알고리즘 추론

알고리즘 추론은 어떤 데이터 분석가도 널리 이용할 수 있는 강력한 컴퓨팅 장치에 의해 실현 가능한 통계 추론 방법의 새로운 발전을 수집한다.이 분야의 주춧돌은 컴퓨터 학습 이론, 세밀한 컴퓨팅, 생물정보학, 그리고 오래 전 구조 확률이다(Fraser 1966).주요 초점은 신뢰할 수 있는 결과를 도출하기 위해 공급해야 하는 데이터의 양과 함께 무작위 현상의 연구를 뒷받침하는 통계를 계산하는 알고리즘에 있다.이것은 수학자들의 관심을 분포 법칙의 연구로부터 통계학의 기능적 특성으로, 컴퓨터 과학자들의 관심을 데이터 처리를 위한 알고리즘에서 그들이 처리하는 정보로 이동시킨다.null

Fisher 매개변수 추론 문제

유통법의 매개변수 식별과 관련하여 성숙한 독자는 20세기 중반에 기준 분포(Fisher 1956), 구조 확률(Fraser 1966), 사전/포스터(Ramsey 1925) 등의 측면에서 변동성의 해석에 관한 오랜 논쟁을 회상할 수 있다.인식론적 관점에서, 이것은 확률의 본질에 관한 동반자 논쟁을 수반했다: 그것은 무작위 변수를 통해 설명되어야 하는 현상의 물리적 특징인가 아니면 현상에 대한 데이터를 합성하는 방법인가?후자를 선택하면서, 피셔는 규격의 표본에서 추론하는 주어진 무작위 변수의 매개변수에 대한 기준 분포 법칙을 정의한다.예를 들어, 그는 "μ(가우스 변수의 평균 - 우리의 노트)가 어떤 할당된 값보다 작을 확률, 또는 어떤 할당된 값 사이에 있을 확률, 즉, 관찰된 표본에 비추어 그 확률 분포"를 계산한다.null

고전적인 해결책

피셔는 베이지스의 후분포, 프레이저의 건설적 확률, 네이만의 신뢰구간 등 유사한 개념에 비해 자신의 매개변수 분포 개념의 차이와 우월성을 방어하기 위해 열심히 싸웠다.반세기 동안 네이먼의 신뢰 구간은 모든 실제적인 목적을 위해 승리했고, 확률의 현상학적 성격을 신뢰했다.이러한 관점에서 가우스 변수를 다룰 때 평균 μ는 관찰 중인 현상의 물리적 특성에 의해 고정되며, 여기서 관측치는 랜덤 연산자이므로 관측된 값은 랜덤 표본의 규격이다.랜덤성 때문에 신뢰도를 나타내는 특정 확률로 고정 μ를 포함하는 표본 고유 구간을 계산할 수 있다.null

예

X는 매개 변수 $[\displaystyle \mu$}과$$(와) ${\displaystyle {\mu \mathrm{}}^{}}$[\$displaystyle \sigma ^{2$}} 및$$${\displaystyle }${$$${\displaystyle {}_{}{}_{}{1\mathrm{}}_{}}$, $displaystyle \{X_{1},\ldots ,X_{m}\}}}}}}}$과(와)가$$ 있는 가우스 변수에서^[1] 추출된 샘플이 되도록 한다.통계 작업

${\displaystyle S_{\mu }=\sum _{i=1}^{m}X_{i}}}}$

그리고

${\displaystyle S_{\sigma ^{2}}=\sum _{i}-{\overline{X}}^{}},{\text{{{}}{{}}}}{{}}}}{{\cline{}}}}}}}}$

표본 평균은 다음과 같다.

${\displaystyle T={\frac {S_{\mu }-m\mu }{\sqrt {S_{\sigma ^{2}}}}}{\sqrt {\frac {m-1}{m}}}={\frac {{\overline {X}}-\mu }{\sqrt {S_{\sigma ^{2}}/(m(m-1))}}}}$

학생 t 분포(Wilks 1962)에 따라 매개변수(자유도) m - 1을 표시한다.

${\displaystyle f_{T}(t)={\frac {\gamma(m/2)}{\gamma((m-1)}{\sqrt{\pi(m-1)}}}}{+{\frac{{t^{{m-1}}\rig)^{m/2}}.}$

두 퀀텀 사이의 T를 측정하고 $\mu$의 함수로서 그 표현을 뒤집으면$\mu$의 $신뢰$ 구간을 얻을 수 있다$$$.$

샘플 사양으로 다음을 수행하십시오.

${\displaystyle \mathbf {x} =\{7.14,6.3,3.9,6.46,0.2,2.94,4.14,4.69,6.02,1.58\}}}$

크기 m = 10을 가지면 통계 $s{\displaystyle {}_{}}$ ${\displaystyle {\mu }_{}}$= ${\displaystyle 43.37}$ ${\displaystyle s_{\mu }=43.37}$ $및{\displaystyle {}_{}}$ s$$ ${\displaystyle {{\mu \mathrm{}}^{}}_{}}$ ${\displaystyle {{}^{}}_{}}$ ${\displaystyle 46.07}$ ${\displaystyle s_{\probma ^{2}}=46.07$을 계산하고, 극한 값(3.03, 5.65)을$$ 갖는$\mu {\displaystyle }${\$displaystylement \muledown$ \muledmulegate \muffic에 대한 신뢰 구간을 얻는다.null

컴퓨터의 도움을 받아 기능 유추

모델링 관점에서 전체 분쟁은 닭갈비 딜레마처럼 보인다. 첫 번째에 의한 고정 데이터와 그 결과로서 그 속성의 확률 분포 또는 관찰된 데이터의 첫 번째와 확률에 의한 고정 특성.고전적인 해결책은 한 가지 이점과 한 가지 단점이 있다.전자는 사람들이 여전히 시트와 연필로 계산을 했을 때 특히 높이 평가되었다.perce, 고정된 매개변수 θ에 대한 Neyman 신뢰구간을 계산하는 작업은 어렵다: θ은 모르지만, 실패할 가능성이 매우 낮은 구간을 처리하는 것을 찾는다.분석 솔루션은 매우 제한된 수의 이론적 사례에 대해 허용된다.반대로, 가우스 분포 주위의 신뢰구간 측면에서 중앙 한계 정리를 통해 많은 다양한 사례가 대략적인 방법으로 신속하게 해결될 수 있다. 그것이 장점이다.단점은 표본 크기가 충분히 클 때 중심 한계 정리를 적용할 수 있다는 것이다.따라서 현대 추론 사례에 포함된 표본에 대한 적용가능성이 점점 낮아진다.고장은 표본 크기에 있지 않다.오히려 추론문제의 복잡성 때문에 이 크기는 충분히 크지 않다.null

대형 컴퓨팅 설비의 가용성과 함께, 과학자들은 고립된 매개변수에서 복잡한 함수 추론, 즉 함수를 식별하는 고도로 중첩된 매개변수 집합에 다시 초점을 맞추었다.이러한 경우, 우리는 매우 유용한 샘플에 기초하여 기능 학습(회귀, 신경 퍼지 시스템 또는 컴퓨터 학습의 예)에 대해 이야기한다.데이터를 연결하는 복잡한 구조를 갖는 첫 번째 효과는 샘플 자유도의 감소, 즉 샘플 포인트의 일부를 태우는 것이다. 따라서 중앙 한계 정리에서 고려해야 할 유효 샘플 크기가 너무 작다.주어진 신뢰 수준에서 제한된 학습 오류를 보장하는 표본 크기에 초점을 맞추면, 이 크기에 대한 하한은 VC 치수나 우리가 배우고자 하는 기능이 속한 클래스의 세부사항과 같은 복잡도 지수와 함께 커진다.null

예

1,000개의 독립 비트의 표본은 최소 0.99의 신뢰도로 기본 베르누이 변수의 매개변수 p의 추정에 대해 최대 0.081의 절대 오차를 보장하기에 충분하다.뉴욕에 사는 20세 남성이 1,000명의 빅애플 거주자들에게서 관찰된 키, 몸무게, 허리선 범위에 맞지 않을 확률로 오차가 확인될 때 동일한 크기가 같은 자신감 0.99로 0.088보다 작은 임계값을 보장할 수는 없다.정확도 부족은 1,000명의 거주자 범위에서 관찰된 VC 치수와 Parallelelepeds 등급의 세부사항이 모두 6과 같기 때문에 발생한다.

피셔 문제를 해결하는 일반적인 반전 문제

표본이 충분히 크지 않은 경우 접근법: 고정 표본 – 무작위 속성은 다음 세 단계로 추론 절차를 제안한다.

1.	샘플링 메커니즘.It consists of a pair ${\displaystyle (Z,g_{\boldsymbol {\theta }})}$, where the seed Z is a random variable without unknown parameters, while the explaining function ${\displaystyle g_{\boldsymbol {\theta }}}$ is a function mapping from samples of Z to samples of the random variable X we are interested in.매개 변수 $벡터{\displaystyle \mathit{}}$ ${{\${\$boldsymbol {\theta}}}$은 랜덤 매개 변수 $\theta {\displaystyle \mathbf{}}${\$displaystyle \mathbf {\\}$의 규격이다.$세타 }$ 그 구성요소는 X 유통법의 매개변수다.적분 변환 정리는 씨앗이${\displaystyle }$[ ${\displaystyle 0}$, ${\displaystyle 1}$ ${\displaystyle ]}$ ${\displaystyle [0,1]$에서 랜덤 변수 Uuniformly 분포와 일치할 때 각 (scalar 또는 벡터) X에 대해 그러한 메커니즘의 존재를 보장한다$.$ 예null 파라미터 a와 k를 포함한 파레토 분포를 따르는 X의 경우. ${\displaystyle F_{X}(x)=\왼쪽(1-{\frac {k}{x}}^{a}\오른쪽)I_{[k,\infit )}(x),}$ 시드 U가 있는 X에 대한$$ 샘플링 메커니즘$({\displaystyle U}$, ${\displaystyle {}_{}}$( ,${\displaystyle k_{}}$)${\displaystyle(U,g_{(a,k)})}:$ ${\displaystyle g_{(a,k)}(u)=k(1-u)^{-{\frac {1}{a}},}$ 또는 동등하게 $g{\displaystyle {}_{(}{a,}_{}}$ ${\displaystyle k{}_{}}$)${\displaystyle {}_{}}$=${\displaystyle k}$ ${\displaystyle {}^{}}$ - ${\displaystyle 1^{}}$ /${\displaystyle {}^{}}$a${\displaystyle {}^{}}$. $displaystyle g_{(a,k)}(u)=ku^{-1/a}.$$}$
2.	마스터 방정식.모델과 관측된 데이터 사이의 실제 연결은 데이터 통계와 샘플링 메커니즘의 상관관계로 간주되는 알려지지 않은 매개변수 사이의 관계 집합에 의해 던져진다.우리는 이러한 관계를 마스터 방정식이라고 부른다.Pivoting around the statistic ${\displaystyle s=h(x_{1},\ldots ,x_{m})=h(g_{\boldsymbol {\theta }}(z_{1}),\ldots ,g_{\boldsymbol {\theta }}(z_{m}))}$, the general form of a master equation is: ${\displaystyle s}$= ${\displaystyle \rho }$ (${\displaystyle \theta \mathit{};}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle }$…${\displaystyle }$, ${\displaystyle z_{}}$ m${\displaystyle {}_{}}$)$${\$displaystyle s=\rho ({\\displaysymbol {\\theta }}};z_{1},\ldots,z_{m$ 이러한 관계를 통해 우리는 표본의 씨앗을 나타내는 씨앗의 특정 설정에서 관찰된 통계량을 사용하여 표본을 생성할 수 있는 매개변수 값을 검사할 수 있다.따라서 표본 씨앗의 모집단은 모수의 모집단에 해당한다.이 모집단이 속성을 깨끗하게 하기 위해서는, 종자 값을 랜덤하게 그리고 충분한 통계량 또는 간단히 말해서, 모수의 .r.t.를 포함하는 것이 충분하다.null For example, the statistics ${\displaystyle s_{1}=\sum _{i=1}^{m}\log x_{i}}$ and ${\displaystyle s_{2}=\min _{i=1,\ldots ,m}\{x_{i}\}}$ prove to be sufficient for parameters a and k of a Pareto random variable X.(같은 형태의) 샘플링 메커니즘 $g{\displaystyle {}_{}}$ ${\displaystyle {(,a}_{}}$ , k${\displaystyle {}_{}}$) ${\$덕분에 우리는$$ 그들을 다음과 같이 읽을 수 있다. ${\displaystyle s_{1}=m\log k+1/a\sum _{i=1}^{m}\log u_{i}}}}}$ ${\displaystyle s_{2}=\min _{i=1,\ldots,m}\{ku_{i}^{-{\frac {1}{a}}\}}}}$ 각각null
3.	모수 모집단.일련의 마스터 방정식을 고친 후, 당신은 표본 씨앗을 모집단 부트스트랩을 통해 숫자적으로 또는 비틀림 인수를 통해 분석적으로 매개변수에 매핑할 수 있다.따라서 씨앗의 모집단에서 모수의 모집단을 얻는다.null 예null 위의 마스터 방정식으로부터 다음과 같은 방정식 시스템을 풀어서 관측된 샘플과 호환되는 한 쌍의 파라미터${\displaystyle (,}$ , k )$$${\displaystyle (a,k)}$을 그릴 수 있다. ${\displaystyle a={\frac {\sum \log u_{i}-m\log \min\{u_{i}\}}}{s_{1}-m\log s_{2}}.}$ ${\displaystyle k=\mathrm {e}^{\frac {as_{1}-\sumlog u_{i}}{ma}}}}$ 여기서 $s{\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$ ${\$및$$ $s{\displaystyle {}_{}}$ ${\displaystyle {2\mathrm{}}_{}}$ ${\$}}개의 관측된 통계와$$ ${\displaystyle {u\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$,${\displaystyle }$u, ${\displaystyle u_{}}$ m ${\$일정한$$ 씨앗 집합이다.씨앗에 영향을 미치는 확률(밀도)을 모수에 전달하면 관찰한 통계와 호환되는 랜덤 모수 A와 K의 분포 법칙을 얻게 된다.null 호환성은 호환 가능한 모집단의 매개변수, 즉 관측된 통계를 발생시키는 표본을 생성할 수 있는 모집단의 매개변수를 나타낸다.이 개념을 다음과 같이 공식화할 수 있다.

정의

For a random variable and a sample drawn from it a compatible distribution is a distribution having the same sampling mechanism ${\displaystyle {\mathcal {M}}_{X}=(Z,g_{\boldsymbol {\theta }})}$ of X with a value ${\displaystyle {\boldsymbol {\theta }}}$ of the random parameter ${\displaystyle$$\mathbf {\$$세타 }$}은(는) 예의 통계 s에 근거한 마스터 방정식에서 도출되었다$$.null

예

파레토 매개변수 A와 K의 분포 법칙은 왼쪽 그림과 같이 모집단 부트스트랩 방법의 구현 사례로 볼 수 있다.null

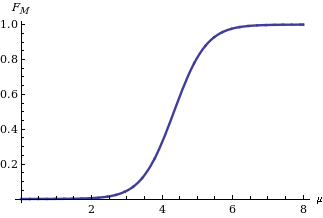
Implementing the twisting argument method, you get the distribution law ${\displaystyle F_{M}(\mu )}$ of the mean M of a Gaussian variable X on the basis of the statistic ${\displaystyle s_{M}=\sum _{i=1}^{m}x_{i}}$ when ${\displaystyle \Sigma ^{2}}$ is known to be equal t$o\sigma {\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$아폴로니, 말치오디 & 가이토 2006).그 표현은 다음과 같다.

${\displaystyle F_{M}(\mu )=\Phi \left({\frac {m\mu -s_{M}}}{\sigma {\sqrt{m}}\right),}$

$오른쪽{\displaystyle \mathrm{}}$ 그림에 표시된 φ ${\displaystyle \Phi }$은(는) 표준 정규 분포의 누적 분포 함수다.null

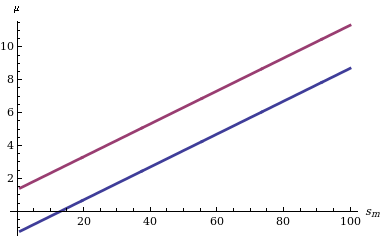
분포 함수를 주어진 M에 대한 신뢰 구간을 계산하는 것은 간단하다. 즉, 꼬리 확률에서 수준 Δ Δ의 신뢰 구간을 원하는 경우 2개의 $\Delta {\displaystyle /2\mathrm{}}${\${\displaystyle \mathrm{displaystyle}}$ $\delta /2}$ $및$ 1 - Δ${\displaystyle /2\mathrm{}}${\$displaystyle 1-\delta /2}$ 정량분위수만$$ 찾으면 된다.서로 다른 통계_m s 값에 대한 두 개의 한계의 동작을 보여주는 도표의 왼쪽에 표시.null

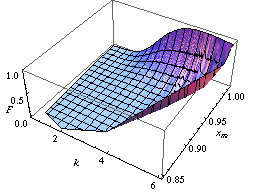
피셔 접근법의 아킬레스건은 가우스 분포의 평균과 분산이라는 두 개 이상의 매개변수의 공동 분포에 있다.반대로 마지막 접근법(그리고 위에서 언급한 방법: 모집단 부트스트랩과 비틀림 주장)으로 우리는 많은 매개변수의 공동 분포를 배울 수 있다.예를 들어, 두 개 이상의 모수의 분포를 중심으로 아래 그림에서 학습할 함수가 90%의 신뢰도로 떨어지는 두 개의 신뢰 영역을 보고한다.전자는 확장 지원 벡터 시스템이 이진 레이블 1을${\displaystyle }$( x ,${\displaystyle }$y${\displaystyle }$) ${\displaystyle (x,y)}$ 평면의$$ 점에 귀속시킬 확률을 다룬다.두 표면은 특정 유통법에 따라 라벨이 표시된 일련의 샘플 포인트에 기초하여 그려진다(Apoloni et al. 2008).후자는 검열된 표본에서 계산한 유방암 재발 위험률의 신뢰 영역에 관한 것이다(Apoloni, Malchiodi & Gaito 2006).null

쌍곡선 접선 프로필 함수가 부여된 지원 벡터 머신 계열에 대한 90% 신뢰 영역

검열 표본 =( > 12 > > ${\$검열된 시간을 나타낸다.

메모들

이 글은 일반적인 참고문헌 목록을 포함하고 있지만, 그에 상응하는 인라인 인용구가 충분하지 않기 때문에 대체로 검증되지 않은 상태로 남아 있다. 좀 더 정밀한 인용구를 도입하여 이 기사를 개선할 수 있도록 도와주십시오.(2011년 7월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

참조

• Fraser, D. A. S. (1966), "Structural probability and generalization", Biometrika, 53 (1/2): 1–9, doi:10.2307/2334048, JSTOR 2334048.
• Fisher, M. A. (1956), Statistical Methods and Scientific Inference, Edinburgh and London: Oliver and Boyd
• Apolloni, B.; Malchiodi, D.; Gaito, S. (2006), Algorithmic Inference in Machine Learning, International Series on Advanced Intelligence, vol. 5 (2nd ed.), Adelaide: Magill, Advanced Knowledge International
• Apolloni, B.; Bassis, S.; Malchiodi, D.; Witold, P. (2008), The Puzzle of Granular Computing, Studies in Computational Intelligence, vol. 138, Berlin: Springer, ISBN 9783540798637
• Ramsey, F. P. (1925), "The Foundations of Mathematics", Proceedings of the London Mathematical Society: 338–384, doi:10.1112/plms/s2-25.1.338.
• Wilks, S.S. (1962), Mathematical Statistics, Wiley Publications in Statistics, New York: John Wiley