해밍 거리

이 문서에는 일반적인 참조 목록이 포함되어 있지만 대응하는 충분한 인라인 인용이 없습니다. 좀 더 정밀한 인용문을 도입하여 이 글의 개선에 도움을 주시기 바랍니다.(2015년 5월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

해밍 거리

해밍 거리를 찾기 위한 4비트 바이너리 테서랙트. 거리 예: 0100→1001의 거리는 3이고 0110→1110의 거리는 1입니다.
학급	문자열 유사성
data 구조	스트링
최악의 경우 성능	${\displaystyle O(n)}$
베스트 케이스 성능	${\displaystyle O(1)}$
평균 성능	${\displaystyle O(n)}$
최악의 경우 공간의 복잡성	${\displaystyle O(n)}$

해밍 거리를 찾기 위한 3비트 이진 큐브

두 가지 예제 거리: 100→011은 거리 3이고, 010→2012는 거리 2입니다.

두 꼭지점 사이의 최소 거리는 두 이진 문자열 사이의 해밍 거리입니다.

정보 이론에서, 동일한 길이의 두 문자열 사이의 해밍 거리는 대응하는 기호가 다른 위치의 수입니다.즉, 하나의 문자열을 다른 문자열로 변경하기 위해 필요한 최소 대체 횟수 또는 하나의 문자열을 다른 문자열로 변환했을 가능성이 있는 최소 오류 수를 측정합니다.보다 일반적인 맥락에서 해밍 거리는 두 시퀀스 간의 편집 거리를 측정하기 위한 몇 가지 문자열 메트릭 중 하나입니다.그것은 미국 수학자 리처드 해밍의 이름을 따서 지어졌다.

주요한 응용은 부호화 이론, 특히 블록 코드에 관한 것으로, 같은 길이의 문자열이 유한 필드상의 벡터이다.

정의.

동일한 길이의 두 기호 문자열 사이의 해밍 거리는 해당 기호가 서로 ^[1]다른 위치의 수입니다.

예

기호는 문자, 비트 또는 십진수 등이 될 수 있습니다.예를 들어, 다음 사이의 해밍 거리입니다.

• "카롤린"과 "카롤린"은 3이다.
• "카롤린"과 "커스틴"은 3이다.
• "carsrin"과 "cerstin"은 4입니다.
• 0000과 1111은 4입니다.
• 2173896 및 2233796은 3입니다.

특성.

고정 길이 n의 경우, 해밍 거리는 길이 n(해밍 공간이라고도 함)의 단어 집합의 메트릭으로, 두 단어가 동일한 경우에만 음이 아닌 대칭의 조건을 충족하기 때문에 두 단어의 해밍 거리는 0이며 삼각 부등식도 ^[2]충족합니다.실제로 3개의 단어 a, b, c를 고정하면 a의 ih와 c의 ih 사이에 차이가 있을 때마다 a의 ih와 b의 ih와 c의 ih 사이에 차이가 있을 것이다.따라서 a와 c 사이의 해밍 거리는 a와 b, b와 c 사이의 해밍 거리의 합보다 크지 않다.두 단어 a와 b 사이의 해밍 거리는 두 정수 사이의 차이가 숫자 ^{[clarification needed]}선에서 0으로부터의 거리로 볼 수 있는 것과 마찬가지로 적절한 연산자 선택에 대한 a - b의 해밍 가중치로 볼 수도 있습니다.

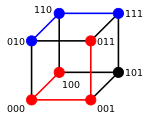
이진 문자열 a 및 b의 경우 Hamming 거리는 XOR ^[3]b의 1의 수(인구 카운트)와 같습니다.길이 n 이진 문자열의 메트릭 공간은 해밍 거리를 가진 해밍 큐브라고 합니다. 하이퍼 큐브 그래프에서 정점 사이의 거리 집합에 대한 메트릭 공간과 동일합니다.또한 문자열의 각 기호를 실제 좌표로 처리함으로써 길이 n의 이진 문자열 n을 R$$ \$displaystyle \mathbb {R}$^{$n}$의 벡터로 볼 수 있습니다. 이 삽입으로 문자열은 n차원 하이퍼 큐브의 정점을 형성하고 문자열의 해밍 거리는 ver 사이의 맨해튼 거리에 해당합니다.티스

오류 검출 및 오류 수정

최소 해밍 거리는 오류 검출 및 오류 수정 코드와 같은 코딩 이론의 몇 가지 필수 개념을 정의하는 데 사용됩니다.특히, 코드 C는, 그 2개의 코드워드 사이의 최소 해밍 거리가 k+1 ^[2]이상일 경우에만 k 에러 검출이라고 한다.

예를 들어, "000"과 "111" 두 개의 코드 워드로 구성된 코드를 생각해 보십시오.이 두 단어 사이의 해밍 거리는 3이므로 k=2 오류 탐지입니다.즉, 한 비트가 플립되거나 두 비트가 플립되면 오류를 감지할 수 있습니다.3비트가 플립되면 "000"이 "111"이 되고 오류를 검출할 수 없습니다.

코드 C는 기초 해밍 공간 H 내의 워드 w마다 w와 c 사이의 해밍 거리가 k가 되도록 (C로부터의) 코드 워드 c가 1개 이상 존재하면 k-오류 보정이라고 한다.즉, 2개의 부호어 중 하나 사이의 최소 해밍 거리가 적어도 2k+1인 경우에만 k-오류 보정이 된다.이것은 구별되는 코드워드를 중심으로 한 반지름 k의 닫힌 공들이 ^[2]분리되기 때문에 기하학적으로 더 쉽게 이해된다.이 ^[4]공들은 이런 맥락에서 해밍구라고도 불린다.

예를 들어, "000"과 "111"의 2개의 코드 워드로 구성된 동일한 3비트 코드를 고려합니다.Hamming 공간은 8개의 단어 000, 001, 010, 011, 100, 101, 110 및 111로 구성됩니다.코드워드 「000」및 싱글비트 에러워드 「001」, 「010」, 「100」은 모두 해밍 거리 1 ~ 「000」이하입니다.마찬가지로 코드워드 '111'과 그 싱글비트 에러워드 '110', '101', '011'은 모두 원래 '111'의 1 해밍 거리 내에 있다.이 코드에서 단일 비트 오류는 항상 원래 코드의 1 Hamming 거리 내에 있으며, 코드는 1-오류 수정(k=1)일 수 있습니다."000"과 "1000" 사이의 최소 해밍 거리는 3으로, 2k+1 = 3을 만족합니다.

따라서 코드워드 사이에 최소 해밍 거리d를 가지는 코드는, 최대 d-1 에러를 검출할 수 있어 「(d-1)/2」^[2]에러를 수정할 수 있습니다.후자의 숫자를 패킹 반지름 또는 코드 ^[4]오류 수정 능력이라고도 합니다.

이력 및 응용 프로그램

해밍 거리는 1950년 ^[5]해밍 코드, 오류 감지 및 오류 수정 코드에 대한 기초 논문에서 개념을 소개한 리처드 해밍의 이름을 딴 것이다.비트의 해밍 무게 분석은 정보 이론, 부호화 이론 및 암호학을 포함한 여러 분야에서 사용됩니다.

이는 통신에서 오류 추정치로서 고정 길이 이진 워드의 플립 비트 수를 세는 데 사용되며, 따라서 신호 ^[6]거리라고도 합니다.크기 q ≤ 2의 알파벳을 넘는 q-ary 문자열의 경우, q-ary 대칭 채널의 경우 해밍 거리가 적용되며, Li 거리는 위상 편이 키 입력 또는 보다 일반적으로 동기 에러의 영향을 받기 쉬운 채널에 사용됩니다.^[7]$q\mathrm{}$$$${\displaystyle =}$ $({displaystyle q=$2$$$})$ $또는{\displaystyle }$ ${\displaystyle \mathrm{q}}$ $=$ 3({$displaystyle$$$q$=3$)인$$ $경우{\displaystyle }$$,$ Z / 2 $Z\mathbb{}$ {$textstyle$ \$mathbb${Z$$} / 2 \$mathbb$$${Z} $}$$또는\mathbb{}$ Z /$$3 $Z\mathbb{}$ {$textstyle$ \$mathbbb$ {Z}$}$의 요소 쌍이(\textstyle \mathbb${Z})$는 모두 거리가 1개씩 다르기 때문에 두 거리가 일치합니다.

해밍 거리는 계통학에서도 유전적 ^[8]거리 측정으로 사용됩니다.

단, 길이가 다른 문자열이나 치환뿐만 아니라 삽입이나 결락이 예상되는 문자열을 비교할 경우에는 Levenshtein 거리처럼 보다 정교한 측정기준이 적합합니다.

알고리즘의 예시

Python 3으로 작성된 다음 함수는 두 문자열 사이의 해밍 거리를 반환합니다.

방어하다 해밍_거리(문자열 1, 스트링2):  dist_counter(카운터) = 0  위해서 n 에 범위(렌(문자열 1)):   한다면 문자열 1[n] != 스트링2[n]:    dist_counter(카운터) += 1  돌아가다 dist_counter(카운터) 

또는 간단히 말하면 다음과 같습니다.

합(xi != 이 위해서 xi, 이 에 지퍼(x, y)) 

함수hamming_distance()Python 2.3+에서 구현된 이 기능은 길이가 같은 두 문자열(또는 다른 반복 가능한 개체) 사이의 해밍 거리를 계산하기 위해 두 입력의 대응하는 위치 간의 불일치 및 일치를 나타내는 부울 값 시퀀스를 만든 다음 False 및 True 값을 0 및 1로 해석하여 합산합니다.

방어하다 해밍_거리(s1, s2) -> 인트:     "같은 길이의 시퀀스 사이의 해밍 거리를 반환합니다."""     한다면 렌(s1) != 렌(s2):         올리다 값 오류("길이가 같지 않은 시퀀스에 대해 정의되지 않음")     돌아가다 합(el1 != el2 위해서 el1, el2 에 지퍼(s1, s2)) 

여기서 zip() 함수는 같은 길이의 2개의 컬렉션을 쌍으로 Marge합니다.

다음 C 함수는 두 정수(이진수 값, 즉 비트 시퀀스로 간주)의 해밍 거리를 계산합니다.이 절차의 실행 시간은 입력의 비트 수가 아니라 해밍 거리에 비례합니다.비트 배타적 비트 또는 두 입력 중 하나를 계산한 다음 가장 낮은 순서의 비트를 반복적으로 찾아 지우는 Wegner(1960) 알고리즘을 사용하여 결과의 해밍 가중치(비제로 비트 수)를 찾습니다.일부 컴파일러는 __builtin_popcount 함수를 지원합니다.이 함수는 사용 가능한 경우 전용 프로세서하드웨어를 사용하여 계산할 수 있습니다.

인트 해밍_거리(서명되어 있지 않다 x, 서명되어 있지 않다 y) {     인트 일그러뜨리다 = 0;      // ^ 연산자는 다른 비트만 1로 설정합니다.     위해서 (서명되어 있지 않다 값 = x ^ y; 값 > 0; ++일그러뜨리다)     {         // 그런 다음 Peter Wegner 방식을 사용하여 비트를 1로 카운트합니다.         값 = 값 & (값 - 1); // 0 val의 최하위 1로 설정     }      // 다른 비트 수를 반환합니다.     돌아가다 일그러뜨리다; } 

더 빠른 대안은 모집단 카운트(팝 카운트) 어셈블리 명령을 사용하는 것입니다.GCC 및 Clang 등의 특정 컴파일러에서는 다음 기능을 통해 사용할 수 있습니다.

// 32비트 정수에 대한 해밍 거리 인트 해밍_거리32(서명되어 있지 않다 인트 x, 서명되어 있지 않다 인트 y) {     돌아가다 __builtin_popcount(x ^ y); }  // 64비트 정수의 경우 해밍 거리 인트 해밍_거리64(서명되어 있지 않다 긴 긴 x, 서명되어 있지 않다 긴 긴 y) {     돌아가다 __builtin_popcountll(x ^ y); } 

「 」를 참조해 주세요.

• 가장 가까운 문자열
• 다메라우-레벤슈테인 거리
• 유클리드 거리
• 갭 해밍 문제
• 그레이 코드
• 자카드 지수
• 레벤슈테인 거리
• 마할라노비스 거리
• 만하임 거리
• 쇠렌센 유사도 지수
• 스퍼스 분산 메모리
• 단어 사다리

레퍼런스

추가 정보

• 이 문서에는 General Services Administration 문서의 퍼블릭도메인 자료가 포함되어 있습니다.
• Wegner, Peter (1960). "A technique for counting ones in a binary computer". Communications of the ACM. 3 (5): 322. doi:10.1145/367236.367286. S2CID 31683715.
• MacKay, David J. C. (2003). Information Theory, Inference, and Learning Algorithms. Cambridge: Cambridge University Press. ISBN 0-521-64298-1.