칸토어 집합

수학에서 칸토어 집합(Cantor set)은 여러 개의 의도하지 않은 속성을 가진 단일 선분 위에 있는 점 집합입니다.이것은 1874년 헨리 존 스티븐^[1][2][3][4] 스미스에 의해 발견되었고 1883년 ^[5][6]독일 수학자 게오르크 칸토에 의해 소개되었다.

이 집합을 고려함으로써, Cantor와 다른 사람들은 현대 포인트 집합 토폴로지의 기초를 마련하는 데 도움을 주었다.가장 일반적인 구조는 칸토어 삼원 집합으로, 선분의 중간 1/3을 제거한 다음 나머지 짧은 세그먼트로 프로세스를 반복하여 구축됩니다.칸토어는 더 일반적인 생각의 예로서, 어느 곳에서도 조밀하지 않은 완벽한 집합의 3원 구조를 지나가는 말로만 언급했다.

보다 일반적으로, 위상학에서, 칸토어 공간은 칸토어 삼원 집합(부분 공간 위상이 장착된)과 동형인 위상 공간입니다.브루어의 정리에 따르면, 이것은 완전 비고, 콤팩트하고,^[7] 0차원적인 것과 같다.

삼원 집합의 구조 및 공식

Cantor 3진수 $집합{\displaystyle \mathcal{}}$C(\$displaystyle\mathcal {C})$는 선분 집합에서 열린 중간 1/3을 반복적으로 삭제하여 생성됩니다.첫 번째는 [$0\mathrm{}$$]{$$$$displaystyle \textstyle \left$ [ $0$, $1\frac{\mathrm{}}{}$$$\ $right$][$$0$$, 1$$$][$ 0 , $\frac{3}{}][$ \ $textstyle$ \ $\frac{\mathrm{textstyle}}{}$ \ left ][ $0$ , $1$ \ textstyle ][ 0 , $3$] [ \ textstyleft$]$의 두 줄 세그먼트를 남기고 열린 가운데$$세 $번째\frac{\mathrm{}}{}$ ( $\frac{1}{}$$$)를$삭제합니다.$${\frac {$2$}$ {3$},$1\right$]$다음으로는 나머지 각 세그먼트의 열린 중간 1/3이 삭제되고 4개의 라인 세그먼트가 남습니다$.[$ $\frac{0}{}$, $1\frac{\mathrm{}}{}\frac{9}{}$]$$[ [ $\frac{2}{}$ $3\frac{\mathrm{}}{}$, $7$ $]$[ [ $\frac{8}{}$ , 1$]{$ $text style$ \ [ $0$, \ $frac${ $9 }$ { $9$} { 9 \ $fright ]$$,{\frac {7}{9}\right]\cup \left[{\frac {8}{9}},1\right$칸토어 3진수 세트에는 이 무한 프로세스의 어떤 단계에서도 삭제되지 않는 $]({displaystyle [0,1])$ 간격의$$ 모든 포인트가 포함됩니다.동일한 사실은 설정에 의해 재귀적으로 설명될 수 있다.

${\displaystyle C_{0}:=[0,1]}$

그리고.

${\displaystyle C_{n}:=cup {C_{n-1}{3}}\cup \leftfrac {2}{3}+{\right}=cup {1}{\bigl(}C_{n-1}\cup \left(2+1C})$

n${\displaystyle 1}$1 \ $displaystyle$n \ $geq$ 1$$$n{\displaystyle }$ 、

${\displaystyle \mathcal{C}}$: $=$ { $displaystyle${$c$} ${\displaystyle \underset{}{lim}}$$$${\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{n\mathrm{}\to }}$ $C$n ${\displaystyle \underset{}{\overset{}{}}}$ ${\displaystyle \underset{\mathrm{}}{\overset{}{n}}}$n = 0 ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle C_{}}$ n ${\displaystyle {}_{}}$ ${\displaystyle \underset{}{\overset{}{m}}}$ ${\displaystyle \underset{}{\overset{}{=}}}$ ${\displaystyle \underset{}{\overset{}{}}{}_{}}$ ${\displaystyle \underset{}{\overset{}{\mathrm{}}}}$ ${\displaystyle C_{}}$ n$$= $m = cap cap$ { $n }^{ displaystyle$ { $블루$} \ $lim$$$_ {$n }$

이 프로세스의 첫 번째 6단계는 다음과 같습니다.

$자기{\displaystyle {}_{}}$ 유사 변환 개념을 사용하여 T ${\displaystyle L_{}}$(${\displaystyle x}$ ) ${\displaystyle =x}$ /${\displaystyle 3\mathrm{}}$ ,$${ $displaystyle T_{L$}$= x$ / 3$,$} $T$${\displaystyle {}_{}}$ ${\displaystyle R_{}}$(${\displaystyle x}$ ) ${\displaystyle =}$ ( ${\displaystyle 2}$+${\displaystyle x}$) /$$ ( \ $displaystyle T_{R}$ (x ) = ($2$ +$x$ ) /$$3 , ${\displaystyle C_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$- ${\displaystyle {\mathrm{L}}_{}}$ )${\displaystyle {}_{}（}$ ${\displaystyle {}_{}}$ )칸토르 세트는^[8]

${\displaystyle {mathcal {C}=[0,1],\setminus,\bigcup _{n=0}^{\infty}\bigcup _{k=0}^3^{n}-1}\leftfrac {3k+1},{\frac {3k+2}{\n}}{\n}}}}\bigcup_{\infty}}}}}\light}$

여기서 모든 중간 1/3이 $열린\frac{\mathrm{}}{}$$$간격$($$\frac{3}{}$$\frac{\mathrm{k}}{}$ + $\frac{{\mathrm{}}^{}}{}$ $\frac{{\mathrm{}}^{}}{}$$\frac{{}^{}}{}$$\frac{n^{}}{}$ +$\frac{{}^{}}{}\frac{1^{}}{}$ , $3\frac{\mathrm{}k}{}$ + $\frac{{\mathrm{}}^{}}{}$ $\frac{3^{}}{}$n +$\frac{{}^{}}{}\frac{1^{}}{}$) { $textstyle$\$left$\ $frac${ $3 k$ + $1 }$ , { \ $frac${ $3$k + $2 }$ , { \ frac { $3$$\frac{k^{}}{}$ + $\frac{1^{}}{}$$}$ , 3 $\frac{k}{}$+ $\frac{1^{}}{}$$}$ )에서 $제거$됩니다.$xtstyle \left[{\frac {3k+0}{3^{n+1}},{\frac {3k+3}{3^{n+1}}\right]=\left[{\frac {k+0}{3$$}$$^{n}},$ {\$frac {k+1}{3^{n}}}\right]}$ 주변$$ 또는

$\displaystyle {\mathcal {C}=\bigcap _{n=1}^{\infty}\bigcup _{k=0}^{3^{n-1}\left[\frac {3k+0}{3}^{n}},{\frac {3k+1}{3^{n}}\right]\cup \left[{\frac {3k+2}{3}^{n}},{\frac {3k+3}{3^{n}}\right]\!,}$

여기서 중간$$세 번째($\frac{\mathrm{3k}}{}$+ $\frac{1}{}$ $\frac{{3n}^{}}{}$ $\frac{\mathrm{3k}}{}$ $\frac{+}{}$ $\frac{{\mathrm{}}^{}}{}$ $)$ {$textstyle \leftfrac {3k+1}{3^{n}},$ {\$frac {3k+2}{3$},$^{n}}\right)$ 위의$$ 닫힌$$간격의 [$k\frac{}{}$ $\frac{+}{}$ $\frac{{\mathrm{}}^{}}{}$ $\frac{{3n}^{}}{}$-$\frac{{}^{}}{}1\frac{}{}$,$\frac{}{}$k + $\frac{1}{}$ $\frac{{3n}^{}}{}$- $\frac{1^{}}{}$ $=$ [ $\frac{\mathrm{3k}}{}$+ $\frac{{\mathrm{}}^{}}{}$ $\frac{{3n}^{}}{}\frac{{}^{}}{}$ $\frac{\mathrm{3k}}{}$ $\frac{+}{}$ $]({\$ {\$frac$ {3$^{n-1}\$fright})\fright$}\fr=$$^{n}},$ {\$frac {3k$$\frac{+}{}$$3}{3^{n}}\right]$는 [$3k\frac{\mathrm{}}{}$ + $\frac{{\mathrm{}}^{}}{}$ $\frac{{3n}^{}}{}$ $\frac{\mathrm{3k}}{}$ $\frac{+}{}$ $\frac{1}{}$ $\frac{{3n}^{}}{}]\cup$ [ $\frac{\mathrm{3k}}{}$ $\frac{+}{}$ $\frac{{\mathrm{}}^{}}{}$ $\frac{{3n}^{}}{}$ $\frac{\mathrm{3k}}{}$ $\frac{+}{}$ $].$ {\$textstyle \left$[ {\$frac {3k$+ $0}}{$3k + 3n}}}}와$$교차하여 삭제됩니다.$^{n}},{\frac {3k+1}{3^{n}}\right]\cup \left[{\frac {3k+2}{3$$}$$^{n}}, {\frac {3k+3}{3^{n}}}\right]\!$$}$

중간 3분의 1을 제거하는 이 과정은 유한 분할 규칙의 간단한 예입니다.칸토어 3진수 집합은 프랙탈 문자열의 예입니다.

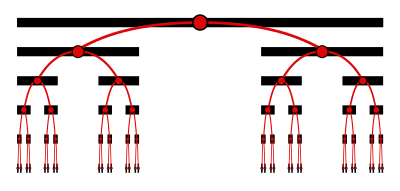
산술적 용어로 칸토어 세트는 숫자 1이 필요 없는 단위${\displaystyle }$간격 [$]({displaystyle [0,1])$의 모든 실수로 구성됩니다.위 다이어그램에서 알 수 있듯이 칸토어 집합의 각 점은 무한히 깊은 이진 트리를 통과하는 경로에 따라 고유하게 배치되며, 각 레벨에서 해당 지점이 삭제된 세그먼트의 어느 쪽에 위치하느냐에 따라 경로가 좌회전 또는 우회전합니다.각 좌회전 수를 0으로 나타내고 각 우회전 수를 2로 나타내면 점의 삼원 분수가 산출됩니다.

구성.

칸토어 세트는 제외되지 않은 포인트 세트로 정의되므로, 남은 단위 간격의 비율(즉, 측정)은 제거된 총 길이만큼 확인할 수 있습니다.이 합계는 기하급수이다.

${\displaystyle \sum _{n=0}^{\infty}{\frac {2^{n+1}}=black {1}{3}+{\frac {2}{9}+{\frac {4}+{\frac {8}+\cdots {3}좌}{frac {3}}}$

따라서 왼쪽 비율은 1 - 1 = 0입니다.

이 계산에 따르면 칸토어 집합은 길이가 0이 아닌 간격을 포함할 수 없습니다.결국 제거된 간격의 길이의 합계는 원래 간격의 길이와 동일하기 때문에 남는 것이 있다는 것은 놀라운 일이 될 수 있습니다.그러나 프로세스를 자세히 살펴보면 각 간격의 "중간 1/3"을 제거하면 열린 집합(엔드포인트가 포함되지 않은 집합)을 제거하는 작업이 포함되므로 남은 것이 있음을 알 수 있습니다.따라서 선분을 삭제합니다(원래 구간 [0, 1]의 1/3, 2/3)은 점 1/3과 2/3 뒤에 남습니다.제거되는 간격은 항상 나머지 간격의 내부에 있기 때문에 후속 절차에서는 이러한 엔드포인트(또는 다른 엔드포인트)는 제거되지 않습니다.따라서 칸토어 집합은 비어 있지 않고 실제로 셀 수 없이 많은 점들이 포함되어 있습니다(무한 이진 트리의 경로 측면에서 위의 설명과 같습니다).

건설 세그먼트의 끝점만 남은 것처럼 보일 수 있지만, 그렇지 않습니다.예를 들어, 숫자 1/4은 고유한 3진수 형식 0.0202를 가집니다.= 0.02.3분의 1 아래, 3분의 1 위, 3분의 1 아래 등입니다.중간 세그먼트 중 하나에 포함되지 않기 때문에 제거되지 않습니다.그러나 중간 세그먼트의 엔드포인트도 아닙니다. 1/3의 ^[9]배수가 아니기 때문입니다.세그먼트의 모든 끝점은 삼원 분수를 종단하며 세트에 포함됩니다.

$\displaystyle \left \{x\in [0,1]\mid \exists i\in \mathbb {N} _{0:x,3^{i}\in \mathbb {Z} \right\}\qquad {Bigl (}\subset \mathbbb {N} _{0,3^{N} {N} {0}} {0} {n}} {0}Bigr )}}:$

셀 수 있을 만큼 무한 집합입니다.카디널리티에 관해서는 칸토어 집합의 거의 모든 요소가 구간의 끝점이나 1/4과 같은 유리점이 아닙니다.사실 전체 칸토어 세트는 셀 수 없다.

특성.

카디널리티

이 프로세스에는 처음부터 많은 포인트가 남아 있으므로 칸토어 세트는 셀 수 없습니다.이를 확인하기 위해 칸토어 $집합{\displaystyle \mathcal{}}$C(\$displaystyle\mathcal {C})$에서 $닫힌{\displaystyle \mathcal{}}$ 간격 [0,1]까지 C(\$displaystyle\mathcal {C})$의 카디널리티가 C$(\$보다 작도록 함수의 f가 있음을 보여준다.C$(\$는 [0,1]의 부분집합이므로, 그 카디널리티도 크지 않기 때문에 칸토르-베른슈타인-슈뢰더 정리에 의해 두 기수는 사실상 동일해야 한다.

이 함수를 구성하려면 [0, 1] 구간의 점을 기저 3(또는 3진수) 표기법으로 고려하십시오.보다 정확하게는 (${\displaystyle Z\mathbb{}}$ ${\displaystyle \{}$ { ${\displaystyle 0}$ ${\displaystyle \}}$ )${\displaystyle {\mathrm{}}^{{\mathbb{}}_{}}}$ - ${\displaystyle {{\mathrm{}}_{}}^{}}$ 0$$( \ $displaystyle$ \ $bigl ($ } \$mathbb$ { Z } \$setminus$ \ { 0 \ } { \ $bigr$} } \ $cdot$ 3$^{$ - \ $mathbbb$ { N$$$\}{\displaystyle }$_ { $0$} } )의 요소는 이 표기법에서와 같이 둘 이상의 표현을 받아들입니다.= 0.02₃ 및 2/3 (0₃.2 = 0₃.20으로 쓸 ₃수 있지만 0.122로도 쓸 수 있음)...= 0.^[10]12₃.가운데 세 번째를 제거하면 0.1xxxxxxxxx 형식의 ₃3진수 숫자가 포함됩니다.여기서 xxxxx...₃엄밀히 말하면 00000 ₃사이...및 22222...₃그래서 첫 번째 단계 뒤에 남은 숫자는

• 0.0xxxxxxxx ₃형식의 번호...(0.022222 ₃포함)= 1/3)
• 0.2xxxxxxxx 형식의 번호...₃(0.22222 ₃포함)= 1)

이는 기수점 뒤의 첫 자릿수가 1이 아닐 정도로 3진수 표현을 가진 숫자가 첫 번째 스텝 뒤에 남은 숫자라고 요약할 수 있다.

두 번째 단계에서는 0.01xxxxx ₃형식의 번호를 삭제합니다.0.21xxxxxx...₃와 (엔드포인트에 대해 적절한 주의를 기울이면) 나머지 숫자는 첫 번째 두 자리 모두 1이 아닌 삼진수 숫자라는 결론을 내릴 수 있습니다.

이와 같이 스텝 n에서 제외되지 않기 위해서는 n번째 자리가 1이 아닌 3진수 표현을 가져야 한다.칸토어 집합에 숫자가 포함되려면 어떤 단계에서도 제외되어서는 안 되며, 0과 2로 구성된 숫자 표현을 모두 허용해야 합니다.

1, 1/3 = 0.1 및₃ 7/9 = 0.21과₃ 같은 숫자는 모두 0과 2로 ₃구성된 3진수이므로 칸토어 집합에 있다는 점을 강조할 필요가 있다.= 0₃.2, 1/3 = 0.0222...₃= 0.02₃ 및 7/9 = 0.1402...₃= 0.120₃.후자의 숫자는 모두 "소수"이며, 이 예들은$$C(\$displaystyle\mathcal {C$의 오른쪽 한계점입니다. C$(\$의 $왼쪽{\displaystyle \mathcal{}}$ 한계점에서도 마찬가지입니다(예: 2/3 = 0.122...).₃= 0.12₃ = 0₃.20 및 8/9 = 0.212222...₃= 0.212₃ = 0₃.220.이러한 모든 끝점은 p/q 형식의 적절한 3원 분수(Z${\displaystyle }$⋅${\displaystyle {}^{\mathrm{}}}$ - ${\displaystyle {{\mathbb{}}_{}}^{}}$ ${\displaystyle {{\mathrm{}}_{}}^{}}$\ $displaystyle \mathbb {Z}$ \$cdot$ 3$^{-\mathbb {N}$ ${0$이다. 여기서 분모는 분수가 환원 불가능한 형태일 ^[9]때 3의 거듭제곱이다.이러한 분수의 3진수 표현은 끝(즉, 유한) 또는 (각각 적절한 3진수 분수가 2개의 표현을 가지고 있다는 것을 위에서 상기하면) 무한하며 무한히 많은 반복 0 또는 무한히 많은 반복 2s에서 "끝"된다.이러한 분수는 3진수 표현에 1이 없고 무한히 많은 반복 0으로 끝나는 경우 C$(\$의 $왼쪽{\displaystyle \mathcal{}}$ 한계점이 됩니다.$마찬가지$로, 3진수 분수는 다시 3진수 팽창에 1이 없고 무한히 많은 반복 2s에서 "끝$"$이 있는 경우$C$의 $오른쪽{\displaystyle \mathcal{}}$ 한계점이 됩니다.

이 엔드포인트 세트는 C${\style$ {\$mathcal {C}}}($단, [0, 1]에서는 조밀하지 않음)로 조밀하며 셀 수 있을 만큼 무한 집합을 구성한다.끝점이 아닌 C$(\$ {$C})$의 숫자도 3진수 표현에 0과 2만 포함되지만 숫자 0이나 숫자 2의 무한 반복으로 끝날 수 없습니다. 그러면 끝점이 되기 때문입니다.

C$(\$ {C})에서 [$0{\displaystyle \mathcal{}}$,1]까지의 함수는 모두 0과 2로 구성된 3진수를 취하여 모든 2를 1로 대체하고, 그 시퀀스를 2진수 표현으로 해석함으로써 정의됩니다.공식에서

${\displaystyle f}$( ${\displaystyle \sum \underset{}{}}$ ${\displaystyle \underset{}{kn\mathbb{}}}$ ${\displaystyle \underset{}{N}{}_{}}$ a ${\displaystyle k_{}{}^{}{}_{}{\mathrm{}}^{}}$ -${\displaystyle {}^{}{k}^{}}$ ) ${\displaystyle =\underset{k}{}}$ k${\displaystyle \underset{}{n}\frac{{}_{}}{}}$ N a $2$- ${\displaystyle k^{}}$( \ $displaystyle f in bigg$ ($}$ \ sum _ { $k$\ in \ $mathbb$ { N } )$=$ \ $sum$_ {$k$ \$in$ \ $mathbbb$ {$N$ } { k $} =$ \ $fraca${ k }$}$

[0,1]의 임의의 숫자 y에 대해 모든 1을 2로 대체하여 이진수 표현을$$C의 $숫자{\displaystyle \mathcal{}}$ x(\$displaystyle\mathcal {C})$의 3진수 표현으로 변환할 수 있습니다.이 경우 f(x) = y이므로 y는 f의 범위에 속합니다.예를 들어 y = 3/5 = 0.10011001이면...₂= 0.1001, x = 0.2002 = 0.22002...₃라고 씁니다.= 10년 7월그 결과, f는 투영적이다.단, f는 주입식이 아닙니다.f(x)가 일치하는 값은 제거된 중간 3분의 1의 반대쪽 끝에 있는 값입니다.예를 들어,

1/3 = 0.02₃($C(\$displaystyle$\mathcal {C})$의 $오른쪽{\displaystyle \mathcal{}}$ 한계점, 중간 1/3의 왼쪽 한계점) 및

2/3 = 0.20₃($C(\$displaystyle$\mathcal {C})$의 왼쪽 한계점 및 중간 1/3의 오른쪽 한계점)

그렇게

${\displaystyle {array} {lcl} fcl bigl (} {}^{1}\!/\!_{3}{\bigr}=f(0.0 오버라인 {2}}_{3})=0.0 오버라인 {1}}_{2}=\!&!\!0.1_{2}\!&\!\=0.1 오버라인 {0}_{2}=f(0.2 오버라인 {0}_{3})=fbigl(}{}^2}\!\!/\!_{3}{\bigr}}.\ & \ \ \ & { }^{1} \!/\!_{2}\end{array}}$

따라서 칸토어 집합에는 [0, 1] 간격과 같은 수의 포인트가 있습니다(이 간격은 셀 수 없는 $카디널리티{\displaystyle \mathfrak{}}$ ${\displaystyle {\mathrm{}}^{}}$ $=$ ${\displaystyle {{2\mathrm{}}_{}}^{}}$ ${\$ 0({$style {mathfrak {c$}}=$2^{\aleph$ _${0$}}}).$$그러나 제거된 간격의 끝점 집합은 셀 수 있으므로 칸토어 집합에는 간격 끝점이 아닌 셀 수 없이 많은 숫자가 있어야 합니다.위에서 설명한 바와 같이, 이러한 숫자의 한 예는 1/4로, 0.020202로 ₃표기할 수 있습니다.= 0.02(삼진법).$실제로{\displaystyle }$ ${\displaystyle \in }$[ -${\displaystyle 1}$, 1$$]{ $displaystyle$ a \ $in$[ -$1$, 1$$]{ $displaystyle$x , $y$ $mathcal${$C$}}에는$$= ${\displaystyle y\mathcal{}}$${\displaystyle }$-$$ { $displaystyle$ a $= y$ -$$x $\}$ 가 $존재$합니다.이것은 1917년 스타인하우스에 의해 처음 입증되었고, 그는 기하학적 인수를 통해 {${\displaystyle }$(${\displaystyle x\mathcal{}}$ ${\displaystyle ,y}$ )${\displaystyle {\mathbb{}}^{}}$ R ${\displaystyle {}^{}y}$ y $=$ + ${\displaystyle a}$ ${\displaystyle \}}{\displaystyle (}$ (${\displaystyle }$C ×${\displaystyle C\mathcal{}}$ ) $∅$ { $display$ style \ { ($x$ ,$y$ )\$in$\$mathbb${ $R }^{2}\mid y+\cap$ ; \cap ;이 건설 C×C{\displaystyle{{C\mathcal}에}{{C\mathcal}}}, 우리는 C×C([− 1,1])c{\displaystyle{{C\mathcal}}[− 1,1]{\displaystyle[-1,1]}에서 주사 \times{{C\mathcal}}\geq[-1,1]={\mathfrak{c}}}a\times을 제공한다 스타일 a\in}.[11][-1,1]한 있습니다.직접적인 귀결론${\displaystyle \mathrm{무한}}$ $집합{\displaystyle }$A에 ${\displaystyle 대해}$ A × A ${\displaystyle =}$A {\$displaystyle$ A$$$= A$}(Tarski에 의해 선택된 공리와 동등한 문장으로 표시됨)라고 가정하면, ${\displaystyle 이}$는$$C = c${\$displaystyle {C$}$$=$ c {displaystyle {$c}$이라는 또 다른 데모를 제공한다.

칸토어 집합에는 가져온 간격만큼 많은 점이 포함되지만, 칸토어 집합에는 길이가 0이 아닌 간격이 포함되지 않습니다.무리수는 같은 성질을 가지지만 칸토어 집합은 닫힌다는 추가적인 성질을 가지기 때문에 모든 구간에서 밀도가 높은 무리수와 달리 어떤 구간에서도 밀도가 높지 않습니다.

모든 대수적 무리수는 정규수라고 추측되어 왔다.칸토어 집합의 구성원은 정규가 아니기 때문에, 이는 칸토어 집합의 모든 구성원은 합리적이거나 초월적이라는 것을 의미합니다.

자기유사성

칸토르 세트는 프랙탈의 원형이다.각 복사본이 3배 축소되어 번역되는 경우, 두 개의 복사본과 같기 때문에 이 복사본은 자기 자신과 유사합니다.보다 정확하게는 칸토어 세트는 T ${\displaystyle L_{}x)}$ $=$ /$$ {$displaystyle$ T_${L}(x$)=$x/3$} 및$$ ${\displaystyle T_{}}$ R${\displaystyle {}_{}x)}$ $=$ (${\displaystyle 2}$ ${\displaystyle +}$ ${\displaystyle x)}$/ 3$${$displaystyle T_{R(x)=3}$의 두 $기능$의 결합과 동일합니다.$=$$displaystyle T_{L}({\mathcal {C}})\cong$$T_{L}({\mathcal {C}})\cup T_{R}({\mathcal {C}})$$}$

${\displaystyle T_{}}$ L$${ $display style$ T _ { $L$$$} $t$ ${\displaystyle t_{}}$ T$$R { $display style$T _$${ R$$ } $の{\displaystyle {}_{}}$ 반복을 무한 이진 트리로 시각화할 수 있습니다.즉, 트리의 각 노드에서 왼쪽 또는 오른쪽에 있는 하위 트리를 고려할 수 있습니다.$\{{\displaystyle {}_{}}$ L${\displaystyle {}_{}}$ ${\displaystyle T_{}}$ R$}({displaystyle \{T_{L},T_{R}\})$ 세트를$$ 함수 성분과 함께 취함으로써 모노이드인 2차원 모노이드를 형성한다.

바이너리 트리의 자기동형은 쌍곡선 회전이며 모듈러 그룹에 의해 제공됩니다.따라서 칸토어 $집합{\displaystyle \mathcal{}}$ C$(\$})의$두$ 점 x(\$displaystyle$ x$)$와$$y(\$displaystyle$ ${$C})에$$ 대해${\displaystyle }$C(\$display$ h$:{\mathcal {C})$와$$Y$(\$$mathcal {C})$의 $동형성$이 존재한다는 점에서 칸토어 집합은 균질한 공간이다${\displaystyle .}$$h(x$)=$y$ 칸토어가 이산${\displaystyle }$공간 {${\displaystyle 0,}$ $}({displaystyle$\{$0,$ 1$\backslash \})$의 셀 수 없을 정도로 많은 복사본의 곱공간으로 설정되어 있는 경우 h$({displaystyle$h})의 명시적 구성을 보다 쉽게 설명할 수 있습니다. 그런 다음 지도 $h{\displaystyle :}$ {${\displaystyle 0,}$ 1} ${\displaystyle {N\mathbb{}}^{}}$ {${\displaystyle 0,}$ 1${\displaystyle {}^{}}$ ${\displaystyle {N\mathbb{}}^{}}$ $디스플레이$ {$0, 1}.$${\displaystyle \mathrm{b<img\; alt="\{\backslash displaystyle\; h:\backslash \{0,1\backslash \}^\{\backslash mathbb\; \{N\}\; \}\backslash to\; \backslash \{0,1\backslash \}^\{\backslash mathbb\; \{N\}\; \}\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/04a231be5db72348abd6eaa536ff8cba819653f2"\; style="vertical-align:\; -0.838ex;\; width:21.095ex;\; height:3.176ex;">}}$${N}$ :${\displaystyle ={}_{}{u}_{}}$ n${\displaystyle {}_{}}$+ ${\displaystyle {}_{}{n}_{}}$ + ${\displaystyle {}_{}}$ ${\displaystyle n{}_{}}$ ${\displaystyle mod\mathrm{}}$2 { $displaystyle h_${n$}(u):$$=u_{$n}+$x_{$n}+$y_{n$}\$mod2}$는 x({$displaystyle$$$x$$$})$와 y({$displaystyle$y$})$를 교환하는 인볼루티브 동형사상입니다$.$

보존법

어떤 형태의 보존 법칙은 항상 규모와 자기 유사성의 배후에 있다는 것이 밝혀졌습니다.칸토르 세트의 경우, 시공 과정의 모든 단계에서 생존하는 간격의 d ${\displaystyle f_{}}${\$displaystyle d_{f}$ / ${\displaystyle \ln }$ ${\displaystyle （3}$） { displaystyle $d_{f}=\ln(2)/\ln(3)}$번째$$$$ 모멘트가 $동일$한 경우임을 알 수 있다.t.^[12][13] 시스템의 구성 $단계{\displaystyle }$ n$(\displaystyle$ n$)$ 단계에서$$ 크기${\displaystyle }1{\displaystyle \mathrm{}}$/$(\$1/$3^{n})$ 간격이 N ${\displaystyle =}$ $(\$ N$=2^{n})$인 것을 알고 있습니다.${\displaystyle {}_{}}$ 다음 생존 ${\displaystyle {간격}_{}}$에 x ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$x${\displaystyle {}_{}}$2, ${\displaystyle \dots ,}$ ${\displaystyle {x{\mathrm{}}^{}}_{}}$ ${\displaystyle {2^{}}_{}}$n({$displaystyle x_{1},x_{2},\$ldots$,x_{2^{n}})$이라고 라벨을 붙이면$$d ${\displaystyle f_{}}$ {{$displaystyle$d_${$f$$}}}$번째{\displaystyle {}_{}}$ ${\displaystyle {모멘트}_{}^{}}$는 ${\displaystyle {{}_{}}_{}^{}}$ ${\displaystyle {1_{}}_{}^{}}$d ${\displaystyle {}_{}^{}}$+ ${\displaystyle {{}_{}}_{}^{}}$ 2${\displaystyle {{}_{}}_{}^{}{d_{}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ + ${\displaystyle {x{\mathrm{}}^{}}_{}^{}}$ ${\displaystyle {2^{}}_{}^{}}$ ${\displaystyle {{}^{}}_{{}_{}}^{}}$ $=$ 1 {$displaystyle$ x_${1_{f$}^{$f}$입니다.$}^{d_{f}}+\cdots +x_{2$$^{n}}^{d_{f}=1}($${\displaystyle {x1\mathrm{}}_{}}$ $=$ ${\displaystyle {x2\mathrm{}}_{}}$ ${\displaystyle =}$ ${\displaystyle {{x2}^{}}_{}}$ n ${\displaystyle =}$ ${\displaystyle x2{\mathrm{}}^{}}$ n ${\displaystyle {{}^{}}_{}}$1/3 $n({$} =$x_{2$}=\$cdots = x_{2$^{n} $=$1/$3^{n$ } $이후$).

칸토어 집합의 하우스도르프 치수는 ln(2)/ln(3) 0 0.631입니다.

토폴로지 및 분석 특성

"the" Cantor set"은 일반적으로 위에서 설명한 원래의 3분의 1 칸토어 집합을 가리키지만, 위상학자들은 종종 "a" 칸토어 집합에 대해 이야기하는데, 이는 (위상적으로) 동형인 위상 공간을 의미합니다.

위의 summary 인수에서 알 수 있듯이 칸토어 집합은 셀 수 없지만 르베그 측정값이 0입니다.칸토어 집합은 열린 집합의 결합을 보완하기 때문에, 칸토어 집합 자체가 실수의 닫힌 부분 집합이므로 완전한 메트릭 공간이다.이것은 또한 완전히 한정되어 있기 때문에, 하이네-보렐 정리는 그것이 작아야 한다고 말한다.

칸토어 집합의 임의의 점 및 점의 임의의 작은 근방에 대해, 3진수 숫자가 1을 포함하는 숫자뿐만 아니라 0과 2s의 다른 숫자도 있습니다.따라서 칸토어 집합의 모든 점은 칸토어 집합의 누적점(클러스터 점 또는 한계점이라고도 함)이지만 내부점은 아닙니다.모든 점이 누적점인 닫힌 집합을 위상에서는 완전 집합이라고도 하지만 내부 점이 없는 간격의 닫힌 부분 집합은 간격에서 밀도가 높지 않습니다.

칸토어 세트의 모든 점은 칸토어 세트의 보완점이기도 합니다.

칸토어 집합의 임의의 2개의 포인트에 대해서, 각각 다른 3진수가 있습니다.하나는 0, 다른 하나는 2가 됩니다.칸토어 집합을 이 자리 값에 따라 "반쪽"으로 분할하면 칸토어 집합의 파티션을 원래 두 점을 구분하는 두 개의 닫힌 집합으로 얻을 수 있습니다.칸토어 집합의 상대 토폴로지에서는 점이 클로닝 집합으로 구분되어 있습니다.그 결과, 칸토어 세트는 완전히 절단됩니다.칸토르 세트는 완전히 분리된 콤팩트 하우스도르프 공간으로서 스톤 공간의 한 예입니다.

위상 공간으로서 칸토어 세트는 공간${\displaystyle }${${\displaystyle 0,}$ $}({displaystyle$\{$0,1$의 셀 수 없을 정도로 많은 복사본의 곱과 자연스럽게 동형입니다. 여기서 각 복사본은 이산 토폴로지를 전송합니다.이것은 모든 시퀀스의 두 자리 숫자 공간입니다.

$\displaystyle 2^{\mathbb {N}=\{(x_{n})\mid x_{n}\in \{0,1\}{\text{}n\in \mathbb {N}\}$

또한 2-adic 정수 집합으로도 식별할 수 있습니다.제품 토폴로지의 열린 집합의 기본은 실린더 집합입니다. 동형사상은 칸토어 집합이 실제 라인의 자연 토폴로지로부터 상속하는 부분 공간 토폴로지에 매핑합니다.칸토어 공간을 콤팩트 공간의 산물로 특징짓는 것은 티코노프의 정리를 통해 칸토어 공간이 콤팩트하다는 두 번째 증거를 제시합니다.

위의 특성으로부터 칸토어 집합은 p-adic 정수와 동형이며, 여기서 한 점이 제거되면 p-adic 숫자와 동형이다.

칸토어 집합은 실수의 부분집합이며, 이는 통상 거리 측정 기준과 관련된 메트릭 공간입니다. 따라서 칸토어 집합 자체는 동일한 메트릭을 사용하여 메트릭 공간입니다.또는 $p-adic$ 메트릭을${\displaystyle }$2 ${\displaystyle N_{}{\mathrm{}}^{}}$2^{\$mathbb {N$에 $사용$할 수 있다. 2 N$($n${\displaystyle }$), ( y n )${\displaystyle }$$2$ 2 N($x _$ { n$},$ ( $y_ { n$})\$in$ 2$^{\mathbb { N}}})$${\displaystyle =}$ ${\displaystyle n_{}}$(${\displaystyle {}_{}}$ ,${\displaystyle }$n${\displaystyle {}_{}}$이 주어졌을 때, n${\displaystyle {}_{}}$의 거리는${\displaystyle {}_{}}$이다${\displaystyle .}$${\displaystyle }$k$(\displaystyle$ k$)$는 x ${\displaystyle k_{}{}_{}}$ ${\displaystyle y_{}}$k(\$displaystyle x_{k}\neq y_{k$와 $같은{\displaystyle {}_{}}$ 최소 인덱스입니다.${\displaystyle 이}$ 인덱스가 존재하지 않는 경우 두 시퀀스는 동일하며 하나는 거리를 0으로 정의합니다.이 두 메트릭은 칸토어 집합에서 동일한 토폴로지를 생성합니다.

위에서 칸토어 세트는 완전히 단절된 완벽한 콤팩트 미터법 공간임을 확인했습니다.실제로, 이것은 유일한 의미입니다: 비어 있지 않은 모든 완전 단절된 완전 콤팩트 메트릭 공간은 칸토어 집합과 동형입니다.칸토어 집합과 동형 공간에 대한 자세한 내용은 칸토어 공간을 참조하십시오.

콤팩트 메트릭 공간이 칸토어 집합의 연속 이미지이기 때문에 칸토어 집합은 때때로 콤팩트 메트릭 공간의 범주에서 "범용"으로 간주됩니다. 그러나 이러한 구성은 고유하지 않으며 따라서 칸토어 집합은 정확한 범주적 의미에서 보편적이지 않습니다."범용" 속성은 함수 분석에서 중요한 응용 분야를 가지며, 여기서 콤팩트 메트릭 공간에 ^[14]대한 표현 정리라고도 한다.

임의의 정수 q ≤ 2에 대해 그룹 G = Z_q^ω(계수 가능한 직접합) 상의 위상은 이산적이다.Pontrjagin 듀얼 δ도_q^ω Z이지만 δ의 토폴로지는 콤팩트합니다.δ는 완전히 단절되고 완벽하다는 것을 알 수 있으며, 따라서 칸토어 세트와 동형이다.사례 q = 2일 때 동형사상을 명시적으로 쓰는 것이 가장 쉽다. (Rudin 1962 페이지 40 참조)

칸토어 집합의 기하 평균은 약 0.274974입니다.^{[15][unreliable source?]}

측정 및 확률

칸토어 집합은 2진수 시퀀스의 콤팩트한 그룹으로 볼 수 있으며, 따라서 자연스러운 Haar 측정이 부여됩니다.세트의 측정값이 1이 되도록 정규화하면 무한 연속 동전 던지기 모델입니다.또, 이 간격에 있어서의 통상적인 르베게 측정이 칸토어 집합상의 하르 측정의 화상이며, 3진 집합으로의 자연 주입은 단수 측정의 표준적인 예임을 나타낼 수 있다.또한 Haar 측정값이 확률의 이미지이므로 칸토어가 어떤 방식으로든 보편적 확률 공간을 설정한다는 것을 보여줄 수 있습니다.

르베게 측정 이론에서 칸토르 집합은 셀 수 없고 ^[16]측정값이 0인 집합의 예입니다.반면, 이 세트는 로그 2 / 로그 ^[17]3의 치수에 하우스도르프 측정값이 1입니다.

칸토어 수

칸토어 번호를 칸토어 세트의 멤버로 정의하면^[18]

1. [0, 2]의 모든 실수는 두 칸토어 숫자의 합이다.
2. 두 개의 칸토어 번호 사이에 칸토어 번호가 아닌 번호가 있습니다.

기술 집합론

칸토어 집합은 [0,1]의 부분 집합(또는 첫 번째 범주의 집합)이다(Baire 공간이기 때문에 그 자체의 부분 집합은 아니지만).따라서 칸토어 집합은 카디널리티, 측정치 및 (바이어) 범주에서 "크기"의 개념이 일치하지 않아도 된다는 것을 보여준다.Cantor $집합{\displaystyle \mathcal{}}$ C$(\$$\mathbb {Q}$ \$cap [0,1$는 $집합{\displaystyle \mathbb{}}$ Q ${\displaystyle [}$ [${\displaystyle 0}$ , $]{$ displaystyle $\mathcal {C})$와 마찬가지로 null 집합(측정값 0의 집합)이며 [0,1]의 미미한 부분 집합이라는 점에서 "작음"입니다.단, Q${\displaystyle }$display [${\displaystyle 0}$ , $]{$ $displaystyle$ \ $mathbb { Q$} \$cap$ [$0$ , $1$$$ . $display$$style$ \ $aleph _${ 0 $\}$과 달리 C$\$ $displaystyle$\ $mathcal${ $C$$}$의 카디널리티는 [0, $cfrak$ style]와 $동일합니다{\displaystyle \mathfrak{}}$.카디널리티 감각사실, 그건 또한" 뚱뚱한"칸토어의 측정 λ의 C({\displaystyle{{C\mathcal}}^{(n)}} 가져오거나 설정하)(스미트 박사를 가산 노조(n− 1)/n{\displaystyle \lambda =(n-1)/n}를 취함으로써[0,1]의지만 긍정적인 조치의 빈약한 하위 집합도 측정 0의non-meagre 하위 집합:[19]를 건설하는 것이 가능하다.h–구성에 대해 아래에 설정된 Volterra-Cantor) 집합 $A\mathcal{}$: $=$ $\underset{}{\overset{}{}}$ $\underset{}{\overset{}{n}}$ $\underset{}{\overset{}{=}}$ $\underset{}{\overset{}{1}}{\mathcal{}}^{}$C ( $n$) : = $\ bigcup _$ { n$=$}^{ \ $infty$}$${ \ $mathcal$ { $C$}^{ ($$n ) } { \ mathcal { C }^{ ( n ) } { n }는$$ 각각 양수이지만 meag 1이므로 구문에 있습니다.$그런{\mathcal{}}^{}$ 다음 ${집합}^{\mathrm{}}$ A c$=$ [$0$ , 1 ] $\setminus$ $\underset{}{\overset{}{n}}$ $\underset{}{\overset{}{=}}$ $\underset{}{\overset{}{1}}$ $\underset{}{\overset{}{\mathrm{}}}{}^{}\underset{}{\overset{}{}}{\mathcal{}}^{}$ ($n^{}$) { $textstyle$\ $mathcal${ $A$} = [ $0$, $1 ]$ \ $setminus$\ $bigcup$_ { $n = 1$} { \ $infty$} { \ $mathcal${ $C$${\displaystyle =}$ 1 } （ ${\displaystyle {\mathcal{}}^{}}$ ）$$[ ${\displaystyle C^{\mathrm{}}}$ 。$e${{$mathcal$$${$A}}^{\mathrm {c}}}$은(는) 미량일 수 없지만${\displaystyle }$μ(${\displaystyle A)}$ $=$(\$displaystyle \mu(A$})=$1$이므로 A ${\$은(는) 측정값이 0이어야 합니다.

변종

스미스-볼테라-캔터 집합

칸토어 세트와 같이 모든 피스의 중간을 반복하여 제거하는 것이 아니라 중간에서 다른 고정 비율(0%와 100% 이외)을 계속 제거할 수 있습니다.간격의 중간 8/10이 제거된 경우, 매우 쉽게 접근할 수 있습니다. [0,1]의 모든 숫자는 0과 9로 구성되어 있습니다.각 스테이지에서 고정 퍼센티지가 제거되면 제한 세트는 0이 됩니다${\displaystyle .}$그 는${\displaystyle }$0f $1$과 $f{\displaystyle }$ {\$displaystyle$ $(1-f$$)$ $n$ ${\displaystyle {}^{}}$ ${\displaystyle 0}$$$$0$ n$$${\displaystyle \mathrm{\to }}$ \ $displaystyle$n$\to$ \$infty$$}$의 나머지 $길이$(${\displaystyle \mathrm{1-f}{}^{}}$ ${\displaystyle \mathrm{n}}$ → 0 {\ ∞ ∞ ∞ ∞ ∞ ∞ → $displaystyle$ $0$∞ the the the the the the the the the the the $the$ the the the the the the the the the the the

한편, 각 반복에서 세그먼트 중앙의 더 작은 부분을 제거함으로써 양의 측정값의 "팻 칸토어 세트"를 생성할 수 있다.따라서 아직 밀도가 낮은 상태에서 양의 르베그 측정값을 갖는 칸토어 집합과 동형 집합을 구성할 수 있습니다.$길이{\displaystyle {}^{}}$r n({$displaystyle$ r$^{n})($${\displaystyle 1}$1 / $({displaystyle$r\$leq$1/$3$의 간격을 n번째 반복 시 각 세그먼트의 중간에서 제거하면 제거된 총 길이는$\underset{n}{\overset{}{}}$ n $\underset{}{\overset{}{=}}$ $1\underset{}{\overset{}{}}{\mathrm{}}^{}$ 2$n^{}$ - $1$ ${}^{}{}^{}$ $=\mathrm{r}$ / ($1$ -$$2$$r ){ $style$\$sum$_ { n$$=$$1 \ n }^2 } inftyle $}$ $^$2 } 입니다.et의 Lebegue 측정값은 $\lambda {\displaystyle =}$ ( ${\displaystyle 1}$-${\displaystyle 3}$r )${\displaystyle }$/ ( ${\displaystyle 1}$ -$$ ){ $display$\ $specda =$ ( 1 - ${\displaystyle \mathrm{3r}}$ ) / ( 1 - $2r )$} 입니다.따라서 중간 칸토어 세트는 r ${\displaystyle =1}$ /$$3 { $displaystyle$ r $= 1$/$$ $\{$ $displaystyle$0 <$r$<$1$ / $3$인 $경우{\displaystyle }$ 나머지는 0< \ $displaystyle$0 <\ $displayda < 1$ 인 양의 측정값이 됩니다.$케이스{\displaystyle }$ r ${\displaystyle =}$ ${\displaystyle 1}$/$$4 { $style$ r $=$1/$4}$은 Smith-Volterra-Cantor 집합으로 알려져 있으며, 르베그 측정값은 $({displaystyle$1/$2$입니다.

확률 칸토어 집합

칸토어 집합의 구성은 균등하게 나누지 않고 무작위로 나누어서 수정할 수 있다.또한 시간을 통합하기 위해 모든 사용 가능한 간격을 분할하는 대신 각 단계에서 사용 가능한 간격 중 하나만 분할할 수 있습니다.확률적 3차 칸토어 집합의 경우 결과 과정은 다음 속도^[12][13] 방정식으로 설명할 수 있다.

${\displaystyle {\frac c(x,t)}{\frac {x^{2}}{2}}c(x,t)+2\int _{x}^{\infty }(y-x)c(y,t),dy,}$

확률적 쌍방향 칸토어^[20] 집합은

${{displaystyle {{\display c(x,t)}\over {display t}=-xc(x,t)+(1+p)\int _{x}^{\infty }c(y,t),dy,}$

$여기$서 c${\displaystyle }$(${\displaystyle x}$ ,${\displaystyle t}$ ) ${\displaystyle d}$x { $display$ $style$ c $( x$ ,$t$ ) spec$$}는$$x { $display$ style$$x } ~$x$+ ${\displaystyle d}$ { $display style$ x + spec$\}$ $사이$의 크기 간격 수입니다.3차원 칸토어 세트의 경우 프랙탈 치수는 0.$(\displaystyle$0.$5616)$으로, 결정론적 칸토어 $세트$의${\displaystyle 0}$.6309$(\style$0.$6309$보다 작습니다.확률적 쌍방향 캔터 집합의 경우 프랙탈 치수는 p$(\displaystyle$$$p$)$로 결정론적 ${\displaystyle \mathrm{상대}}$ ln${\displaystyle }$(${\displaystyle 1}$+ ${\displaystyle p}$) / ${\displaystyle \ln }$ 2(\$displaystyle \ln(1+p$)/\$ln$ 2)보다$$작습니다. 확률적 쌍방향 캔터 집합의 경우 c$(x$,$tisplay style$ sc$(\$display style sc$)$에 $대해{\displaystyle }$ 솔루션을 설정합니다.장기 제한에서 해법으로 aling은 $t{\displaystyle {}^{}}$- ( 1${\displaystyle {}^{}}$+ ${\displaystyle {d_{}}^{}}$f )${\displaystyle {}^{}{}^{}{}^{}}$ - ${\displaystyle x^{}}$ ${\displaystyle t^{}}${ \ $displaystyle$ t^ { - ($1$ + d$_ f$) } $e^{$ - $xt$}이다$.$ 여기서$$ 확률적 쌍방향 캔터의 프랙탈 치수는 d ${\displaystyle {}_{}}$ ${\displaystyle p}$ {$$\ $displaystyle d_$${$ f$}$ $= p$}이다. 어느 경우든, 3방향 캔터 $d_styledisplaystyle$ ${\displaystyle {d\_f}_{}}$}${}^{}c$ $($ x$$,$t$ )$d$ x $=$ $\text{확률적}$ 3진수 및 2진수 칸토어 집합의 상수$${\$textstyle$ \$int x^{d_{f}c(x,t),$ qual$=squaltext{f$도 보존량이다.

칸토르 분진

칸토어 더스트는 칸토어 세트의 다차원 버전입니다.칸토어 집합의 유한 데카르트 곱을 가져와서 칸토어 공간을 만들 수 있다.칸토어 세트와 마찬가지로 칸토어 분진도 제로 ^[21]측정입니다.

캔터 분진(2D)

캔터 분진(3D)

칸토르 세트의 다른 2D 아날로그는 Sierpinski 카펫입니다. 이 카펫에서는 정사각형이 9개의 작은 정사각형으로 분할되고 가운데 정사각형이 제거됩니다.나머지 정사각형은 각각 9개로 분할되고 가운데는 제거되는 등 무한히 분할됩니다.^[22]이것의 3D 아날로그 중 하나가 Menger 스폰지입니다.

이력 코멘트

칸토어 소위 말하는 오늘은 칸토어 ternary C{\displaystyle{{C\mathcal}을 세웠다}}어떤 간격에everywhere-dense지 않은 완벽한 point-set, 그러나 작은 하나의 예를``를 소개했다.모든 실수를 폼으로"[23][24]칸토어 3진의 확대기의 조건{\displaystyle{\mathcal{C}}}에 C를 묘사하다."the이다.ula: $z{\displaystyle }$ ${\displaystyle =}$ ${\displaystyle {c\mathrm{}}_{}}$ 1${\displaystyle {}_{}}$/${\displaystyle 3\mathrm{}}$ + ${\displaystyle {c\mathrm{}}_{}}$2 / ${\displaystyle {3\mathrm{}}^{}}$2 +${\displaystyle \cdots }$ + / + ${\displaystyle {}_{}{\nu }_{}}$ / ${\displaystyle 3{\mathrm{}}^{}}$+ + c$_$ 、$$ $display style$ z$= c_{1}$ / 3 +$c_{$2} / $3$^{\nu$}$ + 3 ^{\$nu$} + 3 ^{\cdots$$} $}$ 계수가 ${\displaystyle {임의}_{}}$로 사용되는$경우$

$위상공간{\displaystyle }$ P$(\displaystyle$ P$)$는 그 모든 점이 한계점일 경우 또는 그 $도출집합{\displaystyle {}^{}}$ P$(\$ P$\text{'})$와 일치할 경우 완벽합니다$.$ C(\$displaystyle {C$와 같이 실제 라인의 부분 집합은 유도 ^[7]부분공간에서 위상공간으로 볼 수 있습니다.

칸토르는 삼각 ^[24]급수의 특이성에 대한 그의 결과에 의해 파생 집합의 연구를 이끌었다.후자는 그가 무한집합에 대한 추상적이고 일반적인 이론을 발전시키는 과정에 많은 기여를 했다.

「 」를 참조해 주세요.

• 칸토어 세트의 표시기 기능
• 스미스-볼테라-캔터 집합
• 육각형(I칭)
• 칸토어 함수
• 칸토르 입방체
• 앙투안 목걸이
• 코흐 눈꽃
• 크나스터 쿠라토스키 팬
• 하우스도르프 차원에 따른 프랙탈 목록
• 모세르-드 브루인 수열

메모들

레퍼런스

외부 링크

• "Cantor set", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• 칸토어 세트 및 칸토어 세트 및 기능(컷 더 노트)
• 플라토닉 영역에 있는 칸토르 세트