드람 곡선

이 문서에는 참고 자료, 관련 읽기 또는 외부 링크가 포함되어 있지만 인라인 인용이 부족하여 출처가 불분명합니다. 좀 더 정밀한 인용문을 도입하여 이 글의 개선에 도움을 주시기 바랍니다.(2019년 1월) (이 템플릿메시지 삭제 방법 및 삭제 시기 확인)

수학에서, 드 람 곡선은 조르주 드 람의 이름을 따서 명명된 프랙탈 곡선의 한 종류이다.

칸토르 함수, 세자로 곡선, 민코프스키 물음표 함수, 레비 C 곡선, 블랑망지 곡선, 코흐 곡선 모두 일반적인 드 람 곡선의 특수한 경우이다.

건설

완전한 메트릭 공간$({\displaystyle M}$ ${\displaystyle ,d}$) {$displaystyle (M,d)}($$일반적$으로 R$$\$style \mathbb {R}$ 표시$$²) 및 M 위의 한 쌍의 수축 맵을 고려합니다.

${\displaystyle d_{0}:\M\toM}$

$(\displaystyle d_{1}:\M\toM).}$

바나흐 고정점 정리에 따르면, 이들은 각각 $고정점{\displaystyle {}_{}}$ $($ 스타일 $p_{0})$과 $($ 스타일 $p_{1$})을$$ 가진다.x를 [$]({displaystyle$ [$0,1$${\displaystyle }$간격의 실수(이진수 전개)로 합니다.

${\displaystyle x=\sum _{k=1}^{\infty}{\frac {b_{k}}{2^{k}}}}$

$여기$서 각$$(\$displaystyle b_{k})$는 0 또는 1입니다.지도를 검토하다

$\displaystyle c_{x:\M\toM}$

정의하다

$\displaystyle c_{x}=d_{b_{1}}\displays d_{b_{2}\cdots\cdots d_{b_{k}\displays \cdots,}$

여기서 $"\displaystyle\display"$는 함수 구성을 나타냅니다.$각{\displaystyle {}_{}}$ ${\displaystyle c_{}}$x {\$displaystyle c_{x$$}$는 d$$ {\$displaystyle d_{0}$ $및$ d$$ {\$displaystyle d_$${1$$}}$의 공통 흡인 분지를$M$ {\$displaystyle$M$\}$의 $단일{\displaystyle {}_{}}$ ${\displaystyle {포인트}_{}}$p x${{$x$$}에 매핑하는 것을 알 수 있습니다.$$ x {\$displaystyle p_x$ 파라미터, i단일 실제 매개변수 x에 의해 zed되며, de Rham 곡선으로 알려져 있습니다.

연속성 조건

고정점이 다음과 같이 쌍으로 구성된 경우

${\displaystyle d_{0}(p_{1})=d_{1}(p_{0})}$

그러면 결과 $곡선{\displaystyle {}_{}}$ p$$ {\$displaystyle p_{x}}$이 x의 연속 함수임을 알 수 있다.곡선이 연속인 경우 일반적으로 미분할 수 없습니다.

이 페이지의 나머지 부분에서는 곡선이 연속이라고 가정합니다.

특성.

De Rham 곡선은 구조상 자기 유사하다.

${\displaystyle p}$(${\displaystyle x}$ ) $=$ ${\displaystyle {d\mathrm{}}_{}}$0 (${\displaystyle p}$ ( ${\displaystyle 2}$x $){$ d _ 0 } （ display $style$p ( x )= $d$_ { 0 ${\displaystyle （}$ $p$( 2 x )$$） } 。$x$ ${\displaystyle \in }$ x x [ ${\displaystyle 0}$ ,${\displaystyle }$1 / 2$]{$ $display style$x \$in$ [$0$ ,$1$ / $2$] ） 。

${\displaystyle }$${\displaystyle \mathrm{p<img\; alt="p(x)=d\_1(p(2x-1))"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/ddc2a5759813a2c7b9b2f43c128db4bc77301b84"\; style="vertical-align:\; -0.838ex;\; margin-left:\; -0.089ex;\; width:21.042ex;\; height:2.843ex;">}}$${\displaystyle }$(${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle {d\mathrm{}}_{}}$1 (${\displaystyle p}$ ( ${\displaystyle 2}$x -$){$ d _ { 1${\displaystyle （}$$display style$p ( x ) = d _ { $1 （ p$ ( ${\displaystyle \mathrm{2x}}$ -$$1 ) ${\displaystyle ）}$ ${\displaystyle \}}$ $。{$ $displaystyle$x \ $in [ 1$ / $2,$1 ${\displaystyle \}}$ ） 。$}$

모든 de Rham 곡선의 자기 대칭성은 무한 이진 트리 또는 칸토어 집합의 대칭성을 설명하는 모노이드에 의해 제공됩니다.이른바 주기배율모노이드는 모듈러 그룹의 서브셋입니다.

곡선의 이미지({${\displaystyle p}$ (${\displaystyle x}$) , ${\displaystyle x}$ ${\displaystyle [}$ [${\displaystyle 0}$ , ${\displaystyle 1}$]$}$ { $displaystyle$\ {p$(x$, $x$) ,$x$ \$in$ [ 0 , 1$$]$$} )는 반복 함수시스템에 의해 construction${\displaystyle }$mapping ${\displaystyle {}_{}}${${\displaystyle {}_{}}$d ${\displaystyle \text{0}{}_{}}$ , d$$} { $displaystyle$\ { $d _ 0$} $)$를 사용하여 얻을 수 있지만 결과는 $다음과 같습니다.$수축 매핑이 연속성 조건을 충족하는 경우에만 de Rham 곡선.

자기 유사성에 대한 상세하고 가공된 예는 칸토어 함수와 민코프스키의 물음표 함수에 관한 기사에서 찾을 수 있다.정확히 같은 자기유사성 모노이드의 쌍방향 모노이드는 모든 드 람 곡선에 적용된다.

분류 및 예시

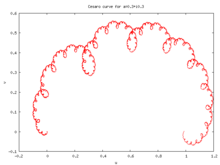
세자로 곡선

세자로 곡선(또는 세자로-페이버 곡선)은 방향을 보존하는 아핀 변환에 의해 생성된 드 람 곡선이며, $고정점{\displaystyle {}_{}}$ p ${\displaystyle 0}$ $=$$$0 (\$displaystyle p_{0$}=$0$$})$ $및{\displaystyle {}_{}}$ ${\displaystyle {p\mathrm{}}_{}}$ 1 $(\displaystyle p_{1$}=1$\})$이다.

이러한 제약조건으로 인해 Cesaro 곡선은 $a$에 의해 고유하게 결정되므로 $(디스플레이 스타일$a$$<$1$) 1$(디스플레이$ 스타일 $1-a$$< 1$)이 .

수축 매핑 ${\displaystyle {d\mathrm{}}_{}}$ 0$({$ 및$$ $d{\displaystyle {}_{}}$ $({$은 다음과 같이 복합 평면에서 복잡한 함수로 정의됩니다.

${\displaystyle d_{0}(z)=az}$

$\displaystyle d_{1}(z)=a+(1-a)z.}$

a $=$ ( ${\displaystyle 1}$+${\displaystyle i}$) / ${\displaystyle 2\mathrm{}}${{$displaystyle$ a=($1+i)/2$의 값의 경우 결과 곡선은 Lévy C 곡선입니다.

코흐-페아노 곡선

마찬가지로 Koch-Peano 곡선 패밀리를 방향을 반전시키는 아핀 변환에 의해 생성된 De Rham 곡선 세트로 정의할 수 있으며, $고정점{\displaystyle {}_{}}$ p ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ { $display$ style $p_{0}$= ${\displaystyle \mathrm{1<img\; alt="p\_0=0"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/7d9da57af25134722e43acddbdfecfa21839889a"\; style="vertical-align:\; -0.671ex;\; margin-left:\; -0.089ex;\; width:6.574ex;\; height:2.509ex;">}}${ $displaystyle p_{$1} $=$$1$ 입니다.

이러한 매핑은 z$${\$displaystyle$z$\}$의 복합 켤레인$$z ${\$ {\$displaystyle$ {$z$의 함수로 복소 평면에 표현됩니다.

${\displaystyle d_{0}(z)=오버라인 {z}}$

${\displaystyle d_{1}(z)=a+(1-a){\overline {z}}.}$

그 가족의 이름은 가장 유명한 두 가족에게서 유래되었다.Koch 곡선은 다음을 설정하여 얻을 수 있습니다.

$({displaystyle a_{\text{Koch}}=paramfrac {1}{2}}+i440frac {{6}})$

Peano 곡선은 다음 항목에 해당합니다.

${\displaystyle a_{\text{Peano}}=paramfrac {(1+i)}{2}}.}$

일반 아핀 맵

Cesaro-Faber 곡선과 Peano-Koch 곡선은 모두 복소 평면에서 아핀 선형 변환 쌍의 일반적인 경우이다.곡선의 한쪽 끝점을 0으로 고정하고 다른 한쪽 끝점을 0으로 고정하면 두 변환에서 반복하여 일반적인 경우를 얻을 수 있습니다.

$\displaystyle d_{0}=pmatrix1&0&\alpha&\varepsilon\end{pmatrix}}$

그리고.

$({displaystyle d_{1}=pmatrix}1&0\alpha&1-\alpha&\zeta &-\alpha&\geta\end{pmatrix}).}$

아핀 변환이므로 이러한 변환은 벡터에 작용하여 2-D 평면의 점$({\displaystyle u}$,${\displaystyle v}$) {$displaystyle (u, v)}$에 작용합니다.

$(*displaystyle {pmatrix}1\u\v\end{pmatrix})}$

곡선의 중간점은 (${\displaystyle u}$,${\displaystyle v}$ ) $=$ $({\displaystyle \alpha }$ ${\displaystyle ,}$β$$) {$displaystyle (u,v$)=(\$alpha ,\display$에 있으며, 다른 4개의 매개변수를 변경하여 다양한 곡선을 생성할 수 있습니다.

$파라메타$w의 블랑망주 $곡선$은 ${\displaystyle \alpha }$ ${\displaystyle =}$${\displaystyle \beta }$ ${\displaystyle =}$ 1/$2({displaystyle \$$alpha$ =\$display =\$$zeta = 0)$ ${\displaystyle \mathrm{및}}$ ${\displaystyle =}$ ${\displaystyle =}$ ${\displaystyle w}${$display$$$style $\valpsilon$$$=\$eta$$= 0$$}$로 $설정$하면 얻을 수 있다.

${\displaystyle d_{0}=pmatrix}1&0\\0&1/2&0\0&w\end{pmatrix}$

그리고.

$({displaystyle d_{1}=pmatrix}1&0\1/2&1/2&0\1/2&w\end{pmatrix})}$

$파라메타{\displaystyle }$ ${\displaystyle \mathrm{w}}$ ${\displaystyle =}$ ${\displaystyle 1\mathrm{}}$ /$$4 { $displaystyle$ w ${\displaystyle =}$$1$ /$$4$$ }의 블랑망주 곡선은$방정식$ ( ${\displaystyle x}$ )$=$ $x$($$1 - ${\displaystyle x}$)의 포물선이기 때문에 경우에 따라서는 De Rham 곡선이 매끄럽다는 것을 알 수 있다.

민코프스키 물음표 함수

민코프스키의 물음표 함수는 지도 쌍에 의해 생성된다.

${\displaystyle d_{0}(z)=squalfrac {z}{z+1}}$

그리고.

$({displaystyle d_{1}(z)=snapsfrac {1}{z+1}).}$

일반화

세 개 이상의 축소 매핑을 사용하면 정의를 쉽게 일반화할 수 있습니다.n개의 매핑을 사용하는 경우, 실수의 2진수 확장 대신 x의 n-ary 분해를 사용해야 합니다.연속성 조건은 다음과 같이 일반화해야 합니다.

${\displaystyle d_{}}$i ( ${\displaystyle p_{}}$n -${\displaystyle {}_{}{1}_{}}$ )$=$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$+ 1${\displaystyle {}_{}}$( ${\displaystyle {\mathrm{p}}_{}}$ 0 $){$ $displaystyle d_{i}(p_{n-1$})= $d_{i+1}(p_{0})$($i{\displaystyle }$ $0$ …${\displaystyle n}$ ${\displaystyle -}$ $.\display style$ i= 0$\ldots n-2).$$}$

이 연속성 조건은 다음 예에서 이해할 수 있습니다.가 10번 기지에서 작동한다고 가정해봐그럼 0.999...= 1.000...모든 갭에서 적용되어야 하는 연속성 방정식입니다.즉, 10진수 ${\displaystyle {b\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}{b\mathrm{}}_{}}$2, ${\displaystyle "",}$ ${\displaystyle {}_{}}$ $(\$$displaystyle b_$${1}, b_{2},\cdots, b_$${k$$},$ b_${$$k},$ ${\displaystyle b_{}9}$9$)$를 지정하면 다음과 같이 됩니다.

$\displaystyle b_{1}, b_{2},\cdots,b_{k},9,9,\cdots=b_{1},b_{2},\cdots,b_{k}+1,0,0,0,0,\cdots}$

이러한 일반화를 통해 예를 들어 시에르핀스키 삼각형을 생성하는 반복 함수 시스템의 수축 매핑을 사용하여 시에르핀스키 화살촉 곡선을 생성할 수 있다.

다분할 곡선

Ornstein과 다른 사람들은 고정된 기반에서 일하는 것이 아니라 가변 기반에서 일하는 다분할 시스템을 설명합니다.

가변 베이스의 제품 공간 고려 - ${\displaystyle {}_{}}$ \ $displaystyle m_{n}$ 이산 공간

$\displaystyle \Omega = \displays _ {n\in \mathbb {N} }A_{n}$

${\displaystyle A_{}}$ n ${\displaystyle {}_{}Z\mathbb{}}$ / ${\displaystyle m{}_{}}$ ${\displaystyle n_{}}$ ${\displaystyle {}_{}\mathbb{}}$ ${\displaystyle =}$ {${\displaystyle 0}$ ,${\displaystyle 1}$ , ${\displaystyle ,}$ , ${\displaystyle {}_{}{n}_{}}$ - $}$ { $display$ $style$ A _ { n }$= m$_ { $n$} \ $mathbb { Z$} = \ { $0 , 1$ , \ $cdots$, m _ { $n$$$ - $1$\ } 의$$ $경우{\displaystyle {}_{}}$, $2_ge style$ m _ group단위 간격 내의 모든 실수는${\displaystyle }$${n$의 각 $(\$ style$$$a_{1$$},$로 전개할 수 있습니다. 보다 정확하게는 $displayx display$1 입니다${\displaystyle .}$

${\displaystyle x=\sum _{n=1}^{\infty}{\frac {a_{n}}{\frac _{k=1}^{n}m_{k}}}}$

모든 ${\displaystyle n_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle 0}$ { $displaystyle$ $a$_ { n } =$0$some$$ K < $n$ $some$ in, has 。이 경우, 다음과 같이 됩니다.

$\displaystyle a_{1}, a_{2},\cdots,a_{K},0,\cdots=a_{1},m_{K+1}-1,m_{K+2}-1,\cdots}$

이러한 점은 2진수 팽창의 2진수 유리수와 유사하며, 곡선의 연속성 방정식을 이러한 점에 적용해야 합니다.

각 ${\displaystyle A_{}}$n { $displaystyle$ A _ {$n$${\displaystyle {<img\; alt="A\_\{n\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/730f6906700685b6d52f3958b1c2ae659d2d97d2"\; style="vertical-align:\; -0.671ex;\; width:2.962ex;\; height:2.509ex;">}_{}^{}}$} each 、 2개의 $포인트{\displaystyle {}_{}^{}}$ ${\displaystyle {p\mathrm{}}_{}^{}}$0 ( $n$ ) ${\displaystyle 、}$ $p{\displaystyle {}_{}^{}}$ 1${\displaystyle {}_{}^{}}$( ${\displaystyle n_{}^{}}$ $){$ $displaystyle$ $p$$_$ { $1$$$}^{ ($n$$$)$$} $n$ a n n n n n n n n n n$$n n n n n n${\displaystyle {}_{}^{}}$n n n ${\displaystyle {for}_{}^{}}$ for for 0 0 0 0 0 0 p 0 ( n ){ $displaystyle$ $p_$${$0 ( n$）^$$0$ ( n ) ） and$$$$ and 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 11${\displaystyle {}_{11\mathrm{}}^{}}$ $11$ (1 of1 of$(\displaystyle$ j$\in$ A_${n})$그러면 연속성 조건은 위와 같습니다.

${\displaystyle d_{}^{}}$j (${\displaystyle n_{}^{}}$) ( ${\displaystyle {}_{}^{}{}_{1\mathrm{}}^{}}$ (${\displaystyle n_{}^{}}$ +${\displaystyle 1_{}^{}}$) ${\displaystyle ={\mathrm{d}}_{}^{}}$ j${\displaystyle {}_{}^{}}$+ 1${\displaystyle {}_{}^{}}$(${\displaystyle {}_{}^{}{}_{}^{}}$ ) (${\displaystyle {}_{p\mathrm{}}^{}}$ 0${\displaystyle {}_{}^{}}$( ${\displaystyle {\mathrm{n}}_{}^{}}$ +$$1 ){ $displaystyle d_{$j}^{($n+1)} = d_{j+$1}^{($n)}$ ($p_{$0}^{($n+$1$)\}$ ), j ${\displaystyle =}$ ${\displaystyle 0}$ - 0${\displaystyle ,}$ ${\displaystyle {}_{}}$ ${\displaystyle n_{}\mathrm{+}}$1) 。$}$

Ornstein의 원래 사용 예

$\displaystyle \Omega = \left(\mathbb {Z} / 2\mathbb {Z} \right)\times \left(\mathbb {Z} / 3\mathbb {Z} \right)\times \tes \left(\mathbbb {Z} / 4\right)\cdots$

「 」를 참조해 주세요.

• 반복 기능 시스템
• 리페일러블 기능
• 모듈러 그룹
• 푸치안군

레퍼런스

추가 정보

• Georges de Rham, 함수 방정식에 의해 정의된 몇 가지 곡선에 대하여(1957)는 프랙탈에 관한 고전, ed.제럴드 A.Edgar (Addison-Wesley, 1993), 페이지 285–298.
• Georges de Rham, Sur Quelques courbes는 par des 방정식을 정의한다.대학교.e Politec.토리노.렌드, Sem. Mat., 1957, 16, 101 – 113
• Linas Vepstas, A Gallery of de Rham curves, (2006).
• Linas Vepstas, Period-Doubling Maps, (2006).(프랙탈 곡선의 모듈러 군 대칭에 대한 일반적인 탐구).