두아디토끼

Douady 토끼는 복잡한 2차 맵에 대한 Mandelbrot 세트의 중심 주기 3 싹 근처의 매개 변수와 관련된 다양한 특정 채워진 Julia 세트 중 하나입니다.

• 

  색상은 반복을 나타낸다.

• 

  회색 레벨은 무한대 또는 매력적인 사이클로의 수렴 속도를 나타냅니다.

• 

  수준 집합의 경계

• 

  이원 분해

• 
• 

  척추를 가지고

• 

  외부 광선이 고정 $지점{\displaystyle {}_{}}$ ${\displaystyle {\alpha }_{}}$ c${\displaystyle {}_{}}$\$displaystyle \alpha$ _${c$에 착지합니다.

이름.

• 토끼^[1]
• 두아디토끼
• 드래곤^[2][3] 프랙탈

그것은 프랑스 ^[4]수학자 Adrien Douady에 의해 처음 묘사되었기 때문에 Douady의 토끼라고 불립니다.

본체(성분)에 두 개의^[5] 돌출된 귀(성분)가 붙어 있고 ^[6]토끼처럼 생겼기 때문에 토끼라고 불린다.

변종

꼬임 토끼 또는^[7] 꼬임 귀를 가진 토끼 = ^[8]ᄃ의 n제곱이 귀를 중심으로 꼬임으로 이루어진 "꼬임" 다항식의 구성이다.

Corabbit은 토끼의 대칭적인 이미지입니다.여기서 $파라미터{\displaystyle }$ c${\displaystyle }$θ -${\displaystyle 0}$.${\displaystyle 1226}$- ${\displaystyle 0.\mathrm{7449}}$i (\$displaystyle c\apprough$ -0$.1226-0.7449i)$는 임계 후 세트의 동일한 치환을 유도하는 다른 2개의 다항식 중 하나입니다.

3D

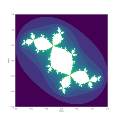
4분위 줄리아 세트는 매개변수 c = -0,123 + 0.745i이고 XY 평면에 단면이 있습니다."Douady Rabbit" 줄리아 세트가 단면에서 보입니다.

• 

내장

• 

줄리아^[9] 세트 중앙에 작은 동종 토끼 모형이 있는 것을 볼 수 있습니다.

뚱뚱해요.

뚱뚱한 토끼 또는 통통한 토끼는 만델브로트 세트의 1/3 림브 뿌리 부분에 c를 가지고 있습니다.그것은 3개의 ^[10]꽃잎이 있는 포물선 모양의 고정점을 가지고 있다.

• 

  뚱뚱한 토끼

• 

  포물선 체스판

n번째 귀

• 네 번째 토끼=귀가^[11] 세 개 달린 토끼

섭동했다

섭동토끼^[12]

• 섭동토끼
• 

  섭동토끼

• 

  섭동토끼 줌

복소 2차 지도의 형태

$복소$ 2차 맵$M$에는 두 가지 일반적인 $형식$이 있습니다$.$복잡한 로지스틱 맵이라고도 불리는 첫 번째 맵은 다음과 같이 작성됩니다.

$({displaystyle z_{n+1}={M}z_{n}=\gamma z_{n}\left(1-z_{n}\오른쪽)})$

$여기$서$$z(\$displaystyle$ z$)$는 복소 변수이고,$display$(\displaystyle$\display)$는 복소 파라미터입니다.두 번째 일반적인 형태는

${\displaystyle w_{n+1}=smathcal {M}w_{n}=w_{n}^{2}-\mu .}$

$여기$서 w$\displaystyle$w는$$ 복소 $변수$이고$$μ\$displaystyle\mu$는 복소 파라미터입니다.$변수{\displaystyle }$z 및 $w{\displaystyle }${$displaystyle$$$w$}$는 다음 방정식과 관련이 있습니다.

${\displaystyle z=-{\frac {w}{\frac}}+{\frac {1}{2}}$

$파라미터{\displaystyle }$ ${\(\displaystyle\$displaystyle$\mu$)와$$μ(\$displaystyle\mu)$는 방정식으로 관련지어집니다.

${{displaystyle \mu =\leftfrac {1}{2}\right}^{2}-{\frac {1}{4}}\display,\displays\pm = 1\pm {1+4\mu}}}.}$

$\mu {\displaystyle }$$${\$displaystyle \mu}$는 ${\displaystyle \to 2}$ -${\$ {\$displaystyle \to 2-display$ 치환에서는 불변합니다.

만델브로트와 채워진 줄리아 세트

M$(\displaystyle {M$에는 2개의 평면이 관련지어져 있습니다.이 중 하나인 z$($$또는{\displaystyle }$ w$(\displaystyle$ w$)$ 평면은$$$M{\displaystyle }$(\$displaystyle {M})$이 이 평면을 자체 전송하므로 $매핑{\displaystyle \mathcal{}}$ 평면이라고 불립니다.$다른$ 하나는 컨트롤 플레인이라고 $불립니다.$

M$(\$을 $반복적$으로 적용했을 때 맵플레인에서 발생하는 동작의 성질은 컨트롤 플레인 내의$\mu {\displaystyle }$(\$displaystyle\gamma)($$또는{\displaystyle }$μ\$displaystyle\mu$의 위치에 따라 달라집니다.채워진 Julia 세트는 M$\$style$\display\mathcal$ {$M$의 무한 반복 적용 하에서 이미지가 경계로 유지되는 매핑 평면 내의 모든 점으로 구성됩니다.Mandelbrot 세트는 매핑 평면에서 연결된 채워진 Julia 세트가 연결되도록 제어면의 해당 점으로 구성됩니다.

그림 1은$\mu {\displaystyle }$ {\$displaystyle \gamma}$가 제어 파라미터일 때의 Mandelbrot 세트, 그림 2는$$μ {\$displaystyle \mu}$가 제어 파라미터일 $때$의 Mandelbrot 세트입니다.z$(\displaystyle$$)$와 w(\$displaystyle$ w$)$는 서로 아핀 변환(선형 변환과 변환)이기 $때문$에 채워진 Julia$$$세트$는 $z$(\$displaystyle$ z$)$$또는$ w(\$displaystyle$ w$)$ 평면에서 거의 동일하게 보입니다.

두아디토끼

^{[검증 필요]}

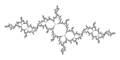
Douady 토끼는 그림 1(위)과 같이 Mandelbrot 세트의 관점에서 가장 쉽게 설명된다.이 그림에서 Mandelbrot 세트는 적어도 멀리서 볼 때 새싹이 있는 두 개의 연속 장치 디스크로 나타납니다.오른쪽 디스크의 1시와 5시 위치에 새싹을 배치하거나 왼쪽 디스크의 7시와 11시 위치에 새싹을 배치하십시오.$【{$ $displaystyle \gamma }$가 이 4개의 새싹 중 하나일 때, 지도 평면에 설정된 관련 채워진 줄리아는 Douady 토끼입니다.$이러한 {\$ {\$displaystyle$\displaystyle$$$\}$의$값$에 대해$$M {\$displaystyle$ {M$}$은 ${\displaystyle \mathrm{z}}$ $=$ 0($표시 스타일$ z$=$$0})$ 및$$ 기타 1개의 불안정한(제어) $고정점$으로서 z $=$ ${\displaystyle \mathrm{=}}$ $display$ {\$displaystyle$z=\infty$}$을 매력적인 고정점으로 갖는 $것$을 알 수 있다.$게다가$ 지도 $($스타일 {M$}}^{3})$에는 3개의 매력적인 고정점이 있습니다.Douady의 토끼는 3개의 매력적인 $고정점{\displaystyle {}_{}}$ $($ 스타일 $z_{1$ $($ 스타일 $z_{2$ $($ 스타일 $z_{3$})와$$ 그 매력적인 분지로 구성되어 있습니다.

예를 들어, 그림 3은 디스크 오른쪽의 5시 싹에 있는 $지점$인 ${\displaystyle =}$ D ${\displaystyle \mathrm{d}}$ D${\displaystyle \mathrm{}{}_{}}$ 2.${\displaystyle 55268}$-${\displaystyle 0.959456}$ \$displaystyle$ \$displate =\displate$ _${D$} $= 2.55268-0.959456i$일 때 Z$평면$에 있는 Douady의 토끼를 보여줍니다.이 $값$인 ${\$ {\$displaystyle$$\$displaystyle$}$의 경우 맵$M$의 $고정점{\displaystyle }$ ${\displaystyle \mathrm{z}}$ $=$ 0(\$displaystyle$ $z$$=$$0)$ 및$$ $z{\displaystyle }$ ${\displaystyle \mathrm{=}}$ .${\displaystyle 656747}$ $-$.${\displaystyle \mathrm{129015}}$i(\$displaystyle$ z=.$656747-129015i$의 값을 나타냅니다.$({$주기 3 고정점이라고도 함)의 3개의 매력적인 고정점에는 위치가 있습니다.

$(\displaystyle z^{1}=0.49997032420304-(1.221880225696050\times 10^{-6})i20204;}{\;}{\mathrm {(빨간색)}}}}$

${\displaystyle z^{2}=0.63816999974373-(0.239864000011495)i20;}{\;}{\mathrm {(녹색)}}}}$

${\displaystyle z^{3}=0.799901291393262-(0.107547238170383)i420;}{\;}{\mathrm {(노란색)}}}.}$

$빨간색{\displaystyle {\mathcal{}}^{}}$$,$ 녹색 및 노란색 포인트는 M ${\displaystyle 3^{}}$의$$B${\displaystyle (\backslash }$$displaystyle$ {$M}^{3$ $분지{\displaystyle }$ ${\displaystyle {}^{}}$${\displaystyle (\backslash }$$displaystyle$B${\displaystyle {}^{}{displaystyle\mathrm{}}^{}}$ B$($$z$$^{$$2$}) 및 $B(\$$(z^{3})$에 각각 있습니다.흰색 포인트는$$M$\displaystyle\mathcal$ {M$}$의$$$B$ $분지$에 있습니다.

이 고정점에 대한 M$(\displaystyle$ {$M})$의 작용은 관계에 의해 주어진다.

${\displaystyle {M}}z^{1}=z^{2}$

$({displaystyle {M}}z^{2}=z^{3})$

$(\displaystyle {M}}z^{3}=z^{1}).}$

이러한 관계에 대응한 결과가 있습니다.

${\displaystyle {M}B(z^{1})=B(z^{2}){\;}{\mathrm {or}}{\;}{\mathrm {red}}\displayeq {mathrm {green}}}}$

${\displaystyle {M}B(z^{2})=B(z^{3}){\;}{\mathrm {or}}{\;}{\mathrm {green}}\displayeq {\mathrm {y}}{\;}}$

${\displaystyle {M}B(z^{3})=B(z^{1}){\;}{\mathrm {or}{\;}{\mathrm {nellow}}\mathrm {red}}}.$

분지 경계에 있는 놀라운 프랙탈 구조에 주목하세요.

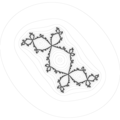
두 번째 예로서 $그림{\displaystyle }$ 4는 ${\displaystyle =}$ 2${\displaystyle }$- ${\displaystyle {\gamma }_{}}$ D${\displaystyle \mathrm{=}}$ - .${\displaystyle 559268\mathrm{}}$+ .${\displaystyle \mathrm{959456}}$i (\$displaystyle \display$ $=$ $2$- \ $displaystyle$ _ {D} $=$ - $55268$+ $959456i$$)$일 때 Douady 토끼를 나타내고 있습니다($앞서 설명$한 바와 $같이{\displaystyle }$).토끼는 이제 페이지에 대칭적으로 앉아 있습니다.주기 - 3개의 고정점은 다음 위치에 있습니다.

$(\displaystyle z^{1}=0.5003730675024+(6.968273875812428\times 10^{-6})i2020;}{\;}({\mathrm {red}}),}$

$\displaystyle z^{2}=-0.1640169999969259+(0.239864000061970)i420;}{\;}({\mathrm {green}}}),}$

${\displaystyle z^{3}=-0.238618870661709-(0.264884797354373)i20;}{\;}({\mathrm {yellow}}}),}$

M$(\$style {\$mathcal {M})$ $자체$의 역방향 고정점은 z ${\displaystyle =}$ $(\style$ z$=$$0$$)$ $및{\displaystyle }$ z ${\displaystyle =1.450795}$+${\displaystyle 0.7825835}$ $(\displaystyle$ z= 1.$450795+0.7825835i$에 $있습니다{\displaystyle }$.왼쪽의 3대 로브는 고정점 ${\displaystyle {z\mathrm{}}^{}}$ 1$({$ z$^{1$ $z{\displaystyle {}^{}}$$$2({$displaystyle$ z$^{2$ ${\displaystyle {z\mathrm{}}^{}}$3({$displaystyle$ z$^{3$로 구성되어 있으며, 오른쪽의 3대 로브는 $고정점{\displaystyle }$ z ${\displaystyle =}$$({$$displaystyle$ z$=0$에서 만난다.원점근처에 대한 M$(\$ {$M})$의 효과는 ${\displaystyle \arg }$δ$(\displaystyle$ \displaystyle(\displaystyle \$display(\displaystyle$$))$의 원점근점에 대한 반시계방향 회전 또는 매우 ${\displaystyle {\mathrm{가까운}}^{}}$ 120$$${\displaystyle \mathrm{\delta }}$(\$displaystyle$ 120$^{\d$에 이어${\displaystyle \mathrm{}=1253}$의 배율로 스케일링(확장)하는 것으로 나타난다.${\displaystyle 8}$(\$displaystyle$ \ displaystyle =$1.1402538$)

토끼 꼬임 문제

1980년대 초, 허바드는 이른바 꼬인 토끼 문제를 제기했습니다.다항식 분류 문제입니다.목표는 보통 공식에 의해 주어지지 않는 복소수 함수의 서스턴 동등성 유형을 결정하는 것이다(이것을 위상 다항식이라고 한다)."^[13]

• 3주기와 주기적인 분기점이 있는 위상 2차 다항식이 주어졌을 때, 어느 2차 다항식에 해당합니까?
• "뒤틀린 토끼"의 당량 클래스를 결정한다. 즉, "토끼" 다항식의 콤포지타이며, 덴강의 귀 둘레에 n제곱이 있다.

그것은 원래 Laurent Bartholdi와 Volodymyr Nekrashevych에^[14] 의해 반복된 단색 그룹을 사용하여 해결되었다.

사후 임계점의 수가 임의로 큰 경우의 트위스트 래빗 문제의 일반화도^[15] 해결된다.

「 」를 참조해 주세요.

• 용곡선
• 허먼 링
• 시겔 원반

레퍼런스

외부 링크

• Weisstein, Eric W. "Douady Rabbit Fractal". MathWorld.
• Dragt, A. "Lie Methods for Nonlinear Dynamics with Applications to Accelerator Physics".
• Adrien Douady: La dynamique du lapin (1996년) - 유튜브 동영상

이 문서에는 Creative Commons Attribution/Share-Alike License에 따라 라이센스가 부여된 PlanetMath의 Douady Rabbit의 자료가 포함되어 있습니다.