정규 4폴리토프

큐빅은 6개의 볼록한 일반 4폴리토프 중 하나이다.

수학에서 규칙적인 4 폴리토프는 규칙적인 4차원 폴리토프다.그것들은 3차원의 일반 다면체와 2차원의 일반 다면체의 4차원 유사점이다.

볼록은 6개, 별정규 4폴리탑은 10개로 총 16개가 주어진다.

역사

볼록한 규칙적인 4폴리토프는 19세기 중반 스위스 수학자 루드비히 슐레플리에 의해 처음 묘사되었다.^[1]그는 정확히 6개의 그러한 수치가 있다는 것을 발견했다.

슐래플리는 또한 그랜드 120 셀, 그레이트 스틸 120 셀, 그랜드 600 셀, 그리고 그레이트 스틸 120 셀의 네 개의 일반 별 4 폴리탑을 발견했다.그는 세포나 꼭지점 수치에서 오일러 특성이 실패한 형태를 허용하지 않기 때문에 나머지 6개를 건너뛰었다.F − E + V = 2).그것은 위대한 도데카헤드론 {5}과 같은 세포와 꼭지점 수치를 제외한다.5/2} 및 작은 스티커 도데카헤드론 { 5/2,5}.

에드먼드 헤스(1843~1903)는 1883년 독일 책 아인레이퉁의 다이스 레레 폰 데어 쿠겔테이룽 미트(Die Lehre von der Kougeltiung mitder Berücksichtung ihung ihrer Anwendung auf die Theory der Gleichfichechen und der.

건설

규칙적인 4-폴리토프 $\{p,q,r\}$ { $\{p,q,r\}$ , $\{p,q,r\}$ , r $}$ {\ $displaystyle \{p,q,$ r\}}의 존재는 세포를 형성하는 일반 $\{p,q\},\{q,r\}$ 다면체 { $\{p,q\},\{q,r\}$ , ${\$ displaystyle $\{p,q,r\}}$ 의 존재에 의해 제약된다 $\{p,q,r\}$ .

\sin {\frac {\pi }{p}\sin {\frac {\pi }{r}}}\coses {\frac {\pi }{q}}}}}

세포가 만나 닫힌 3각형을 이루도록 하기 위해서입니다.

기술된 6개의 볼록한 부분과 10개의 별 다극체가 이러한 제약조건에 대한 유일한 해결책이다.

유효한 세포 {p,q}과 정점 그림 {q,r}을(를) 가지고 있고 이음계 시험을 통과하지만 유한한 수치를 생성하지 못하는 비콘벡스 Schléfli 기호 {p,q,r}이(가) 4개 있다: {3,5/2,3}, {4,3,4}, {5,2,3,4}, {5/2}.

정규 볼록 4폴리톱

정규 볼록 4폴리탑은 플라토닉 고형분의 4차원 아날로그와 2차원 볼록 정규 폴리곤이다.

6개 중 5개는 해당 5개의 플라토닉 고형물과 분명히 유사하다.6번째, 24-셀은 3차원에서는 정규 아날로그가 없다.단, 불규칙 고형물 한 쌍인 큐옥타헤드론과 그 이중인 롬빅 도데헤드론이 존재하는데, 이는 24세포와 부분적인 유사(보완적인 방법으로)이다.그들은 함께 24-셀의 3차원 아날로그로 볼 수 있다.

각각의 볼록한 규칙적인 4-폴리토프는 동일한 종류와 크기의 플라토닉 고체인 3차원 세포 세트로 경계를 이룬다.이들은 각자의 얼굴(대면)을 따라 규칙적으로 함께 장착된다.

특성.

이들의 3차원 아날로그처럼 볼록한 4폴리토프는 같은 반지름에 대한 4차원 함량(하이퍼볼륨)의 척도로 크기별로 자연스레 주문할 수 있다.순서에서 각각의 큰 폴리토프는 동일한 반경 내에 더 많은 내용을^[2] 포함하면서 이전보다 더 둥글다.4심플렉스(5셀)는 한계 최소 케이스, 120셀은 최대 케이스다.복잡성(구성 행렬 또는 정점 수를 비교하여 측정)은 동일한 순서를 따른다.

정규 볼록 4폴리톱
대칭군	A을₄	B₄		F₄	H₄
이름	5세포 초계면체 5점	16 셀 초옥타헤드론 8점	8셀 하이퍼큐브 16점	24셀 24점	600셀 고이코사면체 120점	120 셀 초도면체 600점
슐레플리 기호	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
콕시터 미러
그래프
정점	5	8	16	24	120	600
가장자리	10	24	32	96	720	1200
얼굴	삼각형 10개	삼각형 32개	24제곱	96개의 삼각형	1200 삼각형	펜타곤 720개
세포	5 사면체	사면체 16	8입방체	24옥타헤드라	사면체 600개	도데카헤드라로120번길
토리	5축면체 1개	2 8수면체	2 4시 30분	4 6옥타이드론	30수면체 20	10도면체 12개
새겨진	120 셀에 120	16 셀 1	16-182로 2	3 8시 30분	5 24 x 5	600 x 2의 5 x 2
그레이트 폴리곤		2㎛/2제곱×3	직사각형 4개/2개 x 3개	4㎛/3헥사곤 x 4	12㎛/5데카곤 x 6	50 //15 도데카곤 x 4
페트리 폴리곤	1오각형	팔각형 1개	옥타곤 2개	도데카곤 2개	30-gon 4개	30-gon 20
이소크라인 폴리곤		1 {8/2}=2{4} x {8/2}=2{4}	2 {8/2}=2{4} x {8/2}=2{4}	2 {12/2}=2{6} x {12/6}=6{2}	4 {30/2}=2{15} x 30{0}	20 {30/2}=2{15} x 30{0}
긴 반지름	1	1	1	1	1	1
모서리 길이	√5/√2 ≈ 1.581	√2 ≈ 1.414	1	1	1/ϕ ≈ 0.618	1/√2ϕ² ≈ 0.270
단반경	1/4	1/2	1/2	√2/2 ≈ 0.707	1 - (√2/2√3φ)² ≈ 0.936	1 - (1/2√3φ)² ≈ 0.968
면적	10•√8/3 ≈ 9.428	32•√3/4 ≈ 13.856	24	96•√3/4 ≈ 41.569	1200•√3/8φ² ≈ 99.238	720•25+10√5/8φ⁴ ≈ 621.9
볼륨	5•5√5/24 ≈ 2.329	16•1/3 ≈ 5.333	8	24•√2/3 ≈ 11.314	600•1/3√8φ³ ≈ 16.693	120•2 + φ/2√8φ³ ≈ 18.118
4-내용	√5/24•(√5/2)⁴ ≈ 0.146	2/3 ≈ 0.667	1	2	쇼트∙볼/4 ≈ 3.907	쇼트∙볼/4 ≈ 4.385

다음 표에는 6개의 볼록형 일반 4폴리탑의 몇 가지 특성이 나열되어 있다.이들 4-폴리탑의 대칭 그룹은 모두 Coxeter 그룹이며, 이 기사에서 설명한 표기법으로 제시되어 있다.그룹 이름 뒤에 오는 번호는 그룹 순서다.

이름	가족	슐레플리 콕시터	V	E	F	C	Vert. 무화과를 만들다	이중	대칭군
5세포 펜타코론 펜타토프 사오백스	n-제곱스 (가족_n)	{3,3,3}	5	10	10 {3}	5 {3,3}	{3,3}	자화자기의	A₄ [3,3,3]	120
16 셀 헥사데카초론 4인조	무정통의 (B가족_n)	{3,3,4}	8	24	32 {3}	16 {3,3}	{3,4}	8셀	B₄ [4,3,3]	384
8셀 옥타코론 큐테릭트 4시 15분	하이퍼큐브 n-11 (B가족_n)	{4,3,3}	16	32	24 {4}	8 {4,3}	{3,3}	16 셀	B₄ [4,3,3]	384
24셀 이코시테트라초론 옥타플렉스 다옥타헤드론 (pO)	F_n 패밀리	{3,4,3}	24	96	96 {3}	24 {3,4}	{4,3}	자화자기의	F₄ [3,4,3]	1152
600셀 헥사코시코론 테트라플렉스 다면체 (pT)	n-자갈 폴리토프 (H_n 패밀리)	{3,3,5}	120	720	1200 {3}	600 {3,3}	{3,5}	120 셀	H₄ [5,3,3]	14400
120 셀 헤카토노사초론 도데카콘타초론 도데카플렉스 다면체 (pD)	n-자갈 폴리토프 (H_n 패밀리)	{5,3,3}	600	1200	720 {5}	120 {5,3}	{3,3}	600셀	H₄ [5,3,3]	14400

존 콘웨이는 심플렉스, 직교, 테세락트, 옥타플렉스 또는 폴리옥타헤드론(pO), 테트라플렉스 또는 폴리테트라헤드론(pT), 도데카플렉스 또는 폴리도데카헤드론(pD) 등의 명칭을 주창했다.^[3]

Norman Johnson advocated the names n-cell, or pentachoron, hexadecachoron, tesseract or octachoron, icositetrachoron, hexacosichoron, and hecatonicosachoron (or dodecacontachoron), coining the term polychoron being a 4D analogy to the 3D polyhedron, and 2D polygon, expressed from the Greek roots poly ("many") and choros ("room" or "space").^[4]^[5]

모든 4-폴리탑에 대한 오일러 특성은 0이며, 오일러의 다면 공식의 4차원 아날로그가 있다.

N_{0}-N_{1}+N_{2}-N_{3}=0\,

여기서 N은_k 폴리토프의 k-faces 수를 나타낸다(정점수는 0면, 가장자리는 1면 등).

주어진 4 폴리토프의 위상은 베티 번호와 비틀림 계수로 정의된다.^[6]

구성으로

일반 4 폴리토프는 구성 요소 요소의 카운트를 포함하는 구성 매트릭스로 완전히 설명될 수 있다.행과 열은 꼭지점, 가장자리, 면 및 셀에 해당한다.대각선 숫자(왼쪽 위부터 오른쪽 아래까지)는 각 원소가 전체 4폴리토프에서 얼마나 많이 발생하는지 알려준다.비대각 숫자는 열의 요소 중 몇 개가 열의 요소 안에서 또는 열 요소에서 발생하는지를 나타낸다.예를 들어, 각 가장자리에는 2개의 정점이 있으며(각 가장자리는 2개의 정점을 가지고 있다), 어떤 규칙적인 4폴리토프에서 2개의 셀이 각 얼굴(각 얼굴은 2개의 셀에 속한다)에서 만난다.듀얼 폴리토프의 구성은 매트릭스를 180도 회전시켜 얻을 수 있다는 점에 유의하십시오.^[7]^[8]

5세포 {3,3,3}	16 셀 {3,3,4}	큐테릭트 {4,3,3}	24셀 {3,4,3}	600셀 {3,3,5}	120 셀 {5,3,3}
${\displaysty}{bmatrix}{\\n4&6&4\\\2&10&3&3\\3&10&2\4&4&5\end{bmatrix}}}}$	${\displaysty}{bmatrix}{\\\n8&6&12&8\\2&24&4\\3&3&32&2\\4&4&16\end{bmatrix}}}}}$	${\displaysty}{bmatrix}{\\\\n3\2&n4&4&4&3\\4&3\4&24&2\\8&12&8\end{bmatrix}}}}}}$	${\displaystyle{bmatrix}{\\\nf}24&#2&#8&12&6\\2&963\\3&96&2\\\6&12&8&24\end{bmatrix}}}}}$	${\displaysty}{bmatrix}{\\\\120&30&20\\2<3<3<2\4&4&600\end{bmatrix}}}}}$	${\displaystyle {\displaysty}{bmatrix}{\\nf}600&4&6&4\\\2&n3\5&n3\\5&nf&n3\\\2\20&30&120&120&120\end{bmatrix}}}}}}}\end{bmatrix}}}}}}}}}}}}}}}}}}?$

시각화

다음 표는 이러한 4-폴리토프의 일부 2차원 투영을 보여준다.기타 다양한 시각화는 아래 외부 링크에서 확인할 수 있다.Coxeter-Dynkin 다이어그램 그래프도 Schléfli 기호 아래에 제시되어 있다.

A₄ = [3,3,3]	B₄ = [4,3,3]		F₄ = [3,4,3]	H₄ = [5,3,3]
5세포	16 셀	8셀	24셀	600셀	120 셀
{3,3,3}	{3,3,4}	{4,3,3}	{3,4,3}	{3,3,5}	{5,3,3}

입체 3D 직교 투영
사면체 봉투 (셀/셀렉스 중심)	세제곱 봉투 (세포 중심)	큐빅 봉투 (세포 중심)	큐폭타헤드랄 봉투 (세포 중심)	펜타키스 이코시다데코헤드랄 봉투 (제곱 중심)	잘린 롬빅 삼권면체 봉투 (세포 중심)
와이어프레임 슐레겔 도표(내성 투영)
세포 중심	세포 중심	세포 중심	세포 중심	꼭지점 중심	세포 중심
와이어프레임 입체 투영(3-sphere)

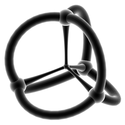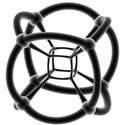정규성(슐라펠리-헤스) 4폴리토페스

이것은 4차원 별무늬 다상체 사이의 관계를 보여준다.2개의 볼록한 형태와 10개의 별 모양은 3D로 큐옥타헤드론의 정점으로 볼 수 있다.^[9]

8개 사이의 관계의 하위 집합은 120 셀의 다면체(pD)로부터 형성된다.세 가지 작업 {a,g,s}은(는) 입방체 프레임워크를 정의하는 동시 실행 가능한 작업이다.수직 위치에는 7개의 밀도가 있으며, 2개의 이중 형태가 동일한 밀도를 가진다.

슐레플리-헤스 4-폴리토페스는 10개의 규칙적인 자기 교차 항성 폴리초라(4차원 폴리토페스)로 이루어진 완전한 세트다.^[10]그들은 그들의 발견자들을 기리기 위해 이름 지어졌다: Ludwig Schléfli와 Edmund Hess.각각은 숫자 중 하나가 5/2인 슐레플리 기호 {p,q,r}로 표현된다.따라서 그것들은 일반적인 비콘벡스 케플러-푸인소트 다면체와 유사하며, 차례로 펜타그램과 유사하다.

이름

그들의 이름은 존 콘웨이가 케플러-푸인소트 다면체의 이름을 확장하면서 붙여준 것인데, 케플리-푸인소트 다면체의 이름을 확장시켰으며, 그는 기품 있고 위대한 수식어를 덧붙인다.Conway는 다음과 같은 운영 정의를 제공했다.

스텔레이션 – 동일한 선에서 가장자리를 긴 가장자리로 대체한다(예: 펜타그램으로 펜타곤 스텔링).
증조 – 동일한 평면에서 큰 면으로 얼굴을 대체한다. (예: 증조된 이코사면체는 증조하여 큰 이코사면체가 된다.)
재배열 – 동일한 3-공간에서 큰 셀로 대체한다. (예: 600 셀은 그랜드 600 셀로 확장됨)

John Conway names the 10 forms from 3 regular celled 4-polytopes: pT=polytetrahedron {3,3,5} (a tetrahedral 600-cell), pI=polyicoshedron {3,5,5/2} (an icosahedral 120-cell), and pD=polydodecahedron {5,3,3} (a dodecahedral 120-cell), with prefix modifiers: g, a, and s for great, (ag)grand, and stellated.마지막 절개, 거대한 절개된 다면체에는 모두 숨이 막힐 정도로 들어있다.

대칭

10개의 모든 폴리초라에는 [3,3,5] (H₄) 육각 대칭이 있다.그것들은 6개의 관련 Goursat tetrahedra 합리 순서 대칭 그룹에서 생성된다: [3,5/2], [5,5/2,5], [5,5,5/2], [5,5/2], [3,5/2].

각 그룹에는 2개의 정규 별-폴리초라가 있는데, 2개의 그룹이 있고, 2개의 그룹이 있고, 1개의 그룹만 있다.그래서 10개의 일반 별 폴리초라 중 4개의 듀얼페어와 2개의 셀프듀얼 형태가 있다.

특성.

참고:

120셀과 600셀의 정점과 일치하는 두 개의 독특한 정점 배열이 있다.
와이어프레임 직교 투영으로 표시되는 4개의 고유한 가장자리 배치가 있다.
고형(얼굴색) 직교 투영으로 표시된 7가지 고유한 얼굴 배치가 있다.

세포(폴리헤드라), 얼굴(폴리곤), 다각형 가장자리 형상 및 다면 정점 형상은 Schléfli 기호로 식별된다.

이름 콘웨이(약칭)	슐레플리 콕시터	C {p, q}	F {p}	E {r}	V {q, r}	밀스.	χ
이코사헤드랄120세포 다면체(pI)	{3,5,5/2}	120 {3,5}	1200 {3}	720 {5/2}	120 {5,5/2}	4	480
소형강관 120셀 Stelled polydodecahedron (spD)	{5/2,5,3}	120 {5/2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	−480
그레이트 120 셀 다면체(gPD)	{5,5/2,5}	120 {5,5/2}	720 {5}	720 {5}	120 {5/2,5}	6	0
그랜드 120 셀 다면체(apdodecahedron, apD)	{5,3,5/2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5/2}	20	0
그레이트 스틸 120 셀 대절단 폴리도데카헤드론(gspD)	{5/2,3,5}	120 {5/2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0
그랜드 스틸 120 셀 대절단 폴리도데카헤드론(aspD)	{5/2,5,5/2}	120 {5/2,5}	720 {5/2}	720 {5/2}	120 {5,5/2}	66	0
대그랜드 120 셀 거대 다면체(ground polydodecahedron, gapD)	{5,5/2,3}	120 {5,5/2}	720 {5}	1200 {3}	120 {5/2,3}	76	−480
대이심면 120세포 다면체(gPI)	{3,5/2,5}	120 {3,5/2}	1200 {3}	720 {5}	120 {5/2,5}	76	480
그랜드 600 셀 대 폴리테트라헤드론(apT)	{3,3,5/2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5/2}	191	0
대그랜드 스티어 120셀 대망원형 폴리도데카헤드론(gaskdecaderon, gaspD)	{5/2,3,3}	120 {5/2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0

참고 항목

일반 폴리토프
일반 폴리토페스 목록
무한 일반 4폴리 토플:
- 일반 유클리드 벌집 1개: {4,3,4}
- 소형 일반 쌍곡선 허니컴 4개: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
- 11개의 파라콤팩트 정규 쌍곡선 벌집: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,3}, {3,3}, {3,6}, {6,3,3}, {6,4,4},4,4},4,4},5},6,6}.
추상 일반 4폴리 토픽:
- 11셀 {3,5,3}
- 57셀 {5,3,5}
이 6가지 정규 양식으로 구성된 균일한 4 폴리토프 균일 4 폴리토프 패밀리.
플라토닉 고체
케플러-푸인소트 다면체 - 일반 항성 다면체
항성 폴리곤 - 일반 항성 폴리곤
4칸짜리
5칸 반
6시 반경

참조

인용구

^ Coxeter 1973, 페이지 141, §7-x. 역사적 발언.
^ Coxeter 1973, 페이지 292–293, 표 I(ii):4차원의 16개의 일반 폴리토페 {p,q,r}: [각 4-폴리토프의 20개 메트릭스를 에지 길이 단위로 제공하는 귀중한 표.단위 반지름의 폴리토페스를 비교하기 위해 대수적으로 변환해야 한다.]
^ Conway, Burgiel & Goodman-Strass 2008, 26장.하이더 스틸
^ "콘벡스 및 추상 폴리토페스", 프로그램 및 추상화, MIT, 2005
^ Johnson, Norman W. (2018). "§ 11.5 Spherical Coxeter groups". Geometries and Transformations. Cambridge University Press. pp. 246–. ISBN 978-1-107-10340-5.
^ Richeson, David S. (2012). "23. Henri Poincaré and the Ascendancy of Topology". Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. pp. 256–. ISBN 978-0-691-15457-2.
^ Coxeter 1973, § 1.8 구성
^ Coxeter, 복합 일반 폴리토페스, 페이지 117
^ Conway, Burgiel & Goodman-Strass 2008, 페이지 406, 그림 26.2
^ Coxeter, Star polytopes 및 Schléfli 함수 f{α,β,³) 페이지 122 2.슐라플리-헤스 다층동물

참고 문헌 목록

Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover.
Coxeter, H.S.M. (1969). Introduction to Geometry (2nd ed.). Wiley. ISBN 0-471-50458-0.
D.M.Y. Sommerville (2020) [1930]. "X. The Regular Polytopes". Introduction to the Geometry of n Dimensions. Courier Dover. pp. 159–192. ISBN 978-0-486-84248-6.
Conway, John H.; Burgiel, Heidi; Goodman-Strass, Chaim (2008). "26. Regular Star-polytopes". The Symmetries of Things. pp. 404–8. ISBN 978-1-56881-220-5.
Hess, Edmund (1883). "Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder".
Hess, Edmund (1885). "Uber die regulären Polytope höherer Art". Sitzungsber Gesells Beförderung Gesammten Naturwiss Marburg: 31–57.
Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
- (10 용지)
Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. ISBN 978-0-521-39490-1.
McMullen, Peter; Schulte, Egon (2002). "Abstract Regular Polytopes" (PDF).

외부 링크

Weisstein, Eric W. "Regular polychoron". MathWorld.
조나단 바우어스, 16개의 정규 4폴리토프
일반 4D 폴리토프 접기
Polytope Images의 카탈로그 4폴리토페의 입체 투영 모음입니다.
균일한 폴리토페스의 카탈로그
치수 4차원에 대한 2시간 필름(모든 일반 4폴리탑의 입체 투영 포함)
Olshevsky, George. "Hecatonicosachoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Olshevsky, George. "Hexacosichoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Olshevsky, George. "Stellation". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Olshevsky, George. "Greatening". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Olshevsky, George. "Aggrandizement". Glossary for Hyperspace. Archived from the original on 4 February 2007.
레굴레 폴리토페
더 레귤러 스타 폴리초라
과포화합물

[FOOTNOTECoxeter1973141§7-x._Historical_remarks-1] Coxeter 1973, 페이지 141, §7-x. 역사적 발언.

[FOOTNOTECoxeter1973292–293Table_I(ii):_The_sixteen_regular_polytopes_{''p,q,r''}_in_four_dimensions-2] Coxeter 1973, 페이지 292–293, 표 I(ii):4차원의 16개의 일반 폴리토페 {p,q,r}: [각 4-폴리토프의 20개 메트릭스를 에지 길이 단위로 제공하는 귀중한 표.단위 반지름의 폴리토페스를 비교하기 위해 대수적으로 변환해야 한다.]

[3] Conway, Burgiel & Goodman-Strass 2008, 26장.하이더 스틸

[4] "콘벡스 및 추상 폴리토페스", 프로그램 및 추상화, MIT, 2005

[5] Johnson, Norman W. (2018). "§ 11.5 Spherical Coxeter groups". Geometries and Transformations. Cambridge University Press. pp. 246–. ISBN 978-1-107-10340-5.

[richeson-6] Richeson, David S. (2012). "23. Henri Poincaré and the Ascendancy of Topology". Euler's Gem: The Polyhedron Formula and the Birth of Topology. Princeton University Press. pp. 256–. ISBN 978-0-691-15457-2.

[7] Coxeter 1973, § 1.8 구성

[8] Coxeter, 복합 일반 폴리토페스, 페이지 117

[9] Conway, Burgiel & Goodman-Strass 2008, 페이지 406, 그림 26.2

[10] Coxeter, Star polytopes 및 Schléfli 함수 f{α,β,³) 페이지 122 2.슐라플리-헤스 다층동물

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

Search