몬티 홀 문제
Monty Hall problem몬티홀 문제는 미국의 텔레비전 게임쇼 렛츠 어 딜(Let's Make a Deal)을 느슨하게 기반으로 한 확률 퍼즐 형태의 브레인 티저로 원래 진행자인 몬티 홀의 이름을 따서 명명된 것이다.이 문제는 원래 스티브 셀빈이 1975년 미국 통계학자에게 보낸 편지에서 제기되었다.[1][2]그것은 독자 크레이그 F의 질문으로 유명해졌다.휘태커가 1990년 퍼레이드 잡지에 실린 마릴린 보스 사반트의 "마릴린에게 물어봐" 칼럼에서 인용한 편지는 다음과 같다.[3]
게임 쇼에 참가하면 세 개의 문을 선택할 수 있다고 가정합시다.한 문 뒤에는 차가 있고, 다른 문 뒤에는 염소들이 있다.문을 따면 1번이라고 하고, 문 뒤에 무엇이 있는지 아는 주인이 다른 문을 열고, 염소가 있는 3번이라고 말한다.그리고 나서 그는 너에게 "2번 문을 고르고 싶니?"라고 말했어. 너의 선택을 바꾸는 것이 너에게 유리하니?
참가자가 다른 문으로 갈아타야 한다는 것이 Vos Savant의 반응이었다.[3]표준 가정 하에서 스위칭 전략에는 2/3분의 2의 승산이 있는 반면, 초기 선택과 함께 남아 있는 전략은 1/3 확률에 불과하다.
선수가 먼저 선택했을 때, 선택되지 않은 문들 중 하나 뒤에 차가 있을 확률이 2/3이다.숙주가 한 마리의 염소 뒤에 염소를 드러낸 후에 이 확률은 변하지 않는다.주최자가 2개의 언초센 도어에 대한 정보를 제공할 때(그 중 한 개는 뒤에 차가 없는 것으로 확인), 2/3 확률의 미초센 도어는 참가자가 처음에 선택한 도어 뒤에 차가 있을 확률의 1/3 확률과는 반대로, 미초센 도어에 놓여 있다.
주어진 확률은 주최자와 참가자가 자신의 문을 선택하는 방법에 대한 구체적인 가정에 따라 달라진다.중요한 통찰력은 이러한 표준 조건 하에서 1번 도어가 플레이어에 의해 선택되었을 때 경기 초반에 사용되었던 것보다 2번과 3번 도어에 대한 정보가 더 많다는 것이다: 진행자의 의도적인 행동은 그가 제거하려고 선택하지 않은 도어에 가치를 더하지만, 원래 참가자가 선택한 도어에 가치를 더한다.또 다른 통찰은 첫 번째 행동이 이전의 정보를 사용하고 후자는 그렇지 않기 때문에, 문을 바꾸는 것은 두 개의 남은 문 사이에서 무작위로 선택하는 것과는 다른 행동이라는 것이다.설명한 것과 다른 호스트의 다른 가능한 동작은 다른 추가 정보를 노출하거나 전혀 노출하지 않으며 다른 확률을 산출할 수 있다.
Vos Savant's 칼럼의 많은 독자들은 교체가 유익하다고 믿기를 거부했고 그녀의 설명을 거부했다.이 문제가 퍼레이드에 등장한 후, 거의 1,000명의 박사들을 포함한 약 1만 명의 독자들이 이 잡지에 썼는데, 그들 대부분은 vos Savant를 틀렸다고 부른다.[4]설명, 시뮬레이션, 형식적인 수학적 증명서가 주어졌을 때에도, 많은 사람들은 여전히 전환이 최선의 전략이라는 것을 받아들이지 않았다.[5]역사상 가장 다작의 수학자 중 한 명인 폴 에르디스는 vos Savant의 예측 결과를 보여주는 컴퓨터 시뮬레이션이 보여질 때까지 납득이 가지 않았다.[6]
문제는 진부한 유형의 역설이다. 왜냐하면 Vos Savant의 해결책은 너무나 반직관적이어서 불합리하게 보일 수 있지만 그럼에도 불구하고 명백하게 사실이기 때문이다.몬티 홀 문제는 수학적으로 이전의 세 죄수 문제와 훨씬 오래된 베르트랑의 박스 역설과 밀접하게 관련되어 있다.
역설
스티브 셀빈은 1975년 미국 통계학자에게 게임쇼 렛츠 어 딜(Let's Make a Deal)을 바탕으로 문제를 기술하는 편지를 썼고,[1] 후속 편지에서 이를 "몬티 홀 문제"로 더빙했다.[2]문제는 수학적으로 1959년[7] 사이언티픽 아메리칸의 마틴 가드너의 '수학적 게임' 칼럼에 기술된 '세 명의 죄수 문제'와 가드너의 저서 '아하 고트차'에 기술된 '세 개의 조개 문제'에 해당한다.[8]
표준 가정
표준 가정 하에서 전환 후 승산이 2/3이다.이 해결책의 핵심은 호스트의 행동이다.퍼레이드 버전의 모호함은 호스트의 프로토콜을 명시적으로 정의하지 않는다.그러나 휘태커의 질문과 함께 인쇄된 Marilyn vos Savant의[5] 솔루션은 다음과[3] 같이 진행자의 역할을 명시적으로 정의하고[1] 있다.
- 주최자는 항상 참가자가 선택하지 않은 문을 열어야 한다.[9]
- 주인은 항상 문을 열어 염소를 드러내야 하고, 절대로 차를 드러내지 말아야 한다.
- 주최자는 항상 원래 선택한 문과 닫힌 나머지 문 사이를 전환할 기회를 제공해야 한다.
이러한 가정 중 어떤 것이든 변동될 경우, 아래 절에서 상세히 기술한 바와 같이 도어를 전환함으로써 승산이 바뀔 수 있다.또한 일반적으로 차는 처음에 문 뒤에 무작위로 숨겨져 있고, 만약 선수가 처음에 차를 고른다면, 주최자가 어떤 염소치기 문을 열 것인지를 선택하는 것은 무작위로 추정된다.[10]독립적이든 포괄적이든 어떤 저자는 플레이어의 초기 선택도 무작위라고 가정한다.[1]
간단한 솔루션
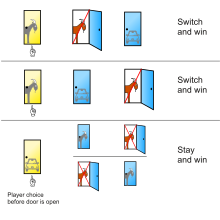
Vos Savant가 퍼레이드에서 제시한 해결책은 세 개의 문 뒤에 한 대의 차와 두 마리의 염소가 가능한 세 가지 배열과 각각의 경우에 처음 1번 문을 선택한 후 머무르거나 교체한 결과를 보여준다.[11]
1번 문 뒤 2번 문 뒤 3번 문 뒤 1번 출입문에 머문 경우 결과 도어로 전환할 경우 나타나는 결과 염소 염소 자동차 염소를 이기다 윈즈 카 염소 자동차 염소 염소를 이기다 윈즈 카 자동차 염소 염소 윈즈 카 염소를 이기다
초기의 선택에 머무르는 선수가 똑같이 가능성이 있는 가능성 중 세 가지 중 한 가지에만 승리하는 반면, 전환한 선수는 세 가지 중 두 가지에 승리한다.
직관적인 설명은 참가자가 처음에 염소를 고르면(3도어 중 2개) 다른 염소를 고를 수 없기 때문에 다른 염소를 고를 수 없기 때문에 다른 염소를 고를 수 없기 때문에 교환하여 우승하는 반면, 참가자가 처음에 차를 고르면(3도어 중 1개) 교환으로 우승하지 않는다는 것이다.[12]따라서 스위칭 전략을 사용하는 경우, 승패는 참가자가 처음에 염소(2/3 확률)를 선택했는지 아니면 자동차(2/3 확률)를 선택했는지에 따라서만 결정된다.숙주가 이어서 한 개의 언초센 문에서 염소를 드러낸다는 사실은 초기 확률에 대해 아무것도 바꾸지 않는다.[13]
대부분의 사람들은 문이 열리지 않은 두 개와 차가 한 대 있기 때문에 개폐는 중요하지 않으며, 50/50 선택이라고 결론짓는다.주최자가 임의로 문을 연다면 이는 사실이지만 그렇지 않다. 열린 문은 플레이어의 초기 선택에 따라 달라지기 때문에 독립성에 대한 가정은 유지되지 않는다.호스트가 문을 열기 전에 자동차가 각 문 뒤에 있을 확률은 1/3이다.자동차가 1번 도어 뒤에 있는 경우, 호스트는 2번 도어 또는 3번 도어를 열 수 있으므로, 자동차가 1번 도어 뒤에 있고 3번 도어를 열 확률은 1/3 × 1/2 = 1/6이다.자동차가 2번 도어(그리고 플레이어가 1번 도어를 선택한 경우) 뒤에 있는 경우, 호스트는 3번 도어를 열어야 하므로, 자동차가 2번 도어 뒤에 있고 3번 도어를 열 확률은 1/3 × 1 = 1/3이다.주최자가 3번 도어를 여는 경우는 이 밖에 없기 때문에 플레이어가 1번 도어를 선택하고 3번 도어를 열면 1번 도어에 비해 2번 도어의 뒤에 있을 가능성이 높다.핵심은 차량이 2번 문 뒤에 있을 경우 호스트가 3번 문을 열어야 하지만 1번 문 뒤에 있을 경우 호스트가 어느 한쪽 문을 열 수 있다는 것이다.
그 해결책을 이해하는 또 다른 방법은 두 개의 원래 언코젠 문을 함께 고려하는 것이다.[14][15][16][17][18]세실 아담스의 말처럼,[14] "몬티는 사실상 한 문을 지키거나 다른 두 개의 문을 가질 수 있다고 말하고 있다."차의 위치를 알고 있는 몬티가 염소를 노출할 것이 확실하기 때문에 이 문들 중 하나를 열어도 2/3 가능성은 변하지 않았다.그러므로 주최자가 문을 연 후 플레이어의 선택은 주최자가 플레이어에게 원래 선택한 도어에서 나머지 두 도어의 세트로 전환하는 옵션을 제공했을 때와 다르지 않다.이 경우의 스위치는 플레이어가 자동차를 선택할 확률을 2/3로 명확하게 해준다.
키스 데블린의 말대로 [15]"문을 열어서 몬티는 참가자에게 '당신이 선택하지 않은 문이 두 개 있는데, 그 중 한 개 뒤에 상이 있을 확률은 2/3이다.상이 어디 있는지 내 지식을 이용하여 그 두 개의 문 중 하나를 열어 상을 숨기지 않는다는 것을 보여줌으로써 너를 돕겠다.이제 이 추가 정보를 이용할 수 있다.당신이 선택한 문 A는 3분의 1의 승자가 될 가능성이 있다.나는 그것을 바꾸지 않았다.그러나 C문을 제거함으로써 B문이 상을 숨길 확률은 3분의 2라는 것을 보여 주었다.'
Vos Savant는 솔루션이 3개보다 100만 개의 문으로 더 직관적일 것이라고 제안한다.[3]이 경우 뒤에 염소가 있는 문은 99만9999개, 상이 있는 문은 1개다.플레이어가 문을 고른 후, 진행자는 나머지 문 중 99만9998개를 연다.평균 100만 번 중 99만9999번이면 나머지 문에는 상금이 들어간다.직관적으로, 플레이어는 백만 개의 문이 주어진 상황에서, 처음에 적절한 문을 고른 것이 얼마나 그럴 가능성이 있는지 물어봐야 한다.Stibel 등은[18] Monty Hall 문제 동안 작업 메모리 수요에 세금이 부과되며 이로 인해 사람들이 그들의 선택을 똑같이 가능한 두 가지 옵션으로 "축소"하도록 강요할 것이라고 제안했다.그들은 선택의 폭을 7개(7도어) 이상으로 늘리면 사람들이 더 자주 바꾸는 경향이 있다고 보고하지만, 대부분의 참가자들은 여전히 50:50으로 성공 확률을 잘못 판단하고 있다.
Vos Savant와 언론의 열광
"네가 날려버렸고, 크게 날려버렸어!네가 여기서 일하는 기본 원리를 이해하는 데 어려움을 겪는 것 같으니, 내가 설명해 줄게.사회자가 염소를 공개한 후, 당신은 이제 1대 2로 맞힐 가능성이 있다.선택을 바꾸든 말든 승산은 같다.이 나라에는 수학적 문맹이 충분하며, 세계 최고의 IQ를 더 전파할 필요가 없다.수치심!"
Scott Smith, Ph.D. University of Florida[3]
Vos Savant는 Monty Hall 문제에 대한 그녀의 첫 칼럼에서 플레이어가 전환해야 한다고 썼다.[3]그녀는 독자들로부터 수천 통의 편지를 받았다. 이 편지들 중 대부분은 박사학위를 가진 독자들로부터, 그녀의 대답에 동의하지 않았다.1990-1991년 동안, 퍼레이드에 실린 그녀의 칼럼들 중 세 개가 더 그 역설에 바쳐졌다.[19]Vos Savant's 칼럼의 독자들이 보낸 수많은 편지들의 예는 <몬티 홀 딜레마>에서 제시되고 논의된다. 인지적 환상 파 탁월함.[20]
토론은 다른 장소(예: 세실 아담스의 "스트레이트 도프[14]" 신문 칼럼)에서 재연되었고 뉴욕타임스 등 주요 신문에 보도되었다.[4]
그녀는 자신의[8] 대답을 명확히 하기 위해 "너희들은 외면하고, 나는 세 개의 껍질 중 하나에 완두콩을 넣는다"고 설명했다.그럼 조개껍질 위에 손가락을 올려달라고 부탁한다.당신의 선택이 완두콩을 포함할 확률은 1/3이다, 동의하십니까?그리고 남은 두 개에서 빈 껍데기만 들어 올린다.네가 무엇을 선택했든 나는 이것을 할 수 있고(그리고 의지할 수 있기 때문에, 우리는 네 손가락 아래의 껍질에 있는 확률을 우리가 수정할 수 있도록 허락하는 것을 아무것도 배우지 못했어."그녀는 또한 세 장의 카드를 가지고 비슷한 시뮬레이션을 제안했다.
Vos Savant는 일부 독자들이 주최자가 항상 염소를 노출시켜야 한다고 가정해야 한다는 것을 깨닫지 못해 혼란이 발생했지만, 그녀의 거의 모든 특파원들은 문제 가정을 정확히 이해했고, 여전히 처음에 Vos Savant의 대답("스위치")이 틀렸다고 확신했다고 논평했다.
혼란과 비판
혼돈의 원인
몬티 홀 문제를 처음 제시했을 때, 압도적으로 많은 사람들이 각각의 문이 동일한 확률을 가지고 있다고 가정하고 전환은 중요하지 않다고 결론짓는다.[9]한 연구에서 228개 과목 중 13%만이 전환을 선택했다.[21]그의 책에서 권력 논리적 Thinking,[22]인지 심리학자 마시모 Piattelli Palmarini[그것]의:"어떤 다른 통계 퍼즐 너무[그리고]심지어 노벨 물리학자들 체계적으로, 그리고 그들이 그곳에 그들은 인쇄에 사용하는 사람들 리를 제안합니다 비난할 준비가 되었다 주장하는 그 오답을 모든 시간 모든 사람들이 장난에 가깝다고 쓴다.ght비둘기들이 이 문제에 반복적으로 노출되는 것은 그들이 인간과 달리 항상 바꾸는 법을 빨리 배운다는 것을 보여준다.[23]
문제의 대부분의 진술, 특히 퍼레이드에 나오는 진술은 실제 게임 쇼의 규칙과 일치하지 않으며 진행자의 행동을 완전히 명시하거나 자동차의 위치를 무작위로 선택한다는 것을 명시하지 않는다.[21][4][24]Krauss와 Wang은 명시적으로 언급되지 않더라도 사람들이 표준적인 가정을 한다고 추측한다.[25]
비록 이러한 문제들이 수학적으로 중요하지만, 심지어 이러한 요소들을 통제할 때에도, 거의 모든 사람들은 여전히 미개봉된 두 개의 문 각각이 동일한 확률을 가지고 있다고 생각하고 전환은 중요하지 않다고 결론짓는다.[9]이 "평등 확률" 가정은 뿌리 깊은 직관이다.[26]사람들은 확률이 있든 없든 간에 존재하는 많은 미지의 것에 고르게 분포되어 있다고 강하게 생각하는 경향이 있다.[27]
그 문제는 계속해서 인지심리학자들의 관심을 끌고 있다.대다수의 전형적인 행동, 즉 전환이 아닌 행동은 심리학 문헌에서 알려진 현상에 의해 다음과 같이 설명될 수 있다.
- 이미 "소유"된 문에서 이미 선택한 문(이미 "소유"된)의 당첨 확률을 과대평가하는 경향이 있는 기부 효과.[28]
- 사람들이 이미 그들이 만든 문 선택을 고수하기를 선호하는 [29]현상적 편견.
- 누락의 오류 대 커미션 효과의 오류,[30] 즉 다른 모든 것이 동일하다면 사람들은 행동(스위치)과 반대로 행동하지 않음(스테이)을 통해 오류를 범하는 것을 선호한다.
실험 증거는 이러한 설명이 확률 직관에 의존하지 않는 그럴듯한 설명임을 확인시켜 준다.[31][32]또 다른 가능성은 사람들의 직관이 단순히 문제의 교과서적인 버전을 다루는 것이 아니라 실제 게임쇼 설정으로 다루는 것이다.[33]그곳에서 쇼 마스터는 처음에 자동차가 있는 문이 선택되었을 경우에만 다른 문을 열어 기만적인 행동을 할 가능성이 있다.반을 기만적으로 연기하는 쇼 마스터는 "같은 확률"로 바꾸자는 제안을 받을 경우에 승산이 있는 기회를 수정한다.
간단한 해결책에 대한 비판
이미 언급한 바와 같이, 많은 입문 확률 교과서를 포함한 확률 분야의 대부분의 출처는 참가자가 처음에 1번 도어를 선택하고 3번 도어를 여는 점, 다양한 방법으로 유도하고 유도하는 방법, 다양한 방법 등을 고려할 때, 자동차가 1번 도어 뒤에 있고 2번 도어가 1/3과 2/3(1/2와 1/2이 아닌)이라는 조건부 확률을 보여줌으로써 문제를 해결한다.이 결과가 이전 하위 섹션에 제시되었다는 것을 이해한다.
이러한 출처들 중에는 대중적으로 제시된 "단순한" 해결책들을 명백히 비판하고 있는 몇몇 사람들이 있는데, 이러한 해결책들은 "틀림없지만..."이라고 말한다.흔들리는"[34] 또는 "위장된 문제를 해결"[35]하거나, "위장"하거나,[36] "위장하고 오해의 소지가 있는"[37] 또는 "거짓말"이 아니다.[38]
사샤 볼로크(2015년)는 "문 1의 확률은 1/3이었고, 그 어떤 것도 바꿀 수 없다"는 식의 설명은 자동적으로 수상하다: 확률은 세상에 대한 우리의 무지를 표현하는 것이고, 새로운 정보는 우리의 무지의 정도를 바꿀 수 있다"[39]고 썼다.
어떤 사람들은 이러한 해결책들이 약간 다른 질문에 대답한다고 말한다. 한 표현은 "전환할 계획이 있는지 문이 열리기 전에 발표해야 한다"[40]이다.
간단한 해결책은 다양한 방법으로 전환하기로 결정한 참가자가 2/3 확률로 자동차를 우승할 것이며, 따라서 플레이어가 "항상 전환"과 "항상 유지" 중 하나를 미리 선택해야 한다면 전환이 승리 전략이라는 것을 보여준다.다만 플레이어가 1번 도어를 선택하고 3번 도어를 개최자가 열었다고 볼 때 항상 스위칭으로 승리할 확률은 논리적으로 구분되는 개념이다.한 정보원이 말하듯이, "[이 질문들]의 구별은 많은 것을 혼란스럽게 하는 것 같다."[38]이 두 개 확률이 서로 다른 숫자 값을 갖도록 문제를 변화시킴으로써 이 두 개 확률이 다르다는 사실을 알 수 있다.예를 들어, 참가자가 몬티가 모든 법적 대안 중에서 두 번째 문을 무작위로 고르지 않고 대신 두 개의 문을 잃을 때 몬티가 오른쪽 문을 열 것이라고 가정하자.이 상황에서 다음의 두 질문은 서로 다른 답을 가지고 있다.
- 항상 바꿔서 차를 탈 확률이 얼마나 될까?
- 선수가 1번 도어를 선택하고 3번 도어를 연 경우, 우승 확률이 얼마나 되는가?
첫 번째 질문에 대한 답은 "단순한" 해결책에서 올바르게 나타난 바와 같이 2/3이다.그러나 두 번째 질문에 대한 대답은 이제 다르다: 호스트가 3번 도어를 열었을 때, 자동차가 1번 도어나 2번 도어 뒤에 있을 조건부 확률은 1/2이다.몬티가 가장 오른쪽 문을 선호하는 것은 자동차가 1번 문(원래 확률 1/3로) 뒤에 있거나 2번 문(원래 확률 1/3로) 뒤에 있을 경우 3번 문을 여는 것을 의미하기 때문이다.이 변형에 대해, 두 질문은 다른 답을 산출한다.단, 각 문 뒤에 차가 있는 초기 확률이 1/3인 한, 개폐에 의한 승산이 항상 1/2 이상이기 때문에, 절대로 참가자가 개폐하는 것이 불리하지 않다.[38]
모건 외 연구진에서는 4명의 대학교수들이 <아메리칸 통계학>에 vos Savant가 올바른 조언을 했지만 잘못된 주장을 했다고 주장하는 기사를 실었다.[38]이들은 1번 문과 3번 문이 열린 플레이어의 초기 선택으로 인해 2번 문 뒤에서 차의 가능성을 묻는 질문이 나왔다고 믿었고, 이 기회가 주어진 진행자의 결정 과정에 따라 1/2과 1/1 사이라는 것을 보여주었다.결정이 완전히 무작위화 될 때에만 기회는 2/3이다.
초청된 논평과[41] 편집자에게 보낸 후속 편지에서,[42][43][44][45] 모건 외는 다른 사람들에 의해 비판된 몇몇 작가들의 지지를 받았다; 각각의 경우, 모건 외 에 의한 반응은 The American Statisticsian에 있는 편지나 논평과 함께 발표된다.특히 vos Savant는 자신을 강력하게 변호했다.모건 외 알은 vos Savant에[42] 대한 그들의 반응에서 vos Savant가 여전히 그들 자신의 요점에 실제로 반응하지 않았다고 불평했다.나중에 Hogbin과 Nijdam,[45]에 대한 그들의 반응에서 그들은 그들이 그 숙주 그리고 뒸을 때 선택의 여지가 있나 완전히 무작위로 개최하는 방향을 택한다고 생각하는 것은 당연했다 합의했습니다가 갖고 있는 동일(즉, 조건부 그리고 그는 그의 선택을 해야 합니다의 선수는 이런 상황) 옮김으로써 승자의 조건부 확률잘 지내니lue, 2/3은 스위칭에 의한 무조건적인 우승 확률로 (즉, 가능한 모든 상황에 대한 평균)이러한 평등은 이미 벨(1992)에 의해 강조되었는데, 벨(1992)은 모건 외가 수학적으로 관여된 해법이 통계학자에게만 어필할 것이라고 제안한 반면, 대칭의 경우 조건적 해법과 무조건적 해법의 동등성은 직관적으로 명백했다.
문헌에서는 퍼레이드에서 제시된 바와 같이 vos Savant의 문제 제형이 첫 번째 질문을 던지는 것인지 두 번째 질문을 던지는 것인지, 그리고 이러한 차이가 유의미한 것인지에 대해 의견이 분분하다.[46]베렌즈 교수는 "두 분석이 모두 맞는지 주의깊게 검토해야 한다"고 결론짓는데, 그렇다고 해서 두 분석이 동일하다는 뜻은 아니다.[47]원작과 함께 기고가 게재된 [38]모건 외 연구원의 논문에 대한 몇몇 비평가들은 저자들이 Vos Savant의 표현을 바꾸고 그녀의 의도를 잘못 해석했다고 비판했다.[46]한 토론자(윌리엄 벨)는 (표준 조건 하에서) 주최자가 어느 문을 열었는지에 대해 명시적으로 언급하는지는 자신이 전환해야 하는지 여부와 무관하다고 봤다.
단순한 해법 중에서, 우리가 오즈의 개념과 베이지스의 정리를 이용한 접근에 대한 논의에서 보았듯이, "결합된 문 해법"은 조건부 해법에 가장 가깝다.이미 알려진 정보를 공개하는 것은 확률에 영향을 미치지 않는다는 뿌리 깊은 직관에 바탕을 두고 있다.그러나 사회자가 염소를 보여주기 위해 두 개의 언초센 문 중 하나를 열 수 있다는 것을 아는 것은 특정한 문을 여는 것이 처음에 선택한 문 뒤에 자동차가 있을 확률에 영향을 미치지 않는다는 것을 의미하지는 않는다.요점은 숙주가 문을 열고 염소를 드러낼 것을 미리 알고 있지만, 어느 문을 열지는 알 수 없다는 것이다.호스트가 염소를 숨기는 문 사이에 균일하게 (표준 해석에서와 같이) 선택한다면, 이 확률은 실제로 변하지 않지만, 만약 호스트가 그러한 문들 사이에서 무작위로 선택할 수 있다면, 호스트가 여는 특정 문은 추가 정보를 노출한다.주최자는 언제나 염소를 드러내는 문을 열 수 있고 (문제의 표준 해석에서) 처음에 선택한 문 뒤에 차가 있을 확률은 변하지 않지만, 후자가 사실이라는 것은 전자 때문은 아니다.진행자의 행동이 처음에 선택한 사람의 뒤에 자동차가 있을 가능성에 영향을 줄 수 없다는 주장에 기초한 해결책은 설득력이 있어 보이지만, 만약 그가 선택할 수 있다면, 진행자의 두 가지 선택이 똑같이 가능성이 있지 않다면, 그 주장은 단순히 사실이 아니다.[48]그러므로 그 주장은 정당화될 필요가 있다. 명분이 주어지지 않으면 해결책은 기껏해야 불완전하다.답은 정확할 수 있지만 그것을 정당화하기 위해 사용되는 추리는 결함이 있다.
조건부 확률 및 기타 솔루션을 사용한 솔루션
위의 간단한 해결책은 전환 전략을 가진 선수가 전반적인 확률 2/3으로, 즉 호스트가 어떤 문을 열었는지 고려하지 않고 자동차를 이긴다는 것을 보여준다.[49][13]이와는 대조적으로 확률 분야의 대부분의 출처는 참가자가 처음에 1번 도어를 선택하고 3번 도어를 여는 경우, 차량이 1번 도어 뒤에 있고 2번 도어가 1/3과 2/3인 조건부 확률을 계산한다.[2][38][50][35][13][49][36]이 섹션의 해결책은 플레이어가 도어 1을 선택하고 호스트가 도어 3을 연 경우만 고려한다.
간단한 솔루션 개선
만약 호스트에게 선택권이 주어졌을 때 임의로 문을 연다고 가정한다면, 호스트가 어느 문을 여는지는 우리에게 자동차가 1번 문 뒤에 있는지 여부에 대한 정보를 전혀 주지 않는다.간단한 해결책에서, 우리는 이미 자동차가 1번 문 뒤에 있을 확률, 즉 플레이어가 처음에 선택한 문이 3분의 1이라는 것을 관찰했다.더구나 주최자는 분명히 (다른) 문을 열 것이기 때문에 (어떤 문이 지정되지 않았는지) 문을 여는 것은 이것을 바꾸지 않는다. 1/3은 주최자가 2번 문을 선택한 것과 3번 문을 택한 것을 볼 때 차가 1번 문 뒤에 있을 가능성이 평균적인 확률이어야 한다. 왜냐하면 이 두 가지 가능성밖에 없기 때문이다.그러나 이 두 가지 확률은 같다.따라서 둘 다 1/3과 같다.[38]이는 플레이어가 처음에 이 문을 선택했고, 주최자가 3번 문을 열었다는 점을 감안하면 1번 문 뒤에 차가 있을 확률은 1/3이고, 이어 플레이어가 1번 문을 선택했고, 주최자가 3번 문을 열었다는 점을 볼 때 2번 문 뒤에 차가 있을 확률은 2/3이라는 것을 보여준다.분석은 또한 항상 전환함으로써 달성된 2/3의 전체적인 성공률은 개선될 수 없다는 것을 보여주며, 이미 직감적으로 명백했을 수 있는 것을 강조한다: 플레이어가 마주한 선택은 처음에 선택한 문 사이의 선택이고, 호스트가 닫은 다른 문은 이 문들의 구체적인 숫자는 무관하다는 것이다.
직접 계산에 의한 조건부 확률
정의에 따르면, 처음에 참가자가 1번 도어를 선택하고 3번 도어를 여는 경우에 승산이 있는 조건부 확률은 "차가 2번 도어에 뒤에 있고 3번 도어를 여는" 이벤트의 확률을 "3번 도어를 여는 호스트" 확률로 나눈 값이다.이러한 확률은 아래의 조건부 확률표 또는 오른쪽에 보이는 동등한 의사결정 트리를 참고하여 결정할 수 있다.[50][13][49]스위칭으로 우승할 수 있는 조건부 확률은 1/3/1/3 + 1/6로 2/3이다.[2]
아래의 조건부 확률표는 선수가 처음에 1번 도어를 선택한 300개의 경우를 평균적으로 차 위치와 주최자가 열 수 있는 도어의 선택에 따라 어떻게 분할되는지를 보여준다.
베이즈 정리
확률론 분야의 많은 확률 텍스트 책과 기사는 베이즈의 정리의 공식적인 적용을 통해 조건부 확률 해답을 도출하는데, 그 중에서도 길과[51] 헨제의 책이다.[52]흔히 베이즈의 지배라고 불리는 베이즈의 정리의 승산 형식을 사용하면 그러한 파생을 더욱 투명하게 만든다.[34][53]
처음에 자동차는 세 개의 문 중 어느 하나에나 뒤쪽에 있을 가능성이 있다: 1번 문, 2번 문, 3번 문에서의 확률은 1:1이다.이것은 선수가 독립적으로 1번 문을 선택한 후에도 그대로 남아 있다.베이스의 규칙에 따르면, 숙주가 3번 도어를 연다고 가정했을 때, 자동차의 위치에 대한 후발 확률은 베이즈 요인 또는 우도에 곱한 이전의 승산과 같으며, 이는 정의상 (호스트가 3번 도어를 여는 확률)이 고려된 각 가설 하에서 새로운 정보 조각(호스트가 3번 도어를 여는 확률)의 확률이다.지금은 처음에 1번 도어를 선택했기 때문에 1번 도어에 차가 있으면 호스트가 3번 도어를 열 확률은 50%이고 2번 도어에 차가 있으면 100%이고 3번 도어에 뒤가 있으면 0%이다.따라서 베이지 인수는 비율 1/2 : 1 : 0 또는 동등하게 1 : 2 : 0으로 구성되며, 이전 승산은 1 : 1 : 1이었다.따라서 후발 확률은 베이즈 인자 1 : 2 : 0과 같아진다.주최자가 3번 도어를 연 것을 감안하면 차가 3번 도어의 뒤에 있을 확률은 0이며, 1번 도어에 비해 2번 도어의 뒤에 있을 확률은 2배이다.
리차드 길은[54] 사회자가 3번 문을 열 가능성을 다음과 같이 분석한다.차가 1번 문 뒤에 있지 않다는 점을 감안하면 2번 문이나 3번 문 뒤에 있을 가능성도 똑같이 있다.따라서 호스트가 3번 문을 열 확률은 50%이다.차가 1번 문 뒤에 있다는 점을 감안하면, 호스트가 3번 문을 열 확률도 50%나 된다. 왜냐하면, 호스트가 선택권이 있을 때, 어느 쪽이든 똑같이 선택할 가능성이 있기 때문이다.따라서 차가 1번 문 뒤에 있든 없든 호스트가 3번 문을 열 확률은 50%이다."호스트 오픈 도어 3" 정보는 차량이 1번 도어 뒤에 있는지 여부에 대한 베이즈 계수 또는 1:1의 우도 비율을 제공한다.처음에, 차를 숨긴 1번 문이 2:1이었다.따라서 차를 숨기는 도어 1에 대한 후방 확률은 이전 확률인 2: 1과 동일하게 유지된다.
즉, 사회자에 의해 열리는 정보(도어 2나 도어 3?)는 자동차가 1번 도어 뒤에 있는지 여부에 대한 정보를 전혀 드러내지 않고, 이것이 바로 간단한 해결책의 지지자들에 의해 직관적으로 명백하다고 주장되는 것이나, "확실히 사실, 대칭에 의해" 수학적 증거의 관용어를 사용하는 것이다.[44]
직접계산
차량이 i번 도어 뒤에 있음을 나타내는 Ci 이벤트를 고려하고, 플레이어의 선택에 있어 Xi 값을, 그리고 문을 여는 호스트에게 Hi 값을 부여한다.플레이어는 처음에 도어 i = 1, C = X1을 선택하고 호스트는 도어 i = 3, C = H3을 연다.
이 경우 다음을 수행하십시오.
P(H3 X1) = 1/2 왜냐하면 이 식은 어떤 Ci에도 의존하지 않고 X1에만 의존하기 때문이다.So, in this particular expression, the choosing of the host does not depend on where the car is, and there's only two remaining doors once X1 is chosen (for instance, P(H1 X1) = 0); and P(Ci,Xi) = P(Ci)P(Xi) because Ci and Xi are independent events (the player does not know where the car is in order to make a choice).
그 후, 플레이어가 처음에 1번 도어를 선택하고, 호스트가 3번 도어를 열면, 우리는 스위칭에 의한 조건부 우승 확률을 다음과 같이 증명한다.
베이지족의 규칙으로 볼 때, 우리는 P(A,B) = P(A B)P(B) = P(B)P(A)를 알고 있다.이 논리를 여러 사건(예: A, B, C)으로 확장하면 다음과 같은 조건부 확률 계산을 단순화하는 도구로서 교차로 확률을 계산하기 위해 {A, B, C}의 서로 다른 하위 집합을 가지고 놀 수 있다는 것을 알 수 있다.
우리의 경우 P(H3 C2,X1)가 1이라는 것을 알고 있기 때문에 우리는 운이 좋다.
전략적 우위 솔루션
다시 날레부프로 돌아가면 몬티 홀 문제는 게임 이론과 결정 이론에 관한 문헌에서도 많이 연구되고 있으며, 몇몇 인기 있는 해결책도 이 관점에 해당된다.[55]Vos Savant는 기회가 아니라 결정을 요구한다.그리고 자동차가 어떻게 숨겨져 있는지, 어떻게 문이 열려있는지에 대한 우연한 측면은 알려지지 않았다.이런 관점에서 볼 때, 플레이어가 선택할 수 있는 두 가지 기회가 있다는 것을 기억해야 한다: 첫째, 처음에 어느 문을 선택해야 할지, 둘째, 전환해야 할지 말아야 할지.차가 어떻게 숨겨져 있는지, 진행자가 어떻게 선택을 하는지 모르기 때문에 진행자를 포함한 퀴즈쇼를 진행하는 팀의 행동을 무력화시키는 것이었기에 첫 번째 선택 기회를 활용할 수도 있을 것이다.
Gill에 이어,[56] 참가자의 전략은 두 가지 행동을 포함한다. 즉, 처음에 선택한 문과 주최자가 개폐를 제공하는 문 양쪽 모두에 의존할 수 있는 문 전환(또는 고정)의 결정.예를 들어, 한 참가자의 전략은 "1번 도어를 선택한 다음, 제공된 경우 2번 도어로 전환하고, 제공된 경우 3번 도어로 전환하지 말라"이다.참가자의 12가지 결정론적 전략이 존재한다.
참가자의 전략의 기초적인 비교를 보면, 모든 전략 A에 대해, 그것을 지배하는 또 다른 전략 B가 있다는 것을 알 수 있다.[57]차가 어떻게 숨겨져 있든, 주인이 염소 두 마리 중에서 선택권이 있을 때 어떤 규칙을 쓰든 간에, 만약 A가 승차를 하면 B도 승차를 한다.예를 들어 전략 A는 "1번 문을 따고 나서 항상 그 문을 고수하라"는 전략 B가 지배하고 있다: 1번 문이 문을 가리면 A가 승리하고, 2번 문과 3번 문이 차를 가리킬 때 B가 승리한다.마찬가지로 전략 A는 전략 B "3번 도어를 선택한 후 2번 도어로 전환(제공된 경우)하지만 3번 도어로 전환하지 말라"는 전략 B "3번 도어를 선택한 후 항상 전환한다"가 지배한다.
우위는 참가자가 결정을 내리는 환경에 대한 상당히 일반적인 가정 하에 항상 변화하는 전략들 사이에서 해결책을 모색해야 하는 강력한 이유다.특히 대칭 또는 비대칭 3면 다이(symmetric side die)와 같은 어떤 무작위화 장치에 의해 자동차가 숨겨져 있는 경우, 이 우세는 승산이 최대화된 전략이 세 가지 항상 교환되는 전략 중 하나가 될 것임을 암시한다. 즉, 초기에 가장 가능성이 낮은 도어를 선택한 다음 교환하는 전략이 될 것이다.es 호스트가 어느 문을 바꿀지에 상관없이.
전략적 우위는 몬티 홀 문제를 게임 이론과 연결시킨다.길의 제로섬 게임 설정에서,[56] 비스위치 전략을 버리면, 경기는 다음과 같은 단순한 변형으로 줄어든다. 주최자(또는 TV-팀)는 차를 숨기기 위해 문을 결정하고, 참가자는 두 개의 문(즉, 플레이어의 첫 번째, 명목상, 선택 뒤에 남은 두 개의 문)을 선택한다.그녀가 선택한 두 문 중 한 문 뒤에 차가 있으면 참가자가 이긴다(그리고 그녀의 상대는 진다).
시뮬레이션에 의한 솔루션
스위칭 전략이 표준 가정으로 세 번 중 두 번을 이긴다는 것을 증명하는 간단한 방법은 카드를 가지고 게임을 시뮬레이션하는 것이다.[58][59]일반 갑판에서 나온 세 장의 카드는 세 개의 문을 나타내기 위해 사용된다; 한 장의 '특별한' 카드는 차와 함께 문을 나타내고, 두 장의 다른 카드는 염소 문을 나타낸다.
시뮬레이션은 게임의 여러 라운드를 시뮬레이션하기 위해 여러 번 반복될 수 있다.플레이어는 세 개의 카드 중 하나를 고른 다음, 남은 두 개의 카드를 보면서 '호스트'는 염소 카드를 없앤다.주최자의 손에 남아 있는 카드가 카카드일 경우 이는 전환승으로 기록되고, 주최자가 염소카드를 들고 있을 경우 라운드는 체류승으로 기록된다.이 실험은 여러 라운드에 걸쳐 반복되기 때문에 각 전략에 대해 관측된 승률은 대수의 법칙에 따라 이론적 승리 확률에 근접한 것으로 보인다.
플레이가 반복되면 왜 스위칭이 더 나은 전략인지 더 분명해진다.선수가 자신의 카드를 고른 후, 스위칭이 그 선수의 라운드에서 이길지는 이미 결정되었다.이것이 설득력이 없다면 전체 갑판으로 시뮬레이션이 가능하다.[58][14]이 변종에서 카카드는 52장 중 51장으로 진행자에게 가고, 비카드가 아무리 많이 버려져도 진행자와 함께 지낸다.
변형
몇몇 학술적 저자들이 표준적인 문제로 가정하는 문제의 일반적인 변형은 사회자가 개방할 문을 균일하게 선택해야 한다는 단순화 가정을 만드는 것이 아니라, 그 대신 그가 어떤 다른 전략을 사용한다는 가정을 만든다.특히 이 변종이 플레이어에 대한 항상 스위치 전략의 최적성을 변경하지 않고 증거를 더 많이 포함시키기 때문에 공식화가 권위적인 혼란은 상당한 신랄함을 초래했다.이 변종에서 플레이어는 관찰된 진행자의 선택에 따라 승산이 다를 수 있지만, 어떤 경우든 스위칭에 의한 승산은 적어도 1/2(그리고 1만큼 높을 수 있음)인 반면, 스위칭에 의한 승산은 여전히 정확히 2/3이다.그 변형은 확률론과 게임 이론의 기초를 가르치기 위한 교과서와 기사에 연달아 제시되기도 한다.다른 일반화들도 상당히 많이 연구되었다.
기타 호스트 동작
1990년 퍼레이드에서 발행된 몬티홀 문제의 버전에는 주최자가 항상 다른 문을 열거나, 항상 교환할 수 있는 선택권을 제공하거나, 심지어 자동차가 드러나는 문을 절대 열지 않는다는 내용이 구체적으로 명시되어 있지 않았다.그러나 Vos Savant는 두 번째 후속 칼럼에서 의도된 호스트의 행동이 그녀가 원래 대답으로 준 2/3 확률로 이어질 수 밖에 없다는 것을 분명히 했다."다른 것은 다른 질문이다."[5] "분명히 나의 비평가들은 의도된 시나리오를 이해했다.나는 개인적으로 거의 3천 통의 편지를 읽었고 (수천 통의 추가 편지 중에서) 거의 모든 사람이 단순히 두 가지 옵션이 남아있기 때문에 (또는 그에 상응하는 오류로) 가능성은 반반이라고 주장하는 것을 발견했다.극소수만이 애매성에 대해 의문을 제기했고, 실제로 칼럼에 게재된 글자들은 그 몇 안 되는 글자에 속하지 않았다."[60]어떤 문 뒤에든 임의로 차를 세워놓으면 진행자는 플레이어의 초기 선택과 상관없이 염소를 드러내는 문을 열어야 하고, 두 개의 문이 있다면 어떤 문을 무작위로 열어야 할지를 선택해야 한다.[9]아래 표는 다양한 가능한 호스트 동작과 스위칭 성공에 미치는 영향을 보여준다.
주최자가 준수해야 하는 주어진 다른 규칙 집합 내에서 플레이어의 최선의 전략을 결정하는 것은 게임 이론에서 연구된 문제의 유형이다.예를 들어, 만약 호스트가 플레이어에게 교환 제안을 할 필요가 없다면, 플레이어가 처음에 자동차를 선택한 경우, 호스트가 악의적인지 의심하고 제안을 더 자주 할 수 있다.일반적으로, 이러한 종류의 질문에 대한 답은 호스트의 행동에 대해 만들어진 특정 가정에 따라 달라지며, "호스트를 완전히 무시"에서 "앞면이 나오면 동전을 던져 전환"까지 다양할 수 있다. 아래 표의 마지막 줄을 참조하라.
모건 외 연구원과[38] 길먼은[35] 둘 다 차가 무작위로 (균일하게) 놓여있지만, 만약 선수가 처음에 차를 선택했다면 호스트가 균일하게 무작위로 선택하도록 제약받지 않는 더 일반적인 해결책을 보여주는데, 이것이 바로 그 둘 다 저자의 부인에도 불구하고 퍼레이드에서 문제의 진술을 해석하는 방법이다.둘 다 문제를 다시 풀 때 그 점을 강조하기 위해 퍼레이드 버전의 표현을 바꿨다.그들은 호스트가 0과 1 사이의 값을 갖는 확률 q로 표현되는 선호도를 가진 두 마리의 염소를 노출하는 것 사이에서 선택하는 시나리오를 고려한다.호스트가 임의로 q를 선택하는 경우, 호스트가 어느 문을 여든 간에 2/3 확률로 스위칭이 승리한다.플레이어가 1번 도어를 선택하고 3번 도어에 대한 호스트의 선호도가 q인 경우, 호스트가 3번 도어를 열고 자동차가 2번 도어를 뒤에 있을 확률은 1/3인 반면, 호스트가 3번 도어를 열고 자동차가 1번 도어를 뒤에 있을 확률은 1/3이다.이는 호스트가 3번 도어를 여는 유일한 경우여서 3번 도어를 개폐하여 승산이 있는 조건부 확률은 1/3/1/3 + q로 단순화된다. q는 0과 1 사이에 차이가 날 수 있기 때문에 이 조건부 확률은 1/2과 1/1 사이에 차이가 날 수 있다.이것은 만약 선수가 처음에 자동차를 선택했을 때 호스트가 무작위로 선택하도록 제한하지 않더라도, 플레이어가 스위치를 끄는데 있어 결코 나쁘지 않다는 것을 의미한다.그러나 어느 출처도 플레이어가 q의 가치가 무엇인지 알지 못하기 때문에 플레이어가 vos Savant가 암묵적으로 가정했던 2/3 이외의 확률을 탓할 수 없다고 암시하지 않는다.
| 지정되지 않은 문제에서 발생할 수 있는 호스트 동작 | |
|---|---|
| 호스트 동작 | 결과 |
| 호스트는 문제의 특정 버전에 명시된 대로 행동한다. | 스위칭은 시간의 2/3를 이긴다. (p = q = 1/2로 아래 일반화된 형태의 구체적인 경우) |
| 숙주는 항상 염소를 드러내고 항상 스위치를 제공한다.선택권이 있다면 확률 p(선수의 초기 선택에 따라 달라질 수 있음)가 있는 가장 왼쪽 염소와 확률 q = 1 - p가 있는 가장 오른쪽 문을 선택한다.[38][34][53] | 호스트가 가장 오른쪽 도어를 열면 전환이 확률 1/(1+q)로 승리한다. |
| "지옥에서 온 몬티": 진행자는 플레이어의 초기 선택이 우승문일 때만 전환할 수 있는 옵션을 제공한다.[4] | 바꾸면 항상 화가 난다. |
| "Mind-reading Monty":호스트는 손님이 어쨌든 머물기로 결정되거나 손님이 염소로 전환될 경우에 대비하여 전환 옵션을 제공한다.[33] | 바꾸면 항상 화가 난다. |
| "엔젤리크 몬티":진행자는 플레이어가 잘못 선택한 경우에만 전환할 수 있는 옵션을 제공한다.[61] | 교체가 항상 차를 이긴다. |
| "Monty Fall" 또는 "Ignorant Monty":진행자는 문 뒤에 무엇이 있는지 모르고, 우연히 차를 드러내지 않기 위해 무작위로 문을 연다.[62][34][53] | 교체가 시간의 반을 이긴다. |
| 진행자는 문 뒤에 무엇이 있는지 알고, (선수가 선택하기 전에) 어떤 염소를 드러낼지 무작위로 선택한다.그는 선수의 선택이 자신과 다를 때만 바꿀 수 있는 옵션을 제공한다. | 교체가 시간의 반을 이긴다. |
| 주최자는 문을 열고 참가자가 처음에 차를 고르면 100% 전환하고, 그렇지 않으면 50% 전환 제안을 한다.[9] | 스위칭은 내쉬 평형에서 1/2의 시간을 이긴다. |
| 4단계 2인용 게임-테오레틱.[63][56]그 선수는 사회자가 포함된 쇼 주최자(TV 방송국)와 경기를 하고 있다.첫 번째 단계: 주최자는 문을 선택한다(선수에게 비밀로 하는 선택).두 번째 단계: 플레이어는 예비 문 선택을 한다.세 번째 단계: 호스트가 문을 연다.네 번째 단계: 플레이어가 최종 선택을 한다.그 선수는 차를 타고 싶어하고, TV 방송국은 차를 갖고 싶어 한다.이것은 제로섬 2인칭 게임이다.게임 이론에서 본 노이만의 정리, 양쪽이 완전히 무작위화된 전략을 허용한다면 미니맥스 해결책이나 내시 평형이 존재한다.[9] | 미니맥스 솔루션(Nash 평형): 차는 처음에는 무작위로 균일하게 숨겨져 있다가 나중에 호스트가 차체를 노출시키지 않고 열 수 있는 균일한 무작위 도어를 선택하고 플레이어는 먼저 균일한 무작위 도어를 선택하고 나중에는 항상 닫힌 다른 도어로 전환한다.그의 전략으로, 그 선수는 최소한 2/3의 승률을 가지고 있지만, TV 방송국은 경기를 하고, TV 방송국의 전략으로, 그 선수는 경기를 하지만, TV 방송국은 최대 2/3의 확률로 질 것이다.이 두 가지 전략이 일치한다는 사실(최소 2/3, 최대 2/3)은 미니맥스 솔루션을 형성한다는 것을 증명한다. |
| 이전처럼, 그러나 이제 호스트는 문을 전혀 열지 않는 옵션을 가지고 있다. | 미니맥스 솔루션(Nash 평형): 자동차는 처음에는 무작위로 균일하게 숨겨져 있다가 나중에는 호스트가 절대 문을 열지 않는다; 플레이어는 먼저 무작위로 균일하게 문을 선택하고 나중에는 절대 바꾸지 않는다.플레이어의 전략은 최소 1/3의 승차를 보장한다.TV 방송국의 전략은 기껏해야 1/3의 손해율을 보장한다. |
| 딜 또는 노딜 사례: 진행자가 플레이어에게 문을 열어달라고 한 다음, 차가 드러나지 않은 경우에 대비하여 스위치를 제공한다. | 교체가 시간의 반을 이긴다. |
N도어
D. L. Ferguson (1975 in a letter to Selvin[2]) suggests an N-door generalization of the original problem in which the host opens p losing doors and then offers the player the opportunity to switch; in this variant switching wins with probability .이 확률은 항상 {\보다 크므로 전환은 항상 이점을 가져다 준다.
호스트가 단 하나의 문(= {\1} )만 열어도 플레이어는 모든 경우에 스위치 조작을 하는 것이 좋다.N이 커질수록 이점은 줄어들고 0에 가까워진다.[64]다른 극단에서는, 호스트가 1개(p = N - 2)를 제외하고 모든 실점 도어를 열면 N이 커질수록 이점이 커진다(스위칭으로 승리할 확률은 N - 1/N이며, N이 매우 커질수록 1에 접근한다).
양자 버전
역설의 양자 버전은 양자역학 시스템의 상태로 인코딩된 것처럼 고전적이거나 비양자적인 정보와 양자 정보의 관계에 대한 몇 가지 점을 보여준다.그 공식은 양자 게임 이론에 느슨하게 기초하고 있다.세 개의 문은 양자체제로 대체되어 세 가지 대안이 있는데, 문을 열고 그 뒤를 살피는 것은 특정한 측정을 하는 것으로 해석된다.규칙은 이 언어로 명시될 수 있으며, 다시 한 번 플레이어의 선택은 초기 선택을 고수하거나 다른 "직관적" 옵션으로 변경하는 것이다.후자의 전략은 고전적인 경우와 마찬가지로 두 배의 확률로 나타난다.하지만 쇼호스트가 완전 양자역학적으로 상금의 위치를 무작위로 결정하지 않았다면 플레이어는 훨씬 더 잘할 수 있고 때로는 확실하게 상을 탈 수도 있다.[65][66]
역사
몬티 홀 문제와 관련된 몇 가지 가능성 퍼즐 중 가장 이른 것은 1889년 조셉 버트랜드가 캘컬 데스 확률에서 제기한 베르트랑의 박스 패러독스다.[67]이 퍼즐에는 금화 두 개가 들어 있는 상자, 은화 두 개가 들어 있는 상자, 그리고 각각 한 개가 들어 있는 상자 등 세 개의 상자가 있다.무작위로 상자를 선택하고 우연히 금화가 되는 동전을 무작위로 한 개씩 인출한 뒤, 다른 동전이 금일 확률이 얼마나 되느냐는 것이다.몬티홀 문제에서처럼 직관적인 대답은 1/2이지만, 실제로 가능성은 2/3이다.
1959년 사이언티픽 아메리칸에 있는 마틴 가드너의 수학 게임 칼럼에 실린 세 죄수 문제는 몬티 홀 문제와 맞먹는다.이 문제에는 세 명의 사형수들이 연루되어 있는데, 그들 중 한 명은 비밀리에 사면되도록 선택되었다.수감자 중 한 명은 소장에게 처형될 다른 한 사람의 이름을 말해달라고 애원하며, 이는 자신의 운명에 대한 정보는 밝히지 않지만 사면될 가능성은 1/3에서 1/2로 증가한다고 주장한다.교도소장은 묻는 죄수가 사면될 경우 어떤 이름을 제공할 것인지 결정하기 위해 동전을 던질 의무가 있다.문제는 소장의 대답을 아는 것이 죄수의 사면 가능성을 바꾸느냐 하는 것이다.이 문제는 몬티 홀 문제와 맞먹는다. 이 질문을 하는 죄수는 여전히 사면될 확률이 1/3이지만 그의 이름 없는 동료는 2/3의 가능성이 있다.
스티브 셀빈은 1975년 미국 통계학자에게 보낸 편지에서 몬티 홀 문제를 제기했다.[1][2]첫 번째 편지는 15년 후 퍼레이드에서의 발표와 가까운 버전으로 문제를 제시했다.두 번째는 "몬티 홀 문제"라는 용어의 첫 번째 용어로 보인다.문제는 사실상 게임쇼의 외삽이다.몬티 홀은 흥분을 쌓기 위해 문을 잘못 열었지만, 문을 바꾸는 선택보다는 현금 100달러와 같은, 알려진 적은 상금을 제공했다.몬티 홀은 셀빈에게 다음과 같이 썼다.
그리고 만약 당신이 내 쇼에 출연한다면, 그 규칙은 당신을 위한 것이다. 선택 후에는 트레이드 박스가 없다.
— Monty Hall[68]
3년 후 퍼레이드에 등장한 것과 매우 유사한 문제의 버전은 1987년 경제관점 저널의 퍼즐 섹션에 발표되었다.나중 수학적 경제학의 작가로서, 나일부프는 이 문제를 게임 이론의 단순하고 재미있는 연습으로 본다.[55]
필립 마틴의 1989년 브릿지 투데이 기고문인 '몬티 홀 트랩'은 마틴이 비랜덤 정보를 무작위적으로 취급하는 확률 트랩이라고 부르는 셀빈의 문제를 예로 제시하며, 이를 브릿지 게임의 개념과 연관시킨다.[69]
셀빈 문제의 재작성된 버전은 1990년 9월 퍼레이드의 Marilyn vos Savant's Ask Marilyn 질의 응답란에 나타났다.[3]Vos Savant는 전환이 3분의 2를 차지할 것이라는 정답을 제시했지만, 그녀는 이 잡지가 수학과와 과학과의 레터헤드에 관한 많은 PhDs가 서명한 거의 1,000통의 편지를 포함하여 1만통의 편지를 받아 자신의 해결책이 잘못되었다고 선언했다고 추정했다.[4]압도적인 반응으로 인해, 퍼레이드는 이 문제에 대해 전례 없는 4개의 칼럼을 게재했다.[70]홍보의 결과로 그 문제는 "마릴린과 염소"라는 대체 이름을 얻게 되었다.
1990년 11월, 똑같이 논쟁적인 vos Savant의 기사에 대한 토론이 세실 아담스의 칼럼 "The Straight Dope"[14]에서 이루어졌다.아담스는 처음에 남은 두 개의 문이 각각 둘 중 하나일 가능성이 있다고 잘못 대답했다.한 독자가 아담스의 분석의 수학을 수정하기 위해 편지를 쓴 후, 아담스는 수학적으로 자신이 틀렸다는 것에 동의했다."네가 1번 문을 골라라.이제 당신은 1번 문을 열거나, 2번 문을 열거나, 3번 문을 열거나,후자의 경우 어느 쪽 문 뒤에 있으면 상금을 보관한다.1인 3타수보다는 2타수 3타수 2안타를 하는 게 낫지 않겠는가?생각해보면, 원래의 문제는 기본적으로 똑같은 선택을 제공한다.몬티는 사실상 한 문을 지키거나 다른 두 개의 문을 가질 수 있다고 말하고 있는데, 그 중 한 문은 내가 열어 줄게."애덤스는 퍼레이드 버전이 결정적인 제약조건을 완화하지 않게 만들었고, 그러한 제약조건이 없다면, 반드시 3점 만점에 2점이 될 가능성은 없다고 말했다(예를 들어, 주최자가 항상 문을 연다고 가정하는 것은 합리적이지 않았다).그러나 수많은 독자들은 아담스가 "처음에는 옳았다"고 썼고 정확한 기회는 둘 중 하나라고 주장했다.
퍼레이드 칼럼과 그 반응은 몬티 홀이 직접 인터뷰한 뉴욕 타임즈의 1면 기사 등 언론에서 상당한 관심을 받았다.[4]홀은 기자에게 자동차 키로 시범을 보이고, 렛츠 어 딜에서 실제 게임 플레이가 퍼즐의 규칙과 어떻게 다른지를 설명하면서 문제를 이해했다.이 글에서 홀은 참가자의 심리를 이용해 경기 진행 방식을 통제했기 때문에, 이 프로그램의 실제 게임 플레이에는 이론적 해결책이 적용되지 않았다고 지적했다.그는 "확률이 2점 만점에 1점이라는 전문가들의 주장에 놀라지 않았다"면서 "내가 한 문 뒤에 아무것도 없다는 것을 보여준 후 쇼에서 참가자들이 할 가정과 똑같다"고 말했다."그들은 이제 자기 집 문 위의 승산이 2분의 1까지 올랐다고 생각할 테니까, 내가 아무리 돈을 내놓아도 문을 포기하는 것을 싫어했을 거야.그 문을 열어서 우리는 압력을 가하고 있었다.우리는 그것을 헨리 제임스 치료라고 불렀다.그것은 '나사의 턴'이었다." 홀은 게임쇼 진행자로서 자신이 vos Savant 칼럼의 퍼즐의 규칙을 따를 필요가 없었고, 항상 다른 사람에게 전환의 기회를 허락할 필요가 없다고 명확히 했다(예를 들어, 만일 그것이 패배한 문이라면 그는 즉시 문을 열 수도 있고, 그들에게 패배한 문에서 승리로 전환하지 않을 수 있는 돈을 줄 수도 있다.닝 도어(ning door, 또는 그들이 승리하는 문이 있어야만 전환할 수 있는 기회를 줄 수 있다)그는 "주최자가 항상 문을 열고 스위치를 제시해야 한다면 스위치를 받아야 한다"고 말했다."하지만 만약 그가 스위치를 허용할지 말지를 선택할 수 있다면, 조심해라.주의사항 비우기.모든 것은 그의 기분에 달려 있다고 말했다.
참고 항목
- 신화 버스터즈 에피소드 177 "신화의 바퀴" – 문 고르기
- 선택 제한 원칙 – 계약 브리지에서 베이지안 업데이트의 유사한 적용
확률과 의사결정 이론에서 유사한 퍼즐
참조
- ^ a b c d e 셀빈 1975a.
- ^ a b c d e f 셀빈 1975b.
- ^ a b c d e f g Vos Savant 1990a.
- ^ a b c d e f 티어니 1991.
- ^ a b c Vos Savant 1991a.
- ^ 바즈소니 1999.
- ^ a b 가드너 1959a.
- ^ a b 가드너 1982년
- ^ a b c d e f 뮤저 & 그랜버그 1999.
- ^ a b Krauss & Wang 2003 페이지 9.
- ^ vos Savant 1990b.
- ^ 칼튼 2005 마무리 발언
- ^ a b c d 칼튼 2005.
- ^ a b c d e 아담스 1990.
- ^ a b 데블린 2003.
- ^ 데블린 2005.
- ^ 윌리엄스 2004.
- ^ a b Stibel, Dror & Ben-Zeev 2008.
- ^ vos Savant 2012.
- ^ 그랜버그 2014.
- ^ a b 그랜버그 & 브라운 1995.
- ^ vos Savant 1996, 페이지 15.
- ^ 허브랜슨 & 슈뢰더 2010.
- ^ 버브루겐 2015.
- ^ Krauss & Wang 2003 페이지 10.
- ^ 포크 1992 페이지 202.
- ^ 폭스 & 레바브 2004, 페이지 637.
- ^ Kahneman, Knetch & Thaler 1991.
- ^ 사무엘슨 & 제크하우저 1988.
- ^ 길로비치, 메드벡 & 첸 1995.
- ^ 카이반토, 크롤 & 자빈스키 2014.
- ^ Morone & Fiore 2007.
- ^ a b Enßlin & Westerkamp 2018.
- ^ a b c d 로젠탈 2005a.
- ^ a b c 길먼 1992.
- ^ a b 루카스, 로젠하우스 & 쉐플러 2009.
- ^ 아이젠하우어 2001.
- ^ a b c d e f g h i 모건 외 1991년
- ^ "An "easy" answer to the infamous Monty Hall problem". Washington Post. ISSN 0190-8286. Retrieved 17 June 2021.
- ^ 길먼 1992년, 원작에 강조
- ^ 세이만 1991.
- ^ a b vos Savant 1991c.
- ^ 라오 1992.
- ^ a b 1992년 12월.
- ^ a b 호그빈 & 니즈담 2010.
- ^ a b 로젠하우스 2009.
- ^ 베렌즈 2008.
- ^ 1992년 207쪽 213쪽.
- ^ a b c 그레인스테드 & 스넬 2006, 페이지 137–138.
- ^ a b 1991년 1월.
- ^ Gill 2002.
- ^ 헨즈 2011.
- ^ a b c 로젠탈 2005b.
- ^ Gill 2011a.
- ^ a b 날레부프 1987.
- ^ a b c Gill 2011.
- ^ 그네딘 2011.
- ^ a b c 가드너 1959b.
- ^ Vos Savant 1996, 페이지 8.
- ^ Vos Savant 1996.
- ^ 그랜버그 1996, 페이지 185.
- ^ 그랜버그 & 브라운 1995, 712페이지.
- ^ Gill 2010.
- ^ 그랜버그 1996, 페이지 188.
- ^ 플리트니 앤 애보트 2002.
- ^ 다리아노 외 2002년
- ^ 바바바우 1993.
- ^ 1975년 홀.
- ^ 마틴 1993.
- ^ vos Savant 1996, 페이지 xv.
참고 문헌 목록
- Adams, Cecil (2 November 1990). "On Let's Make a Deal, you pick door #1. Monty opens door #2 – no prize. Do you stay with door #1 or switch to #3?". The Straight Dope. Retrieved 25 July 2005.
- Barbeau, Edward (1993). "Fallacies, Flaws, and Flimflam: The Problem of the Car and Goats". The College Mathematics Journal. 24 (2): 149–154. doi:10.1080/07468342.1993.11973519.
- Behrends, Ehrhard (2008). Five-Minute Mathematics. AMS Bookstore. p. 57. ISBN 978-0-8218-4348-2.
- Bell, William (August 1992). "Comment on Let's make a deal by Morgan et al". The American Statistician. 46 (3): 241. JSTOR 2685225.
- Carlton, Matthew (2005). "Pedigrees, Prizes, and Prisoners: The Misuse of Conditional Probability". Journal of Statistics Education. 13 (2). doi:10.1080/10691898.2005.11910554. S2CID 118792491.
- Chun, Young H. (1991). "Game Show Problem". OR/MS Today. 18 (3): 9.
- D'Ariano, G. M.; Gill, R. D.; Keyl, M.; Kuemmerer, B.; Maassen, H.; Werner, R. F. (21 February 2002). "The Quantum Monty Hall Problem". Quant. Inf. Comput. 2 (5): 355–366. arXiv:quant-ph/0202120. Bibcode:2002quant.ph..2120D.
- Devlin, Keith (July–August 2003). "Devlin's Angle: Monty Hall". The Mathematical Association of America. Retrieved 23 June 2014.
- Devlin, Keith (December 2005). "Devlin's Angle: Monty Hall revisited". The Mathematical Association of America. Retrieved 23 June 2014.
- Eisenhauer, Joseph G. (2001). "The Monty Hall Matrix" (PDF). Teaching Statistics. 22 (1): 17–20. doi:10.1111/1467-9639.00005. Archived from the original (PDF) on 1 March 2012. Retrieved 9 July 2012.
- Enßlin, Torsten A.; Westerkamp, Margret (April 2018). "The rationality of irrationality in the Monty Hall problem". Annalen der Physik. 531 (3): 1800128. arXiv:1804.04948. Bibcode:2019AnP...53100128E. doi:10.1002/andp.201800128. S2CID 56036255.
- Falk, Ruma (1992). "A closer look at the probabilities of the notorious three prisoners". Cognition. 43 (3): 197–223. doi:10.1016/0010-0277(92)90012-7. PMID 1643813. S2CID 39617738.
- Flitney, Adrian P. & Abbott, Derek (2002). "Quantum version of the Monty Hall problem". Physical Review A. 65 (6): 062318. arXiv:quant-ph/0109035. Bibcode:2002PhRvA..65f2318F. doi:10.1103/PhysRevA.65.062318. S2CID 119417490. Art. No. 062318, 2002.
- Fox, Craig R. & Levav, Jonathan (2004). "Partition-Edit-Count: Naive Extensional Reasoning in Judgment of Conditional Probability" (PDF). Journal of Experimental Psychology: General. 133 (4): 626–642. doi:10.1037/0096-3445.133.4.626. PMID 15584810. Archived from the original (PDF) on 10 April 2020.
- Gardner, Martin (October 1959a). "Mathematical Games". Scientific American: 180–182. Reprinted in The Second Scientific American Book of Mathematical Puzzles and Diversions
{{cite journal}}: CS1 maint : 포스트스크립트(링크) - Gardner, Martin (November 1959b). "Mathematical Games". Scientific American: 188.
- Gardner, Martin (1982). Aha! Gotcha: Paradoxes to Puzzle and Delight. W. H. Freeman. ISBN 978-0716713616.
- Gill, Jeff (2002). Bayesian Methods. CRC Press. pp. 8–10. ISBN 1-58488-288-3. (restricted online copy , p. 8, at Google Books)
{{cite book}}:외부 링크 위치postscript= - Gill, Richard (2010). "Monty Hall problem". International Encyclopaedia of Statistical Science. Springer. pp. 858–863. arXiv:1002.3878v2.
- Gill, Richard (February 2011). "The Monty Hall Problem is not a probability puzzle (it's a challenge in mathematical modelling)". Statistica Neerlandica. 65 (1): 58–71. arXiv:1002.0651v3. doi:10.1111/j.1467-9574.2010.00474.x.
- Gill, Richard (17 March 2011a). "The Monty Hall Problem" (PDF). Mathematical Institute, University of Leiden, Netherlands. pp. 10–13.
- Gillman, Leonard (1992). "The Car and the Goats". American Mathematical Monthly. 99 (1): 3–7. doi:10.2307/2324540. JSTOR 2324540.
- Gilovich, T.; Medvec, V.H. & Chen, S. (1995). "Commission, Omission, and Dissonance Reduction: Coping with Regret in the "Monty Hall" Problem". Personality and Social Psychology Journal. 21 (2): 182–190. doi:10.1177/0146167295212008. S2CID 146500989.
- Gnedin, Sasha (2011). "The Mondee Gills Game". The Mathematical Intelligencer. 34: 34–41. doi:10.1007/s00283-011-9253-0.
- Granberg, Donald (2014). The Monty Hall Dilemma: A Cognitive Illusion Par Excellence. Lumad/CreateSpace. ISBN 978-0996100809.
- Granberg, Donald (1996). "To Switch or Not to Switch". In vos Savant, Marilyn (ed.). The Power of Logical Thinking. St. Martin's Press. ISBN 0-312-30463-3. (restricted online copy , p. 169, at Google Books)
{{cite book}}:외부 링크 위치postscript= - Granberg, Donald & Brown, Thad A. (1995). "The Monty Hall Dilemma". Personality and Social Psychology Bulletin. 21 (7): 711–729. doi:10.1177/0146167295217006. S2CID 146329922.
- Grinstead, Charles M. & Snell, J. Laurie (4 July 2006). Grinstead and Snell's Introduction to Probability (PDF). Retrieved 2 April 2008.
- Hall, Monty (1975). "The Monty Hall Problem". LetsMakeADeal.com. Retrieved 15 January 2007. Includes 12 May 1975 letter to Steve Selvin
{{cite web}}: CS1 maint : 포스트스크립트(링크) - Henze, Norbert (2011) [1997]. Stochastik für Einsteiger: Eine Einführung in die faszinierende Welt des Zufalls (in German) (9th ed.). Springer. pp. 50–51, 105–107. ISBN 978-3834818454. (restricted online copy, p. 105, at Google Books)
{{cite book}}:외부 링크 위치postscript= - Herbranson, W. T. & Schroeder, J. (2010). "Are birds smarter than mathematicians? Pigeons (Columba livia) perform optimally on a version of the Monty Hall Dilemma". Journal of Comparative Psychology. 124 (1): 1–13. doi:10.1037/a0017703. PMC 3086893. PMID 20175592.
- Hogbin, M.; Nijdam, W. (2010). "Letter to editor on Let's make a deal by Morgan et al". The American Statistician. 64 (2): 193. doi:10.1198/tast.2010.09227. S2CID 219595003.
- Kahneman, D.; Knetsch, J. L. & Thaler, R. H. (1991). "Anomalies: The endowment effect, loss aversion, and status quo bias". Journal of Economic Perspectives. 5: 193–206. doi:10.1257/jep.5.1.193.
- Kaivanto, K.; Kroll, E. B. & Zabinski, M. (2014). "Bias Trigger Manipulation and Task-Form Understanding in Monty Hall" (PDF). Economics Bulletin. 34 (1): 89–98.
- Krauss, Stefan & Wang, X. T. (2003). "The Psychology of the Monty Hall Problem: Discovering Psychological Mechanisms for Solving a Tenacious Brain Teaser" (PDF). Journal of Experimental Psychology: General. 132 (1): 3–22. doi:10.1037/0096-3445.132.1.3. Retrieved 30 March 2008.
- Lucas, Stephen; Rosenhouse, Jason & Schepler, Andrew (2009). "The Monty Hall Problem, Reconsidered" (PDF). Mathematics Magazine. 82 (5): 332–342. doi:10.4169/002557009X478355. Retrieved 9 July 2012.
- Martin, Phillip (1993) [1989]. Granovetter, Pamela; Granovetter, Matthew (eds.). The Monty Hall Trap. For Experts Only. Granovetter Books.
- Morgan, J. P.; Chaganty, N. R.; Dahiya, R. C. & Doviak, M. J. (1991). "Let's make a deal: The player's dilemma". The American Statistician. 45 (4): 284–287. doi:10.1080/00031305.1991.10475821. JSTOR 2684453.
- Morone, A. & Fiore, A. (2007). "Monty Hall's Three Doors for Dummies". Dipartimento di Scienze Economiche e Metodi Matematici – Università di Bari, Southern Europe Research in Economic Studies – S.E.R.I.E.S. Working Paper no. 0012.
- Mueser, Peter R. & Granberg, Donald (May 1999). "The Monty Hall Dilemma Revisited: Understanding the Interaction of Problem Definition and Decision Making". Experimental. University Library of Munich. Working Paper 99–06. Retrieved 10 June 2010.
- Nalebuff, Barry (Autumn 1987). "Puzzles: Choose a Curtain, Duel-ity, Two Point Conversions, and More". Journal of Economic Perspectives. 1 (2): 157–163. doi:10.1257/jep.1.2.157.
- Rao, M. Bhaskara (August 1992). "Comment on Let's make a deal by Morgan et al". The American Statistician. 46 (3): 241–242. JSTOR 2685225.
- Rosenhouse, Jason (2009). The Monty Hall Problem. Oxford University Press. ISBN 978-0-19-536789-8.
- Rosenthal, Jeffrey S. (September 2005a). "Monty Hall, Monty Fall, Monty Crawl" (PDF). Math Horizons: 5–7.
- Rosenthal, Jeffrey S. (2005b). Struck by Lightning: the Curious World of Probabilities. Harper Collins. ISBN 978-0-00-200791-7.
- Samuelson, W. & Zeckhauser, R. (1988). "Status quo bias in decision making". Journal of Risk and Uncertainty. 1: 7–59. CiteSeerX 10.1.1.632.3193. doi:10.1007/bf00055564. S2CID 5641133.
- Selvin, Steve (February 1975a). "A problem in probability (letter to the editor)". The American Statistician. 29 (1): 67–71. doi:10.1080/00031305.1975.10479121. JSTOR 2683689.
- Selvin, Steve (August 1975b). "On the Monty Hall problem (letter to the editor)". The American Statistician. 29 (3): 134. JSTOR 2683443.
- Seymann, R. G. (1991). "Comment on Let's Make a Deal: The player's dilemma". The American Statistician. 45 (4): 287–288. doi:10.2307/2684454. JSTOR 2684454.
- Stibel, Jeffrey; Dror, Itiel; Ben-Zeev, Talia (2008). "The Collapsing Choice Theory: Dissociating Choice and Judgment in Decision Making" (PDF). Theory and Decision.
- Tierney, John (21 July 1991). "Behind Monty Hall's Doors: Puzzle, Debate and Answer?". The New York Times. Retrieved 18 January 2008.
- Vazsonyi, Andrew (December 1999 – January 1999). "Which Door Has the Cadillac?" (PDF). Decision Line: 17–19. Archived from the original (PDF) on 13 April 2014. Retrieved 16 October 2012.
{{cite journal}}: CS1 maint: 날짜 및 연도(링크) - VerBruggen, Robert (24 February 2015). "The 'Monty Hall' Problem: Everybody Is Wrong". RealClearScience. Retrieved 12 October 2017.
- Volokh, Sasha (2 March 2015). "An 'easy' answer to the infamous Monty Hall problem". The Washington Post. ISSN 0190-8286. Retrieved 12 October 2017.
- vos Savant, Marilyn (2012) [1990–1991]. "Game Show Problem". Parade. Archived from the original on 29 April 2012.
- vos Savant, Marilyn (9 September 1990a). "Ask Marilyn". Parade: 16. Archived from the original on 21 January 2013. Retrieved 12 November 2012.
- vos Savant, Marilyn (2 December 1990b). "Ask Marilyn". Parade: 25. Archived from the original on 21 January 2013. Retrieved 12 November 2012.
- vos Savant, Marilyn (17 February 1991a). "Ask Marilyn". Parade: 12. Archived from the original on 21 January 2013. Retrieved 12 November 2012.
- vos Savant, Marilyn (November 1991c). "Marilyn vos Savant's reply". Letters to the editor. The American Statistician. 45 (4): 347. JSTOR 2684475.
- vos Savant, Marilyn (1996). The Power of Logical Thinking. St. Martin's Press. p. 5. ISBN 0-312-15627-8.
- Williams, Richard (2004). "Appendix D: The Monty Hall Controversy" (PDF). Course notes for Sociology Graduate Statistics I. Retrieved 25 April 2008.
- Whitaker, Craig F. (9 September 1990). "[Formulation by Marilyn vos Savant of question posed in a letter from Craig Whitaker]. Ask Marilyn". Parade: 16.
추가 읽기
- Gill, Richard (2011b). "Monty Hall Problem (version 5)". StatProb: The Encyclopedia Sponsored by Statistics and Probability Societies. Archived from the original on 21 January 2016. Retrieved 3 April 2011.
- vos Savant, Marilyn (7 July 1991b). "Ask Marilyn". Parade: 26. Archived from the original on 21 January 2013. Retrieved 12 November 2012.
- vos Savant, Marilyn (26 November 2006). "Ask Marilyn". Parade: 6.
외부 링크
| Wikibook 알고리즘 구현에 관한 주제의 페이지가 있다: Monty Hall 문제 시뮬레이션 |
| 위키미디어 커먼즈에는 몬티 홀 문제와 관련된 미디어가 있다. |
- 게임 쇼 문제 – Marilyn vos Savant의 웹 사이트에 대한 원래의 질문과 대답
- 캘리포니아 대학교 샌디에이고, 몬티는 버전을 알고 있고 몬티는 버전을 알지 못한다, 게임의 설명
- 컬리의 몬티 홀
- "스틱이냐, 스위치냐? 2013년 9월 11일(영상) BBC 뉴스 매거진 '확률과 몬티홀 문제'수학자 마르쿠스 뒤 사우토이는 몬티 홀의 역설에 대해 설명한다.