점도
Viscosity| 점도 | |
|---|---|
 다양한 점성을 가진 액체의 시뮬레이션.왼쪽 액체는 오른쪽 액체에 비해 점도가 낮다. | |
공통 기호 | η, μ |
에서 파생됨 다른 수량 | μ = G·t |
| 다음에 대한 시리즈 일부 |
| 연속체 역학 |
|---|
유체의 점도는 일정한 비율로 변형에 대한 저항의 척도다.액체의 경우, 그것은 "두꺼움"이라는 비공식적인 개념에 해당한다. 예를 들어, 시럽은 물보다 점성이 더 높다.[1]
점도는 상대 운동 중인 유체의 인접 층 사이의 내부 마찰력을 계량한다.예를 들어, 점성 액체가 튜브를 통해 강제될 때, 그것은 벽 근처보다 튜브의 축 근처로 더 빨리 흐른다.실험 결과, 흐름을 유지하기 위해서는 약간의 스트레스(관 두 끝 사이의 압력 차이 등)가 필요하다는 것을 알 수 있다.상대운동 중인 유체의 층간 마찰을 극복하기 위해서는 힘이 필요하기 때문이다.일정한 유량을 가진 관의 경우 보상력의 강도는 유체의 점도에 비례한다.
일반적으로 점도는 온도, 압력, 변형률 등 유체의 상태에 따라 달라진다.그러나 이러한 특성들 중 일부에 대한 의존은 어떤 경우에는 무시할 수 있다.예를 들어, 뉴턴 액의 점도는 변형 속도에 따라 크게 달라지지 않는다.제로 점도(전단 응력에 대한 저항 없음)는 슈퍼플루이드에서 매우 낮은 온도에서만 관찰된다. 그렇지 않으면 열역학 제2법칙에서는 모든 유체가 양의 점도를 가져야 한다.[2][3]점성이 0인 액체를 이상 또는 비침습이라고 한다.
어원
"점성"이라는 단어는 라틴어 점성("mistletoe")에서 유래되었다.비스코움은 겨우살이 열매에서 추출한 점성 접착제를 지칭하기도 했다.[4]
정의
동적 점도
재료 과학과 공학에서는 재료의 변형에 수반되는 힘이나 스트레스를 이해하는 데 관심이 있는 경우가 많다.예를 들어 물질이 단순한 샘이었다면, 샘에 의해 경험되는 힘은 평형에서 벗어난 거리에 비례한다는 후크의 법칙에 의해 해답이 주어질 것이다.일부 정지 상태에서 물질의 변형에 기인할 수 있는 응력을 탄성응력이라고 한다.다른 재료에서는 시간이 지남에 따라 변형의 변화 속도에 기인하는 응력이 존재한다.이를 점성응력이라고 한다.예를 들어, 물과 같은 액에서 액을 깎을 때 발생하는 스트레스는 액을 깎은 거리에 따라 달라지지 않고, 오히려 얼마나 빨리 깎이는가에 따라 달라진다.
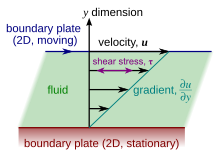
점도는 재료의 점성 응력을 변형률(변형률)과 연관시키는 재료 특성이다.일반 흐름에도 적용되지만 평면 쿠엣 흐름과 같이 단순한 피복 흐름으로 시각화 및 정의하기 쉽다.
쿠엣 흐름에서 유체는 두 개의 무한히 큰 플레이트 사이에 고정된 것과 일정한 속도 에서 병렬 동작하는 것 사이에 갇힌다(오른쪽 그림 참조).상단 플레이트의 속도가 (난류를 피할 수 있을 정도로) 낮으면, 안정 상태에서 유체 입자가 그것과 평행하게 움직이며, 그 속도는 의 0 에서 상단의 까지 다양하다.[5]각각의 액체 층은 그 바로 아래 층보다 더 빨리 움직이며, 그들 사이의 마찰은 그들의 상대적인 움직임에 저항하는 힘을 발생시킨다.특히 액체는 상단 판에 그것의 움직임과 반대 방향으로 힘을 가하며 하단 판에는 동일하지만 반대되는 힘을 가한다.따라서 상단 판이 일정한 속도로 이동하도록 하기 위해서는 외부 힘이 필요하다.
많은 유체에서 유속은 하단의 0에서 상단의 까지 선형적으로 변화하는 것으로 관찰된다.더욱이 상단 판에 작용하는 힘의 크기 은 각 판의 속도 및 면적 A 에 비례하며, 분리 y 에 반비례하는 으로 확인된다
비례 인자는 유체의 동적 점도로서 흔히 점성이라고 부른다.그리스 문자 mu(μ)로 표시된다.동적 점도에는 치수 / e e 이(가) 있으므로 SI 단위와 파생 단위가 발생한다.
전술한 비율 은 전단 변형률 또는 전단 속도의 비율로 불리며, 판에 수직인 방향으로 유체 속도의 파생이다(오른쪽 그림 참조).속도가 과와) 선형적으로 달라지지 않는 경우 적절한 일반화는 다음과 같다.
여기서 = / 및 /∂ u {\u/\ y은 로컬 전단 속도다.이 표현을 뉴턴의 점성 법칙이라고 한다.평면 대칭의 피복유동에서는 를 정의하는 것이다 좌표 없는 형태로 표현할 수 있는 점도의 일반적 정의(아래 참조)의 특수한 경우다.
동적 점성(절대 점성이라고도 함)을 위해 그리스 문자 mu( })를 사용하는 것은 수학자와 물리학자는 물론 기계 및 화학 엔지니어들 사이에서도 흔히 볼 수 있다.[6][7][8]그러나 그리스 문자 eta( )는 화학자, 물리학자, IUPAC에서도 사용된다.[9]점성 을(를) 전단 점성이라고도 한다.그러나 적어도 한 저자는 이 용어의 사용을 단념하며, 은(는) 피복 흐름 외에 비피복 흐름에서도 나타날 수 있다는 점에 주목한다.[10]
키네마틱 점도
유체 역학에서 때로는 유체( visc體)의 밀도에 대한 동적 점성(μ)의 비율로 정의되는 동역학적 점성(일명 모멘텀 디퓨전성)의 관점에서 작업하는 것이 더 적절할 때도 있다.보통 그리스 문자 nu(ν)로 표시된다.
치수 g ) 2/ t 을(를) 가지므로 SI 단위와 파생 단위가 된다.
- specific energy multiplied by time.
일반적 정의
매우 일반적인 용어로 유체의 점성 응력은 다른 유체 입자의 상대 속도에서 발생하는 응력으로 정의된다.이와 같이 점성 응력은 유속의 공간 구배에 따라 달라져야 한다.속도 구배가 작을 경우, 첫 번째 근사치까지 점성 응력은 속도의 첫 번째 파생 모델에 의해서만 결정된다.([11]뉴턴 유체의 경우, 이것 또한 선형 의존이다.)데카르트 좌표에서 일반적인 관계는 다음과 같이 기록될 수 있다.
k은 점성 응력 텐서/∂ rℓ{\displaystyle\partial v_{k}/\partial r_{\ell}}에 τ 나는 j{\displaystyle \tau_{ij}}.[12]기 때문에 이 식의 지수 13까지 다양할 수 있다면 a는 속도 기울기 텐서 ∂ v매핑 됩니다 어디 μ 나는 j k({\displaystyle \mu_{ijk\ell}}는 점도 텐서re8총 1개의 "점도 계수" i j l 그러나 점성 순위 4 텐서가 등방성이라고 가정하면 이들 81 계수가 세 개의 독립 매개변수 {\}로 감소한다
또한 유체가 단순한 강체-신체 회전을 거치고 있을 때 비스코스 힘이 발생하지 않을 것으로 가정하여 = = γ 두 개의 독립 파라미터만 남는다.[11]The most usual decomposition is in terms of the standard (scalar) viscosity and the bulk viscosity such that and . In vector notation this appears as:
여기서 \properties}은 단위 텐서이고, 단도 Δ은 전치(transpose)를 나타낸다.[10][13]이 방정식은 뉴턴의 점성 법칙의 일반화된 형태라고 생각할 수 있다.
대량 점성(볼륨 점성이라고도 함)은 유체의 전단 없는 압축이나 팽창에 저항하는 내부 마찰의 유형을 나타낸다.유체 역학 문제에서는 에 대한 지식이 필요하지 않은 경우가 많다.예를 들어, 압축 불가능한 액체는 = {v} =을(를) 충족하므로 을(를) 포함하는 용어는 제외된다.더욱이 은(는) 단일 원자 이상 기체에서 {\이므로 가스에 대해서는 무시할 수 있는 것으로 간주되는 경우가 많다.[10] 이(가) 중요할 수 있는 한 가지 상황은 스톡스의 음감쇠 법칙에 의해 기술된 음파 및 충격파의 에너지 손실의 계산이다. 이러한 현상은 급속한 팽창과 압축을 수반하기 때문이다.
점도의 정의 방정식은 자연의 근본 법칙이 아니기 때문에 점도의 측정이나 계산 방법은 물론 그 유용성도 별도의 방법을 사용하여 확립해야 한다.잠재적인 문제는 점성이 원칙적으로 시스템 내 모든 입자의 위치와 모멘텀을 포괄하는 유체의 완전한 미시적 상태에 따라 결정된다는 것이다.[14]그러한 고도로 상세한 정보는 일반적으로 현실적인 시스템에서는 이용할 수 없다.그러나 특정 조건에서 이 정보의 대부분은 무시할 수 있는 것으로 나타날 수 있다.특히 평형에 가깝고 경계(불크 상태)에서 멀리 떨어진 뉴턴 유체의 경우 점도는 국소 평형을 정의하는 공간 및 시간에 따른 거시적 영역(온도와 밀도 등)에만 의존한다.[14][15]
그럼에도 불구하고 점도는 온도, 압력 및 외부 강제력의 진폭과 빈도와 같은 몇 가지 시스템 속성에 대해 여전히 불가결한 의존성을 가질 수 있다.따라서 점도의 정밀 측정은 특정 유체 상태에 대해서만 정의된다.[16]실험과 이론 모델 간의 비교를 표준화하기 위해 점성 데이터는 때때로 (가스의 경우) 전단 제한 제로 또는 (가스의 경우) 0 밀도 한계와 같은 이상적인 제한 사례로 외삽된다.
모멘텀 운송
운송 이론은 모멘텀 운송 측면에서 점도의 대안적 해석을 제공한다: 점도는 열전도율이 열 수송을 특징짓는 것과 마찬가지로 유체 내 모멘텀 운송을 특징짓는 물질적 특성이고, (질량) 확산성은 대량 수송을 특징짓는 것이다.[17]이 관점은 뉴턴의 점성 법칙인 = (μ / ) y에 내포되어 있다 왜냐하면 전단 응력 은 단위 면적당 단위 시간 당 모멘텀에 해당하는 단위를 가지 단위가 있기 때문이다.따라서 은(는) 한 유체 계층에서 다음 유체 계층으로 방향으로 모멘텀의 흐름을 지정하는 것으로 해석할 수 있다.뉴턴의 점도의 법칙에 따르면, 이 운동량 흐름은 속도 구배를 가로질러 발생하며, 해당 운동량의 크기는 점도에 의해 결정된다.
열과 질량 전달과의 유사성은 명백하게 만들어질 수 있다.열이 고온에서 저온으로, 질량이 고밀도에서 저밀도로 흐르는 것처럼 운동량은 고속에서 저속으로 흐른다.이러한 행동들은 모두 구성관계라고 불리는 콤팩트한 표현에 의해 설명되며, 그들의 1차원적 형태는 여기에 주어진다.
여기서 은 밀도, { 및 은 질량 및 열 플럭스, t 는 질량 확산도 및 열전도도이다.[18]질량, 운동량 및 에너지(열) 수송이 연속 역학에서 가장 관련성이 높은 과정 중 하나라는 사실은 우연이 아니다. 이것들은 기관 간 충돌에서 극미량 수준으로 보존되는 몇 안 되는 물리적 양에 속한다.따라서, 빠르고 복잡한 미시적 상호작용 시간 척도에 의해 지시되기 보다는, 그들의 역학은 교통 이론과 수역학의 다양한 방정식에 의해 설명되는 거시적 시간 척도에서 발생한다.
뉴턴과 비뉴턴 유체
뉴턴의 점성 법칙은 자연의 근본 법칙이 아니라 점성 스타일 을 정의하는 역할을 하는 구성 방정식(후크의 법칙, 픽의 법칙, 옴의 법칙 등)이다 그 형태는 광범위한 유체에 대해 스타일 이 변형 r과 독립되어 있음을 보여주는 실험에 의해 동기가 된다.먹었어. 그런 액체를 뉴턴이라고 한다.가스, 물, 그리고 많은 일반적인 액체는 일반적인 조건과 맥락에서 뉴턴어로 간주될 수 있다.그러나 이러한 행동에서 현저하게 벗어나는 뉴턴계 이외의 액체가 많다.예를 들면 다음과 같다.
- 전단 변형률에 따라 점도가 증가하는 전단 두께의 액체.
- 전단 변형률에 따라 점도가 감소하는 전단 박리 액체.
- 흔들리거나 흔들리거나, 또는 다른 방법으로 스트레스를 받을 때 시간이 지남에 따라 점성이 낮아지는 소화성 액체.
- 흔들리거나 흔들리거나, 또는 다른 방법으로 스트레스를 받을 때 시간이 지남에 따라 점성이 더해지는 Rheopectic 액체.
- 낮은 스트레스에서는 고체로 작용하지만 높은 스트레스에서는 점성 액체로 흐르는 빙엄 플라스틱.
트라우턴의 비율은 전단 점도에 대한 확장 점도의 비율이다.뉴턴 액체의 경우 트라우턴 비율은 3이다.[19][20]전단 박리 액체는 매우 흔하지만 오해의 소지가 있는 것으로, thixotious라고 표현된다.[21]
뉴턴 액체의 경우에도 점도는 보통 그것의 성분과 온도에 따라 달라진다.기체와 기타 압축성 액체의 경우 온도에 따라 달라지며 압력에 따라 매우 느리게 변화한다.일부 유체의 점도는 다른 요인에 따라 달라질 수 있다.예를 들어 자기장(自體場)에 걸리면 자력학적 액체가 두꺼워지는데, 아마도 고체처럼 행동할 정도로 된다.
고형물 내
유체 흐름 중에 발생하는 점성력은 전단, 압축 또는 연장 응력에 반응하여 고형에서 발생하는 탄성력과 구별된다.후자의 경우 응력은 전단 변형량에 비례하는 반면, 유체에서는 시간 경과에 따른 변형 속도에 비례한다.이 때문에 맥스웰은 유체 점성을 위해 탈주탄력이라는 용어를 사용했다.
그러나 많은 액체(물 포함)는 갑작스러운 스트레스를 받으면 탄성 고형분처럼 잠시 반응하게 된다.반대로, 많은 "솔리드" ( 심지어 화강암도)는 임의의 작은 스트레스에도 불구하고 매우 느리지만 액체처럼 흐를 것이다.[22]이러한 재료는 점성(변형에 대한 반응)과 점성(변형률에 대한 반응)을 모두 갖는 점성(viscoastic)으로 가장 잘 설명된다.
점성 고형물은 전단 점도와 대량 점도를 둘 다 나타낼 수 있다.확장 점도는 연장에 대한 고체 탄성 재료의 반응을 설명하는 전단 및 벌크 점성의 선형 결합이다.중합체의 특성화에 널리 쓰인다.
지질학에서는 탄성 변형보다 최소 3배 이상의 비스코스 변형을 보이는 토자재를 rheids라고 부르기도 한다.[23]
측정
점도는 다양한 유형의 점도계와 온도계로 측정한다.단일한 점도의 값으로 정의할 수 없는 유체에 대해 rhemeter를 사용하므로 점성계의 경우보다 더 많은 파라미터를 설정하고 측정해야 한다.특히 윤활유와 같은 소재에서는 5°C만 변화해도 점도가 두 배가 될 수 있는 정확한 측정을 위해서는 유체의 긴밀한 온도 조절이 필수적이다.[24]
일부 유체의 경우 점도는 광범위한 전단 속도(뉴턴 유체)에 걸쳐 일정하다.일정한 점성이 없는 유체(뉴턴계 이외의 유체)는 단일 숫자로 설명할 수 없다.비뉴턴 액체는 전단 응력과 전단률 사이에 다양한 상관관계를 보인다.
운동학적 점도를 측정하는 가장 일반적인 기구 중 하나는 유리 모세관 점도계다.
코팅 산업에서는 유출 시간을 측정하는 컵으로 점도를 측정할 수 있다.잔컵과 포드 점성컵과 같은 여러 종류의 컵이 있는데, 각 유형의 사용법은 주로 업계에 따라 다르다.
또한 코팅에도 사용되며, Stormer 점도계는 점도를 결정하기 위해 부하 기반 회전을 사용한다.점도는 Stormer 점도계에 고유한 Kerbs 단위(KU)로 보고된다.
진동 점도계는 점도를 측정하는 데도 사용될 수 있다.공명 또는 진동 점도계는 액체 내에 전단파를 생성하여 작용한다.이 방법에서 센서는 유체에 잠기고 특정 주파수에서 공명하도록 만들어진다.센서의 표면이 액체를 통해 가늘어지면 점성으로 인해 에너지가 손실된다.이 비산된 에너지는 측정되어 점성 판독으로 변환된다.점성이 높을수록 에너지 손실이 커진다.[citation needed]
확장 점도는 확장 응력을 적용하는 다양한 온도계로 측정할 수 있다.
겉보기 점도는 오일이나 가스웰 개발에 사용되는 시추액에 대해 수행된 시험에서 도출된 계산이다.이러한 계산과 시험은 엔지니어가 필요한 사양에 따라 드릴링 액의 특성을 개발하고 유지하는 데 도움이 된다.
나노 점도(나노로봇이 감지하는 가시도)는 형광 상관 분광법으로 측정할 수 있다.[25]
단위
동적 점도의 SI 단위는 평방미터당 뉴턴초(N/s2/m)이며, 파스칼초(Pa/s), 초 당 킬로그램(kg·m−1·s−1), 푸아세일리(Pl) 등가형식으로도 자주 표현된다.CGS 단위는 장 레오나르 마리 푸아세유(Jean Léonard Marie Poiseuille)의 이름을 딴 페이즈(P, 또는 g·cm−1·s−1 = 0.1 Pa·s)[26]이다.그것은 일반적으로, 특히 ASTM 표준에서 centipoise (cP)로 표현된다.20℃에서 물의 점도가 약 1 cP이고, 1 centipoise는 SI 밀리파스칼 초(mPa·s)와 같기 때문에 센티포이즈가 편리하다.
키네마틱 점도의 SI 단위는 초당 제곱미터(m2/s)인 반면, 키네마틱 점도의 CGS 단위는 조지 가브리엘 스톡스 경의 이름을 딴 스톡스(St, 또는 cm2/s−1 = 0.00012 m/s−1)이다.[27]미국의 용법에서는 스토크가 단수형태로 쓰이기도 한다.하위 센티스토크(cSt)를 대신 사용하는 경우가 많은데, 1 cSt = 1 mm2/s−1 = 10−6 m2/s이다−1.20 °C에서 물의 동적 점도는 약 1 cSt이다.
미국의 관습, 즉 임페리얼 단위에서 가장 자주 사용되는 시스템은 영국 중력(BG)과 영국 공학(EE)이다.BG 시스템에서 동적 점도는 평방 피트당 파운드-초 단위(lb/s/ft2), EE 시스템에서는 평방 피트당 파운드-강력-초 단위(lbf/s/ft2)를 갖는다.파운드와 파운드 힘은 동등하다. 두 시스템은 힘과 질량이 어떻게 정의되는가에 있어서만 다르다.BG 시스템에서 파운드는 질량의 단위(슬러그)가 뉴턴의 제2법칙에 의해 정의되는 기본 단위인 반면 EE 시스템에서는 힘과 질량의 단위(각각 파운드 힘 및 파운드 질량)가 비례 상수 g를c 사용하여 제2법을 통해 독립적으로 정의된다.
키네마틱 점도에는 BG와 EE 시스템 모두에서 초당 제곱피트(ft2/s) 단위가 있다.
비표준 단위에는 동적 점도의 영국 단위인 레이닌이 포함된다.[citation needed]자동차 산업에서 점성 지수는 온도에 따른 점도의 변화를 설명하기 위해 사용된다.
점도의 역수는 유동성이며, 일반적으로 사용된 규약에 따라 = 1/ F= /−1mu−1 로 상징되며 때로는 rhe라고 불리기도 한다.유동성은 공학적 실무에서 거의 사용되지 않는다.[citation needed]
한때 석유 산업은 세이볼트 점도계를 통해 키네마틱 점도를 측정하고, 세이볼트 범용 초(SUS) 단위로 키네마틱 점도를 표현하는 데 의존했다.[28]SSU(Saybolt seconds universal) 또는 SUV(Saybolt universal scority)와 같은 다른 약어가 사용되기도 한다.센티스토크의 키네마틱 점도는 ASTM D 2161에 제공된 산술 및 기준표에 따라 SUS에서 변환할 수 있다.
분자 기원
기체에서의 모멘텀 운송은 이산적인 분자 충돌에 의해 매개되며, 액체에서는 분자를 서로 가깝게 묶는 매력적인 힘에 의해 매개된다.[17]이 때문에 액체의 동적 점성은 일반적으로 기체의 점보다 훨씬 크다.또한, 점도는 가스의 온도에 따라 증가하고 액체의 온도에 따라 감소하는 경향이 있다.
액체가스 임계점 위에서는 액체와 가스 단계가 단일 초임계 단계로 대체된다.이 정권에서 모멘텀 수송의 메커니즘은 액체와 가스 같은 행동 사이에 보간된다.예를 들어 초임계 이소바르(일정한 압력 표면)를 따라 저온에서 운동점도가 감소하고 고온에서 증가하며, 그 중간에서 최소가 증가한다.[29][30]최소값의 대략적인 추정치는 다음과 같다.
여기서 는 Planck의 상수, 는 전자질량, m m은 분자질량이다.[30]
그러나 일반적으로 계통의 점도는 계통을 구성하는 분자들이 어떻게 상호작용하는가에 따라 세부적으로 달라지며, 계통에 대한 단순하지만 정확한 공식은 없다.가장 간단한 정확한 표현은 1988년 에반스와 모리스가 도출한 선형 전단 점도에 대한 그린-쿠보 관계 또는 과도 시간 상관 함수 표현이다.[31]이러한 표현들은 각각 정확하지만, 이러한 관계를 이용하여 고밀도 유체의 점도를 계산하려면 현재 분자역학 컴퓨터 시뮬레이션을 사용해야 한다.기체 분자가 어떻게 움직이고 상호작용하는가에 대한 기본적인 가정은 점도의 분자 기원에 대한 기본적인 이해로 이어지기 때문에 희석 기체에 대해 다소 더 많은 진전이 있을 수 있다.보다 정교한 치료법은 가스 분자의 운동 방정식을 체계적으로 거칠게 갈아서 만들 수 있다.그러한 치료의 예로는 채프만-엔스코그 이론이 있는데, 이것은 볼츠만 방정식에서 희석된 기체의 점도를 나타내는 표현을 도출한다.[15]
순수 가스
희석가스의 점도의 기초적 계산 좌표에만 의존하는 속도 ) 과 x - 축에 평행으로 이동하는 희석 가스를 고려하십시오.논의를 단순화하기 위해 가스는 온도와 밀도가 균일하다고 가정한다.
이러한 가정 하에서 = 을 통과하는 의 x 속도는 평균 자유 경로 이(가) 시작되었을 때 분자가 가졌던 속도와 동일하다. 은(는) 일반적으로 거시적 척도에 비해 작기 때문에 그러한 분자의 x{\ 속도는 형태를 가진다.
때문에 반 스파이가 어디α{\displaystyle \alpha}숫자의 1{1\displaystyle}의 질서에.(어떤 저자들을 평가한다 α=2/3{\displaystyle \alpha =2/3};[17][32]에 다른 한편으로, 좀 더 치밀한 계산을 위해 엄격한 탄성 영역을 준다 α ≃ 0.998{\displaystyle \alpha \simeq 0.998}.)다음, 상수입니다.cules에양쪽 모두 = 을를) 향해 이동하고 있으며 평균 분자 속도 / ) 1/로 평균적으로 그렇게 하고 있다. 양쪽에서 나오는 모멘텀 플럭스는
= 의 순 모멘텀 플럭스는 다음 두 가지 차이점이다.
점도의 정의에 따르면 이 모멘텀 플럭스는 ( 0) {과 같아야 한다
기체의 점도는 주로 흐름의 층들 사이에서 운동량을 전달하는 분자 확산에서 발생한다.온도 및 밀도 에서 희석 가스에 대한 기본 계산은 다음과 같다.
서 k B 은 볼츠만 상수, 분자 질량, 은 1 {\displaystyle 1}의숫자상수다.평균 자유 경로인수량 은 분자가 충돌 간에 이동하는 평균 거리를 측정한다. 에 대한 사전 지식이 없어도 이 표현은 비교의 의미가 없다특히 은(는) 일반적으로 밀도에 반비례하며 온도에 따라 증가하므로 {\ 자체는 온도에 따라 증가해야 하며 고정온도에 있는 밀도에 독립되어야 한다.사실 이 두 예측 모두 보다 정교한 치료법을 지속하며, 실험적인 관찰을 정확하게 기술한다.반면에 액체 점도는 일반적으로 온도에 따라 감소한다.[17][32]
직경 의 경직성 탄성 구에 대해서는 다음과 같이 계산될 수 있다.
이 경우 은 온도와 무관하므로 / 2 그러나 더 복잡한 분자 모델의 경우 은 비종류의 온도에 따라 달라지며 여기서 사용되는 간단한 운동 논거는 불충분하다.보다 근본적으로, 평균 자유 경로의 개념은 유한한 범위에 걸쳐 상호작용하는 입자에 부정확하게 되며, 이는 실제 가스를 기술하는 개념의 유용성을 제한한다.[33]
채프먼-엔스코그 이론
1900년대 초 시드니 채프먼과 데이비드 엔스코그에 의해 개발된 기법은 의 좀 더 정제된 계산이 가능하다. 볼츠만 방정식에 기초하여, 분자간 상호작용의 관점에서 희석 가스에 대한 통계적 설명을 제공한다[15][34]이 기법은 분자간 명소를 결합한 것과 같이 단단한 탄성구보다 더 사실적인 분자 모델에 대해 스타일 을(를) 정확하게 계산할 수 있다.실험 결과 단단한 탄성 구에 대해 예측된 1/ T 추세보다 더 빠르게 증가하는 의 정확한 온도 의존도를 재현하기 위해서는 그렇게 하는 것이 필요하다[17]실제로 Chapman-Enskog 분석은 다양한 분자 모델에서 매개변수를 변화시킴으로써 예측 온도 의존성을 조정할 수 있음을 보여준다.간단한 예가 서덜랜드 모델인데,[a] 서로 끌어당기는 힘이 약한 단단한 탄성구를 묘사하고 있다.이런 경우 매력적인 힘을 섭동적으로 다룰 수 있어 :
여기서 은 온도와 독립적이며 분자간 끌어당김의 매개 변수에 의해서만 결정된다.실험과 연결하기 위해서는 로 다시 쓰는 것이 편리하다.
여기서 는 온도 에서 점성이며[35] = 에서 실험한 결과 이(가) 알려지고 다른 온도 하나 이상이면 를 계산할 수 있다.이러한 방법으로 얻은 에 대한 표현은 여러 개의 단순한 기체에 대해 질적으로 정확하다.레너드-존스 잠재력과 같은 약간 더 정교한 모델은 실험과 더 나은 합의를 제공할 수 있지만, 온도에 대한 더 불투명한 의존성을 희생해야 한다.일부 시스템에서는 구면 대칭에 대한 가정도 포기해야 하며, HO와2 같은 극성 분자를 가진 증기의 경우도 그러하다.이러한 경우 채프먼-엔스코그 분석은 훨씬 더 복잡하다.[36][37]
벌크 점도
운동 분자 그림에서, 분자의 변환 에너지와 그 내부 에너지 사이의 에너지 교환(예: 회전 및 진동)을 관장하는 비글라이제이션 이완 시간 계산이 있을 때마다 0이 아닌 대량 점도가 기체에서 발생한다.이와 같이 대량 점도는 단원자 이상 기체의 경우 0이며, 이 기체는 분자의 내부 에너지가 무시할 수 있지만, 분자가 회전 에너지와 진동 에너지를 모두 가지고 있는 이산화탄소와 같은 기체의 경우에는 0이 아니다.[38][39]
순수액체
기체와 대조적으로 액체의 점도의 분자 기원에 대한 간단하지만 정확한 그림은 없다.
가장 간단한 설명 수준에서 액체에서 인접한 층들의 상대적인 운동은 주로 층 경계를 가로질러 작용하는 매력적인 분자 힘에 의해 반대된다.이 그림에서 한 (정확히)은 온도가 상승함에 따라 점도가 감소할 것으로 예상한다.온도를 올리면 분자의 무작위 열운동이 증가하기 때문에 분자의 매력적인 상호작용을 쉽게 극복할 수 있기 때문이다.[40]
이 시각화에 기초하여, 간단한 이론은 고체의 이산적 구조와 유사하게 구성될 수 있다: 액체 속의 분자 그룹은 단일 분자를 둘러싸고 둘러싸는 "케이지"를 형성하는 것으로 시각화된다.[41]이러한 우리들은 점령되거나 점령되지 않을 수 있으며, 분자 흡인력이 강한 우리에 해당한다.무작위 열 운동으로 인해 분자는 분자 매력의 강도에 반비례하는 속도로 우리 사이의 "홉"을 한다.평형상태에서 이러한 "홉"은 어떤 방향으로도 치우치지 않는다.한편, 인접한 두 층이 서로 상대적으로 이동하기 위해서는, 「홉」이 상대 운동 방향으로 편향되어야 한다.이 방향 운동을 유지하는 데 필요한 힘은 주어진 전단 속도에 대해 추정할 수 있으며, 이는 다음과 같다.
-
(1)
여기서 는 아보가드로 상수, 는 플랑크 상수, 은 액체 몰의 부피, 는 정상 비등점이다.이 결과는 잘 알려진 경험적 관계와 같은 형태를 가지고 있다.
-
(2)
여기서 {\ 및 은(는) 데이터에서 적합한 상수임.[41][42]반면에, 몇몇 저자들은 이 모델에 대해 주의를 표명한다.실험 데이터에 대한 적합 방정식(2)과 비교하여 방정식(1)을 사용하여 최대 30%의 오차를 만날 수 있다.[41]보다 근본적으로, (1)식의 기초가 되는 물리적 가정은 비판을 받아왔다.[43]또한 등식 (1)의 지수적 의존성이 반드시 단순한 비우수적 표현보다 더 정확하게 실험 관찰을 기술하는 것은 아니라는 주장도 제기되었다.[44][45]
이러한 단점에 비추어 볼 때, 덜 임시적인 모델의 개발은 실제적인 관심의 문제다.정밀도에 호의적인 전술한 단순성으로, 분자에 대한 운동의 기본 방정식부터 시작하여 점도에 대한 엄격한 표현을 쓸 수 있다.이 접근법의 전형적인 예는 어빙-키크우드 이론이다.[46]한편, 그러한 표현은 다중문자 상관 함수에 대한 평균으로 주어지며, 따라서 실무에서 적용하기 어렵다.
일반적으로 경험적으로 파생된 표현식(기존 점성 측정에 기초함)은 액체의 점성을 계산하는 유일한 일관성 있는 신뢰할 수 있는 수단으로 보인다.[47]
혼합 및 혼합
기체 혼합물
같은 분자-키네틱 그림의 단일 성분 기체를 기체 혼합물에도 적용할 수 있다.예를 들어 Chapman-Enskog 접근방식에서 기체의 2진 혼합물인 점성 은 개별 성분 점성 , 각각의 체적분율 및 분자간 상호작용의 측면에서 기록할 수 있다.[15]단일 구성 요소 가스의 경우 분자간 상호작용의 파라미터에 대한 의 의존성은 다양한 충돌 통합을 통해 유입되며, 이는 기본적인 기능으로는 표현되지 않을 수 있다.실험 데이터와 합리적으로 일치하는 에 사용할 수 있는 식을 얻으려면 일반적으로 분석적 계산과 경험적 적합의 조합을 사용하여 충돌 통합을 평가해야 한다.그러한 절차의 예로는 위에서 논의한 단일 구성요소 가스에 대한 서덜랜드 접근법이 있다.
액체의 혼방
순수한 액체의 경우, 액체 혼합의 점도는 분자 원리에서 예측하기 어렵다.한 가지 방법은 순액에 대해 위에서 제시한 분자 "케이지" 이론을 확장하는 것이다.이것은 다양한 수준의 정교함으로 이루어질 수 있다.이러한 분석에서 도출된 한 가지 표현식은 이항 혼합물에 대한 Leader-Roeers 방정식이다.
여기서 은(는) 경험적 매개 변수이고 , 2{\ 및 , 은 구성성분의 각 몰 분율과 점성이다.[48]
혼합은 윤활유와 석유 산업에서 중요한 과정이기 때문에 혼합의 점도를 예측하기 위한 다양한 경험적, 적절성 방정식이 존재한다.[48]
솔루션 및 일시 중단
수용액
수용액 용액은 용액과 농도의 범위에 따라 동일한 온도와 압력에서 순수한 물과 비교하여 점도가 크거나 작을 수 있다.예를 들어 20% 염화염수(염화수소) 용액은 순수수의 1.5배 이상 점성이 있는 반면 20% 요오드칼륨 용액은 약 0.91배 정도 점성이 있다.
희석된 전해액의 이상적인 모델은 용액의 점성 에 대한 다음과 같은 예측으로 이어진다.[49]
여기서 은 용매의 점성, 은 농도, 은 용매와 용액 특성에 모두 의존하는 양의 상수다.그러나 이 표현은 이(가) 0.1 mol/L 미만인 매우 희석된 용액에만 유효하다.[50]고농도의 경우 고차 분자 상관 관계를 설명하는 추가 항이 필요하다.
서 B 및 은(는) 데이터로부터 적합하다.특히 의 음수 값은 일부 용액에서 관측된 점도의 감소를 설명할 수 있다.이러한 상수의 추정값은 25°C 온도에서 염화나트륨과 요오드화칼륨(mol = 몰, L = 리터)에 대해 아래에 제시되어 있다.[49]
| 솔루트 | A몰−1/2 L1/2) | B몰−1 L) | C몰−2 L2) |
|---|---|---|---|
| 염화나트륨(NaCl) | 0.0062 | 0.0793 | 0.0080 |
| 요오드화칼륨(KI) | 0.0047 | −0.0755 | 0.0000 |
정지
고체 입자(예: 오일에서 매달린 미크론 크기의 구)의 서스펜션에서 유효 점도 은(는) 부유 입자 사이의 거리에 비해 큰 볼륨에 걸쳐 평균되지만 거시적 di에 대해서는 작다.마션스[51]그러한 중단은 일반적으로 비뉴턴적 행동을 나타낸다.그러나 일정한 흐름의 묽은 시스템의 경우 동작은 뉴턴식이고 에 대한 표현은 입자 역학에서 직접 도출할 수 있다.매우 희석된 시스템에서 부피 분율 00 부유 입자 간의 상호작용을 무시할 수 있다이러한 경우 각 입자 주위의 흐름 장을 독립적으로 명시적으로 계산할 수 있으며, 그 결과를 결합하여 를 얻을 수 있다 구체의 경우, 다음과 같은 결과를 얻는다.
여기서 은 중단 액체의 점성이다. 에 대한 선형 의존은 인터기사 상호작용을 소홀히 한 결과물이다.일반적으로 묽은 시스템의 경우 이(가) 형태를 취할 것으로 예상한다.
여기서 계수 은(는) 입자 형태(예: 구, 막대, 디스크)에 따라 달라질 수 있다.[52] B 의 정확한 값에 대한 실험적인 판단은 어렵다. 구에 예측 =5 / B=조차 1.5 1.5 범위의 값을 다양한 실험이 결정적으로 검증되지 않았다이러한 결핍은 실험 조건을 통제하기 어려웠기 때문이다.[53]
밀도 높은 서스펜션에서 은(는) 에 비선형 의존성을 획득하며, 이는 인터기사 상호작용의 중요성을 나타낸다.이 정권을 잡기 위한 다양한 분석적, 반감각적 계획들이 존재한다.가장 기본적인 수준에서는 eff{\의 2차적 용어를 에 추가한다
그리고 계수 }는 실험 데이터로부터 적합하거나 현미경 이론으로부터 근사치를 구한다.그러나 일부 저자들은 비뉴턴적 행동이 밀집된 정지(구체의 경우 0 0.25[53]에 나타나거나 연장되거나 유연한 입자의 정지에 나타나기 때문에 이러한 간단한 공식을 적용할 때 주의를 기울여야 한다고 조언한다.[51]
위에서 설명한 고체 입자의 정지와 에멀전 사이에는 구별이 있다.후자는 작은 물방울의 중단인데, 그 자체가 내부 순환을 보일 수도 있다.내부 순환의 존재는 관찰된 유효 점도를 감소시킬 수 있으며, 다른 이론적 또는 반감기적 모델을 사용해야 한다.[54]
무정형 재료
고온 한계와 저온 한계에서 무정형 물질의 점성 흐름(예: 안경과 용해)[56][57][58]은 아르헤니우스 형태를 가진다.
여기서 Q는 분자 매개변수로 주어지는 관련 활성화 에너지, T는 온도, R은 어금니 기체 상수, A는 대략 상수다.활성화 에너지 Q는 고온 또는 저온 한계치 고려 여부에 따라 다른 값을 취한다. 즉, 저온(유리 상태)에서는 고값 Q에서 고온(액체 상태)에서는 저값 Q로HL 변화한다.
중간 온도의 Q 이(가) 온도에 따라 크게 달라지며 단순한 Arrhenius 형식이 실패한다.반면 2배수 방정식은
여기서 C 는 모두 상수로, 전체 온도 범위에서 실험 데이터에 잘 맞는 동시에 저온 및 고온 한계에서 올바른 Arrhenius 형태로 축소된다.이 표현은 원자 수준에서 비정형 물질의 다양한 이론적 모델에서 동기를 부여할 수 있다.[57]
점도에 대한 2-배수 방정식은 과냉각 액체의 Dyre shoubing 모델 내에서 도출될 수 있으며, 여기서 Arrhenius 에너지 장벽은 고유 투입 부피에 고주파 전단 계수 곱으로 식별된다.[59][60]열팽창을 통한 전단 계수의 온도 의존성과 분자간 전위의 반발 부분을 통해 또 다른 2-배수 방정식이 검색된다.[61]
여기서 G 는 유리 전환 와 동일한 온도에서 평가된 소재의 고주파 전단 계수를 나타내며 c V 는 이른바 밀어내기 부피, 즉 관여하는 원자 그룹의 특성 부피다.원자/원자가 가장 가까운 원자의 케이지에서 탈출하는 밀어내기 사건, 일반적으로 소수의 원자가 점유한 부피 순서에 따라 발생한다.더욱이 는 물질의 열팽창계수로서, }은 방사상 분포함수의 첫 번째 봉우리 상승측면의 급경사도를 측정하는 매개변수로, 정량적으로 해당 역행 부분과 관련이 있다.원자간의 [61]전위마지막으로 는 볼츠만 상수를 나타낸다.
에디 점도
유체의 난류를 연구하는 데 있어서, 일반적인 실용적 전략은 운동 중의 작은 규모의 장애물(또는 에디)을 무시하고, 효과적인 점도로 대규모 운동을 계산하는 것인데, 이를 "에디스코스"라고 하며, 이것은 작은 규모의 흐름에서 에너지의 전달과 소산을 특징으로 한다(대형 에디 시뮬레이션 참조).[62][63]열역학 제2법칙에 의해 양성이 되어야 하는 유체 자체의 점도와는 대조적으로 에디 점도는 음성이 될 수 있다.[64][65]
예측
점도는 온도와 압력에 따라 지속적으로 달라지기 때문에 한정된 수의 실험 측정으로 완전히 특성화할 수 없다.관심 온도 및 압력에서 실험 값을 사용할 수 없는 경우 예측 공식이 필요하게 된다.이 기능은 유체의 온도와 압력이 공간과 시간에 따라 지속적으로 달라질 수 있는 열물리학적 시뮬레이션에 중요하다.점도가 구성 유체의 농도 비율에 따라 지속적으로 달라지는 순수 유체의 혼합물에서도 유사한 상황이 발생한다.
희석된 단원자 기체와 그 혼합물과 같은 가장 단순한 유체의 경우, ab initio 양자 기계적 계산은 기본 원자 상수 측면에서, 즉, 기존의 점도 측정을 참조하지 않고 점도를 정확하게 예측할 수 있다.[66]묽은 헬륨의 특별한 경우, 아비니티오 계산 점도의 불확실성은 실험값의 불확실성보다 작은 크기의 두 가지 순서다.[67]
대부분의 유체에서, 그러한 고정밀도, 일차 원칙의 계산은 실현 가능하지 않다.오히려 이론적 또는 경험적 표현은 기존의 점도 측정에 적합해야 한다.그러한 표현이 광범위한 온도 및 압력에 걸쳐 높은 충실도의 데이터에 적합하다면, 그 유동성에 대한 "기준 상관관계"라고 한다.많은 순수한 액체에 대한 참조 상관관계가 발표되었다. 몇 가지 예로는 물, 이산화탄소, 암모니아, 벤젠, 그리고 제논이 있다.[68][69][70][71][72]이 중 다수는 가스, 액체 및 초임계 단계를 포함하는 온도 및 압력 범위를 포함한다.
열물리학적 모델링 소프트웨어는 종종 사용자가 지정한 온도와 압력의 점도를 예측하기 위해 참조 상관관계에 의존한다.이러한 상관관계는 독점적일 수 있다.예를 들어 REPP[73](수용)와 CoolProp[74](오픈 소스)이 있다.
점도는 또한 개별 입자 궤도의 통계학적 관점에서 그것을 표현하는 공식을 사용하여 계산할 수 있다.이러한 공식에는 1988년 에반스와 모리스가 도출한 선형 전단 점도에 대한 그린-쿠보 관계와 과도 시간 상관 함수 식이 포함된다.[75][31]이러한 표현들의 장점은 형식적으로 정확하고 일반 시스템에 유효하다는 것이다.단점은 분자 역학과 같이 계산적으로 비용이 많이 드는 시뮬레이션에서만 이용할 수 있는 입자 궤적에 대한 상세한 지식이 필요하다는 것이다.복잡한 분자의 경우 얻기 어려울 수 있는 정확한 인터기사 상호작용 모델도 필요하다.[76]
선택물질
관측된 점도의 값은 일반 물질의 경우에도 몇 가지 크기의 순서에 따라 달라진다(아래 크기 표 순서 참조).예를 들어, 70%의 자당(설탕) 용액은 물의 400배, 공기의 26,000배 이상의 점도를 가진다.[78]더 극적으로, 음높이는 물의 점도의 2300억 배인 것으로 추정되었다.[77]
물
물의 동적 점도 은(는) 상온(25°C)에서 약 0.89mPa/s이다.켈빈(kelvins)의 온도 함수로서 점도는 반감기 보겔-풀처-탐만 방정식을 사용하여 추정할 수 있다.
여기서 A = 0.02939 mPa·s, B = 507.88 K, C = 149.3 K.[79] 실험적으로 결정된 점도의 값도 아래 표에 제시되어 있다.20 °C에서의 값은 유용한 참고 자료로, 여기서 동적 점도는 약 1 cP, 키네마틱 점도는 약 1 cSt이다.
| 온도(°C) | 점도(mPa/s 또는 cP) |
|---|---|
| 10 | 1.3059 |
| 20 | 1.0016 |
| 30 | 0.79722 |
| 50 | 0.54652 |
| 70 | 0.40355 |
| 90 | 0.31417 |
공기
표준 대기 조건(25°C, 압력 1bar)에서 공기의 동적 점도는 18.5μPa·s로 같은 온도에서 물의 점성보다 약 50배 작다.매우 높은 압력을 제외하면 공기의 점도는 대부분 온도에 달려 있다.온도 의존성에 대한 많은 가능한 근사 공식(점도의 온도 의존도 참조) 중에서 하나는 다음과 같다.[80]
-20 °C ~ 400 °C 범위에서 정확하다.이 공식이 유효하려면 온도를 켈빈으로 지정해야 하며, ; 그러면 Pa 및s의 점도에 해당된다.

기타공통물질
| 물질 | 점도(mPa·s) | 온도(°C) | 참조 |
|---|---|---|---|
| 벤젠 | 0.604 | 25 | [78] |
| 물 | 1.0016 | 20 | |
| 수성. | 1.526 | 25 | |
| 전유 | 2.12 | 20 | [81] |
| 흑맥주 | 2.53 | 20 | |
| 올리브오일 | 56.2 | 26 | [81] |
| 여보 | 2000–10000 | 20 | [82] |
| 케첩[b] | 약 –20000 | 25 | [83] |
| 땅콩버터[b] | 약 4–106 | [84] | |
| 피치 | 2.3×1011 | 10-30 (1998년) | [77] |
규모 추정치 순서
다음 표는 공통 물질에서 관측된 점성 값의 범위를 나타낸다.달리 명시되지 않는 한, 25 °C의 온도와 1 대기의 압력을 가정한다.
열거된 값은 측정 불확도, 재료 정의의 변동성 또는 비뉴턴적 행동을 설명하지 않기 때문에 대표적인 추정치일 뿐이다.
| 요인(Pa/s) | 설명 | 예 | 값(Pa/s) | 참조 |
|---|---|---|---|---|
| 10−6 | 기체 점도의 낮은 범위 | 부탄 | 7.49 × 10−6 | [85] |
| 수소 | 8.8 × 10−6 | [86] | ||
| 10−5 | 기체 점도의 상한 범위 | 크립톤 | 2.538 × 10−5 | [87] |
| 네온 | 3.175 × 10−5 | |||
| 10−4 | 액체 점도의 낮은 범위 | 펜탄 | 2.24 × 10−4 | [78] |
| 가솔린 | 6 × 10−4 | |||
| 물 | 8.90 × 10−4 | [78] | ||
| 10−3 | 소분자에 대한 일반적인 범위 뉴턴 액체 | 에탄올 | 1.074 × 10−3 | |
| 수성. | 1.526 × 10−3 | |||
| 전유(20°C) | 2.12 × 10−3 | [81] | ||
| 피 | 3 × 10−3 ~ 6 × 10−3 | [88] | ||
| 액체강(1550 °C) | 6 × 10−3 | [89] | ||
| 10−2 – 100 | 오일 및 롱 체인 탄화수소 | 린세드 오일 | 0.028 | |
| 올레산 | 0.036 | [90] | ||
| 올리브오일 | 0.084 | [81] | ||
| SAE 10 모터 오일 | 0.085 ~ 0.14 | |||
| 캐스터오일 | 0.1 | |||
| SAE 20 모터 오일 | 0.14 ~ 0.42 | |||
| SAE 30 모터 오일 | 0.42 ~ 0.65 | |||
| SAE 40 모터 오일 | 0.65 ~ 0.90 | |||
| 글리세린 | 1.5 | |||
| 팬케이크 시럽 | 2.5 | |||
| 101 – 103 | 페이스트, 젤 및 기타 세미솔리드 (일반적으로 비뉴턴어) | 케첩 | ≈ 101 | [83] |
| 겨자 | ||||
| 사워 크림 | ≈ 102 | |||
| 땅콩버터 | [84] | |||
| 라드 | ≈ 103 | |||
| ≈108 | 점탄성 고분자 | 피치 | 2.3×108 | [77] |
| ≈1021 | 점탄성 아래의 특정 고형분 설명 | 맨틀(지질학) | ≈ 1019 ~ 1024 | [91] |
참고 항목
참조
각주
인용구
- ^ 시몬 1971.
- ^ 발레스쿠 1975, 페이지 428-429.
- ^ 랜도 & 리프시츠 1987.
- ^ Harper, Douglas (n.d.). "viscous (adj.)". Online Etymology Dictionary. Archived from the original on 1 May 2019. Retrieved 19 September 2019.
- ^ Mewis & Wagner 2012, 페이지 19.
- ^ Streeter, Willie & Bedford 1998.
- ^ 홀맨 2002.
- ^ 인크로페라 외 2007.
- ^ 니치 외 1997.
- ^ a b c 버드, 스튜어트 & 라이트풋 2007, 페이지 19.
- ^ a b 랜도 & 리프시츠 1987, 페이지 44–45.
- ^ Bird, Stewart & Lightfoot 2007, 페이지 18: 이 출처는 대체 기호 규약을 사용하며, 여기서 역전되었다.
- ^ 랜도 & 리프시츠 1987, 페이지 45.
- ^ a b 발레스쿠 1975.
- ^ a b c d 채프먼 & 카울링 1970.
- ^ 밀라트 1996.
- ^ a b c d e 버드, 스튜어트 & 라이트풋 2007.
- ^ 슈뢰더 1999.
- ^ 로자스카 외 2014, 페이지 47–55.
- ^ 트라우트론 1906, 페이지 426–440.
- ^ Mewis & Wagner 2012, 페이지 228–230.
- ^ 쿠마가이, 사사지마 & 이토 1978, 페이지 157–161.
- ^ Scherer, Pardenek & Swiatek 1988, 페이지 14.
- ^ 한난 2007.
- ^ Kwapiszewska 외 2020.
- ^ 맥노트 & 윌킨슨 1997, 침착하라.
- ^ Gyllenbok 2018, 페이지 213.
- ^ ASTM D2161 : Standard Practice for Conversion of Kinematic Viscosity to Saybolt Universal Viscosity or to Saybolt Furol Viscosity, ASTM, 2005, p. 1
- ^ Trachenko & Brazhkin 2020.
- ^ a b 트라첸코 & 브라슈킨 2021.
- ^ a b 에반스 & 모리스 1988.
- ^ a b 벨락, 모르테사뉴 & 바트루니 2004.
- ^ 채프먼 & 카울링 1970, 페이지 103.
- ^ 케르시냐니 1975년
- ^ 서덜랜드 1893, 페이지 507-531.
- ^ Bird, Stewart & Lightfoot 2007, 페이지 25–27.
- ^ 채프먼 & 카울링 1970, 페이지 235–237.
- ^ 채프먼 & 카울링 1970, 페이지 197, 214–216.
- ^ 크레이머 2012 페이지 066102-2.
- ^ 리드 & 셔우드 1958, 페이지 202.
- ^ a b c Bird, Stewart & Lightfoot 2007, 페이지 29–31.
- ^ 리드 & 셔우드 1958 페이지 203–204.
- ^ 힐데브란트 1977.
- ^ 힐드브랜드 1977, 페이지 37.
- ^ 에겔스타프 1992 페이지 264.
- ^ 어빙 & 커크우드 1949 페이지 817–829.
- ^ 리드 & 셔우드 1958 페이지 206–209.
- ^ a b Zhmud 2014, 페이지 22.
- ^ a b Viswanath 외 2007.
- ^ 압둘라가토프, 자이날로바 & 아지조프 2006, 페이지 75–88.
- ^ a b 버드, 스튜어트 & 라이트풋 2007, 페이지 31~33.
- ^ Bird, Stewart & Lightfoot 2007, 페이지 32.
- ^ a b Mueller, Llewellin & Mader 2009, 페이지 1201–1228.
- ^ 버드, 스튜어트 & 라이트풋 2007, 페이지 33.
- ^ 2007년 푸에겔 2007.
- ^ 도레머스 2002 페이지 7619–7629.
- ^ a b 오조반, 트래비스 & 핸드 2007, 페이지 415107.
- ^ 오조반 & 리 2004, 페이지 3803–3810.
- ^ Dyre, Olsen & Christensen 1996, 페이지 2171.
- ^ Hecksher & Dyre 2015.
- ^ a b 크라우저, 샘워 & 자코네 2015, 페이지 13762.
- ^ 버드, 스튜어트 & 라이트풋 2007, 페이지 163.
- ^ Lesieur 2012, 페이지 2–.
- ^ 시바신스키 & 야코트 1985, 페이지 1040.
- ^ 시앤레브첸코 2019, 페이지 045434.
- ^ 샤리포프 & 베니테스 2020.
- ^ Rowland, Al Ghafri & 2020년 5월.
- ^ 휴버 외 2009.
- ^ Laeseke & Muzny 2017.
- ^ 모노게니두, 어사엘 & 휴버 2018.
- ^ Avgeri et al. 2014.
- ^ 벨리아두 외 2021년
- ^ "Refprop". Nist.gov. 18 April 2013. Archived from the original on 2022-02-09. Retrieved 2022-02-15.
- ^ 벨 외 2014.
- ^ 에반스 & 모리스 2007.
- ^ 마긴 외 2019.
- ^ a b c d 엣지워스, 달튼 & 파넬 1984, 페이지 198–200.
- ^ a b c d e 럼블 2018.
- ^ Viswanath & Natarajan 1989, 페이지 714–715.
- ^ tec-science (2020-03-25). "Viscosity of liquids and gases". tec-science. Archived from the original on 2020-04-19. Retrieved 2020-05-07.
- ^ a b c d 2009년 친구들.
- ^ Yanniotis, Scaltsi & Karaburnioti 2006, 페이지 372–377.
- ^ a b 쿠체키 외 2009년, 페이지 596–602.
- ^ a b Citerne, Carreau & Moan 2001, 페이지 86–96.
- ^ 케스틴, 칼리파 & 웨이크햄 1977.
- ^ 어사엘 외 2018.
- ^ Kestin, Ro & Wakeham 1972.
- ^ Rosenson, McCormick & Uretz 1996.
- ^ 자오 외 2021.
- ^ 사그데프 외 2019년.
- ^ 월저, 헨델 & 바움가드너 N.D.
원천
- Abdulagatov, Ilmutdin M.; Zeinalova, Adelya B.; Azizov, Nazim D. (2006). "Experimental viscosity B-coefficients of aqueous LiCl solutions". Journal of Molecular Liquids. 126 (1–3): 75–88. doi:10.1016/j.molliq.2005.10.006. ISSN 0167-7322.
- Assael, M. J.; et al. (2018). "Reference Values and Reference Correlations for the Thermal Conductivity and Viscosity of Fluids". Journal of Physical and Chemical Reference Data. 47 (2): 021501. Bibcode:2018JPCRD..47b1501A. doi:10.1063/1.5036625. ISSN 0047-2689. PMC 6463310. PMID 30996494.
- Avgeri, S.; Assael, M. J.; Huber, M. L.; Perkins, R. A. (2014). "Reference Correlation of the Viscosity of Benzene from the Triple Point to 675 K and up to 300 MPa". Journal of Physical and Chemical Reference Data. AIP Publishing. 43 (3): 033103. Bibcode:2014JPCRD..43c3103A. doi:10.1063/1.4892935. ISSN 0047-2689.
- Balescu, Radu (1975). Equilibrium and Non-Equilibrium Statistical Mechanics. John Wiley & Sons. ISBN 978-0-471-04600-4. Archived from the original on 2020-03-16. Retrieved 2019-09-18.
- Bell, Ian H.; Wronski, Jorrit; Quoilin, Sylvain; Lemort, Vincent (2014-01-27). "Pure and Pseudo-pure Fluid Thermophysical Property Evaluation and the Open-Source Thermophysical Property Library CoolProp". Industrial & Engineering Chemistry Research. American Chemical Society (ACS). 53 (6): 2498–2508. doi:10.1021/ie4033999. ISSN 0888-5885. PMC 3944605. PMID 24623957.
- Bellac, Michael; Mortessagne, Fabrice; Batrouni, G. George (2004). Equilibrium and Non-Equilibrium Statistical Thermodynamics. Cambridge University Press. ISBN 978-0-521-82143-8.
- Bird, R. Byron; Stewart, Warren E.; Lightfoot, Edwin N. (2007). Transport Phenomena (2nd ed.). John Wiley & Sons, Inc. ISBN 978-0-470-11539-8. Archived from the original on 2020-03-02. Retrieved 2019-09-18.
- Bird, R. Bryon; Armstrong, Robert C.; Hassager, Ole (1987), Dynamics of Polymeric Liquids, Volume 1: Fluid Mechanics (2nd ed.), John Wiley & Sons
- Cercignani, Carlo (1975). Theory and Application of the Boltzmann Equation. Elsevier. ISBN 978-0-444-19450-3.
- Chapman, Sydney; Cowling, T.G. (1970). The Mathematical Theory of Non-Uniform Gases (3rd ed.). Cambridge University Press. ISBN 9780521075770.
- Citerne, Guillaume P.; Carreau, Pierre J.; Moan, Michel (2001). "Rheological properties of peanut butter". Rheologica Acta. 40 (1): 86–96. doi:10.1007/s003970000120. S2CID 94555820.
- Cramer, M.S. (2012). "Numerical estimates for the bulk viscosity of ideal gases". Physics of Fluids. 24 (6): 066102–066102–23. Bibcode:2012PhFl...24f6102C. doi:10.1063/1.4729611. hdl:10919/47646. Archived from the original on 2022-02-15. Retrieved 2020-09-19.
- Doremus, R.H. (2002). "Viscosity of silica". J. Appl. Phys. 92 (12): 7619–7629. Bibcode:2002JAP....92.7619D. doi:10.1063/1.1515132.
- Dyre, J.C.; Olsen, N. B.; Christensen, T. (1996). "Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids". Physical Review B. 53 (5): 2171–2174. Bibcode:1996PhRvB..53.2171D. doi:10.1103/PhysRevB.53.2171. PMID 9983702.
- Edgeworth, R.; Dalton, B.J.; Parnell, T. (1984). "The pitch drop experiment". European Journal of Physics. 5 (4): 198–200. Bibcode:1984EJPh....5..198E. doi:10.1088/0143-0807/5/4/003. Archived from the original on 2013-03-28. Retrieved 2009-03-31.
- Egelstaff, P. A. (1992). An Introduction to the Liquid State (2nd ed.). Oxford University Press. ISBN 978-0-19-851012-3.
- Evans, Denis J.; Morriss, Gary P. (2007). Statistical Mechanics of Nonequilibrium Liquids. ANU Press. ISBN 9781921313226. JSTOR j.ctt24h99q. Archived from the original on 2022-01-10. Retrieved 2022-01-10.
- Evans, Denis J.; Morriss, Gary P. (October 15, 1988). "Transient-time-correlation functions and the rheology of fluids". Physical Review A. 38 (8): 4142–4148. Bibcode:1988PhRvA..38.4142E. doi:10.1103/PhysRevA.38.4142. PMID 9900865.
- Fellows, P. J. (2009). Food Processing Technology: Principles and Practice (3rd ed.). Woodhead. ISBN 978-1845692162.
- Fluegel, Alexander (2007). "Viscosity calculation of glasses". Glassproperties.com. Archived from the original on 2010-11-27. Retrieved 2010-09-14.
- Gibbs, Philip (January 1997). "Is glass liquid or solid?". math.ucr.edu. Archived from the original on 29 March 2007. Retrieved 19 September 2019.
- Gyllenbok, Jan (2018). "Encyclopaedia of Historical Metrology, Weights, and Measures: Volume 1". Encyclopaedia of Historical Metrology, Weights, and Measures. Vol. 1. Birkhäuser. ISBN 9783319575988.
- Hannan, Henry (2007). Technician's Formulation Handbook for Industrial and Household Cleaning Products. Waukesha, Wisconsin: Kyral LLC. p. 7. ISBN 978-0-6151-5601-9.
- Hecksher, Tina; Dyre, Jeppe C. (2015-01-01). "A review of experiments testing the shoving model". Journal of Non-Crystalline Solids. 7th IDMRCS: Relaxation in Complex Systems. 407: 14–22. Bibcode:2015JNCS..407...14H. doi:10.1016/j.jnoncrysol.2014.08.056. ISSN 0022-3093. Archived from the original on 2022-02-15. Retrieved 2021-10-17.
- Hildebrand, Joel Henry (1977). Viscosity and Diffusivity: A Predictive Treatment. John Wiley & Sons. ISBN 978-0-471-03072-0.
- Holman, Jack Philip (2002). Heat Transfer. McGraw-Hill. ISBN 978-0-07-112230-6. Archived from the original on 2020-03-15. Retrieved 2019-09-18.
- Huber, M. L.; Perkins, R. A.; Laesecke, A.; Friend, D. G.; Sengers, J. V.; Assael, M. J.; Metaxa, I. N.; Vogel, E.; Mareš, R.; Miyagawa, K. (2009). "New International Formulation for the Viscosity of H2O". Journal of Physical and Chemical Reference Data. AIP Publishing. 38 (2): 101–125. Bibcode:2009JPCRD..38..101H. doi:10.1063/1.3088050. ISSN 0047-2689.
- Incropera, Frank P.; et al. (2007). Fundamentals of Heat and Mass Transfer. Wiley. ISBN 978-0-471-45728-2. Archived from the original on 2020-03-11. Retrieved 2019-09-18.
- Irving, J.H.; Kirkwood, John G. (1949). "The Statistical Mechanical Theory of Transport Processes. IV. The Equations of Hydrodynamics". J. Chem. Phys. 18 (6): 817–829. doi:10.1063/1.1747782.
- Kestin, J.; Ro, S. T.; Wakeham, W. A. (1972). "Viscosity of the Noble Gases in the Temperature Range 25–700°C". The Journal of Chemical Physics. 56 (8): 4119–4124. Bibcode:1972JChPh..56.4119K. doi:10.1063/1.1677824. ISSN 0021-9606.
- Kestin, J.; Khalifa, H.E.; Wakeham, W.A. (1977). "The viscosity of five gaseous hydrocarbons". The Journal of Chemical Physics. 66 (3): 1132. Bibcode:1977JChPh..66.1132K. doi:10.1063/1.434048.
- Koocheki, Arash; et al. (2009). "The rheological properties of ketchup as a function of different hydrocolloids and temperature". International Journal of Food Science & Technology. 44 (3): 596–602. doi:10.1111/j.1365-2621.2008.01868.x.
- Krausser, J.; Samwer, K.; Zaccone, A. (2015). "Interatomic repulsion softness directly controls the fragility of supercooled metallic melts". Proceedings of the National Academy of Sciences of the USA. 112 (45): 13762–13767. arXiv:1510.08117. Bibcode:2015PNAS..11213762K. doi:10.1073/pnas.1503741112. PMC 4653154. PMID 26504208.
- Kumagai, Naoichi; Sasajima, Sadao; Ito, Hidebumi (15 February 1978). "Long-term Creep of Rocks: Results with Large Specimens Obtained in about 20 Years and Those with Small Specimens in about 3 Years". Journal of the Society of Materials Science (Japan). 27 (293): 157–161. NAID 110002299397. Archived from the original on 2011-05-21. Retrieved 2008-06-16.
- Kwapiszewska, Karina; Szczepański, Krzysztof; Kalwarczyk, Tomasz; Michalska, Bernadeta; Patalas-Krawczyk, Paulina; Szymański, Jędrzej; Andryszewski, Tomasz; Iwan, Michalina; Duszyński, Jerzy; Hołyst, Robert (2020). "Nanoscale Viscosity of Cytoplasm Is Conserved in Human Cell Lines". The Journal of Physical Chemistry Letters. 11 (16): 6914–6920. doi:10.1021/acs.jpclett.0c01748. PMC 7450658. PMID 32787203.
- Laesecke, Arno; Muzny, Chris D. (2017). "Reference Correlation for the Viscosity of Carbon Dioxide". Journal of Physical and Chemical Reference Data. AIP Publishing. 46 (1): 013107. Bibcode:2017JPCRD..46a3107L. doi:10.1063/1.4977429. ISSN 0047-2689. PMC 5514612. PMID 28736460.
- Landau, L. D.; Lifshitz, E.M. (1987). Fluid Mechanics (2nd ed.). Elsevier. ISBN 978-0-08-057073-0. Archived from the original on 2020-03-21. Retrieved 2019-09-18.
- Maginn, Edward J.; Messerly, Richard A.; Carlson, Daniel J.; Roe, Daniel R.; Elliott, J. Richard (2019). "Best Practices for Computing Transport Properties 1. Self-Diffusivity and Viscosity from Equilibrium Molecular Dynamics [Article v1.0]". Living Journal of Computational Molecular Science. University of Colorado at Boulder. 1 (1). doi:10.33011/livecoms.1.1.6324. ISSN 2575-6524. S2CID 104357320.
- Monogenidou, S. A.; Assael, M. J.; Huber, M. L. (2018). "Reference Correlation for the Viscosity of Ammonia from the Triple Point to 725 K and up to 50 MPa". Journal of Physical and Chemical Reference Data. AIP Publishing. 47 (2): 023102. Bibcode:2018JPCRD..47b3102M. doi:10.1063/1.5036724. ISSN 0047-2689. PMC 6512859. PMID 31092958.
- Lesieur, Marcel (2012). Turbulence in Fluids: Stochastic and Numerical Modelling. Springer. ISBN 978-94-009-0533-7. Archived from the original on 2020-03-14. Retrieved 2018-11-30.
- Mewis, Jan; Wagner, Norman J. (2012). Colloidal Suspension Rheology. Cambridge University Press. ISBN 978-0-521-51599-3. Archived from the original on 2020-03-14. Retrieved 2018-12-10.
- McNaught, A. D.; Wilkinson, A. (1997). "poise". IUPAC. Compendium of Chemical Terminology (the "Gold Book"). S. J. Chalk (2nd ed.). Oxford: Blackwell Scientific. doi:10.1351/goldbook. ISBN 0-9678550-9-8.
- Millat, Jorgen (1996). Transport Properties of Fluids : Their Correlation, Prediction and Estimation. Cambridge: Cambridge University Press. ISBN 978-0-521-02290-3. OCLC 668204060.
- Mueller, S.; Llewellin, E. W.; Mader, H. M. (2009). "The rheology of suspensions of solid particles". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 466 (2116): 1201–1228. doi:10.1098/rspa.2009.0445. ISSN 1364-5021.
- Nič, Miloslav; et al., eds. (1997). "dynamic viscosity, η". IUPAC Compendium of Chemical Terminology. Oxford: Blackwell Scientific Publications. doi:10.1351/goldbook. ISBN 978-0-9678550-9-7.
- Ojovan, M.I.; Lee, W.E. (2004). "Viscosity of network liquids within Doremus approach". J. Appl. Phys. 95 (7): 3803–3810. Bibcode:2004JAP....95.3803O. doi:10.1063/1.1647260.
- Ojovan, M.I.; Travis, K. P.; Hand, R.J. (2007). "Thermodynamic parameters of bonds in glassy materials from viscosity-temperature relationships" (PDF). J. Phys.: Condens. Matter. 19 (41): 415107. Bibcode:2007JPCM...19O5107O. doi:10.1088/0953-8984/19/41/415107. PMID 28192319. Archived (PDF) from the original on 2018-07-25. Retrieved 2019-09-27.
- Plumb, Robert C. (1989). "Antique windowpanes and the flow of supercooled liquids". Journal of Chemical Education. 66 (12): 994. Bibcode:1989JChEd..66..994P. doi:10.1021/ed066p994. Archived from the original on 2005-08-26. Retrieved 2013-12-25.
- Rapaport, D.C. (2004). The Art of Molecular Dynamics Simulation (2nd ed.). Cambridge University Press. ISBN 9780521825689. Archived from the original on 2018-06-25. Retrieved 2022-01-10.
- Reid, Robert C.; Sherwood, Thomas K. (1958). The Properties of Gases and Liquids. McGraw-Hill.
- Reif, F. (1965), Fundamentals of Statistical and Thermal Physics, McGraw-Hill. 고급 치료법.
- Rosenson, R S; McCormick, A; Uretz, E F (1996-08-01). "Distribution of blood viscosity values and biochemical correlates in healthy adults". Clinical Chemistry. Oxford University Press (OUP). 42 (8): 1189–1195. doi:10.1093/clinchem/42.8.1189. ISSN 0009-9147. PMID 8697575.
- Rowland, Darren; Al Ghafri, Saif Z. S.; May, Eric F. (2020-03-01). "Wide-Ranging Reference Correlations for Dilute Gas Transport Properties Based on Ab Initio Calculations and Viscosity Ratio Measurements". Journal of Physical and Chemical Reference Data. AIP Publishing. 49 (1): 013101. Bibcode:2020JPCRD..49a3101X. doi:10.1063/1.5125100. ISSN 0047-2689. S2CID 213794612.
- Różańska, S.; Różański, J.; Ochowiak, M.; Mitkowski, P. T. (2014). "Extensional viscosity measurements of concentrated emulsions with the use of the opposed nozzles device" (PDF). Brazilian Journal of Chemical Engineering. 31 (1): 47–55. doi:10.1590/S0104-66322014000100006. ISSN 0104-6632. Archived (PDF) from the original on 2020-05-08. Retrieved 2019-09-19.
- Rumble, John R., ed. (2018). CRC Handbook of Chemistry and Physics (99th ed.). Boca Raton, FL: CRC Press. ISBN 978-1138561632.
- Sagdeev, Damir; Gabitov, Il'giz; Isyanov, Chingiz; Khairutdinov, Vener; Farakhov, Mansur; Zaripov, Zufar; Abdulagatov, Ilmutdin (2019-04-22). "Densities and Viscosities of Oleic Acid at Atmospheric Pressure". Journal of the American Oil Chemists' Society. Wiley. 96 (6): 647–662. doi:10.1002/aocs.12217. ISSN 0003-021X. S2CID 150156106.
- Scherer, George W.; Pardenek, Sandra A.; Swiatek, Rose M. (1988). "Viscoelasticity in silica gel". Journal of Non-Crystalline Solids. 107 (1): 14. Bibcode:1988JNCS..107...14S. doi:10.1016/0022-3093(88)90086-5.
- Schroeder, Daniel V. (1999). An Introduction to Thermal Physics. Addison Wesley. ISBN 978-0-201-38027-9. Archived from the original on 2020-03-10. Retrieved 2018-11-30.
- Sharipov, Felix; Benites, Victor J. (2020-07-01). "Transport coefficients of multi-component mixtures of noble gases based on ab initio potentials: Viscosity and thermal conductivity". Physics of Fluids. AIP Publishing. 32 (7): 077104. arXiv:2006.08687. Bibcode:2020PhFl...32g7104S. doi:10.1063/5.0016261. ISSN 1070-6631. S2CID 219708359.
- Sivashinsky, V.; Yakhot, G. (1985). "Negative viscosity effect in large-scale flows". The Physics of Fluids. 28 (4): 1040. Bibcode:1985PhFl...28.1040S. doi:10.1063/1.865025.
- Streeter, Victor Lyle; Wylie, E. Benjamin; Bedford, Keith W. (1998). Fluid Mechanics. WCB/McGraw Hill. ISBN 978-0-07-062537-2. Archived from the original on 2020-03-16. Retrieved 2019-09-18.
- Sutherland, William (1893). "LII. The viscosity of gases and molecular force" (PDF). The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. 36 (223): 507–531. doi:10.1080/14786449308620508. ISSN 1941-5982. Archived (PDF) from the original on 2019-07-20. Retrieved 2019-09-18.
- Symon, Keith R. (1971). Mechanics (3rd ed.). Addison-Wesley. ISBN 978-0-201-07392-8. Archived from the original on 2020-03-11. Retrieved 2019-09-18.
- Trachenko, K.; Brazhkin, V. V. (2020-04-22). "Minimal quantum viscosity from fundamental physical constants". Science Advances. American Association for the Advancement of Science (AAAS). 6 (17): eaba3747. arXiv:1912.06711. Bibcode:2020SciA....6.3747T. doi:10.1126/sciadv.aba3747. ISSN 2375-2548. PMC 7182420. PMID 32426470.
- Trachenko, Kostya; Brazhkin, Vadim V. (2021-12-01). "The quantum mechanics of viscosity" (PDF). Physics Today. AIP Publishing. 74 (12): 66–67. Bibcode:2021PhT....74l..66T. doi:10.1063/pt.3.4908. ISSN 0031-9228. S2CID 244831744. Archived (PDF) from the original on 2022-01-10. Retrieved 2022-01-10.
- Trouton, Fred. T. (1906). "On the Coefficient of Viscous Traction and Its Relation to that of Viscosity". Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 77 (519): 426–440. Bibcode:1906RSPSA..77..426T. doi:10.1098/rspa.1906.0038. ISSN 1364-5021.
- Velliadou, Danai; Tasidou, Katerina A.; Antoniadis, Konstantinos D.; Assael, Marc J.; Perkins, Richard A.; Huber, Marcia L. (2021-03-25). "Reference Correlation for the Viscosity of Xenon from the Triple Point to 750 K and up to 86 MPa". International Journal of Thermophysics. Springer Science and Business Media LLC. 42 (5): 74. Bibcode:2021IJT....42...74V. doi:10.1007/s10765-021-02818-9. ISSN 0195-928X. PMC 8356199. PMID 34393314.
- Viswanath, D.S.; Natarajan, G. (1989). Data Book on the Viscosity of Liquids. Hemisphere Publishing Corporation. ISBN 0-89116-778-1.
- Viswanath, Dabir S.; et al. (2007). Viscosity of Liquids: Theory, Estimation, Experiment, and Data. Springer. ISBN 978-1-4020-5481-5.
- Walzer, Uwe; Hendel, Roland; Baumgardner, John (n.d.), Mantle Viscosity and the Thickness of the Convective Downwellings, archived from the original on 2007-06-11
- Xie, Hong-Yi; Levchenko, Alex (23 January 2019). "Negative viscosity and eddy flow of the imbalanced electron-hole liquid in graphene". Phys. Rev. B. 99 (4): 045434. arXiv:1807.04770. Bibcode:2019PhRvB..99d5434X. doi:10.1103/PhysRevB.99.045434. S2CID 51792702.
- Yanniotis, S.; Skaltsi, S.; Karaburnioti, S. (February 2006). "Effect of moisture content on the viscosity of honey at different temperatures". Journal of Food Engineering. 72 (4): 372–377. doi:10.1016/j.jfoodeng.2004.12.017.
- Zhao, Mengjing; Wang, Yong; Yang, Shufeng; Li, Jingshe; Liu, Wei; Song, Zhaoqi (2021). "Flow behavior and heat transfer of molten steel in a two-strand tundish heated by plasma". Journal of Materials Research and Technology. Elsevier BV. 13: 561–572. doi:10.1016/j.jmrt.2021.04.069. ISSN 2238-7854. S2CID 236277034.
- Zhmud, Boris (2014). "Viscosity Blending Equations" (PDF). Lube-Tech:93. Lube. No. 121. pp. 22–27. Archived (PDF) from the original on 2018-12-01. Retrieved 2018-11-30.
- "NIST Reference Fluid Thermodynamic and Transport Properties Database (REFPROP): Version 10". nist.gov. NIST. 2018-01-01. Archived from the original on 2021-12-16. Retrieved 2021-12-23.
- tec-science (2020-03-25). "Viscosity of liquids and gases". tec-science. Archived from the original on 2020-04-19. Retrieved 2020-05-07.
외부 링크
| 무료 사전인 Wiktionary에서 점도를 찾아 보십시오. |
| Wikisource는 The New Student's Reference Work 기사 "Viscosity of Liquids"의 본문을 가지고 있다. |
| Wikiquote에 관련된 인용구가 있음: 점도 |
- 유체 특성 – 자주 접하는 순액과 가스의 점도의 높은 정확도 계산
- 온도 함수로서의 가스 점도 계산기
- 온도 및 압력 함수로서의 공기 점도 계산기
- 유체 특성 차트 – 다양한 유체의 점성 및 증기 압력 표
- 가스 다이내믹스 도구 상자 – 가스 혼합물의 점도 계수 계산
- 유리 점성 측정 – 점성 측정, 점성 단위 및 고정점, 유리 점성 계산
- 키네마틱 점도 – 키네마틱과 동적 점도 사이의 변환
- 물의 물리적 특성 - 온도의 함수로서 물의 점성표
- 보겔-탐만-풀처 방정식 매개변수
- 일부 공통 구성 요소의 온도에 따른 동적 특성 계산
- "도로 및 비도로 엔진 및 옴니버스 기술 수정 테스트 절차" – 미국 환경 보호청
- 인공 점도
- 공기의 점도, 동적 및 동역학적, 엔지니어 에지



 0
0 




![{\displaystyle [\mu ]={\frac {\rm {kg}}{\rm {m\cdot s}}}={\frac {\rm {N}}{\rm {m^{2}}}}\cdot s={\rm {Pa\cdot s}}=}](https://wikimedia.org/api/rest_v1/media/math/render/svg/94672cf9c544af92f8e598bdd2b764795ad29697)
 전단 변형률 또는 전단 속도의
전단 변형률 또는 전단 속도의 

 로컬 전단 속도다.이 표현을 뉴턴의 점성 법칙이라고 한다.평면 대칭의 피복유동에서는
로컬 전단 속도다.이 표현을 뉴턴의 점성 법칙이라고 한다.평면 대칭의 피복유동에서는 



![{\displaystyle [\nu ]={\frac {\rm {m^{2}}}{\rm {s}}}=\mathrm {{\frac {\rm {N\cdot m}}{\rm {kg}}}\cdot s} =\mathrm {{\frac {\rm {J}}{\rm {kg}}}\cdot s} =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d3199a04f1776c84ac6126806304099e08dbe61)










![{\displaystyle {\boldsymbol {\tau }}=\mu \left[\nabla \mathbf {v} +(\nabla \mathbf {v} )^{\dagger }\right]-\left({\frac {2}{3}}\mu -\kappa \right)(\nabla \cdot \mathbf {v} )\mathbf {\delta } ,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5e5b06e2df4001df52d323172cd43795795fff66)





![{\displaystyle {\begin{aligned}\mathbf {J} &=-D{\frac {\partial \rho }{\partial x}}&&{\text{(Fick's law of diffusion)}}\\[5pt]\mathbf {q} &=-k_{t}{\frac {\partial T}{\partial x}}&&{\text{(Fourier's law of heat conduction)}}\\[5pt]\tau &=\mu {\frac {\partial u}{\partial y}}&&{\text{(Newton's law of viscosity)}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6380b89b0d24d9c9deb9ef04f333430b073c45cc)




 질량 확산도 및 열전도도이다.
질량 확산도 및 열전도도이다.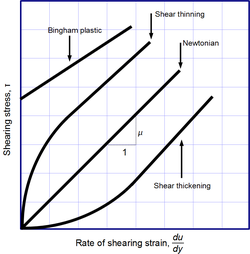





 분자질량이다.
분자질량이다.

 (가) 시작되었을 때 분자가 가졌던 속도와 동일하다
(가) 시작되었을 때 분자가 가졌던 속도와 동일하다



















 (가) 알려지고
(가) 알려지고




 액체
액체  .이 결과는 잘 알려진 경험적 관계와 같은 형태를 가지고 있다.
.이 결과는 잘 알려진 경험적 관계와 같은 형태를 가지고 있다.
 (는) 데이터에서 적합한 상수임.
(는) 데이터에서 적합한 상수임.





 농도,
농도, 















![{\displaystyle \mu =AT\exp \left({\frac {B}{RT}}\right)\left[1+C\exp \left({\frac {D}{RT}}\right)\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/38aa9224e9ac73624655cd20405e140af63a62eb)
![{\displaystyle \mu =\exp {\left\{{\frac {V_{c}C_{G}}{k_{B}T}}\exp {\left[(2+\lambda )\alpha _{T}T_{g}\left(1-{\frac {T}{T_{g}}}\right)\right]}\right\}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d7c6670713177337446c22a7976e9664d2008526)


 이른바 밀어내기 부피, 즉 관여하는 원자 그룹의 특성 부피다.원자/원자가 가장 가까운 원자의 케이지에서 탈출하는 밀어내기 사건, 일반적으로 소수의 원자가 점유한 부피 순서에 따라 발생한다.더욱이
이른바 밀어내기 부피, 즉 관여하는 원자 그룹의 특성 부피다.원자/원자가 가장 가까운 원자의 케이지에서 탈출하는 밀어내기 사건, 일반적으로 소수의 원자가 점유한 부피 순서에 따라 발생한다.더욱이 








