호환성(기차)

이 기사의 주요 부분을 다시 써야 할 수도 있다. 리드 레이아웃 가이드를 사용하여 해당 섹션이 위키백과의 규범을 따르고 모든 필수 세부사항을 포함하는지 확인하십시오. (2010년 1월) (이 템플릿 메시지를 제거하는 방법과 시기 알아보기)

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

연속체 역학에서 신체의 호환 가능한 변형(또는 변형) 텐서 장은 신체가 연속적인 단일값의 변위장을 받을 때 획득되는 독특한 텐서장이다. 양립성은 그러한 변위장이 보장될 수 있는 조건에 대한 연구다. 호환성 조건은 통합성 조건의 특별한 경우로서, 1864년 Barre de Saint-Venant에 의해 선형 탄성을 위해 처음으로 유도되었고 1886년 Beltrami에 의해 엄격하게 증명되었다.^[1]

단단한 신체에 대한 연속적인 설명에서 우리는 신체가 최소한의 부피나 물질적인 점들의 집합으로 구성될 것이라고 상상한다. 각 권은 틈이나 겹치지 않고 이웃과 연결되는 것으로 가정한다. 연속체 본체가 변형되었을 때 간격/오버랩이 발생하지 않도록 하기 위해 특정 수학 조건을 만족시켜야 한다. 틈새나 오버랩이 생기지 않고 변형되는 몸을 양립체라고 한다. 적합성 조건은 특정 변형이 신체를 호환 가능한 상태로 둘 것인지를 결정하는 수학적 조건이다.^[2]

극소수의 변형 이론의 맥락에서, 이러한 조건들은 변종을 통합하여 체내의 변위를 얻을 수 있다고 말하는 것과 같다. Such an integration is possible if the Saint-Venant's tensor (or incompatibility tensor) ${\displaystyle {\boldsymbol {R}}({\boldsymbol {\varepsilon }})}$ vanishes in a simply-connected body^[3] where ${\displaystyle {\boldsymbol {\varepsilon }}}$ is the infinitesimal strain tensor and

${\displaystyle {\boldsymbol {R}:={\boldsymbol {\nabla }\time ({\boldsymbol {\barepsilon }}}}}^{{\\\boldsymbol}}}}}}}{{{{{}}}}}}}}}}}}}}}}}}}}}}}}}}}}})T}={\boldsymbol{0}}~~}$

유한변형의 경우 호환성 조건은 다음과 같다.

${\displaystyle {\boldsymbol{R}:={\boldsymbol {\nabla}}\time {\boldsymbol{F}={\boldsymbol{0}}}}}}$

여기서 $F{\displaystyle \mathit{}}$ ${\$은(는) 변형 구배입니다.

최소 변종에 대한 호환성 조건

선형탄성에서의 호환성 조건은 3가지 미지의 변위 기능인 변형-변위 관계가 6가지임을 관찰하여 얻는다. 이는 세 가지 변위를 정보 손실 없이 방정식 시스템에서 제거할 수 있음을 시사한다. 균주의 관점에서만 결과적인 표현은 가능한 변형 영역의 형태에 제약을 제공한다.

2시 30분

2차원 평면 변형 문제의 경우 변형-변형 관계는 다음과 같다.

${\displaystyle \varepsilon _{11}={\cfrac {\partial u_{1}}{\partial x_{1}}}~;~~\varepsilon _{12}={\cfrac {1}{2}}\left[{\cfrac {\partial u_{1}}{\partial x_{2}}}+{\cfrac {\partial u_{2}}{\partial x_{1}}}\right]~;~~\varepsilon _{22}={\cfrac {\partial u_{2}}{\partial x_{2}}}}$

이러한$$ 관계의 반복적인 분화를 통해 $변위{\displaystyle {}_{}}$ $u{\displaystyle {}_{}}$ ${\$1} 및 ${\displaystyle {u\mathrm{}}_{}}$2 {\$displaystyle u_{$2}}:$$균주에 대한 2차원 호환성 조건을 얻을 수 있다.

${\displaystyle {\cfrac {\partial ^{2}\varepsilon _{11}}{\partial x_{2}^{2}}}-2{\cfrac {\partial ^{2}\varepsilon _{12}}{\partial x_{1}\partial x_{2}}}+{\cfrac {\partial ^{2}\varepsilon _{22}}{\partial x_{1}^{2}}}=0}$

호환 가능한 평면 변형률 필드에서 허용되는 유일한 변위장은 평면 변위 필드, $즉{\displaystyle \mathbf{}}$u =${\displaystyle {}_{}}$(${\displaystyle {x\mathrm{}}_{}}$ ${\displaystyle {}_{}}$,${\displaystyle {}_{}}$x${\displaystyle {}_{}{2\mathrm{}}_{}}$ ) ${\displaystyle \mathbf {u}$=\$mathbf {u}(x_{1},x_{$2})이다$.$

3시 30분

3차원에서는 2차원에 대해 보이는 2개의 형태 방정식 외에 3개의 형태 방정식이 더 있다.

${\displaystyle {\cfrac {\partial ^{2}\varepsilon _{33}}{\partial x_{1}\partial x_{2}}}={\cfrac {\partial }{\partial x_{3}}}\left[{\cfrac {\partial \varepsilon _{23}}{\partial x_{1}}}+{\cfrac {\partial \varepsilon _{31}}{\partial x_{2}}}-{\cfrac {\partial \varepsilon _{12}}{\partial x_{3}}}\right]}$

따라서 3⁴=81 부분 미분방정식이 있지만 대칭조건으로 인해 이 숫자는 6개의 다른 호환성조건으로 감소한다. 우리는 이 조건들을 다음과^[4] 같이 색인 표기법으로 쓸 수 있다.

${\displaystyle e_{ikr}~e_{jls}~\varepsilon _{ij,kl}=0}$

여기서$$ $e{\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\displaystyle k_{}}$ ${\$는 순열 기호다. 직접 텐서 표기법

${\displaystyle {\basymbol {\baslia}}\{\\basymbol {\barembol {\barepsilon}}}^{{}T}={\boldsymbol{0}}$

where the curl operator can be expressed in an orthonormal coordinate system as ${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\varepsilon }}=e_{ijk}\varepsilon _{rj,i}\mathbf {e} _{k}\otimes \mathbf {e} _{r}}$.

2차 텐서

${\displaystyle {\boldsymbol{R}:={\boldsymbol {\nabla}\time ({\boldsymbol {\nabla }}}}}\\boldsymbol {\baldsylon }}^{T}~;~R_{rs}:=e_{ikr}~e_{jls}~\varepsilon _{ij,kl}}$

비호환성 텐서로 알려져 있으며, 생베넌트 호환성 텐서와 동일하다.

유한 균주의 적합성 조건

변형이 작을 필요가 없는 고형물의 경우 적합성 조건은 형태를 취한다.

${\displaystyle {\boldsymbol {\nabla}\time {\boldsymbol{F}={\boldsymbol {0}}}$

여기서 $F{\displaystyle \mathit{}}$ ${\$은(는) 변형 구배입니다. 데카르트 좌표계에 관한 구성요소의 관점에서 우리는 이러한 호환성 관계를 다음과 같이 작성할 수 있다.

${\displaystyle e_{ABC}~{\cfrac {\partial F_{iB}}{\partial X_{A}}=0}$

변형이 연속적이고 매핑 $x{\displaystyle \mathbf{}}$ = ${\displaystyle =}$ (${\displaystyle X}$, ${\displaystyle t\mathbf{}}$) ${\displaystyle \mathbf {x} ={\boldsymbol${\$chi }}(\mathbf {X}$ ,$t)}$에서 파생되는 경우 이 조건이 필요하다($$한정변형 변형률 이론 참조). 단순히 연결된 본체에서도 호환성을 확보하기에 같은 조건이면 충분하다.

오른쪽 Cauchy-Green 변형 텐서 호환성 조건

오른쪽 Cauchy-Green 변형 텐서의 호환성 조건은 다음과 같이 표현할 수 있다.

${\displaystyle R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\Gamma _{\alpha \rho }^{\gamma }]+\Gamma _{\mu \rho }^{\gamma }~\Gamma _{\alpha \beta }^{\mu }-\Gamma _{\mu \beta }^{\gamma }~\Gamma _{\alpha \rho }^{\mu }=0}$

여기서 $\gamma {\displaystyle {\mathrm{}}_{}^{}}$ i ${\displaystyle {}_{}^{}}$ ${\displaystyle k_{}^{}}$ ${\${ij$}^{k}}}}$는 두 번째 종류의 크리스토펠 기호다. $수량{\displaystyle {}_{}^{}}$ ${\displaystyle {Rii}_{}^{}}$ ${\displaystyle {\mathrm{jk}}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$은 리만-크리스토펠 곡률 텐서의 혼합 성분을 나타낸다$$.

일반적인 호환성 문제

연속체 역학의 호환성 문제에는 단순히 연결된 신체에 허용되는 단일 값 연속적 장의 결정이 포함된다. 더 정확히 말하면, 그 문제는 다음과 같은 방법으로 명시될 수 있다.^[5]

그림 1에 나타난 차체의 변형을 고려한다. 참조 좌표계${\displaystyle }${${\displaystyle }$(${\displaystyle {\mathrm{}}_{}}$ 1,${\displaystyle {}_{}{\mathrm{}}_{}}$ 2,${\displaystyle {}_{}{\mathrm{}}_{}}$ ${\displaystyle {}_{}}$)${\displaystyle }$, ${\displaystyle O}$ ${\displaystyle \}}$ ${\displaystyle \{{{{(\mathbf {E} _{1},\mathbf {E} _{2},\mathbf {E} _{3}),$$O$ 체내의 한 점의 변위는 다음과 같이 주어진다.

${\displaystyle \mathbf {u} =\mathbf {x} -\mathbf {X} ~;~u_{i}=x_-X_{i}}}}$

또한

${\displaystyle {\boldsymbol {\nabla }}\mathbf {u} ={\frac {\partial \mathbf {u} }{\partial \mathbf {X} }}~;~~{\boldsymbol {\nabla }}\mathbf {x} ={\frac {\partial \mathbf {x} }{\partial \mathbf {X} }}}$

주어진$$ 2차 텐서 필드 $A{\displaystyle \mathit{}(}$ X${\displaystyle }$) ${\displaystyle {\boldsymbol {A}(\mathbf {X})}$의 조건이 충족되는 고유한$$ 벡터 필드 $v{\displaystyle \mathbf{}(}$ ${\displaystyle X\mathbf{}}$) ${\displaystyle \mathbf {v}(\mathbf {X})$가 존재하기에 충분하고 필요한 조건

${\displaystyle {\boldsymbol {\nabla}\mathbf {v} ={\boldsymbol {A}\quad \quad \quad v_{i,j}=A_{ij}}$

필요조건

필요한 조건의 경우 $필드{\displaystyle \mathbf{}}$v {\$displaystyle \mathbf${v}이$($가) 존재하며$$ ${\displaystyle v_{}}$ i${\displaystyle {}_{}}$, j${\displaystyle {}_{}}$= ${\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$을(를) 만족한다고 가정한다.$A_{ij$ 그러면

${\displaystyle v_{i,jk}=A_{ij,k}~;~v_{i,kj}=A_{ik,j}}$

차별화 순서를 바꾸는 것은 결과에 영향을 미치지 않기 때문에 우리는 다음과 같이 한다.

${\displaystyle v_{i,jk}=v_{i,kj}}$

그러므로,

${\displaystyle A_{ij,k}=A_{ik,j}}$

텐서의 굴림에 대해 잘 알려진 정체성으로부터 우리는 필요한 조건을 얻는다.

${\displaystyle {\boldsymbol {\nabla}\time {\boldsymbol{A}={\boldsymbol {0}}}$

충분한 조건

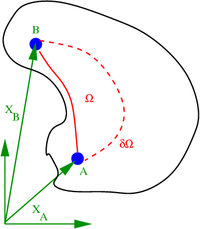
To prove that this condition is sufficient to guarantee existence of a compatible second-order tensor field, we start with the assumption that a field ${\displaystyle {\boldsymbol {A}}}$ exists such that ${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {A}}={\boldsymbol {0}}}$. We will integrate this field $지점$ A$$ ${\$ $A$$}$과$($) B {\displaystyle B} 사이의 선을 따라 벡터 필드 v {\$displaystyle$ $\mathbf$ {$v}$}을(를) 찾으려면($$그림 2 $참조$).

${\displaystyle \mathbf {v} (\mathbf {X} _{B})-\mathbf {v} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {v} \cdot ~d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {A}}(\mathbf {X} )\cdot d\mathbf {X} }$

벡터 필드 $v{\displaystyle \mathbf{}}$ ${\$을(를) 단일 값으로 하려면$$ 적분 값이 $A{\displaystyle }$ ${\displaystyle A}$에서 $B{\displaystyle }$ ${\displaystyle B}($으)로$$ 이동하는 데 사용된 경로와 독립적이어야 한다$.$

스톡스의 정리로부터, 닫힌 길을 따라가는 제2차 순서 텐서(tensor)의 적분은 다음과 같이 주어진다.

${\displaystyle \partial \Oomega}{\boldsymbol {A}\cdot d\mathbf {s} =\int_{\Oomega}\mathbf {n}\cdot({\boldsymbol{\nabla}}}\time {\\bmbolda})~da}$

$A{\displaystyle \mathit{}}$ ${\$의 컬이 0이라고$$ 가정하면

${\displaystyle \partial \Oomega}{\boldsymbol {A}\cdot d\mathbf {s} =0\quad \implies \quad \quad \quad \int_{AB}{\boldsymboll {A}\cdmathbf}+X}A}{\boldsymbol {A}\cdot d\mathbf {X} =0}$

따라서 본질은 경로에 독립적이며, 본문이 단순히 연결되어 있다면 호환성 조건은 고유한 $v{\displaystyle \mathbf{}}$ ${\$ 필드를$$ 보장하기에 충분하다.

변형 구배 적합성

변형 구배 적합성 조건은 위의 증거에서 다음과 같이 직접 구한다.

${\displaystyle {\boldsymbol {F}={\cfrac {\partial \mathbf {x}{\partial \mathbf{X}}}={\boldsymbol {\nabla}}}}}}}}}$

그렇다면 단순히 연결된 본체 위에 호환되는 $F{\displaystyle \mathit{}}$ ${\$ 필드가$$ 존재하기 위한 필요하고도 충분한 조건은 다음과 같다.

${\displaystyle {\boldsymbol {\nabla}\time {\boldsymbol{F}={\boldsymbol {0}}}$

극소수 균주의 호환성

소형 변종의 적합성 문제는 다음과 같이 명시할 수 있다.

대칭적인 두 번째 순서 텐서 필드 $ϵ{\displaystyle \mathit{}}$ ${\$이(가) 지정되면 다음과$$ 같은$$ 벡터 필드 $u{\displaystyle \mathbf{}}$ ${\$를) 구성할 수 있는가?

${\displaystyle {\boldsymbol {\epsilon}}={\frac {1}{1}:{2}}:[{\boldsymbol {\nabla }}}+({\boldsymbol {\\nabla }}}}}}})^{T}}}}}$

필요조건

$ϵ{\displaystyle \mathit{}}$ ${\$$displaystyle${\$mathbf {u$$}$에 대한 식이 유지되는$$ u {\displaystyle ${\boldsymbol {\epsilon$}}이$($가) 있다고 가정하십시오. 지금

${\displaystyle {\bmbol {\bla }\mathbf {u} = {\\bmithmbol {\epsilon }+{\bmbol {\omega}}}}}$

어디에

${\displaystyle {\boldsymbol {\omega}:={\frac {1}{1}:{2}}[{\boldsymbol {\nabla }}}-({\boldsymbol {\\nabla }}}})^{T}}}}}$

따라서, 색인 표기법에서는

${\displaystyle {\boldsymbol {\nabla }}{\boldsymbol {\omega }}\equiv \omega _{ij,k}={\frac {1}{2}}(u_{i,jk}-u_{j,ik})={\frac {1}{2}}(u_{i,jk}+u_{k,ji}-u_{j,ik}-u_{k,ji})=\varepsilon _{ik,j}-\varepsilon _{jk,i}}$

$\Omega {\displaystyle \mathit{}}$ ${\$이(가) 계속 다를 경우 $\Omega {\displaystyle {}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {j,}_{}}$ ${\displaystyle k_{}}$ =${\displaystyle {}_{}{}_{}}$ ${\displaystyle i_{}}$ ${\displaystyle {j,}_{}}$ ${\displaystyle l_{}}$ ${\displaystyle k_{}}$ ${\$ 따라서

${\displaystyle \varepsilon _{ik,jl}-\varepsilon _{jk,il}-\varepsilon _{jl,ik}=0}$

직접 텐서 표기법

${\displaystyle {\symbol {\bla }\pcsymbol {\bla }{\bla }\psymbol {\epsilon }}^{{}}T}={\boldsymbol{0}}$

위의 조건은 필수 조건이다. If ${\displaystyle \mathbf {w} }$ is the infinitesimal rotation vector then ${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} +{\boldsymbol {\nabla }}\mathbf {w} ^{T}}$. Hence the necessary condition may also be written as ${\displaystyle \mathbf{\nabla }\times (\mathbf{\nabla }}$${\$$T}={\boldsymbol{0$

충분한 조건

${\displaystyle 이제\mathit{}}$ ${\displaystyle {조건}^{}}$ $\nabla {\displaystyle \mathbf{}}$ ${\displaystyle \times }$ (${\displaystyle \mathbf{}}$× ${\displaystyle \times }$ ${\displaystyle \times {}^{}}$ ) T${\displaystyle {}^{}}$= ${\displaystyle 0\mathbf{}}${\$displaystyle${\$boldsymbol${\$nabla$}}\time ({\$boldsymbol${\$nabla }}}}}\time {\boldsymbol{\bla}}}}}^{{{}}}}}}}}}}}}}}}}}}}}$$T}={\boldsymbol{0}}}}$은(는) 신체 일부에서 만족한다$$. 이 조건은 연속적인 단일 값 변위 $필드{\displaystyle \mathbf{}}$ ${\$의 존재를$$보장하기에 충분한가$?$

프로세스의 첫 번째 단계는 이 조건이 최소 회전 텐서 $\Omega {\displaystyle \mathit{}}$ ${\$이(가) 고유하게 정의되었음을$$ 함축한다는 것을 보여주는 것이다. ${\displaystyle {}_{}}$를 위해 ${\displaystyle X\mathbf{}}{\displaystyle \mathbf{}}$${\displaystyle {}_{}}$ ${\$$displaystyle {\boldsymbol {\nabla }}\mathbf$${X} _{A}$에서 $X{\displaystyle {\mathbf{}}_{}}$ B ${\$$_{B}$ } 경로를 따라$$along$$ w ${\$displaystystylement \matbf{\{\c}, 즉,

${\displaystyle \mathbf {w} (\mathbf {X} _{B})-\mathbf {w} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {w} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }})\cdot d\mathbf {X} }$

참조 $w{\displaystyle \mathbf{}}$( ${\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$) ${\displaystyle \mathbf {w}(\mathbf {X} _{A})$를 알아야 강체 회전을 고정할 수 있다는 점에 유의하십시오. $w{\displaystyle \mathbf{}}$( ${\displaystyle X\mathbf{}}$) ${\displaystyle \mathbf {w}(\mathbf${X$})(\$mathbf {$X})$ 필드는 $X{\displaystyle {\mathbf{}}_{}}$ ${\displaystyle {}_{}}$ ${\$$displaystyle \mathbf$$${$X} _{b}$ 사이의$$ 닫힌 윤곽선을 따라 통합된 윤곽선이 0인$$ 경우에만 고유하게 결정된다$$.

${\displaystyle \point _{\mathbf{X} _{A}^{\mathbf{X} _{B}}({\boldsymbol{\nabla }}})\회 {\boldsymbol {\epsilon}}\cdot d\mathbf{X}}}}}}$

그러나 단순하게 연결된 몸을 위한 스토크스의 정리로부터 그리고 호환성을 위해 필요한 조건으로부터.

${\displaystyle \point _{\mathbf{X} _{A}^{\mathbf {X} _{B}}({\boldsymbol {\nabla }}}}\boldsymbol {\epsilon})\cdot d\mathbf {X}{{{\int_{{{{}}}}}}}}AB}\mathbf{n} \cdot({\boldsymbol {\nabla }}\time {\boldsymbol {\nabla }}}}\time {\boldsymbol {\epsilon }}})~da={\boldsymbol{0}}}$

$따라서{\displaystyle \mathbf{}}$ ${\$ 필드가 고유하게 정의되며$$, 이는 본체가 단순하게 연결되어 있다면 최소 회전 텐서르 $\Omega {\displaystyle \mathit{}}$ ${\$도 고유하게 정의됨을$$ 의미한다.

다음 단계에서는 변위 구배를 통합하기 전에 변위장 ${\$의 고유성을 고려할 것이다$.$

${\displaystyle \mathbf {u} (\mathbf {X} _{B})-\mathbf {u} (\mathbf {X} _{A})=\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}{\boldsymbol {\nabla }}\mathbf {u} \cdot d\mathbf {X} =\int _{\mathbf {X} _{A}}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon }}+{\boldsymbol {\omega }})\cdot d\mathbf {X} }$

From Stokes' theorem and using the relations ${\displaystyle {\boldsymbol {\nabla }}\times {\boldsymbol {\epsilon }}={\boldsymbol {\nabla }}\mathbf {w} =-{\boldsymbol {\nabla }}\times \omega }$ we have

${\displaystyle \point _{\mathbf {X} _{A}^{\mathbf {X} _{B}}({\boldsymbol {\epsilon}}}+{\boldsymbol {\\mathbf {X}} = {\int_{{\Oomega_}){{{{}}}}}}}}}}}}}}AB}\mathbf{n} \cdot({\boldsymbol {\nabla }}}\time {\boldsymbol {\epsilon }}}}}}\time {\boldsymbol {\omega })~da={\\boldsymbol {0}}}}$

따라서 변위 필드 $u{\displaystyle \mathbf{}}$ ${\$도 고유하게 결정된다$$. 따라서 호환성 조건은 단순히 연결된 본체에서 고유한$$ 변위 필드 $u{\displaystyle \mathbf{}}$ ${\$의 존재를 보장하기에 충분하다.

우측 카우치-녹색변형장치의 적합성

Right Cauchy-Green 변형 영역의 호환성 문제는 다음과 같이 제기할 수 있다.

문제: $C{\displaystyle \mathit{}}$( ${\displaystyle X\mathbf{}}$) ${\displaystyle {\boldsymbol {C}(\mathbf {X})$을 참조 구성에 정의된 양의 한정 대칭 텐서 필드로 설정하십시오$$. $C{\displaystyle \mathit{}}$ ${\$${\displaystyle C\mathbf{}}$$}$의 어떤 조건에서 다음과 같은 $위치{\displaystyle \mathbf{}}$ 필드${\displaystyle }$x${\displaystyle }$( X$$) {\$displaystyle \mathbf${x$$$}(\mathbf${X$})$로 표시된 변형된 구성이 있는가$$?

${\displaystyle(1)\quad \left({\frac {\partial \mathbf {x}{\partial \mathbf {X}}}}\오른쪽)^{T}\왼쪽({\frac {\partial \mathbf {x}{}}{\partial \mathbf {X}}}}\오른쪽)={\boldsymbol {C}}}}$

필요조건

조건 (1)을 충족하는 필드 $x{\displaystyle \mathbf{}}$ (${\displaystyle X\mathbf{}}$) ${\displaystyle \mathbf {x}(\mathbf {X})$가 존재한다고$$ 가정합시다. 직사각형 데카르트 기반에 대한 구성 요소 측면

${\displaystyle {\frac {\partial x^{i}{\partial x^{\alpha }{\partial x^{i}}{\partial X^{\beta}}}=C_{\partial \alpha \beta \beta }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

유한 변형률 이론으로부터 $우리$는 C ${\displaystyle {\alpha }_{}}$ ${\displaystyle {\beta }_{}}$= g ${\displaystyle {\alpha }_{}}$ ${\displaystyle {\beta }_{}}$ ${\$ $\}\}\}\}\}\}$그러므로 쓸 수 있다.

${\displaystyle \delta _{ij}~{\frac {\partial x^{\alpha }}{\partial x^{j}}{\partial X^{\partial X^{\beta}}}=g_{\alpha \beta \veta }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

일대일로 매핑된 두 개의 대칭 2차 텐서 필드의 경우에도 관계가 있다.

${\displaystyle G_{ij}={\frac {\partial X^{\alpha}}{\partial X^{i}}}{\partial X^{\beta}}{\partial x^{j}}}}{\alpha \beta \}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}:{\partfrac$

$Gi{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ ${\$과(${\displaystyle {와}_{}}$) $β$ {\$displaystyle$ g_${\\alpha \beta}}}$의 관계에서 $\Delta {\displaystyle {}_{}}$ i ${\displaystyle j_{}}$= G ${\displaystyle i_{}}$ ${\displaystyle j_{}}$ ${\$

${\displaystyle _{(x)}\감마 _{ij}^{k}=0}$

그러면 관계상으로는.

${\displaystyle {\frac {\partial ^{2}x^{m}}{\partial X^{\alpha }\partial X^{\beta }}}={\frac {\partial x^{m}}{\partial X^{\mu }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-{\frac {\partial x^{i}}{\partial X^{\alpha }}}~{\frac {\partial x^{j}}{\partial X^{\beta }}}\,_{(x)}\Gamma _{ij}^{m}}$

우리는 가지고 있다.

${\displaystyle {\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }\qquad ;~~F_{~\alpha }^{i}:={\frac {\partial x^{i}}{\partial X^{\alpha }}}}}}$

유한한 변형 이론으로부터 우리는 또한

${\displaystyle _{(X)}\Gamma _{\alpha \beta \gamma }={\frac {1}{2}}\left({\frac {\partial g_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial g_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial g_{\alpha \beta }}{\partial X^{\gamma }}}\right)~;~~_{(X)}\Gamma _{\alpha \beta }^{\nu }=g^{\nu \gamma }\,_{(X)}\Gamma _{\alpha \beta \gamma }~;~~g_{\alpha \beta \}=C_{\alpha \beta };~~g^{\g^{\alpha \beta }}}}}}}}$

그러므로

${\displaystyle \,_{(X)}\Gamma _{\alpha \beta }^{\mu }={\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)}$

그리고 우리는

${\displaystyle {\frac {\partial F_{~\alpha }^{m}}{\partial X^{\beta }}}=F_{~\mu }^{m}~{\cfrac {C^{\mu \gamma }}{2}}\left({\frac {\partial C_{\alpha \gamma }}{\partial X^{\beta }}}+{\frac {\partial C_{\beta \gamma }}{\partial X^{\alpha }}}-{\frac {\partial C_{\alpha \beta }}{\partial X^{\gamma }}}\right)}$

다시 말하지만, 분화 순서의 역순성을 이용하여, 우리는

${\displaystyle {\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\beta }\partial X^{\rho }}}={\frac {\partial ^{2}F_{~\alpha }^{m}}{\partial X^{\rho }\partial X^{\beta }}}\implies {\frac {\partial F_{~\mu }^{m}}{\partial X^{\rho }}}\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]={\frac {\partial F_{~\mu }^{m}}{\partial X^{\beta }}}\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]}$

또는

${\displaystyle F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\mu }]=F_{~\gamma }^{m}\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }+F_{~\mu }^{m}~{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\mu }]}$

용어를 모은 후 우리는 얻는다.

${\displaystyle F_{~\gamma }^{m}\left(\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }+{\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamm}]\오른쪽)=0}$

$F{\displaystyle {}_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$의 정의에서 우리는 그것이$$ 되돌릴 수 없으므로 0이 될 수 없음을 관찰한다. 그러므로

${\displaystyle R_{\alpha \beta \rho }^{\gamma }:={\frac {\partial }{\partial X^{\rho }}}[\,_{(X)}\Gamma _{\alpha \beta }^{\gamma }]-{\frac {\partial }{\partial X^{\beta }}}[\,_{(X)}\Gamma _{\alpha \rho }^{\gamma }]+\,_{(X)}\Gamma _{\mu \rho }^{\gamma }\,_{(X)}\Gamma _{\alpha \beta }^{\mu }-\,_{(X)}\Gamma _{\mu \beta }^{\gamma }\,_{(X)}\Gamma _{\alpha \rho }^{\mu }=0}$

우리는 이것들이 리만-크리스토펠 곡률 텐서의 혼합 성분임을 보여줄 수 있다. 따라서 $C{\displaystyle \mathit{}}$ ${\$ -호환성에$$ 필요한 조건은 변형의 리만-크리스토펠 곡률이 0이라는 것이다.

충분한 조건

충분하다는 증거가 좀 더 개입되어 있다.^[5][6] 우리는 다음과 같은 가정으로부터 출발한다.

${\displaystyle R_{\alpha \beta \rho }^{\gamma }=0~;~g_{\alpha \beta }=C_{\alpha \beta }}}}}}}}}}}}}}}}}"$

$우리$는 $다음$과$$같은 x {\$displaystyle \mathbf$ {$x}$과$($) X ${\displaystyle$\mathbf$$ {$X}$이(가) 존재함을 보여줘야 한다.

${\displaystyle {\frac {\partial x^{i}{\partial x^{\alpha }{\partial x^{i}}{\partial X^{\beta}}}=C_{\partial \alpha \beta \beta }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

T.Y.의 정리로부터.토마스 우리는 방정식의 체계를 안다.

${\displaystyle {\frac {\partial F_{~\alpha }^{i}}{\partial X^{\beta }}}}}=F_{~\gamma }{{{{}}}}}\gamma _{\alpha \beta }{}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

단순히 연결된 도메인에 대해$$ 고유한 솔루션 $F{\displaystyle {}_{}^{}}$ ${\displaystyle {\alpha }_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$을(를) 가지고 있는 경우

${\displaystyle _{(X)}\감마 _{\alpha \beta \beta }^{(X)}\감마 _{\beta \alpha \alpha }^{~R_{\alpha \rho }^{}^{\gamma }=0}}}}$

이 중 첫 번째는 $\gamma {\displaystyle {\mathrm{}}_{}^{}}$ ${\displaystyle j_{}^{}}$ ${\displaystyle {}_{}^{}}$ i ${\$jk$}^{i}}}$의 정의에서 따르며, 두$$ 번째는 가정한다. 따라서 가정 조건은 ${\displaystyle {}_{}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$$alpha }^{$$i}}{{}}}}}{$i$}}}$을(를) 연속적으로$$ $우리$에게 제공한다.

다음으로 방정식의 체계를 고려한다.

${\displaystyle {\frac {\partial x^{i}{\partial X^{\\alpha }}}=F_{~\alpha }^{i}}}}$

$F{\displaystyle {}_{}^{}}$ ${\displaystyle {\alpha }_{}^{}}$ ${\displaystyle {}_{}^{}}$ ${\$$alpha$ $}^{i$}}}{i$}}$은(는) $C{\displaystyle {}^{}}$ ${\displaystyle {2\mathrm{}}^{}}$ ${\$$displaystyle$ C$^{i}}}}}}}$이$(가$) 단순히 연결되어 있기 때문에 위의 방정식에 대한 일부$$ 용액 $x{\displaystyle {}^{}}$ ${\displaystyle i^{}}$ X$$ ${\displaystyle {}^{}}$가$있다$. $x{\displaystyle {}^{}}$ ${\displaystyle i^{}}$ ${\$도 그 속성을 만족시킨다는 것을 보여줄 수 있다.

${\displaystyle \det \왼쪽 {\frac {\partial x^{i}{\partial X^{\alpha }}\오른쪽 \neq 0}$

우리는 또한 그 관계가

${\displaystyle {{\frac {\partial x^{i}{\partial x^{\alpha }}~g^{\partial x^{j}{\partial X^{\partial X^{\}}}=\delta ^{ij}}}}}}}}}}$

라는 뜻을 내포함하다

${\displaystyle g_{\alpha \beta }=C_{\alpha \beta }={\frac {\partial x^{k}}{\partial x^{k}}}{\partial X^{\beta}}}}}}}}}}}}}}}}}}:{\partial X^{partial X^{\frac$

이 수량을 텐서 필드와 ${\displaystyle \frac{연결}{}}$하면 $\partial {\displaystyle \frac{\mathrm{}}{}}$ x ${\displaystyle \frac{\partial }{\mathrm{}}}$ X ${\$은(는) 변환 불가능하며 생성된 텐서 필드는 C ${\$에 대한 식을 만족한다는 것을 알 수 있다$.$

참고 항목

• 생베난트의 호환성 조건
• 선형탄성
• 변형(기전)
• 무한변형론
• 유한변형 이론
• 텐서 유도체(연속역학)
• 곡선 좌표

참조

외부 링크

• 아미트 아차랴의 iMechanicalica 호환성에 관한 노트
• J. Lubliner에 의한 가소성, 초 1.2.4 페이지 35