질량 보존

이 글은 검증을 위해 인용구가 추가로 필요하다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선할 수 있도록 도와주십시오. 공급되지 않은 재료는 도전하여 제거할 수 있다. 출처 찾기: "미사 보존" – 뉴스 · 신문 · 책 · 학자 · JSTOR (2020년 5월) (이 템플릿 메시지를 제거하는 방법과 시기 학습)

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

물리학과 화학에서 질량보존의 법칙이나 질량보존의 원리는 물질과 에너지의 모든 전달에 닫힌 어떤 시스템의 경우 시스템의 질량이 변할 수 없기 때문에 시스템의 질량은 시간이 지남에 따라 일정하게 유지되어야 하므로 질량을 더하거나 제거할 수 없다고 명시하고 있다. 따라서 질량의 양은 시간이 지남에 따라 보존된다.

이 법은 질량이 우주로 재배열되거나 관련 실체가 형태적으로 변경될 수 있지만 생성되거나 파괴될 수 없다는 것을 암시하고 있다. 예를 들어, 화학 반응에서, 반응 전의 화학 성분의 질량은 반응 후의 성분 질량과 동일하다. 따라서 격리된 시스템에서 화학반응과 저에너지 열역학 프로세스 중에 반응물질 또는 시동물질의 총 질량은 제품의 질량과 같아야 한다.

대량 보존의 개념은 화학, 역학, 유체 역학과 같은 많은 분야에서 널리 사용되고 있다. 역사적으로 화학 반응에서의 대량 보존은 미하일 로모노소프에 의해 독립적으로 증명되었고 이후 18세기 후반에 앙투안 라부아지에에 의해 재발견되었다. 이 법칙의 제정은 연금술에서 현대 화학의 자연과학으로 발전하는 데 결정적인 중요성이 있었다.

실제로 질량의 보존은 대략적으로만 유지되며 고전역학에서 일련의 가정의 일부로 간주된다. 에너지와 질량이 하나의 보존량을 형성한다는 질량에너지 동등성 원칙에 따라 양자역학과 특수상대성이론의 법칙을 준수하도록 법이 수정돼야 한다. 매우 에너지 넘치는 시스템의 경우, 입자 물리학에서 핵반응과 입자-항문자 전멸의 경우처럼 질량만을 보존하는 것이 유지되지 않는 것으로 보인다.

질량 또한 일반적으로 개방형 시스템에 보존되지 않는다. 다양한 형태의 에너지와 물질이 시스템에 들어오거나 빠져나갈 수 있는 경우가 이에 해당한다. 그러나 방사능이나 핵반응이 개입되지 않는 한 열, 기계 작업 또는 전자기 방사선과 같은 시스템에서 탈출(또는 유입)하는 에너지의 양은 보통 시스템 질량의 감소(또는 증가)로 측정하기에는 너무 작다.

큰 중력장을 포함하는 시스템의 경우 일반상대성이성을 고려해야 한다. 따라서 질량 에너지 보존은 다른 정의에 따라 더욱 복잡한 개념이 되며 질량도 에너지도 특수상대성이론처럼 엄격하게 단순하게 보존되지 않는다.

공식화 및 예시

질량 보존의 법칙은 오직 고전적인 역학에서만 공식화될 수 있는데, 이 역학에서는 격리된 시스템과 관련된 에너지 $척도$가 m ${\displaystyle {c\mathrm{}}^{}}$ 2 ${\$ m$^{2$}}보다 훨씬 작다$.$ $여기$서 m$${\$displaystyle m}$은 물체가 정지해 있는 참조 프레임에서 측정된 시스템 내 대표적인 물체의 질량이다.d $[\displaystyle c}$는 빛의 속도다.

법칙은 유체역학과 연속역학의 분야에서 수학적으로 공식화할 수 있는데, 질량의 보존은 보통 연속성 방정식을 사용하여 표현되는데, 여기서 다음과 같이 미분 형태로 주어진다.

${\displaystyle {\frac {\reship \rho }{\reshold t}+\cdla \cdot(\rho \mathbf {v} )=0,}$

여기서 $\rho$ ${\$$textstyle \rho}$은$$ 밀도(단위 볼륨당 질량), t ${\textstyle$ t$}$은 $시간$, } , ∇$textstyle \nabla \cdot}$은 발산, v {\$textstyle \mathbf {v}}$은 흐름 속도 필드. 질량에 대한 연속성 방정식의 해석은 다음과 같다. 시스템에서 주어진 닫힌 표면의 경우, 표면으로 둘러싸인 질량의 변화는 그 시간 간격 동안 표면을 가로지르는 질량과 동일하다. 물질이 들어가면 양이고 물질이 나가면 음이다. 전체 격리된 시스템의 경우, 이 조건은 전체 $질량$ M ${\textstyle$ M$},$즉 시스템 내 모든 구성 요소의 질량 합계가 시간이 지남에 따라 변하지 않는다는 것을 의미한다.

${\displaystyle {\frac {{\text{d}}$$M}{{\text{d}}}}={\frac {\text{d}}}{{\text{d}}}\int \rho {\text}V=0$

여기서 $d$ $V$ ${\textstyle {\text{d}V}$는 시스템의 전체 볼륨에 걸쳐 적분을 정의하는 차등이다.

질량에 대한 연속성 방정식은 유체 역학의 오일러 방정식의 일부분이다. 많은 다른 대류-확산 방정식은 주어진 시스템에서 질량과 물질의 보존과 흐름을 설명한다.

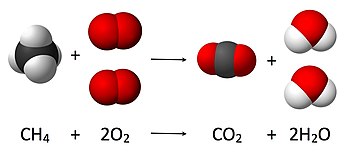
화학에서는 화학반응에서 반응물질과 제품의 양, 즉 스토이치측정법(stoichometry)의 계산이 질량보존의 원리에 근거한다. 원리는 화학 반응 동안 반응 물질의 총 질량이 제품의 총 질량과 같다는 것을 의미한다. 예를 들어, 다음과 같은 반응에서

CH
₄ + 2 O
₂ → CO
₂ + 2 H
₂O,

여기서 메탄(CH
₄) 1개 분자와 산소 분자 O
₂ 2개가 이산화탄소(CO
₂) 1개 분자와 물(HO
₂) 2개로 변환된다. 반응으로 인한 분자의 수는 처음에는 수소 원자 4개, 산소 원자 4개, 탄소 원자 1개가 존재하므로(최종 상태에서도 마찬가지) 생성된 물 분자의 수는 정확히 1개의 이산화탄소 분자당 2개여야 한다.

많은 공학적인 문제들은 시간이 지남에 따라 주어진 시스템의 대량 분배를 따라 해결된다; 이 방법론은 질량 균형이라고 알려져 있다.

역사

기원전 520년에 마하비라의 가르침에 근거한 비창조주의 철학인 자인철학은 우주와 물질과 같은 그 구성요소는 파괴되거나 창조될 수 없다고 명시했다.^[4] 자인 문자 Tattvartasutra(2세기 CE)는 물질은 영구적이지만 그 모드는 생성과 파괴에 의해 특징지어진다.^[5]

고대 그리스 철학에서 중요한 생각은 "무에서 오는 것은 없다"는 것이었고, 그래서 지금 존재하는 것은 항상 존재해 왔다. 전에는 없었던 곳에 새로운 물질이 존재할 수 없다. 이에 대한 명시적 진술은 아무것도 무로 전멸할 수 없다는 추가적인 원칙과 함께 엠페도클레스(기원전 4세기경)에서 발견된다: "무엇이든 없는 것에서 오는 것은 불가능하며, 무엇이든지 완전히 파괴되어야 한다는 것을 가져오거나 들을 수 없기 때문이다."^[6]

기원전 3세기경 에피쿠로스는 우주의 본질을 설명하면서 "사물의 총체성은 항상 지금과 같았고, 앞으로도 그럴 것"^[7]이라고 썼다.

물질 보존의 원칙도 나스르 알-딘 알-투스 (CE 13세기경)에 의해 명시되었다. 그는 "물질의 몸체가 완전히 사라질 수는 없다. 단지 형태, 조건, 구성, 색상 및 기타 특성만 변화시키고 다른 복합 물질이나 기본적인 물질로 변한다."^{[8][better source needed]}

화학의 발견

18세기에 이르러 화학반응 중 질량보존의 원리가 널리 사용되었고,^[9] 조셉 블랙, 헨리 캐번디쉬, 장 레이의 작품에서 볼 수 있듯이 정의가 정식으로 성립되기 이전에도 실험 중 중요한 가정이었다.^[10] 그 원리를 처음으로 개괄한 것은 1756년 미하일 로모노소프였다. 그는 실험에 의해 그것을 증명했을지도 모르며 1748년 레온하르트 오일러와 교신하면서 분명히 그 원리에 대해 논의했을 것이다,^[11] 비록 그 주제에 대한 그의 주장이 때때로 도전받고 있기는 하지만 말이다.^[12][13] 소련의 물리학자 야코프 도프만에 따르면:

보편적 법칙은 로모노소프에 의해 일반적인 철학적 유물론적 고려에 기초하여 공식화되었고, 그에 의해 질문이나 실험된 적은 없지만, 반대로 평생에 걸친 모든 연구에서 확고한 출발지위로서 기능했다. ^[14]

이후 앙투안 라부아지에가 1773년 자신의 결론을 표명하고 질량 보존의 원리를 대중화시킨 더욱 정제된 일련의 실험이 진행되었다. 그 원리의 시연은 연소 과정과 열 과정에서 질량을 얻거나 잃을 수 있다는 당시의 대중적인 phlogiston 이론을 반증했다.

지구 대기의 부력이 기체의 무게에 미치는 영향 때문에 질량 보존은 수천 년 동안 모호했다. 예를 들어, 나무 조각은 불에 탄 후 무게가 덜 나간다; 이것은 나무 덩어리의 일부가 사라지거나 변형되거나 없어지는 것을 암시하는 것처럼 보였다. 이는 밀봉된 유리 앰플에서 녹슬기 등 화학반응이 일어날 수 있도록 세심한 실험을 하기 전까지는 반증되지 않았으며, 화학반응으로 밀봉된 용기의 무게와 내용물이 바뀌지 않은 것으로 밝혀졌다. 17세기에 진공 펌프가 발명되기 전까지는 비늘을 이용한 기체의 무게를 측정할 수 없었다.

일단 이해되면, 질량의 보존은 연금술에서 현대 화학으로 발전하는 데 매우 중요했다. 일단 초기 화학자들이 화학 물질은 결코 사라지지 않고 같은 무게의 다른 물질로만 변형된다는 것을 깨달았을 때, 이 과학자들은 처음으로 물질의 변화에 대한 양적 연구에 착수할 수 있었다. 질량 보존에 대한 관념과 특정한 "원소 물질"도 화학 반응에 의해 다른 물질로 변형될 수 없다는 추측은 차례로 화학 원소에 대한 이해로 이어졌고, 모든 화학적 과정과 변화(연소 및 대사 반응 등)는 불변량 사이의 반응이라는 관념으로 이어졌다. 또는 이러한 화학 원소의 무게.

라부아지에의 선구적인 작업에 이어 장 스타스의 철저한 실험은 비록 다른 의도를 가지고 수행되었음에도 불구하고 ^[15]화학 반응에서 이 법칙의 일관성을 뒷받침했다. 그의 연구는^[16][17] 특정 반응에서 손실이나 이득이 10만분의 2에서 4부분 이상일 수 없다는 것을 보여주었다.^[18] 한편으로 라부아지에가 지향하고 달성한 정확도, 다른 한편으로 몰리와 스타스가 달성한 정확도의 차이는 어마어마하다.^[19]

현대물리학

질량 보존의 법칙은 특수상대성이성의 출현과 함께 도전받았다. 1905년 아인슈타인의 아누스 미라빌리스 논문 중 하나에서 그는 질량과 에너지의 동등성을 제시했다. 이 이론은 시스템의 내부 에너지가 전체 시스템의 질량에 기여할 수 있거나 질량이 전자기 방사선으로 변환될 수 있다는 생각처럼 몇 가지 주장을 내포하고 있었다. 그러나 막스 플랑크가 지적한 바와 같이 아인슈타인의 이론에서 예측한 바와 같이 화학적 에너지의 추출이나 추가에 따른 질량의 변화는 이용 가능한 계기로 측정할 수 없을 정도로 작으며 특수 상대성 시험으로 제시될 수 없다. 아인슈타인은 반응 에너지가 시스템에서 제거된 후 질량의 변화를 측정할 수 있도록 새로 발견된 방사능과 관련된 에너지가 이를 생성하는 시스템의 질량과 비교했을 때 충분히 유의하다고 추측했다. 이것은 나중에 실제로 가능했지만, 그것이 결국 1932년에 최초의 인공 핵 투과 반응으로 증명되었고, 콕크로프트와 월튼에 의해 증명되었으며, 에너지 이득과 함께 질량 손실에 관한 아인슈타인의 이론의 첫 번째 성공적인 실험이었다.

질량 보존 법칙과 유사한 에너지 보존 법칙은 질량-에너지 동등성이라고 알려진 보다 일반적인 원리에 의해 최종적으로 기각되었다. 특수 상대성 또한 질량과 에너지의 개념을 재정의하는데, 질량은 서로 교환하여 사용할 수 있고 기준의 틀에 비례하여 정의된다. 입자의 나머지 질량(입자의 나머지 프레임의 질량)과 상대론적 질량(다른 프레임의 질량)과 같이 일관성을 위해 여러 양을 정의해야 했다. 후기는 보통 덜 자주 사용된다.

일반화

이 기사 또는 섹션은 오해의 소지가 있는 부분을 포함할 수 있다. 토크 페이지에 제시된 모든 제안에 따라 이 기사를 명확히 할 수 있도록 도와주십시오. (2017년 12월)

특수상대성

특수상대성이론에서는 체계가 개방되어 에너지가 빠져나갈 경우 질량의 보존이 적용되지 않는다. 그러나 완전히 닫힌(단열된) 시스템에는 계속 적용된다. 에너지가 계통을 벗어날 수 없다면, 그 질량은 감소할 수 없다. 상대성 이론에서, 어떤 종류의 에너지가 시스템 내에 유지되는 한, 이 에너지는 질량을 나타낸다.

또한 질량은 항상 그러한 시스템에서 보존되지만 물질은 격리된 시스템에서 완벽하게 보존되지 않을 수 있으므로 질량은 물질과 구별되어야 한다. 그러나 물질은 화학에 있어서 거의 보존되어 있어서 물질 보존의 위반은 핵 시대까지 측정되지 않았으며, 물질 보존의 가정은 방사능과 핵 반응의 전형적인 높은 에너지를 포함하지 않는 화학 및 다른 연구들의 대부분의 시스템에서 중요한 실용적 개념으로 남아 있다.

화학적 에너지 양과 관련된 질량이 너무 작아서 측정할 수 없다.

원자나 거대한 입자가 빠져나갈 수 없는 특정한 종류의 개방된 시스템의 질량의 변화는 19세기 동안 눈에 띄지 않았다. 왜냐하면 질량의 변화는 열이나 복사 에너지의 소량의 추가나 손실과 관련되기 때문이다.화학 반응의 rgy는 매우 작다. (이론적으로 열과 작업이 출입이 허용되지 않는 격리된 시스템에서 수행된 실험에서는 질량이 전혀 변하지 않을 것이다.)

에너지가 손실되지 않더라도 대량 보존은 올바른 상태를 유지함

관성 프레임을 변경하면 시스템에 대한 총 에너지(상대적 에너지)가 변경될 수 있고, 이 양이 상대적 질량을 결정할 수 있기 때문에 상대적 질량의 보존은 단일 관측자(또는 단일 관성 프레임으로부터의 관점)의 관점을 의미한다.

고전 물리학에서는 사실이지만 입자 체계의 질량이 나머지 질량의 합과 같아야 한다는 원리는 특수 상대성에서는 거짓일 수 있다. 쉼표 질량을 단순히 추가할 수 없는 이유는 이것이 운동 에너지와 전위 에너지와 같은 다른 형태의 에너지와 광자와 같은 질량이 없는 입자를 고려하지 않기 때문이며, 이 모든 것이 시스템의 총 질량에 영향을 미칠 수 있거나 그렇지 않을 수 있다.

시스템 내에서 움직이는 거대한 입자의 경우, 다양한 입자의 나머지 질량을 검사하는 것은 또한 많은 다른 관성 관측 프레임(총 시스템 에너지와 운동량이 보존될 경우 금지됨)을 도입하는 것과 같으며, 또한 한 입자의 나머지 프레임에서 이 절차는 다른 입자의 모멘텀인 휘를 무시한다.ch는 이 프레임에서 다른 입자가 움직이는 경우 시스템 질량에 영향을 미친다.

불변성 질량이라고 하는 특수한 유형의 질량의 경우, 닫힌 시스템 전체에 대해 관성형 관측 프레임을 변경하는 것은 시스템 전체의 관성형 질량을 측정하는 데 아무런 영향을 미치지 않으며, 이는 전체 시스템을 보는 서로 다른 관찰자에게도 보존 및 불변성(불변성)으로 남아 있다. 불변 질량은 어떤 관성 프레임에서든 다양한 입자의 에너지와 모멘텀은 항상 같은 양(운동량이 음수일 수 있으므로 덧셈이 뺄셈에 이를 수 있음)을 더하기 때문에 어떤 관찰자에게도 불변하는 에너지와 운동량의 시스템 결합이다. 불변성 질량은 모멘텀 프레임의 중심에서 볼 때 시스템의 상대성 질량이다. 가능한 모든 관성 프레임에서 볼 때 시스템이 나타낼 수 있는 최소 질량이다.

상대론적 질량과 불변적 질량의 보존은 새로운 입자에 대한 에너지가 다른 입자의 운동 에너지에서 나올 수 있는 쌍 생성에 의해 생성된 입자의 시스템에도 적용되며, 광자 이외에 다른 입자를 포함하는 시스템의 일부로서 하나 이상의 광자에서 발생할 수 있다. 다시 말하지만, 완전히 닫힌(즉, 격리된) 시스템의 상대론적 질량이나 불변적 질량은 새로운 입자가 생성될 때 변하지 않는다. 그러나 서로 다른 관성 관측자들은 상대론적 질량(즉 상대론적 질량은 보존되지만 불변성이 아닌)인 경우 보존된 질량의 가치에 대해 동의하지 않을 것이다. 그러나 모든 관측자는 측정되는 질량이 불변 질량(즉 불변 질량은 보존 및 불변 질량)인 경우 보존 질량의 값에 동의한다.

질량 에너지 동등성 공식은 비절연 시스템에서 다른 예측을 제시하는데, 에너지가 시스템에서 빠져나갈 수 있도록 허용되면 상대론적 질량과 불변성 질량도 모두 빠져나갈 것이기 때문이다. 이 경우 질량 에너지 동등성 공식은 시스템의 질량 변화가 추가 또는 감산되는 에너지로 인한 에너지 변화와 관련이 있다고 예측한다: ${\displaystyle \Delta }$ m${\displaystyle }$= ${\displaystyle \mathrm{\Delta }}$ E${\displaystyle }$/ ${\displaystyle c}$ ${\displaystyle {2\mathrm{}}^{}}$.$${\$displaystyle \Delta$ m$=\Delta$E/$c^{2}.$$$ 변화를 수반하는 이 형태는 아인슈타인에 의해 원래 제시된 이 유명한 방정식이었다. 이러한 의미에서, 시스템에서 추가되거나 제거된 에너지의 질량을 고려한다면 어떤 시스템의 질량 변화도 간단히 설명된다.

이 공식은 시스템이 바인딩된 후 바인딩 에너지가 시스템에서 탈출할 수 있도록 허용되었을 경우 바인딩된 시스템이 부품의 합보다 불변 질량(시스템에 대한 정지 질량)을 더 적게 갖는다는 것을 의미한다. 이는 시스템 전위 에너지를 운동 에너지나 광자와 같은 다른 종류의 활성 에너지로 변환하여 발생할 수 있으며, 이는 바운드 시스템을 쉽게 탈출한다. 질량 결함이라 불리는 시스템 질량의 차이는 바운드 시스템의 결합 에너지, 즉 시스템을 분해하는 데 필요한 에너지의 척도다. 질량 결함이 클수록 결합 에너지도 커진다. 결합 에너지(그 자체가 질량을 갖는 것)는 부품이 결합하여 결합 시스템을 형성할 때 (빛이나 열로) 방출되어야 하며, 이것이 결합 시스템의 질량이 에너지가 시스템을 떠날 때 감소하는 이유다.^[20] 총 불변 질량은 실제로 보존되는데, 이때 빠져나온 결합 에너지의 질량이 고려된다.

일반상대성

일반 상대성에서는, 팽창하는 공간의 부피에 있는 광자의 총 불변성 질량이 그러한 팽창의 적색 이동으로 인해 감소할 것이다. 따라서 질량과 에너지의 보존은 그러한 시스템의 중력 전위 에너지의 변화로 인해 이론에서 에너지에 대해 이루어진 다양한 보정에 의존한다.

참고 항목

• 전하보전
• 보존법
• 픽의 확산 법칙
• 일정한 비율의 법칙
• 다중 비율의 법칙

참조