소성(물리학)
Plasticity (physics)| 시리즈의 일부 |
| 연속체 역학 |
|---|
물리학 및 재료 과학에서, 소성 변형이라고도 알려진 가소성은 적용된 [1][2]힘에 반응하여 돌이킬 수 없는 형태의 변화인 영구 변형을 겪는 고체 물질의 능력입니다.예를 들어 단단한 금속 조각이 구부러지거나 새로운 모양으로 두들겨지면 재료 자체 내에서 영구적인 변화가 발생할 때 가소성이 나타납니다.공학에서는 탄성 거동에서 소성 거동으로 전환하는 것을 굴곡이라고 합니다.
대부분의 물질, 특히 금속, 토양, 암석, 콘크리트 및 발포체에서 소성 [3][4][5][6]변형이 관찰됩니다.그러나 소성 변형을 일으키는 물리적 메커니즘은 매우 다양할 수 있습니다.결정적 규모에서 금속의 가소성은 일반적으로 전위의 결과이다.이러한 결함은 대부분의 결정성 물질에서 비교적 드물지만 결정 구조의 일부 및 일부에 많이 있습니다. 이러한 경우 플라스틱 결정성이 발생할 수 있습니다.바위, 콘크리트 및 뼈와 같은 부서지기 쉬운 재료에서 가소성은 주로 마이크로 크랙에서의 미끄러짐으로 인해 발생합니다.액체 발포체나 생체 조직과 같은 세포 물질에서 가소성은 주로 기포 또는 세포 재배열, 특히 T1 과정의 결과이다.
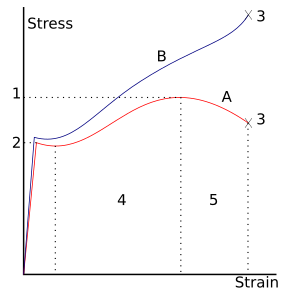
많은 연성 금속의 경우 시료에 가해지는 인장 하중에 의해 시료가 탄력적으로 동작하게 됩니다.하중의 각 증분은 비례적인 증분을 수반한다.하중이 제거되면 조각이 원래 크기로 돌아갑니다.단, 하중이 임계값(항복 강도)을 초과하면 탄성 영역보다 확장이 더 빠르게 증가합니다.이제 하중이 제거되면 어느 정도의 확장이 유지됩니다.
그러나 탄성 변형은 근사치이며, 그 품질은 고려된 시간 범위와 적재 속도에 따라 달라집니다.반대쪽 그래프에 나타나 있듯이 변형에 탄성변형이 포함되는 경우에는 흔히 '탄성소성변형' 또는 '탄성소성변형'이라고도 한다.
완벽한 가소성은 응력이나 하중의 증가 없이 돌이킬 수 없는 변형을 겪는 재료의 특성입니다.냉간 성형과 같은 이전 변형으로 경화된 플라스틱 재료는 더 이상 변형하기 위해 점점 더 높은 응력을 필요로 할 수 있습니다.일반적으로 소성 변형은 변형 속도에 따라 달라지며, 즉 변형 속도를 높이기 위해 일반적으로 더 높은 응력을 적용해야 합니다.이러한 재료는 점착적으로 변형된다고 한다.
기여 속성
물리 메커니즘
금속제
순수 금속 결정의 가소성은 주로 결정 격자의 두 가지 변형 모드, 즉 슬립과 트윈닝에 의해 발생합니다.슬립은 원자가 초기 위치에 비해 원자간 거리를 많이 이동하는 전단 변형입니다.트윈닝은 주어진 금속 조각에 가해지는 일련의 힘에 의해 두 평면을 따라 발생하는 소성 변형입니다.
대부분의 금속은 차가울 때보다 뜨거울 때 더 많은 가소성을 보인다.납은 실온에서 충분한 가소성을 나타내지만, 주철은 뜨거워도 단조 작업에 충분한 가소성을 가지고 있지 않습니다.이 특성은 금속에 대한 성형, 성형 및 압출 작업에 중요합니다.대부분의 금속은 가열에 의해 플라스틱으로 만들어지며, 따라서 뜨거운 모양으로 형성된다.
슬립 시스템
결정성 물질에는 원자의 균일한 평면이 장거리의 순서로 배열되어 있습니다.슬립 시스템 페이지에 나와 있는 것처럼 비행기는 촘촘한 방향을 따라 서로 미끄러질 수 있습니다.그 결과 결정 및 소성 변형 내에서 영구적인 형상 변화가 발생합니다.전위의 존재는 평면의 가능성을 높인다.
가역 소성
나노 스케일에서 단순한 면중심 [7]입방금속의 1차 소성 변형은 크로스슬립 형태의 물질 수송이 없는 한 가역적입니다.니티놀 와이어와 같은 형상기억합금은 가소성의 가역적 형태를 나타내며, 이를 의사탄성이라고 한다.
전단 밴딩
결정 내에 다른 결함이 있으면 전위가 얽히거나 미끄러지지 않을 수 있습니다.이 경우 가소성은 재료의 특정 부위에 국한됩니다.결정의 경우, 이러한 국소적 가소성 영역을 전단 밴드라고 합니다.
미세 소성
미세 가소성은 금속의 국소적인 현상이다.이는 금속이 전체적으로 탄성 영역에 있는 반면 일부 국소 영역은 [8]플라스틱 영역에 있는 응력 값에 대해 발생합니다.
비정질 재료
크래징
비정질 재료에서는 전체 재료에 장거리 순서가 없기 때문에 "전위"에 대한 설명은 적용할 수 없습니다.이 재료들은 여전히 소성 변형을 겪을 수 있다.폴리머와 같은 비정질 재료는 질서가 좋지 않기 때문에 많은 양의 자유 부피 또는 낭비된 공간을 포함합니다.이러한 재료를 팽팽하게 당기면 이러한 영역이 열리고 재료가 흐릿하게 보일 수 있습니다.이러한 흐릿함은 크래징의 결과로, 높은 정수압 응력 영역에서 재료 내에 섬유섬유가 형성됩니다.소재는 정돈된 모양에서 변형과 스트레치 자국이 "미친" 패턴으로 바뀔 수 있습니다.
셀룰러 재료
이러한 재료는 굽힘 모멘트가 완전 플라스틱 모멘트를 초과하면 소성 변형됩니다.이는 셀 벽에 벤딩 모멘트가 가해지는 개방 셀 폼에 적용됩니다.발포재는 단단한 폴리머와 금속을 포함한 플라스틱 항복점이 있는 모든 재료로 만들 수 있습니다.이 폼을 빔으로 모델링하는 방법은 폼 밀도 대 물질의 밀도 비율이 0.3 미만일 경우에만 유효합니다.이는 빔이 휘어지는 대신 축방향으로 산출되기 때문입니다.밀폐형 셀폼에서는 셀의 표면을 가로지르는 막에 의해 재료가 장력을 받으면 항복강도가 증가한다.
흙과 모래
토양, 특히 점토는 하중을 받으면 상당한 양의 비탄력을 보인다.토양에서 가소성의 원인은 매우 복잡할 수 있으며 미세 구조, 화학 성분 및 수분 함량에 따라 크게 좌우됩니다.토양에서의 가소성 행동은 주로 인접한 곡물의 군집 재배치에 의해 야기된다.
암석 및 콘크리트
암석과 콘크리트의 비탄성 변형은 주로 이러한 균열과 관련된 미세 균열의 형성 및 슬라이딩 운동에 의해 발생한다.고온 및 압력에서 플라스틱 거동은 미세 구조의 개별 입자의 전위 움직임에도 영향을 받을 수 있습니다.
결정성[9] 재료의 시간에 의존하지 않는 항복 및 소성 흐름
단결정 및 다결정에서의 시간 의존적인 플라스틱 플로우는 임계/최대 분해 전단 응력(θCRSS)에 의해 정의되며, 단일 슬립 시스템의 평행 슬립 평면을 따른 전위 이동을 개시함으로써 결정성 재료에서의 탄성으로부터 소성 변형 거동에 대한 전이를 정의한다.
단결정 내 시간 독립 항복 및 소성 흐름
단결정에 대한 임계 분해 전단 응력은 Schmid의 법칙 = = δCRSSy/m에 의해 정의되며, 여기서y δ는 단결정의 항복 강도, m은 Schmid 계수이다.Schmid 계수는 슬립 평면 방향과 가해지는 인장력 사이의 각도, 슬립 평면 법선과 가해지는 인장력 사이의 각도를 정의하는 두 개의 변수 θ와 θ로 구성된다.특히 m > 1이기 때문에, 「 > 」입니다yCRSS.
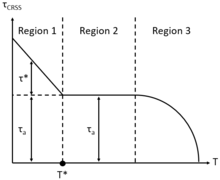
온도, 변형률, 점결함에 따른 중대 분해 전단응력 의존성
임계 분해 전단 응력에는 온도의 함수로서 세 가지 특징 영역이 있습니다.저온영역 1(T 0 0.25Tm)에서는 변형률 θ가 높아야 전위활공과 등가소성흐름을 시작할 수 있는 θ가CRSS 높아진다.영역 1에서 임계 분해 전단 응력은 다른 전위 존재 하에서 전위 이동에 필요한 응력에서 발생하는 아테르말(θa) 및 열(θ*) 전단 응력과 전위 이동에 대한 점 결함 장애물의 저항이라는 두 가지 성분을 가진다.T=T*이나 중도파 온도 지역 2(0.25Tm<T>0.7에서.Tm)정의는 어디서 열 전단 변형력 성분 τ*→ 0,을 대표하는 탈락 점결함 임피던스에 탈구 이민이다.그러므로temperature-independent critical 전단 응력 τCRSS)τa기 전까지 지역 3정의된 남은 것을 해결했다.지역 2에 특히 적당한 온도time-dependent 플라스틱 변형( 기다)solute-drag 같은 메커니즘을 고려하여야 한다.게다가, 가장 높은 온도 지역 3에(T≥ 0.7.Tm)έ, 낮은 τCRSS에 기여하는 하지만 플라스틱 흐름 여전히 Nabarro– 같은 열로 작동 고온time-dependent 플라스틱 변형 메커니즘 때문에 발생할 것이 낮을 수 있다.Herring(NH)과 격자는 단결정의 평면을 Coble확산 흐름, 각각, 뿐만 아니라 탈구 climb-glide 아첨꾼이다.
시간에 구애받지 않는 플라스틱 흐름 단계, 항복 후
이지 글라이드 스테이지 1에서는 전단 스트레인에 대한 전단 응력 변화(dd/d with)로 정의되는 워크 경화율이 낮아 대량의 전단 스트레인을 유도하기 위해 필요한 소량의 전단 응력을 대표한다.패실 전위 활공 및 대응하는 흐름은 평행 슬립 평면을 따른 전위 이동(즉, 하나의 슬립 시스템)에 기인한다.평행 슬립 평면을 따른 전위 이동에 대한 적당한 임피던스는 이러한 전위 사이의 약한 응력장 상호작용에 따라 나타나며, 이는 평면 간 간격이 작을수록 높아진다.전체적으로 단일 슬립 시스템 내에서 이동되는 이러한 전위는 흐름에 대한 약한 장애물로 작용하며 항복 응력에 비해 응력이 약간 상승하는 것이 관찰된다.흐름의 선형 경화 단계 2에서는 비평행 슬립 평면(즉 다중 슬립 시스템)으로 이동하는 전위의 응력장 상호작용을 극복하기 위해 상당한 응력이 요구되어 흐름의 강한 장애물로 작용하기 때문에 작업 경화율이 높아진다.작은 균주의 지속적인 전위 이동을 촉진하기 위해서는 많은 스트레스가 필요하다.전단 흐름 응력은 전위 구성의 진화에 관계없이 전위 밀도의 제곱근(θflow ~θ½)에 정비례하며, 존재하는 전위 수에 대한 경화의 의존성을 나타낸다.이러한 전위 구성의 진화에 관해, 작은 변형률에서 전위 배열은 교차선의 무작위 3D 배열이다.적당한 균주는 세포 경계에서의 큰 전위 밀도 및 세포 내부에서의 작은 전위 밀도를 가진 이종 전위 분포의 세포 전위 구조에 대응한다.더 큰 균주에서는 세포 전위 구조가 최소 크기에 도달할 때까지 크기가 감소합니다.마지막으로 소성류 경화단계 3의 탈진 포화상태에서는 전단응력이 작을수록 전단응력이 커지기 때문에 작업경화율이 다시 낮아진다.특히 가해진 응력에 대해 복수의 슬립계가 유리하게 배향되어 있는 경우, 이들 계통의 θ는CRSS 유사할 수 있으며, 비평행 슬립면을 가진 복수의 슬립계를 따른 전위 이동에 따라 산출되어 2단계의 전형적 특징인 1단계의 워크 경화율을 나타낼 수 있다.마지막으로, 체심 입방체 전이 금속과 면심 입방 금속의 시간 비의존적 소성 변형 사이의 차이를 아래에 요약한다.
| 체심입방 전이금속 | 면심입방금속 |
|---|---|
| 임계 분해 전단 응력 = 높은(매우) 온도 의존성 | 임계 분해 전단 응력 = 낮은(완전하게) 온도의존성 |
| 작업 경화율 = 온도에 의존하지 않음 | 작업경화율 = 온도 의존 |
| 넥킹 변형률은 온도에 따라 증가합니다. | 넥킹 변형률은 온도에 따라 감소합니다. |
다결정에서의 시간 의존 항복 및 소성 흐름
다결정에서의 가소성은 활성 슬립면의 전체 길이를 따라 전위 이동을 방해함으로써 플라스틱 흐름에 매우 강력한 장애물로 작용하는 입자 경계(GB) 평면 결함의 존재로 인해 단결정에서의 가소성과는 크게 다르다.따라서 전위는 입자 경계를 넘어 한 입자에서 다른 입자로 전달될 수 없습니다.다음 절에서는 파괴 전에 다결정체의 광범위한 소성 변형과 개별 결정체 내의 미시적 항복이 다결정체의 거시적 항복에 미치는 영향에 대한 특정 GB 요구 사항을 살펴봅니다.다결정 임계 분해 전단 응력은 Schmid의 법칙(θCRSS=θy/θ)으로도 정의되며, 여기서 θ는y 다결정 항복 강도이고 θ는 가중치 Schmid 계수이다.가중치 Schmid 계수는 GB를 구성하는 입자의 가장 바람직한 방향의 슬립 시스템 중 가장 바람직하지 않은 방향의 슬립 시스템을 반영한다.
다결정에서의 입자 경계 제약
다결정용 GB의 제약은 구성, 구조 및 슬립 시스템이 동일하지만 서로 방향이 맞지 않는 2개의 단결정 A와 B 사이의 xz 평면 내 입자 경계를 고려하는 것으로 설명할 수 있습니다.는 빈 공간 개별적으로 deforming 알들 사이에 형성되지 않아 보장하기 위해서, bicrystal의 GB제약 조건은 εxxA)εxxB(그 GB에서x-axial 변형으로 환산하야 한다 A와 B), εzzA)εzzB(그 GB에서z-axial 변형으로 환산하야 한다 A와 B)고,xz-GB 비행기 함께 εxzA)εxzB 자세한 내용은 xz 전단 변형과 동등한 것이 틀림 없다.A와 B).또한 이 GB 제약에 따라 GB를 구성하는 결정체별로 5개의 독립 슬립 시스템을 활성화해야 합니다.특히 독립 슬립 시스템은 다른 슬립 시스템의 평면을 따라 위치 이동의 어떤 조합으로도 전위 이동을 재현할 수 없는 슬립 평면으로 정의되기 때문에 주어진 결정 시스템의 기하학적 슬립 시스템의 수는 정의상 슬립 시스템의 조합으로 구성될 수 있다.y는 독립 슬립 시스템보다 크다.유의적으로, 7개의 결정계 각각에 대해 최대 5개의 독립 슬립계가 있지만, 모든 7개의 결정계가 이 상한을 얻는 것은 아니다.실제로 특정 결정계 내에서도 조성물과 Bravais 격자는 독립 슬립계의 수를 다양화한다(아래 표 참조).다결정 결정체가 5개의 독립된 슬립계를 얻지 못할 경우 GB 조건을 충족할 수 없기 때문에 개별 결정체의 시간 의존적인 변형에 의해 다결정체의 GB에 균열이나 공극이 발생하고 곧 파단이 실현된다.따라서 특정 조성 및 구조에서 5개 미만의 독립 슬립 시스템을 가진 단일 결정이 다결정 형태보다 더 강합니다(더 큰 범위의 가소성을 나타냄).
| 브라바 격자 | 프라이머리 재료 클래스: # 독립 슬립 시스템 |
|---|---|
| 면중심입방체 | 금속: 5, 세라믹(공가): 5, 세라믹(이온): 2 |
| 본체 중심 입방체 | 금속: 5 |
| 심플 큐빅 | 세라믹(이온): 3 |
| 육각형 | 금속: 2, 세라믹(혼합): 2 |
다결정에서의 입자 경계 제약의 영향
상기 절에서 설명한 2개의 결정체 A와 B는 동일한 슬립계를 가지지만 서로 방향이 틀리고, 따라서 가해지는 힘에 대해 방향이 틀린다.따라서 결정체 내부에서의 미시적 수율은 단결정 시간 의존 수율을 지배하는 규칙에 따라 발생할 수 있다.결국, 곡물 내부 내의 활성화된 슬립 평면을 통해 많은 전위가 기하학적으로 필요한 전위로 축적되는 GB로의 전위 이행을 허용합니다.이 축적은 GB 근처의 전위 밀도가 곡물 내부보다 커 접촉하는 인접 곡물에 스트레스를 가하기 때문에 개별 곡물에 걸친 변형률 구배에 해당합니다.AB의 바이크리스탈 전체를 생각할 때, A에서 가장 바람직한 방향의 슬립계는 B의 것이 아니라 θACRSSCRSS θBCRSS paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount paramount the the the the the the the the the the the the the the the the the the the the the a the the the 따라서, 주어진 구성 및 구조에서, 5개의 독립적인 슬립 시스템을 가진 다결정체는 단일 결정 형태보다 더 강합니다(가소성이 더 높습니다).이에 따라 단결정보다 다결정에서 응력이 더 많이 필요하기 때문에 응력이 더 높아진다.중요한 것은 단결정 흐름 응력과 마찬가지로 δflow~δ이지만½ 평균 입경의 제곱근(θflow~d-½)에 반비례한다는 것입니다.따라서, 다결정체의 유동 응력, 즉 다결정체의 강도는 입자 크기가 작을수록 증가한다.그 이유는 작은 알갱이가 활성화되는 슬립면의 수가 상대적으로 적어 GB로 이동하는 전위 수가 적기 때문에 전위 누적으로 인해 인접한 알갱이에 유발되는 응력이 적기 때문이다.또한 특정 부피의 다결정에서 입자가 작을수록 장애물 입자의 경계가 더 강해집니다.이 두 가지 인자는 왜 미세 다결정에서 거시적 흐름의 시작이 거친 다결정에서보다 더 큰 응력에서 발생하는지에 대한 이해를 제공합니다.
수학적 설명
변형 이론

가소성에 [12]대한 수학적인 설명이 몇 가지 있습니다.하나는 변형 이론이다(예: 참조).후크의 법칙)에서 코시 응력 텐서(d차원에서의 순서 d-1)는 변형 텐서의 함수이다.이 설명은 물질의 작은 부분이 증가하는 하중(예: 변형률 하중)을 받는 경우 정확하지만, 이 이론은 불가역성을 설명할 수 없습니다.
연성 재료는 파손 없이 큰 플라스틱 변형을 견딜 수 있습니다.그러나 연성 금속이라도 변형률이 충분히 커지면 깨질 수 있습니다. 이는 재료의 작업 경화로 인해 재료가 부서지기 쉬워지기 때문입니다.어닐링 등의 열처리를 통해 워크피스의 연성을 회복할 수 있으므로 성형처리를 계속할 수 있습니다.
흐름 가소성 이론
1934년, 에곤 오로완, 마이클 폴라니, 제프리 잉그램 테일러는 연성 물질의 소성 변형이 전위 이론의 관점에서 설명될 수 있다는 것을 대략 동시에 깨달았다.가소성의 수학적 이론인 흐름 가소성 이론은 일련의 비선형, 비적분 방정식을 사용하여 이전 상태와 약간의 변형 증가에 대한 변형과 응력의 변화를 기술합니다.
수율기준
응력이 위에서 언급한 바와 같이 임계값을 초과할 경우 재료는 소성, 즉 돌이킬 수 없는 변형을 겪습니다.이 임계 응력은 인장 또는 압축될 수 있습니다.Tresca와 von Mises 기준은 재료의 산출 여부를 결정하기 위해 일반적으로 사용된다.그러나 이러한 기준은 광범위한 재료에 적합하지 않은 것으로 입증되었으며 다른 여러 산출량 기준도 광범위하게 사용되고 있다.
트레스카 기준
Tresca 기준은 재료가 파손될 때 전단에서 파괴된다는 개념에 기초하고 있으며, 이는 금속을 고려할 때 비교적 좋은 가정이다.주 응력 상태가 주어지면, 우리는 모어의 원을 사용하여 우리의 물질이 경험할 최대 전단 응력에 대해 해결할 수 있고 재료가 다음과 같이 실패할 것이라는 결론을 내릴 수 있다.
여기서 θ는1 최대 법선응력, θ는3 최소 법선응력, θ는0 단축하중으로 재료가 고장나는 응력이다.항복면을 구성할 수 있으며, 이 개념을 시각적으로 표현할 수 있다.항복면 내부는 탄성이 있다.표면적으로는 변형은 플라스틱이다.재료가 항복 표면 밖에 응력 상태를 갖는 것은 불가능하다.
Huber-von Mises 기준
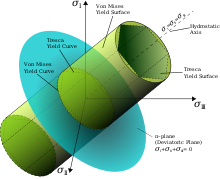
Huber-von Mises[13] 기준은 Tresca 기준에 기초하지만 정수적 응력이 재료 고장에 기여하지 않는다는 가정을 고려한다.M. T. Huber는 전단 [14][15]에너지의 기준을 최초로 제안한 사람이다.Von Mises는 단축 부하에서 유효 응력을 해결하여 정수압 부하를 뺀 후 단축 부하에서 재료 고장을 일으키는 것보다 큰 모든 유효 응력이 소성 변형을 초래한다고 기술합니다.
다시 타원형상을 취하는 상기 방정식을 이용하여 항복면의 시각적 표현을 구성해도 된다.표면 내부에서는 재료가 탄성 변형을 일으킨다.표면에 도달한다는 것은 재료가 소성 변형을 겪는다는 것을 의미합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ Lubliner, J. (2008). Plasticity theory. Dover. ISBN 978-0-486-46290-5.
- ^ Bigoni, D. (2012). Nonlinear Solid Mechanics: Bifurcation Theory and Material Instability. Cambridge University Press. ISBN 978-1-107-02541-7.
- ^ Jirasek, M.; Bazant, Z. P. (2002). Inelastic analysis of structures. John Wiley and Sons. ISBN 0-471-98716-6.
- ^ Chen, W.-F. (2008). Limit Analysis and Soil Plasticity. J. Ross Publishing. ISBN 978-1-932159-73-8.
- ^ Yu, M.-H.; Ma, G.-W.; Qiang, H.-F.; Zhang, Y.-Q. (2006). Generalized Plasticity. Springer. ISBN 3-540-25127-8.
- ^ Chen, W.-F. (2007). Plasticity in Reinforced Concrete. J. Ross Publishing. ISBN 978-1-932159-74-5.
- ^ Gerolf Ziegenhain과 Herbert M.Urbasek:FCC 금속의 가역 소성.입력: Philosical Magazine Letters. 89 (11) : 717-723, 2009 DOI
- ^ Maaß, R.; Derlet, P.M. (January 2018). "Micro-plasticity and recent insights from intermittent and small-scale plasticity". Acta Materialia. 143: 338–363. arXiv:1704.07297. doi:10.1016/j.actamat.2017.06.023. S2CID 119387816.
- ^ Courtney, Thomas (2005). Mechanical Behavior of Materials (Second ed.). Long Grove, Illinois: Waveland Press, Inc. ISBN 978-1-57766-425-3.
- ^ Partridge, Peter (1969). Deformation and Fatigue of Hexagonal Close Packed Metals. University of Surrey.
- ^ Grooves, G.W.; Kelly, A. (1963). "Independent Slip Systems in Crystals". Philosophical Magazine. 8 (89): 877–887. doi:10.1080/14786436308213843.
- ^ Hill, R. (1998). The Mathematical Theory of Plasticity. Oxford University Press. ISBN 0-19-850367-9.
- ^ von Mises, R. (1913). "Mechanik der festen Körper im plastisch-deformablen Zustand". Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. Mathematisch-Physikalische Klasse. 1913 (1): 582–592.
- ^ Huber, M. T. (1904). "Właściwa praca odkształcenia jako miara wytezenia materiału". Czasopismo Techniczne. Lwów. 22. 로 번역됨
- ^ 참조
추가 정보
- Ashby, M. F. (2001). "Plastic Deformation of Cellular Materials". Encyclopedia of Materials: Science and Technology. Vol. 7. Oxford: Elsevier. pp. 7068–7071. ISBN 0-08-043152-6.
- Han, W.; Reddy, B. D. (2013). Plasticity: Mathematical Theory and Numerical Analysis (2nd ed.). New York: Springer. ISBN 978-1-4614-5939-2.
- Kachanov, L. M. (2004). Fundamentals of the Theory of Plasticity. Dover Books. ISBN 0-486-43583-0.
- Khan, A. S.; Huang, S. (1995). Continuum Theory of Plasticity. Wiley. ISBN 0-471-31043-3.
- Simo, J. C.; Hughes, T. J. (1998). Computational Inelasticity. Springer. ISBN 0-387-97520-9.
- Van Vliet, K. J. (2006). "Mechanical Behavior of Materials". MIT Course Number 3.032. Massachusetts Institute of Technology.








![\sigma _{v}^{2}={\tfrac {1}{2}}[(\sigma _{{11}}-\sigma _{{22}})^{2}+(\sigma _{{22}}-\sigma _{{33}})^{2}+(\sigma _{{11}}-\sigma _{{33}})^{2}+6(\sigma _{{23}}^{2}+\sigma _{{31}}^{2}+\sigma _{{12}}^{2})]](https://wikimedia.org/api/rest_v1/media/math/render/svg/918b083c9c0c4f9cb190d778ecfdc3fd9eb6e4f9)