전단 계수

전단 계수
공통 기호	G, S
SI 단위	파스칼
파생상품 기타 수량	G = / / γ G = E / 2 (1+n)

재료과학에서 전단계수 또는 강성계수(G, 때로는 S 또는 μ)는 재료의 탄성 전단강성을 측정하는 것으로 전단변형에 ^[1]대한 전단응력의 비율로 정의된다.

${\displaystyle G\{stackrel {def}{=}\frac _{xy}}=flac {F/A}{\Delta x/l}=flac {Fl}{A\Delta x}}}}$

어디에

${\displaystyle {\theta }_{}}$ x y${\displaystyle {}_{}}$=${\displaystyle F}$ /$A${$displaystyle$ \ $displaystyle$_ {$xy}$ = $F/A,}$ $$= ${\displaystyle {\mathrm{전단응력}}_{}}$

$(Displaystyle$ F$)$는 동작하는 힘입니다.

$\displaystyle$A는$$ 힘이 작용하는 ${\displaystyle \mathrm{영역}}$입니다.

${\displaystyle {\gamma }_{}}$x y \$displaystyle _${xy}$$ = 전단 ${\displaystyle {\mathrm{변형률}}_{}}$.엔지니어링 분야 : ${\displaystyle =}$ ${\displaystyle \delta }$ x${\displaystyle }$/ ${\displaystyle l}$ $=$ tan ${\displaystyle }$display$$ （ { $displaystyle$ : =\$Delta$x/l =\$tan$\$theta$$$$}$ 、 ${\displaystyle \mathrm{other}}$ :=$$） 。

$x (\ displaystyle$ \$Delta$ x )는 횡방향 변위입니다.

$\displaystyle$l은$$ 영역의 초기 길이입니다.

전단률의 SI 단위는 파스칼(Pa)이지만 일반적으로 기가파스칼(GPA) 또는 평방인치당 1000파운드(ksi)로 표시됩니다.그 치수 형태는¹⁻¹⁻² MLT이며 힘을 질량 곱하기 가속도로 대체한다.

★★★

★★★	의 인 값 (상온에서)
[2]	478.0
★★★ [3]	79.3
★ [4]	52.5
★★★ [5]	44.7
티타늄 titanium [3]	41.4
★★★ [3]	26.2
루루늄늄 [3]	25.5
[3]	0.117
★★★ [6]	0.0006
[7] [8]	24
[7] [8]	1.6
[7] [8]	24
[7] [8]	3.2
★★★ [7] [8]	0.4
★★★	4

전단계수는 재료의 강성을 측정하는 몇 가지 수량 중 하나입니다.모두 일반화된 후크의 법칙에서 비롯됩니다.

• Young's modulus E는 이 응력 방향의 단축 응력에 대한 재료의 변형 반응을 나타냅니다(와이어가 길어지고 기둥의 높이가 줄어드는 와이어의 끝을 잡아당기거나 기둥 위에 무게를 싣는 것과 같습니다).
• 포아송 비율 θ는 이 단축 응력에 직교하는 방향의 반응을 나타냅니다(배선은 얇아지고 기둥은 두꺼워짐).
• 벌크 계수 K는 (균일한) 정수압에 대한 물질의 반응을 설명한다(대양 바닥의 압력이나 깊은 수영장,
• 전단 계수 G는 전단 응력에 대한 재료의 반응을 나타냅니다(예: 둔한 가위로 절단).

이러한 모듈리는 독립적이지 않으며 등방성 재료의 경우 방정식을^[9] 통해 연결됩니다.

$E)=displaystyle E=2G(1+\nu)=3K(1-2\nu)}$

전단 계수(shear modulus)는 표면 중 하나에 평행한 힘을 경험하는 반면 반대 면은 반대 힘(마찰 등)을 경험할 때 고체의 변형과 관련이 있습니다.직사각형 프리즘처럼 생긴 물체의 경우, 그것은 평행입방체로 변형됩니다.목재, 종이 및 기본적으로 모든 단결정과 같은 이방성 재료는 서로 다른 방향으로 테스트했을 때 응력 또는 변형에 대해 서로 다른 재료 반응을 보입니다.이 경우 단일 스칼라 값 대신 탄성 상수의 완전한 텐서 식을 사용해야 할 수 있다.

유체의 가능한 정의 중 하나는 전단 계수가 0인 물질이다.

★★★★

균질 및 등방성 고체에는 압력파와 전단파의 두 종류가 있다.전단파의 속도${\displaystyle }$(${\displaystyle v_{}}$ s$)({displaystyle (v_{s})}$는 전단계수에 의해 제어된다.

$({displaystyle v_{s}={frac {G}{\rho }})$

서 ''는

G 단 단 수 이 이 이 계 계 계 계 계 g g g g g g

$δ(\displaystyle$ \rho$$$)$는 고체의 밀도입니다.

의 전단

금속의 전단 계수는 일반적으로 온도가 상승할수록 감소하는 것으로 관찰된다.고압에서 전단계수는 가해지는 압력에 따라 증가하는 것으로 보인다.많은 ^[13]금속에서 용해 온도, 공실 형성 에너지 및 전단 계수 사이의 상관 관계가 관찰되었습니다.

금속(그리고 합금)의 전단 계수를 예측하려는 여러 모델이 있습니다. 흐름 은 다음과 같습니다.

1. MTS(Mechanical Threshold Stress, MTS) 플라스틱 흐름 응력 ^[15][16]모델에 의해 개발되어^[14] 함께 사용되는 MTS 전단 계수 모델.
2. Steinberg-Cochran-Guian(SCGL) 흐름 응력 모델에 의해 개발되어^[17] SCGL(Steinberg-Cochran-Guian-Lund)과 함께 사용되는 전단 계수 모델.
3. 린데만 이론을 사용하여 온도 의존성을 결정하는 나달과 르포악(NPoac) 전단 계수 모델과^[12] 전단 계수 압력 의존성에 대한 SCG 모델.

MTS 델 m

은 다음과 . MTS 전단 계수 모델에는 MTS가 있습니다.

$_displaystyle \mu(T)=\mu _{0}-{\frac {D}{\exp(T_{0}/T)-1}}}}\displaystyle \muyle \xp(T)$

$여기$서 ${\displaystyle {\mu \mathrm{}}_{}}$ 0$({$ _${$$0})$은 T $=$ ${\displaystyle 0}$K의 $전단{\displaystyle }$ $계수$이고 D({$displaystyle$ T=0K$\})$$$$및{\displaystyle {}_{}}$ T $({$은$$ 재료 상수입니다$.$

모모

하며 Steinberg-Cochran-Guian(SCG)의 형식을 .

$}{\^{\{ \}{\ T \ {{\}$

여기서₀ μ는 기준상태에서의 전단계수(T = 300 K, p = 0, θ = 1)이고 p는 압력, T는 온도이다.

NP 형

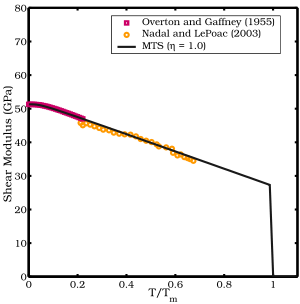
나달-르 포악(NP) 전단 계수 모델은 SCG 모델의 변형 버전입니다.SCG 모델에서 전단률의 경험적 온도 의존성은 린데만 용해 이론에 기초한 방정식으로 대체된다.NP 전단 계수 모형의 형식은 다음과 같습니다.

${\displaystyle\mu(p,T)={\frac{1}{{{J\mathcal}}\left({\hat{T}}\right)}}\left[\left(\mu_{0}+{\frac{\partial \mu}{\partial p}}{{p}{\eta ^{\frac{1}{3}}}}\right)\frac \left(1-{\hat{T}}\right)+{\frac{\rho}{Cm}}~T\right],(\displaystyle \mu(p,T)=param frac{1}{{J\mathcal}}\left({\hat{T}\right)}}\left-LSB- \mu _0}+{\frac{p}{\frac{p}{\eta ^{\frac.1}{3}}}}\left}{\left}}}{\left}{\left}}}}}{\left}}{\left}}}}}{\fright}}}{\fright}\quad C:={\frac{\left(6\pi ^{2}\right)^{{2\frac}{3}}}{3}}f^{2}}\contrac C:=frac{left(6\pi^{2}\right)^{{2\frac}}{3}}{3}}}{f^{2}}.$

어디 어디에

${\= \ { {\T}: = style {T}],}T_{m}\in [0,6+\zeta],}$

μ는₀ 절대 0 및 주변 압력에서의 전단 계수, μ는 면적, m은 원자 질량, f는 린데만 상수이다.

$전단완화계수{\displaystyle }$ G${\displaystyle (}$ ${\displaystyle t}$) {$displaystyle$ G$(t)}$는 $전단계수$^[18] G$(\displaystyle$ G$)$의 시간 의존적 일반화이다.

${\displaystyle G}$ ${\displaystyle =}$ ${\displaystyle \underset{}{lim}}$ t ${\displaystyle \underset{}{\to }}$ ${\displaystyle \underset{}{\mathrm{\infty }}\underset{}{}}$ (${\displaystyle t}$) { $displaystyle$ G = \$lim$_ {$t\to$ \infty$}G(t$

「」도 .

• 강도 강 shear

균질 등방성 선형 탄성 재료는 이들 중 2개의 모듈리에 의해 고유하게 결정되는 탄성 특성을 가지고 있으며, 따라서 임의의 2개의 모듈리가 주어진 경우 3D 재료(표 제1부) 및 2D 재료(제2부) 모두에 대해 제공되는 이들 공식에 따라 다른 탄성 모듈을 계산할 수 있다.
	$K=displaystyle K=}$	$E=displaystyle E=}$	$=displaystyle\displayda =,}$	$G=displaystyle G=}$	$=displaystyle \nu =,}$	$M=displaystyle M=}$	★★★★★
$displaystyle(K,E)}$			$displaystyle {3K(3K-E)}{9K-E}$	$9K-E}}{\displaystyle\tfrac{3}KE}{9K-E}}$	$displaystyle\tfrac{3K-E}{6K})$	$displaystyle {3K(3K+E)}{9K-E}$
${\displaystyle(K,,\lambda)}$		${\displaystyle {9K(K-\lambda)}{3K-\lambda }}$		${\displaystyle {3(K-\lambda)}{2}}$	$(\displaystyle\tfrac\lambda}{3K-\lambda}}$	$({displaystyle 3K-2\lambda})$
${\displaystyle(K,G)}$		${\displaystyle\tfrac{9KG}{3K+G}}$	${\displaystyle K-{\tfrac {2G}{3}}$		$(\displaystyle\tfrac{3K-2G}{2(3K+G)})$	$\displaystyle K+{\tfrac {4G}{3}}$
${\displaystyle(K,,\nu)}$		${\displaystyle 3K(1-2\nu),}$	${\displaystyle {3K\nu}{1+\nu }}$	${\displaystyle {3K(1-2\nu)}{2(1+\nu)}}$		${\displaystyle {3K(1-\nu)}{1+\nu }}$
${\displaystyle(K,M)}$		${\displaystyle {9K(M-K)}{3K+M}}$	$(\displaystyle\tfrac{3K-M}{2})$	${\displaystyle {3(M-K)}{4}}$	${\displaystyle\tfrac{3K-M}{3K+M}}$
${\displaystyle(E,,\lambda)}$	${\displaystyle {E+3\lambda +R}{6}}$			${\displaystyle {E-3\lambda +R}{4}}$	${\displaystyle {tfrac {2\lambda}{E+\lambda +R}}$	${\displaystyle {E-\lambda +R}{2}}$	$({displaystyle R=sqrt {E^{2}+9\lambda ^{2}+2E\lambda }})$
${\displaystyle(E,G)}$	${\displaystyle\tfrac{EG}{3(3G-E)}}$		${\displaystyle {G(E-2G)}{3G-E}}$		${\displaystyle\tfrac{E}{2G}}-1}$	${\displaystyle {G(4G-E)}{3G-E}}$
${\displaystyle(E,,\nu)$	${\displaystyle\tfrac{E}{3(1-2\nu)}}$		${\displaystyle {E\nu}{(1+\nu)(1-2\nu)}}$	${\displaystyle {E}{2(1+\nu)}}$		${\displaystyle {E(1-\nu)}{(1+\nu)(1-2\nu)}}$
${\displaystyle(E,M)}$	$(\displaystyle\tfrac{3M-E+S}{6})$		$\ displaystyle \ tfrac { M - E + S } { 4}}}$	$(\displaystyle\tfrac{3M+E-S}{8})$	${\displaystyle\tfrac{E-M+S}{4M}}}$		$\displaystyle S=\pm {E^{2}+9M^{2}-10EM}}}$ 두 가지 유효한 해결책이 있습니다. 플러스 기호는 ${\displaystyle 0}$으로$$이어집니다.\ $displaystyle \ nu$ \ $geq$ 0$$${\displaystyle 。}$ 빼기 부호는 ${\displaystyle 0}$으로$$이어집니다$.\displaystyle$\ $nu$ \$leq$ 0$$${\displaystyle 。}$
$\displaystyle(\lambda,,G)}$	$\displaystyle \lambda +{\tfrac {2G}{3}}$	${\displaystyle {G(3\lambda +2G)}{\lambda +G}}$			$(\displaystyle\tfrac\lambda}{2(\lambda+G)})$	$(\displaystyle \lambda + 2G, )$
$\displaystyle(\displayda,\nu)}$	$(\displaystyle\tfrac(1+\nu){3\nu }}$	$(*displaystyle (1+\nu) (1-2\nu)) {\nu }$		${\displaystyle\tfrac(1-2\nu)}{2\nu }$		$(\displaystyle\tfrac(1-\nu){\nu }}$	${\displaystyle \mathrm{\nu }}$ ${\displaystyle =}$ 0 ${\displaystyle \iff }$ ${\displaystyle =}$ { $displaystyle \nu$=$$0 \$left$ rightarrow \sqda =$0$}인 경우에는 사용할 수 없습니다.
${\displaystyle(\lambda,,M)}$	${\displaystyle {M+2\lambda}{3}}$	${\displaystyle {(M-\lambda)(M+2\lambda)}{M+\lambda}}$		${\displaystyle {M-\lambda}{2}}$	$(\displaystyle\tfrac\lambda}{M+\lambda}})$
${\displaystyle(G,\nu)}$	${\displaystyle {2G(1+\nu)}{3(1-2\nu)}}$	${\displaystyle 2G(1+\nu),}$	${\displaystyle {2G\nu}{1-2\nu }}$			${\displaystyle {2G(1-\nu)}{1-2\nu }}$
${\displaystyle(G,M)}$	${\displaystyle M-{\tfrac {4G}{3}}$	${\displaystyle {G(3M-4G)}{M-G}}$	${\displaystyle M-2G,}$		${\displaystyle {M-2G}{2M-2G}}$
${\displaystyle(\nu,,M)}$	${\displaystyle {M(1+\nu)}{3(1-\nu)}}$	${\displaystyle {M(1+\nu)(1-2\nu)}{1-\nu }}$	${\displaystyle {M\nu}{1-\nu }}$	${\displaystyle {M(1-2\nu)}{2(1-\nu)}}$
이차원 공식	${\displaystyle K_{\mathrm {2D} =,}$	${\displaystyle E_{\mathrm {2D} =,}$	${\displaystyle \displayda _{\mathrm {2D} =,}$	${\displaystyle G_{\mathrm {2D} =,}$	$\displaystyle \nu _{\mathrm {2D} =,}$	${\displaystyle M_{\mathrm {2D} =,}$	메모들
$({displaystyle(K_{\mathrm {2D}}},E_{\mathrm {2D}})}$			$({displaystyle {tfrac {2K_{\mathrm {2D}}) {2K_{\mathrm {2D}}) {4K_{\mathrm {2D}}-E_{\mathrm {2D}}}})$	${\displaystyle {K_{\mathrm {2D}}E_{\mathrm {2D}}}{4K_{\mathrm {2D}}-E_{\mathrm {2D}}}}}$	${\displaystyle {tfrac {2K_{\mathrm {2D}}-E_{\mathrm {2D}}}{2K_{\mathrm {2D}}}}}$	$({displaystyle {tfrac {4K_{\mathrm {2D}}^{2}}) {4K_{\mathrm {2D}}-E_{\mathrm {2D}}}})$
$\displaystyle (K_{\mathrm {2D}},\lambda _{\mathrm {2D}})}$		$(\displaystyle {tfrac {4K_{\mathrm {2D}}-\lambda _{\mathrm {2D}}) {2K_{\mathrm {2D}}-\lambda _{\mathrm {2D}}}}}})$		${\displaystyle K_{\mathrm {2D}}-\lambda _{\mathrm {2D}}}$	$({displaystyle {tfrac {\mathrm {2D}}) {2K_{\mathrm {2D}}-\lambda_{\mathrm {2D}}}})$	${\displaystyle 2K_{\mathrm {2D}}-\lambda _{\mathrm {2D}}}$
$({displaystyle(K_{\mathrm {2D}},G_{\mathrm {2D}})})$		${\displaystyle {tfrac {4K_{\mathrm {2D}}G_{\mathrm {2D}}}{K_{\mathrm {2D}}+G_{\mathrm {2D}}}}}}$	$\displaystyle K_{\mathrm {2D}}-G_{\mathrm {2D}}$		${\displaystyle {K_{\mathrm {2D}}-G_{\mathrm {2D}}}{K_{\mathrm {2D}}+G_{\mathrm {2D}}}}}$	${\displaystyle K_{\mathrm {2D}}+G_{\mathrm {2D}}}$
$\displaystyle (K_{\mathrm {2D}},\nu _{\mathrm {2D}})}$		${\displaystyle 2K_{\mathrm {2D}}}(1-\nu _{\mathrm {2D} }),$	${\displaystyle {tfrac {2K_{\mathrm {2D}}\nu _{\mathrm {2D}}}{1+\nu _{\mathrm {2D}}}}}}$	${\displaystyle {K_{\mathrm {2D}}(1-\nu _{\mathrm {2D}})}{1+\nu _{\mathrm {2D}}}}}$		${\displaystyle {2K_{\mathrm {2D}}}}{1+\nu _{\mathrm {2D}}}}}$
$(\displaystyle(E_{\mathrm {2D}},G_{\mathrm {2D} })}$	${\displaystyle {E_{\mathrm {2D}}G_{\mathrm {2D}}}}{4G_{\mathrm {2D}}-E_{\mathrm {2D}}}}}}$		${\displaystyle {2G_{\mathrm {2D}}(E_{\mathrm {2D}}-2G_{\mathrm {2D}}}}}}{4}G_{\mathrm {2D}}-E_{\mathrm {2D}}}}}}$		${\displaystyle {E_{\mathrm {2D}}}{2G_{\mathrm {2D}}}-1}$	${\displaystyle {4G_{\mathrm {2D} {{2}} {4}G_{\mathrm {2D}}-E_{\mathrm {2D}}}}}}$
$\displaystyle (E_{\mathrm {2D}},\nu _{\mathrm {2D}})}$	${\displaystyle {E_{\mathrm {2D}}}}{2(1-\nu _{\mathrm {2D}}}}}$		${\displaystyle {E_{\mathrm {2D}}\nu _{\mathrm {2D}}}}{(1+\nu _{\mathrm {2D}}}}}}{\nu _{\mathrm {2D}}}}}$	${\displaystyle {E_{\mathrm {2D}}}}{2(1+\nu _{\mathrm {2D}}}}}$		${\displaystyle {E_{\mathrm {2D}}}}{(1+\nu _{\mathrm {2D}}}}}}$
${\displaystyle(\lambda _{\mathrm {2D}},G_{\mathrm {2D}})}$	${\displaystyle \lambda _{\mathrm {2D}}+G_{\mathrm {2D}}}$	$(\displaystyle { tfrac { 4G _ { \ mathrm { 2D } } \ mathrm { 2D } } ) { \ lambda _ { \ mathrm { 2D } } + 2G _ { \ mathrm { 2D } } } } } } }$			${\displaystyle {\mathrm {2D}}{\lambda _{\mathrm {2D}}}+2G_{\mathrm {2D}}}}}$	$\displaystyle \lambda _{\mathrm {2D}}+2G_{\mathrm {2D}},}$
${\displaystyle(\lambda _{\mathrm {2D}},\nu _{\mathrm {2D}})}$	$({displaystyle {tfrac {\mathrm {2D}}) {2\nu _{\mathrm {2D}}}}) {2\nu _{\mathrm {2D}}}}$	$({displaystyle {tfrac {\mathrm {2D}}) (1+\nu _{\mathrm {2D}}) {\nu _{\mathrm {2D}}})$		$({displaystyle {tfrac {\mathrm {2D}}) {2\nu _{\mathrm {2D}}}}) {2\nu _{\mathrm {2D}}}}$		$(\displaystyle {tfrac {\mathrm {2D}}) {\nu _{\mathrm {2D}}})$	${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {\mathrm{2}}_{}}$ D ${\displaystyle {=}_{}}$ ${\displaystyle 0}$ ${\displaystyle \iff }$ ${\displaystyle {2\mathrm{}}_{}}$ ${\displaystyle {\mathrm{D}}_{}}$ ${\displaystyle {=}_{}}$ \ $displaystyle$\ $nu$ _ { \ $mathrm${ 2$D$ } $= 0$ \ 왼쪽 $화살표$\ $sqda$ _ { \ $mathrm${ 2$D$ } =$0$}인 경우에는 사용할 수 없습니다.
$\displaystyle (G_{\mathrm {2D}},\nu _{\mathrm {2D}})}$	${\displaystyle {G_{\mathrm {2D}}(1+\nu _{\mathrm {2D}})}{1-\nu _{\mathrm {2D}}}}}$	${\displaystyle 2G_{\mathrm {2D}}}(1+\nu _{\mathrm {2D}}),$	${\displaystyle {tfrac {2G_{\mathrm {2D}}\nu _{\mathrm {2D}}}{1-\nu _{\mathrm {2D}}}}}}$			${\displaystyle {2G_{\mathrm {2D}}}}{1-\nu _{\mathrm {2D}}}}}$
${\displaystyle(G_{\mathrm {2D}},,M_{\mathrm {2D}})}$	${\displaystyle M_{\mathrm {2D}}-G_{\mathrm {2D}}}$	$({displaystyle {4G_{\mathrm {2D}})(M_{\mathrm {2D}}) {M_{\mathrm {2D}}}) {M_{\mathrm {2D}}}}}}$	${\displaystyle M_{\mathrm {2D}}-2G_{\mathrm {2D}},}$		${\displaystyle {M_{\mathrm {2D}}-2G_{\mathrm {2D}}}{M_{\mathrm {2D}}}}:$