마찰 접촉 역학

다음에 대한 시리즈 일부
연속체 역학
${\displaystyle J=-D{\frac {d\varphi }{dx}}}$ 픽의 확산 법칙
법 컨버지 미사 모멘텀 에너지 불평등 클라우시우스-듀헴 (엔트로피)
고체 역학 변형 탄력성 일직선의 가소성 후크의 법칙 스트레스 유한변형 무한 변형률 호환성. 벤딩 접촉 역학 마찰의 물질적 고장 이론 파단 역학
유체역학 유체 통계학 · 역학 아르키메데스의 원리 · 베르누이의 원리 나비에-스토크스 방정식 푸아세유 방정식 · 파스칼의 법칙 점도 (뉴턴어 · 비뉴턴어) 부력 · 믹싱 · 압력 액체 접착 모세관 작용 크로마토그래피 응집(화학) 표면장력 가스 대기 보일의 법칙 찰스의 법칙 복합가스법 픽의 법칙 게이 루삭의 법칙 그레이엄의 법칙 플라즈마
리히로지 점탄성 레호메트리 레히미터 스마트 유체 전기오류 자기 지질학 페로플루이드
과학자들 베르누이 보일 카우치 찰스 오일러 픽 게이 루삭 그레이엄 훅 뉴턴 나비에르 노울 파스칼 스톡스 트뤼셀
v t

접촉 역학은 하나 이상의 지점에서 서로 접촉하는 고체의 변형을 연구하는 학문이다.^[1][2] 이는 인터페이스에 수직인 방향의 압축력과 접착력, 접선 방향의 마찰력으로 나눌 수 있다. 마찰 접촉 역학은 마찰 효과의 존재에 있어서 신체의 변형에 관한 연구인 반면, 마찰 없는 접촉 역학은 그러한 영향이 없다고 가정한다.

마찰 접촉 역학은 다양한 스케일의 넓은 범위에 관련된다.

• 거시적 규모로, 신체 접촉 운동의 조사에 적용한다(연락처 역학 참조). 예를 들어 표면에 고무공이 튀는 것은 접촉면에서의 마찰 상호작용에 따라 달라진다. 여기서 총 하중 대 수축 및 측면 변위가 주된 관심사다.
• 중간 규모에서는 접촉 구역 안과 근처에 있는 접촉 기관의 국소 응력, 변형 및 변형에 관심이 있다. 예를 들어 거시적 척도로 접촉 모델을 도출하거나 검증하거나 접촉하는 신체 표면의 마모 및 손상을 조사한다. 이 척도의 적용 영역은 타이어-포장 상호작용, 철도 휠-레일 상호작용, 롤러 베어링 분석 등이다.
• 마지막으로, 현미경 및 나노스케일에서는 접촉 역학을 사용하여 유전체계에 대한 이해도를 높이고(예를 들어 마찰의 기원을 조사) 원자력 현미경 및 MEMS 장치와 같은 첨단 장치의 엔지니어링을 한다.

이 페이지는 주로 두 번째 척도와 관련이 있다. 즉, 접촉 패치의 내부와 주변의 스트레스와 변형에 대한 기본적인 통찰력을 얻는 것이다.

역사

몇몇 유명한 과학자, 엔지니어, 수학자가 마찰에 대한 우리의 이해에 기여했다.^[3] 레오나르도 다빈치, 기욤 아몬턴스, 존 테오필루스 데사굴리에스, 레온하르트 오일러, 샤를 아우구스틴 드 쿨롱 등이 그것이다. 후에 니콜라이 파블로비치 페트로프, 오스본 레이놀즈, 리처드 스트리벡은 윤활 이론으로 이러한 이해를 보충하였다.

고체 물질의 변형은 17세기와 18세기에 로버트 후크, 조셉 루이스 라그랑주에 의해, 19세기와 20세기에 달렘베트와 티모셴코가 조사되었다. 접촉 역학에 관해서는 하인리히 헤르츠의^[4] 고전적 공헌이 돋보인다. 또한 (선형적으로) 탄성체제의 마찰 접촉 문제를 조사하기 위해서는 부신섹과 세루티의 근본적인 해결책이 일차적으로 중요하다.

진정한 마찰 접촉 문제에 대한 고전적인 결과는 F.W. 카터(1926)와 H. 프롬(1927)의 논문과 관련이 있다. 그들은 Coulomb의 건조 마찰 법칙(아래 참조)^[5]을 사용하여 평면의 실린더 또는 두 실린더에 대한 크리프 대 크리프 힘 관계를 독립적으로 제시했다. 이는 철도 기관차 견인 및 철도 차량의 사냥 진동 이해에 적용된다. 슬라이딩과 관련하여 고전적인 해결책은 C 때문이다. 비행기에서 구의 접선적 이동을 고려했던 카타네오(1938년)와 R.D.민들린(1949년)은 다음과 같다.^[1]

1950년대에는 철도 바퀴의 구르는 접촉에 대한 관심이 커졌다. 1958년에 Kenneth L. Johnson은 측면 또는 스핀 크립페이지 중 하나로 헤르츠 기하학의 3D 마찰 문제에 대한 대략적인 접근방식을 제시했다. 다른 것들 중에서 그는 접점 패치의 중심에 대칭인 스핀 크립이 굴림 조건에서 순 횡력으로 이어진다는 것을 발견했다. 이는 접점 패치의 트랩 분포에서 전후반 차이 때문이다.

1967년, Joost Jacques Kalker는 롤링 접점을 위한 선형 이론에 대한 그의 획기적인 박사 논문을 발표했다.^[6] 이 이론은 슬립 영역이 사라지는 무한 마찰 계수의 상황에 정확하며, 비파니싱 크립 페이지에 근사적이다. 그것은 어느 정도는 깨끗한 표면을 필요로 하는 쿨롱의 마찰 법칙을 가정한다. 이 이론은 철도 차륜-철도 접촉과 같은 거대한 몸을 위한 이론이다. 도로와 타이어의 상호작용과 관련하여 중요한 기여는 한스 파세즈카의 이른바 매직 타이어 공식에 관한 것이다.^[7]

1970년대에는 많은 숫자 모델이 고안되었다. 특히 듀바우트와 라이온의 존재와 고유성 이론에 의존하는 것과 같은 가변적 접근법. 시간이 지남에 따라, 이것들은 일반 재료 모델과 기하학과의 접촉 문제에 대한 유한 요소 접근법, 그리고 선형 탄성 재료에 대한 소위 매끄러운 모서리의 접촉 문제에 대한 반공간 기반 접근법으로 성장했다. 첫 번째 범주의 모델은 로르센과^[8] 리거스가 선보였다.^[9] 후자의 범주의 예는 칼커의 CONTER 모델이다.^[10]

근거가 충분한 변동 접근법의 단점은 큰 계산 시간이다. 따라서, 다양한 근사적 접근법도 고안되었다. 롤링컨택 문제에 대해 잘 알려진 몇 가지 근사 이론은 Kalker의 FASTSIM 접근법, Shen-Hedrick-Elkins 공식, Polach의 접근법이다.

휠/레일 접촉 문제의 이력에 대한 자세한 내용은 노데의 논문을 참조하십시오.^[5] 게다가 존슨은 그의 책에서 접촉 역학과 관련 주제에 대한 엄청난 양의 정보를 수집했다.^[1] 롤링 컨택트 메카니즘에 관해서도 칼커는 다양한 이론의 개요를 제시한다.^[10] 마지막으로, CISM 과정의 진행은 관심의 대상이며, 이것은 롤링 접점 이론의 더 진보된 측면에 대한 소개를 제공한다.^[11]

문제 제식

마찰 접촉 문제의 분석에서 중심은 각 신체 표면의 응력이 공간적으로 변화한다는 것을 이해하는 것이다. 결과적으로 신체의 변종과 변형은 위치에 따라 달라진다. 그리고 접촉하는 신체들의 입자의 움직임은 서로 다른 위치에서 다를 수 있다: 반대되는 신체들의 접촉 패치 입자의 일부에서는 서로 달라붙을 수 있는 반면, 접촉 패치 상대적 움직임의 다른 부분에서는 발생한다. 이 국부적 상대적 슬라이딩은 마이크로슬립이라고 불린다.

이렇게 접촉 부위를 막대(접착)와 미끄러짐 영역으로 세분화하면 초조해하는 마모가 드러난다. 마모는 전원이 방전된 경우에만 발생하며, 두 표면 사이의 응력과 국소 상대적 변위(슬립)가 필요하다.

콘택트 패치 자체의 크기와 모양, 접착력과 미끄러짐 부위는 일반적으로 사전에 알려져 있지 않다. 이런 것들이 알려지면 두 신체의 탄성장은 서로 독립적으로 해결될 수 있고 문제는 더 이상 접촉 문제가 되지 않을 것이다.

접촉 문제에서 세 가지 다른 구성요소를 구별할 수 있다.

1. 우선, 표면에 가해지는 하중에 대한 반응으로 분리된 신체의 변형이 있다. 이것은 일반적인 연속체 역학의 주제다. 그것은 신체의 기하학적 구조와 그들의 (대안) 물질적 행동(예: 탄성 대 플라스틱 반응, 동질 대 층 구조 등)에 크게 좌우된다.
2. 둘째로, 서로에 대한 몸의 전반적인 움직임이 있다. 예를 들어 신체는 휴식(통계)에 있거나 서로 빠르게 접근(충격)할 수 있으며, 서로 위로 이동(슬라이딩)하거나 회전(롤링)할 수 있다. 이러한 전반적인 동작은 일반적으로 고전 역학에서 연구된다. 예를 들어 멀티바디 역학을 참조한다.
3. 마지막으로 접점 인터페이스에는 인터페이스에 수직인 방향의 압축과 접착, 접선 방향의 마찰과 마이크로 미끄럼 등의 프로세스가 있다.

마지막 측면은 접촉 역학의 주요 관심사다. 이른바 접촉 조건의 측면에서 기술하고 있다. 인터페이스에 수직인 방향의 경우, 정상 접촉 문제의 경우 접착 효과는 대개 작으며(더 큰 공간적 척도에서) 다음과 같은 조건이 일반적으로 사용된다.

1. ${\displaystyle {두}_{}}$ 표면 사이의$$ 간격 $e{\displaystyle {}_{}}$ ${\$은(는) 0(접점) 또는 엄격히 양(분리, > $({\displaystyle e_{n}>0})$이어야 한다.
2. 각 몸에 작용하는$$ 정상 응력 ${\$는 0(분리) 또는 압축(> ${\displaystyle p_{n}>0}$ 접촉 중)이다.

Mathematically: ${\displaystyle e_{n}\geq 0,p_{n}\geq 0,e_{n}\cdot p_{n}=0\,\!}$. Here ${\displaystyle e_{n},p_{n}}$ are functions that vary with the position along the bodies' surfaces.

접선 방향에서는 흔히 다음과 같은 조건을 사용한다.

1. The local (tangential) shear stress ${\displaystyle {\vec {p}}=(p_{x},p_{y})^{\mathsf {T}}\,\!}$ (assuming the normal direction parallel to the ${\displaystyle z}$-axis) cannot exceed a certain position-dependent maximum, the so-called traction bound ${\displaystyle g}$;
2. Where the magnitude of tangential traction falls below the traction bound ${\displaystyle \ {\vec {p}}\ <g\,\!}$, the opposing surfaces adhere together and micro-slip vanishes, ${\displaystyle {\vec {s}}=(s_{x},s_{y})^{\mathsf {T}}={\vec {0}}\,\!}$;
3. 마이크로 미끄럼은 접선 트립이 트랙션 바운드에 있을 때 발생한다. 접선 트랙션의 방향은 마이크로 $미끄럼{\displaystyle \stackrel{}{}}$p${\displaystyle }$→${\displaystyle }$= - ${\displaystyle g\stackrel{}{}s\stackrel{}{}}$→ /${\displaystyle s\stackrel{}{}}$ s → ${\displaystyle \stackrel{}{\to }}$ s →$‖{\vec}=-g{\vec$의 방향과 반대다.

트랙션 바운드의 정확한 형태는 이른바 국소마찰법이다. 이 쿨롱의 (글로벌) 마찰 법칙은 ${\displaystyle \mathrm{종종}}$ 국지적으로 적용된다:${\displaystyle }$: ${\displaystyle p\stackrel{}{}}$→${\displaystyle \Vert }$ g =${\displaystyle \mu }$ p = ${\displaystyle {\mu }_{}}$ ${\displaystyle {}_{}}$ ${\vec{p}\\leq$ g$=\mu p_{n}\,\},$$\mu {\displaystyle }$$$${\displaystyle \mu \}$의 마찰$$ 계수를 가지고 있다. 온도 $T{\displaystyle }$ ${\displaystyle$ T$\},$ 국부 슬라이딩 속도 $\Vert {\displaystyle s\stackrel{}{}}$→$‖{\displaystyle \{\vec}\}$등에 따라$$ $\mu {\displaystyle }$ ${\displaystyle \mu }$을(를) 갖는 등 보다 상세한 공식도 가능하다.

정적 사례에 대한 솔루션

볼라드 위의 밧줄, 캡스턴 방정식

동일한 힘($예{\displaystyle {}_{}}$: F ${\displaystyle {\text{hold}}_{}}$ = ${\displaystyle 400\mathrm{}{}_{}}$N ${\$이 양쪽에 작용하는 로프를 고려하십시오. 이에 의해 로프가 약간 늘어나며 내부 $장력{\displaystyle }$ T ${\displaystyle T}$이(가) 유도된다(로프를 따라 모든 $$에서${\displaystyle }$T = ${\displaystyle 400}$ ${\displaystyle N\mathrm{}}$ ${\$ 로프는 볼라드와 같은 고정된 품목에 감겨 있다. 로프는 구부러지고 접촉 각도를 통해 품목의 표면에 접촉한다(예: ${\displaystyle {180}^{}}$˚${\$circle $}).$ 밧줄과 볼라드 사이에 정상적인 압력이 들어오지만 아직 마찰은 일어나지 않는다. 다음으로 볼라드 한쪽의 힘은 더 높은 값으로 증가한다(예: F ${\displaystyle {\text{부하}}_{}}$= ${\displaystyle 600N\mathrm{}}$ ${\$ {$N} }).$ 이것은 접촉 부위에서 마찰전단 응력을 유발한다. 마지막 상황에서 볼라드는 정적 상황이 발생하도록 로프에 마찰력을 행사한다.

이 최종 상황에서 로프의 장력 분포는 캡스턴 방정식으로 설명되며, 용액은 다음과 같다.

${\displaystyle {\reasoned}T(\phi )&=T_{\text{hold},&\phi &\in \왼쪽[\phi _{\text{hold},\phi _{\text{intf}}\오른쪽]\T(\phi )&=T_{\text{load}e^{-\mu \pi },&\pi &\in \왼쪽[\phi _{\text{intf},\phi _{\text{load}\오른쪽]\\phi _{\text{intf}&={\frac {1}{\mu }}\log \left({\frac {T_{\text{load}}}}}}}{\frac {1}}}}{\log}}{\frac}}}}}}{T_{\text{hold}}}\오른쪽)&\end{aigned}}$

The tension increases from ${\displaystyle T_{\text{hold}}}$ on the slack side (${\displaystyle \phi =\phi _{\text{hold}}}$) to ${\displaystyle T_{\text{load}}}$ on the high side ${\displaystyle \phi =\phi _{\text{load}}}$. When viewed from the high side, the tension drops 기하급수적으로 $\varphi {\displaystyle }$= ${\displaystyle {}_{}}$ ${\displaystyle {\text{intf}}_{}}$ ${\$에서 하중에 도달할 때까지. 거기서부터 이 값으로 일정하게 된다$.$ 전환점 $\varphi {\displaystyle {}_{}}$ ${\displaystyle {\text{intf}}_{}}$ ${\$은(는) 두 하중 비율과 마찰 계수에 의해 결정된다$$. 여기서 긴장 $T{\displaystyle }$ ${\displaystyle T}$이(가) 뉴턴에 있고$$ 각도 $\varphi {\displaystyle }$ ${\displaystyle \phi }$이(가) 라디안으로 표시된다.

최종 상황에서 로프의$$ 장력 $T{\displaystyle }$ ${\displaystyle T}$은(는) 초기 상태에 대해 증가된다. 그러므로 로프는 약간 길다. 이것은 로프의 모든 표면 입자가 볼라드 표면에서 초기 위치를 유지할 수 없다는 것을 의미한다. 적재 과정 중에, 로프는 슬립 영역인 볼라드 표면을 따라 약간 미끄러져 나갔다${\displaystyle .}$$\varphi {\displaystyle }$ [${\displaystyle {}_{}}$ ${\displaystyle {\text{intf}}_{},{}_{}{}_{}}$ ${\displaystyle {\text{load}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle \phi \in[\phi _{\text{intf},\phi _{\text{load}}].$ 이 전표는 최종 상태에서 발생하는 연장에 도달할 수 있을 만큼 충분히 크다. 최종 상태에서는 미끄러짐 현상이 발생하지 않는다는 점에 유의하십시오. 미끄러짐 영역이라는 용어는 적재 프로세스 중에 발생한 미끄러짐을 가리킨다. 또한 미끄러짐 영역의 위치는 초기 상태와 적재 프로세스에 따라 결정된다는 점에 유의하십시오. 초기 장력이 $(\$이고 장력이 느슨한 쪽에서$$ $(\$으)로 감소하면 접점 부위의 느슨한 쪽에서 미끄러짐 영역이 발생한다. $400$ ${\$$displaystyle 400}$과 $사이$의 초기 장력에 대해서는 양쪽에 스틱 영역이 사이에 있는 슬립 영역이 있을 수 있다$.$

임의의 직교이방성 표면에 놓여 있는 로프의 일반화

로프가 거친 직교방성 표면의 접선력 하에서 평형을 이루면 다음 세 가지 조건(모두)이 충족된다.

이 일반화는 Konyukhov A에 의해 얻어졌다.^[12][13]

평면 위의 구면, (3D) Cattaneo 문제

평면(반쪽 공간)에 눌린 다음 평면 표면 위로 이동한 구를 고려한다. 구체와 평면이 강성체로 이상화되면 단 한 지점에서 접촉이 일어나며, 적용된 접선력이 최대 마찰력에 도달할 때까지 구체가 움직이지 않는다. 그런 다음 적용된 힘이 다시 줄어들 때까지 표면 위로 미끄러지기 시작한다.

탄성 효과를 고려한 현실은 상황이 많이 다르다. 탄성 구를 같은 물질의 탄성 면에 압착하면 양쪽 신체가 변형되고, 원형 접촉 영역이 생겨나고, (헤르츠어) 정상 압력 분포가 발생한다. 구의 중심은 접근이라 불리는$$ ${\displaystyle {\Delta n}_{}}$ ${\$ 거리에 의해 아래로 이동하는데, 이는 비정형 표면의 최대 침투에 해당한다. 반경 $R{\displaystyle }$ ${\displaystyle R}$ 및 탄성$$ $상수{\displaystyle }$ E ,${\displaystyle \nu }$ ${\displaystyle$ E$,\nu }$의 경우 이$$ 헤르츠어 솔루션은 다음과 같이 읽는다.

${\displaystyle {\signified}p_{n}(x,y)&=p_{0}{\sqrt{1-{\frac{2}}:{a^{2}}:}&r&={\sqrt{x^{2}+y^{2}}{2}}}}}}}\leq a&a&={\sqrt {R\delta _{n}}}\\p_{0}&={\frac {2}{\pi }}E^{*}{\sqrt {\frac {\delta _{n}}{R}}}&F_{n}&={\frac {4}{3}}E^{*}{\sqrt {R}}\delta _{n}^{\frac {3}{2}}&E^{*}&={\frac {E}{2\왼쪽(1-\nu ^{2}\오른쪽)}}}\end{aigned}}}$

이제 쿨롬 마찰 결합 ${\displaystyle {\mu F}_{}}$ ${\$$displaystyle F_{n$}보다 낮은 접선력 F ${\displaystyle x_{}}$ ${\$$displaystyle μF$ {\$mu$ F_${$$n}}$이 적용되는$$ 것을 고려한다$.$ 그 후 구의 중심은 시프트라고 불리는$$ 작은 거리 $\Delta {\displaystyle {}_{}}$ ${\displaystyle x_{}}$ ${\$에 의해 옆으로 이동하게 된다. 정적 평형상태는 탄성변형과 접촉면에서의 마찰전단 응력이 발생하는 곳에서 얻는다. 이 경우 접선력이 감소하면 탄성 변형과 전단 응력도 감소한다. 접촉 패치의 국부적 미끄러짐으로 인해 발생하는 마찰 손실을 제외하고 구는 대체로 원래 위치로 다시 이동한다.

이 접촉 문제는 분석적 접근법을 사용하여 Cattaneo에 의해 대략적으로 해결되었다. 평형 상태에서 응력 분포는 두 부분으로 구성된다.

${\displaystyle {\begin{aligned}p_{x}(x,y)&=\mu p_{0}\left({\sqrt {1-{\frac {r^{2}}{a^{2}}}}}-{\frac {c}{a}}{\sqrt {1-{\frac {r^{2}}{c^{2}}}}}\right)&0\leq {}&r\leq c\\p_{x}(x,y)&=\mu p_{n}(x,y)&c\leq {}&r\leq a\\p_{x}(x,y)&=0&a\leq {}&r\end{aligned}}}$

In the central, sticking region ${\displaystyle 0\leq r\leq c}$, the surface particles of the plane displace over ${\displaystyle u_{x}=\delta _{x}/2}$ to the right whereas the surface particles of the sphere displace over ${\displaystyle u_{x}=-\delta _{x}/2}$ to the lefT. 구 전체가 평면에 상대적인 Δ x{\displaystyle \delta_{)}위로 이동해도 이러한 표면 입자는 서로 상대적으로 이동하지 않았다. 바깥쪽 고리 c $c{\displaystyle }$ r${\displaystyle r}$ r ${\displaystyle c\leq r\leq r}$에서 표면 입자는 서로 상대적으로 움직였다$.$ 그들의 지역 교대조는 다음과 같다.

${\displaystyle s_{x}(x,y)=\filename _{x}+u_{x}^{\text}}(x,y)-u_{x}^{\text{plane}}}(x,y)}}}$

이 이동 s ${\displaystyle x_{}}$ (${\displaystyle {}_{}x}$, ${\displaystyle y}$) ${\displaystyle s_{x}(x,y)}$은 정확하게$$ 크기 때문에 이 소위 슬립 영역에서 결합된 트랙션에서 전단 응력으로 정적 평형을 얻는다.

그래서 구의 접선하중에서는 부분 슬라이딩이 발생한다. 따라서 접촉 영역은 표면이 서로 상대적으로 움직이는 미끄러짐 영역과 그렇지 않은 막대기 영역으로 나뉜다. 평형 상태에서는 더 이상 슬라이딩이 진행되지 않는다.

동적 슬라이딩 문제 해결

접촉 문제의 해결책은 인터페이스의 상태(접촉이 있는 경우, 접촉 부위를 스틱과 슬립 존으로 나누고, 정상 및 전단 응력 분포)와 신체 내부 내부의 탄성장으로 구성된다. 이 해결책은 접촉 내역에 따라 달라진다. 이는 위에서 설명한 캣타네오 문제의 연장선에서 알 수 있다.

• 캣타네오 문제에서는 구를 먼저 비행기에 눌린 다음 접선적으로 이동시킨다. 이것은 위에서 설명한 부분적인 슬립을 산출한다.
• 구를 먼저 접선으로 이동한 다음 평면에 압착하면 반대 표면 사이에 접선 변위 차이가 없고 결과적으로 접점 인터페이스에 접선 응력이 없다.
• 정상 방향과 접선 이동의 접근방식이 동시에 증가한다면("비끄럼 압축") 국부 슬립 없이 접선 응력을 통해 상황을 달성할 수 있다.^[2]

이것은 접촉 인터페이스의 상태가 두 신체의 상대적 위치뿐만 아니라 그들의 운동 이력에 의존한다는 것을 보여준다. 구를 원래 위치로 다시 이동시키면 또 다른 예가 발생한다. 처음에는 접점 인터페이스에 접선 응력이 없었다. 초기 변속 마이크로 슬립이 발생한 후 이 마이크로 미끄럼틀은 뒤로 옮겨서 완전히 풀린 것은 아니다. 따라서 최종 상황에서 접선 스트레스는 인터페이스에 남아 원래의 것과 동일한 구성으로 보인다.

동적 접촉(충돌)에 대한 마찰의 영향을 자세히 고려한다. ^[14]

롤링 접점 문제 해결

롤링 컨택트 문제는 컨택트 체계가 서로에 대해 지속적으로 움직이고 있는 역동적인 문제들이다. 동적 슬라이딩 접촉 문제의 차이점은 표면 입자의 상태에 더 많은 다양성이 있다는 것이다. 슬라이딩 문제의 접점 패치는 지속적으로 동일한 입자로 구성되는 반면, 롤링 접점에서는 접점 패치를 끊임없이 출입한다. 게다가, 미닫이 문제에서는 접점의 표면 입자들이 거의 모든 곳에서 동일한 접선 이동에 의해 영향을 받는 반면, 굴림 문제에서는 표면 입자들이 다소 다른 방식으로 스트레스를 받는다. 접점 패치에 들어갈 때 스트레스를 받지 않고 반대 표면의 한 입자에 달라붙어 두 신체 사이의 전체적인 움직임 차이로 인해 경직되어 국부적인 트랙션 바운드가 초과되고 국부 슬립이 들어갈 때까지. 이 과정은 접촉 영역의 다른 부분에 대해 서로 다른 단계에 있다.

만약 신체의 전체적인 움직임이 일정하다면, 전체적인 안정 상태가 달성될 수 있다. 여기서 각 표면 입자의 상태는 시간에 따라 다르지만 전체 분포는 일정할 수 있다. 이는 접점 패치와 함께 이동하는 좌표계를 사용하여 공식화된다.

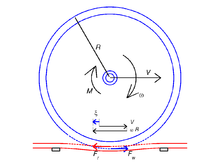
평면에서 롤링하는 실린더(2D) 카터-프롬 솔루션

일정한 조건 하에서 평면 위로 굴러가는 실린더(반공간)를 고려하되, 실린더 끝단에서 멀리 떨어진 시간에 독립적인 세로 방향 연면 페이지 ${\displaystyle \xi$}. (상대적으로) 평면 변형 상황이 발생하며 문제는 2차원이다.

실린더와 평면이 동일한 재료로 구성되면 정상적인 접촉 문제는 전단 응력에 영향을 받지 않는다. 접촉 영역은 스트립 $x{\displaystyle }$ ${\displaystyle \in [,a}$ ${\displaystyle ]}$ ${\displaystyle x\in [-a,a]}$이고$,$ 압력은 (2D) 헤르츠 용액에 의해 설명된다.

${\displaystyle {\regated}p_{n}(x)&={\frac{p_{0}}{a}{\sqrt{a^{a^{2}-x^{2}}}&#################{2}={\leq a^{4}F_{n}R}{\pi E^{*}}\p_{0}&={\frac {2F_{n}}{\pi a}{{n}}{\pi a}&E^{*&}={\frac {E}{2\nu ^{2}\오른쪽)}}}&\end{정렬}}$

전단 응력의 분포는 Carter-Fromm 용액으로 설명된다. 접점 구역의 가장자리에는 접착 영역, 가장자리에는 미끄러짐 영역으로 구성된다. The length of the adhesion area is denoted ${\displaystyle 2a'}$. Further the adhesion coordinate is introduced by ${\displaystyle x'=x+a-a'}$. In case of a positive force ${\displaystyle F_{x}>0}$ (negative creepage ${\displaystyle \xi <0}$) it is:

${\displaystyle {\begin{aligned}p_{x}(x)&=0& &x \geq a\\p_{x}(x)&={\frac {\mu p_{0}}{a}}\left({\sqrt {a^{2}-x^{2}}}-{\sqrt {a'^{2}-x'^{2}}}\right)&a-2a'\leq {}&x\leq a\\p_{x}(x)&=\mu p_{n}(x)&&x\leq a-2a'\end{aligned}}}$

접착 영역의 크기는 연면, 휠 반지름 및 마찰 계수에 따라 달라진다.

${\displaystyle {\begin{aligned}a'&=a{\sqrt {1-{\frac { F_{x} }{\mu F_{n}}}}},&{\mbox{for }} F_{x} \leq \mu F_{n}\\\xi &=-\operatorname {sign} (F_{x})\,{\frac {\mu (a-a')}{R}},&{\mbox{i.e. \xi \leq {\frac}{R}\\F_{x}=-\operatorname {sign}(\xi )\,\mu F_{n}\좌측(1+{\R \xi }\오른쪽)^{2}\i1}{{{{{R}}}}\riged}}}}}}}}}}$

크립 페이지의 경우 전체 슬라이딩이 ${\displaystyle \mathrm{발생}}$하는${\displaystyle {}^{}}such$${\displaystyle }$= 0 ${\displaystyle$ a$'=0}$

절반의 공간 기반 접근 방식

중간 공간 척도의 접촉 문제를 고려할 때, 소형의 물질적 불균형과 표면 거칠기는 무시된다. 본체는 매끄러운 표면과 균일한 물질로 구성된 것으로 간주된다. 응력, 균주 및 변위가 (부분적으로) 연속 함수로 설명되는 경우 연속형 접근법을 취한다.

반공간 접근방식은 이른바 '매끈한' 또는 '집중된' 접촉 문제에 대한 우아한 솔루션 전략이다.

1. 거대한 탄성체가 표면의 작은 부분에 적재된 경우, 탄성 $응력$은${\displaystyle }$1/${\displaystyle d}$ ${\displaystyle i}$ ${\displaystyle t}$ ${\displaystyle a}$ n ${\displaystyle {}^{}}$ e ${\displaystyle {2\mathrm{}}^{}}$ ${\$${\displaystyle \}\}}$에 비례하고 탄성 변위는 $1{\displaystyle \mathrm{}}$/${\displaystyle d}$ t ${\displaystyle a}$ n ${\displaystyle c}$ ${\displaystyle e}$ ${\displaystyle 1/distance}$ 이 표면적에서 멀어질$$ 때 1/${\displaystyle \mathrm{di}}$이다.
2. If a body has no sharp corners in or near the contact region, then its response to a surface load may be approximated well by the response of an elastic half-space (e.g. all points ${\displaystyle (x,y,z)^{\mathsf {T}}\in \mathbb {R} ^{3}\,\!}$ with ${\displaystyle z>0\,\!}$).
3. 탄성 반공간 문제는 분석적으로 해결된다. Boussinesq-Cerruti 솔루션을 참조하십시오.
4. 이 접근방식의 선형성 때문에 복수의 부분적 해법이 중첩될 수 있다.

반공간에 대한 근본적인 해결책을 사용하여 전체 3D 접촉 문제는 신체의 경계 표면의 2D 문제로 감소한다.

만약 두 몸이 "기하학적으로 그리고 탄성적으로 유사하다"면 더 단순화된다. 일반적으로, 한 방향의 신체 내부의 스트레스는 수직 방향의 변위를 유발한다. 따라서 접촉 문제의 정상 응력과 접선 변위 사이에 교호작용이 있고 접선 응력과 정상 변위 사이에 교호작용이 있다. 그러나 접촉 인터페이스의 정상적인 응력으로 양쪽 접촉 신체에서 동일한 접선 변위를 유도하는 경우, 두 표면의 상대적인 접선 변위는 없다. 이 경우 정상 및 접선성 접촉 문제는 분리된다. 이 경우 두 기체를 준정체라고 한다. 예를 들어 접촉면에 대해 신체가 거울 대칭이고 동일한 탄성 상수를 갖는 경우 이러한 현상이 발생한다.

반공간 접근법에 기초한 고전적 해결책은 다음과 같다.

1. 헤르츠는 단순한 기하학(곡률 반경이 일정한 곡선 표면)에 대해 마찰이 없는 상태에서 접촉 문제를 해결했다.
2. 카터는 위에서 설명한 대로 실린더와 평면 사이의 롤링 접점을 고려했다. 접선 트랙션을 위한 완전한 분석 솔루션이 제공된다.
3. 카타네오는 위에서 설명한 바와 같이 두 개의 구체의 압축과 이동을 고려하였다. 이 분석 용액은 근사치라는 점에 유의하십시오. 실제로는 ${\displaystyle {무시}_{}}$되는 작은 접선트레이닝 $p{\displaystyle {}_{}}$ ${\$이 발생한다$$.

참고 항목

참조

외부 링크

• [1]^{[permanent dead link]} Prof.dr.ir의 전기. J.J. 칼커(델프트 공과대학)
• [2] 칼커의 헤르츠안/비 헤르츠안 컨택트 소프트웨어.