데비-휘켈 이론

데비-후켈 이론은 전해질과 플라스마의 용액에서 이상성으로부터 벗어나는 이론적 설명으로 Peter Debye와 Erich Hückel에 의해 제안되었습니다. ^[1] 이것은 선형화된 포아송-볼츠만 모델로, 매우 단순화된 전해질 용액 모델을 가정하지만 그럼에도 불구하고 희석 용액의 이온에 대한 평균 활성 계수의 정확한 예측을 제공합니다. 데비-Hückel 방정식은 전해질 용액의 비이상성을 현대적으로 처리하기 위한 출발점을 제공합니다.^[2]

개요

전해질 용액의 화학에서 이상적인 용액은 응집 특성이 용질의 농도에 비례하는 용액입니다. 실제 솔루션은 이러한 종류의 이상에서 벗어나는 것을 보여줄 수 있습니다. 이러한 효과를 용액의 열역학에 수용하기 위해 활성의 개념이 도입되었습니다. 그 다음 특성은 이온의 활성에 비례합니다. 활동량 a는 농도 c에 비례합니다. 비례 상수는 활동 계수,$$γ $\{\backslash$displaystyle$$\gamma}로 알려져 있습니다.

${\displaystyle a=\gamma c/c^{0}}$

이상적인 전해질 용액에서 모든 이온의 활성 계수는 1과 같습니다. 전해질 용액의 이상성은 매우 희석된 용액에서만 달성할 수 있습니다. 더 농축된 용액의 비이상성은 주로(단독적이지는 않지만) 정전기 힘으로 인해 반대 전하의 이온이 서로 끌어당기는 반면 같은 전하의 이온은 서로 밀어내기 때문에 발생합니다. 결과적으로 이온은 이상적인 해에 있을 때처럼 해 전체에 무작위로 분포되지 않습니다.

전해질 용액은 양전하를 띤 이온과 음전하를 띤 이온을 모두 포함해야 하기 때문에 단일 이온의 활성 계수를 실험적으로 측정할 수 없습니다. 대신$평균$ 활동 계수인 γ$$± {\$displaystyle \gamma$_{\pm}}가 정의됩니다. 예를 들어, 전해질 NaCl로

${\displaystyle \gamma _{\pm }=\left(\gamma _{\mathrm {Na^{+}}\gamma _{\mathrm {Cl^{-}}\right)^{1/2}}$

일반적으로, 화학식 AB의_nm 완전 해리된 전해질의 평균 활성 계수는 다음과^[4] 같이 주어집니다.

${\displaystyle \gamma _{\pm }=\left ({\gamma _{A}}^{\gamma _{B}}^{m}\right)^{1/(n+m)}}$

활성 계수는 전해질의 농도가 증가함에 따라 이온간 상호작용의 양이 증가함에 따라 그 자체로 농도의 함수입니다. Debye와 Hückel은 단일 이온 활성 계수를 계산할 수 있는 이론을 개발했습니다. 이들로부터 평균 활동 계수를 계산함으로써 이론을 실험 데이터와 비교하여 검정할 수 있습니다. "희석" 솔루션에 대한 탁월한 합의를 제공하는 것으로 나타났습니다.

모델이

데비에 대한 설명-휴켈 이론은 가정과 그 한계, 그리고 수학적 발전과 응용에 대한 매우 상세한 논의를 포함합니다.^[5]

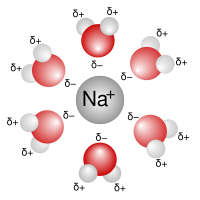
이상화된 전해질 용액의 2차원 단면 스냅샷이 그림에 표시되어 있습니다. 이온은 단위 전하를 갖는 구체로 표시됩니다. 용매(파란색)는 구조가 없는 균일한 매질로 표시됩니다. 평균적으로 각각의 이온은 비슷한 전하의 이온보다 반대 전하의 이온으로 더 가까이 둘러싸여 있습니다. 이 개념들은 z가 임의의 정수일 수 있는 전하₁⁺ ze와 ze의₂⁻ 이온을 포함하는 정량 이론으로 발전되었습니다. 주요 가정은 이상성에서 벗어나는 것은 쿨롱의 법칙에 의해 매개되는 이온들 사이의 정전기적 상호작용 때문이라는 것입니다: 상대 유전율 ε의 매질에서 거리로 분리된 두 전하 사이의 상호작용 힘 r은 다음에 의해 주어집니다.

${\displaystyle {\text{force}}={\frac {z_{1}z_{2}e^{2}}{4\pi \epsilon _{0}\epsilon _{r}r^{2}}}$

또한 다음과 같이 추정됩니다.

• 그 용질은 완전히 분리되어 있습니다. 그것은 강한 전해질입니다.
• 이온은 구형이며 주변 전기장에 의해 편광되지 않습니다. 이온의 유효한 크기를 결정하는 한 이온의 용해는 무시됩니다.
• 용매는 일정한 상대 유전율(유전율)의 매질을 제공하는 것 외에는 아무런 역할도 하지 않습니다.
• 전기적 제약이 없습니다.
• "중앙" 이온을 둘러싸고 있는 개별 이온은 통계적으로 평균화된 연속 전하 밀도의 구름으로 표현될 수 있으며, 최소 접근 거리는 최소입니다.

마지막 가정은 각 양이온이 다른 이온들의 구형 대칭 구름에 의해 둘러싸여 있다는 것을 의미합니다. 클라우드에는 순 음전하가 있습니다. 마찬가지로 각 음이온은 알짜 양전하를 띤 구름으로 둘러싸여 있습니다.^[7]

수학적 전개

이상성으로부터의 편차는 이온과 주변 구름 사이의 정전기적 상호작용으로 인한 위치 에너지의 함수로 간주됩니다. 이 에너지를 계산하려면 두 단계가 필요합니다.

첫 번째 단계는 포아송 방정식을 통해 이온 j의 정전기량을 지정하는 것입니다.

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\rho _{j}(r)}$

ψ(r)은 중심 이온으로부터의 거리에서의 총 퍼텐셜이고, r은 그 거리에서의 주변 구름의 평균 전하 밀도입니다. 이 공식을 적용하려면 구름이 구면 대칭을 갖는 것이 필수적인데, 즉 전하 밀도는 중심 이온과의 거리에 대한 함수이기 때문에 각도 의존성이 없는 구면 좌표로 포아송 방정식을 주조할 수 있습니다.^[8]

두 번째 단계는 볼츠만 분포를 통해 전하 밀도를 계산하는 것입니다.

${\displaystyle n'_{i}=n_{i}\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}\right)}$

여기서 k는_B 볼츠만 상수이고 T는 온도입니다. 이 분포는 또한 잠재적인 ψ(r)에 따라 다르며 이는 중첩 원리 측면에서 심각한 어려움을 초래합니다. 그럼에도 불구하고 두 방정식을 결합하여 포아송-볼츠만 방정식을 생성할 수 있습니다.^[9]

${\displaystyle \nabla ^{2}\psi _{j}(r)=-{\frac {1}{\epsilon _{0}\epsilon _{r}}}\sum _{i}\left\{n_{i}(z_{i}e)\exp \left({\frac {-z_{i}e\psi _{j}(r)}{k_{\rm {B}}T}\right)\right\}$

이 방정식의 해법은 간단하지 않습니다. Debye와 Hückel은 절단된 테일러 급수로서 지수를 1차로 확장했습니다. 0차 항은 평균적으로 전기적으로 중성이므로(따라서 σ n z = 0이 됨) 1차 항만 남게 되므로 사라집니다. 결과는 헬름홀츠 방정식의^[10] 형태를 갖습니다.

${\displaystyle {\mathrm{\nabla }}^{}}{\displaystyle {\mathrm{}}^{}{\mathrm{2}}^{}{\psi }_{}}$$abla ^{2}\psi _{j}(r)=\kappa ^{2}\psi _{j}(r)\qquad {\text{with}}\qquad \kappa ^{2}={\frac {e^{2}}{\epsilon _{0}\epsilon _{r}k_{\rm {B}}$$T}}\sum _{i}n_{i}z_{i}^{2}}$,

분석적인 해결책을 가지고 있습니다. 이 방정식은 각 전하의 이온 수가 같은 전해질에 적용됩니다. 비대칭 전해질은 ψ과 함께 또 다른 용어가 필요합니다. 대칭 전해질의 경우, 이것은 수정된 구형 베셀 방정식으로 감소합니다.

${\displaystyle(\partial _{r}^{2}+{\frac {2}{r}}\partial _{r}-\kappa^{2})\psi _{j}=0\qquad {\text{with solutions}}\qquad \psi _{j}(r)=A'{\frac {e^{-\kappa r}}{r}}+A''{\frac {e^{\kappa r}}{r}}}$

계수 $A{\displaystyle {\text{'}}^{}}$ ${\displaystyle A'}$ 및 $A$″ {\$displaystyle$A'}은 경계 조건에 의해 고정됩니다. $r$ → ∞ {\$displaystyle r\rightarrow$$infty$}이므로 ψ$${\displaystyle \psi }가 발산되어서는 안 $되므로$ A$$″ = ${\displaystyle 0_{}}$ {\displaystyle A''= 0}입니다. $이온$의 가장 가까운 접근 거리인 r = 0 {\display r=a_{0}에서 전하가 작용하는 힘은 다른 이온의 힘과 균형을 이루어야 합니다. ${\displaystyle {부과}_{}}$ ∂ ${\displaystyle {}_{}}$ ψ j (${\displaystyle {}_{}{0}_{}}$) = -$$ $j$ / (4 π ϵ 0 ϵ r a 02) {\displaystyle \partial _{r}\psi _{j}(a_{0})=-z_{j}e/(4\pi \epsilon _{0}\epsilon _{r}a_{0}^{2}}, 여기서 A' {\displaystyle A'}이(가) 발견되어 생성됩니다.

${\displaystyle \psi _{j}(r)={\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {e^{\kappa a_{0}}}{1+\kappa a_{0}}}{\frac {e^{-\kappa r}}{r}}}$

$r$ = ${\$display r = 0}에서 이온의 정전기 전위 에너지$({\display u_{j$는 다음과 같습니다.

${\displaystyle u_{j}=z_{j}e{\Big (}\psi _{j}(a_{0})-{\frac {z_{j}e}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {1}{a_{0}}}{\Big )}=-{\frac {z_{j}^{2}e^{2}}{4\pi \varepsilon _{0}\varepsilon _{r}}}{\frac {\kappa }{1+\kappa a_{0}}}}$

이것은 용액 내 단일 이온의 위치 에너지입니다. 정전기로부터 다중 전하 일반화를 통해 전체 용액의 위치 에너지를 표현할 수 있습니다(다음 항목 참조). 데비–휴켈 방정식). 평균 활동 계수는 이 수량의 로그로 다음과 같이 표시됩니다(참조: 이론의 확장)^[11]

${\displaystyle \log _{10}\gamma _{\pm}=-Az_{j}^{2}{\frac {\sqrt {I}}{1+Ba_{0}{\sqrt {I}}}$

${\displaystyle A={\frac {e^{2}B}{2.303\times 8\pi \epsilon _{0}\epsilon _{r}k_{\rm {B}}T}}}$

${\displaystyle B=\left({\frac {2e^{2}N}{\epsilon_{0}\epsilon_{r}k_{\rm {B}}T}\right)^{1/2}$

여기서 I는 이온 강도이고 a는₀ 이온의 가장 가까운 접근 거리를 나타내는 매개 변수입니다. 25 °C A = 0.51 mold 및 B = 3.29 nm mold의 수용액의 경우

이 결과의 가장 중요한 측면은 평균 활성 계수가 전해질 농도보다는 이온 강도의 함수라는 예측입니다. 이온 강도의 매우 낮은 값의 경우 위의 식에서 분모의 값은 거의 1과 같아집니다. 이 경우 평균 활동 계수는 이온 강도의 제곱근에 비례합니다. 이것은 데비라고 알려져 있습니다.휴켈 제한법.

제한 및 확장

$로그$⁡ γ ± {\displaystyle$\$log \gamma _{\pm }}에 대한 이 방정식은 일반적으로 10 mol/L 미만의 낮은 전해질 농도에 대한 실험 측정과 만족스러운 일치를 제공합니다. 이론에서 벗어나는 것은 더 높은 농도와 더 높은 전하의 이온, 특히 비대칭 전해질을 생성하는 전해질에서 발생합니다. 기본적으로 이러한 편차는 모형이 지나치게 단순화되어 있으므로 모형을 약간 조정해도 얻을 것이 거의 없습니다.^[14] 개별 가정에 차례로 도전할 수 있습니다.

• 완전한 해리. 이온 결합은 특히 더 높은 전하를 가진 이온과 일어날 수 있습니다. 이것은 닐스 비에룸이 자세히 설명했습니다. 비제룸 길이는 두 이온 사이의 정전기 상호작용이 kT와 비슷한 크기의 분리입니다.
• 약한 전해질. 약한 전해질은 완전히 해리되지 않은 전해질입니다. 따라서 해리 상수가 있습니다. 해리 상수는 해리 정도를 계산하는 데 사용할 수 있으므로 활성 계수를 계산하는 데 필요한 보정을 수행합니다.^[15]
• 이온은 점전하가 아닌 구형이며 편광되지 않습니다. 질산염 이온, NO와₃⁻ 같은 많은 이온은 구형이 아닙니다. 다원자 이온도 분극이 가능합니다.
• 용매의 역할. 용매는 구조가 없는 매질이 아니라 분자로 이루어져 있습니다. 수용액의 물 분자는 쌍극성이면서 분극성입니다. 양이온과 음이온은 모두 강한 1차 용해 쉘과 약한 2차 용해 쉘을 가지고 있습니다. Debye에서 이온-용매 상호작용은 무시됩니다.휴켈 이론.

더욱이 이온 반경은 무시할 수 있다고 가정되지만 고농도에서는 이온 반경이 이온 대기의 반경과 비슷해집니다. 데비에 대한 대부분의 확장들-휴켈 이론은 본질적으로 경험적입니다. 그들은 보통 데비를 허용합니다.Hückel 방정식은 낮은 농도에서 따라야 하며 실험 관측치에 맞게 이온 강도의 일부 거듭제곱에 대한 항을 추가합니다. 주요 확장은 데이비스 방정식, 피처 방정식 및 특정 이온 상호 작용 이론입니다.

전해질 혼합물

이 이론은 혼합 전해질의 묽은 용액에도 적용될 수 있습니다. 어는점 함몰 측정은 이 목적을 위해 사용되었습니다.^[16]

전도성

지금까지 주어진 치료법은 외부 전기장의 영향을 받지 않는 시스템에 대한 것입니다. 전도도를 측정할 때 시스템은 용액에 잠긴 전극에 AC 전압을 인가하기 때문에 진동하는 외부 필드의 영향을 받습니다. 데비와 휘켈은 1926년에 그들의 이론을 수정했고 1927년 라스 온세거에 의해 그들의 이론은 더 수정되었습니다. 원래 이론의 모든 가설은 유지되었습니다. 또한 전기장이 전하 구름을 구형 대칭에서 벗어나 왜곡시키는 것으로 가정했습니다.^[17] 이를 고려한 후, Onsager는 점도 및 전기영동 효과와 같은 이동 이온의 특정 요구 사항과 함께 몰 전도도인 λ에 대한 Kohlrausch's Law로 알려진 경험적 관계를 설명하기 위한 이론적 표현을 도출할 수 있었습니다.

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-K{\sqrt {c}}}$

$m$ 0 {\displaystyle \Lambda _{m}^{0}}는 제한 몰 전도도로 알려져 있으며, K는 경험 상수이고 c는 전해질 농도입니다. 여기서 제한은 "무한 희석의 한계에서"를 의미합니다. 온세저의 표정은.

${\displaystyle \Lambda _{m}=\Lambda _{m}^{0}-(A+B\Lambda _{m}^{0}){\sqrt {c}}}$

여기서 A와 B는 온도, 이온의 전하량, 용매의 유전상수 및 점도와 같은 알려진 양에만 의존하는 상수입니다. 이것은 데비라고 알려져 있습니다.Hückel-Onsager 방정식. 그러나 이 방정식은 매우 희석된 용액에만 적용되며 Fuoss와 Onsager, 1932년과 1957년 이후로 인해 다른 방정식으로 대체되었습니다.^[18]

참고문헌