자연의 패턴
Patterns in nature

자연의 패턴은 자연계에서 볼 수 있는 형태의 눈에 보이는 규칙성입니다.이러한 패턴은 다른 맥락에서 반복되며 때로는 수학적으로 모델링될 수도 있습니다.자연 패턴에는 대칭, 나무, 나선형, 구불구불한 모양, 파도, 거품, 테셀레이션, 균열 및 줄무늬가 포함됩니다.[1]플라톤, 피타고라스 그리고 엠페도클레스가 자연의 질서를 설명하려고 시도하면서 초기 그리스 철학자들은 패턴을 연구했습니다.눈에 보이는 패턴에 대한 현대적인 이해는 시간이 지나면서 점차적으로 발전했습니다.
19세기에 벨기에의 물리학자 조셉 플라토는 비누 필름을 조사했고, 그가 최소 표면의 개념을 공식화하도록 이끌었습니다.독일의 생물학자이자 예술가인 에른스트 해켈은 대칭성을 강조하기 위해 수백 개의 해양 생물을 그렸습니다.스코틀랜드의 생물학자 D'Arcy Thompson은 식물과 동물 모두의 성장 패턴에 대한 연구를 개척했고, 간단한 방정식이 나선형 성장을 설명할 수 있다는 것을 보여주었습니다.20세기에 영국의 수학자 앨런 튜링은 점과 줄무늬 패턴을 만드는 형태형성 메커니즘을 예측했습니다.헝가리 생물학자 아리스티드 린덴메이어와 프랑스계 미국인 수학자 베노 î트 만델브로는 프랙탈의 수학이 어떻게 식물의 성장 패턴을 만들 수 있는지 보여주었습니다.
수학, 물리학, 화학은 자연의 패턴을 다양한 수준과 척도로 설명할 수 있습니다.생물의 패턴은 자연 선택과 성적 선택의 생물학적 과정에 의해 설명됩니다.패턴 형성에 대한 연구는 컴퓨터 모델을 사용하여 다양한 패턴을 시뮬레이션합니다.
역사
초기 그리스 철학자들은 현대의 개념을 예상하면서 자연의 질서를 설명하려고 시도했습니다.피타고라스 (c. 570–c. 495 BC)는 음악의 조화와 같은 자연의 패턴을 그가 존재의 기본적인 구성 요소로 삼은 수에서 발생하는 것으로 설명했습니다.[a]Empedocles (c. 494–c. 434 BC)는 유기체의 구조에 대한 다윈의 진화론적 설명을 어느 정도 예상했습니다.[b]플라톤 (c. 427–c. 347 BC)은 자연적인 보편성의 존재를 주장했습니다.그는 이것들이 물리적인 물체가 불완전한 복제품에 지나지 않는 이상적인 형태(εἶδος eidos: "형태")로 구성되어 있다고 생각했습니다.따라서, 꽃은 대략 원형일 수 있지만, 결코 완벽한 원형은 아닙니다.[2]테오프라스토스 (c. 372–c. 287 BC)는 식물들이 "평활한 잎을 가진 식물들이 그것들을 규칙적인 계열로 가지고 있다"고 언급했습니다; 대 플리니 (23–79 AD)는 그것들의 무늬가 있는 원형 배열에 주목했습니다.[3]수 세기 후, 레오나르도 다빈치 (1452–1519)는 나무 줄기가 나이가 들면서 연속적인 고리를 얻는다는 잎 패턴의 나선형 배열에 주목했고, 나뭇가지의 단면적에 의해 충족된다고 알려진 규칙을 제안했습니다.[4][3]
1202년 레오나르도 피보나치는 그의 책 Liber Abaci로 피보나치 수열을 서양에 소개했습니다.[5]피보나치는 이상화된 토끼 개체군의 성장에 대한 사고 실험을 제시했습니다.[6]요하네스 케플러 (1571–1630)는 일부 꽃들의 오각형 형태를 설명하기 위해 피보나치 수열의 자연에서의 존재를 지적했습니다.[3]1658년, 영국의 의사이자 철학자인 토마스 브라운 경은 숫자 5와 퀸쿤크스 패턴의 플라톤적 형태를 포함하는 피타고라스 숫자학을 인용하면서 키루스의 정원에서 "자연 기하학의 방법"에 대해 논의했습니다.담론의 중심 장에는 식물학의 퀸쿤크스에 대한 예시와 관찰이 담겨 있습니다.[7]1754년, 찰스 보닛은 식물의 나선형 필로축이 시계방향과 반시계방향의 황금 비율 시리즈로 자주 표현되는 것을 관찰했습니다.[3]필로타시스에 대한 수학적 관찰은 카를 프리드리히 심퍼와 그의 친구 알렉산더 브라운의 1830년과 1830년 각각의 연구와 뒤따랐습니다. 오귀스트 브라베와 그의 형 루이는 1837년에 필로타시스 비율을 피보나치 수열과 연결시켰고, 소나무와 파인애플에서 필로타시스가 나타나는 것에 주목했습니다.[3]독일의 심리학자 아돌프 자이징은 1854년 저서에서 식물의 부분 배열, 동물의 골격, 혈관과 신경의 가지 패턴, 그리고 결정체로 표현된 황금 비율을 탐구했습니다.[8][9][10]
19세기 벨기에의 물리학자 요제프 플라토 (1801–1883)는 현재 그의 이름을 따서 명명된, 주어진 경계를 갖는 최소 표면의 존재에 대한 수학적 문제를 공식화했습니다.그는 비누 필름을 집중적으로 연구하여 필름에 의해 형성된 구조를 설명하는 고원의 법칙을 만들었습니다.[11]켈빈 경은 1887년에 동일한 부피의 세포를 거품처럼 포장하는 가장 효율적인 방법의 문제를 발견했습니다. 그의 해결책은 플라토의 법칙을 충족시키기 위해 표면이 매우 약간 휜, 비트라운 큐빅 벌집을 단 하나만 사용합니다.1993년 데니스 위어와 로버트 펠란이 위어를 제안하기 전까지는 더 나은 해결책을 찾을 수 없었습니다.펠란 구조물; 베이징 국가수족센터는 2008년 하계 올림픽에서 외벽을 위해 이 구조물을 개조했습니다.[12]Ernst Haeckel (1834–1919)은 해양 생물, 특히 Radiolaria의 아름다운 삽화를 그렸고, 그의 가짜 다윈 진화 이론을 뒷받침하기 위해 그것들의 대칭을 강조했습니다.[13]미국 사진작가 윌슨 벤틀리(Wilson Bentley)는 1885년에 눈송이의 첫 현미경 사진을 찍었습니다.[14]
20세기에, A. H. Church는 그의 1904년 책에서 필로택스의 패턴을 연구했습니다.[15]1917년, D'Arcy Wentworth Thompson은 "성장과 형태"를 출판했습니다. 식물의 나선형 성장 패턴에 대한 그의 설명, 즉 식물의 나선형 성장 패턴에 대한 수학적 관계는 간단한 방정식이 동물의 뿔과 연체동물의 나선형 성장 패턴을 설명할 수 있다는 것을 보여주었습니다.[16]1952년, 컴퓨터 과학자 알란 튜링 (1912–1954)은 형태생성이라고 불리는 과정에서 생물체에서 패턴을 만드는 데 필요한 메커니즘의 분석인 형태생성의 화학적 기초를 썼습니다.[17]그는 진동하는 화학 반응, 특히 벨루소프-자보틴스키 반응을 예측했습니다.튜링은 이러한 활성화 억제 메커니즘은 동물의 줄무늬와 점의 패턴("튜링 패턴"이라 불리는)을 생성하고 식물의 필로택스에서 볼 수 있는 나선형 패턴에 기여할 수 있다고 제안했습니다.[18]1968년 헝가리의 이론생물학자 아리스티드 린덴마이어(1925–1989)는 프랙탈 스타일의 식물 성장 패턴을 모델링하는 데 사용할 수 있는 공식 문법인 L-시스템을 개발했습니다.[19]L-시스템에는 생산 규칙을 사용하여 조합할 수 있는 기호 알파벳과 생성된 문자열을 기하학적 구조로 변환하는 메커니즘이 있습니다.1975년에, 고트프리트 라이프니츠, 게오르크 칸토어, 헬게 폰 코흐, 와츠와프 시에르피 ń스키와 다른 사람들에 의해 패턴의 수학이 몇 세기 동안 천천히 발전한 후, 베노 î트 만델브로는 "영국의 해안은 얼마나 길까?"라는 유명한 논문을 썼습니다. 통계적 자기 유사성과 분수 차원, 수학적 사고를 프랙탈의 개념으로 결정화합니다.[20]
-
피보나치 수 패턴은 퀸사고(Queen Sago), 사이카스 서키날리스(Cycas circinalis)와 같은 식물에서 널리 발생합니다.
-
다르시 톰슨(D'Arcy Thompson)은 1917년 저서에서 성장과 형태에 대한 연구를 개척했습니다.
원인들

난초, 벌새, 공작의 꼬리와 같은 생물들은 예술가들이 맞추기 힘든 형태, 패턴, 색깔의 아름다움을 가진 추상적인 디자인을 가지고 있습니다.[21]자연에서 사람들이 지각하는 아름다움은 다양한 수준에서 원인을 갖는데, 특히 물리적으로 어떤 패턴을 형성할 수 있는지를 지배하는 수학과 자연 선택의 영향을 받는 생물 중 패턴이 어떻게 진화하는지를 지배하는 생물에서 특히 그렇다.[22]
수학은 모든 종류의 추상적인 패턴이나 규칙성을 발견하고 설명하려고 합니다.[23][24]자연의 시각적 패턴은 혼돈 이론, 프랙탈, 로그 나선, 위상 및 기타 수학적 패턴에서 설명을 찾습니다.예를 들어, L-시스템은 다양한 나무 성장 패턴의 설득력 있는 모델을 형성합니다.[19]
물리학의 법칙은 수학의 추상화를 마치 완벽한 것처럼 현실 세계에 적용합니다.예를 들어, 결정은 전위와 같은 구조적 결함이 없고 완전히 대칭일 때 완벽합니다.정확한 수학적 완벽함은 실제 물체에만 근사할 수 있습니다.[25]자연에서 보이는 패턴은 물리적 법칙에 의해 지배됩니다. 예를 들어, 구불구불한 것은 유체 역학을 사용하여 설명될 수 있습니다.
생물학에서, 자연 선택은 위장,[26] 성적 선택,[26] 모방과[27] 청소 공생을 포함한 다양한 종류의 신호 전달을 포함한 여러 가지 이유로 생물체에 패턴의 발달을 야기할 수 있습니다.[28]식물에서는, 백합과 같이 곤충을 수분시킨 꽃의 모양, 색깔, 패턴이 벌과 같은 곤충을 유인하도록 진화해왔습니다.자외선에서만 볼 수 있는 방사형 패턴의 색상과 줄무늬는 멀리서도 볼 수 있는 과즙 가이드 역할을 합니다.[29]
패턴의 종류
대칭성
대칭성은 생명체에 만연해 있습니다.동물들은 주로 식물의 잎과 난초와 같은 꽃들처럼 양쪽 또는 거울 대칭을 갖습니다.[30]식물들은 많은 꽃들과 말미잘과 같은 몇몇 동물들처럼 방사상 또는 회전 대칭을 갖습니다.불가사리, 성게, 그리고 백합을 포함하는 그룹인 극피동물에서 다섯 배의 대칭이 발견됩니다.[31]
무생물 중 눈송이는 눈에 띄는 여섯 겹의 대칭성을 가지고 있는데, 각각의 조각의 구조는 결정화 동안의 다양한 상태에 대한 기록을 형성하며, 여섯 개의 팔 각각에 거의 동일한 성장 패턴을 가지고 있습니다.[32]일반적으로 결정은 다양한 대칭과 결정 습관을 갖는데, 입방정계 또는 팔면체가 될 수 있지만, 실제 결정은 준결정과 달리 다섯 겹의 대칭을 가질 수 없습니다.[33]회전대칭성은 생물이 아닌 것들 사이에서 발견되는데, 물방울이 연못에 떨어졌을 때 형성되는 왕관 모양의 물보라 무늬와 [34]토성과 같은 행성의 구상 모양과 고리 모두에서 발견됩니다.[35]
대칭성에는 다양한 원인이 있습니다.방사상 대칭성은 성체가 움직이지 않는 말미잘과 같은 유기체에 적합합니다. 먹이와 위협은 어느 방향에서든 도달할 수 있습니다.하지만 한 방향으로 움직이는 동물들은 반드시 위와 아래, 머리와 꼬리 끝이 있고, 따라서 왼쪽과 오른쪽을 가지고 있습니다.머리는 입과 감각 기관으로 전문화되고 (세팔화), 몸은 좌우 대칭이 됩니다 (내부 기관이 그럴 필요는 없지만).[36]더 혼란스러운 것은 극피의 다섯 배 대칭에 대한 이유입니다.초기의 극피동물은 유충이 아직도 그러하듯이 양쪽으로 대칭적이었습니다.Sumrall과 Wray는 오래된 대칭성의 상실이 발달적인 원인과 생태학적인 원인 둘 다를 가지고 있다고 주장합니다.[37]
나무, 프랙탈
나무의 가지무늬는 레오나르도 다빈치에 의해 이탈리아 르네상스에 묘사되었습니다.A Treatise on Painting에서 그는 다음과 같이 말했습니다.
높이의 모든 단계에서 나무의 모든 가지를 합치면 줄기의 두께는 [그 아래]와 같습니다.[38]
보다 일반적인 버전에서는 부모 분기가 두 개 이상의 자식 분기로 분할될 때 자식 분기의 표면적이 부모 분기의 표면적과 합산된다고 말합니다.[39]동일한 공식은 부모 가지가 두 개의 자식 가지로 분할되는 경우 부모 가지의 단면 직경과 두 개의 자식 가지가 직각 삼각형을 형성한다는 것입니다.한 가지 설명은 이것이 나무들이 강한 바람을 더 잘 견딜 수 있게 해준다는 것입니다.[39]생체역학 모형의 시뮬레이션은 규칙과 일치합니다.[40]
프랙탈은 프랙탈 차원을 갖는 무한히 유사하고 반복되는 수학적 구조입니다.[20][41][42]무한 반복은 본질적으로 불가능하기 때문에 모든 '프랙탈' 패턴은 근사치에 불과합니다.예를 들어, 양치식물과 우산꽃의 잎은 2, 3, 4단계와 자기적으로 비슷할 뿐입니다.양치류와 유사한 성장 패턴은 식물과 동물에서 발생합니다. 브리오조아, 산호, 공기 양치류와 같은 하이드로조아, 세르툴라리아 아르젠테아, 그리고 생물이 아닌 것, 특히 전기 방전을 포함합니다.린덴메이어 시스템 프랙탈은 분기 각도, 노드 또는 분기점 사이의 거리(노드 길이), 분기점당 분기 수 등의 소수의 매개 변수를 변경하여 다양한 트리 성장 패턴을 모델링할 수 있습니다.[19]
프랙탈과 유사한 패턴은 구름, 강 네트워크, 지질 단층선, 산, 해안선,[43] 동물 색, 눈송이,[44] 수정,[45] 혈관 분기,[46] 푸르킨제 세포,[47] 작용 세포골격, 바다 [48]파도와 같은 다양한 현상에서 자연에서 광범위하게 발생합니다.[49]
-
어떤 나무들의 성장 패턴은 이 린덴메이어 시스템 프랙탈과 비슷합니다.
-
바오밥나무 가지무늬
-
소 파슬리의 잎, Anthriscus sylvestris는 무한이 아닌 2- 또는 3-피네이트입니다.
-
프랙탈 나선: 로마네스코 브로콜리가 자기 유사한 형태를 보임
-
나무: 수지상 구리 결정(현미경상)
나선형
나선형은 식물과 일부 동물, 특히 연체동물에서 흔히 볼 수 있습니다.예를 들어, 두족류 연체동물인 노틸러스에서, 껍질의 각 방은 상수 인자에 의해 축척되고 로그 나선형으로 배열된 다음 방의 대략적인 복사본입니다.[50]프랙탈에 대한 현대적인 이해를 고려할 때, 성장 나선은 자기 유사성의 특별한 경우로 볼 수 있습니다.[51]
식물의 나선형은 솔방울의 비늘 모양 뿐만 아니라, 식물의 줄기 위의 잎의 배열, 그리고 해바라기와 같은 복합적인 꽃의 머리와 씨앗의 머리와 파인애플과[15][53]: 337 뱀 열매와 같은 과일 구조와 같은 다른 부분의 배열(기생충[52])에서 볼 수 있습니다.다수의 나선이 시계방향과 반시계방향으로 달리는 곳입니다.이러한 배열에는 수학, 물리학, 화학, 생물학 등 다양한 수준의 설명이 있습니다. 각각 개별적으로 정확하지만 모두 함께 필요합니다.[54]Phylotaxis 나선은 Fibonacci 비율로부터 생성될 수 있습니다. Fibonacci 시퀀스는 1, 1, 2, 3, 5, 8, 13...(각각의 후속 숫자는 앞의 두 숫자의 합입니다.)예를 들어 잎이 줄기를 번갈아 올라가면 나선형의 한 회전이 두 잎에 닿기 때문에 패턴이나 비율이 1/2이 됩니다.헤이즐에서는 1/3, 살구에서는 2/5, 배에서는 3/8, 아몬드에서는 5/13입니다.[55]
해바라기나 데이지와 같은 원반형 꽃차례에서, 꽃차례는 페르마의 나선형을 따라 배열되지만, 연속되는 꽃차례는 137.508°(황금 비율로 원을 나누는 것)만큼 멀리 떨어져 있기 때문에 위장된다; 꽃차례가 성숙하여 모든 원소들이 같은 크기일 때,이 간격은 더 명백한 나선의 피보나치 수를 만듭니다.[56]
물리학의 관점에서 보면, 나선은 동적 시스템에서 자기 조직화 과정을 통해 자발적으로 나타나는 최저 에너지 구성입니다[57].[58]화학의 관점에서, 나선은 활성화와 억제를 모두 포함하는 반응-확산 과정에 의해 생성될 수 있습니다.필로택스는 줄기 주위의 꽃봉오리의 상대적인 각도를 조절하기 위해 다른 메커니즘과 함께 메리스템 성장을 활성화하는 식물 호르몬인 옥신의 농도를 조절하는 단백질에 의해 조절됩니다.[59]생물학적 관점에서, 주어진 공간에서 나뭇잎들을 가능한 한 멀리 떨어져 배열하는 것은 자원들, 특히 광합성을 위한 햇빛에 대한 접근을 극대화하기 때문에 자연 선택에 의해 선호됩니다.[53]
-
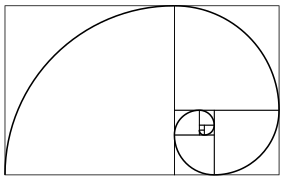
피보나치 나선형
-
큰뿔양
-
나선형: 나선형 알로에의 필로택스, 알로에 폴리필라
-
다중 피보나시선: 단면의 적양배추
-
나선형 껍질의 트로초이데아 리베트루티
-
물방울은 축축하고 회전하는 공을 등각의 나선형으로 날아갑니다.
혼돈, 흐름, 구불구불한 길
수학에서, 역학계는 위상 혼합과 밀도 높은 주기 궤도의 수학적 특성을 필요로 하는 초기 조건(일명 "나비 효과")[60]에 매우 민감한 경우 혼돈 상태에 빠집니다.[61]
카오스 이론은 프랙탈과 더불어 본질적으로 자연의 패턴에 대한 보편적인 영향으로 평가됩니다.혼돈과 프랙탈 사이에는 관계가 있습니다. 혼돈 시스템의 이상한 끌개들은 프랙탈 차원을 가지고 있습니다.[62]패턴을 생성하는 간단한 수학 규칙 집합인 일부 세포 오토마타는 혼란스러운 행동을 보이는데, 특히 스티븐 울프람의 규칙 30이 그렇습니다.[63]
소용돌이 거리는 대부분 공기나 물로 이루어진 유체의 불안정한 흐름이 방해하는 물체를 덮으면서 생기는 소용돌이의 지그재그 패턴입니다.[64]유체의 점도에 비해 장애물의 크기나 흐름의 속도가 충분히 커지면 매끄러운 (층형) 흐름이 끊어지기 시작합니다.
구불구불한 것은 강이나 다른 수로에서 연속적으로 구부러진 것으로, 유체(주로 물)가 굽은 것을 중심으로 흐르면서 형성됩니다.나선형 흐름이 모래와 자갈 등의 물질을 강을 가로질러 굴곡 안쪽으로 끌고 가면서 길이가 약간 곡선을 그리자마자 각 고리의 크기와 곡률이 증가합니다.루프 외부는 깨끗하고 보호되지 않은 상태로 남아 있으므로 침식이 가속화되어 강력한 양의 피드백 루프에서 사행을 더욱 증가시킵니다.[65]
-
혼돈: 복족류 연체동물의 껍질 금 원뿔의 천, Conus 텍스타일, 규칙 30 세포 자동화와 닮음
-
흐름: 후안 페르난데스 제도의 소용돌이 구름 거리
-
구불구불한 구불구불한 쿠바 리오 카초의 길
-
구불구불한 구불구불: 구불구불한 뱀이 기어 다닙니다.
-
구불구불: 대칭형 뇌산호, Diploria strigosa
파도,사구
파도는 움직임에 따라 에너지를 전달하는 교란입니다.기계파는 공기 또는 물과 같은 매질을 통해 전파되어 통과할 때 진동합니다.[66]풍파는 거대한 수역의 특징적인 혼돈 패턴을 만드는 해수면 파도이지만, 그들의 통계적 행동은 풍파 모델로 예측될 수 있습니다.[67]물이나 바람에 있는 파도가 모래 위를 지나갈 때, 파도는 잔물결의 패턴을 만듭니다.바람이 거대한 모래 위로 불어올 때, 그것들은 모래 언덕을 형성하고, 때때로 타클라마칸 사막에서처럼 넓은 사구밭에 있습니다.사구는 초승달 모양, 매우 긴 직선 모양, 별 모양, 돔 모양, 포물선 모양, 세로 모양('검' 모양 등 다양한 모양을 형성할 수 있습니다.[68]
바르칸이나 초승달 사구는 사막의 모래 위에 작용하는 바람에 의해 만들어집니다; 초승달의 두 뿔과 미끄럼틀은 아래 바람을 향합니다.수평에서 약 15도 정도 되는 바람면 위로 모래가 불어와 미끄러진 면 위로 떨어져 약 35도 정도의 모래의 휴식각까지 쌓입니다.미끄럼면이 휴식각을 넘으면 모래 눈사태가 발생하는데, 이것은 비선형적인 행동입니다. 많은 양의 모래를 첨가하면 큰 일이 일어나지 않지만, 더 많은 양의 모래를 첨가하면 갑자기 많은 양의 눈사태가 발생합니다.[69]이러한 비선형성과는 별개로, 바칸은 고독한 파도처럼 행동합니다.[70]
거품,거품
비눗방울은 면적(최소 표면)이 최소인 구(球)를 형성하는데, 이는 동봉된 부피에 대해 가능한 최소 표면적입니다.두 기포는 함께 더 복잡한 모양을 형성합니다. 두 기포의 외부 표면은 구형입니다. 이 표면은 작은 기포가 큰 기포로 약간 불룩해지면서 세 번째 구형 표면이 결합됩니다.[11]
거품은 거품 덩어리입니다. 다양한 물질의 거품은 자연에서 발생합니다.비누막으로 구성된 발포체는 플라토의 법칙을 따르는데, 플라토의 법칙은 세 개의 비누막을 120°의 각 모서리에서 만나고 네 개의 비누 모서리를 사면체 각도 약 109.5°의 각 꼭지점에서 만나야 합니다.플래토의 법칙은 필름이 매끄럽고 연속적이어야 하며, 모든 지점에서 일정한 평균 곡률을 가져야 합니다.예를 들어, 필름은 한 방향(예: 왼쪽에서 오른쪽으로)으로 휘어져 있고 다른 방향(예: 앞에서 뒤로)으로 아래로 휘어져 평균적으로 거의 평평하게 유지될 수 있습니다.[71][72]최소한의 표면을 가진 구조물은 텐트로 사용할 수 있습니다.
살아있는 세포의 규모에서 거품 패턴은 흔합니다. 방사선학자, 스폰지 스파이큘, 규편모 외골격 및 성게의 석회암 골격인 시다리스 루고사는 모두 플래토 폼 경계의 광물 주조물과 유사합니다.[73][74]에른스트 해켈이 그린 아름다운 해양 형태인 방사형의 뼈대인 아울로니아 육각형은 육각형 전체로 구성된 구처럼 보이지만 이는 수학적으로 불가능합니다.오일러 특성은 임의의 볼록 다면체에 대해 면의 수와 꼭짓점(모서리)의 수를 더한 수가 가장자리의 수와 2를 더한 수와 같다는 것을 나타냅니다.이 공식의 결과는 육각형의 닫힌 다면체는 축구공, 벅민스터 풀러 지오데식 돔 또는 플러렌 분자와 같이 정확히 12개의 오각형을 포함해야 한다는 것입니다.이것은 육각형의 그물이 닭 철사 한 장처럼 평평하지만 추가된 각 오각형이 그물을 구부리도록 강요한다는 것을 주목함으로써 시각화할 수 있습니다(모퉁이가 적어 그물이 당겨집니다).[75]
-
Haeckel's Spumellaria; 이 Radiolaria의 골격은 거품과 같은 형태를 가지고 있습니다.
-
Buckminster 풀러렌 C60: Richard Smalley와 동료들은 1985년에 풀러렌 분자를 합성했습니다.
-
표면거품의 등구(기체거품)
-
서커스 텐트는 최소 표면에 근접합니다.
테셀레이션
모자이크식 세공은 평평한 표면 전체에 타일을 반복하여 형성된 패턴입니다.타일링은 17개의 벽지 그룹이 있습니다.[76]예술과 디자인에서는 흔하지만, 정확히 반복되는 타일링은 생물체에서 찾기가 덜 쉽습니다.사회적 말벌의 종이 둥지에 있는 세포와 꿀벌이 만든 벌집에 있는 왁스 세포가 대표적인 예입니다.동물, 경골 어류, 파충류, 판골린, 또는 살락과 같은 과일들 중에서, 이것들은 다소 정확하게 반복되는 단위를 형성하지만, 사실 그 크기는 계속적으로 다릅니다.꽃들 중에서, 뱀의 머리 부분인 Fritillaria meleagris는 꽃잎에 테셀레이션 된 체커보드 무늬를 가지고 있습니다.광물의 구조는 3차원 배열을 규칙적으로 반복하는 좋은 예를 제공합니다.수십만 개의 알려진 광물에도 불구하고 결정 구조, 결정계, 점군에 의해 정의되는 결정 내 원자 배열의 가능한 유형은 거의 없습니다. 예를 들어, 3차원 공간에 있는 7개의 격자계에 대해 정확히 14개의 브라베 격자가 있습니다.[77]
-
틸링스: 뱀 머리 프릴리알리스 테셀레이션 꽃
-
틸링: 스네이크 열매 또는 살락, 살락카잘락카의 겹침 비늘
-
테셀레이트 포장도로: 태즈먼 반도의 희귀한 암석층
균열
균열은 응력을 완화하기 위해 재료에 형성되는 선형 개구입니다.탄성이 있는 물질이 균일하게 늘어나거나 줄어들면 결국 파단강도에 도달했다가 갑자기 사방으로 실패하면서 120도 관절로 균열이 생기므로 한 마디에서 세 개의 균열이 만나게 됩니다.반대로 비탄성 재료가 고장나면 직선 균열이 생겨 응력이 완화됩니다.같은 방향으로 응력을 가하면 기존 균열이 열리게 됩니다. 직각으로 응력을 가하면 기존 균열에 90도로 새로운 균열이 생길 수 있습니다.따라서 균열의 패턴은 재료의 탄성 여부를 나타냅니다.[78]참나무 껍질처럼 질긴 섬유질에 균열이 생겨 평소처럼 스트레스를 해소하지만, 강한 탄성섬유 다발에 의해 성장이 방해되면서 오래 자라지 않습니다.각 종의 나무는 세포와 분자 수준의 구조를 가지고 있기 때문에, 각각의 나무껍질에는 그것의 고유한 패턴이 있습니다.[79]
-
오래된 도자기 표면, 주로 90° 균열이 있는 흰색 유약
-
주로 90° 균열이 발생한 Kutch Ran에서의 비탄성 진흙 건조
-
주로 120° 균열이 있는 시칠리아의 탄성 진흙 건조
-
가지 모양의 수직 균열이 있는 팜 트렁크(및 수평 잎 흉터)
점, 줄무늬
표범과 무당벌레가 눈에 띄고, 천사 물고기와 얼룩말은 줄무늬가 있습니다.[80]이 패턴들은 진화론적인 설명을 가지고 있습니다: 그것들은 패턴화된 동물의 자손들이 번식하기 위해 살아남을 가능성을 증가시키는 기능을 가지고 있습니다.동물 패턴의 한 가지 기능은 위장입니다.[26] 예를 들어, 보기 힘든 표범은 더 많은 먹이를 잡습니다.다른 기능은 신호를 보내는[27] 것입니다. 예를 들어, 레이디버드는 대담한 경고색을 가지고 있고, 불쾌하게 쓰거나 독이 있거나, 다른 혐오스러운 곤충들을 모방할 경우, 시각으로 사냥하는 포식적인 새들에게 공격을 당할 가능성이 적습니다.어린 새는 무당벌레처럼 경고무늬가 있는 곤충을 보고 그것을 먹으려 할지도 모르지만, 이것은 단지 한 번만 할 것입니다; 곧 그것은 쓰디쓴 곤충을 뱉어낼 것입니다; 그 지역의 다른 무당벌레들은 방해받지 않고 남아있을 것입니다.어린 표범과 레이디버드는 어떻게든 얼룩을 만드는 유전자를 물려받아 살아남습니다.하지만 이러한 진화론적이고 기능적인 논쟁들은 이 동물들이 그들의 패턴을 필요로 하는 이유를 설명해 주지만, 패턴이 어떻게 형성되는지는 설명해 주지 않습니다.[80]
-
꽃미녀나비, 콜로부라 꽃미녀
-
그레비얼룩말, 에쿠스 그레비
-
왕당귀, Pygoplites diacanthus
-
표범
-
G.G. Jacobson의 무당벌레 모음
-
갑오징어의 번식 패턴, Sepia Officialis
패턴형성
앨런 튜링과 [17]후에 수학 생물학자 제임스 머레이는 자발적으로 점무늬나 줄무늬 패턴을 만드는 반응-확산 시스템을 설명했습니다.[81][82]어린 유기체의 세포는 화학적 신호인 모포겐에 의해 전환될 수 있는 유전자를 가지고 있는데, 이것은 어두운 색소를 띤 피부의 한 부분이라고 하는 특정한 형태의 구조의 성장을 초래합니다.만약 모포겐이 모든 곳에 존재한다면, 그 결과는 흑표범에서처럼 고른 색소 침착이 됩니다.그러나 만약 그것이 불균등하게 분포되어 있다면, 반점이나 줄무늬가 생길 수 있습니다.튜링은 모포겐 자체의 생성에 대한 피드백 조절이 있을 수 있다고 제안했습니다.이것은 몸 주위에 퍼지면서 모포겐의 양에 지속적인 변동을 일으킬 수 있습니다.두 번째 메커니즘은 정상 파동 패턴을 만들기 위해 필요합니다. 즉, 모포겐의 생성을 차단하고, 그 자체가 모포겐보다 더 빨리 몸을 통해 확산되어 활성화제-억제제 체계를 생성하는 억제제 화학물질입니다.벨루소프-자보틴스키 반응은 이러한 종류의 체계의 비생물학적인 예로 화학 발진기가 있습니다.[82]
이후의 연구는 얼룩말 줄무늬, 기린 얼룩, 재규어 반점(어두운 고리로 둘러싸인 중간-어두운 반점), 무당벌레 껍질 무늬(점과 줄무늬의 기하학적 다양한 레이아웃, 그림 참조)와 같이 다양한 패턴의 설득력 있는 모델을 만들어냈습니다.[83]튜링의 연구로부터 개발된 Richard Prum의 활성화 억제 모델은 6개의 변수를 사용하여 가장 단순한 중심 색소 패치, 막대, 쉐브론, 눈 점, 한 쌍의 중심 점, 한 쌍의 쌍으로 이루어진 점, 그리고 일련의 점들을 통해 관찰된 9개의 기본적인 깃털 내 색소 패턴의 범위를 설명합니다.[84][85]좀 더 정교한 모델은 기니새 누미다 멜레아그리의 복잡한 깃털 패턴을 모방합니다. 이 패턴에서 개별 깃털은 밑 부분의 막대에서 끝 부분의 일련의 점으로 전환됩니다.이를 위해서는 공간과 시간 모두에서 상호작용을 하는 두 가지 억제 신호에 의해 생성되는 진동이 필요합니다.[85]
패턴은 호랑이 덤불과[86] 전나무 파도의 식생지형에서 다른 이유로 형성될 수 있습니다.[87]호랑이 덤불 줄무늬는 식물의 성장이 강우에 의해 제한되는 건조한 경사지에서 발생합니다.대략적으로 수평을 이루는 각각의 식생은 바로 위에 있는 맨 공간으로부터 빗물을 효과적으로 모읍니다.[86]전나무 파도는 바람의 교란 후, 재생 중에 산비탈의 숲에서 발생합니다.나무가 쓰러지면 그동안 피했던 나무들이 그대로 드러나 훼손될 우려가 커지기 때문에 바람을 타고 간격이 넓어지는 경향이 있습니다.한편 바람이 부는 쪽에는 남아있는 키 큰 나무들의 바람 그림자에 보호를 받으며 어린 나무들이 자랍니다.[87]미국 북서부와 일부 다른 지역의 미마 언덕에서와 같이 동물들에 의해 자연적인 패턴이 형성되기도 하는데, 이는 포켓 고퍼들의 굴을 파는 활동에 의해 수년에 걸쳐 형성된 것으로 보이는 [88]반면, 나미비아의 소위 요정 서클은 모래 흰개미의 경쟁적인 집단들의 상호작용에 의해 형성된 것으로 보입니다.사막의 식물들 사이에 물을 얻기 위한 경쟁과 함께.[89]
매년 동결과 해빙의 영향을 받는 활성 상층을 가진 영구 동토에서, 패턴화된 지반이 형성되어 원, 그물, 얼음 쐐기 다각형, 계단 및 줄무늬가 생성될 수 있습니다.열 수축은 수축 균열을 형성하게 합니다. 해빙기에는 물이 균열을 채우고 다음에 얼었을 때 얼음을 형성하며 균열을 쐐기로 넓힙니다.이러한 균열은 결합하여 다각형 및 기타 모양을 형성할 수 있습니다.[90]
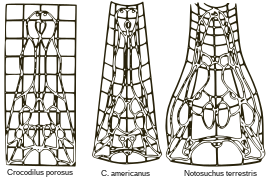
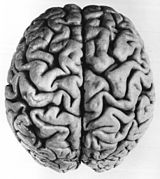
척추동물의 뇌에서 발생하는 균열 패턴은 두 가지 기하학적 매개변수, 즉 상대적인 접선 피질 확장과 피질의 상대적인 두께에 의존하는 제한된 확장의 물리적 과정에 의해 발생합니다.용매를 첨가한 후 바깥 층(피질을 나타내는)의 팽창으로 인한 압축 기계적 힘에 의한 패턴과 함께 매끄러운 층층이 있는 겔에서 시작하는 뇌의 모델에서 유사한 패턴이 입증되었습니다.컴퓨터 시뮬레이션의 수치 모델은 표면 접힘 패턴이 더 큰 뇌에서 증가한다는 자연적이고 실험적인 관찰을 뒷받침합니다.[91][92]
-
대왕복어, 테트라오돈엠부
-
대왕 복어 피부 패턴 상세
-
벨루소프-자보틴스키 반응 시뮬레이션 스냅샷
-
헬멧을 쓴 기니새, 누미다 메레그리, 깃털이 빗장에서 점박이로, 깃털 안에서 그리고 새를 가로질러 이동합니다.
참고 항목
참고문헌
각주
- ^ 수학을 처음으로 시작한 이른바 피타고라스 사람들은 이 과목을 발전시켰을 뿐만 아니라 그것에 포화되어 수학의 원리가 만물의 원리라고 생각했습니다.아리스토텔레스, 형이상학 1–5, c. 기원전 350년
- ^ 아리스토텔레스는 엠페도클레스가 주장하는 바에 따르면, "어떤 목적을 위해 일어난 일이라면 모든 것이 그렇게 되고, 그곳에서 생물들이 살아남고, 우연히 적절한 방법으로 복합되었다. 하지만 이런 일이 일어나지 않은 곳에서 생물들은 죽었다."라고 합니다.The Physics, B8, 198b29 in Kirk, et al., 304).
인용문
- ^ 스티븐스 1974, 3쪽.
- ^ Balaguer, Mark (7 April 2009) [2004]. "Platonism in Metaphysics". Stanford Encyclopedia of Philosophy. Retrieved 4 May 2012.
- ^ a b c d e Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number (First trade paperback ed.). New York: Broadway Books. p. 110. ISBN 978-0-7679-0816-0.
- ^ Da Vinci, Leonardo (1971). Taylor, Pamela (ed.). The Notebooks of Leonardo da Vinci. New American Library. p. 121.
- ^ Singh, Parmanand (1986). "Acharya Hemachandra and the (so called) Fibonacci Numbers". Mathematics Education Siwan. 20 (1): 28–30. ISSN 0047-6269.
- ^ Knott, Ron. "Fibonacci's Rabbits". University of Surrey Faculty of Engineering and Physical Sciences.
- ^ Browne, Thomas (1658). How Nature Geometrizeth.
{{cite book}}:work=무시됨(도움말) - ^ Padovan, Richard (1999). Proportion: Science, Philosophy, Architecture. Taylor & Francis. pp. 305–306. ISBN 978-0-419-22780-9.
- ^ Padovan, Richard (2002). "Proportion: Science, Philosophy, Architecture". Nexus Network Journal. 4 (1): 113–122. doi:10.1007/s00004-001-0008-7.
- ^ Zeising, Adolf (1854). Neue Lehre van den Proportionen des meschlischen Körpers. preface.
- ^ a b Stewart 2001, 페이지 108–109.
- ^ 볼 2009a, 페이지 73–76.
- ^ 볼 2009a, 페이지 41.
- ^ Hannavy, John (2007). Encyclopedia of Nineteenth-Century Photography. Vol. 1. CRC Press. p. 149. ISBN 978-0-415-97235-2.
- ^ a b Livio, Mario (2003) [2002]. The Golden Ratio: The Story of Phi, the World's Most Astonishing Number. New York: Broadway Books. p. 111. ISBN 978-0-7679-0816-0.
- ^ Wayback Machine에서 D'Arcy Archived 2017-07-01에 대한 정보.다르시 150.던디 대학교와 세인트앤드류스 대학교.2012년 10월 16일 회수.
- ^ a b Turing, A. M. (1952). "The Chemical Basis of Morphogenesis". Philosophical Transactions of the Royal Society B. 237 (641): 37–72. Bibcode:1952RSPTB.237...37T. doi:10.1098/rstb.1952.0012.
- ^ Ball 2009a, pp. 163, 247–250.
- ^ a b c 로젠베르크, 그레고르츠; 살로마아, 아르토.L 시스템의 수학적 이론.학술출판사, 뉴욕, 1980.ISBN 0-12-597140-0
- ^ a b Mandelbrot, Benoît B. (1983). The fractal geometry of nature. Macmillan.
- ^ 포브스, 피터.쓸모없는 아름다움.가디언지.리뷰: 논픽션. 2012년 2월 11일.
- ^ 스티븐스 1974년 222쪽
- ^ Steen, L.A. (1988). "The Science of Patterns". Science. 240 (4852): 611–616. Bibcode:1988Sci...240..611S. doi:10.1126/science.240.4852.611. PMID 17840903. S2CID 4849363.
- ^ 데블린, 키스.수학: 패턴의 과학: 생명, 마음, 우주의 질서를 찾아서 (Scientific American Paperback Library) 1996
- ^ Tatarkiewicz, Władysław. "Perfection in the Sciences. II. Perfection in Physics and Chemistry". Dialectics and Humanism. 7 (2 (spring 1980)): 139.
- ^ a b c 다윈, 찰스.종의 기원에 관하여.1859년, 4장.
- ^ a b Wickler, Wolfgang (1968). Mimicry in plants and animals. New York: McGraw-Hill.
- ^ Poulin, R.; Grutter, A.S. (1996). "Cleaning symbioses: proximate and adaptive explanations". BioScience. 46 (7): 512–517. doi:10.2307/1312929. JSTOR 1312929.
- ^ Koning, Ross (1994). "Plant Physiology Information Website". Pollination Adaptations. Retrieved 2 May 2012.
- ^ Stewart 2001, 페이지 48-49.
- ^ Stewart 2001, 페이지 64-65.
- ^ 스튜어트 2001, 페이지 52.
- ^ Stewart 2001, 페이지 82-84.
- ^ 스튜어트 2001, 60쪽.
- ^ 스튜어트 2001, 71쪽.
- ^ Hickman, Cleveland P.; Roberts, Larry S.; Larson, Allan (2002). "Animal Diversity" (PDF). Chapter 8: Acoelomate Bilateral Animals (Third ed.). p. 139. Archived from the original (PDF) on 17 May 2016. Retrieved 25 October 2012.
- ^ Sumrall, Colin D.; Wray, Gregory A. (January 2007). "Ontogeny in the fossil record: diversification of body plans and the evolution of "aberrant" symmetry in Paleozoic echinoderms". Paleobiology. 33 (1): 149–163. doi:10.1666/06053.1. JSTOR 4500143. S2CID 84195721.
- ^ Richter, Jean Paul, ed. (1970) [1880]. The Notebooks of Leonardo da Vinci. Dover. ISBN 978-0-486-22572-2.
{{cite book}}: CS1 유지 관리: 위치 누락 게시자(링크) - ^ a b Palca, Joe (December 26, 2011). "The Wisdom of Trees (Leonardo Da Vinci Knew It)". Morning Edition. NPR. Retrieved 16 July 2019.
- ^ Minamino, Ryoko; Tateno, Masaki (2014). "Tree Branching: Leonardo da Vinci's Rule versus Biomechanical Models". PLoS One. Vol. 9, no. 4. p. e93535. doi:10.1371/journal.pone.0093535.
- ^ Falconer, Kenneth (2003). Fractal Geometry: Mathematical Foundations and Applications. John Wiley.
- ^ Briggs, John (1992). Fractals:The Patterns of Chaos. Thames and Hudson. p. 148.
- ^ Batty, Michael (4 April 1985). "Fractals – Geometry Between Dimensions". New Scientist. 105 (1450): 31.
- ^ Meyer, Yves; Roques, Sylvie (1993). Progress in wavelet analysis and applications: proceedings of the International Conference "Wavelets and Applications," Toulouse, France – June 1992. Atlantica Séguier Frontières. p. 25. ISBN 9782863321300.
- ^ Carbone, Alessandra; Gromov, Mikhael; Prusinkiewicz, Przemyslaw (2000). Pattern formation in biology, vision and dynamics. World Scientific. p. 78. ISBN 978-9810237929.
- ^ Hahn, Horst K.; Georg, Manfred; Peitgen, Heinz-Otto (2005). "Fractal aspects of three-dimensional vascular constructive optimization". In Losa, Gabriele A.; Nonnenmacher, Theo F. (eds.). Fractals in biology and medicine. Springer. pp. 55–66.
- ^ Takeda, T; Ishikawa, A; Ohtomo, K; Kobayashi, Y; Matsuoka, T (February 1992). "Fractal dimension of dendritic tree of cerebellar Purkinje cell during onto- and phylogenetic development". Neurosci Research. 13 (1): 19–31. doi:10.1016/0168-0102(92)90031-7. PMID 1314350. S2CID 4158401.
- ^ Sadegh, Sanaz (2017). "Plasma Membrane is Compartmentalized by a Self-Similar Cortical Actin Meshwork". Physical Review X. 7 (1): 011031. arXiv:1702.03997. Bibcode:2017PhRvX...7a1031S. doi:10.1103/PhysRevX.7.011031. PMC 5500227. PMID 28690919.
- ^ Addison, Paul S. (1997). Fractals and chaos: an illustrated course. CRC Press. pp. 44–46.
- ^ Elie, Maor: The Story of a Number.프린스턴 대학 출판부, 2009.135페이지.
- ^ Ball 2009a, pp. 29–32.
- ^ "Spiral Lattices & Parastichy". Smith College. Archived from the original on 26 May 2010. Retrieved 24 September 2013.
- ^ a b Kappraff, Jay (2004). "Growth in Plants: A Study in Number" (PDF). Forma. 19: 335–354.
- ^ 볼 2009a, 페이지 13.
- ^ Coxeter, H. S. M. (1961). Introduction to geometry. Wiley. p. 169.
- ^ Prusinkiewicz, Przemyslaw; Lindenmayer, Aristid (1990). The Algorithmic Beauty of Plants. Springer-Verlag. pp. 101–107. ISBN 978-0-387-97297-8.
- ^ Levitov, L. S. (15 March 1991). "Energetic Approach to Phyllotaxis". Europhysics Letters. 14 (6): 533–539. Bibcode:1991EL.....14..533L. doi:10.1209/0295-5075/14/6/006. S2CID 250864634.
- ^ Douady, S.; Couder, Y. (March 1992). "Phyllotaxis as a physical self-organized growth process". Physical Review Letters. 68 (13): 2098–2101. Bibcode:1992PhRvL..68.2098D. doi:10.1103/PhysRevLett.68.2098. PMID 10045303.
- ^ Ball 2009a, pp. 163, 249–250.
- ^ Lorenz, Edward N. (March 1963). "Deterministic Nonperiodic Flow". Journal of the Atmospheric Sciences. 20 (2): 130–141. Bibcode:1963JAtS...20..130L. doi:10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
- ^ Elaydi, Saber N. (1999). Discrete Chaos. Chapman & Hall/CRC. p. 117.
- ^ Ruelle, David (1991). Chance and Chaos. Princeton University Press.
- ^ Wolfram, Stephen (2002). A New Kind of Science. Wolfram Media.
- ^ von Kármán, Theodore (1963). Aerodynamics. McGraw-Hill. ISBN 978-0070676022.von Kármán, Theodore (1963). Aerodynamics. McGraw-Hill. ISBN 978-0070676022.도버 (1994):ISBN 978-0486434858.
- ^ Lewalle, Jacques (2006). "Flow Separation and Secondary Flow: Section 9.1" (PDF). Lecture Notes in Incompressible Fluid Dynamics: Phenomenology, Concepts and Analytical Tools. Syracuse, New York: Syracuse University. Archived from the original (PDF) on 29 September 2011..
- ^ French, A. P. (1971). Vibrations and Waves. Nelson Thornes.
- ^ Tolman, H. L. (2008). "Practical wind wave modeling" (PDF). In Mahmood, M.F. (ed.). CBMS Conference Proceedings on Water Waves: Theory and Experiment. Howard University, USA, 13–18 May 2008. World Scientific Publications.
- ^ "Types of Dunes". USGS. 29 October 1997. Retrieved May 2, 2012.
- ^ Strahler, A.; Archibold, O. W. (2008). Physical Geography: Science and Systems of the Human Environment (4th ed.). John Wiley. p. 442.
- ^ Schwämmle, V.; Herrman, H. J. (11 December 2003). "Solitary wave behaviour of sand dunes". Nature. 426 (6967): 619–620. Bibcode:2003Natur.426..619S. doi:10.1038/426619a. PMID 14668849. S2CID 688445.
- ^ 볼 2009a, 페이지 68.
- ^ Almgren, Frederick J. Jr.; Taylor, Jean E. (July 1976). "The geometry of soap films and soap bubbles". Scientific American. 235 (235): 82–93. Bibcode:1976SciAm.235a..82A. doi:10.1038/scientificamerican0776-82.
- ^ Ball 2009a, 페이지 96–101.
- ^ Brodie, Christina (February 2005). "Geometry and Pattern in Nature 3: The holes in radiolarian and diatom tests". Microscopy-UK. Retrieved 28 May 2012.
- ^ 볼 2009a, 51-54쪽.
- ^ Armstrong, M.A. (1988). Groups and Symmetry. New York: Springer-Verlag.
- ^ 훅, J. R.; 홀, H. E. 솔리드 스테이트 물리학 (제2판)맨체스터 물리학 시리즈, John Wiley & Sons, 2010.ISBN 978-0-471-92804-1
- ^ 스티븐스 1974, 페이지 207.
- ^ 스티븐스 1974, 페이지 208.
- ^ a b 볼 2009a, 페이지 156-158
- ^ Murray, James D. (9 March 2013). Mathematical Biology. Springer Science & Business Media. pp. 436–450. ISBN 978-3-662-08539-4.
- ^ a b Ball 2009a, pp. 159-167
- ^ 볼 2009a, 페이지 168-180
- ^ 로텐버그 2011, 93-95쪽.
- ^ a b Prum, Richard O.; Williamson, Scott (2002). "Reaction–diffusion models of within-feather pigmentation patterning" (PDF). Proceedings of the Royal Society of London B. 269 (1493): 781–792. doi:10.1098/rspb.2001.1896. PMC 1690965. PMID 11958709.
- ^ a b Tongway, D. J.; Valentin, C.; Seghieri, J. (2001). Banded vegetation patterning in arid and semiarid environments. New York: Springer-Verlag.
- ^ a b D'Avanzo, C. (22 February 2004). "Fir Waves: Regeneration in New England Conifer Forests". TIEE. Retrieved 26 May 2012.
- ^ Morelle, Rebecca (2013-12-09). "'Digital gophers' solve Mima mound mystery". BBC News. Retrieved 9 December 2013.
- ^ Sample, Ian (18 January 2017). "The secret of Namibia's 'fairy circles' may be explained at last". The Guardian. Retrieved 18 January 2017.
- ^ "Permafrost: Patterned Ground". US Army Corps of Engineers. Archived from the original on 7 March 2015. Retrieved 17 February 2015.
- ^ Ghose, Tia. "Human Brain's Bizarre Folding Pattern Re-Created in a Vat". Scientific American. Retrieved 5 April 2018.
- ^ Tallinen, Tuoma; Chung, Jun Young; Biggins, John S.; Mahadevan, L. (2014). "Gyrification from constrained cortical expansion". Proceedings of the National Academy of Sciences of the United States of America. 111 (35): 12667–12672. arXiv:1503.03853. Bibcode:2014PNAS..11112667T. doi:10.1073/pnas.1406015111. PMC 4156754. PMID 25136099.
서지학
선구적인 저자
- 피보나치, 레오나르도리버 아바시, 1202호
- ———— 시글러 번역, 로렌스 E.피보나치의 리베르 아바치.스프링어, 2002년.
- 헤켈, 에른스트.쿤스트포멘더나투르 (자연 속의 예술 형태), 1899-1904.
- 톰프슨, 달시 웬트워스.성장과 형태에 관해.1917년 캠브리지.
일반도서
- 아담, 존 A.자연에서의 수학: 자연계의 모델링 패턴.프린스턴 대학 출판부, 2006.
- Ball, Philip (2009a). Nature's Patterns: a tapestry in three parts. 1: Shapes. Oxford University Press.
- Ball, Philip (2009b). Nature's Patterns: a tapestry in three parts. 2: Flow. Oxford University Press.
- Ball, Philip (2009c). Nature's Patterns: a tapestry in three parts. 3. Branches. Oxford University Press.
- 볼, 필립.자연의 패턴.2016년 시카고
- 머피, 팻, 닐, 윌리엄자연의 디자인으로.크로니클 북스, 1993.
- Rothenberg, David (2011). Survival of the Beautiful: Art, Science and Evolution. Bloomsbury Press.
- Stevens, Peter S. (1974). Patterns in Nature. Little, Brown & Co.
- Stewart, Ian (2001). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson.
자연의 패턴 (예술로서의)
- 에드마이어, 버나드지구의 패턴.파이돈 출판사, 2007
- 맥냅, 매기.자연에 의한 디자인: 유니버설 폼과 디자인 원칙을 사용합니다.뉴 라이더즈, 2012년.
- 나카무라, 시게키.패턴 소스북: 자연에서 영감을 받은 250가지 패턴..1권과 2권.록포트, 2009.
- 오닐, 폴리.표면 및 질감: 비주얼 소스북.블랙, 2008년.
- 포터, 엘리엇, 글릭, 제임스.자연의 혼돈.바이킹 펭귄, 1990년.