복소 이차 다항식

복소수 2차 다항식은 계수와 변수가 복소수인 2차 다항식입니다.

특성.

2차 다항식에는 형식에 관계없이 다음과 같은 특성이 있습니다.

• 그것은 유니크 다항식이다. 즉, 복합 평면에 하나의 유한 임계점이 있다. 동적 평면은 최대 2개의 분지로 구성된다: 무한대의 유역과 유한 임계점의 유역(유한 임계점이 탈출하지 않는 경우)
• 임계점은 주기적 또는 사전 ^[1]주기적이기 때문에 임계점의 궤도는 유한할 수 있다.
• 그것은 하나의 기능이다.
• 이건 합리적인 함수야
• 그것은 전체 기능이다.

폼

2차 다항식에 변수(단변량)가 하나만 있는 경우 다음과 같은 네 가지 주요 형식을 구분할 수 있습니다.

• 일반적인 형식:${\displaystyle }f{\displaystyle }$ (${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}^{}}$ ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}{}_{}}$ + ${\displaystyle {a\mathrm{}}_{}}$ 0$${ { $displaystyle$ f$(x$ ) =$a_{2}$ x$^{2$} +$a_{1$$}x+a_{$0$$}: ${\displaystyle {여기}_{}}$서 a 2$†$ $0$(\$displaystyle a_{$2}\$neq$0$)$
• 로지스틱 맵에 사용되는 인수 형식: $f{\displaystyle {}_{}{r}_{}}$ (${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle r}$x (${\displaystyle 1}$ -${\displaystyle x}$) { $displaystyle$f_${r$}(x) $=$flash($1-x)}$
• ${\displaystyle {}_{}}$f^[2]${\displaystyle {}_{}{\theta }_{}}$ (${\displaystyle x}$ ) ${\displaystyle =}$ ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle \lambda }$x { \ $displaystyle$ f $_${ \ $theta$} ( x ) = $x^$ {$2}$ + \ $displayda$ x$$$$} = e 2$$ i$${ \ $displaystyle \ pi$ \ $theta$i$$ } $f{\displaystyle }$ f f f f f f f f ${\displaystyle {}^{}}$ f f f f f f $=$ e $f$ point f f f f f f f f f f f f f f f f f f point f
• 일원 중심 형식 ${\displaystyle f_{}}$ ${\displaystyle c{}_{}}$(${\displaystyle }$x ) $=$ ${\displaystyle {x\mathrm{}}^{}}$2 +$$ \ $displaystyle f_{c}(x$)=$x^{2}+c}$

모니크 및 중심 형태는 광범위하게 연구되어 왔으며 다음과 같은 특성이 있습니다.

• 이 값은 계수(모수)가 1개인 가장 단순한 비선형 함수 형식입니다.
• 중심 다항식(임계점의 합계는 0)^[3]입니다.
• 이항식이다

람다 $형태{\displaystyle {}_{}}$ ${\displaystyle f}$ ${\displaystyle {}_{}}$ (${\displaystyle }$z ) $=$ ${\displaystyle {}^{}{2\mathrm{}}^{}}$ + ${\displaystyle z}$z {\$displaystyle$ f_${\displayda }(z$)=$z^{2}+\displayda$z}는$$ 다음과 같습니다.

• 비수습 $시스템$의 가장 단순한 비수습 섭동 z ${\displaystyle \mapsto }$ ${\$ {\ ${\displaystyle z}$ \ $displaystyle$z\ $mapsto$\$displayda$z }
• "작은 약수 문제가 ^[4]안정되었을 때 명시적으로 필요하고 충분한 조건을 알고 있는 동적 시스템의 첫 번째 패밀리"

활용

양식 사이

${\displaystyle f_{}}$ c${\displaystyle {}_{}}$(${\displaystyle x}$) {$displaystyle f_{c}(x)}$는 2차 다항식의 일반적인 형태에 아핀 켤레이기 $때문$에 복잡한 역학을 연구하고 만델브로트, 줄리아 및 파투 집합의 이미지를 만드는 데 자주 사용된다.

$§(\displaystyle\theta)$에서 c$(\displaystyle$ c$)$^[5]로 변경하는 경우:

${\displaystyle c=c(\theta)=snapfrac {e^{2\pi \theta i}{2}}\left(1-{\frac {e^{2\pi \theta i}}}{2}}\오른쪽).}$

$\displaystyle$r에서$$ c$\backslash$$displaystyle$c로 $변경$하는 경우 파라미터 변환은^[6] 다음과 같습니다.

${{displaystyle c=c(r)=snapfrac {1-(r-1)^{2}}{4}=-{\frac {r}{2}\left\flac {r-2}{2}}\right}}}$

${\displaystyle z_{}}$ t${\displaystyle {}_{}}$+ ${\displaystyle 1_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}^{}}$ ${\displaystyle {\mathrm{}}_{}^{}}$ 2${\displaystyle {}_{}^{}}$+$$ {\$displaystyle z_{t+1$} =$z_{t}^{2}+$$c$} ${\displaystyle {및}_{}}$x ${\displaystyle {\mathrm{t}}_{}}$ + ${\displaystyle 1}$ ${\displaystyle {}_{}}$ ${\displaystyle {}_{}\mathrm{x}}$ t (${\displaystyle }$1 -${\displaystyle {}_{}{x}_{}}$ )(\$displaystyle x_{t+$1} = syslog_${t}(1-x_{t})$의 $변수{\displaystyle {}_{}}$ 변환은 다음과 같습니다.

$(\displaystyle z=r\leftfrac {1}{2}}-x\right).}$

더블링 맵 포함

2차 변환(더빙 맵)과 2차 다항식 c = –2 사이에는 반비례성이 있다.

표기법

반복

$여기$서 ${\displaystyle {fn}^{}}${\$displaystyle$ f$^{n}$은 $함수{\displaystyle }$f {\$displaystyle$ f$\}$의 n번째 반복을 나타냅니다.

${\displaystyle f_{c}^{n}(z)=f_{c}^{1}(f_{c}^{n-1}(z)}$

그렇게

${\displaystyle z_{n}=f_{c}^{n}(z_{0}).}$

지수와 혼동될 수 있기 때문에 일부 $저자$는 $f$의 n번째 반복에 f$$$n$n {\$displaystyle$$f$^{\circ $n$$\}$을 $씁니다{\displaystyle {}^{}}$.

파라미터

${\displaystyle {중심}_{}}$ 형태 f c (${\displaystyle x}$ )$=$ ${\displaystyle {x\mathrm{}}^{}}$ 2 +$$ $displaystyle f_{c}(x$)=$x^{2}+c}$는 다음과 같이 표시할 수 있습니다.

• $파라미터{\displaystyle }$ c$\displaystyle$ c$}$
• 도달하는 광선의 외부 $(\displaystyle\theta$$):$
  • 파라미터 평면에 설정된 Mandelbrot의 c에서
  • 임계값:z = 동적 평면에 설정된 Julia의 c

즉, 다음과 같이 됩니다.

${\displaystyle f_{c}=f_{\theta }}$

${\displaystyle c=carreta\theta }}$

예:

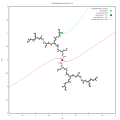
• c는 만델브로트 집합의 1/6 외부 광선의 착지점으로 z->z^2+i이다(여기서 i^2=-1).
• c는 5/14 외부 광선의 착지점으로 z->z^2+c이며, c = -1.2392255538957 + 0.412602181604*i

• 

  1/4

• 

  1/6

• 

  9/56

• 

  129/16256

지도

2차 ^[7]다항식의 Douady-Hubbard 계열로 불리기도 하는 monic 및 중심 형태는 $일반적$으로 변수$$z {\$displaystyle$ z$}$ 및$$ $매개변수{\displaystyle }$c {\$displaystyle$ c$\}$와 함께 사용된다.

${\displaystyle f_{c}(z)=z^{2}+c}$

이산 비선형 동적 시스템의 진화 함수로 사용되는 경우

${\displaystyle z_{n+1}=f_{c}(z_{n})$

2차 ^[8]맵이라고 합니다.

$({displaystyle f_{c:z\to z^{2}+c})$

Mandelbrot 집합은 초기 조건₀ z = 0으로 인해 반복이 무한대로 분산되지 않는 매개변수 c의 값 집합입니다.

중요 항목

임계점

복소 평면

${\displaystyle f_{}}$c {\$displaystyle f_{c}$의 임계점은 동적 평면상의 ${\displaystyle z_{}}$ c$$ {\$displaystyle z_{$cr$$}$점$이며 도함수가 사라집니다.

$\displaystyle f_{c}'(z_{cr})=0.}$

부터

${\displaystyle f_{c}'(z)=param frac {d}{dz}f_{c}(z)=2z}$

암시하다

${\displaystyle z_{cr}=0,}$

${\displaystyle f_{}}$c { $displaystyle$ f$_$ { $c$} ${\displaystyle \mathrm{is<img\; alt="f\_\{c\}"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/d2b64a46c31800830b9fecc59b22812390e18c05"\; style="vertical-align:\; -0.671ex;\; width:2.083ex;\; height:2.509ex;">}}$ z point point point ${\displaystyle {point}_{}}$ point point point point point point point point point point point point point c c c c c c c c c c c c c c $z_{cr}=0$$점뿐임$을 알 수 있다.

${\displaystyle {z\mathrm{}}_{}}$ 0$(\$은 Mandelbrot 집합 ^[9]반복의 초기 지점입니다.

$2차족{\displaystyle {}_{}}$ ${\displaystyle f_{}}$ c${\displaystyle {}_{}}$(${\displaystyle z}$ ) $=$ ${\displaystyle {z\mathrm{}}^{}}$2 +$$ {\$displaystyle f_{c}(z$)=$z^{2}+c}$의 경우 임계점 z = 0은 Julia 집합 ^[10]Jc의 대칭 중심이므로 Jc에서 두 점의 볼록한 조합이다.

확장 복소 평면

리만 구에서 다항식은 2d-2 임계점을 가진다.여기서 0과 무한은 임계점입니다.

임계치

$c$의 $임계치{\displaystyle {}_{}}$ ${\displaystyle z_{}}$v {\$displaystyle$ $z_{cv$$}$는 임계점의 이미지입니다.

${displaystyle z_{cr}=f_{c}(z_{cr})$

부터

${\displaystyle z_{cr}=0}$

우리는 가지고 있다.

${\displaystyle z_{display}=c.}$

$따라서{\displaystyle }$ 파라미터 c$\displaystyle$c는$$ f ${\displaystyle c_{}}$(${\displaystyle z}$ $)\displaystyle f_{c}(z)$의 임계치입니다$.$

임계 수준 곡선

임계 레벨은 임계점을 포함하는 레벨 곡선을 곡선화합니다.동적 평면의 골격과^[11] 같은 역할을 합니다.

예: 레벨 곡선은 특수 유형의 임계점인 새들 지점에서 교차합니다.

• 

  끌리다

• 

  끌리다

• 

  끌리다

• 

  포물선

• 내부 레이 0에 따른 c용 비디오

임계 한계 설정

임계 한계 설정은 모든 임계 지점의 전방 궤도 집합입니다.

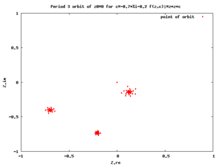
임계 궤도

임계점의 전방 궤도를 임계 궤도라고 합니다.임계 궤도는 매우 중요합니다. 왜냐하면 모든 끌어당기는 주기적 궤도가 임계점을 끌어당기기 때문입니다. 그래서 임계 궤도를 연구하는 것은 파투 ^[12][13][14]집합의 역학을 이해하는 데 도움을 줍니다.

${\displaystyle z_{0}=z_{cr}=0}$

$\displaystyle z_{1}=f_{c}(z_{0})=c}$

$\displaystyle z_{2}=f_{c}(z_{1})=c^{2}+c}$

${\displaystyle z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c}$

$\displaystyle \ vdots }$

이 궤도는 존재하는 경우 매력적인 주기 주기에 빠집니다.

크리티컬 섹터

임계 섹터는 임계점을 포함하는 동적 평면의 섹터입니다.

크리티컬 세트

Critical set은 중요한 포인트 세트입니다.

임계 다항식

${\displaystyle P_{n}(c)=f_{c}^{n}(z_{cr})=f_{c}^{n}(0)}$

그렇게

${\displaystyle P_{0}(c)=0}$

${\displaystyle P_{1}(c)=c}$

${\displaystyle P_{2}(c)=c^{2}+c}$

${\displaystyle P_{3}(c)=(c^{2}+c)^{2}+c}$

이러한 다항식은 다음 용도로 사용됩니다.

• 주기 n의 이러한 Mandelbrot 집합 성분의 중심을 찾습니다.중심은 n번째 중요 다항식의 근이다.

${\displaystyle\text{c}=\{c:P_{n}(c)=0\}$

• 주기 n의 Mandelbrot 세트 구성 요소 루트 찾기(국소 $최소{\displaystyle {}_{}}$ ${\displaystyle {Pn}_{}}$(${\displaystyle c}$) {$displaystyle P_{n}(c$ )
• 미시우레비치 포인트

${\displaystyle M_{n,k}=\{c:P_{k}(c)=P_{k+n}(c)\}$

임계 곡선

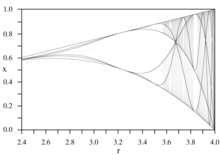
임계 다항식의 도표는 임계 ^[15]곡선이라고 불립니다.

이러한 곡선은 분기 다이어그램의 ^[16][17]골격(어두운 선)을 생성합니다.

공간, 평면

4D 공간

Julia-Mandelbrot 4차원(4D) 공간을 사용하여 이 동적 ^[18]시스템을 전체적으로 분석할 수 있습니다.

이 공간에는 두 가지 기본 2D 평면 유형이 있습니다.

• 동적(동적) 평면, ${\displaystyle f_{}}$ c ${\$}} - 평면$$ 또는 C 평면
• 파라미터 평면 또는 z 평면

또한 평면을 사용하여 이러한 동적 시스템을 분석하는 데 사용되는 다른 평면이 있습니다.

• 활용면^[19]
• 모형^[20] 평면

2D 매개변수 평면

• 파라미터 평면 유형
• 

  r 모수 평면(로지스틱 지도)

• 

  c 파라미터 평면

2차 맵의 위상 공간을 매개변수 평면이라고 합니다.여기:

${\displaystyle {z\mathrm{}}_{}}$ 0 $=$ ${\displaystyle {}_{}}$ ${\displaystyle c_{}}$ {\$displaystyle z_{0$}=$z_{cr}$은(는) $상수$이고$$c {\$displaystyle$ c$}$은(는) 변수입니다.

여기에는 역동성이 없습니다.파라미터 값의 세트일 뿐입니다.매개변수 평면에 궤도가 없습니다.

파라미터 평면은 다음과 같이 구성됩니다.

• 만델브로트 세트
  • 분기 궤적 = 다음과 같은 Mandelbrot 세트의 경계
    • 루트 포인트
  • 만델브로트 집합의 경계 쌍곡선 성분 = 내부 광선이 있는 만델브로트^[21] 집합의 내부
• 로 설정된 만델브로트의 외부
  • 외부 광선
  • 등전위선

파라미터 ^[22][23]평면에는 다양한 서브타입이 있습니다.

다음 항목도 참조해 주세요.

• 만델브로트 세트의 외부를 유닛 디스크의 외측에 매핑하는 Boetcher 지도
• 만델브로트 세트의 쌍곡선 성분 내부를 단위 원반 내부에 매핑하는 승수 지도

2D 동적 평면

"다항식 Pc는 각 동적 광선을 각도를 두 배로 하는 다른 광선(0 = 1 = 2µ rad = 360°)과 무한대에 가까운 다항식 "직선 광선처럼"의 동적 광선에 매핑합니다.이를 통해 Mandelbrot와 Julia 집합을 조합적으로 연구할 수 있으며 동적 평면을 단위 원으로, 광선을 각도로, 2차 다항식을 2배 모듈로 하나의 맵으로 대체할 수 있습니다."비르피^[24] 카우코

동적 평면에서 다음을 찾을 수 있습니다.

• 줄리아 세트
• 채워진 줄리아 세트
• 파투 세트
• 궤도

동적 평면은 다음과 같이 구성됩니다.

• 파투 집합
• 줄리아 세트

$여기$서 c$\displaystyle$c는$$ 상수이고 $\displaystyle$z는$$ 변수입니다.

2차원 동적 평면은 연속 동적 시스템의 ^[25][26]3차원 공간의 Poincaré 단면으로 취급할 수 있다.

동적 z 평면은 두 그룹으로 나눌 수 있습니다.

• ${\displaystyle {f\mathrm{}}_{}}$ 0$${\${\displaystyle \mathrm{displaystyle}}$ $f_{0}$ c$$ ${\displaystyle =}$0 {$displaystyle$ c$=0}$ $평면{\displaystyle }$(복잡한 스쿼링 맵 참조)
• ${\displaystyle f_{}}$ c$(\$ 플레인$$(다른 모든 ${\displaystyle \mathrm{플레인}}$($c{\displaystyle }$for 0(\$displaystyle$ c$\neq$ 0$)$

리만 구

확장된 복합 평면 + 무한대 지점

• 리만 구

파생상품

c에 관한 제1도함수

파라미터 평면에서:

• $\displaystyle$c는$$ 변수입니다.
• ${\displaystyle {z\mathrm{}}_{}}$ 0 $=$ $({displaystyle z_{0$}=$0}$은(는) 상수입니다.

c에 대한 ${\displaystyle f_{}^{}}$ ${\displaystyle {}_{}^{}}$n ( ${\displaystyle {}_{}{0\mathrm{}}_{}}$ $){displaystyle f_{c}^{n}(z_{0})$의 첫 번째 도함수는 다음과 같다.

${\displaystyle z_{n}=f_{c}{n}(z_{0})}$

이 도함수는 다음과 같이 시작하는 반복을 통해 찾을 수 있습니다.

${\displaystyle z_{0}=f_{c}{0}(z_{0})=1}$

연속되는 모든 단계에서 교체합니다.

$({displaystyle z_{n+1}'=f_{c}{n+1}(z_{0})=2\cdot {}f_{c}{n}(z)\cdot {frac {d}{dc}{c}{n}{n}^{n}(z_cdc})^{n}{n}{cdot}(z_cdot})}$

이는 도함수에 대한 체인 규칙을 사용하면 쉽게 확인할 수 있습니다.

이 도함수는 Mandelbrot 집합을 그리기 위한 거리 추정 방법에 사용됩니다.

z에 관한 제1도함수

동적 평면에서:

• $(\displaystyle$ z$)$는 변수입니다.
• $\displaystyle$c는$$ 상수입니다.

${\displaystyle {고정점\mathrm{}}_{}}$ z 0$(\$에서

${\displaystyle f_{c}'(z_{0})=f_{c}(z_{0})=2z_{0}.}$

주기 p의 주기점₀ z에서 함수의 첫 번째 도함수

$({displaystyle (f_{c}^{p}), (z_{0})=p_{c}{p}(z_{0})=\param _{i=0}{p-1}f_{c}'(z_{i})=2^{p}\p}\p}{p1}{p-1}{p-1}'(z}{p}{p}'(z}{da})={da}={da}{da}{da}{da}{da}{da}{da}{d$

는 $종종{\displaystyle }$ ${\(\displaystyle\lambda)$로 나타나며 승수 또는 랴푸노프 특성수로 불립니다.그것의 로그는 랴푸노프 지수로 알려져 있다.승수의 절대값은 주기적(고정적) 점의 안정성을 확인하는 데 사용됩니다.

비주기적 ${\displaystyle {점}_{}^{}}$에서는 z n ${\$ {$displaystyle z'_{n$로 $표시$된 도함수를 다음부터 반복하여 찾을 수 있습니다.

${\displaystyle z'_{0}=1,}$

그 후 를 사용하여

${\displaystyle z'_{n}=2*z_{n-1}*z'_{n-1}.}$

이 도함수는 줄리아 집합까지의 외부 거리를 계산하는 데 사용됩니다.

슈바르츠 도함수

f의 슈바르츠 도함수(SD)는 다음과 같다.^[27]

${{displaystyle(Sf)(z)=flac {f''(z)}{f'(z)}}-{\frac {3}{2}\flac {f'(z)}{f'(z)}}\right}{2}$

「 」를 참조해 주세요.

• 미시우레비치 점
• 복소 2차 매핑의 주기점
• 만델브로트 집합
• 줄리아 세트
• 밀너-서스턴 반죽 이론
• 텐트 지도
• 로지스틱 맵

레퍼런스

외부 링크

• 모니카 네빈스와 토마스 D.로저스, "p-adic 번호의 동적 시스템으로 4차 지도"
• Wolf Jung : Mandelbrot 집합의 가장자리에 있는 동형사상.2002년 박사 논문
• 2차 맵에 대한 자세한 내용은http://https://mathworld.wolfram.com/QuadraticMap.html