X선 결정학

이 기사는 너무 길어서 편하게 읽고 탐색할 수 없습니다. 콘텐츠를 하위 기사로 분할하거나 압축하거나 하위 제목을 추가하는 것을 고려하십시오. 기사의 토크 페이지에서 이 문제에 대해 논의해 주시기 바랍니다. (2023년 2월)

X선 결정학은 결정의 원자와 분자 구조를 결정하는 실험 과학으로, 결정 구조는 입사된 X선 빔을 여러 특정 방향으로 회절시키는 원인이 됩니다. 이 회절된 빔의 각도와 강도를 측정함으로써 결정학자는 결정 내 전자의 밀도에 대한 3차원 그림을 생성할 수 있습니다. 이 전자 밀도로부터 결정 안에 있는 원자들의 평균 위치와 화학적 결합, 결정학적 장애, 그리고 다양한 다른 정보들을 알아낼 수 있습니다.

X선 결정학은 소금, 금속, 광물, 반도체는 물론 다양한 무기 분자, 유기 분자, 생물 분자 등 많은 물질이 결정을 형성할 수 있기 때문에 많은 과학 분야의 발전에서 기본적인 역할을 해왔습니다. 이 방법은 사용 첫 수십 년 동안 원자의 크기, 화학 결합의 길이와 종류, 다양한 물질, 특히 광물과 합금 사이의 원자 규모 차이를 결정했습니다. 이 방법은 또한 비타민, 약물, 단백질 및 DNA와 같은 핵산을 포함한 많은 생물학적 분자의 구조와 기능을 밝혀냈습니다. X선 결정학은 여전히 새로운 물질의 원자 구조를 특성화하고 다른 실험들에 의해 비슷하게 보이는 물질들을 구별하는 주요한 방법입니다. 또한 X선 결정 구조는 물질의 특이한 전자적 또는 탄성적 특성을 설명하거나 화학적 상호작용과 과정을 조명하거나 질병에 대한 의약품을 설계하는 데 기초가 될 수 있습니다.

X선 결정학은 원자 구조를 결정하기 위한 여러 가지 다른 방법과 관련이 있습니다. 전자나 중성자를 산란시켜 비슷한 회절 패턴을 만들 수 있고, 중성자 산란도 푸리에 변환으로 비슷하게 해석할 수 있습니다. 충분한 크기의 단결정을 얻을 수 없는 경우 다른 다양한 X선 방법을 적용하여 덜 상세한 정보를 얻을 수 있습니다. 이러한 방법에는 섬유 회절, 분말 회절 및 (샘플이 결정화되지 않은 경우) 소각 X선 산란(SAXS)이 포함됩니다. 조사 중인 물질이 나노결정 분말 형태로만 이용 가능하거나 결정성이 떨어지는 문제가 있는 경우에는 전자 회절, 투과 전자 현미경, 전자 결정학의 방법을 원자 구조를 결정하는 데 적용할 수 있습니다.

역사

결정체와 X선의 초기 과학사

크리스탈은 규칙성과 대칭성으로 오랫동안 존경받았지만 17세기가 되어서야 과학적으로 조사되었습니다. 요하네스 케플러는 그의 작품인 Strenase de Nive Sexangula (육각형 눈의 새해 선물) (1611)에서 눈송이 결정의 육각형 대칭은 구형의 물 입자가 규칙적으로 채워지기 때문이라고 가설을 세웠습니다.^[1] 덴마크의 과학자 니콜라스 스테노 (1669)는 결정 대칭성에 대한 실험적인 연구를 개척했습니다. 스테노는 얼굴 사이의 각도가 특정한 종류의 결정의 모든 예시에서 동일하다는 것을 보여주었습니다.^[2] 르네 저스트 하우이(René Just Haüy)는 결정체의 모든 면이 같은 모양과 크기의 블록들을 단순하게 쌓는 패턴으로 묘사될 수 있다는 것을 발견했습니다. 따라서 1839년 윌리엄 할로우스 밀러는 각각의 얼굴에 세 개의 작은 정수들로 이루어진 독특한 라벨을 부여할 수 있었는데, 이 라벨들은 수정 얼굴들을 식별하는 데 사용되고 있습니다. 하우이의 연구는 결정이 원자와 분자의 규칙적인 3차원 배열(브라바 격자)이라는 아이디어로 이어졌습니다. 단 하나의 단위 셀은 세 가지 주요 방향을 따라 무한히 반복됩니다. 19세기에 요한 헤셀,^[3] 오귀스트 브라바이스,^[4] 에브그라프 페도로프,^[5] 아서 쇤플라이스^[6], 윌리엄 발로우(1894)에 의해 결정체의 가능한 대칭에 대한 완전한 목록이 작성되었습니다. 발로우는 1880년대에 몇 가지 결정 구조를 제안했는데, 이 결정 구조는 나중에 X선 결정학에 의해 검증되었습니다.^[7] 그러나 1880년대에는 사용 가능한 데이터가 너무 부족하여 그의 모델을 결정적인 것으로 받아들이지 못했습니다.

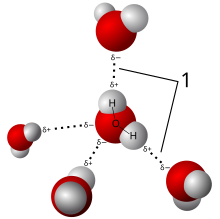
빌헬름 뢴트겐은 1895년에 X선을 발견했습니다.^[8] 물리학자들은 엑스레이의 본질에 대해서는 확신하지 못했지만, 곧 그것들이 전자기 방사선의 파동이라고 의심했습니다. 전자파 복사의 맥스웰 이론은 잘 받아들여졌고, 찰스 글로버 바클라의 실험은 X선이 가시 파장에서 관찰된 것과 유사한 가로 편광 및 스펙트럼 선을 포함하여 전자파와 관련된 현상을 나타냄을 보여주었습니다. 바클라는 1909년에 X선 표기법을 만들었는데, 처음에는 두 종류의 회절광을 "A"와 "B"로 명명한 다음, "A" 이전에 선이 있을 수 있다고 가정하고 "K"로 시작하는 알파벳 번호를 시작했습니다."^[9]아놀드 소머펠트의 실험실에서 단일 슬릿^[9][10] 실험은 엑스레이의 파장이 약 1 옹스트롬임을 시사했습니다.^[11] X-선은 파동일 뿐만 아니라 광자이기도 하며, 소머펠트가 이 파동과 같은 형태의 회절을 위해 브렘스트랄룽이라는 이름을 공동으로 사용하게 하는 입자 특성을 가지고 있습니다.^[10] 알버트 아인슈타인은 1905년에 광자 개념을 ^[12]소개했지만 1922년 ^[13][14]아서 콤프턴이 전자에서 X선이 산란되어 그것을 확인하기 전까지는 널리 받아들여지지 않았습니다.^[15] 기체의 이온화와 같은 X선의 입자 같은 특성은 1907년 윌리엄 헨리 브래그가 X선이 전자기 방사선이 아니라고 주장하게 만들었습니다.^{[16][17][18][19]} 브래그의 견해는 인기가 없다는 것이 증명되었고 1912년^[20] 막스 폰 라우에가 X선 회절을 관찰한 결과 X선은 전자기 방사선의 한 형태임이 확인되었습니다.

결정체가 X선의 회절격자로 사용될 수 있다는 생각은 1912년 뮌헨의 잉글리시 가든에서 열린 폴 피터 에발트와 막스 폰 라우에의 대화에서 비롯되었습니다. Ewald는 논문을 위해 결정의 공명기 모델을 제안했지만 파장이 공명기 사이의 간격보다 훨씬 크기 때문에 가시광선을 사용하여 이 모델을 검증할 수 없었습니다. 폰 라우에는 더 짧은 파장의 전자기 방사선이 필요하다는 것을 깨닫고 X선이 결정체의 단위 셀 간격과 비슷한 파장을 가질 수 있다고 제안했습니다. Von Laue는 두 명의 기술자 Walter Friedrich와 그의 조수 Paul Kniping과 함께 황산구리 결정을 통해 X선 광선을 비추고 그 회절을 사진판에 기록했습니다. 플레이트는 개발된 후 중앙보가 생성하는 스폿을 중심으로 교차하는 원의 패턴으로 배열된 잘 정의된 스폿이 다수 나타남을 알 수 있었습니다. 그 결과는 1912년 6월 바이에른 과학 및 인문학 아카데미에 "인터페렌스-에르샤이눙겐베이 뢴트겐스트랄렌"(X-선 간섭 현상)으로 발표되었습니다.^[21][22] 폰 라우에는 산란각과 결정 내 단위 셀 간격의 크기와 방향을 연결하는 법칙을 개발하여 1914년 노벨 물리학상을 수상했습니다.^[23]

1912~1920년 개발

Von Laue의 선구적인 연구 이후, 이 분야는 빠르게 발전했고, 가장 유명한 것은 물리학자 William Lawrence Bragg와 그의 아버지 William Henry Bragg입니다. 1912-1913년에 더 젊은 브래그는 관측된 산란과 결정 내의 균일한 간격의 평면으로부터의 반사를 연결하는 브래그의 법칙을 개발했습니다.^{[8][24][25][26]} 아버지와 아들인 브래그 부부는 결정학 분야에서의 업적으로 1915년 노벨 물리학상을 공동 수상했습니다. 초기의 구조는 일반적으로 단순했고 1차원 대칭으로 특징지어졌습니다. 그러나 다음 수십 년 동안 계산 및 실험 방법이 향상됨에 따라 단위 셀에서 원자의 더 복잡한 2차원 및 3차원 배열에 대한 신뢰할 수 있는 원자 위치를 추론하는 것이 가능해졌습니다.

화학적 및 유체역학적 실험을 통해서만 모호하게 알려진 분자와 광물의 구조를 결정하는 X선 결정학의 가능성은 바로 실현되었습니다. 초기의 구조는 단순한 무기 결정과 광물이었지만, 이마저도 물리학과 화학의 기본 법칙을 밝혀냈습니다. 1914년에 "해결"(즉, 결정)된 최초의 원자-해상도 구조는 식용 소금의 구조였습니다.^[27][28][29] 표-염 구조의 전자 분포는 결정이 반드시 공유 결합 분자로 구성되어 있지는 않다는 것을 보여주었고, 이온 화합물의 존재를 증명했습니다.^[30] 다이아몬드의 구조는 같은 해에 해결되어 ^[31][32]화학적 결합의 사면체 배열을 증명하고 C-C 단일 결합의 길이가 1.52 옹스트롬임을 보여주었습니다. Other early structures included copper,^[33] calcium fluoride (CaF₂, also known as fluorite), calcite (CaCO₃) and pyrite (FeS₂)^[34] in 1914; spinel (MgAl₂O₄) in 1915;^[35][36] the rutile and anatase forms of titanium dioxide (TiO₂) in 1916;^[37] pyrochroite (Mn(OH)₂) and, by extension, brucite (Mg(OH)₂) in 1919.^[38][39] 또한 1919년에는 랄프 월터 그레이스톤 와이코프(Ralph Walter Graystone Wyckoff)에 의해 질산나트륨(NaNO₃)과 다이클로로아이오다이드(CsICL₂)가 결정되었고 1920년에는 워츠자이트(hexagonal ZnS) 구조가 알려지게 되었습니다.^[40]

흑연의 구조는 1916년에^[41] Peter Debye와 Paul Scherrer에 의해 그리고 1917년에 Albert Hull에 의해 각각 개발된 분말 회절법에 의해 해결되었습니다.^[42][43] 흑연의 구조는 1924년에 단결정 회절로부터 두 그룹에 의해 독립적으로 결정되었습니다.^[44][45] 헐은 또한^[46] 분말법을 사용하여 철과 마그네슘과 같은 다양한 금속의 구조를 결정했습니다.^[47]

화학 및 재료 과학에 대한 기여

X선 결정학은 화학적 결합과 비공유 상호작용에 대한 더 나은 이해로 이어졌습니다. 초기의 연구는 원자의 전형적인 반경을 밝혀냈고 다이아몬드 구조에서 탄소의 사면체 결합,^[31] 육염화암모늄(IV)에서 관찰되는 금속의 팔면체 결합,^[48] 그리고 평면 탄산염기와^[34] 방향족 분자에서 관찰되는 공명과 같은 화학적 결합의 많은 이론적 모델을 확인했습니다.^[49] 1928년 Kathleen Lonsdale의^[50] 헥사메틸벤젠 구조는 벤젠의 육각대칭성을 확립하고 지방족 C-C 결합과 방향족 C-C 결합 사이의 결합 길이에 분명한 차이를 나타냈으며, 이 발견은 화학적 결합 사이의 공명에 대한 생각으로 이어졌으며, 이는 화학의 발전에 지대한 결과를 가져왔습니다.^[51] 그녀의 결론은 1921년 다른 분자를 기반으로 한 나프탈렌과 안트라센 모델을 발표한 윌리엄 헨리 브래그에 의해 예상되었습니다.^[49][52]

또한 1920년대에 Victor Moritz Goldschmidt와 후에 Linus Pauling은 화학적으로 가능성이 없는 구조를 제거하고 원자의 상대적인 크기를 결정하는 규칙을 개발했습니다. 이러한 규칙은 브루카이트의 구조와 루타일, 브루카이트 및 이산화티타늄의 아나타제 형태의 상대적 안정성에 대한 이해로 이어졌습니다.

결합된 두 원자 사이의 거리는 결합 강도와 결합 순서에 대한 민감한 척도입니다. 따라서 X선 결정학 연구를 통해 무기 화학에서 금속-금속 이중 결합, 금속-금속 4중 ^[53][54][55]결합,^[56][57][58] 3중심, 2전자 결합과 같은 훨씬 더 이국적인 유형의 결합이 발견되었습니다.^[59] X선 결정학, 또는 엄밀히 말하면 비탄성 콤프턴 산란 실험은 또한 수소 결합의 부분적 공유 특성에 대한 증거를 제공했습니다.^[60] 유기금속 화학 분야에서 페로센의 X선 구조는 샌드위치 화합물에 대한 과학적 연구를 시작한 ^[61][62]반면, Zeise의 염의 구조는 "등결합"과 금속-파이 복합체에 대한 연구를 자극했습니다.^{[63][64][65][66]} 마지막으로, X선 결정학은 초분자 화학의 발전, 특히 크라운 에테르의 구조와 숙주-손님 화학의 원리를 명확히 하는 데 선구적인 역할을 했습니다.

재료 과학에서는 풀러렌, 메탈로포르피린 및 기타 복잡한 화합물과 같은 많은 복잡한 무기 및 유기 금속 시스템이 단결정 방법을 사용하여 분석되었습니다. 단결정 회절은 제약 산업에서도 사용됩니다. 단결정 구조의 품질에 영향을 미치는 주요 요인은 결정의 크기와 규칙성이며, 소분자 결정에서 이러한 요인을 개선하기 위해 일반적으로 사용되는 방법은 재결정화입니다. Cambridge Structural Database는 2019년 6월 기준으로 1,000,000개 이상의 구조를 포함하고 있으며, 이 구조의 99% 이상이 X선 회절에 의해 결정되었습니다.^{[citation needed]}

광물학과 야금학

1920년대부터 X선 회절은 광물과 금속의 원자 배열을 결정하는 주요 방법이었습니다. X선 결정학을 광물학에 적용한 것은 1924년 멘저에 의해 결정된 가넷의 구조에서 시작되었습니다. 규산염에 대한 체계적인 X선 결정학 연구가 1920년대에 수행되었습니다. 이 연구는 Si/O 비율이 변화함에 따라 규산염 결정이 원자 배열에 상당한 변화를 보임을 보여주었습니다. 마차츠키는 이러한 통찰력을 알루미늄이 규산염의 실리콘 원자를 대체하는 광물로 확장했습니다. X선 결정학을 야금학에 처음으로 적용한 것도 1920년대 중반입니다.^{[68][69][70][71][72][73]} 특히 리누스 폴링의 합금 MgSn의₂^[74] 구조는 복잡한 이온 결정의 안정성과 구조에 대한 그의 이론으로 이어졌습니다.^[75]

2012년 10월 17일, 록네스트 화성에 있는 큐리오시티 탐사선은 화성 토양의 X선 회절 분석을 처음으로 수행했습니다. 탐사선의 CheMin 분석 결과는 장석, 파이록센 및 감람석을 포함한 여러 광물의 존재를 밝혀냈고 샘플에 포함된 화성 토양이 하와이 화산의 "풍화된 기저 토양"과 유사함을 시사했습니다.^[67]

초기 유기 분자 및 작은 생물 분자

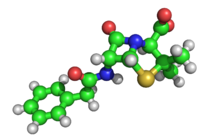
최초의 유기 화합물인 헥사메틸렌테트라민의 구조는 1923년에 해결되었습니다.^[76] 그 뒤로 생물막의 중요한 성분인 긴 사슬 지방산에 대한 여러 연구가 이어졌습니다.^{[77][78][79][80][81][82][83][84][85][excessive citations]} 1930년대에는 2차원의 복잡성을 가진 훨씬 더 큰 분자들의 구조가 해결되기 시작했습니다. 중요한 진보는 헴, 코린 및 엽록소와 같은 생물학에서 중요한 포르피린 분자와 밀접한 관련이 있는 큰 평면 분자인 ^[86]프탈로시아닌의 구조였습니다.

생물 분자의 X선 결정학은 콜레스테롤(1937), 페니실린(1946), 비타민 B₁₂(1956)의 구조를 해결한 도로시 크로풋 호지킨과 함께 발전하여 1964년 노벨 화학상을 수상했습니다. 1969년에 그녀는 인슐린의 구조를 해결하는 데 성공했고,^[87] 30년 넘게 연구했습니다.

생물학적 거대분자 결정학

단백질의 결정 구조(불규칙하고 콜레스테롤보다 수백 배 큰)는 1950년대 후반부터 해결되기 시작했고,^[88] 1962년 막스 페루츠와 함께 노벨 화학상을 공동 수상한 존 코더리 켄드루 경의 향유고래 미오글로빈 구조에서 시작했습니다.^[89] 그 성공 이후로 단백질, 핵산 및 기타 생물학적 분자의 13만 개 이상의 X선 결정 구조가 결정되었습니다.^[90] 분석된 구조의 수에서 가장 근접한 경쟁 방법은 핵자기공명(NMR) 분광법으로 10분의 1 미만의 분해능을 가지고 있습니다.^[91] 결정학은 임의로 큰 분자의 구조를 해결할 수 있는 반면, 용액 상태의 NMR은 상대적으로 작은 분자(70 kDa 미만)로 제한됩니다. X선 결정학은 제약 약물이 단백질 표적과 어떻게 상호 작용하고 어떤 변화가 이를 개선시킬 수 있는지를 결정하는 데 일상적으로 사용됩니다.^[92] 그러나 본질적인 막단백질은 세제나 다른 변성제를 필요로 하기 때문에 결정화에 어려움이 있고, 이러한 세제는 결정화를 방해하는 경우가 많습니다. 막단백질은 유전체의 큰 구성요소로 이온채널, 수용체 등 생리학적으로 매우 중요한 단백질을 많이 포함하고 있습니다.^[93][94] 헬륨 극저온은 단백질 결정의 방사선 손상을 방지하는 데 사용됩니다.^[95]

단백질 결정학은 구조 생물학에서 매우 귀중한 도구임에도 불구하고 데이터 해석을 방해하는 방법론에서 몇 가지 고유한 문제를 가지고 있습니다.

결정화 과정에서 만들어지는 결정격자에는 수많은 단위의 정제된 단백질이 들어 있고, 이들은 결정 내에 촘촘하고 대칭적으로 뭉쳐 있습니다. 이전에 알려지지 않은 단백질을 찾을 때 결정 격자 내에서 그 모양과 경계를 파악하는 것은 어려울 수 있습니다. 단백질은 보통 더 작은 소단위체로 구성되는데 소단위체를 구별하고 실제 단백질을 식별하는 작업은 숙련된 결정학자들에게도 어려울 수 있습니다.

결정화 중에 발생하는 비생물적 계면은 결정-패킹 접촉(또는 간단히 결정 접촉)으로 알려져 있으며 결정학적 수단으로는 구별할 수 없습니다. 새로운 단백질 구조가 X선 결정학에 의해 해결되고 단백질 데이터 뱅크에 축적되면, 그 저자들은 기능적이고 생물학적으로 관련된 단백질을 구성할 "생물학적 집합체"를 지정하도록 요청 받습니다. 그러나 데이터를 제출하는 동안 오류, 누락된 데이터 및 부정확한 주석은 구조를 모호하게 만들고 데이터베이스의 신뢰성을 손상시킵니다.

결함 있는 주석만으로 인한 단백질 데이터베이스 오류율은 6.6%^[96] 또는 약 15%^[97] 이상인 것으로 보고되었으며, 퇴적된 구조의 수를 고려할 때 사소한 크기라고 할 수 있습니다. 이 "인터페이스 분류 문제"는 일반적으로 계산 접근 방식으로 해결되며 구조 생물정보학에서 인정받는 주제가 되었습니다.

산란기법

탄성 vs 비탄성 산란

X-선 결정학은 탄성 산란의 한 형태입니다. 나가는 X-선은 방향만 바뀐 채 들어오는 X-선과 같은 에너지를 가지므로 파장이 같습니다. 비탄성 산란은 에너지가 유입되는 X선에서 결정으로 전달될 때 발생합니다. 예를 들어 내부 쉘 전자를 더 높은 에너지 수준으로 자극함으로써 발생합니다. 비탄성 산란은 물질의 이러한 여기를 조사하는 데 유용하지만 X선 결정학의 목표인 물질 내 산란체의 분포를 결정하는 데는 유용하지 않습니다.

X선의 파장은 10~0.01 나노미터이며, 일반적으로 결정학에 사용되는 파장은 1Å(0.1nm)이며,^[98] 이는 공유 화학 결합의 규모이며 단일 원자의 반지름입니다. 파장이 긴 광자(예: 자외선 복사)는 원자 위치를 결정하기에 충분한 해상도를 가지고 있지 않습니다. 다른 극단에서는 감마선과 같은 더 짧은 파장의 광자가 대량으로 생성되기 어렵고, 초점을 맞추기 어렵고, 물질과 너무 강하게 상호작용하여 입자-반입자 쌍을 생성합니다. 따라서 X선은 종종 전자기 방사선의 산란으로부터 원자 분해능 구조를 결정하는 "스위트 스팟"입니다.

기타 X선 기법

단결정 회절 외에 탄성 X선 산란의 다른 형태로는 분말 회절, 소각 X선 산란(SAXS) 및 여러 종류의 X선 섬유 회절이 있으며, 이는 로잘린드 프랭클린이 DNA의 이중 나선 구조를 결정하는 데 사용했습니다. 일반적으로 단결정 X선 회절은 이러한 다른 방법보다 구조적인 정보를 더 많이 제공하지만, 충분히 크고 규칙적인 결정이 필요하며, 이는 항상 이용 가능한 것은 아닙니다.

이러한 산란 방법은 일반적으로 단색 X선을 사용하며 편차가 작은 단일 파장으로 제한됩니다. 또한 광범위한 스펙트럼의 X선(즉, 파장이 다른 X선의 혼합)을 사용하여 X선 회절을 수행할 수 있으며, 이를 Laue 방법이라고 합니다. 이것은 원래 X선 회절의 발견에 사용된 방법입니다. 라우에 산란은 X선 빔에 대한 짧은 노출만으로 많은 구조적 정보를 제공하므로 매우 빠른 사건(Time resolved crystalography)의 구조 연구에 사용됩니다. 그러나 결정의 전체 원자 구조를 결정하는 데 단색 산란만큼 적합하지 않으므로 비교적 간단한 원자 배열의 결정에 더 잘 작동합니다.

라우 백 반사 모드는 넓은 스펙트럼 소스에서 뒤로 흩어진 X선을 기록합니다. X선이 투과하기에 샘플이 너무 두꺼울 경우 유용합니다. 결정에서 회절 평면은 회절 평면에 대한 법선이 입사 빔과 회절 빔 사이의 각도를 이등분한다는 것을 알고 결정됩니다. Greninger 차트를 사용하여^[99] 후면 반사 Laue 사진을 해석할 수 있습니다.

전자와 중성자 회절

전자나 중성자와 같은 다른 입자를 사용하여 회절 패턴을 생성할 수 있습니다. 전자, 중성자, X선 산란은 서로 다른 물리적 과정을 기반으로 하지만 결과적인 회절 패턴은 동일한 회절 기법을 사용하여 분석됩니다.

아래에서 도출된 바와 같이 결정 및 회절 패턴 내의 전자 밀도는 종종 단순한 수학적 방법인 푸리에 변환에 의해 관련되며, 이를 통해 패턴으로부터 밀도를 비교적 쉽게 계산할 수 있습니다. 그러나 이것은 산란이 약한 경우, 즉 산란된 빔이 들어오는 빔보다 훨씬 덜 강렬한 경우에만 작동합니다. 약하게 산란된 X선 또는 중성자 빔은 결정의 나머지 부분을 두 번째 산란 이벤트를 거치지 않고 통과합니다. 이렇게 다시 산란되는 파동을 '2차 산란' 또는 '역학적 회절'이라고 하며 분석을 변경합니다. 충분히 두꺼운 결정은 동적 회절을 일으키지만 X선과 중성자는 물질과 비교적 약하게 상호작용하기 때문에 일반적으로 사용할 때 큰 문제가 되지 않습니다.

쿨롱을 통해 상호작용하기 때문에 물질에 의한 전자의 산란은 X선보다 1000배 이상 강합니다. 따라서 전자 빔은 상대적으로 얇은 결정(>10 nm)에도 강력한 동적 산란을 생성합니다. 존 M의 책에서 볼 수 있듯이 X선과 전자의 회절 사이에는 유사점이 있습니다. 카울리,^[100] 이 접근법은 운동학적 또는 브래그의 법칙적 접근법이 아닌 상대론적 전자에 대한 한스 베테의^[101] 원래 접근법과 슈뢰딩거 방정식을 푸는 것에 기초하기 때문에 일반적으로 다릅니다. 단일 원자까지 매우 작은 영역에 대한 정보가 가능합니다. 고에너지 전자를 사용한 전자 회절, 투과 전자 현미경 및 투과 전자 결정학의 응용 범위는 광범위합니다. 자세한 내용과 인용은 관련 링크를 참조하십시오. 저에너지 전자 회절은^[102] 투과법 외에도 표면에 전자를 역산란시키는 방법으로 원자 규모의 표면 구조를 결정하는 데 광범위하게 사용되어 왔으며, 반사 고에너지 전자 회절은 박막 성장을 측정하는 데 광범위하게 사용되고 있습니다.^[103]

중성자 회절은 중성자의 강렬한 단색 빔을 충분한 양으로 얻기는 어려웠지만 구조를 결정하는 데 탁월한 방법입니다. 전통적으로 원자로가 사용되었지만, 분열에 의해 중성자를 생성하는 소스가 점점 더 이용 가능해지고 있습니다. 대전되지 않은 중성자는 전자보다 원자핵에서 훨씬 더 쉽게 흩어집니다. 따라서 중성자 산란은 X선 회절에서 본질적으로 보이지 않는 전자가 거의 없는 가벼운 원자, 특히 수소의 위치를 관찰하는 데 매우 유용합니다. 중성자 산란은 일반 물인 HO와₂ 중수인 DO의₂ 비율을 조절하여 용매를 보이지 않게 만들 수 있다는 놀라운 특성도 가지고 있습니다.

방법들

단결정 X선 회절 개요

X선 결정학의 가장 오래되고 정확한 방법은 단결정 X선 회절인데, X선 빔이 단결정에 부딪혀 산란된 빔을 생성합니다. 이 빔들은 필름이나 다른 검출기 위에 착륙할 때 점들의 회절 패턴을 만들고, 결정이 점차 회전하면서 이 빔들의 강도와 각도가 기록됩니다.^[a] 각 점은 결정 내의 균일한 간격의 평면 한 세트에서 나오는 X선의 반사에 해당하기 때문에 반사라고 불립니다. 순도와 규칙성이 충분한 단일 결정의 경우 X선 회절 데이터는 평균 화학 결합 길이와 각도를 각각 옹스트롬의 수천 분의 1 이내와 10분의 1 이내로 결정할 수 있습니다. 결정 안의 원자들은 정적인 것이 아니라, 보통 10분의 1 이하의 옹스트롬으로 그들의 평균적인 위치에 대해 진동합니다. X선 결정학을 통해 이러한 진동의 크기를 측정할 수 있습니다.

절차.

단결정 X선 결정학 기술은 세 가지 기본 단계가 있습니다. 첫 번째, 그리고 종종 가장 어려운 단계는 연구 대상 물질의 적절한 결정을 얻는 것입니다. 결정은 충분히 커야 하며(일반적으로 모든 치수에서 0.1mm보다 커야 합니다), 조성이 순수하고 구조가 규칙적이어야 하며 균열이나 쌍동과 같은 큰 내부 불완전성이 없습니다.

두 번째 단계에서는 일반적으로 단일 파장(단색 X선)의 강렬한 X선 빔에 결정체를 배치하여 일반적인 반사 패턴을 생성합니다. 회절된 X선의 각도와 강도가 측정되며, 각 화합물은 고유한 회절 패턴을 가지고 있습니다.^[104] 결정이 점차 회전하면서 이전의 반사가 사라지고 새로운 반사가 나타납니다. 모든 지점의 세기는 결정의 모든 방향에서 기록됩니다. 여러 개의 데이터 세트를 수집해야 할 수 있으며, 각 세트는 결정의 반 이상의 전체 회전을 포함하고 일반적으로 수만 개의 반사를 포함합니다.

세 번째 단계에서는 이러한 데이터를 상호 보완적인 화학 정보와 계산적으로 결합하여 결정 내의 원자 배열 모델을 생성하고 개선합니다. 현재는 결정 구조라고 불리는 원자 배열의 최종적이고 정제된 모델은 일반적으로 공개 데이터베이스에 저장됩니다.

한계

결정의 반복 단위인 단위 셀이 점점 커지고 복잡해짐에 따라 X선 결정학에 의해 제공되는 원자 수준의 그림은 주어진 수의 관찰된 반사에 대해 덜 잘 분해(더 "퍼지")됩니다. X선 결정학의 두 가지 제한적인 경우, 즉 연속적인 무기 고체를 포함하는 "소분자"와 "대분자" 결정학이 종종 발견됩니다. 소분자 결정학은 일반적으로 비대칭 단위에 원자가 100개 미만인 결정을 포함합니다. 이러한 결정 구조는 일반적으로 매우 잘 분해되어 원자가 전자 밀도의 고립된 "블롭"으로 식별될 수 있습니다. 이에 비해 고분자 결정학은 단위 셀에 수만 개의 원자를 포함하는 경우가 많습니다. 이러한 결정 구조는 일반적으로 덜 잘 분해됩니다(더 "스미어 아웃"됨). 원자와 화학 결합은 고립된 원자가 아니라 전자 밀도의 튜브로 나타납니다. 일반적으로 작은 분자도 거대 분자보다 결정화하기 쉽지만 X선 결정화는 향상된 결정화 이미징과 기술을 통해 수십만 개의 원자를 가진 바이러스와 단백질에도 가능하다는 것이 입증되었습니다.^[105] 일반적으로 X선 결정학은 샘플이 결정 형태일 경우에만 수행할 수 있지만 비결정 형태의 샘플을 샘플링하는 새로운 연구가 수행되었습니다.^[106]

결정화

결정학은 불순하거나 불규칙한 결정의 장애를 특성화하는 데 사용될 수 있지만, 결정학은 일반적으로 원자의 복잡한 배열 구조를 해결하기 위해 규칙성이 높은 순수한 결정을 필요로 합니다. 순수하고 규칙적인 결정은 금속, 광물 또는 기타 거시적인 물질의 샘플과 같은 천연 또는 합성 물질에서 얻을 수 있습니다. 이러한 결정의 규칙성은 때때로 고분자 결정 어닐링^{[107][108][109]} 및 기타 방법으로 향상될 수 있습니다. 그러나 많은 경우 회절 품질의 결정을 얻는 것이 원자-해상도 구조를 해결하는 데 가장 큰 장벽이 됩니다.^[110]

소분자 및 고분자 결정학은 회절 품질의 결정을 생성하는 데 사용되는 가능한 기술의 범위가 다릅니다. 작은 분자는 일반적으로 구조적 자유도가 거의 없으며 화학 기상 증착 및 재결정화와 같은 광범위한 방법에 의해 결정화될 수 있습니다. 이에 비해 거대분자는 일반적으로 많은 자유도를 가지며 안정적인 구조를 유지하기 위해서는 결정화를 수행해야 합니다. 예를 들어 단백질과 더 큰 RNA 분자는 3차 구조가 펼쳐지면 결정화할 수 없기 때문에 결정화 조건의 범위는 그러한 분자가 접힌 상태를 유지하는 용액 조건으로 제한됩니다.

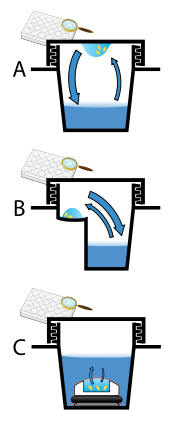
단백질 결정은 거의 항상 용액에서 성장합니다. 가장 일반적인 방법은 구성 분자의 용해도를 매우 점진적으로 낮추는 것인데, 너무 빨리 하면 용액에서 분자가 침전되어 용기 바닥에 쓸모없는 먼지나 비정질 겔이 형성됩니다. 용액에서 결정 성장은 두 단계로 특징지어집니다: 마이크로 결정체의 핵 생성(아마도 분자가 100개뿐일 수 있음), 그 다음에 그 결정체가 회절 품질의 결정체로 성장합니다.^[111][112] 첫 번째 단계(핵화)를 선호하는 해 조건이 두 번째 단계(후속 성장)를 선호하는 조건과 항상 동일한 것은 아닙니다. 결정학자의 목표는 더 큰 결정이 분자의 향상된 분해능을 제공하기 때문에 단일의 큰 결정의 개발에 유리한 용액 조건을 식별하는 것입니다. 결과적으로, 용액 조건은 첫 번째 단계(핵 생성)를 불리하게 하고 두 번째 단계(성장)를 유리하게 하여 액적당 하나의 큰 결정이 형성되도록 해야 합니다. 핵생성이 너무 선호되면 하나의 큰 결정체가 아니라 작은 결정체들의 소나기가 물방울 안에서 형성될 것이고, 너무 적게 선호되면 어떤 결정체도 형성되지 않을 것입니다. 다른 접근법은 결정화 단백질을 오일 아래에서 포함하는데, 여기서 단백질 수용액은 액체 오일 아래에서 분배되고 물은 오일 층을 통해 증발합니다. 오일마다 증발 투과율이 다르기 때문에 다른 지각/단백질 혼합물에서 농도 변화가 발생합니다.^[113]

잘 정돈된 결정의 핵 생성이나 성장을 위한 좋은 조건을 예측하는 것은 극히 어렵습니다.^[114] 실제로는 스크리닝을 통해 유리한 조건을 확인하고 매우 많은 양의 분자를 준비하고 다양한 결정화 용액을 테스트합니다.^[115] 성공적인 솔루션을 찾기 전에 일반적으로 수백, 심지어 수천 개의 솔루션 조건을 시도합니다. 다양한 조건은 분자의 용해도를 낮추기 위해 하나 이상의 물리적 메커니즘을 사용할 수 있습니다. 예를 들어, 일부는 pH를 변화시킬 수 있고, 일부는 Hofmeister 계열의 염 또는 용액의 유전 상수를 낮추는 화학 물질을 포함합니다. 그리고 또 다른 것들은 폴리에틸렌 글리콜과 같은 큰 폴리머를 함유하고 있어 엔트로픽 효과에 의해 분자를 용액 밖으로 몰아냅니다. 결정화를 촉진하기 위해 여러 온도를 시도하거나 용액이 과포화되도록 온도를 점차 낮추는 것도 일반적입니다. 이러한 방법은 결정화하기 위해 고농도의 분자를 사용하기 때문에 많은 양의 표적 분자를 필요로 합니다. 이렇게 많은 양(밀리그램)의 결정화 등급 단백질을 얻기 어려워 100나노리터 정도의 결정화 시험 방울을 부피로 정확하게 분사할 수 있는 로봇이 개발됐습니다. 이것은 손으로 직접 설정한 결정화 실험(1마이크로리터 순서)과 비교했을 때 실험당 10배 적은 단백질이 사용된다는 것을 의미합니다.^[116]

결정화를 억제하거나 손상시키는 몇 가지 요인이 알려져 있습니다. 성장하는 결정은 일반적으로 일정한 온도로 유지되고 결정화를 방해할 수 있는 충격이나 진동으로부터 보호됩니다. 분자 또는 결정화 용액의 불순물은 종종 결정화에 부정적입니다. 분자의 구조적 유연성은 또한 엔트로피로 인해 결정화 가능성을 낮추는 경향이 있습니다. 일반 나선으로 자가 조립되는 경향이 있는 분자는 종종 결정으로 조립되는 것을 꺼립니다.^{[citation needed]} 결정은 쌍방향으로 손상될 수 있으며, 이는 단위 셀이 여러 방향으로 동등하게 유리하게 포장될 수 있을 때 발생할 수 있습니다. 그러나 최근 계산 방법의 발전으로 일부 쌍방향 결정의 구조를 해결할 수 있습니다. 목표 분자를 결정화하는 데 실패한 결정학자는 분자의 약간 변형된 버전으로 다시 시도할 수 있습니다. 분자 특성의 작은 변화로도 결정화 동작에 큰 차이가 발생할 수 있습니다.

자료수집

크리스털 장착

크리스털은 X선 빔에 고정되어 회전할 수 있도록 측정을 위해 장착됩니다. 여러 가지 장착 방법이 있습니다. 과거에는 결정화 용액(모액)으로 유리 모세관에 결정을 담았습니다. 오늘날 일반적으로 작은 분자의 결정은 나일론이나 플라스틱으로 만들어진 유리 섬유나 루프에 오일이나 접착제로 부착되어 고체 막대에 부착됩니다. 단백질 결정은 루프로 퍼낸 다음 액체 질소로 급속 동결됩니다.^[117] 이러한 결빙은 X선의 방사선 손상뿐만 아니라 열 운동으로 인한 브래그 피크의 소음(Debye-Waller effect)을 감소시킵니다. 그러나 처리되지 않은 단백질 결정은 플래시 냉동 시 종종 갈라지기 때문에 일반적으로 동결 전에 동결 보호제 용액에 미리 담근다.^[118] 이 사전 침지는 결정 자체가 균열을 일으켜 결정을 손상시킬 수 있습니다. 일반적으로 성공적인 크라이오 조건은 시행착오를 통해 식별됩니다.

모세관 또는 루프는 고니오미터에 장착되어 있어 X선 빔 내에 정확하게 위치하고 회전할 수 있습니다. 수정과 빔이 모두 매우 작기 때문에 수정은 ~25 마이크로미터의 정확도 내에서 빔의 중심을 잡아야 하며, 이는 수정에 초점을 맞춘 카메라의 도움을 받습니다. 고니오미터의 가장 일반적인 유형은 "카파 고니오미터"로 세 가지 회전 각도를 제공합니다: 빔에 수직인 축을 중심으로 회전하는 ω 각도, ω 축에 대해 ~50°의 축을 중심으로 회전하는 κ 각도, 그리고 마지막으로 루프/모세관 축을 중심으로 하는 φ 각도. κ 각도가 0이면 ω 축과 φ 축이 정렬됩니다. κ 회전은 수정체가 장착된 암을 결정자 쪽으로 스윙할 수 있기 때문에 수정체를 편리하게 장착할 수 있습니다. 데이터 수집 중에 수행되는 진동(아래에 언급됨)에는 ω 축만 포함됩니다. 고니오미터의 오래된 유형은 4원 고니오미터와 6원 고니오미터와 같은 동족입니다.

엑스레이 소스

회전음극

일반적으로 이미지 플레이트 검출기와 결합된 로컬 X선 튜브 소스를 사용하여 소규모 결정학을 수행할 수 있습니다. 이들은 비교적 저렴하고 유지보수가 용이하며, 신속한 선별과 시료 채취가 가능하다는 장점이 있습니다. 그러나 생성되는 빛의 파장은 다양한 양극 재료의 사용 가능성에 의해 제한됩니다. 또한 양극이 녹는 것을 방지하기 위해 적용되는 전력과 사용 가능한 냉각 용량에 의해 강도가 제한됩니다. 이러한 시스템에서 전자는 음극에서 증발하여 ~50kV의 강한 전위를 통해 가속됩니다. 전자는 고속에 도달하면 금속 플레이트와 충돌하여 금속 내부 쉘 전자의 여기에 해당하는 브렘스트랄롱 및 일부 강한 스펙트럼 라인을 방출합니다. 가장 많이 사용되는 금속은 구리로 열전도율이 높아 쉽게 냉각할 수 있으며 강한 K선과_α K선을_β 생성합니다. K선은 얇은(~10 µm) 니켈박으로 억제되기도 합니다. 가장 간단하고 저렴한 다양한 밀폐형 X선 튜브에는 고정 양극(Crookes tube)이 있으며 ~2kW의 전자 빔 전력으로 작동합니다. 더 비싼 품종에는 ~14kW의 전자빔 전력으로 구동되는 회전 양극 유형의 소스가 있습니다.

X선은 일반적으로 단일 파장(단색으로 제작됨)으로 필터링되고 결정에 부딪히기 전에 단일 방향으로 시준됩니다. 필터링은 데이터 분석을 단순화할 뿐만 아니라 유용한 정보를 제공하지 않고 결정을 저하시키는 방사선을 제거합니다. 시준은 시준기(기본적으로 긴 튜브)를 사용하거나 부드럽게 휘어진 거울을 교묘하게 배열하여 수행합니다. 미러 시스템은 작은 결정(0.3mm 미만) 또는 큰 단위 셀(150Å 이상)에 사용하는 것이 좋습니다.

회전 양극은 양자 우물 레이저의 품질 관리를 위한 대형 InGaAsP 박막 웨이퍼의 빠른(실시간 생산) 스크리닝을 위한 X선의 힘을 입증한 첫 번째^[119][120] 실험에서 Joanna(Joka) Maria Vandenberg에 의해 사용되었습니다.

미세초점관

보다 최근에 개발된 것은 마이크로포커스 튜브로, 적어도 회전 애노드 소스만큼 높은 빔 플럭스(시준 후)를 전달할 수 있지만 몇 킬로와트가 아닌 수십 또는 수백 와트의 빔 파워만을 필요로 합니다.

싱크로트론 복사

싱크로트론 방사원은 지구에서 가장 밝은 광원들 중 일부이며 엑스레이 결정학자들이 이용할 수 있는 가장 강력한 도구들 중 일부입니다. 엑스레이 빔은 전기로 대전된 입자들, 종종 전자를 가속시키는 싱크로트론이라고 불리는 큰 기계들에서 발생됩니다. 거의 빛의 속도에 도달하고 자기장을 사용하여 (roughly) 원형 고리에 가둡니다.

싱크로트론은 일반적으로 국가 시설이며, 각 시설에는 데이터가 중단 없이 수집되는 여러 개의 전용 빔 라인이 있습니다. 싱크로트론은 원래 아원자 입자와 우주 현상을 연구하는 고에너지 물리학자들이 사용하도록 설계되었습니다. 각 싱크로트론의 가장 큰 구성 요소는 전자 저장 링입니다. 이 고리는 사실 완벽한 원이 아니라 다각형입니다. 폴리곤 또는 섹터의 각 모서리에는 정확하게 정렬된 자석이 전자 스트림을 구부립니다. 전자의 경로가 휘어지면서 X선 형태로 에너지를 폭발시킵니다.

싱크로트론 방사선을 사용하는 경우 X선 결정학에 대한 특정 요구 사항이 있는 경우가 많습니다. 강렬한 이온화 방사선은 샘플, 특히 고분자 결정에 방사선 손상을 일으킬 수 있습니다. 저온 결정학은 결정을 액체 질소 온도(~100K)에서 동결함으로써 샘플을 방사선 손상으로부터 보호합니다.^[121] 저온 결정법은 가정용 소스 회전 양극 소스에도 적용됩니다.^[122] 그러나 싱크로트론 방사는 종종 사용자가 선택할 수 있는 파장의 장점을 가지고 있어 비정상적인 신호를 최대화하는 비정상적인 산란 실험을 가능하게 합니다. 이는 단일 파장 이상 분산(SAD) 및 다중 파장 이상 분산(MAD)과 같은 실험에서 매우 중요합니다.

자유전자레이저

자유 전자 레이저는 X선 결정학에 사용하기 위해 개발되었습니다.^[123] 이것들은 현재 사용 가능한 가장 밝은 X선 소스입니다. X선은 펨토초 버스트로 제공됩니다. 소스의 강도는 원자 분해능 회절 패턴이 수집하기에는 너무 작은 결정에 대해 분해될 수 있도록 합니다. 그러나 강렬한 광원도 샘플을 파괴하여 여러 ^[124]결정을 촬영해야 합니다. 각 결정이 빔에 무작위로 배열되어 있으므로 완전한 데이터 세트를 얻기 위해서는 수십만 개의 개별 회절 이미지를 수집해야 합니다. 이 방법인 직렬 펨토초 결정학은 여러 단백질 결정 구조의 구조를 해결하는 데 사용되었으며, 때때로 싱크로트론 소스에서 수집된 동등한 구조와의 차이에 주목했습니다.^[125]

데이터 분석

반사 기록

결정체를 장착하고 강렬한 X선 빔에 노출시키면 X선을 점이나 반사 패턴으로 분산시켜 결정체 뒤의 화면에서 관찰할 수 있습니다. 컴팩트 디스크에 레이저 포인터를 비추면 비슷한 패턴을 볼 수 있습니다. 이 점들의 상대적인 강도는 결정 내 분자의 배열을 원자적으로 상세히 결정하는 정보를 제공합니다. 이러한 반사의 강도는 사진 필름, 영역 검출기(예: 픽셀 검출기) 또는 전하 결합 장치(CCD) 이미지 센서로 기록될 수 있습니다. 작은 각도의 피크는 저해상도 데이터에 해당하는 반면, 높은 각도의 피크는 고해상도 데이터를 나타냅니다. 따라서 구조의 최종 해상도에 대한 상한은 처음 몇 개의 이미지에서 결정될 수 있습니다. 피크 폭에서 관찰되는 결정의 모자이크성과 전체적인 무질서와 같은 회절 품질의 일부 측정은 이 시점에서 결정될 수 있습니다. 구조를 해결하기에 적합하지 않은 결정의 일부 병리학도 이 시점에서 빠르게 진단할 수 있습니다.

한 점의 이미지는 전체 결정을 재구성하기에 충분하지 않습니다. 전체 푸리에 변환의 작은 조각만 나타냅니다. 필요한 모든 정보를 수집하려면 수정을 180°까지 단계적으로 회전해야 하며, 모든 단계에서 이미지가 기록됩니다. 실제로는 에발트 구의 곡률 때문에 상호 공간을 덮기 위해 180°를 약간 초과해야 합니다. 그러나 결정체의 대칭성이 더 높은 경우에는 90° 또는 45°와 같은 더 작은 각도 범위가 기록될 수 있습니다. 회전축에 가까운 상호 공간에 "사각지대"가 생기지 않도록 회전축을 한 번 이상 변경해야 합니다. 일반적으로 0.5~2°씩 수정을 약간씩 흔들어 상호 공간의 넓은 영역을 잡는 것이 일반적입니다.

특정 단계 방법에는 여러 데이터 세트가 필요할 수 있습니다. 예를 들어, 다중 파장 이상 분산 단계에서는 들어오는 X선 방사선의 최소 3개(일반적으로 중복성을 위해 4개) 파장의 산란을 기록해야 합니다. 방사선 손상으로 인해 한 데이터 세트를 수집하는 동안 단결정이 너무 많이 저하될 수 있으며, 이 경우 여러 결정에 대한 데이터 세트를 수집해야 합니다.^[126]

결정 대칭, 단위 셀 및 이미지 스케일링

기록된 일련의 2차원 회절 패턴은 각각 다른 결정 방향에 대응하여 전자 밀도의 3차원 모델로 변환됩니다. 변환은 푸리에 변환의 수학적 기법을 사용하여 다음과 같이 설명됩니다. 각 점은 전자 밀도의 다른 유형에 해당합니다. 결정학자는 어떤 변화가 어떤 점(인덱스)에 해당하는지, 다른 이미지에 있는 점( 병합 및 스케일링)의 상대적 강도, 그리고 변화를 결합하여 총 전자 밀도(위상)를 산출하는 방법을 결정해야 합니다.

데이터 처리는 반사를 인덱싱하는 것으로 시작됩니다. 이는 단위 셀의 치수와 어떤 이미지 피크가 상호 공간의 어느 위치에 해당하는지 식별하는 것을 의미합니다. 인덱싱의 부산물은 결정의 대칭성, 즉 공간 그룹을 결정하는 것입니다. 일부 공간 그룹은 처음부터 제거할 수 있습니다. 예를 들어, 카이랄 분자에서는 반사 대칭이 관찰될 수 없습니다. 따라서 거의 항상 카이랄인 단백질 분자에는 가능한 230개의 65개의 공간 그룹만 허용됩니다. 인덱싱은 일반적으로 자동 인덱싱 루틴을 사용하여 수행됩니다.^[127] 대칭이 할당되면 데이터가 통합됩니다. 이를 통해 수천 개의 반사가 포함된 수백 개의 이미지를 하나의 파일로 변환하고, 각 반사의 밀러 인덱스(Miller index)에 대한 (적어도) 기록으로 구성됩니다. 그리고 각 반사의 강도(이 상태에서 파일에는 종종 오류 추정 및 편파 측정(해당 이미지에 기록된 특정 반사의 부분)도 포함됩니다.

전체 데이터 세트는 결정의 다른 방향에서 촬영된 수백 개의 개별 이미지로 구성될 수 있습니다. 첫 번째 단계는 이러한 다양한 이미지를 병합하고 스케일하는 것, 즉 두 개 이상의 이미지에 나타나는 피크(peak)를 식별하고 일관된 강도 스케일을 갖도록 상대 이미지를 스케일하는 것입니다. 피크의 상대적인 강도가 구조를 결정하는 핵심 정보이기 때문에 강도 척도를 최적화하는 것은 매우 중요합니다. 결정학적 데이터 수집의 반복적인 기술과 결정적 물질의 높은 대칭성으로 인해 회절계는 많은 대칭성 등가 반사를 여러 번 기록하게 됩니다. 이를 통해 대칭 관련 R-팩터를 계산할 수 있으며, 이는 측정된 대칭 등가 반사의 강도가 얼마나 유사한지에 기반한 신뢰성 지수이며,^{[clarification needed]} 따라서 데이터의 품질을 평가할 수 있습니다.

초기단계

회절 실험에서 수집된 데이터는 결정 격자의 상호 공간 표현입니다. 각 회절 '스팟'의 위치는 단위 셀의 크기와 모양, 결정 내의 고유한 대칭성에 의해 결정됩니다. 각 회절 '스팟'의 세기가 기록되며, 이 세기는 구조 인자 진폭의 제곱에 비례합니다. 구조 계수는 파동의 진폭과 위상에 관련된 정보를 포함하는 복소수입니다. 해석 가능한 전자 밀도 지도를 얻기 위해서는 진폭과 위상을 모두 알아야 합니다(전자 밀도 지도를 통해 결정학자는 분자의 시작 모델을 구축할 수 있습니다). 회절 실험 중에는 위상을 직접 기록할 수 없습니다. 이를 위상 문제라고 합니다. 초기 단계 추정치는 다음과 같은 다양한 방법으로 얻을 수 있습니다.

• 초기 단계 또는 직접 방법 – 일반적으로 작은 분자(<1000개의 비수소 원자)에 대한 선택 방법이며, 작은 단백질에 대한 상 문제를 해결하는 데 성공적으로 사용되었습니다. 데이터의 해상도가 1.4 Å(140 pm) 이상이면 특정 반사 그룹 간의 알려진 위상 관계를 활용하여 위상 정보를 얻는 데 직접 방법을 사용할 수 있습니다.^[128][129]
• 분자 대체 – 관련 구조가 알려져 있는 경우 분자 대체에서 검색 모델로 사용하여 단위 세포 내 분자의 방향과 위치를 결정할 수 있습니다. 이렇게 얻은 상은 전자 밀도 지도를 생성하는 데 사용할 수 있습니다.^[130]
• 비정상적인 X선 산란(MAD 또는 SAD 단계) – X선 파장은 원자의 흡수 가장자리를^[b] 지나 스캔되어 알려진 방식으로 산란을 변경할 수 있습니다. 세 가지 다른 파장(훨씬 아래, 훨씬 위 및 흡수 가장자리 중간)에서 반사의 전체 세트를 기록함으로써 비정상적으로 회절하는 원자의 하부 구조 및 따라서 전체 분자의 구조를 해결할 수 있습니다. 비정상적인 산란 원자를 단백질에 통합하는 가장 일반적인 방법은 셀레늄 원자를 포함하는 셀레노-메티오닌이 풍부한 배지에서 메티오닌 영양요구성(메티오닌을 합성할 수 없는 숙주)으로 단백질을 발현하는 것입니다. 그런 다음 다파장 비정상 분산(MAD) 실험을 흡수 가장자리 주변에서 수행할 수 있으며, 이는 초기 단계를 제공하는 단백질 내 메티오닌 잔기의 위치를 산출해야 합니다.^[131]
• 중원자 방법(다중 동형 치환) – 전자 밀도가 높은 금속 원자가 결정에 도입될 수 있는 경우 직접 방법 또는 패터슨 공간 방법을 사용하여 위치를 결정하고 초기 상을 얻을 수 있습니다. 이러한 무거운 원자는 무거운 원자를 함유한 용액에 결정을 담그거나 공결정화(무거운 원자가 존재하는 상태에서 결정을 성장시킴)에 의해 도입될 수 있습니다. 다파장 이상 분산 단계에서와 마찬가지로 산란 진폭의 변화를 해석하여 위상을 생성할 수 있습니다. 이것이 단백질 결정 구조를 해결한 독창적인 방법이지만, 셀레노메티오닌을 사용한 다파장 이상 분산 단계로 대체되었습니다.^[130]

모델 구축 및 단계 개선

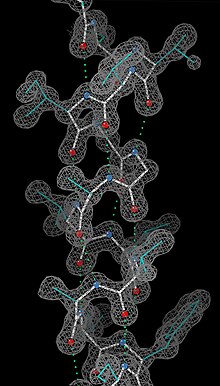
초기 단계를 획득하면 초기 모델을 구축할 수 있습니다. 모델의 원자 위치와 각각의 Debye-Waller 인자(또는 원자의 열 운동을 설명하는 B-팩터)를 관찰된 회절 데이터에 맞게 정제하여 이상적으로 더 나은 위상 세트를 산출할 수 있습니다. 그런 다음 새로운 모델을 새로운 전자 밀도 맵에 맞출 수 있고 연속적인 개선 작업이 수행됩니다. 이 반복 과정은 회절 데이터와 모형 사이의 상관 관계가 최대가 될 때까지 계속됩니다. 일치는 다음과 같이 정의된 R-팩터에 의해 측정됩니다.

${\displaystyle R={\frac {\sum_{\text{all reflections}\left F_{\text{obs}-F_{\text{calc}}\right}}{\sum_{\text{all reflections}\left F_{\text{obs}\right}}}$

여기서 F는 구조 인자입니다. 유사한 품질 기준은 구조 개선에 포함되지 않은 반사의 부분 집합(~10%)에서 계산되는 R입니다_free. 두 R 요인 모두 데이터의 해상도에 따라 달라집니다. 경험상 R은_free 대략 10으로 나눈 옹스트롬의 해상도여야 합니다. 따라서 2Å 해상도의 데이터 세트는 최종 R_free ~ 0.2를 산출해야 합니다. 입체화학, 수소 결합, 결합 길이와 각도의 분포와 같은 화학 결합 기능은 모델 품질의 보완적인 척도입니다. 반복적인 모델 구축에서 위상 편향 또는 모델 편향이 발생하는 것이 일반적입니다. 위상 추정은 모델에서 나오기 때문에 계산된 맵의 각 라운드는 밀도가 있는지 여부에 관계없이 모델이 밀도가 있는 곳이면 밀도를 표시하는 경향이 있습니다. 이 심각한 문제는 생략 맵을 사용하여 최대 가능성 가중치를 부여하고 검사함으로써 완화될 수 있습니다.^[134]

비대칭 단위의 모든 원자를 관찰하는 것은 불가능할 수 있습니다. 많은 경우에 결정학적 장애는 전자 밀도 지도를 번지게 합니다. 수소와 같이 약하게 산란하는 원자는 일상적으로 보이지 않습니다. 단일 원자가 전자 밀도 맵에 여러 번 나타나는 것도 가능합니다. 예를 들어, 단백질 측쇄가 여러 개(<4) 허용되는 형태를 갖는 경우. 또 다른 경우, 결정학자는 분자에 대해 추론된 공유 구조가 잘못되었거나 변경되었음을 감지할 수 있습니다. 예를 들어, 단백질은 절단되거나 결정화 이전에는 감지되지 않았던 번역 후 변형을 겪을 수 있습니다.

무질서

결정 구조를 개선하는 데 있어 일반적인 문제는 결정학적 장애에서 비롯됩니다. 장애는 여러 형태로 나타날 수 있지만 일반적으로 두 가지 이상의 종 또는 형태가 공존하는 것을 포함합니다. 장애를 인식하지 못하면 잘못된 해석을 하게 됩니다. 장애의 부적절한 모델링으로 인한 함정은 결합 스트레치 이성질체의 할인된 가설에 의해 설명됩니다.^[135] 무질서는 성분들의 상대적인 모집단(종종 두 개)과 그들의 정체성을 기준으로 모델링됩니다. 큰 분자와 이온의 구조에서 용매와 반대 이온은 종종 무질서합니다.

응용 전산 데이터 분석

분말 X-선 회절 데이터 분석을 위한 계산 방법의 사용이 일반화되었습니다. 일반적으로 도구 매개변수를 고려하여 실험 데이터를 모델 구조의 시뮬레이션된 회절도와 비교하고 최소 제곱 기반 최소화 알고리즘을 사용하여 모델의 구조적 또는 미세 구조적 매개변수를 개선합니다. 단계 식별 및 구조 개선을 가능하게 하는 대부분의 사용 가능한 도구는 Rietveld 방법을 기반으로 하며,^[136][137] 일부는 FullProf Suite,^[138][139] Jana2006,^[140] MAUD,^{[141][142][143]} Rietan,^[144] GSAS ^[145]등과 같은 개방형 및 자유 소프트웨어이며, 다른 일부는 Diffrac과 같은 상용 라이센스로 사용할 수 있습니다.제품군 TOPAS,^[146] Match!^[147] 등 이러한 도구의 대부분은 또한 자체적으로 결정학적 구조를 고려하지 않고, Le Bail 정제(프로파일 매칭이라고도 함), 즉 Bragg 피크 위치 및 피크 프로파일에 기초한 셀 파라미터의 정제를 가능하게 합니다. 보다 최근의 도구를 사용하면 FullProf Suite에 포함된 FALS 프로그램과 같이 구조적 데이터와 미세 구조적 데이터를 모두 개선할 수 있습니다.^[148] 이를 통해 평면 결함(예: 적층 결함, 쌍끌이, 상호 성장)이 있는 구조를 개선할 수 있습니다.

구조물의 퇴적

분자 구조의 모델이 확정되면 종종 Cambridge Structural Database(소분자의 경우), ICSD(무기화합물의 경우) 또는 단백질 데이터 뱅크(단백질 및 때로는 핵산의 경우)와 같은 결정학적 데이터베이스에 저장됩니다. 의학적으로 관련된 단백질을 결정화하기 위해 민간 상업 벤처에서 얻은 많은 구조는 공공 결정학 데이터베이스에 저장되지 않습니다.

회절이론

X선 회절의 기초

결정체는 원자들의 규칙적인 배열이며, X선은 전자기 방사선의 파동으로 간주될 수 있습니다. 원자는 주로 원자의 전자를 통해 X선 파동을 산란시킵니다. 등대에 부딪히는 바다의 파동이 등대에서 뿜어져 나오는 2차 원파를 생성하는 것처럼, 전자에 부딪히는 X선은 전자에서 뿜어져 나오는 2차 원파를 생성합니다. 이 현상을 탄성 산란이라고 하고, 전자(또는 등대)를 산란이라고 합니다. 산란자들의 규칙적인 배열은 구면파의 규칙적인 배열을 생성합니다. 이러한 파동은 파괴적인 간섭을 통해 대부분의 방향에서 서로 상쇄되지만 몇 가지 특정 방향에서 건설적으로 추가됩니다.

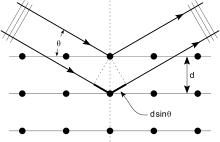
X선 회절에 대한 직관적인 이해는 회절의 브래그 모델에서 얻을 수 있습니다. 이 모델에서 주어진 반사는 보통 결정 격자의 원자 중심을 통과하는 결정을 통과하는 균일한 간격의 시트 세트와 관련이 있습니다. 특정 시트 집합의 방향은 세 가지 밀러 지수(h, k, l)로 식별되며 간격은 d로 표시됩니다. 윌리엄 로렌스 브래그(William Lawrence Bragg)는 들어오는 X선이 각 평면에서 (거울처럼) 특정하게 산란되는 모델을 제안했습니다. 평면과 X선 사이의 각도 θ가 X선 파장 λ의 정수배 n인 경로 길이 차이를 초래할 때 인접 평면에서 산란된 X선은 건설적으로 결합합니다(건설적 간섭).

${\displaystyle 2d\sin \theta = n\lambda.}$

반사는 알려진 파장과 산란 각도 2 θ에서 밀러 지수(또는 더 정확하게는 상호 격자 벡터 성분)가 식별되었을 때 지수화된다고 합니다. 이러한 인덱싱은 단위 셀 매개변수, 단위 셀의 길이 및 각도 및 공간 그룹을 제공합니다. 그러나 브래그의 법칙은 반사의 상대적 강도를 해석하지 않기 때문에 일반적으로 단위 셀 내의 원자 배열을 해결하기에는 불충분합니다. 이를 위해서는 푸리에 변환 방법이 수행되어야 합니다.

산란

X선 산란은 결정 내 전자의 밀도에 의해 결정됩니다. X선의 에너지는 원자가 전자의 에너지보다 훨씬 크므로 산란은 전자파선과 자유 전자의 상호작용인 톰슨 산란으로 모델링될 수 있습니다. 이 모델은 일반적으로 산란된 방사선의 편광을 설명하기 위해 채택됩니다.

질량 m과 기본 전하 q를 가진 한 입자에 대한 톰슨 산란의 강도는 다음과 같습니다.^[149]

${\displaystyle I_{o}=I_{e}\left({\frac {q^{4}}{m^{2}c^{4}}}\right){\frac {1+\cos ^{2}2\theta }{2}}=I_{e}7.94\times 10^{-26}{\frac {1+\cos ^{2}2\theta }{2}}=I_{e}f}$

따라서 전자보다 훨씬 무거운 원자핵은 흩어진 X선에 무시할 정도로 기여합니다. 결과적으로, 원자에서 검출된 가간섭성 산란은 시스템 내의 전자로부터의 집단 산란을 분석함으로써 정확하게 근사화될 수 있습니다.^[150]

X선 결정학의 주요 목표는 결정 전체에 걸쳐 전자 f(r)의 밀도를 결정하는 것이며, 여기서 r은 결정 내의 3차원 위치 벡터를 나타냅니다. 이를 위해 X선 산란을 사용하여 푸리에 변환 F(q)에 대한 데이터를 수집하고, 이를 수학적으로 반전시켜 실제 공간에서 정의된 밀도를 구하는 공식을 사용합니다.

${\displaystyle f(\mathbf {r})={\frac {1}{\left(2\pi \right)^{3}}\int F(\mathbf {q})e^{\mathrm {i} \mathbf {q} \cdot \mathbf {r}\mathrm {d} \mathbf {q},}$

여기서 적분은 q의 모든 값을 인수합니다. 3차원 실수 벡터 q는 상호 공간의 한 점, 즉 q가 가리키는 방향으로 움직일 때 전자 밀도의 특정 진동을 나타냅니다. q의 길이는 $진동$의$$으로 나눈 2 π ${\displaystyle$ 2\pi}에 해당합니다. 푸리에 변환에 해당하는 공식은 아래에서 사용됩니다.

${\displaystyle F(\mathbf {q})=\int f(\mathbf {r})\mathrm {e} ^{-\mathrm {i} \mathbf {q} \cdot \mathbf {r}\mathrm {d} \mathbf {r},}$

여기서 적분은 결정 내 위치 벡터 r의 가능한 모든 값에 대해 합산됩니다.

푸리에 변환 F(q)는 일반적으로 복소수이며, 따라서 F(q)의 크기와 방정식과 관련된 위상 φ(q)를 갖습니다.

${\displaystyle F(\mathbf {q})=\left F(\mathbf {q})\right \mathrm {e} ^{\mathrm {i} \phi(\mathbf {q})}.$

X선 회절에서 관찰된 반사 강도는 F(q)의 크기를 제공하지만 φ(q)의 위상은 제공하지 않습니다. 상을 얻기 위해, 반사의 전체 세트는 특정 흡수 에지를 지나 파장을 변조하거나 수은과 같은 강한 산란(즉, 전자 밀도가 높은) 금속 원자를 추가함으로써 산란에 대한 알려진 변경과 함께 수집됩니다. 크기와 위상을 결합하면 완전한 푸리에 변환 F(q)가 생성되며, 이를 반전하여 전자 밀도 f(r)를 얻을 수 있습니다.

크리스탈은 종종 완벽한 주기적인 것으로 이상화됩니다. 이상적인 경우, 원자들은 완벽한 격자 위에 위치하고, 전자 밀도는 완벽하게 주기적이며, 푸리에 변환 F(q)는 q가 상호 격자(이른바 브래그 피크)에 속하는 경우를 제외하고는 0입니다. 그러나 실제로는 결정이 완벽하게 주기적인 것은 아니며, 원자는 그들의 평균 위치에 대해 진동하고, 결정화된 분자의 형태에 모자이크, 전위, 여러 가지 점 결함, 이질성 등 다양한 형태의 무질서가 있을 수 있습니다. 따라서 브래그 피크는 유한한 폭을 가지며 브래그 피크 사이에 떨어지는 산란된 X선의 연속체인 상당한 확산 산란이 있을 수 있습니다.

푸리에 변환으로서의 산란

들어오는 X선 빔은 편광을 가지고 있으며 벡터 파동으로 표현되어야 합니다. 그러나 단순화를 위해 여기서 스칼라 파동으로 표현하도록 합니다. 또한 파동의 시간 의존성이라는 복잡한 문제를 무시하고 파동의 공간 의존성에만 집중합니다. 평면파는 파동 벡터 k로 표현될 수 있고, 따라서 시간 t = 0에서 들어오는 파동의 세기는 다음과 같이 주어집니다.

${\displaystyle A\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\mathrm {in}\cdot \mathbf {r}}$

표본 내 위치 r에서 산란체의 밀도가 f(r)가 되도록 합니다. 이러한 산란체는 유입파의 국부 진폭과 r에 대한 작은 부피 dV의 산란체 수에 비례하는 진폭의 산란된 구형파를 생성해야 합니다.

${\displaystyle {\text{산란파의 amplitude}}=A\mathrm {e} ^{\mathrm {i} \mathbf {k} \cdot \mathbf {r} }Sf(\mathbf {r})\mathrm {d} V,}$

여기서 S는 비례 상수입니다.

k의_out 나가는 파동 벡터와 함께 떠나고 r에서_screen 화면을 타격하는 산란파의 비율을 고려해 보십시오. 에너지가 손실되지 않기 때문에(비탄성 산란이 아닌 elastic) 파장은 파동-vectors k=k의 크기와 같습니다. 광자가 r로 산란된 시점부터 r로 흡수될 때까지 광자는 위상 변화를 겪습니다.

${\displaystyle e^{i\mathbf {k} _{\text{out}}\cdot \left(\mathbf {r} _{\text{screen}}-\mathbf {r} \r} \right)}}$

r에_screen 도달하는 순 방사선은 결정 전체에 흩어진 모든 파동의 합입니다.

${\displaystyle AS\int \mathrm {d} \mathbf {r} f(\mathbf {r} )\mathrm {e}^{\mathbf {i} _{\text{in}}\cdot \mathbf {r}e^{i\mathbf {k} _{\text{out}\cdot \left(\mathbf {r} _{\text{screen} -\mathbf {r} \right)} =ASe^{i\mathbf {k}_{\text{out}}\cdot \mathbf {r}_{\text{screen}}\int \mathrm {d} \mathbf {r} f(\mathbf {r})\mathrm {e}^{\mathrm {i} \left(\text{in}}-\mathbf {k}_{\text{out}\right)\cdot \mathbf {r}}$

푸리에 변환으로 기록될 수 있습니다.

${\displaystyle AS\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\text{out}\cdot \mathbf {r} _{\text{screen}}\int d\mathbf {r} f(\mathbf {r})\mathrm {i} \mathbf {q} \cdot \mathbf {r} } =AS\mathrm {e} ^{\mathrm {i} \mathbf {k} _{\text{out}\cdot \mathbf {r} _{\text{screen}} F(\mathbf {q}),$

여기서 q = k – k. 측정된 반사 강도는 이 진폭의 제곱입니다.

${\displaystyle A^{2}S^{2}\left F(\mathbf {q})\right ^{2}.$

프리델과 비즈보엣의 짝

역수 공간의 한 점 q에 해당하는 모든 반사에 대해 반대 점 -q에서 동일한 세기의 다른 반사가 있습니다. 이 반대 반사는 원래 반사의 프리델 메이트로 알려져 있습니다. 이 대칭성은 위치 r에서 전자 f(r)의 밀도가 항상 실수라는 수학적 사실에서 비롯됩니다. 위에서 언급한 바와 같이, f(r)는 푸리에 변환 F(q)의 역변환이지만, 이러한 역변환은 일반적으로 복소수입니다. f(r)가 실수임을 보장하려면 푸리에 변환 F(q)는 프리델 짝 F(-q)와 F(q)가 서로 복소 켤레가 되어야 합니다. 따라서 F(-q)는 F(q)와 동일한 크기를 갖지만 반대 위상, 즉 φ(q) = - φ(-q)을 갖습니다.

${\displaystyle F(-\mathbf {q})=\left F(-\mathbf {q})\right \mathrm {e} ^{\mathrm {i} \phi(-\mathbf {q})} =F^{*}(\mathbf {q})=\left F(\mathbf {q})\right \mathrm {e} ^{-\mathrm {i} \phi(\mathbf {q})}}$

그들의 크기의 동일성은 프리델 메이트가 동일한 강도 F를 갖는 것을 보장합니다. 이 대칭성은 예를 들어 결정을 완전한 360° 회전 대신 180°보다 약간 더 회전시킴으로써 역수 공간의 절반에서만 완전한 푸리에 변환을 측정할 수 있게 해줍니다. 대칭성이 큰 결정에서는 훨씬 더 많은 반사가 동일한 강도(Bijvoet mates)를 가질 수 있습니다. 이러한 경우에는 상호 공간이 훨씬 더 적을 수 있습니다. 대칭성이 높은 유리한 경우에는 때때로 90° 또는 45°의 데이터만 있으면 상호 공간을 완전히 탐색할 수 있습니다.

Friedel-mate 제약은 역 푸리에 변환의 정의로부터 유도될 수 있습니다.

${\displaystyle f(\mathbf {r})=\int {\frac {d\mathbf {q}}{\left(2\pi \right)^{3}}F(\mathbf {q})\mathrm {e} ^{\mathrm {i} \mathbf {q} \cdot \mathbf {r} =\int {\frac {d\mathbf {r} } {\left(2\pi \right)^{3}}\left F(\mathbf {q})\right \mathrm {e} ^{\mathbf {q}}\mathrm {e}^{\mathbf {i} \cdot \mathbf {r}}$

오일러의 공식은 e = cos(x) + in(x)를 의미하므로, 역 푸리에 변환은 순수한 실수부와 순수한 허수부의 합으로 분리될 수 있습니다.

${\displaystyle f(\mathbf {r})=\int {\frac {d\mathbf {q} {\left(2\pi \right)^{3}}\left F(\mathbf {q})\right \mathrm {e}^{\i}\left(\phi +\mathbf {q} \cdot \mathbf {r} \right)}=\int {\frac {d\mathbf {q} {\left(2\pi \right)^{3}}\left F(\mathbf {q})\right \cos \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)+i\int {\frac {d\mathbf {q} }{\left(2\pi \right)^{3}}\left F(\mathbf {q})\right \sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right)=I_{\mathrm {cos} }+iI_{\mathrm {sin} }.}$

함수 f(r)는 두 번째 적분 I가_sin r의 모든 값에 대하여 0인 경우에만 실수입니다. 결국, 이는 위의 제약 조건을 만족하는 경우에만 참입니다.

${\displaystyle I_{\sin} =\int {\frac {d\mathbf {q} {\left(2\pi \right)^{3}}\left F(\mathbf {q})\right \sin \left(\phi +\mathbf {q} \cdot \mathbf {r} \right) =\int {\frac {d\mathbf {q} {\left(2\pi \right)^{3}}\left F(\mathbf {-q})\right \sin \left (-\phi -\mathbf {q} \cdot \mathbf {r} \right) =-I_{\sin}}$

나는 = -나는 내가 =0임을 암시하기 때문입니다.

에발트 구

각 X선 회절 이미지는 Ewald 구 구성에서 볼 수 있는 것처럼 상호 공간의 구형 슬라이스인 슬라이스만을 나타냅니다. k와_out k는_in 파장이 변하지 않았기 때문에 탄성 산란으로 인해 길이가 같습니다. 따라서 주어진 회절 이미지에서 샘플링된 q 값을 보여주는 상호 공간의 구에서 두 개의 방사형 벡터로 표현될 수 있습니다. 들어오는 X선 빔의 들어오는 파장에 약간의 확산이 있기 때문에 F(q)의 값은 해당 반지름에 해당하는 두 구 사이에 위치한 q 벡터에 대해서만 측정할 수 있습니다. 따라서 전체 푸리에 변환 데이터 세트를 얻기 위해서는 180°를 약간 초과하거나, 충분한 대칭이 존재하는 경우에는 그 이하로 결정을 회전시켜야 합니다. 실제 함수의 푸리에 변환(전자 밀도 등)에 고유한 대칭 때문에 전체 360° 회전은 필요하지 않지만, 에발트 구의 곡률 때문에 주어진 해상도 내에서 모든 상호 공간을 덮기 위해서는 180°보다 "약간 더" 필요합니다. 실제로 크리스탈은 소량(0.25~1°)으로 흔들립니다. 구면 에왈드의 껍질 경계 근처에 반사를 포함합니다.

패터슨 함수

푸리에 변환의 잘 알려진 결과는 함수 f(r)의 자기 상관 c(r)를 나타내는 자기 상관 정리입니다.

${\displaystyle c(\mathbf {r})=\int d\mathbf {x} f(\mathbf {x})f(\mathbf {x} +\mathbf {r})=\int {\frac {d\mathbf {q} {\left(2\pi \right)^{3}}C(\mathbf {q})e^{i\mathbf {q} \cdot \mathbf {r}}}$

F(q)의 제곱 크기인 푸리에 변환 C(q)가 있습니다.

${\displaystyle C(\mathbf {q}) =\left F(\mathbf {q})\right ^{2}$

따라서 전자 밀도의 자기 상관 함수 c(r)는^[151] 위상을 계산하지 않고 반사 강도에서 직접 계산할 수 있습니다. 이를 이용하여 결정구조를 직접 결정하는 것이 원칙이지만 실제로는 실현하기가 어렵습니다. 자기 상관 함수는 결정 내의 원자들 간의 벡터 분포에 해당하므로 단위 셀 내의 N개 원자의 결정은 패터슨 함수에서 N(N-1)개의 피크를 가질 수 있습니다. 강도를 측정할 때 피할 수 없는 오류와 원자간 벡터에서 원자 위치를 재구성하는 수학적 어려움을 고려할 때, 이 기술은 가장 단순한 결정을 제외하고는 구조를 해결하는 데 거의 사용되지 않습니다.

결정의 장점

원칙적으로 단 하나의 분자에도 X선 산란을 비결정질 샘플에 적용하여 원자 구조를 결정할 수 있습니다. 그러나 결정체는 주기성 때문에 훨씬 더 강한 신호를 제공합니다. 결정질 샘플은 정의상 주기적이며, 결정은 세 개의 독립적인 방향으로 무한히 반복되는 많은 단위 셀로 구성됩니다. 이러한 주기적 시스템은 브래그 피크(Bragg peaks)로 알려진 상호 공간에서 주기적으로 반복되는 지점에 집중되는 푸리에 변환을 가지며, 브래그 피크는 회절 이미지에서 관찰되는 반사 스팟에 해당합니다. 이러한 반사에서의 진폭은 산란체의 수 N에 따라 선형적으로 증가하기 때문에 이러한 점들의 관찰된 강도는 N과² 같이 2차적으로 증가해야 합니다. 즉, 결정을 사용하면 개별 단위 셀의 약한 산란이 훨씬 강력하고 일관된 반사로 집중되어 노이즈 위에서 관찰할 수 있습니다. 이것은 건설적인 간섭의 한 예입니다.

액체, 분말 또는 비정질 샘플에서 해당 샘플 내의 분자는 임의의 방향으로 배열됩니다. 이러한 샘플은 SAXS에서 관찰되는 바와 같이 진폭이 균일하게 퍼지는 연속 푸리에 스펙트럼을 가지고 있어 측정된 신호 세기를 감소시킵니다. 더 중요한 것은 오리엔테이션 정보가 손실된다는 것입니다. 이론적으로는 가능하지만, 그러한 회전 평균 데이터로부터 복잡한 비대칭 분자의 원자 분해능 구조를 얻는 것은 실험적으로 어렵습니다. 중간 케이스는 서브 유닛들이 적어도 하나의 차원에서 주기적으로 배열되는 섬유 회절입니다.

X선 결정학과 관련된 노벨상

연도	수상자	상	이론적 근거
1914	막스 폰 라우에	물리학	"결정에 의한 X선의 회절을 발견한 그의 업적"[152]은 X선 분광학 발전의 중요한 단계입니다.
1915	윌리엄 헨리 브래그	물리학	"X선을 이용한 결정구조 분석에 대한 그들의 공로"[153]
	윌리엄 로렌스 브래그
1962	Max F. Perutz	화학	"구체 단백질의 구조에 대한 그들의 연구를 위해"[154]
	존 C. 켄드루
1962	제임스 듀이 왓슨	약	"핵산의 분자 구조와 생체 물질에서의 정보 전달에 대한 중요성에 대한 그들의 발견"[155]
	프랜시스 해리 콤프턴 크릭
	모리스 휴 프레드릭 윌킨스
1964	도로시 호지킨	화학	"중요한 생화학 물질의 구조를 X선 기술로 측정하기 [156]위해"
1972	스탠퍼드 무어	화학	"리보뉴클레아제 분자의 활성 중심의 화학 구조와 촉매 활성 사이의 연관성을 이해하는 데 기여한 공로"[157]
	윌리엄 H. 스타인
1976	윌리엄 립스컴	화학	"화학결합의 문제점을 조명하는 보레인의 구조에 대한 그의 연구를 위해"[158]
1985	제롬 칼	화학	"결정구조 측정을 위한 직접적인 방법을 개발한 그들의 뛰어난 업적"[159]
	허버트 A. 하우프트만
1988	요한 데이젠호퍼	화학	"광합성 반응 중심의 3차원 구조 측정을 위해"[160]
	하르트무트 미셸	화학
	로버트 휴버	화학
1997	존 E. 워커	화학	"아데노신 삼인산(ATP) 합성의 기초가 되는 효소 메커니즘을 설명하기 위해"[161]
2003	로더릭 맥키넌	화학	"이온 채널의 구조적, 기계적 연구를 위해 세포막의 채널에 관한 발견을 위해 [...]"[162]
	피터 아그레		"수로 발견을 위한 세포막의 수로에 관한 발견[...]"[162]
2006	로저 D. 콘베르그	화학	"진핵생물 전사의 분자적 기초에 대한 그의 연구를 위해"[163]
2009	Ada E. Yonath	화학	"리보솜의 구조와 기능에 대한 연구를 위해"[164]
	토마스 A. 슈타이츠
	벤카트라만 라마크리슈난
2012	브라이언 코빌카	화학	"G-단백질 결합 수용체 연구용"[165]

참고 항목

참고문헌

더보기

국제결정표

제본된 물품 모음

교재

응용 전산 데이터 분석

히스토리컬

외부 링크

라이브러리 리소스 정보 X선 결정학

라이브러리의 리소스 다른 라이브러리의 리소스

자습서

• 결정학 배우기
• 단순한 비기술적 소개
• 영국왕실연구소의 '크리스탈로그라피 컬렉션', 비디오 시리즈
• Illinois Institute of Technology 웹사이트의 "Small Molecular Crystalization" (PDF)
• 국제 결정학 연합
• 결정학 101
• 2D 결정의 회절 패턴의 특성을 보여주는 대화형 구조 인자 튜토리얼.
• 2D로 결정과 회절 패턴의 관계를 보여주는 푸리에 변환의 그림책.
• X선 결정학 및 구조결정에 관한 강의 노트
• Richard J. Mattyi의 나노크기 재료해석을 위한 현대 X선 산란법 온라인 강의
• 영국 왕립 기관의 웨이백 기계에서 보관된 상호 작용 결정학 타임라인 2021-06-30

기본 데이터베이스

• COD(Crystalography Open Database)
• 단백질 데이터 뱅크(PDB)
• NDB(핵산데이터뱅크)
• 캠브리지 구조 데이터베이스
• 무기결정구조 데이터베이스
• 생체 고분자 결정화 데이터베이스

파생 데이터베이스

• PDBsum
• Proteopedia – 단백질 및 기타 분자의 협업 3D 백과사전
• RNABase
• Wayback Machine에서 보관된 PDB 리간드의 HIC-Up 데이터베이스 2020-08-08
• 단백질의 구조분류 데이터베이스
• CATH 단백질 구조 분류
• Wayback Machine에서 보관된 3D 구조가 알려진 막횡단 단백질 목록 2011-04-11
• 막 데이터베이스에서 단백질의 방향에 관한 연구

구조검증

• MolProbity 구조적 검증 제품군
• ProSA-web
• NQ-Flipper(Asn 및 Gln 잔기의 불리한 로타머 확인)
• DALI 서버(특정 단백질과 유사한 단백질 식별)