섬유 회절

섬유 회절은 산란의 하위 영역이며, 산란 데이터(일반적으로 X선, 전자 또는 중성자)로부터 분자 구조가 결정되는 영역입니다.섬유 회절에서는 샘플이 고유 축(섬유 축)을 중심으로 회전하기 때문에 산란 패턴이 변경되지 않습니다.이러한 단축 대칭은 생물학적 또는 인공 고분자로 구성된 필라멘트나 섬유에서 자주 발생한다.결정학에서 섬유대칭은 섬유회절 패턴에서 반사가 얼룩져 중복될 수 있기 때문에 결정구조의 결정에 관한 악화이다.재료 과학은 섬유 대칭을 단순화로 간주합니다. 왜냐하면 거의 완전한 구조 정보가 사진 필름 또는 2D 검출기에 노출되는 단일 2차원(2D) 회절 패턴에 있기 때문입니다.섬유 회절을 설명하려면 3개의 좌표 방향이 아닌 2개로 충분합니다.

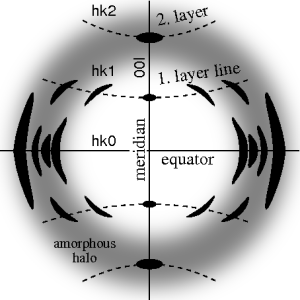
이상적인 섬유 패턴은 4 사분원 대칭을 나타냅니다.이상적인 패턴에서는 섬유축을 자오선이라고 하고 수직 방향을 적도라고 합니다.섬유 대칭의 경우, 단결정 회절보다 훨씬 더 많은 반사가 2D 패턴에 나타납니다.파이버 패턴에서는 이러한 반사가 적도에 거의 평행한 라인(레이어 라인)을 따라 명확하게 배열되어 있습니다.따라서 섬유 회절에서는 결정학의 층선 개념이 뚜렷해진다.레이어 라인이 구부러져 있는 경우는, 패턴을 똑바로 할 필요가 있는 것을 나타냅니다.반사는 밀러 지수 hkl(즉, 3자리)로 표시된다.i층 라인의 반사는 l=i를 공유한다.자오선에서의 반사는 00l-반사입니다.결정학에서 하나의 결정을 축을 중심으로 회전시킴으로써 인공섬유 회절 패턴을 생성한다(회전결정법).

실험에서 이상적이지 않은 섬유 패턴을 얻을 수 있다.그들은 자오선에 대한 거울 대칭만 보여준다.그 이유는 섬유축과 입사빔(X선, 전자, 중성자)이 서로 완전히 수직인 방향을 가질 수 없기 때문입니다.이에 대응하는 기하학적 왜곡은 마이클 폴라니에 의해 에발트의 구와 교차하는 폴라니의 구(독일어: "라겐쿠겔")의 개념을 소개하면서 광범위하게 연구되어 왔다.후에 로잘린드 프랭클린과 레이먼드 고슬링은 그들만의 기하학적 추론을 수행하였고 섬유 기울기 각도 β에 대한 근사 방정식을 제시하였다.분석은 파이버의 대표 평면에 왜곡된 2D 패턴을 매핑하는 것으로 시작됩니다.이것은 실린더 축을 상호 공간에 포함하는 평면입니다.결정학에서는 먼저 반복적으로 정제된 상호공간으로의 매핑 근사치를 계산한다.프레이저 보정이라고 불리는 디지털 방법은 틸트 각도 β에 대한 프랭클린 근사치부터 시작합니다.섬유 기울기를 제거하고 디텍터 이미지를 뒤틀리지 않으며 산란 강도를 보정합니다.β의 결정을 위한 올바른 방정식은 Norbert Stribeck에 의해 제시되었다.

역사적 역할

울이나 면과 같은 섬유질 재료는 정렬된 다발을 쉽게 형성하며, 1930년대 초에 특히 윌리엄 애스트베리에 의해 X선 회절에 의해 연구된 최초의 생물학적 고분자 중 하나였다.섬유 회절 데이터는 구조 생물학 개발에서 몇 가지 중요한 발전을 이끌었다. 예를 들어, α-나선의 원래 모델과 이중 가닥 DNA의 왓슨-크릭 모델이다.

섬유 회절 형상

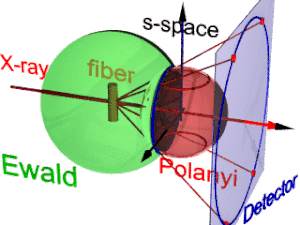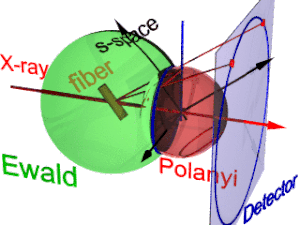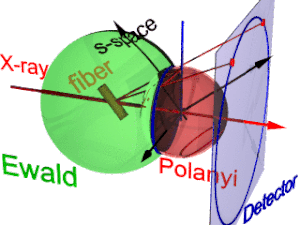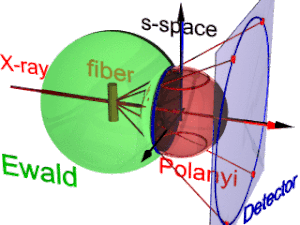
애니메이션은 섬유 회절의 기하학적 구조를 보여줍니다.그것은 폴라니가 제안한 개념에 기초하고 있다.기준 방향은 기본 빔(라벨: X선)입니다.섬유를 수직방향에서 각도β만큼 기울이면 그 역공간에서의 분자구조(s공간이라고 하는 3면체)에 관한 정보도 기울어진다.상호공간에서 에발트 구는 표본에 중심이 있다.반경은 1/µ이며 입사 방사선의 파장은 θ이다.에발트 구의 표면에서 검출기에 의해 보이는 모든 상호 공간의 점이 발견되었다.이러한 점은 중심 투영에 의해 디텍터의 픽셀에 매핑됩니다.

s-공간에서 각 반사는 폴라니-구에서 발견됩니다.본질적으로 이상적인 반사는 s-공간의 한 점이지만, 섬유대칭은 섬유방향에 대한 회전에 의해 얼룩진 링으로 변합니다.산란은 s-공간의 원점에 대해 점 대칭이기 때문에 두 개의 고리는 폴라니 구상의 각 반사를 나타냅니다.검출기에 매핑된 것은 에발트 구와 폴라니 구 둘 다에 있는 s-공간의 반사 지점뿐이다.이 점들은 반사원(파란색 고리)을 형성합니다.파이버가 기울어져 있기 때문에 변화하지 않습니다.슬라이드 프로젝터와 마찬가지로 반사 원은 검출기(검출기 원, 파란색 링)에 투영됩니다(빨간색 이동 광선).모니터링되는 반사의 영상(빨간색 반점)은 최대 4개까지 나타날 수 있습니다.반사 영상의 위치는 기본 빔의 섬유 방향 함수입니다(폴라니 방정식).반대로 Miller 지수 $h{\displaystyle }$ ${\displaystyle k}$ ${\displaystyle l}$$$\ $displaystyle hkl$${\displaystyle \mathrm{0<img\; alt="hkl"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/b11c00a7a2bb17351170f0ecbdcd61cd1581daf3"\; style="vertical-align:\; -0.338ex;\; width:3.243ex;\; height:2.176ex;">}}$0$$\ $displaystyle$h +$k$ \ $neq$ 0$$${\displaystyle \mathrm{0<img\; alt="|h|+|k|\backslash neq\; 0"\; aria-hidden="true"\; class="mwe-math-fallback-image-inline"\; src="https://wikimedia.org/api/rest\_v1/media/math/render/svg/19a3b5f4ae1f4abe501d4953bc3b9f4734605de3"\; style="vertical-align:\; -0.838ex;\; width:12.239ex;\; height:2.843ex;">}}$0 \ $displaystyle$ l \ neq 0$$0 0 \ $displaystyle$ l \ $neq$ 0 is$$${\displaystyle }$${\displaystyle h}$ 0 \ displaystyle l \ $neq$ 0 is 0 0 0 for for for for for for for for for for for for for for for for for for for for섬유회절기하학의 폴라니 표현에서 섬유매핑의 관계는 기본 및 구면기하학에 의해 확립된다.

패턴 보정

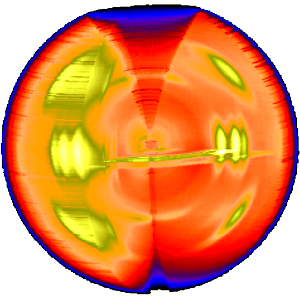
왼쪽 그림은 폴리프로필렌을 서로 다른 공간에 매핑하기 전에 일반적인 섬유 패턴을 보여줍니다.패턴의 미러 축은 수직 방향에 대해 각도$$(\$displaystyle ~\phi)$만큼$$ 회전합니다.이 단점은 그림을 단순 회전시킴으로써 보완된다.4개의 직선 화살표가 선택한 기준 반사의 4개의 반사 영상을 가리킵니다.이러한 위치는 파이버 틸트 $(\displaystyle\beta$를 결정하는 데 사용됩니다. 이미지는 CCD 검출기에 기록됩니다.의사 색 표현에서의 로그 강도를 나타냅니다.여기서 밝은 색상은 높은 강도를 나타냅니다.

β$(\displaystyle\beta)$ $결정$ 후 기준반사의 기존 결정학적 데이터를 사용하여 샘플과 검출기 사이의 거리를 계산하고, 상호공간의 대표섬유 평면에 대해 균일한 격자맵을 구축하여 이 맵에 회절데이터를 입력한다.오른쪽 그림에 결과가 나와 있습니다.비왜곡 과정에서 산란 강도 변화가 고려되었다.에발트 구의 표면 곡률 때문에 자오선에 흰 점이 남아 구조 정보가 누락되어 있습니다.영상 중앙과 산란 $각도{\displaystyle \mathrm{}}$ $(\displaystyle$ 2$\beta)$와 관련된 s-값에서만 자오선에 대한 구조 정보가 있습니다.물론, 지금은 4 사분원 대칭이 존재한다.즉, 패턴 예에서 누락된 정보의 일부가 흰색 영역에 "하반에서 상반부로" 복사될 수 있습니다.따라서 광섬유를 의도적으로 기울이는 것이 적절할 수 있습니다.

3차원 스케치는 이 실험에서 폴리프로필렌 섬유의 분자 구조에 대한 수집된 정보가 거의 완성되었음을 보여줍니다.자오선에 대한 평면 패턴의 회전에 의해 4초 동안 수집된 산란 데이터는 s-공간의 거의 구형 부피를 채운다.이 예에서 4 사분원 대칭은 아직 흰색 점의 일부를 채우는 것으로 간주되지 않았습니다.명확성을 위해 구체의 4분의 1을 잘라냈지만 적도면 자체는 그대로 유지한다.

레퍼런스

• Arnott S & Wonacott A J, X선 데이터와 입체화학적 제약을 이용한 고분자 분자 및 결정구조 개선, 고분자 1966 7 157 - 166
• Bianc W, Wang H, McCullogh I, Stubbs G (2006)"WCEN: 섬유 회절 패턴의 초기 처리를 위한 컴퓨터 프로그램"J. 애플 크리스털로그, 39, 752-756
• 1967년 2월 2일 옥스퍼드 대학교 화학결정학, Bunn C W
• Campbell Smith PJ & Arnott S, LALS 등액타 크리스탈로그르 1978 A34 3 - 11
• 코크란 W, 크릭 FHC, 반드 V(1952년).합성 폴리펩타이드 구조.I. 나선형 원자의 변환.액타 크리스탈로그르, 5, 581-586
• Donohue J, Trueblood, K N, 신뢰성 지수의 신뢰성에 대하여, Acta Crystalogr, 1956, 9, 615
• 프랭클린 RE, 고슬링 RG(1953) "나트륨 티모핵 섬유 구조"II. 원통 대칭 패터슨 기능".액타 크리스털로그르, 6, 678-685
• Fraser RDB, Macrae TP, Miller A, Rowlands RJ(1976)."섬유 회절 패턴의 디지털 처리"J. 애플 크리스털로그 9, 81-94
• Hamilton W C, R-Factors, Statistics and Truth, Paper H5, Amer Cryst Ass Program & Abstracts, 콜로라도 주 볼더, 1961년
• 해밀턴 W C, 결정학 R 인자에 대한 유의성 테스트, Acta Crystalogr 1965 18 502 - 510
• James T W & Mazia D, 디옥시리보핵산 표면 필름, 바이오킴 바이오피스 액타 1953 10 367 - 370
• 마빈 DA(2017) "생물 고분자의 섬유 회절 연구"프로그, 바이오피스 몰, 바이올 127, 43-87
• Millane RP, Arnott S(1985) "배향성 섬유로부터의 X선 회절 패턴의 디지털 처리"J. 마크로몰 Sci. Phys, B24, 193-227
• 폴라니 M(1921) "Das Röntgen-Faserdiagramm (Erste Mitteilung)"Z. Physik, 7, 149-180
• 폴라니 M, 바이센버그 K(1923) "Das Röntgen-Faserdiagramm (Zweite Mitteilung)"Z. Physik, 9, 123-130
• Rajkumar G, AL-Khayat H, Eakins F, He A, Knupp C, Squire J(2005) "파이버 픽스 - 새로운 통합 CCP13 소프트웨어 패키지", 파이버 회절판, 13, 11-18.
• Stribeck N(2009년)."섬유 회절에서의 섬유 기울기 각도 결정에 대하여" Acta Crystalogr, A65, 46-47

교재

• Alexander LE(1979) "폴리머 사이언스의 X선 회절법", 뉴욕주 와일리
• Klug HP, Alexander LE(1974) "다결정 및 비정질 재료용 X선 회절 절차", 뉴욕주 와일리, 제2판
• 워렌 BE(1990) "X선 회절"도버, 도버
• Saad Mohamed(1994) "싱크로트론 방사선 X선을 이용한 힘줄 내 콜라겐 결정 도메인의 저해상도 구조와 패킹 조사, 구조 인자 결정, 동형 치환 방법의 평가 및 기타 모델링"박사학위논문, Université Joseph Fourier Grenoble 1

외부 링크

• WCEN - 파이버 패턴 분석용 소프트웨어(Linux, Mac, Windows)
• 섬유 회절 - 하이델베르크의 Max Planck 의학 연구소 K.C. Holmes 교수에 의해 소개되었습니다.