단위세포

기하학, 생물학, 광물학, 고체 상태 물리학에서 단위 세포는 격자의 점들에 걸쳐 있는 벡터에 의해 형성된 반복 단위다.^[1] 그 선정적인 이름에도 불구하고, 단위 셀은 (예를 들어 단위 벡터와 달리) 반드시 단위 크기, 또는 심지어 특정한 크기를 가지고 있는 것은 아니다. 오히려 원시세포는 주어진 격자에 대해 정해진 크기를 가지고 있고 더 큰 세포가 형성되는 기본 구성블록이기 때문에 단위 벡터와 가장 가까운 유사점이다.

이 개념은 모든 차원에서는 이치에 맞지만 특히 수정 구조를 2차원과 3차원으로 기술하는데 사용된다. 격자는 단위 셀의 기하학적 구조로 특징지어질 수 있다. 단위 셀은 타일링(평행형 또는 병렬형)의 한 부분으로, 번역만 사용하여 전체 타일링을 생성한다.

단위세포에는 원시세포와 재래세포의 두 가지 특별한 경우가 있다. 원시세포는 단일 격자점에 해당하는 단위세포로 가능한 가장 작은 단위세포다. 어떤 경우에는 수정구조의 완전한 대칭이 원시 세포로부터 뚜렷하지 않은 경우도 있는데, 이 경우 재래식 세포가 사용될 수도 있다. 재래식 세포(원시적일 수도 있고 아닐 수도 있음)는 격자의 완전한 대칭을 가진 단위 세포로, 둘 이상의 격자점을 포함할 수 있다. 전통적인 단위 셀은 n차원으로 평행선이다.

원시세포

원시세포는 격자점 하나를 정확히 포함하는 단위세포다. 단위 셀의 경우 일반적으로 $n개$ 의 셀이 공유하는 격자점은 다음과 같이 계산된다. 각 셀에 포함된 격자 점의 1/ $n$ . 예를 들어 8개의 꼭지점에서만 격자 점을 갖는 3차원의 원시 단위 셀은 각 점의 1/8을 포함하는 것으로 간주된다.^[2] 대안 개념화는 주어진 단위 셀에 속할 $n$ 격자점 중 하나만 일관되게 선택하는 것이다(따라서 다른 $1-n$ 격자점은 인접한 단위 셀에 속한다).

원시번역 벡터는 $a \to, 1$ $a \to, 2$ $a \to 3$ 특정 3차원 격자에 대해 가장 작은 부피의 격자세포에 걸쳐 있으며, 결정번역 벡터를 정의하는데 사용된다.

{\vec{T}=u_{1}{\vec {a}_{1}+u_{2}}}{\vec{a}_{2}+u_{3}}}{\vec{a}_{3}

여기서 $u 1$ , $u 2$ , $u$ 는₃ 정수로, 번역은 격자를 불변하게 한다.^{[note 1]} 즉, $격자$ r의 한 점에 대해 점 $배열$ 이 r= = $r$ + $T \to$ $에서$ 와 동일하게 나타난다.^[3]

원시세포는 원시축(벡터) $a \to, 1$ $a \to, 2$ $a \to 3$ 에 의해 정의되기 때문에 원시세포의 체적 $V$ 는_p 위의 축에서 평행한 값으로 주어진다.

V_{\mathrm {p}}=\왼쪽 {\vec {a}_{1}\cdot({\vec {a}_{2}\time {\vec {a}_{3}\오른쪽 .

보통 2차원과 3차원의 원시세포는 세포의 각 모서리에 원자가 있는 평행고그램과 평행고엽의 형태를 취하기 위해 선택된다. 이러한 원시 세포의 선택은 독특하지 않지만, 원시 세포의 부피는 언제나 위의 표현에 의해 주어질 것이다.^[4]

위그너-세이츠 세포

평행한 원시 세포 외에도 모든 브라바 격자에는 위그너-세이츠 세포라고 불리는 또 다른 종류의 원시 세포가 있다. 위그너-세이츠 세포에서 격자 지점은 세포의 중심에 있으며, 대부분의 브라바이스 격자의 경우 형태가 평행사변형이나 평행사변형이 아니다. 이것은 보로노이 세포의 일종이다. 모멘텀 공간에 있는 상호 격자의 위그너-세이츠 셀은 브릴루인 존이라고 불린다.

재래식 세포

각각의 특정 격자에 대해, 계산의 편리성에 기초하여 결정학자에 의해 케이스 바이 케이스 베이스로 재래식 셀을 선택했다.^[5] 이러한 재래식 셀은 단위 셀의 면이나 본체의 중앙에 위치한 추가적인 격자점을 가질 수 있다. 재래식 셀의 부피뿐만 아니라 격자점 수도 원시 셀의 정수 배수(1, 2, 3 또는 4)이다.^[6]

2차원

평행사변형은 비행기의 일반적인 원시 세포다.

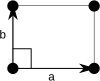
어떤 2차원 격자의 경우, 단위 셀은 평행그램이며, 특별한 경우 직교각 또는 길이가 같거나 둘 다일 수 있다. 5개의 2차원 브라바이스 격자 중 4개는 아래와 같이 전통적인 원시 세포를 사용하여 표현된다.

재래식 원시세포
도형 이름	평행사변형	직사각형	사각형	마름모꼴
브라바이스 격자	원시 사선	원시 직사각형	원시광장	원시 육각형

중심 직사각형 격자 역시 마름모꼴의 원시적인 세포가 있지만 대칭에 근거해 쉽게 구별할 수 있도록 두 개의 격자점을 가진 재래식 세포로 표현된다.

원시세포
도형 이름	마름모꼴
재래식 세포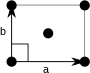
브라바이스 격자	중심 직사각형

삼차원

평행우주는 3차원 공간을 위한 일반적인 원시 세포다.

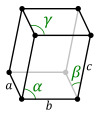
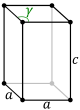
어떤 3차원 격자의 경우, 기존의 단위 셀은 평행하며, 특별한 경우 직교각 또는 길이가 같거나 둘 다일 수 있다. 3차원 브라바이스 격자 14개 중 7개는 아래와 같이 전통적인 원시 세포를 사용하여 표현된다.

재래식 원시세포
도형 이름	파랄레피프	사선 직사각형 프리즘	직사각형 큐빅	사각 큐보이드	삼각 사다리꼴	큐브
브라바이스 격자	원시 트리클린어	원시단백질	원시 정형외과	원시 4각형	원시 림보헤드랄	원시 큐빅	원시 육각형

다른 7개의 브라바이스 격자(중심 격자라고도 함)도 평행한 형태의 원시적인 세포를 가지고 있지만, 대칭에 근거하여 쉽게 구별할 수 있도록 하기 위해 둘 이상의 격자점을 포함하는 전통적인 세포로 표현된다.

원시세포
도형 이름	사선 롬빅 프리즘	우롬비크 프리즘
재래식 세포
브라바이스 격자	베이스 중심 단음계	베이스 중심 정형외과	신체중심 정형외과	얼굴 중심 정형외과	몸 중심 4각형	바디 중심 큐빅	얼굴 중심 큐빅

참고 항목

메모들

^ $n$ 치수에서 결정 변환 벡터는
${\vec{T}=\sum _{i}{\vec{a}_{i}{{i}}},\quad{\mbox{}{{}}\mathb {Z}\quad \all i.$
즉, $격자$ r의 한 점에 대해 점 $배열$ 이 r= = $r$ + $T \to$ $에서$ 와 동일하게 나타난다.

참조

^ Ashcroft, Neil W. (1976). "Chapter 4". Solid State Physics. W. B. Saunders Company. p. 72. ISBN 0-03-083993-9.
^ "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.
^ Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.
^ Mehl, Michael J.; Hicks, David; Toher, Cormac; Levy, Ohad; Hanson, Robert M.; Hart, Gus; Curtarolo, Stefano (2017). "The AFLOW Library of Crystallographic Prototypes: Part 1". Computational Materials Science. Elsevier BV. 136: S1–S828. arXiv:1806.07864. doi:10.1016/j.commatsci.2017.01.017. ISSN 0927-0256.
^ Aroyo, M. I., ed. (2016-12-31). "International Tables for Crystallography". International Tables for Crystallography. Chester, England: International Union of Crystallography. p. 25. doi:10.1107/97809553602060000114. ISBN 978-0-470-97423-0.
^ Ashcroft, Neil W. (1976). Solid State Physics. W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.

[first-3] $n$ 치수에서 결정 변환 벡터는
${\vec{T}=\sum _{i}{\vec{a}_{i}{{i}}},\quad{\mbox{}{{}}\mathb {Z}\quad \all i.$
즉, $격자$ r의 한 점에 대해 점 $배열$ 이 r= = $r$ + $T \to$ $에서$ 와 동일하게 나타난다.

[1] Ashcroft, Neil W. (1976). "Chapter 4". Solid State Physics. W. B. Saunders Company. p. 72. ISBN 0-03-083993-9.

[doitpoms-2] "DoITPoMS – TLP Library Crystallography – Unit Cell". Online Materials Science Learning Resources: DoITPoMS. University of Cambridge. Retrieved 21 February 2015.

[4] Kittel, Charles. Introduction to Solid State Physics (8 ed.). Wiley. p. 4. ISBN 978-0-471-41526-8.

[5] Mehl, Michael J.; Hicks, David; Toher, Cormac; Levy, Ohad; Hanson, Robert M.; Hart, Gus; Curtarolo, Stefano (2017). "The AFLOW Library of Crystallographic Prototypes: Part 1". Computational Materials Science. Elsevier BV. 136: S1–S828. arXiv:1806.07864. doi:10.1016/j.commatsci.2017.01.017. ISSN 0927-0256.

[6] Aroyo, M. I., ed. (2016-12-31). "International Tables for Crystallography". International Tables for Crystallography. Chester, England: International Union of Crystallography. p. 25. doi:10.1107/97809553602060000114. ISBN 978-0-470-97423-0.

[7] Ashcroft, Neil W. (1976). Solid State Physics. W. B. Saunders Company. p. 73. ISBN 0-03-083993-9.

[1]

[2]

[note 1]

[3]

[4]

[5]

[6]

Search

단위세포

네임스페이스

더

목차

원시세포

위그너-세이츠 세포

재래식 세포

2차원

삼차원

참고 항목

메모들

참조