전자 밀도

양자 화학에서, 전자 밀도 또는 전자 밀도는 주어진 점을 둘러싼 공간의 극소수 원소에 전자가 존재할 확률의 척도이다.이 값은 3개의 공간변수에 따른 스칼라 수치로 $보통{\displaystyle }$ "${\displaystyle }$(${\displaystyle r}$) \ $displaystyle \rho$( \ $textbf${ $r$} ) $nた$ 、${\displaystyle }$n (${\displaystyle r}$) \ $displaystyle$ n ( { \ $textbf${$r}$ )$$。밀도는 ${\displaystyle \mathrm{정규화}}$된 N($\mathrm{표시}$ 스타일 N) 전자파 함수에 의해 정의되며, 이 $함수$는$4N$$($$표시$ 스타일 $4N$) 변수$$(3N 공간 좌표$및{\displaystyle }$ N($표시$ 스타일$$$3N)$ 스핀$$ 좌표)에 $따라{\displaystyle \mathrm{}}$ 달라집니다.반대로 밀도는 위상인자까지의 파동함수모듈로를 결정하여 밀도함수이론의 형식적 기초를 제공한다.

양자역학에 따르면, 원자 규모의 불확실성 원리로 인해 전자의 정확한 위치를 예측할 수 없으며, 주어진 위치에 있을 확률만 있을 뿐이다. 따라서 원자와 분자의 전자는 마치 우주에서 "소멸된" 것처럼 작용한다.단일 전자 시스템의 경우, 임의의 지점의 전자 밀도는 파동 함수의 제곱 크기에 비례합니다.

정의.

$정규화$된 N$(\displaystyle$ N$)$ 전자파 함수$\delta {\displaystyle \mathrm{}}$(\$displaystyle \Psi$$)$에 해당하는 전자 밀도는 다음과 같이 정의된다^[1](r$\$ 및 $\displaystyle$s는 공간$$ $변수{\displaystyle }$ 및 스핀 변수를 나타낸다).

$\displaystyle \rho (\mathbf {r})=\Psi \Hat \rho }(\mathbf {r}) \Psi \rangle ,}$

여기서 관측 가능한 밀도에 해당하는 연산자는

$(\displaystyle {\hot {r}}(\mathbf {r})=\sum _{i=1}^{N}\sum (\mathbf {r} -\mathbf {r} _{i}).}$

$위$와 같이 ${\displaystyle (}$ ( ${\displaystyle r\mathbf{}}$) { $displaystyle \rho$( \$mathbf {r}$ )를$$ 계산하면 다음과 같이 식을 단순화할 수 있습니다.

${\displaystyle{\begin{정렬}\rho(\mathbf{r})&, =\sum _{{s}_{1}}\cdots(_{{s}_{N}}\int)\mathrm{d}\mathbf{r}_{1}\ \cdots \int)\mathrm{d}\mathbf{r}_{N}\ \left(\sum_{i=1}^{N}\delta(\mathbf{r}-\mathbf{r}_{나는})\right)\Psi(\mathbf{r}_{1},s_{1},\mathbf{r}_{2},s_{2},...,\mathbf{r}_{N},s_{N})^{2}\\&amp을 말한다.=N\sum _{{s}_{1}}\cdots \sum _{s}_{N}}\int \mathbrm {d} \mathbf {r} _{2} \cdots \int \mathrm {d} \mathbf {r} \Psi (\mathbf {r} , s_{1} , \mathbf {r} _{2} \cdots} \mathbf {r} _{n}$

$즉,$ 하나의 전자가 여전히 제 $위치$에$있는$ 상태로 유지되도록 다른 전자의 $가능$한 모든 배치를 합산합니다$.$인자 N은 모든 전자를 구별할 수 없기 때문에 발생하며, 따라서 모든 적분이 동일한 값으로 평가됩니다.

하트리에서는-Fock 및 밀도 함수 이론에서는 $일반적$으로 파동 함수는$$N$(\$$display$ style$$ N$)$ ${\displaystyle {오비탈}_{}}$ ater k(\$display style$ \$varphi$_$\{$k})로 $구성$된 단일 슬레이터 결정식으로 표현되며, 해당 직업 ${\displaystyle n_{}}$k$(\$$display$ style $n_{k$에서 밀도는 다음과 같이 단순화된다.

$\displaystyle \rho (\mathbf {r})=\sum _{k=1}^{N_{k} \varphi _{k}(\mathbf {r})^{2}.}$

일반 속성

정의상, 전자 밀도는 전자 총수에 통합된 음이 아닌 함수이다.또한 운동 에너지 T를 가진 시스템에서는 밀도가 부등식을^[2] 만족한다.

${\displaystyle {frac {1}{2}}\int \mathbrm {r}\nabla {sqrt {rho(\mathbf {r})}{\leq T}$

$\displaystyle {\frac {3}{2}}\left({\frac {pi }{2}\rft(\int \mathrm {d}\mathbf {r}\rho ^3}(\mathbf {r}\right)^1/3\leq T}.$

유한한 운동 에너지에서, 첫 번째 (더 강한) 부등식은 밀도의 제곱근을 소볼레프 $H$ ($R$3)에 배치합니다. 정규화 $및 비음성과$ 함께 이것은 물리적으로 허용되는 밀도를 포함하는 공간을 다음과 같이 정의합니다.

$\displaystyle {\mathcal {J}}_{\rho \left \rho (\mathbf {r} )\geq 0,\rho ^{1/2}(\mathbf {R})\in H^{1}(\mathbf {R} ^{3}),\int \mathbf {\mathbf} \mathbf} \mathbf} \rf {\rf} \rf} \rf} \rmathbf} \rm {\r}\right\}.}$

두 번째 부등식은 L 공간에 밀도를 배치합니다³.정규화 특성과 ${\displaystyle {함께}_{}}$ JN(\$displaystyle\mathcal {J}}_{N$의 슈퍼셋인 L과³ L의 교차점¹ 내에 허용 밀도를 배치합니다.

토폴로지

원자의 기저 상태 전자 밀도는 ^[3]핵으로부터의 거리의 단조롭게 붕괴하는 함수로 추측된다.

핵교두부 조건

전자 밀도는 무한 전자-핵 쿨롱 전위의 결과로 분자의 각 핵에 쿠스를 표시합니다.이 동작은 Kato cusp 조건에 의해 정량화됩니다.이 조건은 다음과 같이 주어진 핵에^[4] 대해 구면 평균 밀도인 $\delta {\displaystyle \stackrel{}{}}$δ ${\displaystyle \stackrel{}{（}}$ \ $displaystyle$\$bar$\$rho }$） 。

$(\displaystyle\왼쪽).{frac}{\bar r_{\alpha}}{\bar {rho }}(r_{\alpha })\right _{r_{\alpha }=-2Z_{\alpha }{\bar {\rho }}}}}(0).}$

즉, 임의의 핵에서 평가된 평균 밀도의 방사형 도함수는 원자 번호의 음수를 곱한 핵 밀도(${\displaystyle }$\$display Z)$의 2배와 같다.

점근 거동

핵교점 조건은 다음과 같이 핵에 가까운 밀도($small$r\$displaystyle$ r$)$ 거동을 제공합니다.

$\displaystyle \rho (r)\sim e^{-2Z_{\alpha }r},}$

밀도의 장거리($큰{\displaystyle }$ r$\display style$ r$)$ 거동도 알려져 있습니다^[5].

${\displaystyle \rho (r)\sim e^{-2\sqrt {2\mathrm {I}}}r},}$

여기서 I는 시스템의 이온화 에너지입니다.

응답 밀도

밀도의 또 다른 일반적인 정의는 "선형 반응 밀도"^[6][7]입니다.이는 스핀 프리(spin-free)의 1전자 연산자와 계약했을 때 에너지의 도함수로 정의된 관련 특성을 산출하는 밀도이다.예를 들어 다이폴 모멘트는 외부 자기장에 대한 에너지의 도함수이며 파동함수에 대한 연산자의 기대치가 아니다.일부 이론에서는 파동 함수가 수렴될 때 같은 값을 갖습니다.직업 번호는 0에서 2까지의 범위로 제한되지 않으며,^[8] 따라서 응답 밀도조차 공간의 특정 영역에서 음수일 수 있습니다.

개요

분자에서, 큰 전자 밀도의 영역은 보통 원자 주변과 원자 결합 주변에서 발견됩니다.페놀, 벤젠 및 헤모글로빈 및 클로로필과 같은 화합물과 같은 탈국소화 또는 켤레 시스템에서 전자 밀도는 전체 영역에서 유의하다. 즉 벤젠에서 이들은 평면 고리 위와 아래에 발견된다.이것은 때때로 일련의 단일 결합과 이중 결합으로 도식화됩니다.페놀 및 벤젠의 경우, 육각형 내부의 원은 화합물의 탈국재성을 나타낸다.이것은 다음과 같습니다.

서로 연결된 다중 링 시스템을 가진 화합물에서는 더 이상 정확하지 않으므로 단일 결합과 이중 결합을 번갈아 사용합니다.클로로필 및 페놀과 같은 화합물에서는 일부 도표는 단일 ^[9]결합 옆에 전자 밀도가 높은 영역의 비국재화를 나타내는 점선 또는 점선을 나타낸다.복합 시스템은 때때로 다른 파장에서 전자기 복사가 흡수되어 착색된 화합물이 나타나는 영역을 나타낼 수 있습니다.폴리머에서, 이 영역들은 색소체로 알려져 있다.

양자화학적 계산에서 전자밀도 θ(r)는 좌표 r의 함수이며, 따라서 θ(r)dr은 소량 dr 내의 전자수이다.닫힌 껍질 분자의 경우,$$θ ( r ) \ $displaystyle \rho (\mathbf {r}$ )는 기본 함수의 곱의 합으로 $\theta {\displaystyle }$:

$\displaystyle \rho (\mathbf {r})=\sum _{\nu }P_{\mu \nu }\phi _{\mathbf {r}\phi _{\nu }(\mathbf {r})$

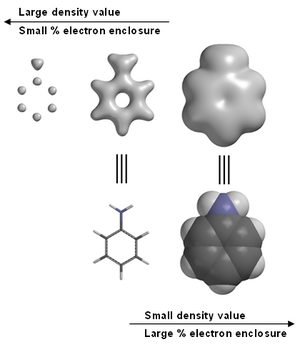
여기서 P는 밀도 행렬입니다.전자 밀도는 종종 선택한 밀도 값 또는 둘러싸인 총 전자 비율에 따라 결정되는 표면의 크기와 모양을 가진 등각면(등각도 표면)으로 표현된다.

분자 모델링 소프트웨어는 종종 전자 밀도의 그래픽 이미지를 제공합니다.예를 들어 아닐린(오른쪽 이미지 참조)입니다.전자 밀도를 포함한 그래픽 모델은 화학 ^[10]교육에서 일반적으로 사용되는 도구입니다.아닐린의 왼쪽 끝 이미지에서 높은 전자 밀도는 탄소 및 질소와 관련되지만 핵에 양성자가 하나만 있는 수소는 보이지 않는다.X선 회절이 수소 위치를 찾는 데 어려움을 겪는 이유다.

대부분의 분자 모델링 소프트웨어 패키지는 사용자가 종종 Iso 값이라고 불리는 전자 밀도 값을 선택할 수 있도록 합니다.일부^[11] 소프트웨어는 또한 둘러싸인 총 전자의 백분율로 전자 밀도를 지정할 수 있습니다.이소값(일반적인 단위는 입방체당 전자) 또는 둘러싸인 총 전자의 비율에 따라 전자 밀도 표면이 원자의 위치를 지정하거나 화학 결합과 관련된 전자 밀도를 강조하거나 전체 분자 크기와 ^[12]모양을 나타내기 위해 사용될 수 있습니다.

그래픽으로 볼 때, 전자 밀도 표면은 다른 전자 특성을 표시할 수 있는 캔버스로도 기능한다.정전 전위 맵(전자 밀도에 매핑된 정전 전위의 특성)은 분자 내 전하 분포를 나타내는 지표입니다.국소 이온화 전위 맵(전자 밀도에 매핑된 국소 이온화 전위 특성)은 전자 친화성의 지표이다.그리고 LUMO 지도(전자 밀도에 매핑된 가장 낮은 빈 분자 궤도)는 친핵성을 ^[13]나타내는 지표가 될 수 있다.

실험

많은 실험 기술들이 전자 밀도를 측정할 수 있다.예를 들어 적절한 파장의 X선을 시료를 대상으로 하고 시간이 지남에 따라 측정을 하는 X선 회절주사를 통한 양자결정학은 전자의 위치를 확률적으로 나타낸다.이러한 위치에서 분자 구조는 종종 결정화된 시스템에 대해 정확한 전하 밀도 분포와 함께 결정될 수 있다.양자 전기 역학 및 양자 이론의 일부 부문은 전자 밀도를 사용하여 비공유 상호작용을 연구할 수 있는 NCI 지수 같은 전자 중첩 및 기타 관련 현상을 연구하고 분석합니다.멀리켄 인구 분석은 분자의 전자 밀도에 기초하고 원자 간 밀도를 분할하여 원자 전하의 추정치를 제공하는 방법입니다.

투과전자현미경법(TEM)과 깊은 비탄성 산란 및 기타 고에너지 입자 실험에서 고에너지 전자는 전자 구름과 상호작용하여 전자 밀도를 직접 나타냅니다.TEM, 주사 터널링 현미경법(STM) 및 원자력 현미경법(AFM)을 사용하여 ^{[citation needed]}특정 개별 원자의 전자 밀도를 조사할 수 있습니다.

스핀 밀도

스핀 밀도는 유리기에 적용되는 전자 밀도입니다.이것은 한 스핀의 전자의 총 전자 밀도에서 다른 스핀의 전자의 총 전자 밀도를 뺀 것으로 정의됩니다.이를 실험적으로 측정하는 방법 중 하나는 전자 스핀 ^[14]공명에 의한 것이며, 중성자 회절은 3D 공간에서 스핀 밀도를 직접 매핑할 수 있습니다.

「 」를 참조해 주세요.

• 차분 밀도 맵
• 전자 구름
• 전자 구성
• 해상도(전자 밀도)
• 전하 밀도
• 밀도 함수 이론
• 확률 전류

레퍼런스