상자 그림
Box plot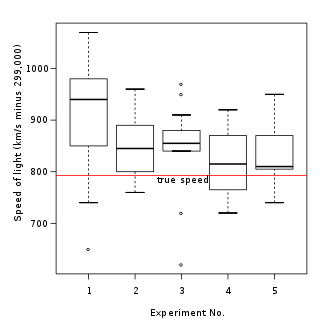
기술 통계량에서 상자 그림 또는 상자 그림은 숫자 데이터의 지역, 산포 및 왜도 그룹을 사분위수에 [1]걸쳐 그래픽으로 보여주는 방법입니다.상자 그림의 상자 외에도 상자로부터 연장된 선(구레나룻이라고 함)이 있을 수 있으므로 상자-구레나룻 그림 및 상자-구레나룻 다이어그램이라고도 합니다.나머지[2] 데이터 집합과 유의하게 다른 특이치는 상자 그림의 수염을 벗어난 개별 점으로 표시될 수 있습니다.상자 그림은 모수가 아닙니다. 기본 통계 분포에[3] 대한 가정을 하지 않고 통계 모집단의 표본에서 변동을 표시합니다(Tukey의 상자 그림은 수염에 대한 대칭성을 가정하고 길이에 대한 정규성을 가정함).상자 그림의 각 하위 섹션에 있는 공백은 데이터의 분산(확산) 및 왜도를 나타내며, 일반적으로 5개 숫자 요약을 사용하여 설명합니다.또한 상자 그림을 사용하면 사분위간 범위, 중간징, 범위, 중간 범위 및 트리만 등 다양한 L-추정자를 시각적으로 추정할 수 있습니다.상자 그림은 수평 또는 수직으로 그릴 수 있습니다.
역사
거리 막대 방법은 메리 엘리노어 스피어가 1952년 그녀의[4] 저서 "통계 차트 작성"에서 처음 소개했고 [5]1969년 그녀의 책 "실제 차트 작성 기술"에서 다시 소개했습니다.박스 앤 수염 플롯은 나중에 [6]1977년 그의 책 "탐색 데이터 분석"에서 이 주제에 대해 발표한 존 투키에 의해 1970년에 처음 소개되었다.
요소들
상자 그림은 최소값, 최대값, 표본 중위수 및 1사분위수와 3사분위수의 5개 숫자 요약을 기반으로 데이터 집합을 표시하는 표준화된 방법입니다.
- 최소값(Q0 또는 0번째 백분위수): 특이치를 제외한 데이터 집합에서 가장 낮은 데이터 점
- 최대값(Q4 또는 100번째 백분위수): 특이치를 제외한 데이터 집합에서 가장 높은 데이터 점
- 중위수(Q2 또는 50번째 백분위수): 데이터 집합의 중간 값
- 첫 번째 사분위수(Q1 또는 25번째 백분위수): 하위 사분위수n q(0.25)라고도 하며 데이터 집합의 하위 절반의 중앙값입니다.
- 제3 사분위수(Q3 또는 75번째 백분위수): 상위n 사분위수 q(0.75)라고도 하며 데이터 [7]집합의 상위 절반의 중앙값입니다.
상자 그림을 구성하는 데 사용되는 최소값과 최대값 외에 상자 그림을 얻는 데 사용할 수 있는 또 다른 중요한 요소는 다음과 같이 사분위간 범위(IQR)입니다.
- 사분위간범위(IQR) : 상위 사분위수와 하위 사분위수 사이의 거리
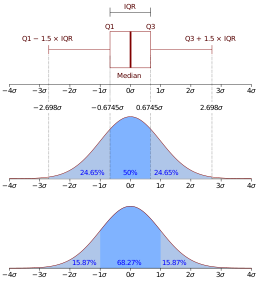
상자 그림에는 일반적으로 그림 2와 같이 상자 하나와 수염 세트가 포함됩니다.이 상자는 Q에서13 Q로 그려지며 가운데에 수평선이 그려져 중위수를 나타냅니다.수염은 다양한 방법으로 정의할 수 있습니다.
가장 간단한 방법에서 아래쪽 수염의 경계가 데이터 세트의 최소값이고 위쪽 수염의 경계가 데이터 세트의 최대값이다.
수염 경계에 대한 또 다른 일반적인 선택은 1.5 IQR 값을 기반으로 합니다.상위 사분위수(Q3) 위에서 IQR의 1.5배 거리를 측정하고 이 거리 내에 있는 데이터 집합에서 가장 큰 관측 데이터 지점까지 수염을 그립니다.마찬가지로 IQR의 1.5배 거리를 하위 사분위수(Q1) 아래로 측정하고 이 거리 내에 있는 데이터 집합에서 가장 낮은 관측 데이터 지점까지 수염을 끌어다 놓습니다.수염은 관측된 데이터 점에서 끝나야 하므로 수염 길이는 양쪽의 IQR이 동일하더라도 같아 보일 수 있습니다.수염 경계 외부에 있는 다른 모든 관측 데이터 점은 [8]특이치로 표시됩니다.특이치는 상자 그림에 점, 작은 원, 별 등으로 표시할 수 있습니다.
그러나 수염은 다음과 같은 몇 가지 다른 의미를 나타낼 수 있습니다.
- 데이터 세트의 최소값과 최대값(그림 2 참조)
- 데이터 집합의 평균보다 위와 아래에 있는 하나의 표준 편차
- 데이터 세트의 9번째 백분위수 및 91번째 백분위수
- 데이터 세트의 두 번째 백분위수 및 98번째 백분위수
드물게 수염 없이 상자 그림을 표시할 수 있습니다.
일부 상자 그림에는 [9][10]데이터의 평균을 나타내는 추가 문자가 포함되어 있습니다.
특이 백분위수 2%, 9%, 91% 및 98%는 7개 숫자 요약을 나타내기 위해 수염 교차 해치와 수염 끝에 사용됩니다.데이터가 정규 분포를 따르는 경우 상자 그림에 있는 7개의 표시 위치가 동일한 간격으로 표시됩니다.일부 상자 그림에서는 각 수염 끝 전에 교차 해치가 배치됩니다.
이러한 변동성으로 인해 상자 그림의 캡션에서 수염과 특이치에 사용되는 관례를 설명하는 것이 적절합니다.
바리에이션
수학자 존 W부터요 Tukey는 1969년에 이러한 유형의 시각적 데이터 디스플레이를 처음 보급했으며, 고전적인 상자 그림에 대한 여러 변형들이 개발되었으며, 가장 일반적으로 발견되는 두 가지 변형은 그림 4에 나온 가변 폭 상자 그림과 노치 상자 그림이다.
가변 폭 상자 그림은 상자의 너비를 그룹의 크기에 비례시켜 데이터가 플롯되는 각 그룹의 크기를 나타냅니다.일반적인 관습은 상자 [11]너비를 그룹 크기의 제곱근에 비례시키는 것입니다.
노치 상자 그림은 상자 중앙값 주위에 "노치" 또는 좁혀진 상자를 적용합니다.노치는 중위수 차이의 유의성에 대한 대략적인 지침을 제공하는 데 유용합니다. 두 상자의 노치가 겹치지 않으면 중위수 [11]사이에 통계적으로 유의한 차이가 있다는 증거를 제공합니다.노치 폭은 표본의 사분위간 범위(IQR)에 비례하며 표본 크기의 제곱근에 반비례합니다.그러나, 가장 적절한 승수에 대한 불확실성이 있다(이것은 [11]표본 분산의 유사성에 따라 달라질 수 있기 때문이다).
이러한 노치의 경계를 구하는 규칙 중 하나는 [12]중앙값 에 ± 1. IQR\pm \{ IQR {n의 거리를 사용하는 것이다.
수정된 상자 그림은 치우침 분포를 설명하기 위한 것으로 치우침의 [13]중위수 통계량에 의존합니다.MC의 중간값 값의 경우 상자 그림에서 위 및 아래 수염의 길이는 각각 다음과 같이 정의됩니다.
대칭 데이터 분포의 경우 중간 쌍은 0이 되며, 이렇게 하면 양쪽 수염에 대해 한 수염 길이 1.5(\ 1.5{IQR의 Tukey 상자 플롯으로 조정된 상자 플롯이 감소합니다.
바이올린 그림 및 콩 그림과 같은 다른 종류의 상자 그림에서는 원래 고전 상자 [6]그림에서는 관찰할 수 없는 단일 모달 분포와 다중 모달 분포의 차이를 나타낼 수 있습니다.
예
특이치가 없는 예제
하루 종일 시간당 기온이 화씨로 측정되었다.기록된 값은 57, 57, 57, 58, 63, 66, 66, 67, 68, 69, 70, 70, 70, 70, 70, 70, 72, 73, 75, 76, 76, 78, 79, 81의 순서로 나열되어 있습니다.
데이터 세트의 상자 그림은 먼저 이 데이터 세트의 관련 값인 최소값, 최대값, 중위수(Q2), 제1 사분위수1(Q) 및 제3 사분위수(Q3)를 계산하여 생성할 수 있습니다.
최소값은 데이터 세트의 최소값입니다.이 경우 기록된 최소 낮 온도는 57°F입니다.
최대값은 데이터 집합의 최대 수입니다.이 경우 기록된 최대 낮 온도는 화씨 81도입니다.
중위수는 순서가 지정된 데이터 집합의 "중간" 숫자입니다.즉, 원소의 50%가 중위수보다 작고 50%가 중위수보다 크다는 것을 의미합니다.이 정렬된 데이터 세트의 중앙값은 70°F입니다.
첫 번째 사분위수 값(Q1 또는 25번째 백분위수)은 순서가 지정된 데이터 세트의 1/4을 표시하는 숫자입니다.즉, 1 사분위수보다 작은 원소는 정확히 25%, 1 사분위수보다 큰 원소는 정확히 75%가 있습니다.첫 번째 사분위수 값은 최소값과 중위수 사이의 "중간값"을 찾으면 쉽게 구할 수 있습니다.시간당 온도의 경우 57°F와 70°F 사이의 "중간" 수치는 66°F입니다.
세 번째 사분위수 값(Q3 또는 75번째 백분위수)은 순서가 지정된 데이터 집합의 3/4을 표시하는 숫자입니다.즉, 3분위수보다 작은 원소는 정확히 75%, 3분위수보다 큰 원소는 25%입니다.세 번째 사분위수 값은 중위수와 최대값 사이의 "중간" 숫자를 찾으면 쉽게 얻을 수 있습니다.시간당 온도의 경우 70°F와 81°F 사이의 "중간" 숫자는 75°F입니다.
사분위간 범위(IQR)는 3분위수 값(Q3)에서 1분위수 값(Q1)을 빼서 계산할 수 있습니다.
1. 5 F .\ 1.text {
제3 사분위수 이상의 1.5 IQR은 다음과 같다.
제1 사분위수 이하의 1.5 IQR은 다음과 같다.
상자 그림의 수염 상한은 세 번째 사분위수 위의 1.5 IQR 내에 있는 가장 큰 데이터 값입니다.여기서, 제3 사분위수 위의 1.5 IQR은 88.5°F이고, 최대값은 81°F이다.따라서 위쪽 수염은 최대값인 81°F에서 그려집니다.
마찬가지로 상자 그림의 수염 하한은 첫 번째 사분위수 아래의 1.5 IQR 내에 있는 가장 작은 데이터 값입니다.여기서, 제1 사분위수 아래의 1.5 IQR은 52.5°F이고, 최소는 57°F이다.따라서 아래쪽 수염은 최소값인 57°F에서 그려집니다.
특이치가 있는 예제
위는 특이치가 없는 예제입니다.다음은 특이치가 있는 상자 그림을 생성하는 추적 예제입니다.
기록된 온도 순서는 (°F): 52, 57, 57, 58, 63, 66, 66, 67, 68, 69, 70, 70, 70, 70, 70, 70, 72, 73, 75, 76, 76, 78, 79, 89 입니다.
이 예에서는 첫 번째와 마지막 번호만 변경됩니다.중위수, 3분위수 및 1분위수는 동일하게 유지됩니다.
이 경우, 이 데이터 세트의 최대값은 89°F이고, 3분위수 이상의 1.5 IQR은 88.5°F입니다.최대값은 1.5 IQR + 3 사분위수이므로 최대값은 특이치입니다.따라서 위쪽 수염은 79°F인 3분위수 위의 1.5 IQR보다 작은 최대값으로 그려집니다.
마찬가지로, 이 데이터 세트의 최소값은 52°F이고, 1분위 이하 1.5 IQR은 52.5°F이다.최소값은 IQR 1.5에서 1분위수를 뺀 값보다 작으므로 최소값도 특이치입니다.따라서 낮은 수염은 첫 번째 사분위수인 57°F 아래의 1.5 IQR보다 작은 값으로 그려집니다.
대규모 데이터셋의 경우
다수의 데이터 점을 포함하는 데이터 집합에서 상자 그림을 얻는 추가 예는 다음과 같습니다.
경험적 분위수를 계산하기 위한 일반 방정식
- 서x (k) { x { () } here points here ( ( ( k、 x( )< ) \ x { ( ) } < (k ) } 。
24개의 데이터 점(n = 24)이 있는 위의 예제를 사용하면 수학적으로나 시각적으로 1사분위수와 3사분위수의 중위수를 계산할 수 있습니다.
: n () ( + (.5 - ) ( ( ) - ( 70+ ( 25 ) ( -70) 70 F {{n} ( 0.5 ) = + 0 cdot - cd 25 25 25 ot 25 . 5 ot 25 . 5 cd
제1 : n (.25 )+ (25 -) + ( 25- ) F { _ n } () _ { - 25 25 } ( ) 。
제3 : n ( (+ (25 - )+ ( 25- ) 75F { () ( 25.75)
시각화
상자 그림은 히스토그램이나 커널 밀도 추정치보다 더 원시적으로 보일 수 있지만 여러 가지 장점이 있습니다.첫째, 상자 그림을 사용하면 통계학자가 하나 이상의 데이터 세트에 대해 간단한 그래픽 검사를 수행할 수 있습니다.상자 그림은 공간을 적게 차지하므로 여러 그룹 또는 데이터 집합 간의 분포를 병렬로 비교할 때 특히 유용합니다(예는 그림 1 참조).마지막으로 히스토그램의 전체 구조와 커널 밀도 추정은 각각 빈 기술의 수와 폭의 선택과 대역폭의 선택에 의해 강하게 영향을 받을 수 있다.
상자 그림을 보는 것보다 통계 분포를 보는 것이 더 일반적이지만, 상자 그림을 정규 N(0,θ2) 분포에 대한 확률 밀도 함수(이론 히스토그램)와 비교하여 그 특성을 직접 관찰하는 것이 유용할 수 있습니다(그림 7 참조).
「 」를 참조해 주세요.
레퍼런스
- ^ C., Dutoit, S. H. (2012). Graphical exploratory data analysis. Springer. ISBN 978-1-4612-9371-2. OCLC 1019645745.
- ^ Grubbs, Frank E. (February 1969). "Procedures for Detecting Outlying Observations in Samples". Technometrics. 11 (1): 1–21. doi:10.1080/00401706.1969.10490657. ISSN 0040-1706.
- ^ Richard., Boddy (2009). Statistical Methods in Practice : for Scientists and Technologists. John Wiley & Sons. ISBN 978-0-470-74664-6. OCLC 940679163.
- ^ Spear, Mary Eleanor (1952). Charting Statistics. McGraw Hill. p. 166.
- ^ Spear, Mary Eleanor. (1969). Practical charting techniques. New York: McGraw-Hill. ISBN 0070600104. OCLC 924909765.
- ^ a b Wickham, Hadley; Stryjewski, Lisa. "40 years of boxplots" (PDF). Retrieved December 24, 2020.
- ^ Holmes, Alexander; Illowsky, Barbara; Dean, Susan (31 March 2015). "Introductory Business Statistics". OpenStax.
- ^ Dekking, F.M. (2005). A Modern Introduction to Probability and Statistics. Springer. pp. 234–238. ISBN 1-85233-896-2.
- ^ Frigge, Michael; Hoaglin, David C.; Iglewicz, Boris (February 1989). "Some Implementations of the Boxplot". The American Statistician. 43 (1): 50–54. doi:10.2307/2685173. JSTOR 2685173.
- ^ Marmolejo-Ramos, F.; Tian, S. (2010). "The shifting boxplot. A boxplot based on essential summary statistics around the mean". International Journal of Psychological Research. 3 (1): 37–46. doi:10.21500/20112084.823.
- ^ a b c McGill, Robert; Tukey, John W.; Larsen, Wayne A. (February 1978). "Variations of Box Plots". The American Statistician. 32 (1): 12–16. doi:10.2307/2683468. JSTOR 2683468.
- ^ "R: Box Plot Statistics". R manual. Retrieved 26 June 2011.
- ^ Hubert, M.; Vandervieren, E. (2008). "An adjusted boxplot for skewed distribution". Computational Statistics and Data Analysis. 52 (12): 5186–5201. CiteSeerX 10.1.1.90.9812. doi:10.1016/j.csda.2007.11.008.
추가 정보
- Tukey, John W. (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 9780201076165.
- Benjamini, Y. (1988). "Opening the Box of a Boxplot". The American Statistician. 42 (4): 257–262. doi:10.2307/2685133. JSTOR 2685133.
- Rousseeuw, P. J.; Ruts, I.; Tukey, J. W. (1999). "The Bagplot: A Bivariate Boxplot". The American Statistician. 53 (4): 382–387. doi:10.2307/2686061. JSTOR 2686061.






 Tukey 상자 플롯으로 조정된 상자 플롯이 감소합니다.
Tukey 상자 플롯으로 조정된 상자 플롯이 감소합니다. 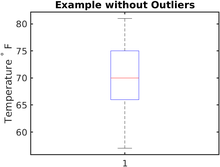






![{\displaystyle {\text{with }}k=[p(n+1)]{\text{ and }}\alpha =p(n+1)-k}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c7fe0c9d05a9554dfbbd8dee8a39f0d779c1d39)






