B 스플라인

이 문서에는 여러 가지 문제가 있습니다.개선을 돕거나 토크 페이지에서 이러한 문제에 대해 논의해 주십시오.(이러한 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 문서의 선두 부분을 다시 써야 할 수 있습니다. 리드 레이아웃 가이드를 사용하여 섹션이 Wikipedia의 규범을 준수하고 모든 필수 세부사항을 포함하도록 하십시오. (2014년 8월) (이 템플릿 메시지 삭제 방법과 시기에 대해 알아보기) 이 기사는 대부분의 독자들이 이해하기에는 너무 전문적일 수 있다. 기술적인 세부사항을 삭제하지 않고 비전문가가 이해할 수 있도록 개선해 주세요.(2022년 1월) (이 템플릿메시지를 삭제하는 방법과 타이밍에 대해 설명합니다) 이 글은 검증을 위해 추가 인용문이 필요합니다. 신뢰할 수 있는 출처에 인용문을 추가하여 이 기사를 개선하는 데 도움을 주십시오. 조달되지 않은 자재는 제거될 수 있습니다.출처 : "B-spline" – 뉴스 · 신문 · 서적 · 학자 · JSTOR (2022년 1월) (이 템플릿 메시지 삭제 방법 및 삭제 시기 확인) (이 템플릿메시지를 삭제하는 방법과 타이밍을 확인합니다)

수치분석의 수학적 서브필드에서 B-스플라인 또는 베이스 스플라인은 주어진 정도, 평활도 및 도메인 분할에 대해 최소한의 지지를 갖는 스플라인 함수이다.주어진 정도의 스플라인 함수는 그 정도의 B 스플라인의 선형 조합으로 표현될 수 있다.카디널 B 스플라인은 서로 등거리에 있는 매듭을 가지고 있다.B 스플라인은 실험 데이터의 곡선 적합 및 수치 미분에 사용할 수 있습니다.

컴퓨터 지원 설계 및 컴퓨터 그래픽스에서 스플라인 함수는 제어점 세트를 가진 B 스플라인의 선형 조합으로 구성된다.

서론

"B-스플라인"이라는 용어는 Isaac Jacob Schoenberg에^[1] 의해 만들어졌으며 기본 스플라인의 ^[2]줄임말이다.$순서$ n${$displaystyle $n{\displaystyle }$$}$의 스플라인 함수는 변수$$x({$displaystyle$x$\})$에서$({displaystyle n-1})$의 구간별 다항식 함수입니다.조각들이 만나는 곳을 매듭이라고 한다.스플라인 함수의 핵심 특성은 매듭의 승수에 따라 스플라인 함수와 그 도함수가 연속적일 수 있다는 것이다.

$순서$$n$의 B 스플라인은 동일한 매듭에 걸쳐 정의된 동일한 순서의 스플라인 함수에 대한 기본 함수입니다. 즉, 가능한 모든 스플라인 함수는 B 스플라인의 선형 조합에서 생성될 수 있으며 각 스플라인 ^[3]함수에 고유한 조합은 하나만 있습니다.

정의.

$순서$ n$(\displaystyle$n$$)의 스플라인은 $변수{\displaystyle }$x(\$displaystyle$x$)$에서$(\displaystyle n-1)$의 구간별 다항식 함수입니다.다항식 조각이 만나는 x$({displaystyle$x})의$$ $값$은 매듭이라고 하며 t ${\displaystyle {0\mathrm{}}_{}}$ ${\displaystyle {}_{}}$ ${\displaystyle {1\mathrm{}}_{}}$,${\displaystyle {}_{}}$t ${\displaystyle {2\mathrm{}}_{}}$,${\displaystyle \dots ,}$ ${\displaystyle {}_{}}$ $({$로 나타나며 비감소 순서로 정렬됩니다.매듭이 구별되면 다항식 $조각$의 첫 $번째{\displaystyle }$n - $2$도함수가$$ 각 매듭에 걸쳐 연속됩니다.$\displaystyle$r노트가$$ 일치하면 스플라인의 첫 $번째{\displaystyle }$ n${\displaystyle }$-${\displaystyle r}$ - ${\displaystyle 1}$ ${\displaystyle n-r-1}$ 도함수만$$ 해당 노트에 걸쳐 연속됩니다.

주어진 매듭 시퀀스에 대해 스케일링 팩터까지 고유한 $스플라인{\displaystyle {}_{}}$ ${\displaystyle B_{}}$ i${\displaystyle {,}_{}{n}_{}}$ (${\displaystyle x}$ $){display style$ B_${i,n}(x)}$가 충족됩니다.

${\displaystyle B_{i,n}(x)=begin{case}0&{\text{if}}x<t_{i}{\text{i+n},\{\text{non-zero}}}&{\text{\text{case}}}}}.\end {case}}$

첫 번째 매듭과 마지막 매듭 사이에 $모든{\displaystyle }$x(\$displaystyle$ x$)$에 대해${\displaystyle \underset{\theta }{}}$ ${\displaystyle \underset{}{}{}_{}}$ B${\displaystyle i_{}}$ ,${\displaystyle {}_{}{n}_{}}$ (${\displaystyle x}$ ) ${\displaystyle =}$ { $displaystyle \sum$ _ ${i$} $B$_ {i , n } ( x ) $= 1$이라는 추가 구속조건을 더하면 ${\displaystyle {Bi}_{}}$ ${\displaystyle {,}_{}}$ ${\displaystyle n_{}}$(${\displaystyle }$x$$) { $displaystyle$ B $_ i$ , $n$} ($x$ )의$$ $스케일{\displaystyle {}_{}}$ 팩터가 고정됩니다.결과적으로 $생성$되는${\displaystyle B_{}}$ ${\displaystyle i_{}}$ ${\displaystyle n}$($$x ) { $displaystyle B_{i,n}(x$)} 스플라인$$ 함수를 B 스플라인이라고 합니다.

또는 B-스플라인은 Cox-de Boor 재귀 공식에 의한 구조에 의해 정의될 수 있다.매듭 시퀀스${\displaystyle \dots ,}$ ${\displaystyle {t\mathrm{}}_{}}$ 0${\displaystyle {}_{}}$ ${\displaystyle {}_{}{}_{}}$1, ${\displaystyle {t\mathrm{}}_{}}$2$…({displaystyle \ldots, t_{0}, t_{1}, t_{2},$ \$ldots$를 지정하면 순서1의 B 스플라인은 다음과 같이 정의됩니다.

${\displaystyle B_{i,1}(x):=param{case}1&{\text{if}}t_{i}\leq x<t_{i+1},\0&{\text{param}}.\end {case}}$

모든$x{\displaystyle }$(\$displaystyle$x)에$$ ${\displaystyle \underset{}{}{}_{}}$ 1${\displaystyle {}_{}x)}$ ${\displaystyle =}$(\$displaystyle \sum$ _${i}B_{i,1}(x$)=1}을$($를) 충족합니다$.$ $왜냐하면{\displaystyle }$ x(\$displaystyle$ x$)$의 $경우{\displaystyle {}_{}{}_{}}$1${\displaystyle (\mathrm{x}}$) $=$ 1(\$displaystyle$B_${i,1}(x$) $=1$및 기타 모든 x$)$ 중 하나이기 때문입니다.

고차 B 스플라인은 재귀에 의해 정의됩니다.

${\displaystyle B_{i,k+1}(x):=\obega _{i,k}(x)B_{i,k}(x)+[1-\obega _{i+1,k}(x)]B_{i+1,k}(x),}$

어디에

$\displaystyle \obega _{i,k}(x):=param{case}{\dfrac {x-t_{i}}{t_{i+k}-t_{i}}},&t_{i+k}\neq t_{i},\0&{\text{i}}}}}.\end {case}}$

특성.

B-스플라인 함수는 제어점이라고 하는 여러 점에 의해 제어되는 유연한 대역의 조합으로 부드러운 곡선을 만듭니다.이러한 기능은 여러 점을 사용하여 복잡한 모양과 표면을 만들고 관리하는 데 사용됩니다.B-스플라인 함수와 Bézier 함수는 형상 최적화 ^[4]방법에 광범위하게 적용된다.

$n$의 B 스플라인$({displaystyle$ n})은 변수$$x({$displaystyle$ x$\})$의$({$displaystyle $n-1})$의 구간별 다항식 함수입니다.이것은${\displaystyle 1}$ + n$(\displaystyle$$t_{j$의 위치 ${\displaystyle {tj}_{}}$(노트 또는 브레이크 포인트)에 $걸쳐{\displaystyle \mathrm{}}$ 정의됩니다.이러한 값은 $내림차순$이 아닌 ${\displaystyle {tj}_{}}$ ${\displaystyle {}_{}{}_{}{t}_{}}$j$$+ $(\$$leq t_{j+1})$이어야 합니다.B 스플라인은 이들 노트의 첫 번째와 마지막 범위에서만 기여하며 그 이외의 경우에는 0입니다.각 매듭이 이전 매듭과 동일한 $거리{\displaystyle }$h({$displaystyle$ h})($$$여기$서 ${\displaystyle {}_{}}$ ${\displaystyle =t_{}}$ ${\displaystyle {\mathrm{j}}_{}}$ +${\displaystyle {}_{}{}_{}}$ -$$t ${\displaystyle j_{}}$ {$displaystyle$ h$=t_{j+1}-t_{j$만큼 떨어져 있으면 매듭 벡터와 대응하는 B-스플라인은 "displaystyle h$"($아래 B-spline 참조)라고 합니다.

0이 아닌 각 유한 매듭 간격에 대해 B 스플라인은 n${\displaystyle }$-$1$의$$$다항식$입니다. B 스플라인은 ^{[note 1]}매듭의 연속 함수입니다.B-스플라인에 속하는 모든 매듭이 구별될 경우, 그 도함수${\displaystyle }n{\displaystyle }$-$$$2$ 도함수까지 연속되며, 주어진 $값{\displaystyle }$x {\$displaystyle$ x$\}$에서 매듭이 일치할 경우 추가로 일치할 때마다 도함수의 연속성이 1씩 감소한다.B 스플라인은 매듭의 서브셋을 공유할 수 있지만 정확히 동일한 매듭에 대해 정의된 2개의 B 스플라인은 동일합니다.즉, B 스플라인은 매듭에 의해 고유하게 정의됩니다.

하나는 내부 매듭과 끝점을 구분합니다.내부 매듭이 x$(디스플레이 스타일$ x$)$ $도메인$을 덮고 있습니다.단일 B 스플라인은 이미 1${\displaystyle }$+$$(\$displaystyle$ 1$+n)$노트$$ $이상$으로 확장되어 있으므로 내부 매듭 간격에 영향을 미치는 첫 번째 및 마지막 B 스플라인을 완전히 지지하기 위해 내부 매듭을 양쪽에 n${\displaystyle }$-$$(\$displaystyle n-1)$개의$$ 엔드 $포인트$로 확장해야 합니다.엔드포인트의 값은 중요하지 않습니다.일반적으로 첫 번째 또는 마지막 내부 매듭만 반복됩니다.

B 스플라인의 유용성은 주어진 매듭 집합에서 순서$n$의$스플라인$ 함수가 B 스플라인의 선형 조합으로 표현될 수 있다는 데 있습니다.

$\displaystyle S_{n,\mathbf {t}}(x)=\sum _{i}\alpha _{i}B_{i,n}(x)}$

B-스플라인은 스플라인 함수 공간에 대한 기본 함수의 역할을 수행하므로 이 이름은 다음과 같습니다.이 특성은 모든 조각이 ^[5]매듭에서 개별 지지 범위 내에서 동일한 연속성 특성을 가지고 있다는 사실에서 비롯됩니다.

다항식 조각의 식은 Cox-de Boor 재귀^[6] 공식에 의해 도출될 수 있다.

${\displaystyle B_{i,0}(x):=param{case}1&{\text{if}}t_{i}\leq x<t_{i+1},\0&{\text{param}}.\end {case}}$

${\displaystyle B_{i,k}(x):=param frac {x-t_{i}{t_{i+k}-{i}}B_{i,k-1}(x)+{\frac {t_{i+k+1}-t_{i+k1}-{i+1}}B_{i+1,k-1}(x)}(x)}$

$즉{\displaystyle {}_{}}$, B${\displaystyle j_{}}$ ,${\displaystyle {}_{}0}$ (${\displaystyle }$x $)({displaystyle B_{j,0}(x$)}은$$(not span j가 반복되는 경우 0) 어떤 not span x가 있는지 나타내는 간격상 상수 1 또는0입니다.재귀 방정식은 다음 두 부분으로 나뉩니다.

$({displaystyle {x-t_{i}}{t_{i+k}-t_{i}}})$

x가 $(\$에서 $(\$로 이동하면 0에서1로 램프가 바뀝니다.

${\displaystyle {t_{i+k+1}-x}{t_{i+k+1}-t_{i+1}}}}$

x가 ${\displaystyle {ti}_{}}$ ${\displaystyle {+}_{}}$ $({$에서 ${\displaystyle {ti}_{}}$ ${\displaystyle {+k}_{}}$ +$$({$displaystyle t_{i+k+1$로 이동하면 1에서0으로 바뀝니다.대응하는 B는, 각각의 범위외에서는 제로입니다.$예$를 들어 ${\displaystyle B_{}}$ i${\displaystyle {,}_{}}$ ${\displaystyle 1_{}}$(${\displaystyle x}$ )$$({$displaystyle B_{i,1$$}($$x)}$은 x ${\displaystyle =}$ ${\displaystyle {ti}_{}}$ ${$$style$ $x=t_$${i$$}}$보다 $작은{\displaystyle }$$$ 삼각형 함수이며 x ${\displaystyle =}$ $ti$ ${\displaystyle {+}_{}}$${\displaystyle 1_{}}$에서 $1$로 램프하고 x ${\displaystyle =}$ ${\displaystyle {t+}_{}}$$i$ +$display$2에서 $다시{\displaystyle }$ 0으로 램프합니다.그러나 B-스플라인 기준 함수는 로컬 지원이 있기 때문에 B-스플라인은 일반적으로 de Boor 알고리즘과 같이 0인 경우 기본 함수를 평가할 필요가 없는 알고리즘에 의해 계산됩니다.

이 관계는 FORTRAN 코드화 알고리즘 BSPLV로 직접 이어지며,^[7] B-스플라인 값은 x에서 n차 값을 생성합니다.다음 방법은 각 순서 n이 왼쪽 순서 n - 1의 B 스플라인 조각의 선형 조합인 방법을 보여 줍니다.

${\displaystyle {begin{matrix}&0&\0&B_{i-2,2}&\B_{i-1,1}&B_{i-1,2}&B_{i,1}&B_{i,1}&B_{i,0}&B_{i,0}&B_{i,0}&B_{i}&0}&0}&0&B_{i}&0&0&0&B_{i}$

( ${\displaystyle 0}$,${\displaystyle 1}$,${\displaystyle 2}$, ${\displaystyle 3}$)$${$displaystyle (0, 1, 2$, 3$)}$의 매듭을 가진${\displaystyle }$재귀 공식을 적용하면 순서 3의 균일한 B 스플라인 조각을 얻을 수 있습니다.

$디스플레이 스타일B_{1}&=x^{2}/2,&0&\leq x <1,\B_{2}&=sq2x{2}+6x-3)/2,&1&\leq x<2,\B_{3}&=(3-x)^{2}/2,\leq x3.\end { aligned}}$

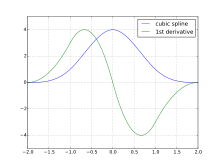
이 조각들은 다이어그램에 나와 있습니다.내부 매듭에서 2차 스플라인 함수와 그 첫 번째 도함수의 연속성 특성은 다음과 같이 설명된다.

${\displaystyle {begin{aligned}&{\text}}x=1\text\B_{1}=0.5,\{frac {dB_{1}{dx}=1.\\[6pt]&{\text{At}}}x=2\text\B_{2}=B_{3}=0.5,\\{frac {dB_{2}}{dx}=bcfrac {dB_{3}{dx}}=-1.\end { aligned}}$

2차 B-스플라인의 두 번째 도함수는 매듭에서 불연속이다.

${\displaystyle {d^{2}B_{1}}{dx^{2}=1, {\frac {d^{2}B_{2}=-2, {\frac {d^{2}B_{3}}{dx^{2}=-1.}$

de Boor 알고리즘의 더 빠른 변형이 제안되었지만,^[8][9] 비교적 낮은 안정성으로 인해 어려움을 겪고 있다.

추기경 B-스플라인

기본 B 스플라인은 매듭 사이에 일정한 간격 h를 가진다.주어진 순서 n에 대한 기본 B 스플라인은 서로 이동된 복사본입니다.그것들은 더 간단한 ^[10]정의에서 얻을 수 있다.

${\displaystyle B_{i,n,t}(x)=param frac {x-t_{i}{h}}n[0,\display,n](\cdot -t_{i})_{+}^n-1}.}$

"플레이스 홀더" 표기법은 2개의 변수 t와 x의 함수$({\displaystyle t}$-${\displaystyle {}_{}^{}x{}_{}^{}}$) +${\displaystyle {}_{}^{}}$ -$$ { $displaystyle (t-x)_{+}^n-1}$의 n번째 나눗셈 차이가 x를 고정하고${\displaystyle }$(${\displaystyle t{}_{}^{}}$- x${\displaystyle {)}_{}^{}}$+ ${\displaystyle {}_{}^{}}$- ${\displaystyle 1_{}^{}}$ { $displaystyle (t-x)$_{+}^{$n-1}}$의 함수만으로${\displaystyle }$간주됨을 나타내기 위해 사용됩니다.

기본 B 스플라인은 균일한 간격의 매듭을 가지므로 매듭 사이의 보간은 평활 커널에 의한 회전과 같다.

예를 들어 B 스플라인 노드 사이에 3개의 값($\$을 보간하는 경우 신호를 다음과 같이 쓸 수 있습니다.

$\displaystyle \mathbf {x} = [\mathbf {b} _{1},0,0,\mathbf {b} _{2},0,0,0,\mathbf {b} _{3},0,\mathbf {b} _{n},0,0}.}$

직사각형 $함수{\displaystyle \mathbf{}}$ h ${\displaystyle =}$ [${\displaystyle 1}$ /${\displaystyle 3\mathrm{}}$,${\displaystyle 1}$ / ${\displaystyle 3\mathrm{}}$ , 1${\displaystyle }$/ ${\displaystyle 3\mathrm{}]}$ ${{$ $displaystyle$ \$mathbf {h} =$ [ $1$/ 3$, 1$/ $3$}}의$$ $신호{\displaystyle \mathbf{}}$x {\ $displaystyle$\ $mathbf {x}}$의 제곱은 1차 보간 B-스플라인 값을 제공합니다.2차 B-스플라인 보간은 직사각형 함수의 ${\displaystyle 2회\mathbf{}}$ y ${\displaystyle =}$ ${\displaystyle x\mathbf{}}$h ${\$ h = \ $display$style \ $mathbf${ y } * \ $mathbf {$ h } * \ $mathbf {$ h $}$에서의 합성이며, 직사각형 함수에 의한 반복 필터링에 의해 고차 보간을 얻을 수 있다.

균일한 샘플 도메인에서의 고속 B 스플라인 보간은 반복 평균 필터링을 통해 수행할 수 있습니다.또는 직사각형 함수는 푸리에 영역에서 sync와 같다.따라서 큐빅 스플라인 보간은 푸리에 영역의 신호에⁴ sync를 곱하는 것과 같습니다.

차수 1~4의 B-스플라인에 대한 대수식은 Irwin-Hall 분포 #특수를 참조하십시오.

P 스플라인

P-spline이라는 용어는 "페널라이즈된 B-spline"을 나타냅니다.이는 계수가 부분적으로 적합될 데이터에 의해 결정되고 부분적으로 ^[11]과적합을 방지하기 위해 평활성을 부과하는 것을 목적으로 하는 추가 패널티 함수에 의해 결정되는 B-스플라인 표현을 사용하는 것을 말한다.

데이터의 2차원 및 다차원 P 스플라인 근사에서는 행렬의 ^[12]면 분할 곱을 사용하여 계산 연산을 최소화할 수 있다.

파생 표현식

k도의 B-스플라인의 도함수는 k - ^[13]1도의 B-스플라인의 함수이다.

${\displaystyle {dB_{i,k}(x)}{dx}=k\left({\frac {B_{i,k-1}(x)}-{\frac {B_{i+1,k-1}(x)}-{\frac {B_{i+i-1}}-{t}-{t}-{t+i_i-1}{t}}}$

이는 을 암시한다.

${\displaystyle {frac {d}\sum _{i}\alpha _{i,k}=\sum _{i=r-k+2}^{s-1}k frac {i}-\alpha _{i-1}{t_{i+k}-t_{i}}B_{i,{text-qu}$

이는 스플라인 함수의 도함수와 1도가 적은 B-스플라인 사이에 단순한 관계가 있음을 보여준다.

일변량 B-스플라인의 모멘트

단변량 B 스플라인, 즉 매듭 위치가 단일 치수에 있는 B 스플라인은 1-d 확률 밀도 $함수{\displaystyle }$ p$)\displaystyle$ p$(x$)\displaystyle p(x$)\backslash$displaystyle n\display n\displine 기본$$ 함수의 $가중치{\displaystyle }$ 합계를 나타낼 수 있으며, 각 영역 정규화된 순서$n{\displaystyle }$(\$displaystyle$ n$)$에 대한 i$\style$ i$\$style basispline 기본 함수의 합입니다.즉, 표준 de-Boor 알고리즘을 사용하여 직접 평가되지 않음)

$\displaystyle p(x)=\sum _{i}c_{i}\cdot B_{i,n,{\textbf {norm}}(x)}$

정규화 상수 제약 ${\displaystyle \underset{}{조건}}$ $\sum {\displaystyle \underset{}{}}$ ${\displaystyle \underset{}{}{}_{}}$ c ${\displaystyle i_{}}$ ${\displaystyle {}_{}}$ { $displaystyle \sum$ _${i} c_{i$} $= 1$ $\}$ 。정규화된 B $스플라인{\displaystyle {}_{}}$ B ${\displaystyle {i,}_{}}$ $,$ ${\displaystyle {\mathbf{\text{norm}}}_{}}$ {$displaystyle B_{i, n,$ {\$textbf {norm}}}$의 k번째 원시 $모멘트{\displaystyle {}_{}}$ ${\displaystyle {\mu }_{}}$k {$displaystyle$ \$mu$_{k$$}}}}는 Carlson의 ${\displaystyle {Dirichlet}_{}}$ $평균{\displaystyle {}_{}}$ R$k$ {\$displaystyle$R_$\{$^[14]k}}}로 표기할 수 있으며, 이는 반복 적분으로서 정확하게 풀 수 있다.

$(\displaystyle \mu _{k}=R_{k}(\mathbf {m};\mathbf {t})=\int _{-\infty}^{k}\cdot B_{i,n,{\textbf {}})(x\mid t_{1}\cdma_{j})Frac=Fr,$

와 함께

${\displaystyle D_{k}=sum frac {1}{k}\sum _{u=1}^{k}\left[\sum \sum _ {i=1}^{j}m_{i}\cdot {t_{u}\right]D_{k-u}\right]$

${\displaystyle {및\mathrm{}}_{}}$ D 0 $=$ {\$displaystyle D_{0$}=$1$ 여기서$$t {\$displaystyle \mathbf$${$$t}$는 j$${\$displaystyle$ j$$$}$ $매듭{\displaystyle }$ 위치의 벡터$,$ $m{\displaystyle \mathbf{}}$ {\$displaystyle$ \$mathbf$ {m$}$은 각 매듭 배수의 벡터입니다.따라서 수치 기법에 의존하지 않고 B 스플라인 기준 함수의 합으로 표현되는$$ 확률 밀도 $함수{\displaystyle }$ p$(x)$의 모멘트를 정확하게 계산할 수 있다.

조각별/복합 베지어와의 관계

Bézier 곡선은 또한 동일한 클래스의 낮은 도 곡선으로부터의 재귀를 사용하여 정의할 수 있고 제어점 측면에서 인코딩될 수 있는 다항식 곡선이지만, 주요 차이점은 Bézier 곡선 세그먼트에 대한 재귀의 모든 항이 동일한 정의 영역(일반적으로 $[{\displaystyle 0,}$1$]\displaystyle [0,1])$을 갖는 반면, 다음과 같은 정의 영역을 갖는다는 것입니다.B-스플라인 재귀의 두 항이 서로 다릅니다(가장 바깥쪽 부분 간격은 일반적이지 않습니다).즉, m${\displaystyle n}$n { $displaystyle$m \ g $n$$$} $제어점$에서 주어진 bézier $곡선{\displaystyle }$n { $displaystyle n$}은${\displaystyle }대부분{\displaystyle }$ 독립된 세그먼트로 구성되며, 같은 파라미터를 가진 B 스플라인은 서브인터벌에서 서브인터벌로 원활하게 이행합니다.베지어 곡선에서 비슷한 것을 얻으려면 세그먼트 간 전환에 평활도 조건을 부과하여 베지어 스플라인(많은 제어점은 평활도 요건에 따라 결정됨)을 생성해야 한다.

분할/복합 베지어 곡선은 적어도 C0 연속성으로 결합된 일련의 베지어 곡선입니다(한 곡선의 마지막 점이 다음 곡선의 시작점과 일치합니다).용도에 따라 평활도 요건(C1 또는 C2 연속성 등)이 ^[16]추가될 수 있습니다.C1 연속형 곡선은 중단점(두 곡선이 만나는 지점)에서 접선이 동일합니다.C2 연속 곡선은 중단점에서 ^[17]동일한 곡률을 가집니다.

곡선 피팅

일반적으로 곡선 적합에서 데이터 점 집합은 일부 수학 함수에 의해 정의된 곡선으로 적합됩니다.예를 들어, 일반적인 유형의 곡선 적합은 다항식 또는 지수 함수 집합을 사용합니다.적합 함수를 선택하는 이론적 근거가 없는 경우 최소 ^{[18][note 2]}제곱법을 사용하여 B 스플라인의 합으로 구성된 스플라인 함수를 곡선에 적합시킬 수 있습니다.따라서 최소 제곱 최소화를 위한 목적 함수는 k도 스플라인 함수의 경우,

$\displaystyle U=\sum _{\text{all}~x}\left\{W(x)\left[y(x)-\sum _{i}\alpha _{i}B_{i,k,t}(x)\right]\right\{2}$

여기서 W(x)는 가중치이고 y(x)는 x의 기준값입니다.${\displaystyle {계수\alpha }_{}}$ i$\$ _${i}$는 결정해야 할 파라미터이다.매듭 값은 고정되거나 매개 변수로 처리될 수 있습니다.

이 프로세스를 적용할 때 가장 큰 어려움은 사용할 매듭의 수와 배치 위치를 결정하는 것입니다.de Boor는 이 문제를 해결하기 위한 다양한 전략을 제안합니다.예를 들어 데이터의 ^{[citation needed]}곡률(2도함수)에 비례하여 매듭 사이의 간격을 줄인다.몇 가지 응용 프로그램이 공개되었습니다.예를 들어 단일 로렌츠 곡선과 가우스 곡선을 맞추기 위해 B-스플라인을 사용하는 것이 조사되었습니다.5, 6, 7노트의 대칭 배열에 기초한 3~7도의 최적 스플라인 함수를 계산했으며, 스펙트럼 ^[19]곡선의 평활화 및 분화에 이 방법을 적용했다.유사한 연구에서, 사비츠키-골레이 필터링의 2차원 버전과 스플라인 방법은 이동 평균 또는 체비셰프 ^[20]필터링보다 더 나은 결과를 도출했다.

컴퓨터 지원 설계 및 컴퓨터 그래픽스

컴퓨터 지원 설계 및 컴퓨터 그래픽스 애플리케이션에서 스플라인 곡선은 실제 $파라미터{\displaystyle }$t${$$displaystyle$ t$\}$의$파라메트릭$ 곡선인 C$)$로 나타나기도 합니다.이 경우 C(t)\$displaystyle$ C($t)$는 두 개 또는 세 개의 개별 좌표 함수$({\displaystyle x)}$로 취급할 수 있습니다.${\displaystyle y}$(${\displaystyle t}$)$${ $displaystyle ( x$${\displaystyle }$($t$ ) ,${\displaystyle y}$$$(${\displaystyle }$t${\displaystyle }$)$$,${\displaystyle z}$(${\displaystyle t}$ )$$} $。\{{\displaystyle }$ $displaystyle ( x$ ($t$ ) , $y$( $t$) , z ( t ) $}$。$좌표{\displaystyle }$ $함수{\displaystyle }$ x${\displaystyle }$( ${\displaystyle t}$) {$displaystyle$ x$(t)}$,${\displaystyle }$y ( ${\displaystyle t}$) {$displaystyle$ y$(t)}$ 및$$${\displaystyle }z{\displaystyle }$ (${\displaystyle t}$) {$displaystyle z$$(t)}$는 $각각$ 스플라인 함수이며, 매듭 $값{\displaystyle {}_{}}$ ${\displaystyle {t1\mathrm{}}_{}}$ $}, t_2},$ \$ldots, t_n$의 공통 집합입니다.

B-스플라인은 기저 함수를 형성하기 때문에, 각 좌표 함수는 B-스플라인의 선형 합계로 표현될 수 있습니다. 그래서 우리는

${\displaystyle {begin{aligned}X(t)&=_{i}x_{i}B_{i}Y_{i}B_{i}(t),\Z(t)&=_sum_i}z_{i}(T){i},{i}.\end { aligned}}$

$무게{\displaystyle {}_{}}$ ${\displaystyle x_{}}$ i$($${\displaystyle i_{}}$}), y$($${i$}), ${\displaystyle z_{}}$ i$($ i${\displaystyle {}_{}}$ ${\displaystyle y_{}}$, $)$의 3차원 공간에 점 $Pi =$ ($x$i,$y, z_{i})$를 형성할 수 있습니다.이러한 $포인트{\displaystyle {}_{}}$ $($ P_${i$})는$$ 일반적으로 컨트롤 포인트라고 불립니다.

반대로 작업하면 일련의 제어점, 매듭 값 및 B-스플라인 순서가 모수 곡선을 정의합니다.제어점에 의한 곡선의 이 표현에는 다음과 같은 유용한 특성이 있습니다.

1. 컨트롤 $포인트{\displaystyle {}_{}}$ $($ P_${i$})는$$ 곡선을 정의합니다.아핀 변환에 의해 변환, 회전, 스케일링 또는 이동되는 등 제어점이 모두 함께 변환되는 경우 해당 곡선은 동일한 방식으로 변환됩니다.
2. B 스플라인은 한정된 수의 매듭 간격에 대해서만 0이 아니므로 단일 제어점이 이동하면 모수 곡선에 대한 해당 변경은 작은 수의 매듭 간격의 매개변수 범위 바로 위에 있습니다.
3. ${\displaystyle \underset{}{i}}{\displaystyle \underset{}{}{}_{}}$ B${\displaystyle i_{}}$ ,${\displaystyle {}_{}n}$ (${\displaystyle }$x ) $=$ ${\displaystyle 1}${ $displaystyle \sum$ _${i,n}(x$${\displaystyle )=}$$1$ 및 $항상{\displaystyle {}_{}}$ ${\displaystyle B_{}}$i ,${\displaystyle {}_{}{n}_{}}$ (${\displaystyle x}$ ) )$$ { $displaystyle B$_ {$i$, $n$} ($x$)\$geq$ 0$\}$ 이므로 곡선은 제어점의 경계 상자 안에 남습니다.또한 어떤 의미에서 곡선은 제어점을 대체로 따릅니다.

모수 곡선이 제어점을 보간하지 않는 것이 바람직하지 않습니다.일반적으로 곡선은 제어점을 통과하지 않습니다.

누르다

컴퓨터 지원 설계, 컴퓨터 지원 제조 및 컴퓨터 그래픽스에서 B 스플라인의 강력한 확장은 NURBS(Non-Uniform real B-splines)입니다.NURBS는 본질적으로 동종 좌표의 B 스플라인입니다.B 스플라인과 마찬가지로 순서, 매듭 벡터 및 제어점 집합으로 정의되지만 단순 B 스플라인과 달리 제어점에는 각각 가중치가 있습니다.가중치가 1인 경우, NURBS는 단순히 B 스플라인이며, 따라서 NURBS는 B 스플라인과 Bézier 곡선 및 표면을 일반화한다. 주요 차이점은 NURBS 곡선을 "합리적으로" 만드는 제어점의 가중치이다.

파라미터의 다양한 값에서 NURBS를 평가함으로써 곡선을 공간을 통해 추적할 수 있습니다. 마찬가지로 두 파라미터의 다양한 값에서 NURBS 표면을 평가함으로써 표면을 데카르트 공간으로 나타낼 수 있습니다.

B-스플라인과 마찬가지로 NURBS 제어점이 곡선의 모양을 결정합니다.곡선의 각 점은 다수의 제어점의 가중치 합계를 취함으로써 계산된다.각 점의 가중치는 지배 모수에 따라 달라집니다.d도 곡선의 경우 모수 공간의 d+1 구간(노트 범위)에서 제어점의 영향은 0이 아닙니다.이 구간 내에서 가중치는 d도의 다항함수(기본함수)에 따라 변화한다.구간의 경계에서는 기본함수가 0으로 부드럽게 진행되며 평활도는 다항식의 정도에 따라 결정된다.

매듭 벡터는 제어점이 NURBS 곡선에 영향을 미치는 위치와 방법을 결정하는 일련의 파라미터 값입니다.노트의 수는 항상 제어점 수에 곡선 각도를 더한 값과 같습니다.파라미터 값이 새로운 매듭 범위에 들어갈 때마다 새로운 제어점이 활성화되고 오래된 제어점은 폐기됩니다.

NURBS 곡선의 형식은 ^[21]다음과 같습니다.

${\displaystyle C(u)=paramfrac {sum _{i=1}^{k}N_{i,n}(u)w_{i}P_{i}}{\sum_{i=1}^{k}N_{i,n}(u)w_{i}}}}$

여기 표기법은 다음과 같습니다.u는 독립 변수(x 대신), k는 제어점 수, N은 B-스플라인(B 대신 사용), n은 다항식 정도, P는 제어점, w는 가중치입니다.분모는 모든 가중치가 1인 경우 1로 평가되는 정규화 요인입니다.

이것을 이라고 쓰는 것이 관례이다.

${{displaystyle C(u)=\sum _{i=1}^{k}R_{i,n}(u)P_{i}}$

그 기능이

${\displaystyle R_{i,n}(u)=param frac {N_{i,n}(u)w_{i}}{\sum _{j=1}^{k}}N_{j,n}(u)w_{j}}}}$

는 합리적 기초함수로 알려져 있습니다.

NURBS 표면은 두 개의 NURBS 곡선의 텐서 곱으로 구해지므로 두 개의 독립적인 매개변수 ^[22]u와 v(각각 지수 i와 j)를 사용한다.

${\displaystyle S(u,v)=\sum _{i=1}^{k}\sum _{j=1}^{\ell}R_{i,j}(u,v)P_{i,j}$

와 함께

${\displaystyle R_{i,j}(u,v)=pfrac {N_{i,n}(u)N_{j,m}(v)w_{i,j}{sum_{p=1}^{\ell}{\ell}N_{p,n}(u){m}{m}{w}{w}{m}$

합리적인 기초 함수로서.

「 」를 참조해 주세요.

• 베지에 곡선
• 박스 스플라인
• 드부르 알고리즘
• I 스플라인
• M 스플라인
• 스플라인 웨이브릿
• T스플라인

메모들

레퍼런스

인용된 작품

• Carl de Boor (1978). A Practical Guide to Splines. Springer-Verlag. ISBN 978-3-540-90356-7.
• Piegl, Les; Tiller, Wayne (1997). The NURBS Book (2nd. ed.). Springer. ISBN 978-3-540-61545-3.

추가 정보

• Richard H. Bartels; John C. Beatty; Brian A. Barsky (1987). An Introduction to Splines for Use in Computer Graphics and Geometric Modeling. Morgan Kaufmann. ISBN 978-1-55860-400-1.
• Jean Gallier (1999). Curves and Surfaces in Geometric Modeling: Theory and Algorithms. Morgan Kaufmann. Chapter 6. B-Spline Curves. 이 책은 절판되어 저자가 무료로 입수할 수 있다.
• Hartmut Prautzsch; Wolfgang Boehm; Marco Paluszny (2002). Bézier and B-Spline Techniques. Springer Science & Business Media. ISBN 978-3-540-43761-1.
• David Salomon (2006). Curves and Surfaces for Computer Graphics. Springer. Chapter 7. B-Spline Approximation. ISBN 978-0-387-28452-1.
• Havey, Chad (2022).Bézier 및 B-Spline 지오메트리의 공식화 및 Python 구현.SAND2022-7702C (153페이지)

외부 링크

• Weisstein, Eric W. "B-Spline". MathWorld.
• Ruf, Johannes. "B-splines of third order on a non-uniform grid" (PDF). Archived from the original (PDF) on 2013-11-06. Retrieved 2012-05-02.
• numpy로부터의 이변량 B-스플린
• JSXGraph를 사용한 인터랙티브 B-스플라인
• TinySpline:다양한 언어의 바인딩을 사용하여 C 라이브러리를 엽니다.
• 균일하고 비합리적인 B-스플라인, 2D 공간에서 모델링 곡선.작성자:스테판 G.벡
• Shukant Pal의 B-Spline 편집기