카트리니얼

점들에 매달린 쇠사슬이 십일조를 이룬다.

자유롭게 매달려 있는 오버헤드 송전선은 또한 Catrene(고전압 라인 및 절연체 근처에 약간의 불완전성이 있는 가장 두드러지게 보이는 선)을 형성한다.

거미줄에 달린 실크는 여러 개의 탄력 있는 용사들을 형성한다.

물리학과 기하학에서 카트리네이션(미국: / /kætənɛri/, 영국: /kətiːnəri/)은 이상화된 매달린 체인이나 케이블이 균일한 중력장에서 끝부분에서만 지지되었을 때 자신의 무게로 가정하는 곡선이다.

격자곡선은 U자형으로 겉보기에는 포물선 아치와 비슷하지만 포물선은 아니다.

곡선은 특정 유형의 아치의 설계에 나타나며 두 개의 평행 원형 고리로 둘러싸인 비누 필름에 의해 가정된 형태인 카테노이드의 단면으로서 나타난다.

카트리얼은 알라이소이드(Alysoid), 체인넷(^[1]chainette) 또는 특히 재료과학에서는 funicular(불구체)라고도 불린다.^[2]로프 스태틱스는 매달린 로프와 관련된 고전적인 스태틱스 문제에서 용사들을 묘사한다.^[3]

수학적으로 Catrene 곡선은 쌍곡선 코사인 함수의 그래프다.카티네이드 곡선인 카티노이드의 회전 표면은 최소 표면이며, 특히 최소의 회전 표면이다.매달려 있는 사슬은 전위 에너지가 가장 적은 것으로 추정되며, 이는 전위 에너지인 것이다.^[4]1638년 갈릴레오 갈릴레이는 포물선과는 다르다는 것을 인식한 <두 개의 새로운 과학>이라는 책에서 카트리네이션에 대해 논했다.카트리네이션 곡선의 수학적 성질은 1670년대 로버트 후크가 연구했으며, 그 방정식은 1691년 라이프니즈, 후이겐스, 요한 베르누이 등이 도출했다.

Catery 및 관련 곡선은 구조 및 엔지니어링에 사용된다(예: 힘이 휨모멘트를 초래하지 않도록 교량 및 아치 설계 시).연안 석유 및 가스 산업에서 "백년제"는 생산 플랫폼과 해저 사이에 매달린 파이프라인인 철갑상어를 말하며, 약 십년제 모양을 채택하고 있다.철도 산업에서 그것은 열차에 전력을 전달하는 오버헤드 배선을 가리킨다.(이는 종종 더 가벼운 접촉 와이어를 지지하며, 이 경우 진정한 격자 곡선을 따르지 않는다.)

광학 및 전자기학에서 쌍곡선 코사인 및 사인 함수는 맥스웰 방정식의 기본 해결책이다.^[5]두 개의 반사파로 구성된 대칭 모드는 대칭 모양을 형성할 것이다.^[6]^[7]^[8]

역사

안토니 가우디의 카사 밀라에서의 카트리네이션 모델

'백년제'라는 단어는 '사슬'을 뜻하는 라틴어 cat catna에서 유래되었다.영어 단어 "catelliance"는 보통 Thomas Jefferson이 ^[9]^[10]Tomas Paine에게 다리 아치 건설에 대해 쓴 편지에서 유래되었다.

나는 최근 이탈리아로부터 압베 마스체로니에 의한 아치의 균형에 관한 논문을 받았다.그것은 매우 과학적인 작품으로 보인다.나는 아직 그것에 관여할 시간이 없었다; 그러나 나는 그의 시위의 결론은, 그 100주년 기념행사의 모든 부분이 완벽한 평형을 이루고 있다는 것을 알게 되었다.^[11]

흔히 갈릴레오는 매달린 사슬의 곡선이 포물선이라고 생각했다고 한다^[12].그러나 갈릴레오는 그의 Two New Science (1638)에서 교수형 코드는 대략적인 포물선일 뿐이며 곡률의 크기가 작아질수록 정확도가 향상되고 고도가 45°^[13] 미만일 때 거의 정확하다는 것을 정확하게 관찰했다고 썼다.쇠사슬에 이은 곡선이 포물선이 아니라는 사실은 요아힘 융기우스(1587–1657)에 의해 증명되었는데, 이 결과는 1669년에 사후에 발표되었다.^[12]

아치 건축에 카트리네이션이 적용된 것은 성 바울 대성당을 재건하는 맥락에서 '진정한 수학적·기계적 형태'가 카트리네이션으로 암시된 로버트 후크 덕분이다.^[14]훨씬 더 오래된 아치들 중 몇몇은 근위대에 가까운 것으로, 그 예로는 크테시폰에 있는 타크이 키스라의 아치(Arch of Taq-i Kisra)가 있다.^[15]

1671년, 후크는 왕립 학회에 아치의 최적 형태 문제를 해결했다고 발표하였고, 1675년 그의 '헬리콥터 설명' 부록에 라틴어 애너그램으로^[16] 암호화된 해결책을 발표하였는데,^[17] 여기서 그는 "모든 형태의 아치들이 건축하는 진정한 수학적이고 기계적인 형태를 발견했다"고 썼다.그는 일생 동안 이 애너그램에^[18] 대한 해결책을 발표하지 않았지만, 1705년에 그의 실행자는 그것을 "유연한 케이블을 매달아서, 뒤집어서, 아치의 만지는 조각들을 서도록 하라"는 뜻의 pendet 연속체, sich stabituum enucuum ridum inversum으로 제공했다.

1691년 고트프리트 라이프니츠, 크리스티안 후이겐스, 요한 베르누이는 야콥 베르누이의 도전에 대응하여 이 방정식을 도출하였다.^[12] 그들의 해결책은 1691년 6월 악타 에루디토룸에 발표되었다.^[19]^[20]David Gregory는 1697년에^[12]^[21] 정확한 미분 방정식의 부정확한 파생을 제공한 caterial에 대한 논문을 썼다.^[20]

오일러는 1744년 X축을 중심으로 회전할 때 주어진 경계 원에 대한 최소 표면적(카테노이드)의 표면을 제공하는 곡선이라는 것을 증명했다.^[1]니콜라스 호들스는 1796년 어떤 힘에서도 사슬의 평형을 설명하는 방정식을 제시하였다.^[22]

역삼각형 아치

가마 건축에는 종종 카트리네이션 아치가 사용된다.원하는 곡선을 만들기 위해 원하는 치수의 매달린 체인의 형상을 벽돌이나 다른 건축자재를 배치하기 위한 가이드로 사용되는 형태로 옮겨진다.^[23]^[24]

성곽의 게이트웨이 아치 미국 미주리 주 루이스는 가끔 (반전) 기념식이라고들 하지만 이것은 틀렸다.^[25]평탄한 천정이라고 하는 보다 일반적인 곡선에 가깝고, $방정식$ y = $ABC$ $($ $Bx)$ 는 $AB$ = $1$ 이면 백정식이다. 백정식은 일정한 두께의 자유로운 아치형이지만, 관문 아치는 상단 가까이에서 더 좁다.미국 국립역사 랜드마크 아치 후보지명에 따르면, 그 대신 "가중치수"라고 한다.그것의 모양은 가운데에 가벼운 고리를 가진 가중 체인이 형성되는 모양에 해당한다.^[26]^[27]맥도날드의 로고인 골든 아치는 포물선을 두 개 붙일 계획이었지만, 포물선을 그리기도 했다.

스페인 바르셀로나 카사 밀라 옥상 아래 카트리네^[28] 아치.
셰필드 윈터 가든은 일련의 아치로 둘러싸여 있다.^[29]
관문 아치는 납작한 천년이다.
임시 형태에 건설 중인 Catelenary 아치 가마

카트리네이션 다리

단순 현수교는 기본적으로 케이블이 두껍게 되어 있으며, catrene 곡선(catelene curve)을 따른다.

우루과이 말도나도의 레오넬 비에라 다리처럼 스트레스를 받는 리본 다리 역시 케이블이 단단한 데크에 박혀 있는 카트리네이션 곡선을 따라간다.

자유행렬 사슬에서 발휘되는 힘은 사슬의 길이에 대해 균일하며, 따라서 사슬은 격자 곡선을 따른다.^[30]단순 현수교나 도로가 케이블을 따라가는 '백년교'도 마찬가지다.^[31]^[32]

스트레스에 시달리는 리본 다리는 같은 모양의 더욱 정교한 구조물이다.^[33]^[34]

단, 노면이 매달린 현수교에서는 체인이나 케이블이 교량의 무게를 지탱하므로 자유롭게 매달려서는 안 된다.대부분의 경우, 도로가 평평하기 때문에 케이블의 무게가 지지되는 무게에 비해 무시할 수 있는 경우, 가하는 힘은 수평 거리에 대해 균일하며, 그 결과는 아래에서 논의한 바와 같이 포물선이 된다(비례적인 의미에서 "catelliance"라는 용어는 여전히 사용된다).케이블이 무겁다면 결과 곡선은 Catably와 Parabola 사이에 있다.^[35]^[36]

동일한 스팬과 처짐이 있는 포물선 아치(검은 점 곡선)와 포물선 아치(빨간색 솔리드 곡선)의 비교.갑판석은 단순 현수교의 종단면 또는 갑판과 행거가 케이블에 비해 미미한 질량을 갖는 현수교의 종단면을 나타낸다.포물선은 케이블과 행거가 갑판과 비교했을 때 무시할 수 있는 질량을 갖는 현수 덱 현수교의 케이블 프로파일을 나타낸다.스팬과 처짐이 동일한 실제 현수교의 케이블 프로파일은 두 곡선 사이에 있다.격자 방정식과 포물선 방정식은 각각

y

=

cosh(x)

및

y =

x

이다².

해양물체 고정

무거운 앵커 체인은 닻을 당기는 각도가 낮은 천장을 형성한다.

중력에 의해 생산된 연대는 무거운 앵커 로드에 이점을 제공한다.앵커 로딩(또는 앵커 라인)은 대개 체인이나 케이블 또는 둘 다로 구성된다.앵커 로드는 해저에 정박해야 하는 선박, 석유 굴착기, 부두, 부유식 풍력 터빈 및 기타 해양 장비에 의해 사용된다.

밧줄이 느슨해졌을 때, 격자 곡선은 거의 직선이었을 때보다 앵커 또는 계류 장치에 더 낮은 당김 각도를 나타낸다.이것은 앵커의 성능을 향상시키고 끌기 전에 저항할 힘의 수준을 높인다.바람이 불어오는 곳에서 갑갑한 모양을 유지하기 위해서는 무거운 쇠사슬이 필요하여, 깊은 물속에 있는 더 큰 배만이 이 효과에 의존할 수 있다.소형 보트들도 최대 보유력을 유지하기 위해 Catelene에 의존한다.^[37]

수학적 설명

방정식

다양

한 가치의 catery

카르테시안 좌표에서 카트리네이션의 방정식은 형태를^[35] 가지고 있다.

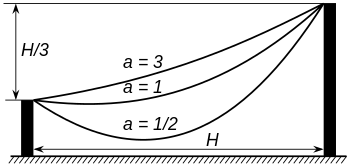
y=a\cosh \left\frac {x}{a}\right)={\frac {a}{a}{a}+e^{-{\frac {x}}\right)}}

여기서 $cosh$ 는 쌍곡 코사인 함수이며, 여기서 $x$ 는 가장 낮은 지점에서 측정된다.^[38]매개변수 $a$ 를 변경하면 곡선의 균일한 스케일링과 같기 때문에 모든 Catifial 곡선은 서로 유사하다.

유월절의 Whwell 방정식이다^[35].

\tan \varphi ={\frac {s}{a}\,

차별화 제공

{\frac {d\varphi }{ds}={\frac {\cos ^{2}\varphi }{a}}}}}

그리고 $φ$ 을 제거하면 cesaro 방정식이^[39] 주어진다.

\kappa ={\frac {a}{s^{2}+a^{2}}}}\,.

그러면 곡률 반경은 다음과 같다.

\rho =a\sec ^{2}\varphi

이 선은 선과 X 축 사이의 곡선에 대해 정규 분포를 따르는 선 길이입니다.^[40]

다른 곡선과의 관계

포물선을 따라 포물선을 그리면 포물선이 초점에 의해 추적되는 룰렛 곡선은 카트리네이션이다.^[41]포물선의 다이렉트릭스의 봉투도 갑갑한 것이다.^[42]정점에서부터의 무의식적인 룰렛, 즉 한 선이 Catwelene에 굴러갈 때 정점에서 시작되는 점으로 추적되는 룰렛은 트랙트릭스다.^[41]

백주에 선을 굴려 형성된 또 다른 룰렛은 또 다른 선이다.이것은 사각형 바퀴가 역삼각형 곡선 형태로 일련의 돌기들로 만들어진 도로에서 완벽하게 굴러갈 수 있다는 것을 의미한다.바퀴는 삼각형을 제외한 모든 일반 다각형이 될 수 있지만, Catelene에는 바퀴의 모양과 치수에 해당하는 매개변수가 있어야 한다.^[43]

기하학적 특성

어떤 수평 간격에서, 그 길이에 대한 Catwelene 이하 영역의 비율은 선택한 간격과 무관하게 $a$ 와 같다.이 성질을 가진 수평선 이외의 평면 곡선은 Catriene이 유일하다.또한, Catrene의 스트레치 아래 면적의 기하학적 중심은 곡선 자체의 중심과 X축을 연결하는 수직 세그먼트의 중간점이다.^[44]

과학

균일한 전기장에서 움직이는 전하가 카트리네일(전하 속도가 빛의 속도 $c$ 보다 훨씬 낮을 경우 포물선을 그리게 된다)을 따라 이동한다.^[45]

최소 표면적을 가진 양쪽 끝의 고정 반지름을 가진 회전 표면은 x축에 대해 회전하는 천년이다.^[41]

분석

체인 및 아치의 모델

수학적 모델에서 체인(또는 코드, 케이블, 로프, 끈 등)은 너무 얇아서 곡선으로 간주할 수 있고 체인에 의해 작용하는 모든 장력의 힘이 체인과 평행하다고 가정하여 이상화된다.^[46]최적의 아치를 위한 곡선의 분석은 장력의 힘이 압축의 힘이 되고 모든 것이 반전된다는 점을 제외하면 유사하다.^[47]기본 원리는 체인이 일단 평형을 이룬 후에는 경직된 신체로 간주될 수 있다는 것이다.^[48]각 지점에서 곡선의 모양과 체인의 장력을 정의하는 방정식은 체인이 정적 평형 상태일 경우 이러한 힘이 균형을 이루어야 한다는 사실을 이용하여 세그먼트에 작용하는 다양한 힘을 세심하게 검사함으로써 도출될 수 있다.

체인 다음에 오는 경로를 $r =$ ( $x,$ $y)$ = ( $x$ ) = ( $s),$ y $(s)$ 로 파라메트릭적으로 주도록 한다. 여기서 $s$ 는 호 길이를 나타내고 $r$ 은 위치 벡터다.이것은 자연적인 매개 변수화이며, 다음과 같은 속성을 가지고 있다.

{\frac {d\mathbf {r}}{ds}=\mathbf {u}}

여기서 $u$ 는 단위 접선 벡터다.

c

에서

r

까지의 1절에서 작용하는 힘의 도표.힘은

c

에서 장력

T 0

,

r

에서

장력

T, 체인의 중량(

0

,

-³

)이다

.

체인이 정지해 있으므로 이 힘의 합은 0이어야 한다.

곡선의 미분 방정식은 다음과 같이 도출할 수 있다.^[49] $c$ 는 사슬에서 가장 낮은 지점이 되게 하고, catial의 꼭지점이라고 한다.^[50].sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw- .sfrac{white-space:nowrap}.mw-parser-output 경사 .mw-parser-output.는 최저 한계점. 곡선의 Parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}dy/dx c에서 경우에만 0입니다.다른 경우는 대칭에 의해 암시되므로 $r$ 이 $c$ 의 오른쪽에 있다고 가정한다. $c$ 에서 $r$ 까지 체인의 단면에 작용하는 힘은 $c$ 에서 체인의 장력, $r$ 에서 체인의 장력, 체인의 중량이다. $c$ 에서의 장력은 $c$ 의 곡선에 접하고 따라서 수직 구성 요소 없이 수평이며, 단면을 왼쪽으로 당겨 힘의 $크기$ 인₀ $(- T 0, 0)$ 라고 쓸 수 있다. $r$ 에서의 장력은 $r$ 의 곡선과 평행하며 단면을 오른쪽으로 당긴다. $r$ 에서의 장력은 두 가지 $요소$ 로나눌 $수$ $있으므로$ $Tu$ = ( $T$ cos $φ$ , T $sin$ φ $)$ 라고 쓸 수 있다. 여기서 $T$ 는 힘의 크기, $φ$ 은 $r$ 과 x 축의 곡선 사이의 각도(접선 각도 참조).마지막으로 체인의 무게는 $(0,$ $-³gs)$ 로 표시되며 여기서 $λ$ 은 단위 길이당 질량이고 $g$ 는 중력의 가속도, $s$ 는 $c$ 와 r $사이$ 의 체인 부분의 길이이다.

사슬은 평형 상태여서 세 힘의 $합$ 이 0이므로

T\cos \varphi =T_{0}

, 그리고

\displaystyle T\sin \varphi =\lambda gs\...}

그리고 이것들을 나누면

{\frac {dy}{dx}}=\tan \varphi ={\frac {\fracda gs}{T_{0}}\,

쓰기가 편하다.

a={\frac {T_{0}{\lambda g}

중량이 $c$ 의 장력과 동일한 체인의 길이.^[51]그러면.

{\frac {dy}{dx}={\frac {s}{a}}}

곡선을 정의하는 방정식이다.

장력의 수평 요소인 $T$ $cos$ $φ$ = $T$ 는₀ 일정하고 장력의 수직 요소인 $T$ $sin$ $φ$ = $λgs$ 는 $r$ 과 정점 사이의 체인 길이에 비례한다.^[52]

곡선에 대한 방정식의 파생

위에 주어진 미분방정식을 풀어 곡선에 대한 방정식을 만들 수 있다.^[53]

보낸 사람

{\frac {dy}{dx}={\frac {s}{a}\}

호 길이 공식은 다음과 같다.

{\frac {ds}{dx}}={\sqrt {1+\left\dfrac}{dx}\right)^{2}}={\prac {\sqrt{a^{2}+s^{2}}}}{a}\, .

그러면.

{\frac {dx}{ds}}={\frac {1}{dx}}={\frac {a}{\sqrt{a^{2}+s^{2}={\frac {1}{\frac {1}{dx}}}}={\frac {a^{2}2}}}}}

, 그리고

{\frac {dy}{d}}={\frac {dy}{dx}}{dx}}={\frac {s}{\sqrt{a^{2}+s^{2}={\frac {d}}}}={\frac {dx}}}}}}}{2}}}}}\,.

이 방정식 중 두 번째 방정식은 다음과 같이 통합될 수 있다.

y={\sqrt {a^{2}+s^{2}}}}+\cHB

그리고 x축의 위치를 이동함으로써 $β$ 를 0으로 취할 수 있다.그러면.

y={\sqrt {a^{2}+s^{2}}}}\\\ft y^{2}=a^{2}+s^{2}\,

이렇게 선택한 x축을 catelene의 directrix라고 한다.

따라서 지점 $(x,$ $y)$ 의 장력의 크기는 $T$ = $λgy$ 이며 점과 다이렉트릭스 사이의 거리에 비례한다.^[52]

이 장력은 $T$ = $T 0$ $y / a$ 로 표현될 수도 있다.

$dx / ds$ 표현식의 적분은 표준^[54] 기법을 사용하여 찾을 수 있으며,

\displaystyle x=a\a\bename {arsinh}\lefts\frac {s}{a}\오른쪽)+\cHB\,}

그리고 다시 y축의 위치를 이동시킴으로써 $α$ 는 0으로 취할 수 있다.그러면.

\displaystyle x=a\a}a\frac {s}{a}\right)\####a=a\sinh \,}

이렇게 선택한 y축은 정점을 통과하여 catial의 축이라고 한다.

$이러한$ 결과는 s 기부를 제거하는 데 사용될 수 있다.

\displaystyle y=a\cosh \lefts\frac {x}{a}\오른쪽)\,}

대체 파생

미분 방정식은 다른 접근법을 사용하여 해결할 수 있다.^[55]보낸 사람

\displaystyle s=a\tan \varphi }

그 뒤를 잇다

{\frac {dx}{d\varphi}}}={\frac {ds}{dds}{d\varphi }}}}=\cos \varphi \cdot a\sec ^{2}\varphi =a\sec \varphi }}}}}}}}}

, 그리고

{\dfrac {dy}{d\varphi}}}}={\frac {ds}{ds}{d\varphi }}}=\sin \varphi \cdot a\sec ^{2}\varphi =a\tan \varphi \varphi \, \varphi \,}

통합 제공,

x=a\ln(\sec \varphi +\tan \varphi )+\propers

, 그리고

\displaystyle y=a\sec \varphi +\displays \,}

이전과 $같이$ x축과 y축은 이동할 수 있으므로 $α$ 와 $β$ 를 0으로 취할 수 있다.그러면.

\sec \varphi +\tan \varphi =e^{\frac {x}{a}\}

그리고 양쪽의 상호작용을 취하는 것

\sec \varphi -\tan \varphi =e^{-{\frac {x}{a}}\,

마지막 두 방정식을 더하고 빼면 용액이 나온다.

y=a=a\sec \varphi =a\cosh \left({\frac {x}{a}\right)\

, 그리고

\displaystyle s=a\tan \varphi =a\sinh \left({\frac {x}{a}\right)\,}

매개변수 결정

수평방향

힘 H

T에 따라 동일한 두 지점을 통과하는 세 명의 용사.

일반적으로 매개변수 $a$ 는 축의 위치다.이 경우 방정식은 다음과 같이 결정할 수 있다.^[56]

필요한 경우 $P$ 가₁ $P$ 의₂ 왼쪽에 오도록 다시 라벨링하고 $H$ 를 수평이 되게 하고 $v$ 를₁ $P$ 에서₂ P까지의 수직 거리가 되게 한다.축을 해석하여 Catrene의 꼭지점이 Y축에 있도록 하고 그 높이 $a$ 를 조정하여 Catrene이 곡선의 표준방정식을 만족하도록 한다.

y=a\cosh \lefts\frac {x}{a}\오른쪽)

$그리고 1$ P와 $P$ 의₂ 좌표는 각각 ( $x 1 1,$ y $)$ 와 $(x 2 2,$ y $)$ 가 되도록 한다.곡선이 이 점들을 통과하기 때문에 높이의 차이는

v=a\cosh \frac {x_{2}}:{a}\right)-a\cosh \cosh \reft({\frac {x_}{a}\right),

그리고 $P$ 에서₁ $P$ 까지의₂ 곡선의 길이는

s=a\sinh \frac {x_{2}}:{a}\right)-a\sinh \reftproc\frac {x_}{1}:{a}\right)\,

$이러한 2$ 식을 사용하여 s - $v$ 를² 확장하면 결과는

s^{2}-v^{2}=2a^{2}\왼쪽(\cosh \왼쪽({\frac {x_{2}-x_{1}:{1}:{a}\오른쪽)=4a^{2}\sinh ^{2}\{2}\왼쪽({\frac {H}}}}}\오른쪽)\}}

그렇게

{\sqrt {s^{2}-v^{2}}=2a\sinh \left({\frac {H}{2a}\오른쪽)\,

이것은 $a$ 의 초월 방정식이며 수치로 풀어야 한다.미적분법을^[57] 통해 알 수 있는데, $0$ 보다 큰 용액이 하나 있고, 따라서 평형의 위치가 하나라는 것이다.

단, 곡선의 양쪽 끝( $P$ 와₁ $P 2$ )이 같은 수준( $y 1$ = $y 2$ )이면, 그 정도를^[58] 알 수 있다.

a={\frac {{\frac {1}{4}L^{2}-h^{2}}:{2h}\,

여기서 L은

P

와₁

P 2

사이의 곡선의 총 길이이고

h

는 Sag(

P 1

,

P 2

및 곡선의 정점 사이의 수직 거리)이다.

라고도 할 수 있다.

L=2a\sinh {\frac {H}{2a}\,

, 그리고

H=2a\operatorname {arcosh} {\frac {h+a}{a},

여기서 H는 동일한 레벨(

H

=

x 2

-

x 1

)에 위치한

P

와₁

P 2

사이의 수평 거리이다.

$P$ 와₁ $P$ 에서₂ 수평 견인력은 $T H$ = $aw$ 이며, $여기$ 서 w는 체인 또는 케이블의 단위 길이당 질량이다.

변이성 제형식

동일한 높이의 두 지점과 거리 $D$ $D$ 에서 매달린 $L$ $길이$ L $L$ 의 체인을 생각해 보십시오 $D$ 곡선은 잠재적 에너지를 최소화해야 한다.

U=\int _{0}^{D}g\rho y{\sqrt{1+y'^{2}}dx

그리고 제약을 받는다.

\int _{0}^{D}{\sqrt {1+y'^{2}}dx=L\,

그러므로 수정된 라그랑지안은

{\mathcal{L}=(g\rho y-\lambda ){\sqrt {1+y'^{2}}}

여기서

\lambda

\lambda

은

\lambda

(는) 결정해야 하는 Lagrange 승수다.독립 변수

x

x

이(가) 라그랑지안에는 나타나지 않으므로

x

벨트라미 아이덴티티를 사용할 수 있다.

{\mathcal {L}-y'{\frac {\partial {L}{\partial y'}=C

여기서

C

C

은

C

(는) 첫 번째 적분을 얻기 위해 통합 상수임

{\frac {(g\rho y-\byda )}{\sqrt {1+y'^{2}}}}=-C

이것은 변수의 분리방법으로 해결할 수 있는 일반적인 1차 차등식이다.그것의 해결책은 제약조건으로부터 매개변수를 얻는 일반적인 쌍곡선 코사인이다.

수직력을 이용한 일반화

통일체 체인

체인의 밀도가 가변적일 경우 위의 분석을 적용하여 밀도가 주어진 곡선에 대한 방정식을 만들거나 곡선을 지정하여 밀도를 찾을 수 있다.^[59]

체인의 단위 길이당 중량을 $나타내면$ 체인의 중량은 크기가 된다.

\int _{\mathbf {c}^{\mathbf {r} }w\,ds\...

여기서 통합의 한계는 $c$ 와 $r$ 이다. 균일 체인에서와 같이 힘의 균형을 맞춘다.

T\cos \varphi =T_{0}

, 그리고

T\sin \varphi =\int _{\mathbf {c}^{\mathbf {r}}w\,ds\...

따라서

{\frac {dy}{dx}}=\tan \varphi ={\frac {1}{}{T_{0}}}\int _{\mathbf {c}^{\mathbf {r}w\,ds\,.

그 후 차별화는 주어진다.

{\dplaystyle w=T_{0}{\frac {d}{d}{dx}}{dx}}={\frac {T_{dx}{d^{2}y}{dx^{dx^}}}}}{1+\dfrac {dy}}{dx\i}}}}:{2}},}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}.}

$φ$ 과 곡률 반경의 측면에서 $ρ$ 이것은 다음과 같다.

w={\frac {T_{0}}{\rho \coses ^{2}\varphi }}\,

현수교 곡선

금문교.대부분의 현수교 케이블은 도로는 케이블보다 훨씬 무겁기 때문에 카트리네이션 곡선이 아닌 포물선을 따른다.

곡선을 찾기 위해 유사한 분석을 수행한 후 수평 차로가 있는 현수교를 지지하는 케이블을 찾을 수 있다.^[60]단위 길이당 도로의 무게가 $w$ 이고 다리를 떠받치는 케이블과 와이어의 무게가 비교해도 무시할 수 있는 경우, $c$ 에서 $r$ 까지의 케이블의 무게(사슬과 아치의 Catnial#Model의 그림 참조)는 $wx$ 이고 여기서 $x$ 는 $c$ 와 $r$ 사이의 수평 거리인 것이다.전과 같이 진행하면 미분 방정식이 제공됨

{\frac {dy}{dx}}=\tan \varphi ={\frac {w}{T_{0}}}x\,

이것은 간단한 통합으로 해결된다.

y={\frac {w}{2}T_{0}}}x^{2}+\베타

그래서 케이블은 포물선을 따라간다.케이블과 지지 와이어의 무게가 무시할 수 없는 경우 분석이 더 복잡하다.^[61]

동일 강도의 반석기

균일강도의 Catelionary에서는 각 지점의 장력의 크기에 따라 케이블이 강화되므로, 케이블의 길이에 따라 파손에 대한 저항성이 일정하게 유지된다.케이블의 강도가 단위 길이당 밀도에 비례한다고 가정하면 체인의 단위 길이당 중량 $w$ , w, 를 $T / c$ 로 표기할 수 있으며, 여기서 $c$ 는 일정하며, 균일하지 않은 체인에 대한 분석을 적용할 수 있다.^[62]

이 경우 장력에 대한 방정식은 다음과 같다.

{\reasoned}T\cos \varphi &=T_{0}\\\\T\sin \varphi &={\frac {1}{c}\int T\,ds\,\ended}}}}

콤비네이션 give

c\tan \varphi =\int \sec \varphi \,ds

그리고 분화로

\displaystyle c=\rho \cos \varphi }

여기서 $ρ$ 은 곡률 반경이다.

이에 대한 해결책은

y=c\ln \left(\sec \leftleft\frac {x}{c}\오른쪽)\,

이 경우, 곡선은 수직 점근법을 가지며, 이는 그 범위를 $cc$ 로 제한한다.다른 관계는

\\displaystyle x=c\varphi \ln s=\ln \left(\tan \left({\frac {\pi +2\varphi }{4}\right)\,\,}

이 곡선은 데이비스 길버트가 1826년에 연구했고, 1836년에 가스파드-구스타브 코리올리가 독자적으로 연구했다.

최근에는 이러한 형태의 카타시네이션이 전자파 메타서페이스의 빌딩 블록 역할을 할 수 있다는 사실이 밝혀져 '동등 위상 그라데이션의 백년제'^[63]로 알려져 있다.

탄성탄수제

탄성 카트리네이션에서, 체인은 긴장에 반응하여 늘어날 수 있는 스프링으로 대체된다.훅의 법칙에 따라 샘물이 뻗어나가는 것으로 추측된다.특히 $p$ 가 스프링 섹션의 자연적인 길이인 경우, $장력$ T가 적용된 스프링의 길이는 길이가 있다.

s=\왼쪽(1+{\frac {T}{E}\오른쪽)p\...

여기서 $E$ 는 $kp$ 와 동일한 상수이고, 여기서 $k$ 는 스프링의 강성이다.^[64]Catrielinary에서는 $T$ 의 값이 가변적이지만, 비율이 로컬 수준에서 유효하기 때문에^[65]

{\frac {ds}{dp}=1+{\frac {T}{E}\,

탄성 스프링이 뒤따르는 곡선은 이제 비탄성 스프링과 유사한 방법으로 도출할 수 있다.^[66]

봄의 장력에 대한 방정식은

\displaystyle T\cos \varphi =T_{0}\...}

, 그리고

T\sin \varphi =\lambda _{0}gp\...

어느 것에서

{\frac {dy}{dx}}=\tan \varphi ={\frac {\fracda _{0}gp}{T_{0}}\...\quad T={\sqrt {T_{0}^{2}+\lambda _{0}^{0}g^{2}p^{2}}\}\}}

여기서 $p$ 는 $c$ 에서 $r$ 까지의 세그먼트의 자연적인 길이, $λ$ 은₀ 장력이 없는 스프링의 단위 길이당 질량이며 $g$ 는 중력의 가속이다.쓰다

a={\frac {T_{0}}{\lambda _{0}g}}

그렇게

{\frac {dy}{dx}}=\tan \varphi ={\frac {p}}{a}\qad {\text{0}}\quad T={\frac {T_}{a}}}}{\sqrt}+p^{2}}}}\,.

그러면.

{\begin{ligned}{\frac {dx}{ds}}&=\cos \varphi ={\frac {T_{0}}}}{\frac}}}}{\frac}}}{0}}}T}\\[6pt]{\frac {dy}{ds}}&=\sin \varphi ={\frac {\lambda _{0}gp}{T}\......\end{aigned}

어느 것에서

{\begin{aignedat}{3}{\frac {dx}{dp}&={\frac {T_{0}}}{{\frac}}}}{{0}}}}}}}{\fracT}{\frac {ds}{dp}&&=T_{0}\왼쪽({\frac {1}{T}+{\frac{1}{E}\오른쪽)&&={\frac{a}{\sqrt{a^{2}+p^{2}}+{\frac{T_{0}\\[6pt]{\frac {d}{dp}}&={\frac {\lambda _{0}gp}{0}}}}}}}{\frac {}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}T}{{\frac {ds}{dp}}&={\frac {T_{0}p}{a}}\왼쪽({\frac {1}{\frac}{1}{p}}}{\frac}{1}{p}}}}{\frac}}{p}}}{T}+{\frac{1}{E}\오른쪽)&&={\frac{p}{\sqrt{a^{2}+p^{2}}+{\frac {T_{0}p}{Ea}}\,\end{aignedat}}

통합은 모수 방정식을 제공한다.

{\displaystyle{\begin}x&=a\operatorname {arsinh} \왼쪽({\frac {p}{a}\right)+{\frac {T_}{0}}}{E}}}}}}}{{}pa+\npt]y&={\sqrt{a^{a^{2}p^{2}}}}+{\frac{T_{0}{2Ea}p^{2}+\beta \,\end{정렬}}}

$다시$ x축과 y축은 이동할 수 있어 $α$ 와 $β$ 를 0으로 취할 수 있다.그렇게

{\begin}x&=a\operatorname {arsinh} \왼쪽({\frac {p}{a}\right)+{\frac {T_{0}}}{{6pt]pt]y&={\sqrt{a^{2}+p^{2}}}}+{\frac{T_{0}}{2Ea}p^{2}\end{arged}}}}

곡선에 대한 모수 방정식이다. $E$ 가 큰 경성 한계에서는 곡선 모양이 비탄성 사슬의 그것까지 감소한다.

기타 일반화

일반적인 힘 아래 쇠사슬을 묶는다.

체인에 작용하는 $G$ 의 힘에 대해 어떠한 가정도 하지 않고, 다음과 같은 분석을 할 수 있다.^[67]

첫째, $T$ = $T (s)$ 를 $s$ 의 함수로서 장력의 힘이 되게 한다.사슬은 유연하기 때문에 자신에게 평행한 힘만 발휘할 수 있다.장력은 체인이 스스로 발휘하는 힘으로 정의되기 때문에 $T$ 는 체인과 평행해야 한다.바꾸어 말하면, 환언하면

\mathbf {T} =T\mathbf {u} \...

여기서 $T$ 는 $T$ 의 크기, $u$ 는 단위 접선 벡터다.

둘째, $G$ = $G (s)$ 를 $s$ 의 함수로 체인의 작은 세그먼트에 작용하는 단위 길이당 외력이 되도록 한다. $s$ 와 $s$ + Δs 사이의 체인의 세그먼트에 작용하는 힘은 세그먼트 한쪽 끝에서 장력 $T$ ( $s$ + Δs $)$ 의 힘, 다른 쪽 끝에서 거의 $반대방향$ 의 힘 -T $(s),$ 그리고 약 $Δs$ 인 세그먼트에 작용하는 외부 힘이다.이 세력들은 그렇게 균형을 잡아야 한다.

\mathbf {T}(s+\Delta s)-\mathbf {T}(s)+\mathbf {G} \delta s\대략 \mathbf {0} \,.

Δs로 나누고 한계치를 Δs → $0$ 으로 취한다.

{\dapplaystyle {\frac {d\mathbf {T}}{ds}+\mathbf {G} =\mathbf {0} \,.}

이러한 방정식은 외부 힘 하에서 작용하는 유연한 사슬의 분석에서 출발점으로 사용될 수 있다.표준 Catriene의 경우, 체인이 단위 길이당 질량 $λ$ 을 갖는 $G =$ $(0,$ $-gg)$ 와 $g$ 는 중력의 가속이다.

참고 항목

카트리나 아치
체인 분수 또는 자가 소각 구슬
오버헤드 캐티너리 – 철도 또는 트램 차량에 전원선이 매달려 있음
룰렛(곡선) – 타원형/하이퍼볼릭 카트리네이션
트로포스케인 – 스펀 로프의 모양
가중카트리네이션

메모들

^ ^a ^b 매트릭월드
^ 예:Shodek, Daniel L. (2004). Structures (5th ed.). Prentice Hall. p. 22. ISBN 978-0-13-048879-4. OCLC 148137330.
^ "Shape of a hanging rope" (PDF). Department of Mechanical & Aerospace Engineering - University of Florida. 2017-05-02. Retrieved 2020-06-04.
^ "The Calculus of Variations". 2015. Retrieved 2019-05-03.
^ Luo, Xiangang (2019). Catenary optics. Singapore: Springer. doi:10.1007/978-981-13-4818-1. ISBN 978-981-13-4818-1. S2CID 199492908.
^ Bourke, Levi; Blaikie, Richard J. (2017-12-01). "Herpin effective media resonant underlayers and resonant overlayer designs for ultra-high NA interference lithography". JOSA A. 34 (12): 2243–2249. Bibcode:2017JOSAA..34.2243B. doi:10.1364/JOSAA.34.002243. ISSN 1520-8532. PMID 29240100.
^ Pu, Mingbo; Guo, Yinghui; Li, Xiong; Ma, Xiaoliang; Luo, Xiangang (2018-07-05). "Revisitation of Extraordinary Young's Interference: from Catenary Optical Fields to Spin–Orbit Interaction in Metasurfaces". ACS Photonics. 5 (8): 3198–3204. doi:10.1021/acsphotonics.8b00437. ISSN 2330-4022.
^ Pu, Mingbo; Ma, XiaoLiang; Guo, Yinghui; Li, Xiong; Luo, Xiangang (2018-07-23). "Theory of microscopic meta-surface waves based on catenary optical fields and dispersion". Optics Express. 26 (15): 19555–19562. Bibcode:2018OExpr..2619555P. doi:10.1364/OE.26.019555. ISSN 1094-4087. PMID 30114126.
^ ""Catenary" at Math Words". Pballew.net. 1995-11-21. Retrieved 2010-11-17.
^ Barrow, John D. (2010). 100 Essential Things You Didn't Know You Didn't Know: Math Explains Your World. W. W. Norton & Company. p. 27. ISBN 978-0-393-33867-6.
^ Jefferson, Thomas (1829). Memoirs, Correspondence and Private Papers of Thomas Jefferson. Henry Colbura and Richard Bertley. p. 419.
^ ^a ^b ^c ^d 록우드 페이지 124
^ Fahie, John Joseph (1903). Galileo, His Life and Work. J. Murray. pp. 359–360.
^ Jardine, Lisa (2001). "Monuments and Microscopes: Scientific Thinking on a Grand Scale in the Early Royal Society". Notes and Records of the Royal Society of London. 55 (2): 289–308. doi:10.1098/rsnr.2001.0145. JSTOR 532102. S2CID 144311552.
^ Denny, Mark (2010). Super Structures: The Science of Bridges, Buildings, Dams, and Other Feats of Engineering. JHU Press. pp. 112–113. ISBN 978-0-8018-9437-4.
^ cf. 다음 단락에 나타난 후크 법칙의 애너그램
^ "Arch Design". Lindahall.org. 2002-10-28. Archived from the original on 2010-11-13. Retrieved 2010-11-17.
^ 원래의 애너그램은 Abccddeeeefgiiiiiiiiiiimmnnnnnnnnnnnnnnnnnnnnnnnoprssttttuuuuuuuuuuux: 알파벳화된 라틴어 구절의 문자였다.
^ Truesdell, C. (1960), The Rotational Mechanics of Flexible Or Elastic Bodies 1638–1788: Introduction to Leonhardi Euleri Opera Omnia Vol. X et XI Seriei Secundae, Zürich: Orell Füssli, p. 66, ISBN 9783764314415
^ ^a ^b Calladine, C. R. (2015-04-13), "An amateur's contribution to the design of Telford's Menai Suspension Bridge: a commentary on Gilbert (1826) 'On the mathematical theory of suspension bridges'", Philosophical Transactions of the Royal Society A, 373 (2039): 20140346, Bibcode:2015RSPTA.37340346C, doi:10.1098/rsta.2014.0346, PMC 4360092, PMID 25750153
^ Gregorii, Davidis (August 1697), "Catenaria", Philosophical Transactions, 19 (231): 637–652, doi:10.1098/rstl.1695.0114
^ 루스 아트 455, 각주
^ Minogue, Coll; Sanderson, Robert (2000). Wood-fired Ceramics: Contemporary Practices. University of Pennsylvania. p. 42. ISBN 978-0-8122-3514-2.
^ Peterson, Susan; Peterson, Jan (2003). The Craft and Art of Clay: A Complete Potter's Handbook. Laurence King. p. 224. ISBN 978-1-85669-354-7.
^ Osserman, Robert (2010), "Mathematics of the Gateway Arch", Notices of the American Mathematical Society, 57 (2): 220–229, ISSN 0002-9920
^ Hicks, Clifford B. (December 1963). "The Incredible Gateway Arch: America's Mightiest National Monument". Popular Mechanics. 120 (6): 89. ISSN 0032-4558.
^ Harrison, Laura Soullière (1985), National Register of Historic Places Inventory-Nomination: Jefferson National Expansion Memorial Gateway Arch / Gateway Arch; or "The Arch", National Park Service 1975년 사진(578KB)에 항공사진 한 장 첨부
^ Sennott, Stephen (2004). Encyclopedia of Twentieth Century Architecture. Taylor & Francis. p. 224. ISBN 978-1-57958-433-7.
^ Hymers, Paul (2005). Planning and Building a Conservatory. New Holland. p. 36. ISBN 978-1-84330-910-9.
^ Byer, Owen; Lazebnik, Felix; Smeltzer, Deirdre L. (2010-09-02). Methods for Euclidean Geometry. MAA. p. 210. ISBN 978-0-88385-763-2.
^ Fernández Troyano, Leonardo (2003). Bridge Engineering: A Global Perspective. Thomas Telford. p. 514. ISBN 978-0-7277-3215-6.
^ Trinks, W.; Mawhinney, M. H.; Shannon, R. A.; Reed, R. J.; Garvey, J. R. (2003-12-05). Industrial Furnaces. Wiley. p. 132. ISBN 978-0-471-38706-0.
^ Scott, John S. (1992-10-31). Dictionary Of Civil Engineering. Springer. p. 433. ISBN 978-0-412-98421-1.
^ Architects' Journal. 207: 51. 1998. {{cite journal}}:누락 또는 비어 있음 title=(도움말)
^ ^a ^b ^c 록우드 페이지 122
^ Kunkel, Paul (June 30, 2006). "Hanging With Galileo". Whistler Alley Mathematics. Retrieved March 27, 2009.
^ "Chain, Rope, and Catenary – Anchor Systems For Small Boats". Petersmith.net.nz. Retrieved 2010-11-17.
^ Weisstein, Eric W. "Catenary". MathWorld--A Wolfram Web Resource. Retrieved 2019-09-21. The parametric equations for the catenary are given by x(t) = t, y(t) = [...] a cosh(t/a), where t=0 corresponds to the vertex [...]
^ 수학월드, eq. 7
^ 루스 아트로444번길
^ ^a ^b ^c Yates, Robert C. (1952). Curves and their Properties. NCTM. p. 13.
^ 예이츠 페이지 80
^ Hall, Leon; Wagon, Stan (1992). "Roads and Wheels". Mathematics Magazine. 65 (5): 283–301. doi:10.2307/2691240. JSTOR 2691240.
^ Parker, Edward (2010). "A Property Characterizing the Catenary". Mathematics Magazine. 83: 63–64. doi:10.4169/002557010X485120. S2CID 122116662.
^ Landau, Lev Davidovich (1975). The Classical Theory of Fields. Butterworth-Heinemann. p. 56. ISBN 978-0-7506-2768-9.
^ 루스 아트 442, 페이지 316
^ Church, Irving Porter (1890). Mechanics of Engineering. Wiley. p. 387.
^ 휴웰 페이지 65
^ 다음 루스 아트 443 페이지 316
^ 루스 아트 443 페이지 317
^ 휴웰 페이지 67
^ ^a ^b 루스 아트 443 페이지 318
^ 다음 루스 아트 443 페이지 317
^ 쌍곡선 함수의 사용은 Maurer 페이지 107에 따른다.
^ 다음 양 페이지 342
^ 토드헌터 미술에 이어. 186
^ 루스 아트를 보라. 447
^ Ghostarchive 및 Wayback Machine에 보관:
^ Routh Art에 이어. 450
^ 다음 루스 아트 452호
^ Ira Freeman은 케이블과 도로만 중요한 경우를 조사하였다. 외부 링크 섹션을 참조하십시오.러스는 지지선만이 상당한 무게를 가지고 있는 경우를 연습으로 제시한다.
^ Routh Art에 이어. 453
^ Pu, Mingbo; Li, Xiong; Ma, Xiaoliang; Luo, Xiangang (2015). "Catenary Optics for Achromatic Generation of Perfect Optical Angular Momentum". Science Advances. 1 (9): e1500396. Bibcode:2015SciA....1E0396P. doi:10.1126/sciadv.1500396. PMC 4646797. PMID 26601283.
^ 루스 아트로489번길
^ 루스 아트로494번길
^ 루스 아트 따라하기 500
^ Routh Art를 따른다. 455

참고 문헌 목록

Lockwood, E.H. (1961). "Chapter 13: The Tractrix and Catenary". A Book of Curves. Cambridge.
Salmon, George (1879). Higher Plane Curves. Hodges, Foster and Figgis. pp. 287–289.
Routh, Edward John (1891). "Chapter X: On Strings". A Treatise on Analytical Statics. University Press.
Maurer, Edward Rose (1914). "Art. 26 Catenary Cable". Technical Mechanics. J. Wiley & Sons.
Lamb, Sir Horace (1897). "Art. 134 Transcendental Curves; Catenary, Tractrix". An Elementary Course of Infinitesimal Calculus. University Press.
Todhunter, Isaac (1858). "XI Flexible Strings. Inextensible, XII Flexible Strings. Extensible". A Treatise on Analytical Statics. Macmillan.
Whewell, William (1833). "Chapter V: The Equilibrium of a Flexible Body". Analytical Statics. J. & J.J. Deighton. p. 65.
Weisstein, Eric W. "Catenary". MathWorld.

추가 읽기

Swetz, Frank (1995). Learn from the Masters. MAA. pp. 128–9. ISBN 978-0-88385-703-8.
Venturoli, Giuseppe (1822). "Chapter XXIII: On the Catenary". Elements of the Theory of Mechanics. Trans. Daniel Cresswell. J. Nicholson & Son.

외부 링크

O'Connor, John J.; Robertson, Edmund F., "Catenary", MacTutor History of Mathematics archive, University of St Andrews
플래닛매트릭스의 카트리니얼.
Catriene 곡선 계산기
지오메트리 센터 카트리네이션
특수 평면 곡선 시각 사전의 "수백주년"
카트리네이션 - 체인, 아치, 비누 영화.
케이블 Sag 오류 계산기 – Catrene 곡선의 직선으로부터의 편차를 계산하고 계산기와 참조의 파생을 제공한다.
동적 및 정적 세백년 곡선 방정식 도출 – 형상(정적 케이스)과 백년의 역학(동적 케이스)을 지배하는 방정식이 도출된다.논의된 방정식에 대한 해결책.
직선, 카트리네일, 브라키스토크론, 원, 페르마트 통합 접근법 등이 일부 지오데오디컬에 접근한다.
Ira Freeman "A General Form of the Suspending Bridge Catelene" Bulletin of AMS

[MathWorld-1] 매트릭월드

[2] 예:Shodek, Daniel L. (2004). Structures (5th ed.). Prentice Hall. p. 22. ISBN 978-0-13-048879-4. OCLC 148137330.

[3] "Shape of a hanging rope" (PDF). Department of Mechanical & Aerospace Engineering - University of Florida. 2017-05-02. Retrieved 2020-06-04.

[4] "The Calculus of Variations". 2015. Retrieved 2019-05-03.

[5] Luo, Xiangang (2019). Catenary optics. Singapore: Springer. doi:10.1007/978-981-13-4818-1. ISBN 978-981-13-4818-1. S2CID 199492908.

[6] Bourke, Levi; Blaikie, Richard J. (2017-12-01). "Herpin effective media resonant underlayers and resonant overlayer designs for ultra-high NA interference lithography". JOSA A. 34 (12): 2243–2249. Bibcode:2017JOSAA..34.2243B. doi:10.1364/JOSAA.34.002243. ISSN 1520-8532. PMID 29240100.

[7] Pu, Mingbo; Guo, Yinghui; Li, Xiong; Ma, Xiaoliang; Luo, Xiangang (2018-07-05). "Revisitation of Extraordinary Young's Interference: from Catenary Optical Fields to Spin–Orbit Interaction in Metasurfaces". ACS Photonics. 5 (8): 3198–3204. doi:10.1021/acsphotonics.8b00437. ISSN 2330-4022.

[8] Pu, Mingbo; Ma, XiaoLiang; Guo, Yinghui; Li, Xiong; Luo, Xiangang (2018-07-23). "Theory of microscopic meta-surface waves based on catenary optical fields and dispersion". Optics Express. 26 (15): 19555–19562. Bibcode:2018OExpr..2619555P. doi:10.1364/OE.26.019555. ISSN 1094-4087. PMID 30114126.

[9] ""Catenary" at Math Words". Pballew.net. 1995-11-21. Retrieved 2010-11-17.

[10] Barrow, John D. (2010). 100 Essential Things You Didn't Know You Didn't Know: Math Explains Your World. W. W. Norton & Company. p. 27. ISBN 978-0-393-33867-6.

[11] Jefferson, Thomas (1829). Memoirs, Correspondence and Private Papers of Thomas Jefferson. Henry Colbura and Richard Bertley. p. 419.

[Lockwood124-12] 록우드 페이지 124

[13] Fahie, John Joseph (1903). Galileo, His Life and Work. J. Murray. pp. 359–360.

[14] Jardine, Lisa (2001). "Monuments and Microscopes: Scientific Thinking on a Grand Scale in the Early Royal Society". Notes and Records of the Royal Society of London. 55 (2): 289–308. doi:10.1098/rsnr.2001.0145. JSTOR 532102. S2CID 144311552.

[15] Denny, Mark (2010). Super Structures: The Science of Bridges, Buildings, Dams, and Other Feats of Engineering. JHU Press. pp. 112–113. ISBN 978-0-8018-9437-4.

[16] . 다음 단락에 나타난 후크 법칙의 애너그램

[17] "Arch Design". Lindahall.org. 2002-10-28. Archived from the original on 2010-11-13. Retrieved 2010-11-17.

[18] 원래의 애너그램은 Abccddeeeefgiiiiiiiiiiimmnnnnnnnnnnnnnnnnnnnnnnnoprssttttuuuuuuuuuuux: 알파벳화된 라틴어 구절의 문자였다.

[19] Truesdell, C. (1960), The Rotational Mechanics of Flexible Or Elastic Bodies 1638–1788: Introduction to Leonhardi Euleri Opera Omnia Vol. X et XI Seriei Secundae, Zürich: Orell Füssli, p. 66, ISBN 9783764314415

[calladine-20] Calladine, C. R. (2015-04-13), "An amateur's contribution to the design of Telford's Menai Suspension Bridge: a commentary on Gilbert (1826) 'On the mathematical theory of suspension bridges'", Philosophical Transactions of the Royal Society A, 373 (2039): 20140346, Bibcode:2015RSPTA.37340346C, doi:10.1098/rsta.2014.0346, PMC 4360092, PMID 25750153

[21] Gregorii, Davidis (August 1697), "Catenaria", Philosophical Transactions, 19 (231): 637–652, doi:10.1098/rstl.1695.0114

[22] 루스 아트 455, 각주

[23] Minogue, Coll; Sanderson, Robert (2000). Wood-fired Ceramics: Contemporary Practices. University of Pennsylvania. p. 42. ISBN 978-0-8122-3514-2.

[24] Peterson, Susan; Peterson, Jan (2003). The Craft and Art of Clay: A Complete Potter's Handbook. Laurence King. p. 224. ISBN 978-1-85669-354-7.

[25] Osserman, Robert (2010), "Mathematics of the Gateway Arch", Notices of the American Mathematical Society, 57 (2): 220–229, ISSN 0002-9920

[26] Hicks, Clifford B. (December 1963). "The Incredible Gateway Arch: America's Mightiest National Monument". Popular Mechanics. 120 (6): 89. ISSN 0032-4558.

[nrhpinv2-27] Harrison, Laura Soullière (1985), National Register of Historic Places Inventory-Nomination: Jefferson National Expansion Memorial Gateway Arch / Gateway Arch; or "The Arch", National Park Service 1975년 사진(578KB)에 항공사진 한 장 첨부

[28] Sennott, Stephen (2004). Encyclopedia of Twentieth Century Architecture. Taylor & Francis. p. 224. ISBN 978-1-57958-433-7.

[29] Hymers, Paul (2005). Planning and Building a Conservatory. New Holland. p. 36. ISBN 978-1-84330-910-9.

[30] Byer, Owen; Lazebnik, Felix; Smeltzer, Deirdre L. (2010-09-02). Methods for Euclidean Geometry. MAA. p. 210. ISBN 978-0-88385-763-2.

[31] Fernández Troyano, Leonardo (2003). Bridge Engineering: A Global Perspective. Thomas Telford. p. 514. ISBN 978-0-7277-3215-6.

[32] Trinks, W.; Mawhinney, M. H.; Shannon, R. A.; Reed, R. J.; Garvey, J. R. (2003-12-05). Industrial Furnaces. Wiley. p. 132. ISBN 978-0-471-38706-0.

[33] Scott, John S. (1992-10-31). Dictionary Of Civil Engineering. Springer. p. 433. ISBN 978-0-412-98421-1.

[34] Architects' Journal. 207: 51. 1998. {{cite journal}}:누락 또는 비어 있음 title=(도움말)

[Lockwood122-35] 록우드 페이지 122

[36] Kunkel, Paul (June 30, 2006). "Hanging With Galileo". Whistler Alley Mathematics. Retrieved March 27, 2009.

[37] "Chain, Rope, and Catenary – Anchor Systems For Small Boats". Petersmith.net.nz. Retrieved 2010-11-17.

[38] Weisstein, Eric W. "Catenary". MathWorld--A Wolfram Web Resource. Retrieved 2019-09-21. The parametric equations for the catenary are given by x(t) = t, y(t) = [...] a cosh(t/a), where t=0 corresponds to the vertex [...]

[39] 수학월드, eq. 7

[40] 루스 아트로444번길

[Yates_13-41] Yates, Robert C. (1952). Curves and their Properties. NCTM. p. 13.

[42] 예이츠 페이지 80

[43] Hall, Leon; Wagon, Stan (1992). "Roads and Wheels". Mathematics Magazine. 65 (5): 283–301. doi:10.2307/2691240. JSTOR 2691240.

[44] Parker, Edward (2010). "A Property Characterizing the Catenary". Mathematics Magazine. 83: 63–64. doi:10.4169/002557010X485120. S2CID 122116662.

[45] Landau, Lev Davidovich (1975). The Classical Theory of Fields. Butterworth-Heinemann. p. 56. ISBN 978-0-7506-2768-9.

[46] 루스 아트 442, 페이지 316

[47] Church, Irving Porter (1890). Mechanics of Engineering. Wiley. p. 387.

[48] 휴웰 페이지 65

[49] 다음 루스 아트 443 페이지 316

[50] 루스 아트 443 페이지 317

[51] 휴웰 페이지 67

[Routh_Art_443_318-52] 루스 아트 443 페이지 318

[53] 다음 루스 아트 443 페이지 317

[54] 쌍곡선 함수의 사용은 Maurer 페이지 107에 따른다.

[55] 다음 양 페이지 342

[56] 토드헌터 미술에 이어. 186

[57] 루스 아트를 보라. 447

[58] Ghostarchive 및 Wayback Machine에 보관:

[59] Routh Art에 이어. 450

[60] 다음 루스 아트 452호

[61] Ira Freeman은 케이블과 도로만 중요한 경우를 조사하였다. 외부 링크 섹션을 참조하십시오.러스는 지지선만이 상당한 무게를 가지고 있는 경우를 연습으로 제시한다.

[62] Routh Art에 이어. 453

[63] Pu, Mingbo; Li, Xiong; Ma, Xiaoliang; Luo, Xiangang (2015). "Catenary Optics for Achromatic Generation of Perfect Optical Angular Momentum". Science Advances. 1 (9): e1500396. Bibcode:2015SciA....1E0396P. doi:10.1126/sciadv.1500396. PMC 4646797. PMID 26601283.

[64] 루스 아트로489번길

[65] 루스 아트로494번길

[66] 루스 아트 따라하기 500

[67] Routh Art를 따른다. 455

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]

[49]

[50]

[51]

[52]

[53]

[54]

[55]

[56]

[57]

[58]

[59]

[60]

[61]

[62]

[63]

[64]

[65]

[66]

[67]

Search

카트리니얼

네임스페이스

더

목차

역사

역삼각형 아치

카트리네이션 다리

해양물체 고정

수학적 설명

방정식

다른 곡선과의 관계

기하학적 특성

과학

분석

체인 및 아치의 모델

곡선에 대한 방정식의 파생

대체 파생

매개변수 결정

변이성 제형식

수직력을 이용한 일반화

통일체 체인

현수교 곡선

동일 강도의 반석기

탄성탄수제

기타 일반화

일반적인 힘 아래 쇠사슬을 묶는다.

참고 항목

메모들

참고 문헌 목록

추가 읽기

외부 링크