드 모르간의 법칙

변환규칙
명제 미적분학
추론 규칙
시사점 소개/제거(modus ponens) 쌍대 도입/제거 접속사 도입/제거 해체소개/제거 분리/가설 삼단 논법 건설적/파괴적 딜레마 흡수/모듀스 톨렌/모듀스 포넨도 톨렌 부정개론
교체규정
연합성 교환성 분배성 이중부정 드 모르간의 법칙 전치 물질적 의미 수출 타우톨로지
술어논리
추론 규칙
보편적 일반화/인스턴스화 실존적 일반화/인스턴스화

드 모르간의 ^[1][2][3][4]법칙은 명제 논리학과 부울 대수학에서 추론 규칙의 유효한 규칙인 변환 규칙입니다. 그들의 이름은 19세기 영국 수학자 아우구스투스 드 모건의 이름을 따서 지어졌습니다. 규칙은 부정을 통해 순수하게 서로에 대한 관점에서 연결과 분리의 표현을 허용합니다.

규칙은 영어로 다음과 같이 표현할 수 있습니다.

• 불협화음의 부정은 부정의 결합입니다.
• 접속사의 부정은 부정의 해체입니다.

아니면

• 두 집합의 결합의 여집합은 그들의 여집합의 교집합과 같습니다.
• 두 집합의 교집합의 여집합은 그들의 여집합들의 합과 같습니다.

아니면

• not (A 또는 B) = (A가 아님) 및 (B가 아님)
• (A와 B)가 아닌 = (A가 아닌) 또는 (B가 아닌)

여기서 "A 또는 B"는 정확히 A 또는 B 중 하나를 의미하는 "exclusive or"가 아니라 A 또는 B 중 적어도 하나를 의미하는 "inclusive or"입니다.

집합론과 부울 대수에서는 다음과 같이 공식적으로 표기됩니다.

${\displaystyle {\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\{\overline {A\cap B}}\={\overline {A}\cup {\overline {B}},\end{aligned}}}$

어디에

• ${\displaystyle A}$ ${\displaystyle A}$와 B ${\displaystyle$ B$}$는 집합입니다.
• $¯${\displaystyle {\$overline${A}}은(는) A ${\displaystyle$ A$\}$의$보체$입니다.
• ${\$이(가) 교차점이고,
• ${\$이(가) 결합입니다.

공식 언어로, 규칙은 다음과 같이 쓰여집니다.

${\displaystyle \neg (P\lor Q)\iff (\negP)\land(\n)egQ),}$

그리고.

${\displaystyle \neg (P\land Q)\iff (\negP)\lor(\n)egQ)}$

어디에

• P와 Q는 명제입니다.
• ${\$$eg}$은(는) 네거티브 로직 연산자(NOT)입니다.
• ${\$은(는) 연결 로직 연산자(AND)입니다.
• ${\$은(는) 분리 논리 연산자(OR)입니다.
• $displaystyle \iff}$는 "논리적 증명에서 대체할 수 있음"을 의미하는 금속학적 기호이며, 종종 "if and only if"로 읽힙니다. P와 Q에 대한 참/거짓 값의 조합에 대해 화살표의 왼쪽과 오른쪽은 평가 후 동일한 참 값을 유지합니다.

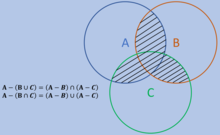
De Morgan 법칙의 또 다른 형태는 오른쪽 그림에서 보는 바와 같이 다음과 같습니다.

${\displaystyle A-(B\cup C)=(A-B)\cap(A-C),}$

${\displaystyle A-(B\cap C)=(A-B)\cup(A-C)}$

규칙의 적용에는 컴퓨터 프로그램 및 디지털 회로 설계에서 논리식의 단순화가 포함됩니다. 드 모건의 법칙은 수학적 이중성에 대한 보다 일반적인 개념의 예입니다.

형식적 표기

연결 규칙의 부정은 다음과 같은 순차적인 표기법으로 작성될 수 있습니다.

$P ∧$$eg (P\land Q)\vdash (\n$$예: P\lor \n$$egQ$

그리고.

${\displaystyle }{\displaystyle (\neg \; P}$$예: P\lor \n$$eg Q)\vdash \n$$eg(P\land$ Q$)\}.$

해체 규칙의 부정은 다음과 같이 기록될 수 있습니다.

$P ∨$$eg (P\lor Q)\vdash (\n$$eg P\land \n$$egQ$

그리고.

${\displaystyle }{\displaystyle (\neg \; P}$$eg P\land \n$$eg Q)\vdash \n$$eg(P\lor$ Q$)\}.$

규칙 형식: 연결 부정

${\displaystyle {\frac {\neg (P\land Q)}{\n따라서 \n예: P\lor \negQ}}$

${\displaystyle {\frac {\n예: P\lor \negQ}{\따라서 \neg (P\land Q)}}}$

그리고 불협화음의 부정.

${\displaystyle {\frac {\neg (P\lor Q)}{\n따라서 \neg P\land \negQ}}$

${\displaystyle {\frac {\neg P\land \negQ}{\따라서 \neg (P\lor Q)}}}$

명제 논리의 진리함수적 항상성 또는 정리로 표현됩니다.

${\displaystyle {\begin{aligned}\neg (P\land Q)&\to (\n예: P\lor \n예 Q),\(\n예: P\lor \negQ)&\n~\neg (P\land Q),\\\neg (P\lor Q)&\to (\neg P\land \n예 Q),\(\neg P\land \negQ)&\n~\neg(P\lor Q),\end{aligned}}$

여기서 $P{\displaystyle }$ ${\displaystyle P}$ 및$$ $Q{\displaystyle }$ ${\displaystyle Q}$는 일부 형식적 시스템에서 표현되는 명제입니다.

대체양식

De Morgan의 법칙은 일반적으로 위의 콤팩트한 형태로 나타나는데, 출력의 음은 왼쪽에, 입력의 음은 오른쪽에 있습니다. 대체할 수 있는 더 명확한 형태는 다음과 같습니다.

${\displaystyle {begin{aligned}(P\land Q)&\왼쪽 긴 화살표\neg(\n)예: P\lor \n예 Q),\(P\lor Q)&\l긴 왼쪽 오른쪽 화살표 \neg(\n)eg P\land \n예).\end{align}}}$

이는 입력과 출력을 모두 반전시키고 대체 작업을 수행할 때 연산자를 변경해야 할 필요성을 강조합니다.

이론 및 부울 대수 설정

집합론과 부울 대수학에서 흔히 "보충 하에서 결합과 교집합 상호작용"이라고 표현되며,^[6] 이는 공식적으로 다음과 같이 표현될 수 있습니다.

${\displaystyle {\begin{aligned}{\overline {A\cup B}}&={\overline {A}}\cap {\overline {B}},\{\overline {A\cap B}}\={\overline {A}\cup {\overline {B}},\end{aligned}}}$

위치:

• $¯$ ${\displaystyle {\overline$ {A}}은(는) A ${\displaystyle$ $A$$\}$이$($) 음인 것이며, 음인 조건 위에 선이 표시됩니다.
• ${\$은(는) 교차점 연산자(AND)이며,
• ${\$은(는) 유니온 연산자(OR)입니다$$.

임의 수의 집합의 합집합과 교집합

일반화된 형태는

${\displaystyle {\bigcap_{i\in I}A_{i}}&\equiv \bigcap_{i\in I}}&\equiv \bigcap_{i\in I}{\equiv {i\in I}A_{i}}&\equiv \bigcap_{i\in I}{\equiv {a_{i}}}$

여기서 저는 아마도 셀 수도 있고 셀 수도 없을 정도로 무한한 인덱싱 집합입니다.

설정된 표기법에서 드 모르간의 법칙은 "선을 끊고 부호를 바꾸다"라는 기호를 사용하여 기억될 수 있습니다.^[7]

공학 기술

전기 및 컴퓨터 공학에서 De Morgan의 법칙은 일반적으로 다음과 같이 쓰여집니다.

${\displaystyle {\overline {(A\cdot B)}}\equiv({\overline {A}}+{\overline {B}})}$

그리고.

${\displaystyle {\overline {A+B}}\equiv {\overline {A}}\cdot {\overline {B}}$

위치:

• ${\$은 논리 AND입니다.
• ${\$은(는) 논리적 논리적 논리적 논리적 논리입니다.
• 오버바는 오버바 아래에 있는 것의 논리적인 NOT입니다.

텍스트검색

De Morgan의 법칙은 일반적으로 부울 연산자 AND, OR, NOT를 사용한 텍스트 검색에 적용됩니다. "고양이"와 "개"라는 단어가 들어 있는 문서 세트를 고려해 보십시오. De Morgan의 법에 따르면 이 두 가지 검색은 동일한 문서 세트를 반환할 것입니다.

검색 A: NOT(고양이 또는 개)

검색 B: (고양이 아님) 및 (개 아님)

"고양이" 또는 "개"를 포함하는 문서의 말뭉치는 다음의 네 가지 문서로 표현될 수 있습니다.

문서 1: "cats"라는 단어만 포함합니다.

문서 2: "개"만 포함합니다.

문서 3: "고양이"와 "개"를 모두 포함합니다.

문서 4: "고양이"와 "개"를 포함하지 않습니다.

검색 A를 평가하기 위해 문서 1, 2, 3에 "(cats OR dogs)" 검색이 적용됩니다. 따라서 해당 검색(즉, 검색 A)의 부정은 다른 모든 것, 즉 문서 4를 강타할 것입니다.

검색 B를 평가하면 검색(NOT cats)은 "cats"가 포함되지 않은 문서(문서 2, 4)에 도달합니다. 마찬가지로 검색(NOT dogs)은 문서 1과 문서 4에 적용됩니다. 이 두 검색(검색 B)에 AND 연산자를 적용하면 이 두 검색에 공통적인 문서(문서 4)가 표시됩니다.

유사한 평가를 적용하여 다음 두 검색이 모두 문서 1, 2, 4를 반환함을 알 수 있습니다.

검색 C: 아니요(고양이와 개),

검색 D: (고양이 아님) 또는 (개 아님).

역사

이 법칙들의 이름은 고전 명제 논리에 이 법칙들의 형식적인 버전을 도입한 ^[8]아우구스투스 드 모르간 (1806–1871)의 이름을 따서 지어졌습니다. De Morgan의 공식은 George Boule이 수행한 논리 대수화의 영향을 받았으며, 나중에 De Morgan의 발견에 대한 주장을 굳혔습니다. 그럼에도 불구하고, 비슷한 관찰이 아리스토텔레스에 의해 이루어졌고, 그리스와 중세의 논리학자들에게 알려졌습니다.^[9] 예를 들어, 14세기에, Ockham의 William은 법을 읽어냄으로써 초래될 단어들을 적었습니다.^[10] 장 부리단(Jean Buridan)은 그의 변증법서(Sumulae de Vatomica)에서 드 모르간의 법칙을 따르는 변환 규칙에 대해서도 설명하고 있습니다.^[11] 여전히 De Morgan은 현대 형식 논리학의 용어로 법칙을 진술하고 논리학 언어에 통합한 공로를 인정받고 있습니다. 드 모건의 법칙은 쉽게 증명될 수 있고, 심지어 하찮게 보일 수도 있습니다.^[12] 그럼에도 불구하고 이 법칙들은 증명과 연역적 논증에서 타당한 추론을 하는 데 도움이 됩니다.

비공식적 증명

드 모르간의 정리는 공식의 전부 또는 일부에서 분해의 부정 또는 연결의 부정에 적용될 수 있습니다.

불협화음의 부정

이의 신청이 기각될 경우 다음과 같은 주장을 고려합니다. "A 또는 B 중 어느 하나가 진실이라는 것은 거짓"이라고 적혀 있습니다.

${\displaystyle \neg(A\lor B).}$

A와 B가 모두 참이 아니라는 것이 확인되면 A와 B가 모두 참이 아니며, 이는 다음과 같이 직접 적을 수 있습니다.

${\displaystyle(\n)eg A)\wedge (\n예 B)}$

A나 B 중 하나가 사실이라면, A와 B의 불일치는 사실일 것이고, 그것의 부정은 거짓이 될 것입니다. 영어로 제시된 이는 "두 가지가 모두 거짓이므로 둘 중 어느 하나가 진실이라는 것도 거짓"이라는 논리를 따른 것입니다.

반대 방향으로 작동하는 두 번째 표현은 A가 거짓이고 B가 거짓(또는 "A가 아니다"와 "B가 아니다"가 참이다)이라고 주장합니다. 이를 알기에 갑과 을의 처분 역시 허위임이 틀림없습니다. 따라서 위 처분의 부정은 사실이어야 하고, 그 결과는 최초의 주장과 동일합니다.

접속사 부정

De Morgan의 정리를 결합에 적용하는 것은 형태와 이론적인 면 모두에서 결합에 적용하는 것과 매우 유사합니다. 다음과 같은 주장을 고려해 보십시오. "A와 B가 모두 진실이라는 것은 거짓입니다"라고 쓰여 있습니다.

${\displaystyle \neg(A\land B).}$

이 주장이 사실이 되려면 A 또는 B 중 어느 하나 또는 둘 다 거짓이어야 합니다. 왜냐하면 둘 다 사실이라면 A와 B의 결합은 사실이므로 부정이 거짓이 될 것입니다. 따라서 A와 B 중 적어도 하나 이상은 거짓이어야 합니다(또는 동등하게 "A 아님"과 "B 아님" 중 하나 이상은 참이어야 합니다). 이것은 직접적으로 다음과 같이 적을 수 있습니다.

${\displaystyle(\n)eg A)\lor(\n)예 B)}$

영어로 제시된 이는 "두 가지가 모두 참이라는 것은 거짓이므로 적어도 그 중 하나는 거짓임에 틀림없다"는 논리를 따른 것입니다.

두 번째 표현은 다시 반대 방향으로 작용하면서 "A가 아니다"와 "B가 아니다" 중 적어도 하나가 참이어야 하며, 또는 동등하게 A와 B 중 적어도 하나가 거짓이어야 한다고 주장합니다. 그들 중 적어도 하나는 거짓이어야 하기 때문에, 그들의 결합도 마찬가지로 거짓일 것입니다. 따라서 해당 결합을 부정하면 참된 표현이 되며, 이 표현은 첫 번째 주장과 동일합니다.

형식적 증명

여기서는 A의 여집합을 나타내기 위해 $A$∁ {\$displaystyle$ A$^{\complement$}}를 사용합니다. The proof that ${\displaystyle (A\cap B)^{\complement }=A^{\complement }\cup B^{\complement }}$ is completed in 2 steps by proving both ${\displaystyle (A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }}$ and ${\displaystyle A^{\complement }\cup B^{\complement }\subseteq (A\cap B{}^{}}$${\displaystyle {)}^{}}$ ${\displaystyle {\complement }^{}}$ ${\displaystyle$A^{\$complement$}\$cup$ B$^{\complement }\subseteq$ ($A\cap$ B$)^{\$complement$$}.

1부

${\displaystyle x}$ ∈${\displaystyle {}^{}}$($A$ ∩ B)를 ∁ {\${\displaystyle \mathrm{displaystyle}}$ x\in (A\cap B)^{\complement }}라고 하자. 그런 다음 $x$ ∉ A ∩ B {\displaystyle x\n$ot$ \$in$ A$\backslash$$cap$ B$}.$

${\displaystyle A}$ ∩ ${\displaystyle B}$ = {${\displaystyle y}$ ∈ $A$ ∧ y ∈ B} {\displaystyle A\cap B =\{\,y\ \ y\in A\weedy\in B\,\}이므로, x ∉ A {\displaystyle x\n}인 경우여야 합니다.$ot$ \in $A} 또는$ x $∉$$B$ {\$displaystyle$ x\n$ot$ \$in$B$\}.$

$만약$ x ∉ A ${\displaystyle$ x\n$ot$ \$in A},$x $∈$$A$ $∁$ ${\displaystyle$ x$in$ A$^{\$complement }}, 따라서 x $∈$ A $∁ ∪$ B $∁$ {\displaystyle x\in A^{\complement }\cup B^{\complement }.

마찬가지로, $만약$ x ∉ B ${\displaystyle$ x\n$ot$ \$in B},$x $∈$$B$ $∁$ ${\displaystyle$ x$in$ B$^{\$complement }}, x $∈$ A $∁ ∪$ B $∁$ {\displaystyle x\in A^{\complement },\cup B^{\complement }.

${\displaystyle 따라서}$ ∀ x${\displaystyle }$(${\displaystyle x}$ ∈ ${\displaystyle ({}^{}}$ ∩ B$)$ ∁ ⟹ $x$∈ A ∁ ∪ B ∁) {\displaystyle \forall x{\Big (}x\in (A\cap B)^{\complement }\cup B^{\complement }{\Big )}};

${\displaystyle 즉},$ (${\displaystyle {}^{}}$ ∩ B) ∁ ⊆ A ∁ ∪ ∁ {\displaystyle (A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }}.

2부

${\displaystyle {}^{}}$을 증명하기 위해, $x$ ∈${\displaystyle {}^{}}$A ∁ ∪ B가 A^{\complement}\cup B^{\complement }에서 {\displaystyle x\$n을$∁한다고 하고, $모순$의 경우 x ∉ ($A$ ∩ B) ∁ {\displaystyle x\n을 가정합니다.$ot$ \in $(A\cap$ B$)^{\complement$ $\}\}.$

${\displaystyle 이}$ 가정 하에서, $x$ ∈ A가 ∩ $B${\$displaystyle$x\in A\cap B}인 경우여야 합니다.

$따라서$ x ∈ A$$${\displaystyle$ x\$in$ A} 및 x ∈ B {\displaystyle x\in B}, 따라서 $x$ ∉ A ∁ {\displaystyle x\n$ot$ \in$A^{\complement }}$ 및 $x$ $∉$ $B$ $∁$ ${\displaystyle$ x\n$ot$ \$in B^{\complement$

그러나 이는 ${\displaystyle {}^{}}$ ∉ A${\displaystyle {}^{}}$∁ ∪ $B$ ∁ {\displaystyle x\n을 의미합니다.$ot$ \$in A^{\complement }\cup$ B$^{\complement }},$ x$∈$$A$$∁ ∪$ B $∁$ ${\$displaystyle x\in A^{\complement }\cup B^{\complement },

$따라서$ 가정 ${\displaystyle x}$ ∉ (A ∩ B) ∁ {\displaystyle x\n${\displaystyle \mathrm{ot}}$$\in (A\cap$ B$)^{\complement }}$는 x${\displaystyle }$$∈$${\displaystyle {}^{}}$A${\displaystyle {}^{}}$$∩$ B)가 ${\displaystyle$ x\$in$(A$\backslash$cap B)^{\complement }를 $∁$한다는 것을 의미합니다.

${\displaystyle 따라서}$,${\displaystyle }$∀ ${\displaystyle {}^{}}$ (${\displaystyle x}$∈ A${\displaystyle }$∁ ∪ B ∈ x ∁ (A ∩ B) ∁ ⟹) {\displaystyle \forall x{\Big (}x\in A^{\complement }\cup B^{\complement }\in (A\cap B)^{\complement }{\Big)}},

$즉$, ${\displaystyle {}^{}}$∁ ∪${\displaystyle }$B ∁ ⊆$(A$ ∩ B$)$ ∁ {\displaystyle A^{\complement }\cup B^{\complement }\subseteq (A\cap B)^{\complement }.

결론

${\displaystyle {}^{}}$∁ ∪${\displaystyle B}$ ∁ ⊆($A$ ∩${\displaystyle {}^{}}$B)가 {\$displaystyle A$^{\$complement$ }\cup B^{\complement }\subseteq (A\cap B)^{\complement }} 및 (A ∩ B) ∁ ⊆ A ∁가 {\displaystyle (A\cap B)^{\complement }\subseteq A^{\complement }\cup B^{\complement }를$$∁하면, $그러면$(${\displaystyle A}$ ∩ B) ∁ = A ∁ ∪$B$ ∁ {\displaystyle (A\cap B)^{\complement } = A^{\complement }\cup B^{\complement }}; 이것은 De Morgan 법칙의 증명을 마칩니다.

$다른$ De Morgan의 ${\displaystyle 법칙}$인$$(${\displaystyle A}$ ∪ B) ∁ = A ∁ ∩$B$ ∁ {\$displaystyle$ (A\cup B)^{\$complement$} = A^{\cap B^{\complement}}도 마찬가지로 증명됩니다.

De Morgan 이중성 일반화

고전 명제 논리의 확장에서 이중성은 여전히 유지됩니다(즉, 모든 논리 연산자에게 항상 이중성을 찾을 수 있음). 부정을 지배하는 정체성이 존재하는 경우 항상 다른 것의 De Morgan 이중인 연산자를 도입할 수 있기 때문입니다. 이는 고전 논리에 기초한 논리학의 중요한 속성, 즉 부정 정상 형태의 존재로 이어집니다. 모든 공식은 부정이 공식의 비논리적 원자에만 적용되는 다른 공식과 동등합니다. 네거티브 노멀 형태의 존재는 많은 응용 프로그램을 추진합니다. 예를 들어, 논리 게이트의 유형을 조작하는 데 사용되는 디지털 회로 설계와 공식의 연결 노멀 형태와 연결 노멀 형태를 찾아야 하는 형식 논리에서 말입니다. 컴퓨터 프로그래머들은 복잡한 논리 조건을 단순화하거나 적절하게 부정하기 위해 이를 사용합니다. 그들은 또한 종종 기초 확률 이론의 계산에 유용합니다.

기본 명제 p, q, ...에 따라 임의의 명제 연산자 P(p, q, ...)의 이중을 정의하면 다음과 같이 정의되는$$ 연산자 ${\displaystyle {Pd}^{}}$ ${\$가 됩니다.

${\displaystyle {\mbox{P}}^{d}(p,q,...)=\neg P(\n)예프,\nq,\dots)}$

술어와 모달 논리로 확장

이 이중성은 양자화기로 일반화될 수 있으므로, 예를 들어 보편적 양자화기와 실존적 양자화기는 이중입니다.

${\displaystyle \ for all x\,P(x)\equiv \neg [\exists x\,\n]eg P(x)}$

${\displaystyle \exists x\,P(x)\equiv \neg [\forall x\,\neg P(x)}$

이러한 계량기 이중성을 De Morgan 법칙과 연관시키기 위해, 도메인 D에 다음과 같은 소수의 요소를 포함하는 모형을 설정합니다.

D = {a, b, c}.

그리고나서

${\displaystyle \fall x\,P(x)\equiv P(a)\land P(b)\land P(c)}$

그리고.

${\displaystyle \exists x\,P(x)\equiv P(a)\lor P(b)\lor P(c).}$

하지만 드 모건의 법칙을 이용하면

${\displaystyle P(a)\land P(b)\land P(c)\equiv \neg(\n)eg P(a)\lor \neg P(b)\lor \neg P(c)}$

그리고.

${\displaystyle P(a)\lor P(b)\lor P(c)\equiv \neg(\n)eg P(a)\land \neg P(b)\land \neg P(c),}$

모델에서 계량기 이중성을 확인합니다.

그런 다음, 양자 이중성은 상자("필수")와 다이아몬드("가능") 연산자를 연관시키는 모달 논리로 더 확장될 수 있습니다.

${\displaystyle \Box p\equiv \n예: \다이아몬드 \negp,}$

${\displaystyle \Diamond p\equiv \neg \Box \n예}$

아리스토텔레스는 가능성과 필요성의 산술 모달리티에 적용할 때 이 사례를 관찰했으며, 일반 모달 로직의 경우 Kripke 시맨틱스를 사용하여 모델을 설정함으로써 이러한 모달 연산자의 정량화에 대한 관계를 이해할 수 있습니다.

직관주의적 논리로

드 모르간 법칙의 네 가지 함의 중 세 가지는 직관주의 논리에 있습니다. 구체적으로, 우리는

${\displaystyle \neg (P\lor Q)\,\leftright 화살표 \,{\big(})(\n)egP)\land(\n)egQ){\big )},}$

그리고.

${\displaystyle {\big(})(\n)egP)\lor(\n)eg Q){\big )}\,\to \,\neg(P\land Q).}$

마지막 암시의 반대는 순수한 직관주의 논리에 성립하지 않습니다. 즉, 합동 ${\displaystyle \mathrm{명제}}$ $P$∧ Q {\$displaystyle P$\land Q}의 실패는 반드시 두 접속사 중 어느 하나의 실패로 해결될 수 없습니다. 예를 들어 앨리스와 밥이 둘 다 데이트 상대에게 나타난 경우가 아니라는 것을 아는 것부터 누가 나타나지 않았는지를 따르지 않는 것입니다. 후자의 원리는 약한 제외된 $중간{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{WEPEM}}$ ${\$의 원리와 동등합니다$.,$

${\displaystyle(\n)egP)\lor\neg(\n)eg P)}$

이 약한 형태는 중간 논리의 기초로 사용될 수 있습니다. 존재 문과 관련된 실패 법칙의 개선된 버전은 덜 제한된 전능 ${\displaystyle \mathrm{LPO}}${\$displaystyle${\$mathrm {LLPO}}}$을(를) 참조하십시오$.$ ${\displaystyle \mathrm{그러나}}$ ${\displaystyle \mathrm{WLP}}${\$displaystyle${\$mathrm {WLPO}}$과는 다릅니다$.$

$부정이$¬ P ${\displaystyle$ \n일 경우 나머지 세 De Morgan 법칙의 유효성은 여전히 유효합니다.$eg P}$은(는) 임의의 상수 술어 C에 $대한$ 암시 ${\displaystyle P}$ $→$ C {\$displaystyle P\$to C}로 대체되며, 이는 위 법칙들이 최소 논리에서 여전히 참임을 의미합니다.

위와 유사하게 계량기 법칙은 다음과 같습니다.

${\displaystyle \fall x\,\nEg P(x)\,\좌우 화살표 \,\neg \exists x\,P(x)}$

그리고.

${\displaystyle \exists x\,\n예를 들어, P(x)\,\to \,\neg \forall x\,P(x).}$

a tautology는 최소 논리에서도 고정된 $Q{\displaystyle }$ ${\displaystyle Q}$를 암시하는 것으로 대체되는 반면$,$ 마지막 법칙의 반대는 일반적으로 참일 필요가 없습니다.

게다가, 아직도 한 사람은

${\displaystyle(P\lor Q)\,\to\,\neg {\big(})(\n)egP)\land(\n)egQ){\big )},}$

${\displaystyle(P\land Q)\,\to\,\n\neg {\big(})(\n)egP)\lor(\n)egQ){\big )},}$

${\displaystyle \ for all x\,P(x)\,\to \,\n예를 들어, \exists x\,\neg P(x),}$

${\displaystyle \는 x\,P(x)\,\에서 \,\n까지 존재합니다.eg \forall x\,\neg P(x),}$

그러나 이들의 반전은 제외된 중간, ${\displaystyle \mathrm{PEM}}${\$displaystyle {\mathrm$ {$PEM}}}$을 의미합니다$.$

컴퓨터공학과

De Morgan의 법칙은 회로 설계의 단순화를 목적으로 컴퓨터 공학과 디지털 논리학에서 널리 사용되고 있습니다.^[13]

참고 항목

• 동형화 – 양의 논리와 음의 논리 사이의 동형화로서 연산자가 아님
• 부울 대수학의 주제 목록
• 설정된 신원 및 관계 목록
• 포지티브 로직

참고문헌

외부 링크

• "Duality principle", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "de Morgan's Laws". MathWorld.
• 행성수학의 드 모건의 법칙.
• 논리와 언어의 이중성, 철학 인터넷 백과사전.