일치 필터

신호 처리에서, 알 수 없는 신호에서 템플릿의 존재를 감지하기 위해 알려진 지연 신호 또는 템플릿을 알 수 없는 신호와 상관시켜 일치하는 필터를 얻는다.^[1][2] 이것은 시간이 경과한 템플릿의 조합된 버전으로 미지의 신호를 교란하는 것과 같다. 일치된 필터는 부가적인 확률적 노이즈가 있는 상태에서 신호 대 잡음 비(SNR)를 최대화하기 위한 최적의 선형 필터다.

일치하는 필터는 일반적으로 알려진 신호가 송신되는 레이더에 사용되며, 반사된 신호는 나가는 신호의 공통 요소를 검사한다. 펄스 압축은 일치하는 필터링의 예다. 그것은 충동 반응이 입력 펄스 신호와 일치하기 때문에 그렇게 불린다. 2차원 일치 필터는 예를 들어 X선 관측치의 SNR을 개선하기 위해 이미지 처리에 일반적으로 사용된다. 일치 필터링은 SNR을 최대화하기 위한 LTI(선형 시간 불변성) 필터를 적용한 계량화 기법이다.^[3] 원래는 북쪽 필터로도 알려져 있었다.^[4]

파생

행렬 대수학을 통한 파생

다음 절은 이산 시간 시스템의 일치 필터를 도출한다. 연속 시간 시스템의 파생은 합산으로 대체되는 합계와 유사하다.

일치하는 필터는 출력 신호 대 잡음 비를 최대화하는 $선형{\displaystyle }$ 필터 h ${\displaystyle h$이다.

${\displaystyle \y[n]=\sum _{k=-\infit }^{\h[n-k]x[k],}$

여기서 $x{\displaystyle }$[ ${\displaystyle k}$ ${\displaystyle ]}$ ${\displaystyle x[k]}$은(는) 독립 변수 $k{\displaystyle }$ ${\displaystyle k$의 함수로서의 입력이고$$ y [${\displaystyle n]}$ ${\displaystyle y[n]}$은(는) 필터링된 출력이다. 위(LTI 시스템 이론 참조)와 같이 우리는 대부분 필터를 콘볼루션 시스템의 임펄스 반응으로 표현하지만, 곧 보게 될 내부 제품의 맥락에서 일치된 필터를 가장 쉽게 생각할 수 있다.

기하학적 인수를 호출하여 출력 신호 대 잡음 비를 최대화하는 선형 필터를 도출할 수 있다. 일치된 필터 뒤의 직관은 수신된 신호(벡터)와 신호와 평행한 필터(다른 벡터)를 상호 연관시켜 내부 제품을 최대화하는 것에 의존한다. 이것은 신호를 강화시킨다. 가법 확률형 노이즈를 고려할 때 노이즈와 직교하는 필터를 선택하여 노이즈로 인한 출력을 최소화해야 하는 추가적인 어려움이 있다.

문제를 공식적으로 정의합시다. 출력 신호 대 잡음 비를 최대화하는 필터($H{\displaystyle }$ ${\displaystyle h$를 구하며, 여기서 출력은 필터의 내부 제품이고 관찰된 신호 $x{\displaystyle }$ ${\displaystyle x$

관측된 신호는 바람직한 신호 $s{\displaystyle }$ ${\displaystyle s}$과(와) $가법{\displaystyle }$ 노이즈$$v {\$displaystyle v}$로 구성된다$.$

${\displaystyle \ x=s+v.\,}$

소음의 공분산 행렬을 정의해 봅시다. 이 행렬이 에르미트 대칭성을 가지고 있다는 것을 상기시켜봅시다. 이 행렬은 파생에서 유용하게 사용될 속성이다.

${\displaystyle \ R_{v}=E\{v^{\mathrm {H}\}\,}$

여기서 v ${\displaystyle {H\mathrm{}}^{}}$ ${\$은(는) v$${\$displaystyle v$의 결합 전이를 나타내고$$ E ${\displaystyle E}$은(는) 기대를 나타낸다. $출력{\displaystyle }$ y {\$displaystyle$ y$}$을(를$)$ 필터의 내부 제품 및 관찰된 신호를 다음과 같이 부르자.

${\displaystyle \y=-\infit _{k=-}^{\nothy}{*]x[k]=h^{\mathrm {H}{}x=h^{}}}}\mathrm {H}}}}}}{v=y_{s}+y}y}y.}$

이제 노이즈로 인해 출력 전력에 대한 원하는 신호로 인한 출력 전력의 비율로 목표 기능인 신호 대 잡음 비를 정의한다.

${\displaystyle \mathrm {SNR} ={\frac { y_{s} ^{2}}:{}E\{{y_{v} ^{2}\}}.}$

위 내용을 다시 작성한다.

${\displaystyle \mathrm {SNR} ={\frac {h^{\mathrm {H}s ^{2}}:{E\{h^{\mathrm {H}{}v{2}\}}}}}}.}$

$h{\displaystyle }$ ${\displaystyle h}$를 선택하여 이 수량을 최대화하고자 함$.$ 목표함수의 분모를 확대하여 다음과 같이 하고 있다.

${\displaystyle \ E\{ h^{\mathrm {H} }v ^{2}\}=E\{(h^{\mathrm {H} }v){(h^{\mathrm {H} }v)}^{\mathrm {H} }\}=h^{\mathrm {H} }E\{vv^{\mathrm {H} }\}h=h^{\mathrm {H} }R_{v}h.\,}$

이제$$ S ${\displaystyle \mathrm{N}}$ ${\displaystyle \mathrm{R}}$ ${\$가)

${\displaystyle \mathrm {SNR} ={\frac {h^{\mathrm {H}s ^{2}}:{h^{\mathrm {H}}}{{R_{v}h}}}.}$

우리는 매트릭스 조작으로 이 표현을 다시 쓸 것이다. 이렇게 비생산적으로 보이는 조치의 이유는 곧 명백해질 것이다. 공분산 행렬 $R{\displaystyle {}_{}}$ ${\displaystyle v_{}}$ ${\$의 은둔자 대칭을 이용하여, 우리는 쓸 수 있다$.$

${\displaystyle \mathrm {SNR} ={\frac { {(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s) ^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}},}$

우리는 이 표현에서 상한을 찾고 싶다. 이를 위해 우리는 먼저 카우치-슈바르츠 불평등의 형태를 인식한다.

${\displaystyle \ a^{\mathrm {H}}b ^{2}\leq (a^{\mathrm {H}}a)(b^{\mathrm {H}b),\,}$

즉, 두 벡터의 내적 생산물의 제곱은 벡터의 개별적 내적 생산물만큼만 클 수 있다. 이 개념은 일치하는 필터 뒤의 직관으로 되돌아간다. 이 상한은 두 벡터 $a{\displaystyle }$ ${\displaystyle a}$과 $b{\displaystyle }$ ${\displaystyle b}$이(가) 평행할$$ 때 달성된다. 위와 같은 기하학적 불평등을 고려하여$$ S $N{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{R}}$ ${\$ {$SNR}}$에 상한선을 표시함으로써 파생을 재개한다.

${\displaystyle \mathrm {SNR} ={\frac { {(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s) ^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq {\frac {\left[{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)\right]\left[{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)\right]}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}.}$

우리의 용감한 매트릭스 조작은 이제 결실을 맺었다. 상한을 나타내는 표현은 다음과 같이 크게 단순화할 수 있다.

${\displaystyle \mathrm {SNR} ={\frac { {(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s) ^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}\leq s^{\mathrm {H} }R_{v}^{-1}s.}$

우리가 선택한다면 이 상한선을 달성할 수 있어

${\displaystyle \ R_{v}^{1/2}h=\알파 R_{v}^{-1/2}s}$

여기서 $\alpha {\displaystyle }$ ${\displaystyle \alpha }$은(는) 임의의 실제 수입니다. 이를 확인하기 위해 ${\displaystyle \mathrm{출력}}$ ${\displaystyle \mathrm{S}}$ N R ${\$ {$SNR} }$에 대한 식을 연결하십시오$.$

${\displaystyle \mathrm {SNR} ={\frac { {(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{-1/2}s) ^{2}}{{(R_{v}^{1/2}h)}^{\mathrm {H} }(R_{v}^{1/2}h)}}={\frac {\alpha ^{2} {(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s) ^{2}}{\alpha ^{2}{(R_{v}^{-1/2}s)}^{\mathrm {H} }(R_{v}^{-1/2}s)}}={\frac { s^{\mathrm {H} }R_{v}^{-1}s ^{2}}{s^{\mathrm {H} }R_{v}^{-1}s}}=s^{\mathrm {H} }R_{v}^{-1}s.}$

따라서, 최적의 일치 필터는

${\displaystyle \ h=\alpha R_{v}^{-1}s.}$

우리는 종종 단일화에 대한 노이즈로 인해 필터 출력 전력의 기대치를 정상화하기로 선택한다. 즉, 우리는 제약한다.

${\displaystyle \ E\{y_{v}^{2}\}=1.\,}$

이 제약조건은 우리가 $해결$할 수 있는$α$ {\displaystyle \$alpha$ $\}$의 값을 의미한다.

${\displaystyle \ E\{y_{v} ^{2}\}=\알파^{2}s^{{}s^{\mathrm {H}}{R_{v}^{-1}s=1,}$

양보하는

${\displaystyle \alpha ={\frac {1}{\sqrt {s^{\mathrm {H}}}{R_{v}^{-1}s}}}},$

정규화된 필터를 제공하고

${\displaystyle \h={\frac {1}{\sqrt {s^{}{{H}}}{R_{v}s}}R_{v}^{1}s.}$

우리가 콘볼루션 시스템 필터의$$ 임펄스 반응 h ${\displaystyle h}$을(를) 쓰고자 한다면, 그것은 $단순히{\displaystyle }$ 입력$$s {\$displaystyle$ s$}$의 복잡한 결합 시간 역전이 된다$.$

이산 시간 내에 일치하는 필터를 도출했지만, 연속 신호 $s{\displaystyle }$( ${\displaystyle t}$) {\$displaystyle$ s($t$ 연속 $노이즈{\displaystyle }$ v${\displaystyle }$( t${\displaystyle }$) ${\displaystyle$ v$(t)}$을$($를) 가정하여 $R{\displaystyle {}_{}}$ {\displaystyle $v_$${v}$를 노이즈의 연속 시간 자기 상관 함수로$$ 대체하면 개념을 연속 시간 시스템으로 확장할 수 있다. ${\displaystyle 및}$ 연속 필터 $h{\displaystyle }$( t${\displaystyle }$) ${\displaystyle h(t$

라그랑지안을 통한 파생

또는, 우리는 라그랑지안과의 최대화 문제를 해결함으로써 일치하는 필터에 대해 해결할 수 있다. 다시 한번, 일치된 필터는 확률적 첨가 노이즈에서 필터링된 결정론적 신호의 출력 신호 대 잡음 비(${\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{N}}$ ${\displaystyle \mathrm{R}}$ ${\$$}$ )를 최대화하기 위해 노력한다. 관찰된 순서는, 다시,

${\displaystyle \ x=s+v,\,}$

노이즈 공분산 행렬과 함께,

${\displaystyle \ R_{v}=E\{v^{\mathrm {H}\}\,}$

신호 대 잡음 비율은

${\displaystyle \mathrm {SNR} ={\frac { y_{s} ^{2}}:{}E\{{y_{v} ^{2}\}}}$

여기서 $y{\displaystyle {}_{}}$ ${\displaystyle s_{}}$= ${\displaystyle H^{}}$ s ${\displaystyle y_{s}=h^{\mathrm {H}s}$ 및$$ $y{\displaystyle {}_{}}$ ${\displaystyle v_{}}$= ${\displaystyle {H\mathrm{}}^{}}$ ${\displaystyle v^{}}$ ${\displaystyle y_{v}=h^{\mathrm {H}}}v$

분자의 표현을 평가해 보면,

${\displaystyle \ y_{s} ^{2}={y_{s}^{}}}^{}y_{s}=h^{}}\mathrm {H}ss^{\mathrm}{h.\},}$

그리고 분모에서는

${\displaystyle \ E\{ y_{v} ^{2}\}=E\{{y_{v}}^{\mathrm {H} }y_{v}\}=E\{h^{\mathrm {H} }vv^{\mathrm {H} }h\}=h^{\mathrm {H} }R_{v}h.\,}$

신호 대 잡음 비율은

${\displaystyle \mathrm {SNR} ={\frac {h^{\mathrm {H}{}ss^{}h}{h^{}{h^{}}\mathrm {H}{}}{{R_{v}h}}}.}$

이제 분모를 1로 제한하면 $S{\displaystyle \mathrm{}}$ ${\displaystyle \mathrm{N}}$ ${\displaystyle \mathrm{R}}$ ${\$의 최대화 문제가 분자의 최대화로 축소된다$$. 그런 다음 Lagrange 승수를 사용하여 문제를 공식화할 수 있다.

${\displaystyle \ h^{\mathrm {H} }R_{v}h=1}$

${\displaystyle \{\mathcal {L}=h^{\mathrm {H}{}ss^{}\mathrm {H}}h+\lambda(1-h^{\mathrmatrm {}}{R_{v}h)}}}$

${\displaystyle \\nabla _{h^{*}{\mathcal {L}=ss^{\mathrm {H}}}h-\lambda R_{v}h=0}$

${\displaystyle \ (ss^{\mathrm {H})h=\lambda R_{v}h}$

우리가 일반화된 고유값 문제로 인식하는 것

${\displaystyle \ h^{\mathrm {H}}}}(ss^{\mathrm {H})h=\lambda h^{\mathrm {H}{}R_{v}h.}$

$s{\displaystyle }$ ${\displaystyle {H\mathrm{}}^{}}$ ${\$이(가) 단위 순위이기$$ 때문에 0이 아닌 고유값이 하나만 있다. 이 고유값이 동일하다는 것을 알 수 있다.

${\displaystyle \lambda _{\max }=s^{\mathrm {H}{}R_{v}^{-1}s,}$

다음과 같은 최적의 일치 필터 생성

${\displaystyle \h={\frac {1}{\sqrt {s^{}{{H}}}{R_{v}s}}R_{v}^{1}s.}$

이는 이전 항에서 발견된 결과와 동일하다.

최소 제곱 추정기로 해석

파생

일치하는 필터링은 또한 주어진 모델 또는 템플릿의 최적 위치와 배율을 위한 최소 제곱 추정기로 해석될 수 있다. 다시 한 번 관찰된 시퀀스를 다음과 같이 정의한다.

${\displaystyle \ x_{k}=s_{k}+v_{k}\,}$

여기서 $v{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$는 상관 관계가 없는 0 평균 노이즈다. 신호 $s{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$은(는) ${\displaystyle {알려진}_{}}$ 모델 시퀀스 $f{\displaystyle {}_{}}$ ${\$의 스케일링 및 시프트 버전으로 가정한다$.$

${\displaystyle \s_{k}=\mu_{0}\cdot f_{k-j_{0}}}$

관측된 시퀀스 $x{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$와 a "prob" 사이의 최소 제곱 잔차를 최소화하여$$ 알 수 없는 시프트 ${\displaystyle {j\mathrm{}}_{}}$ 0 ${\$ 및$$ $스케일링{\displaystyle {}^{}}$ μs$$$\mu {\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}${\$displaystyle \mu _{0}$에 대한 최적 $추정치{\displaystyle {}^{}}$ j${{{\{\$displaystimprob$}$을 구하고자 한다.ig sequence" $h{\displaystyle {}_{}}$ -${\displaystyle j_{}}$ ${\$:

${\displaystyle \j^{*},\mu ^{*}=\arg \min _{j,\mu }\sum _{k}-{k}-\mu \cdot h_{j-k}\오른쪽)^{2}}$

적절한 $h{\displaystyle {}_{}}$ ${\displaystyle j_{}}$ -${\displaystyle k_{}}$ ${\$은(는) 나중에 일치하는 필터로 판명되지만, 아직$$ 지정되지 않았다. $x{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$ 확장 및 합계 내 제곱$$

${\displaystyle \ j^{*},\mu ^{*}=\arg \min _{j,\mu }\left[\sum _{k}(s_{k}+v_{k})^{2}+\mu ^{2}\sum _{k}h_{j-k}^{2}-2\mu \sum _{k}s_{k}h_{j-k}-2\mu \sum _{k}v_$${k}h_{j-k}\right]}$.

괄호 안의 첫 번째 항은 상수(관측 신호가 주어지기 때문에)이며 최적 용액에 영향을 미치지 않는다. 마지막 항은 소음이 상관 관계가 없고 평균이 0이기 때문에 일정한 기대값을 갖는다. 따라서 최적화에서 두 항을 모두 삭제할 수 있다. 기호를 반전시킨 후 등가 최적화 문제를 얻는다.

${\displaystyle \ j^{*},\mu ^{*}=\arg \max _{j,\mu }\left[2\mu \sum _{k}s_{k}h_{j-k}-\mu ^{2}\sum _{k}h_{j-k}^{2}\right]}$.

파생상품 w.r.t. $\mu {\displaystyle }$ ${\displaystyle \mu$}을(를) 0으로$$ 설정하면$$$\mu s{\displaystyle {}^{}}$ ${\$ :

${\displaystyle {㎕\ast }^{}}$=$k$ ${\displaystyle \frac{\underset{}{}{}_{}}{}}$ ${\displaystyle \frac{j_{}}{}}$ -${\displaystyle \frac{k_{}}{}}$ ${\displaystyle \frac{{}_{}}{\underset{}{}}}$ k ${\displaystyle \frac{\underset{}{h}}{}}$ ${\displaystyle \frac{j_{}^{}}{}}$ -${\displaystyle \frac{k_{}^{}}{}}$ ${\displaystyle \frac{{\mathrm{}}_{}^{}}{}}$ ${\$k}h_${j-k}}}}}{j-k}}}}:{2$

이것을 우리의 목표 기능에 삽입하면 $j{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$ ${\$ j$^{*}}$:

${\displaystyle \ j^{*}=\arg \max _{j}{\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}}$.

분자는 Cauchy-Schwarz 부등식을 통해 상한을 지정할 수 있다.

${\displaystyle \ {\frac {\left(\sum _{k}s_{k}h_{j-k}\right)^{2}}{\sum _{k}h_{j-k}^{2}}}\leq {\frac {\sum _{k}s_{k}^{2}\cdot \sum _{k}h_{j-k}^{2}}{\sum _{k$$}h_{j-k}^{2}}=\sum _{k}s_{k}^{2}=\mathrm {const$

최적화 문제는 동일성이 이 식에서 유지될 때 최대치를 가정한다. 카우치-슈바르츠 불평등의 성질에 따르면, 이것은 오직 다음과 같은 경우에만 가능하다.

${\displaystyle h_{}}$ ${\displaystyle j_{}}$ -${\displaystyle k_{}}$=${\displaystyle \nu }$ ${\displaystyle {}_{}}$ ${\displaystyle k_{}}$= ${\displaystyle \kappa }$ f k = ${\displaystyle \cdot }$ ${\displaystyle {}_{}}$ ${\displaystyle k_{}}$- ${\displaystyle {{}_{}}_{}}$ ${\displaystyle {{0\mathrm{}}_{}}_{}}$ ${\$\$h_{j-k}=\nu \cdot s_{k}=\kappa \cdot f_{k-j_{0$

임의의 0이 아닌 상수 ${\displaystyle \nu$} 또는$$ $\kappa {\displaystyle }$ ${\displaystyle \kappa$ $\}\}$의 경우, 원하는 대로$$ $j{\displaystyle {}^{}}$ ${\displaystyle {\ast }^{}}$= ${\displaystyle {}_{}}$ ${\displaystyle {0\mathrm{}}_{}}$ ${\$에서 최적의 솔루션을 얻는다. 따라서 당사의 "프로빙 시퀀스" h${\displaystyle j_{}}$ ${\$은(는) 신호 모델 ${\displaystyle f_{}}$ $k{\displaystyle {}_{}}$- ${\displaystyle {{j\mathrm{}}_{}}_{}}$ ${\displaystyle {{}_{}}_{}}$ ${\$에 비례해야 하며$$, 편리한 선택 $\kappa {\displaystyle }$= ${\displaystyle 1}$ ${\displaysty \kappa =1}$은 일치하는 필터를 생성한다.

${\displaystyle h_{}}$ ${\displaystyle k_{}}$= ${\displaystyle {}_{}}$ -${\displaystyle k_{}}$ ${\$\$h_{k}=f_{-k$

필터가 미러링된 신호 모델이라는 점에 유의하십시오. 이를 통해 최적의 $상태$를 찾기 위해 적용할$$ $\sum {\displaystyle \underset{k}{}}$ ${\displaystyle \underset{}{}{}_{}}$ k ${\displaystyle h_{}}$ ${\displaystyle j_{}}$ -${\displaystyle {}_{}}$k ${\$ 연산 ∑ k ${\$와 일치하는 필터 ${\displaystyle h_{}}$ ${\$ 간의 경합이 실제로 이루어지도록 한다$.$ 필터링된 시퀀스는 관측된 시퀀스 $x{\displaystyle {}_{}}$ ${\displaystyle k_{}}$ ${\$가 신호 모델 ${\displaystyle f_{}}$ ${\$와 가장 잘 일치하는$$ 위치에서 최대값을 가정한다$.$

시사점

일치하는 필터는 다양한 방법으로 파생될 ^[2]수 있지만 최소 제곱 절차의 특별한 경우로서 가우스 소음 모델과 관련 휘틀우도의 맥락에서 최대우도 방법으로 해석될 수도 있다.^[5] 전송된 신호에 알 수 없는 파라미터(예: 도달 시간, 진폭 등)가 없는 경우 일치하는 필터는 Neyman-Pearson 보조정리자에 따라 오류 확률을 최소화한다. 그러나 정확한 신호는 일반적으로 필터링 프로세스에서 효과적으로 추정(또는 장착)되는 알 수 없는 파라미터에 의해 결정되므로 일치하는 필터는 일반화된 최대우도(테스트-) 통계량을 구성한다.^[6] 필터링된 시계열은 종단우도, 시간 매개변수의 함수로써 최대 조건부우도로 해석될 수 있다.^[7] 이는 특히 오류 확률(Neyman과 Pearson의 관점에서, 즉 주어진 거짓 경보 확률에^[8] 대한 탐지 확률의 최대화에 관한 것)이 반드시 최적의 것은 아니라는 것을 암시한다. 일반적으로 일치하는 필터에 의해 최대화되어야 하는 신호 대 잡음비(${\displaystyle \sqrt{SNR\mathcal{}}}$)라고 하는 것은 2 log ${\displaystyle \sqrt{\log }}$ ( L$){\$ ${$$L})}}$에 해당하며$,$ $여기$서 L ${\$ {$L}$은 (조건부) 최대우도비이다$$.^{[7] [nb 1]}

일치하는 필터의 구성은 알려진 소음 스펙트럼에 기초한다. 그러나 실제로는 소음 스펙트럼은 대개 데이터로부터 추정되며 따라서 제한된 정밀도까지만 알려져 있다. 불확실한 스펙트럼의 경우 일치하는 필터는 가우스 노이즈에서도 유리한 특성을 가진 보다 강력한 반복 절차로 일반화할 수 있다.^[7]

주파수 영역 해석

주파수 영역에서 볼 때, 일치된 필터는 가장 큰 신호 대 잡음 비(즉, 노이즈가 상대적으로 낮은 큰 중량)를 나타내는 스펙트럼 구성요소에 가장 큰 가중치를 적용한다는 것이 명백하다. 일반적으로 이것은 평평하지 않은 주파수 응답을 요구하지만, 관련 "분산"은 원래 파형이 알려져 있고 목적은 배경 노이즈에 대해 이 신호를 검출하는 레이더 및 디지털 통신과 같은 상황에서 우려할 만한 이유가 되지 않는다. 기술적 측면에서 일치된 필터는 (열희석성) 주파수 영역 데이터(노이즈 스펙트럼을 통해 "중량"이 결정되는 경우, 이전 섹션 참조)에 기초한 가중 최소 제곱법 또는 동등하게 희어진 데이터에 적용되는 최소 제곱법이다.

예

레이더와 음파탐지기에서 일치하는 필터

일치된 필터는 종종 신호 검출에 사용된다.^[1] 예를 들어, 물체의 신호를 반사하여 물체의 거리를 판단하려고 한다고 가정합시다. 우리는 1 Hz의 순수한 톤의 사인파이를 전송하는 것을 선택할 수 있다. 우리는 수신된 신호가 노이즈가 추가된 전송 신호의 감쇠되고 위상 변화된 형태라고 가정한다.

물체의 거리를 판단하기 위해 수신된 신호를 일치된 필터와 상호 연관시킨다. 백색(상관되지 않은) 노이즈의 경우, 또 다른 순수 톤 1-Hz 사인파이다. 일치된 필터 시스템의 출력이 특정 임계값을 초과하면 수신된 신호가 물체에서 반사되었을 가능성이 높은 것으로 결론을 내린다. 전파속도와 반사신호를 처음 관찰한 시간을 이용하여 물체의 거리를 추정할 수 있다. 특별히 설계된 방법으로 펄스의 모양을 바꾸면 신호 대 잡음 비와 거리 분해능이 일치된 필터링 후에도 향상될 수 있다: 이것은 펄스 압축이라고 알려진 기술이다.

또한 일치하는 필터를 모수 추정 문제에 사용할 수 있다(추정 이론 참조). 이전의 예시로 돌아가기 위해, 우리는 그 위치 외에 그 물체의 속도를 추정하기를 원할지도 모른다. 도플러 효과를 이용하기 위해 수신 신호의 주파수를 추정하고자 한다. 이를 위해 수신된 신호를 다양한 주파수에서 사인파 필터의 몇 가지 일치 필터와 상호 연관시킬 수 있다. 가장 높은 출력의 일치된 필터는 높은 확률로 반사 신호의 주파수를 밝혀내고 물체의 속도를 결정하는 데 도움을 줄 것이다. 이 방법은 사실상 이산 푸리에 변환(DFT)의 간단한 버전이다. DFT는 $N{\displaystyle }$ ${\displaystyle N}$ 값$$ 복합 입력을 취하여 $N{\displaystyle }$ ${\displaystyle N}$의 서로 다른 주파수에서 복합 지수들에 $해당$하는 N$${\$displaystyle$N} 일치$$ 필터와 상호 연관시켜 sinu의 상대적 진폭과 위상에 $해당$하는 N ${\displaystyle N}$ 복합$$ 값 숫자를 산출한다.소이달 구성 요소(대상 표시 이동 참조).

디지털 통신의 일치 필터

일치하는 필터는 통신에도 사용된다. 송신기에서 소음이 많은 채널을 통해 수신기로 이진 메시지를 전송하는 통신 시스템의 맥락에서, 일치하는 필터를 사용하여 소음이 많은 수신 신호에서 전송된 펄스를 검출할 수 있다.

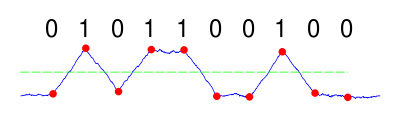
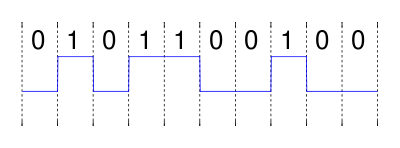
특정 채널을 통해 NRZ(Non-polar Non-return-to-zero)로 코드화된 "0101100100" 시퀀스를 전송한다고 상상해 보십시오.

수학적으로 NRZ 코드의 시퀀스는 단위 펄스 또는 이동된 직장 함수의 시퀀스로 설명될 수 있으며, 각 펄스는 비트가 "1"이면 +1로, 비트가 "0"이면 -1로 가중된다. 공식적으로 $k{\displaystyle {}^{}}$ ${\displaystyle {t\mathrm{}}^{}}$ ${\displaystyle {\mathrm{h}}^{}}$ ${\$ 비트의$$ 스케일링 계수는 다음과 같다.

${\displaystyle \a_{k}={\mbox}+1,&{\mbox{{{}비트 }}}{{k-1,&\mbox{{{mbox{{}}}}}.\end{case}}}$

이동 단위 펄스의 합으로 $M{\displaystyle }$( ${\displaystyle t}$) ${\displaystyle M(t$ 메시지를 나타낼 수 있다.

${\displaystyle \M(t)=\sum _{k=-\flt }^{\nothy }a_{k}\times \Pi \left({\frac {t-kT}{\frc}{\frc}{\flt}{}}{T}\오른쪽).}$

여기서 $T{\displaystyle }$ ${\displaystyle T}$은(는) 1비트의 시간 길이입니다$$.

따라서 송신기에 의해 송신되는 신호는 다음과 같다.

노이즈가 많은 채널을 AWGN 채널로 모델링하면 신호에 흰색 가우스 노이즈가 추가된다. 수신기 끝에서 신호 대 잡음 비율이 3dB인 경우 다음과 같이 보일 수 있다.

첫눈에 원래 전송된 순서가 드러나지 않는다. 원하는 신호의 힘에 비례하는 높은 소음의 힘이 있다(즉, 신호 대 잡음 비율이 낮음). 만약 수신자가 정확한 순간에 이 신호를 샘플링한다면, 결과적인 바이너리 메시지는 아마도 원래 전송된 것을 믿을 것이다.

신호 대 잡음 비율을 높이기 위해 수신된 신호를 일치하는 필터를 통해 전달한다. 이 경우 필터는 NRZ 펄스(NRZ 코드로 코드화된 "1"과 동일)와 일치해야 한다. 정확히 말하면, 백색(비균등) 노이즈를 가정하는 이상적인 일치 필터의 임펄스 응답은 우리가 찾고 있는 신호의 시간 역행 복합 컨버전스 스케일 버전이어야 한다. 우리는 선택한다.

${\displaystyle \ h(t)=\Pi \left({\frac {t}){T}\오른쪽).}$

이 경우 대칭으로 인해 시간 역행 복합 결합 $h{\displaystyle }$( ${\displaystyle t}$) ${\displaystyle h(t)}$이(가)${\displaystyle \mathrm{사실}}$${\displaystyle h}$ ($$t ) {\$displaystyle$ h$(t)}$이(가) 되어$,$ $일치$하는 필터 콘볼루션 시스템의 임펄스$$ 응답을 h${\displaystyle }$( t${\displaystyle }$) ${\displaysty h(t)$라고 부를 수 있다.

올바른 일치 필터를 사용한 후 결과 신호인 $M{\displaystyle {}_{}}$ f ${\displaystyle {\mathrm{i}}_{}}$ t ${\displaystyle {e\mathrm{}}_{}}$ ${\displaystyle {\mathrm{r}}_{}}$ ${\displaystyle {\mathrm{e}}_{}}$ ${\displaystyle d{}_{}}$( t${\displaystyle }$) ${\displaystyle M_{\mathrm {filtered}$ {}($t)}$은(는)

${\displaystyle \ M_{\mathrm {filtered}}(t)=M(t)*h(t)}$

여기서 $\ast {\displaystyle }$ ${\displaystyle *}$은(는) 콘볼루션을 의미한다$$.

이것은 이제 정확한 샘플링 인스타트에서 수신자가 안전하게 샘플링할 수 있으며, 적절한 임계값과 비교하여 이진 메시지를 정확하게 해석할 수 있다.

중력파 천문학에서 일치하는 필터

일치하는 필터는 중력파 천문학의 중심 역할을 한다.^[9] 중력파의 첫 번째 관찰은 예상 형상을 닮은 신호에 대해 각 검출기의 출력을 대규모로 필터링한 후 두 기기 사이의 일치 및 일관성 있는 트리거에 대한 후속 선별에 기초하였다. 거짓 경보 속도 및 그와 함께 검출의 통계적 유의성을 재샘플링 방법을 사용하여 평가하였다.^[10][11] 천체물리학적 소스 파라미터에 대한 추론은 신호 파형에 대한 파라미터화된 이론적 모델과 휘틀우도에 대한 (again)에 기초한 베이지안 방법을 사용하여 완료되었다.^[12][13]

참고 항목

• 치주문자
• 필터링된 백프로젝션(Radon 변환)
• 디지털 필터
• 통계 신호 처리
• 희박한 가능성
• 종단우도
• 검출이론
• 다중 비교 문제
• 채널 용량
• 노이즈 채널 코딩 정리
• 스펙트럼 밀도 추정
• 최소 평균 제곱(LMS) 필터
• 위너 필터
• MUltiple SIgnal Classification(MUSIC), 인기 파라메트릭 초해상도 방법
• SAMV

메모들

참조

추가 읽기

• Turin, G. L. (1960). "An introduction to matched filters". IRE Transactions on Information Theory. 6 (3): 311–329. doi:10.1109/TIT.1960.1057571.
• Wainstein, L. A.; Zubakov, V. D. (1962). Extraction of signals from noise. Englewood Cliffs, NJ: Prentice-Hall.
• Melvin, W. L. (2004). "A STAP overview". IEEE Aerospace and Electronic Systems Magazine. 19 (1): 19–35. doi:10.1109/MAES.2004.1263229.
• Röver, C. (2011). "Student-t based filter for robust signal detection". Physical Review D. 84 (12): 122004. arXiv:1109.0442. Bibcode:2011PhRvD..84l2004R. doi:10.1103/PhysRevD.84.122004.
• Fish, A.; Gurevich, S.; Hadani, R.; Sayeed, A.; Schwartz, O. (December 2011). "Computing the matched filter in linear time". arXiv:1112.4883 [cs.IT].