제복5폴리토프
Uniform 5-polytope 5와섹스 |  수정 5-단순 |  잘린 5-심플렉스 | |||||||||
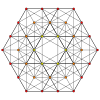 캔터링 5단순 | 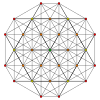 런케이티드 5-심플렉스 | 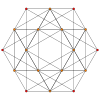 스테로이티드 5심플렉스 | |||||||||
 5형식 |  잘린 5정맥 |  교정된 5정맥류 | |||||||||
 5정음 |  런케이트 5정형 | ||||||||||
 캔터키드 5큐브 |  런케이티드 5큐브 |  스테리커티드 5-큐브 | |||||||||
 5시 15분 |  잘린 5-큐브 | 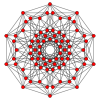 수정 5-큐브 | |||||||||
 5데미큐브 |  잘린 5데미큐브 | ||||||||||
 5데미큐브 |  런케이티드 5데미큐브 | ||||||||||
기하학에서 균일한 5폴리토프는 5차원 균일한 폴리토프다. 정의에 따르면, 균일한 5-폴리토프는 정점 변환이며 균일한 4-폴리토프 면으로 구성된다.
볼록한 제복 5폴리토프의 전체 세트는 결정되지 않았지만, 작은 대칭군에서 와이토프 건설로 많은 것을 만들 수 있다. 이러한 시공 작업은 Coxeter 다이어그램의 링 순열로 표현된다.
발견의 역사
- 일반 폴리탑: (콘벡스 면)
- 볼록 반정형 다상체: (Coxeter의 균일한 범주 이전의 다양한 정의)
- 1900: 소럴드 고셋은 그의 저서 'n차원 공간의 정규 및 반정규 도표에 관한 연구'에서 반정형 반정형 볼록 폴리토프 목록을 정규 면(콘벡스 정규 4폴리토프)으로 열거했다.[1]
- 볼록한 균일한 폴리탑:
- 비콘벡스 균일한 폴리토페즈:
일반 5폴리톱
일반 5폴리탑은 각 면 주위에 s {p,q,r,s}개의 4폴리탑 면이 있는 슐레플리 기호 {p,q,r,s}로 나타낼 수 있다. 그러한 규칙적인 폴리탑이 정확히 세 개 있는데, 모두 볼록한 것이다.
5차원 이상에 비콘벡스 일반 폴리토페스는 없다.
볼록 균일 5폴리톱
104개의 알려진 볼록한 제복 5폴리탑과 다수의 무한가족의 듀오프라즘 프리즘, 그리고 폴리곤-폴리헤드론 듀오프라임이 있다. 대항정신병 프리즘을 제외한 모든 것은 콕시터 그룹과 함께 생성된 반사 대칭인 와이토프 구조에 기초한다.[citation needed]
4차원 균일한 5폴리탑의 대칭
5-심플렉스(simplex)는5 A과에 속하는 정규형식이다. 5관 5관은 B과에5 속하는 정규형식이다. D5 계열의 분기 그래프에는 5정맥과 5정맥이 번갈아 나타나는 5정맥이 들어 있다.
각 반사 균일 5 폴리토프는 Coxeter 다이어그램에서 노드 순열 주변의 링으로 대표되는 Wythoff 구성에 의해 5차원 반사 지점 그룹으로 구성될 수 있다. 미러 하이퍼플레인은 컬러 노드에서 볼 수 있듯이 짝수 분지로 구분하여 그룹화할 수 있다. [a,b,b,a] 형태의 대칭 그룹은 [3,3,3,3,3]과 같이 대칭이 확장되어 대칭 순서를 두 배로 한다. 대칭 링이 있는 이 그룹의 균일한 폴리토프는 이 확장된 대칭을 포함한다.
주어진 균일한 폴리토프에서 주어진 색상의 모든 거울이 비링(비활성)되어 있는 경우, 모든 비활성 미러를 제거하여 더 낮은 대칭 구조를 갖게 된다. 특정 색상의 모든 노드가 링(활성)된 경우, 교류 연산은 "빈" 원형 노드"로 보이는 치랄 대칭으로 새로운 5-폴리토프를 생성할 수 있지만, 일반적으로 기하학적 구조를 조정하여 균일한 솔루션을 만들 수 없다.
- 기본가족[4]
| 그룹 심볼 | 주문 | 콕시터 도표를 찍다 | 브래킷 표기법 | 정류자 부분군 | 콕시터 번호를 붙이다 (h) | 반사 m=5/2시간[5] | ||
|---|---|---|---|---|---|---|---|---|
| A을5 | 720 | [3,3,3,3] | [3,3,3,3]+ | 6 | 15 | |||
| D5 | 1920 | [3,3,31,1] | [3,3,31,1]+ | 8 | 20 | |||
| B5 | 3840 | [4,3,3,3] | 10 | 5 | 20 | |||
- 균일 프리즘
비prismistic 유니폼 4-폴리토페스를 기반으로 한 폴리토페스의 유한한 범주형 균일 프리즘 계열이 5개 있다. 균일한 듀오프라임 {p}×{q}×{{}×{}}}의 프리즘을 바탕으로 5폴리탑의 무한가족이 하나 있다.
| 콕시터 무리를 짓다 | 주문 | 콕시터 도표를 만들다 | 콕시터 표기법 | 정류자 부분군 | 반사 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A4A1 | 120 | [3,3,3,2] = [3,3,3]×[ ] | [3,3,3]+ | 10 | 1 | ||||||
| D4A1 | 384 | [31,1,1,2] = [31,1,1]×[ ] | [31,1,1]+ | 12 | 1 | ||||||
| B4A1 | 768 | [4,3,3,2] = [4,3,3]×[ ] | 4 | 12 | 1 | ||||||
| F4A1 | 2304 | [3,4,3,2] = [3,4,3]×[ ] | [3+,4,3+] | 12 | 12 | 1 | |||||
| H4A1 | 28800 | [5,3,3,2] = [3,4,3]×[ ] | [5,3,3]+ | 60 | 1 | ||||||
| 2중격(이벤의 경우 2p 및 2q 사용) | |||||||||||
| I2(p)I2(q)A1 | 8pq | [p,2,q,2] = [p]×[q]×[ ] | [p+,2,q+] | p | q | 1 | |||||
| I2(2p)I2(q)A1 | 16pq | [2p,2,q,2] = [2p]×[q]×[ ] | p | p | q | 1 | |||||
| I2(2p)I2(2q)A1 | 32pq | [2p,2,2q,2] = [2p]×[2q]×[ ] | p | p | q | q | 1 | ||||
- 유니폼 듀오프리스
균일한 폴리헤드라 및 일반 폴리곤의 카르테시아 제품을 기반으로 하는 폴리토페스의 범주형 균일 2중주의 3개 제품군({q,r}×{p})이 있다.
| 콕시터 무리를 짓다 | 주문 | 콕시터 도표를 만들다 | 콕시터 표기법 | 정류자 부분군 | 반사 | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 프리즘 그룹(짝수에는 2p 사용) | |||||||||||
| A3I2(p) | 48p | [3,3,2,p] = [3,3]×[p] | [(3,3)+,2,p+] | 6 | p | ||||||
| A3I2(2p) | 96p | [3,3,2,2p] = [3,3]×[2p] | 6 | p | p | ||||||
| B3I2(p) | 96p | [4,3,2,p] = [4,3]×[p] | 3 | 6 | p | ||||||
| B3I2(2p) | 192p | [4,3,2,2p] = [4,3]×[2p] | 3 | 6 | p | p | |||||
| H3I2(p) | 240p | [5,3,2,p] = [5,3]×[p] | [(5,3)+,2,p+] | 15 | p | ||||||
| H3I2(2p) | 480p | [5,3,2,2p] = [5,3]×[2p] | 15 | p | p | ||||||
볼록형 균일 5폴리톱 열거
- 심플렉스 패밀리: A5 [34]
- 19개의 제복 5-제복 상의
- 하이퍼큐브/정맥류 가족 : BC5 [4,33]
- 31개의 제복 5-제복 상의
- Demihypercube D5/E5 제품군: [32,1,1]
- 23개의 제복 5-제곱 상단(8개 고유)
- 프리즘 및 듀오프리스:
그 결과: 19+31+8+45+1=104가 된다.
이외에도 다음과 같은 것들이 있다.
- 듀오프리즘 프리즘 계열에 기초한 5-폴리토프 건축물은 무한히 많다: [p]×[q]×[ ]].
- 2중주파 가문에 기초한 5중주형 구조물은 무한히 많다: [3,3]×[p], [4,3]×[p], [5,3]×[p].
A가족5
1개 이상의 링이 있는 Coxeter 다이어그램의 모든 순열을 기준으로 한 19개의 양식이 있다.(16+4-1 사례)
그것들은 와이토프 건설 사업장의 노먼 존슨이 정기적인 5-심플렉스 (헥사테론)로 명명했다.
A5 계열은 순서 720 (6 요인)의 대칭을 가지고 있다. 대칭 링이 있는 Coxeter 다이어그램의 19개 그림 중 7개가 대칭이 2배인 1440번 순서다.
5-단순 대칭의 균일한 5-폴리탑 좌표는 6-공간에서 단순 정수의 순열로 생성될 수 있으며, 모두 정상 벡터(1,1,1,1,1,1,1)가 있는 하이퍼플레인에서 생성된다.
| # | 기준점 | 존슨 명명 시스템 Bowers 이름 및 (acronym) 콕시터 다이어그램 | k-면 요소 계수 | 꼭지점 형상을 나타내다 | 위치별 면 계수: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (6) | [3,3,2] (15) | [3,2,3] (20) | [2,3,3] (15) | [3,3,3] (6) | ||||
| 1 | (0,0,0,0,0,0,1) 또는 (0,1,1,1) | 5와섹스 헥사테론(hix) | 6 | 15 | 20 | 15 | 6 |  {3,3,3} | (5) {3,3,3} | - | - | - | - |
| 2 | (0,0,0,0,1,1) 또는 (0,0,1,1) | 수정 5-단순 정류된 육각형(릭스) | 12 | 45 | 80 | 60 | 15 |  t{3,3}×{ } | (4) r{3,3,3} | - | - | - | (2) {3,3,3} |
| 3 | (0,0,0,0,1,2) 또는 (0,1,2,2,2) | 잘린 5-심플렉스 잘린 육각형(tix) | 12 | 45 | 80 | 75 | 30 |  테트라피르 | (4) t{3,3,3} | - | - | - | (1) {3,3,3} |
| 4 | (0,0,0,1,1,2,2) 또는 (0,1,1,2,2) | 캔터링 5단순 소형 고무 육각형(상어) | 27 | 135 | 290 | 240 | 60 | 프리즘을 이용한 | (3) rr{3,3} | - | - | (1) { }×{3,3} | (1) r{3,3,3} |
| 5 | (0,0,0,1,2,2) 또는 (0,0,1,2,2) | 5-단순 비트런드 비트 처리된 16진수(bittix) | 12 | 60 | 140 | 150 | 60 |  | (3) 2t{3,3} | - | - | - | (2) t{3,3,3} |
| 6 | (0,0,0,1,2,3) 또는 (0,1,2,3,3) | 캔트런치 5-심플렉스 대합성 육각체(garx) | 27 | 135 | 290 | 300 | 120 | 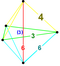 |  tr{3,3} | - | - | { }×{3,3} |  t{3,3,3} |
| 7 | (0,0,1,1,2,2) 또는 (0,1,1,1,2,2) | 런케이티드 5-심플렉스 작은 프리즘으로 된 육각형(스픽스) | 47 | 255 | 420 | 270 | 60 |  | (2) t0,3{3,3,3} | - | (3) {3}×{3} | (3) { }×r{3,3} | (1) r{3,3,3} |
| 8 | (0,0,1,1,2,3) 또는 (0,1,2,3,3) | 런시트드림 5단순수 프리즘(primottrunculated hexateron, pattix) | 47 | 315 | 720 | 630 | 180 | 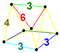 |  t0,1,3{3,3,3} | - | {6}×{3} | { }×r{3,3} |  rr{3,3} |
| 9 | (0,0,1,2,2,3) 또는 (0,1,1,2,3,3) | 런시컨텔링 5단플렉스 프리즘atorhombated 헥사테론(pirx) | 47 | 255 | 570 | 540 | 180 | 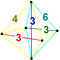 |  t0,1,3{3,3,3} | - |  {3}×{3} | { }×t{3,3} |  2t{3,3} |
| 10 | (0,0,1,2,3,4) 또는 (0,1,2,3,4,4) | 런시칸티트런치드5-심플렉스 대프리즘 육각체(gippix) | 47 | 315 | 810 | 900 | 360 |  인라인 5-셀 |  t0,1,2,3{3,3,3} | - | {3}×{6} | { }×t{3,3} |  rr{3,3} |
| 11 | (0,1,1,2,3) 또는 (0,1,2,2,3) | 스테리트런드 5-심플렉스 세포분열 육각체(카픽스) | 62 | 330 | 570 | 420 | 120 |  |  t{3,3,3} | { }×t{3,3} | {3}×{6} | { }×{3,3} |  t0,3{3,3,3} |
| 12 | (0,1,2,3,4) 또는 (0,1,2,3,4) | 스테리칸티트룬 5-심플렉스 세포호흡기결합헥사테론(cograxrax) | 62 | 480 | 1140 | 1080 | 360 |  tr{3,3} | { }×tr{3,3} | {3}×{6} | {}×r{3,3} |  t0,1,3{3,3,3} | |
| # | 기준점 | 존슨 명명 시스템 Bowers 이름 및 (acronym) 콕시터 다이어그램 | k-면 요소 계수 | 꼭지점 형상을 나타내다 | 위치별 면 계수: [3,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (6) | [3,3,2] (15) | [3,2,3] (20) | [2,3,3] (15) | [3,3,3] (6) | ||||
| 13 | (0,0,0,1,1,1) | 양방향 5단순 도데카테론 (점) | 12 | 60 | 120 | 90 | 20 |  {3}×{3} | (3) r{3,3,3} | - | - | - | (3) r{3,3,3} |
| 14 | (0,0,1,1,2,2) | 바이칸텔레이트 5단플렉스 작은 버혼드 도데카테론 (sibridrid) | 32 | 180 | 420 | 360 | 90 |  | (2) rr{3,3} | - | (8) {3}×{3} | - | (2) rr{3,3} |
| 15 | (0,0,1,2,3,3) | 바이칸티트룬 5-단순 큰 버혼 도데카테론 ( (ridrid) | 32 | 180 | 420 | 450 | 180 | 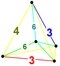 |  tr{3,3} | - |  {3}×{3} | - |  tr{3,3} |
| 16 | (0,1,1,1,1,2) | 스테로이티드 5심플렉스 소세포 도데카테론(scad) | 62 | 180 | 210 | 120 | 30 |  인라인.16 셀 | (1) {3,3,3} | (4) { }×{3,3} | (6) {3}×{3} | (4) { }×{3,3} | (1) {3,3,3} |
| 17 | (0,1,1,2,2,3) | 스테리칸텔화 5단백질 소형 셀리혼합 도데카테론(카드) | 62 | 420 | 900 | 720 | 180 |  |  rr{3,3} | {}×r{3,3} |  {3}×{3} | {}×r{3,3} |  rr{3,3} |
| 18 | (0,1,2,2,3,4) | 스테리룬시티칼 5단백질 celliprismatotrunculated doddecateron (captid) | 62 | 450 | 1110 | 1080 | 360 |  t0,1,3{3,3,3} | { }×t{3,3} |  {6}×{6} | { }×t{3,3} |  t0,1,3{3,3,3} | |
| 19 | (0,1,2,3,4,5) | 옴니트런드 5심플렉스 세포가 많은 도데카테론(고카드) | 62 | 540 | 1560 | 1800 | 720 |  관개 {3,3,3} | (1) t0,1,2,3{3,3,3} | (1) { }×tr{3,3} | (1) {6}×{6} | (1) { }×tr{3,3} | (1) t0,1,2,3{3,3,3} |
B가족5
B5 계열은 순서 3840 (5!×25)의 대칭을 가지고 있다.
이5 패밀리는 2-1=31 Wythoffian 유니폼 폴리토페스를 Coxeter 다이어그램의 하나 이상의 노드를 표시하여 생성한다.
단순성을 위해 각각 12개의 형태를 가진 두 개의 하위그룹과 두 개 모두에 동일하게 속하는 7개의 "중간" 형태로 나뉜다.
5관 5폴리탑 계열은 아래 표에 열거된 기준점의 볼록한 선체에 의해 주어지며, 좌표와 표지의 모든 순열은 다음과 같다. 각 기준점은 구별되는 균일한 5폴리토프를 생성한다. 모든 좌표는 가장자리 길이 2의 균일한 5 폴리 상단과 일치한다.
| # | 기준점 | 이름 콕시터 다이어그램 | 요소 개수 | 꼭지점 형상을 나타내다 | 위치별 면 개수: [4,3,3,3] | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [4,3,3] (10) | [4,3,2] (40) | [4,2,3] (80) | [2,3,3] (80) | [3,3,3] (32) | ||||
| 20 | (0,0,0,0,1)√2 | 5정맥(tactac) | 32 | 80 | 80 | 40 | 10 |  {3,3,4} |  {3,3,3} | - | - | - | - |
| 21 | (0,0,0,1,1)√2 | 수정 5정맥(랫드) | 42 | 240 | 400 | 240 | 40 |  { }×{3,4} |  {3,3,4} | - | - | - |  r{3,3,3} |
| 22 | (0,0,0,1,2)√2 | 잘린 5정형(토트) | 42 | 240 | 400 | 280 | 80 |  (Octah.pyr) |  t{3,3,3} |  {3,3,3} | - | - | - |
| 23 | (0,0,1,1,1)√2 | 양방향 5큐브(nit) (양방향 5정형) | 42 | 280 | 640 | 480 | 80 |  {4}×{3} |  r{3,3,4} | - | - | - |  r{3,3,3} |
| 24 | (0,0,1,1,2)√2 | 5정맥류(사트) | 82 | 640 | 1520 | 1200 | 240 |  프리즘-웨지 | r{3,3,4} | { }×{3,4} | - | - |  rr{3,3} |
| 25 | (0,0,1,2,2)√2 | 비트런드 5정형(비트) | 42 | 280 | 720 | 720 | 240 |  | t{3,3,4} | - | - | - |  2t{3,3} |
| 26 | (0,0,1,2,3)√2 | 캔트런치 5정형(가트) | 82 | 640 | 1520 | 1440 | 480 | 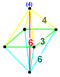 | rr{3,4} | { }×r{3,4} |  {6}×{4} | - |  t0,1,3{3,3,3} |
| 27 | (0,1,1,1,1)√2 | 수정 5-큐브(린) | 42 | 200 | 400 | 320 | 80 |  {3,3}×{ } |  r{4,3,3} | - | - | - |  {3,3,3} |
| 28 | (0,1,1,1,2)√2 | 런케이티드 5정형(스팟) | 162 | 1200 | 2160 | 1440 | 320 |  | r{4,3,3} | - |  {3}×{4} |  t0,3{3,3,3} | |
| 29 | (0,1,1,2,2)√2 | 바이칸텔레이트 5큐브(시번트) (Bicantellated 5정형) | 122 | 840 | 2160 | 1920 | 480 |  |  rr{4,3,3} | - |  {4}×{3} | - |  rr{3,3} |
| 30 | (0,1,1,2,3)√2 | 5정형(특권) | 162 | 1440 | 3680 | 3360 | 960 | 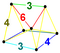 | rr{3,4} | { }×r{3,4} |  {6}×{4} | - |  t0,1,3{3,3,3} |
| 31 | (0,1,2,2,2)√2 | 5-큐브 비트런드(탄) | 42 | 280 | 720 | 800 | 320 |  |  2t{4,3,3} | - | - | - |  t{3,3,3} |
| 32 | (0,1,2,2,3)√2 | 런시컨텔링 5정형(퍼트) | 162 | 1200 | 2960 | 2880 | 960 |  | { }×t{3,4} | 2t{3,4} |  {3}×{4} | - |  t0,1,3{3,3,3} |
| 33 | (0,1,2,3,3)√2 | 바이칸티트룬 5큐브(기브란트) (바이칸티트룬 5정맥) | 122 | 840 | 2160 | 2400 | 960 |  |  rr{4,3,3} | - |  {4}×{3} | - |  rr{3,3} |
| 34 | (0,1,2,3,4)√2 | 런시칸티트룬 5정맥(지핏) | 162 | 1440 | 4160 | 4800 | 1920 |  | tr{3,4} | { }×t{3,4} |  {6}×{4} | - |  t0,1,2,3{3,3,3} |
| 35 | (1,1,1,1,1) | 5인치(뱀) | 10 | 40 | 80 | 80 | 32 |  {3,3,3} |  {4,3,3} | - | - | - | - |
| 36 | (1,1,1,1,1) + (0,0,0,0,1)√2 | 스테리커티드 5큐브(사각형 (긴장 5정형) | 242 | 800 | 1040 | 640 | 160 | 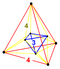 테트르.antiprm |  {4,3,3} |  {4,3}×{ } |  {4}×{3} |  { }×{3,3} |  {3,3,3} |
| 37 | (1,1,1,1,1) + (0,0,0,1,1)√2 | 런케이티드 5큐브(스팬) | 202 | 1240 | 2160 | 1440 | 320 | 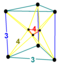 |  t0,3{4,3,3} | - |  {4}×{3} |  { }×r{3,3} |  {3,3,3} |
| 38 | (1,1,1,1,1) + (0,0,0,1,2)√2 | 흉골절제 5정형(카핀) | 242 | 1520 | 2880 | 2240 | 640 | 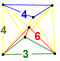 | t0,3{3,3,4} | { }×{4,3} | - | - |  t{3,3,3} |
| 39 | (1,1,1,1,1) + (0,0,1,1,1)√2 | 캔터링된 5큐브(선배) | 122 | 680 | 1520 | 1280 | 320 | 프리즘-웨지 |  rr{4,3,3} | - | - |  { }×{3,3} |  r{3,3,3} |
| 40 | (1,1,1,1,1) + (0,0,1,1,2)√2 | 스테리칸텔레이트 5큐브(카니트) (Stericantellated 5정형식) | 242 | 2080 | 4720 | 3840 | 960 |  |  rr{4,3,3} |  rr{4,3}×{ } |  {4}×{3} |  {}×r{3,3} |  rr{3,3} |
| 41 | (1,1,1,1,1) + (0,0,1,2,2)√2 | 런시컨텔링 5큐브(원리) | 202 | 1240 | 2960 | 2880 | 960 |  |  t0,1,3{4,3,3} | - |  {4}×{3} |  { }×t{3,3} |  2t{3,3} |
| 42 | (1,1,1,1,1) + (0,0,1,2,3)√2 | 스테리칸티트룬 5정맥(코가르트) | 242 | 2320 | 5920 | 5760 | 1920 |  {}×r{3,4} |  t0,1,3{3,3,4} |  {6}×{4} |  { }×t{3,3} |  tr{3,3} | |
| 43 | (1,1,1,1,1) + (0,1,1,1,1)√2 | 잘린 5-큐브(탄) | 42 | 200 | 400 | 400 | 160 |  테트라피르 |  t{4,3,3} | - | - | - |  {3,3,3} |
| 44 | (1,1,1,1,1) + (0,1,1,1,2)√2 | 흉골 절단 5-큐브(캡트) | 242 | 1600 | 2960 | 2240 | 640 | 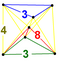 |  t{4,3,3} |  t{4,3}×{ } |  {8}×{3} |  { }×{3,3} |  t0,3{3,3,3} |
| 45 | (1,1,1,1,1) + (0,1,1,2,2)√2 | 런시터드 5큐브(패틴) | 202 | 1560 | 3760 | 3360 | 960 |  |  t0,1,3{4,3,3} | { }×t{4,3} |  {6}×{8} | { }×t{3,3} | t0,1,3{3,3,}]] |
| 46 | (1,1,1,1,1) + (0,1,1,2,3)√2 | 스테리룬시티 절단 5큐브(캡틴트) (멸종 5정형) | 242 | 2160 | 5760 | 5760 | 1920 |  t0,1,3{4,3,3} |  t{4,3}×{ } |  {8}×{6} |  { }×t{3,3} |  t0,1,3{3,3,3} | |
| 47 | (1,1,1,1,1) + (0,1,2,2,2)√2 | 캔트런치 5-큐브(girn) | 122 | 680 | 1520 | 1600 | 640 | 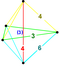 |  tr{4,3,3} | - | - |  { }×{3,3} |  t{3,3,3} |
| 48 | (1,1,1,1,1) + (0,1,2,2,3)√2 | 스테리칸티트룬 5-큐브(코그린) | 242 | 2400 | 6000 | 5760 | 1920 |  tr{4,3,3} |  tr{4,3}×{ } |  {8}×{3} |  { }×t0,2{3,3} |  t0,1,3{3,3,3} | |
| 49 | (1,1,1,1,1) + (0,1,2,3,3)√2 | 런시칸티트룬 5-큐브(지핀) | 202 | 1560 | 4240 | 4800 | 1920 |  |  t0,1,2,3{4,3,3} | - |  {8}×{3} |  { }×t{3,3} |  tr{3,3} |
| 50 | (1,1,1,1,1) + (0,1,2,3,4)√2 | 옴니트룬드 5큐브(가크넷) (5정맥경화) | 242 | 2640 | 8160 | 9600 | 3840 |  관개 {3,3,3} |  tr{4,3}×{ } |  tr{4,3}×{ } |  {8}×{6} |  { }×tr{3,3} |  t0,1,2,3{3,3,3} |
D가족5
D5 계열은 순서 1920 (54! x 2)의 대칭을 가지고 있다.
이 패밀리는 하나 이상의 링이 있는 D5 Coxeter 다이어그램의 3x8-1 순열부터 23개의 와이토피아 유니폼 다면체를 가지고 있다. 15(2x8-1)는 B5 패밀리에서 반복되며 8은 이 패밀리 특유의 것이다.
| # | Coxeter diagram Schläfli symbol symbols Johnson and Bowers names | Element counts | Vertex figure | Facets by location: | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 4 | 3 | 2 | 1 | 0 | [3,3,3] (16) | [31,1,1] (10) | [3,3]×[ ] (40) | [ ]×[3]×[ ] (80) | [3,3,3] (16) | |||
| 51 | h{4,3,3,3}, 5-demicube Hemipenteract (hin) | 26 | 120 | 160 | 80 | 16 |  t1{3,3,3} | {3,3,3} | t0(111) | - | - | - |
| 52 | h2{4,3,3,3}, cantic 5-cube Truncated hemipenteract (thin) | 42 | 280 | 640 | 560 | 160 |  | |||||
| 53 | h3{4,3,3,3}, runcic 5-cube Small rhombated hemipenteract (sirhin) | 42 | 360 | 880 | 720 | 160 | ||||||
| 54 | h4{4,3,3,3}, steric 5-cube Small prismated hemipenteract (siphin) | 82 | 480 | 720 | 400 | 80 | ||||||
| 55 | h2,3{4,3,3,3}, runcicantic 5-cube Great rhombated hemipenteract (girhin) | 42 | 360 | 1040 | 1200 | 480 | ||||||
| 56 | h2,4{4,3,3,3}, stericantic 5-cube Prismatotruncated hemipenteract (pithin) | 82 | 720 | 1840 | 1680 | 480 | ||||||
| 57 | h3,4{4,3,3,3}, steriruncic 5-cube Prismatorhombated hemipenteract (pirhin) | 82 | 560 | 1280 | 1120 | 320 | ||||||
| 58 | h2,3,4{4,3,3,3}, steriruncicantic 5-cube Great prismated hemipenteract (giphin) | 82 | 720 | 2080 | 2400 | 960 | ||||||
Uniform prismatic forms
There are 5 finite categorical uniform prismatic families of polytopes based on the nonprismatic uniform 4-polytopes:
A4 × A1
This prismatic family has 9 forms:
The A1 x A4 family has symmetry of order 240 (2*5!).
| # | Coxeter diagram and Schläfli symbols Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 59 | 5-cell prism | 7 | 20 | 30 | 25 | 10 |
| 60 | Rectified 5-cell prism | 12 | 50 | 90 | 70 | 20 |
| 61 | Truncated 5-cell prism | 12 | 50 | 100 | 100 | 40 |
| 62 | Cantellated 5-cell prism | 22 | 120 | 250 | 210 | 60 |
| 63 | Runcinated 5-cell prism | 32 | 130 | 200 | 140 | 40 |
| 64 | Bitruncated 5-cell prism | 12 | 60 | 140 | 150 | 60 |
| 65 | Cantitruncated 5-cell prism | 22 | 120 | 280 | 300 | 120 |
| 66 | Runcitruncated 5-cell prism | 32 | 180 | 390 | 360 | 120 |
| 67 | Omnitruncated 5-cell prism | 32 | 210 | 540 | 600 | 240 |
B4 × A1
This prismatic family has 16 forms. (Three are shared with [3,4,3]×[ ] family)
The A1×B4 family has symmetry of order 768 (254!).
| # | Coxeter diagram and Schläfli symbols Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| [16] | Tesseractic prism (Same as 5-cube) | 10 | 40 | 80 | 80 | 32 |
| 68 | Rectified tesseractic prism | 26 | 136 | 272 | 224 | 64 |
| 69 | Truncated tesseractic prism | 26 | 136 | 304 | 320 | 128 |
| 70 | Cantellated tesseractic prism | 58 | 360 | 784 | 672 | 192 |
| 71 | Runcinated tesseractic prism | 82 | 368 | 608 | 448 | 128 |
| 72 | Bitruncated tesseractic prism | 26 | 168 | 432 | 480 | 192 |
| 73 | Cantitruncated tesseractic prism | 58 | 360 | 880 | 960 | 384 |
| 74 | Runcitruncated tesseractic prism | 82 | 528 | 1216 | 1152 | 384 |
| 75 | Omnitruncated tesseractic prism | 82 | 624 | 1696 | 1920 | 768 |
| 76 | 16-cell prism | 18 | 64 | 88 | 56 | 16 |
| 77 | Rectified 16-cell prism (Same as 24-cell prism) | 26 | 144 | 288 | 216 | 48 |
| 78 | Truncated 16-cell prism | 26 | 144 | 312 | 288 | 96 |
| 79 | Cantellated 16-cell prism (Same as rectified 24-cell prism) | 50 | 336 | 768 | 672 | 192 |
| 80 | Cantitruncated 16-cell prism (Same as truncated 24-cell prism) | 50 | 336 | 864 | 960 | 384 |
| 81 | Runcitruncated 16-cell prism | 82 | 528 | 1216 | 1152 | 384 |
| 82 | snub 24-cell prism | 146 | 768 | 1392 | 960 | 192 |
F4 × A1
This prismatic family has 10 forms.
The A1 x F4 family has symmetry of order 2304 (2*1152). Three polytopes 85, 86 and 89 (green background) have double symmetry [[3,4,3],2], order 4608. The last one, snub 24-cell prism, (blue background) has [3+,4,3,2] symmetry, order 1152.
| # | Coxeter diagram and Schläfli symbols Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| [77] | 24-cell prism | 26 | 144 | 288 | 216 | 48 |
| [79] | rectified 24-cell prism | 50 | 336 | 768 | 672 | 192 |
| [80] | truncated 24-cell prism | 50 | 336 | 864 | 960 | 384 |
| 83 | cantellated 24-cell prism | 146 | 1008 | 2304 | 2016 | 576 |
| 84 | runcinated 24-cell prism | 242 | 1152 | 1920 | 1296 | 288 |
| 85 | bitruncated 24-cell prism | 50 | 432 | 1248 | 1440 | 576 |
| 86 | cantitruncated 24-cell prism | 146 | 1008 | 2592 | 2880 | 1152 |
| 87 | runcitruncated 24-cell prism | 242 | 1584 | 3648 | 3456 | 1152 |
| 88 | omnitruncated 24-cell prism | 242 | 1872 | 5088 | 5760 | 2304 |
| [82] | snub 24-cell prism | 146 | 768 | 1392 | 960 | 192 |
H4 × A1
This prismatic family has 15 forms:
The A1 x H4 family has symmetry of order 28800 (2*14400).
| # | Coxeter diagram and Schläfli symbols Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 89 | 120-cell prism | 122 | 960 | 2640 | 3000 | 1200 |
| 90 | Rectified 120-cell prism | 722 | 4560 | 9840 | 8400 | 2400 |
| 91 | Truncated 120-cell prism | 722 | 4560 | 11040 | 12000 | 4800 |
| 92 | Cantellated 120-cell prism | 1922 | 12960 | 29040 | 25200 | 7200 |
| 93 | Runcinated 120-cell prism | 2642 | 12720 | 22080 | 16800 | 4800 |
| 94 | Bitruncated 120-cell prism | 722 | 5760 | 15840 | 18000 | 7200 |
| 95 | Cantitruncated 120-cell prism | 1922 | 12960 | 32640 | 36000 | 14400 |
| 96 | Runcitruncated 120-cell prism | 2642 | 18720 | 44880 | 43200 | 14400 |
| 97 | Omnitruncated 120-cell prism | 2642 | 22320 | 62880 | 72000 | 28800 |
| 98 | 600-cell prism | 602 | 2400 | 3120 | 1560 | 240 |
| 99 | Rectified 600-cell prism | 722 | 5040 | 10800 | 7920 | 1440 |
| 100 | Truncated 600-cell prism | 722 | 5040 | 11520 | 10080 | 2880 |
| 101 | Cantellated 600-cell prism | 1442 | 11520 | 28080 | 25200 | 7200 |
| 102 | Cantitruncated 600-cell prism | 1442 | 11520 | 31680 | 36000 | 14400 |
| 103 | Runcitruncated 600-cell prism | 2642 | 18720 | 44880 | 43200 | 14400 |
Grand antiprism prism
The grand antiprism prism is the only known convex non-Wythoffian uniform 5-polytope. It has 200 vertices, 1100 edges, 1940 faces (40 pentagons, 500 squares, 1400 triangles), 1360 cells (600 tetrahedra, 40 pentagonal antiprisms, 700 triangular prisms, 20 pentagonal prisms), and 322 hypercells (2 grand antiprisms  , 20 pentagonal antiprism prisms
, 20 pentagonal antiprism prisms  , and 300 tetrahedral prisms
, and 300 tetrahedral prisms  ).
).
| # | Name | Element counts | ||||
|---|---|---|---|---|---|---|
| Facets | Cells | Faces | Edges | Vertices | ||
| 104 | grand antiprism prism Gappip | 322 | 1360 | 1940 | 1100 | 200 |
Notes on the Wythoff construction for the uniform 5-polytopes
Construction of the reflective 5-dimensional uniform polytopes are done through a Wythoff construction process, and represented through a Coxeter diagram, where each node represents a mirror. Nodes are ringed to imply which mirrors are active. The full set of uniform polytopes generated are based on the unique permutations of ringed nodes. Uniform 5-polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may have two ways of naming them.
Here are the primary operators available for constructing and naming the uniform 5-polytopes.
The last operation, the snub, and more generally the alternation, are the operation that can create nonreflective forms. These are drawn with "hollow rings" at the nodes.
The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.
| Operation | Extended Schläfli symbol | Coxeter diagram | Description | |
|---|---|---|---|---|
| Parent | t0{p,q,r,s} | {p,q,r,s} | Any regular 5-polytope | |
| Rectified | t1{p,q,r,s} | r{p,q,r,s} | The edges are fully truncated into single points. The 5-polytope now has the combined faces of the parent and dual. | |
| Birectified | t2{p,q,r,s} | 2r{p,q,r,s} | Birectification reduces faces to points, cells to their duals. | |
| Trirectified | t3{p,q,r,s} | 3r{p,q,r,s} | Trirectification reduces cells to points. (Dual rectification) | |
| Quadrirectified | t4{p,q,r,s} | 4r{p,q,r,s} | Quadrirectification reduces 4-faces to points. (Dual) | |
| Truncated | t0,1{p,q,r,s} | t{p,q,r,s} | Each original vertex is cut off, with a new face filling the gap. Truncation has a degree of freedom, which has one solution that creates a uniform truncated 5-polytope. The 5-polytope has its original faces doubled in sides, and contains the faces of the dual. | |
| Cantellated | t0,2{p,q,r,s} | rr{p,q,r,s} | In addition to vertex truncation, each original edge is beveled with new rectangular faces appearing in their place.  | |
| Runcinated | t0,3{p,q,r,s} | Runcination reduces cells and creates new cells at the vertices and edges. | ||
| Stericated | t0,4{p,q,r,s} | 2r2r{p,q,r,s} | Sterication reduces facets and creates new facets (hypercells) at the vertices and edges in the gaps. (Same as expansion operation for 5-polytopes.) | |
| Omnitruncated | t0,1,2,3,4{p,q,r,s} | All four operators, truncation, cantellation, runcination, and sterication are applied. | ||
| Half | h{2p,3,q,r} | Alternation, same as | ||
| Cantic | h2{2p,3,q,r} | Same as | ||
| Runcic | h3{2p,3,q,r} | Same as | ||
| Runcicantic | h2,3{2p,3,q,r} | Same as | ||
| Steric | h4{2p,3,q,r} | Same as | ||
| Runcisteric | h3,4{2p,3,q,r} | Same as | ||
| Stericantic | h2,4{2p,3,q,r} | Same as | ||
| Steriruncicantic | h2,3,4{2p,3,q,r} | Same as | ||
| Snub | s{p,2q,r,s} | Alternated truncation | ||
| Snub rectified | sr{p,q,2r,s} | Alternated truncated rectification | ||
| ht0,1,2,3{p,q,r,s} | Alternated runcicantitruncation | |||
| Full snub | ht0,1,2,3,4{p,q,r,s} | Alternated omnitruncation | ||
Regular and uniform honeycombs
There are five fundamental affine Coxeter groups, and 13 prismatic groups that generate regular and uniform tessellations in Euclidean 4-space.[6][7]
| # | Coxeter group | Coxeter diagram | Forms | ||
|---|---|---|---|---|---|
| 1 | [3[5]] | [(3,3,3,3,3)] | 7 | ||
| 2 | [4,3,3,4] | 19 | |||
| 3 | [4,3,31,1] | [4,3,3,4,1+] | 23 (8 new) | ||
| 4 | [31,1,1,1] | [1+,4,3,3,4,1+] | 9 (0 new) | ||
| 5 | [3,4,3,3] | 31 (21 new) | |||
There are three regular honeycombs of Euclidean 4-space:
- tesseractic honeycomb, with symbols {4,3,3,4},








 =
= 





 . There are 19 uniform honeycombs in this family.
. There are 19 uniform honeycombs in this family. - 24-cell honeycomb, with symbols {3,4,3,3},








 . There are 31 reflective uniform honeycombs in this family, and one alternated form.
. There are 31 reflective uniform honeycombs in this family, and one alternated form. - Truncated 24-cell honeycomb with symbols t{3,4,3,3},









- Snub 24-cell honeycomb, with symbols s{3,4,3,3},








 and
and 







 constructed by four snub 24-cell, one 16-cell, and five 5-cells at each vertex.
constructed by four snub 24-cell, one 16-cell, and five 5-cells at each vertex.
- Truncated 24-cell honeycomb with symbols t{3,4,3,3},
- 16-cell honeycomb, with symbols {3,3,4,3},









Other families that generate uniform honeycombs:
- There are 23 uniquely ringed forms, 8 new ones in the 16-cell honeycomb family. With symbols h{4,32,4} it is geometrically identical to the 16-cell honeycomb,








 =
= 






- There are 7 uniquely ringed forms from the ,




 family, all new, including:
family, all new, including: - There are 9 uniquely ringed forms in the : [31,1,1,1]




 family, two new ones, including the quarter tesseractic honeycomb,
family, two new ones, including the quarter tesseractic honeycomb, 



 =
= 







 , and the bitruncated tesseractic honeycomb,
, and the bitruncated tesseractic honeycomb, 



 =
= 







 .
.
Non-Wythoffian uniform tessellations in 4-space also exist by elongation (inserting layers), and gyration (rotating layers) from these reflective forms.
| # | Coxeter group | Coxeter diagram | |
|---|---|---|---|
| 1 | × | [4,3,4,2,∞] | |
| 2 | × | [4,31,1,2,∞] | |
| 3 | × | [3[4],2,∞] | |
| 4 | ×x | [4,4,2,∞,2,∞] | |
| 5 | ×x | [6,3,2,∞,2,∞] | |
| 6 | ×x | [3[3],2,∞,2,∞] | |
| 7 | ×xx | [∞,2,∞,2,∞,2,∞] | |
| 8 | x | [3[3],2,3[3]] | |
| 9 | × | [3[3],2,4,4] | |
| 10 | × | [3[3],2,6,3] | |
| 11 | × | [4,4,2,4,4] | |
| 12 | × | [4,4,2,6,3] | |
| 13 | × | [6,3,2,6,3] | |
Compact regular tessellations of hyperbolic 4-space
There are five kinds of convex regular honeycombs and four kinds of star-honeycombs in H4 space:[8]
| Honeycomb name | Schläfli Symbol {p,q,r,s} | Coxeter diagram | Facet type {p,q,r} | Cell type {p,q} | Face type {p} | Face figure {s} | Edge figure {r,s} | Vertex figure {q,r,s} | Dual |
|---|---|---|---|---|---|---|---|---|---|
| Order-5 5-cell | {3,3,3,5} | {3,3,3} | {3,3} | {3} | {5} | {3,5} | {3,3,5} | {5,3,3,3} | |
| Order-3 120-cell | {5,3,3,3} | {5,3,3} | {5,3} | {5} | {3} | {3,3} | {3,3,3} | {3,3,3,5} | |
| Order-5 tesseractic | {4,3,3,5} | {4,3,3} | {4,3} | {4} | {5} | {3,5} | {3,3,5} | {5,3,3,4} | |
| Order-4 120-cell | {5,3,3,4} | {5,3,3} | {5,3} | {5} | {4} | {3,4} | {3,3,4} | {4,3,3,5} | |
| Order-5 120-cell | {5,3,3,5} | {5,3,3} | {5,3} | {5} | {5} | {3,5} | {3,3,5} | Self-dual |
There are four regular star-honeycombs in H4 space:
| Honeycomb name | Schläfli Symbol {p,q,r,s} | Coxeter diagram | Facet type {p,q,r} | Cell type {p,q} | Face type {p} | Face figure {s} | Edge figure {r,s} | Vertex figure {q,r,s} | Dual |
|---|---|---|---|---|---|---|---|---|---|
| Order-3 small stellated 120-cell | {5/2,5,3,3} | {5/2,5,3} | {5/2,5} | {5} | {5} | {3,3} | {5,3,3} | {3,3,5,5/2} | |
| Order-5/2 600-cell | {3,3,5,5/2} | {3,3,5} | {3,3} | {3} | {5/2} | {5,5/2} | {3,5,5/2} | {5/2,5,3,3} | |
| Order-5 icosahedral 120-cell | {3,5,5/2,5} | {3,5,5/2} | {3,5} | {3} | {5} | {5/2,5} | {5,5/2,5} | {5,5/2,5,3} | |
| Order-3 great 120-cell | {5,5/2,5,3} | {5,5/2,5} | {5,5/2} | {5} | {3} | {5,3} | {5/2,5,3} | {3,5,5/2,5} |
Regular and uniform hyperbolic honeycombs
There are 5 compact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in hyperbolic 4-space as permutations of rings of the Coxeter diagrams. There are also 9 paracompact hyperbolic Coxeter groups of rank 5, each generating uniform honeycombs in 4-space as permutations of rings of the Coxeter diagrams. Paracompact groups generate honeycombs with infinite facets or vertex figures.
| = [(3,3,3,3,4)]: | = [5,3,31,1]: | = [3,3,3,5]: = [4,3,3,5]: |
| = [3,3[4]]: = [4,3[4]]: | = [4,/3\,3,4]: | = [3,4,3,4]: |
Notes
- ^ T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
- ^ Multidimensional Glossary, George Olshevsky
- ^ Uniform Polytera, Jonathan Bowers
- ^ Regular and semi-regular polytopes III, p.315 Three finite groups of 5-dimensions
- ^ Coxeter, Regular polytopes, §12.6 The number of reflections, equation 12.61
- ^ Regular polytopes, p.297. Table IV, Fundamental regions for irreducible groups generated by reflections.
- ^ Regular and Semiregular polytopes, II, pp.298-302 Four-dimensional honeycombs
- ^ Coxeter, The Beauty of Geometry: Twelve Essays, Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213
References
- T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900 (3 regular and one semiregular 4-polytope)
- A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973 (p. 297 Fundamental regions for irreducible groups generated by reflections, Spherical and Euclidean)
- H.S.M. Coxeter, The Beauty of Geometry: Twelve Essays (Chapter 10: Regular honeycombs in hyperbolic space, Summary tables IV p213)
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN978-0-471-01003-6[1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591] (p. 287 5D Euclidean groups, p. 298 Four-dimensionsal honeycombs)
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990) (Page 141, 6.9 List of hyperbolic Coxeter groups, figure 2) [2]
External links
- Klitzing, Richard. "5D uniform polytopes (polytera)".
| Space | Family | / / | ||||
|---|---|---|---|---|---|---|
| E2 | Uniform tiling | {3[3]} | δ3 | hδ3 | qδ3 | Hexagonal |
| E3 | Uniform convex honeycomb | {3[4]} | δ4 | hδ4 | qδ4 | |
| E4 | Uniform 4-honeycomb | {3[5]} | δ5 | hδ5 | qδ5 | 24-cell honeycomb |
| E5 | Uniform 5-honeycomb | {3[6]} | δ6 | hδ6 | qδ6 | |
| E6 | Uniform 6-honeycomb | {3[7]} | δ7 | hδ7 | qδ7 | 222 |
| E7 | Uniform 7-honeycomb | {3[8]} | δ8 | hδ8 | qδ8 | 133 • 331 |
| E8 | Uniform 8-honeycomb | {3[9]} | δ9 | hδ9 | qδ9 | 152 • 251 • 521 |
| E9 | Uniform 9-honeycomb | {3[10]} | δ10 | hδ10 | qδ10 | |
| E10 | Uniform 10-honeycomb | {3[11]} | δ11 | hδ11 | qδ11 | |
| En-1 | Uniform (n-1)-honeycomb | {3[n]} | δn | hδn | qδn | 1k2 • 2k1 • k21 |





































