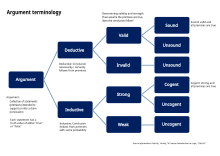
유효성(논리)

논리학에서, 특히 연역적 추론에서, 주장은 전제가 참이고 결론은 ^[1]거짓이 되는 것을 불가능하게 만드는 형식을 취할 경우에만 유효하다.유효한 주장은 실제로 ^[2]사실인 전제를 가질 필요는 없지만, 만약 그것이 사실이라면, 주장의 결론의 진실을 보장할 수 있는 전제를 가질 필요가 있다.유효한 주장은 잘 형성된 공식(wffs 또는 단순 공식이라고도 함)이라고 불리는 문장으로 명확하게 표현되어야 합니다.

주장의 타당성은 시험, 증명 또는 반증될 수 있으며, 논리의 ^[3]형태에 따라 달라집니다.

논쟁들

논리학에서, 논쟁은 전제(경험적 증거와 자명한 사실로 구성된 것)와 증거에 기초한 결론을 표현하는 진술의 집합이다.

주장은 모든 전제가 ^[3]참일 때 결론이 거짓일 경우에만 유효하다.타당성은 전제의 진실성을 요구하는 것이 아니라 논리적 형식의 정확성을 침해하지 않고 작성자로부터 결론을 따를 것을 요구한다.만약 타당한 주장의 전제 또한 사실로 입증된다면,^[3] 이것은 타당하다고 할 수 있다.

유효한 인수의 대응하는 조건은 논리적인 진실이며, 대응하는 조건의 부정은 모순이다.결론은 그 전제의 논리적 결과이다.

유효하지 않은 인수는 "유효하지 않다"고 합니다.

유효한 주장의 예는 다음과 같은 잘 알려진 삼단논법에 의해 제시된다.

모든 사람은 죽는다.

소크라테스는 남자다.

그러므로, 소크라테스는 죽는다.

이것을 타당한 논거로 만드는 것은 그것이 진실한 전제조건과 진실한 결론을 가지고 있다는 것이 아니라 두 가지 전제조건으로 볼 때 결론의 논리적 필요성을 가지고 있다는 것이다.그 주장은 전제와 결론이 틀린 것처럼 타당할 것이다.다음 주장은 논리 형식은 같지만 전제가 틀리고 결론이 틀려 동등하게 유효합니다.

모든 컵이 녹색입니다.

소크라테스는 컵이다.

그러므로, 소크라테스는 녹색이다.

우주가 어떻게 구성되든 간에, 이러한 주장들이 동시에 진실된 전제조건이 아닌 잘못된 결론을 갖는 것으로 밝혀져야 하는 경우는 결코 있을 수 없다.위의 인수는 다음과 같은 비활성 인수와 대조될 수 있습니다.

모든 사람은 불멸이다.

소크라테스는 남자다.

그러므로, 소크라테스는 죽는다.

이 경우 결론은 앞의 전제에서 도출하기보다는 연역적 논리와 모순된다.따라서, 결론은 일반적으로 '참'으로 간주될 수 있지만, 주장은 논리적으로 '무효'하다.'모든 사람은 불멸'이라는 전제는 고전 논리의 틀을 벗어나 잘못된 것으로 여겨질 것이다.하지만, 그 체계 안에서, "참"과 "거짓"은 본질적으로 그 용어들과 보통 연관된 철학 개념보다 이진수 1과 0과 같은 수학적 상태와 더 비슷하게 기능합니다.

표준적인 견해는 논쟁이 유효한지는 논쟁의 논리적 형식의 문제라는 것이다.논리학자들은 논리의 논리적 형태를 나타내기 위해 많은 기법을 사용한다.위의 그림 중 두 가지에 적용된 간단한 예는 다음과 같습니다.남자 집합, 인간 집합, 소크라테스에 각각 'P', 'Q', 'S'를 세우자.이러한 기호를 사용하여 첫 번째 인수는 다음과 같이 축약할 수 있습니다.

모두 P는 Q입니다.

S는 P입니다.

따라서 S는 Q입니다.

마찬가지로 두 번째 인수는 다음과 같습니다.

모든 P가 Q는 아니다.

S는 P입니다.

따라서 S는 Q입니다.

주장은 구조적인 자기 일관성을 갖는 경우, 즉 전제들 사이의 피연산자가 모두 참일 때 도출된 결론도 항상 참일 경우 공식적으로 유효하다.세 번째 예에서는 첫 번째 전제가 논리적으로 결론을 도출할 수 없기 때문에 유효하지 않은 인수로 분류됩니다.

유효한 공식

공식 언어의 공식은 언어의 모든 가능한 해석 하에서 그것이 사실일 경우에만 유효한 공식이다.명제논리학에서 그것들은 동치이다.

진술들

진술은 타당하다고 할 수 있다. 즉, 모든 해석에서 참이라면 논리적인 진실이다.

건전성

추론의 타당성은 전제의 진실이나 결론의 진실성에 영향을 받지 않는다.다음 추론은 완전히 유효하다.

모든 동물들은 화성에 산다.

모든 인간은 동물이다.

그러므로 모든 인간은 화성에 산다.

그 주장의 문제는 그것이 건전하지 않다는 것이다.연역적 논거가 건전하기 위해서는 논거가 유효해야 하며 모든 전제조건이 ^[3]참이어야 한다.

만족도

모델 이론은 적절한 수학적 구조에서 해석의 특정 클래스와 관련하여 공식을 분석합니다.이 해석에서 모든 해석이 사실이라면 공식은 유효하다.추론은 전제를 검증하는 모든 해석이 결론을 검증하는 경우에 유효하다.이것은 의미 ^[4]유효성으로 알려져 있습니다.

보존

진실 보존 타당성에서는 모든 변수에 진실 값 '참'을 할당하는 해석이 진실 값 '참'을 생성합니다.

오보존 타당성에서는 모든 변수에 'false'의 참값 값을 할당하면 참값 'false'^[5]가 된다.

보존 속성	논리 접속문
참 및 거짓 보존:	제안 • 논리적 결합(AND, ${\$ { $displaystyle \land$}$$ ) • 논리적 분리(OR, ${\$ { $displaystyle \lor$}$$ )
실제 보존만:	동어법$( {\$ { $displaystyle$ \ $top$}$$ ) • 바이콘디셔널(XNOR, $↔$ { $displaystyle$$$\ $left$ arrow})$$ • 시사점($→$ { $displaystyle$$$\ $left$ arrow$})$ • 반대 의미($←$ { displaystyle \ }$$ )
잘못된 보존만:	모순( ${\$ { $displaystyle$\ $bot$}$$ ) • 배타적 분리(XOR$, style$ { displaystyle \ oplus })$$ • 비복제$($$style$$${ displaystyle \ n $rightarrow$$$})$$ • 비복제(display { displaystyle \$$n })$$
비보존:	부정( $¬$ { $displaystyle \neg$}$$ ) • 대체 부정($낸드,$ $\uparrow {\displaystyle }$ { $displaystyle$ \up 화살표})$$ • 공동 부정(NOR$,$↓ { $displaystyle$ \$down$ 화살표})$$

「 」를 참조해 주세요.

• 논리적 결과
• 리덕티오 애드 부조리움
• 수학적 오류
• 건전성
• δ-유효성

레퍼런스

추가 정보

• 바와이즈, 존, 에케멘디, 존언어, 실증 및 논리(1999년): 42.
• 맥주, 프란시스 A "유효도: 정치학 관점", 사회 인식론 7, 1(1993): 85-105.