아우프바우 원리

Aufbau principle
"원자력 증강" 리디렉션 핵무기의 확산을 위해서는 핵확산을 보라.
다음 시리즈의 일부
주기율표
전자는 원자의 껍질과 하위껍질을 아우프바우 원리에 따라 대략적으로 점유한다.
주기율표형식
주기율표이력
요소 집합
주기율표 구조별
금속성구분별
다른 특징으로
요소들
화학 원소 목록
요소의 속성
요소의 데이터 페이지

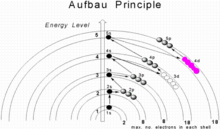
아우프바우 원칙(building-up principe, building-up principle)이라고도 불리는 독일 아우프바우 원칙은 원자나 이온의 지상 상태에서는 전자가 가장 낮은 가용 에너지의 하위껍질을 채운 다음 더 높은 에너지의 하위껍질을 채운다고 명시하고 있다. 예를 들어 1s 하위 쉘은 2s 하위 쉘을 점유하기 전에 채워진다. 이렇게 해서 원자나 이온의 전자는 가능한 한 가장 안정된 전자 구성을 형성한다. 인 원자에 대한 구성 1s2 2s2 2s6 2p2 3s 3p가3 그 예로서, 1s 서브셸에는 2개의 전자가 있다는 것을 의미한다.

전자행동은 훈드의 법칙과 파울리 배타원리와 같은 원자물리학의 다른 원리에 의해 정교하게 설명된다. Hund의 법칙은 동일한 에너지의 여러 궤도를 이용할 수 있다면, 전자가 두 배로 점유되기 전에 단독으로 다른 궤도를 점유할 것이라고 주장한다. 이중 점령이 발생하는 경우, 파울리 배제 원칙은 동일한 궤도상에 점유하는 전자는 반드시 다른 회전(+)을 가져야 한다고 요구한다.½ 및 -1⁄2).

한 요소에서 다음으로 높은 원자 번호의 다른 원소로 전달하면, 중성 원자에 한 번에 한 양성자와 한 전자가 추가된다. 어떤 쉘에서든 최대 전자 수는 2n이며2 여기서 n은 주요 양자수다. 하위 쉘(s, p, d 또는 f)의 최대 전자 수는 2(2l + 1)이며 여기서 l = 0, 1, 2, 3... 따라서 이러한 하위 쉘은 각각 최대 2, 6, 10 및 14개의 전자를 가질 수 있다. 접지 상태에서 전자 구성은 추가된 총 전자 수가 원자 번호와 같을 때까지 가용 가능한 가장 낮은 하위 쉘에 전자를 배치함으로써 구축될 수 있다. 따라서 하위 쉘은 전자 구성을 예측하는 데 도움이 되는 두 가지 일반 규칙을 사용하여 에너지를 증가시키는 순서로 채워진다.

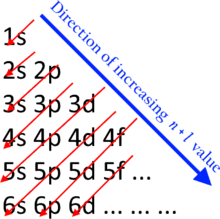
  1. 전자는 n + l의 증가 값 순서로 하위 쉘에 할당된다.
  2. 값이 같은 n + l인 서브쉘의 경우, 낮은 n을 가진 서브셸에 전자가 먼저 할당된다.

핵 쉘 모델이라고 알려진 aufbau 원리의 버전은 원자핵에서 양성자와 중성자의 구성을 예측하는 데 사용된다.[1]

마들룽 에너지 주문 규칙

동일한 빨간색 화살표가 교차하는 상태는 동일한 n + l 값을 갖는다. 빨간색 화살표의 방향은 국가 채우기 순서를 나타낸다.
다극자 원자의 경우 쉘 인터리브의 에너지 스펙트럼이 n + l 규칙을 생성한다.

중성 원자에서, 하위 껍질이 채워지는 대략적인 순서는 n + l 규칙에 의해 주어지며, 또한 다음과 같이 알려져 있다.

여기서 n은 주 양자수 및 방위 양자수 l를 나타낸다. l = 0, 1, 2, 3 값은 각각 s, p, d, f 라벨에 해당한다. 이 규칙에 의한 하위 쉘 순서는 1s, 2s, 2p, 3s, 3p, 4s, 3d, 4p, 4p, 5s, 4d, 5p, 6s, 4f, 5d, 6p, 7s, 5f, 6d, 7d, 7p, 5g, ...이다. 예를 들어 티타늄(Z = 22)은 지상 상태 구성 1s22 2s6 2p2 3s6 3p 4s2 3d를2 가진다.[4]

다른 저자들은 항상 Ti(Z2 = 222) 1s6 2s2 2p6 3p2 3d2 4s와 같이 n을 증가시키는 순서로 하위 쉘을 쓴다.[5] 이 원자가 이온화되면 전자는 대략 4초, 3d, 3p, 3s 등의 순서로 남기 때문에 이것을 "탈진 순서"라고 할 수 있다. 주어진 중립 원자의 경우, 단지 아 껍질 수용만이 물리적 의미를 가지기 때문에 두 개의 표기법은 동등하다.

낮은 n + l 값을 가진 하위 셸은 높은 n + l 값을 가진 하위 셸보다 먼저 채워진다. n + l 값이 같은 경우 n 값이 낮은 하위 쉘이 먼저 채워진다. 마들룽 에너지 순서 규칙은 지상의 중립 원자에만 적용된다. 마들룽 법칙이 정한 전자 구성과는 다른 전자 구성을 예측하는 20개의 원소(d-블록의 16개, f-블록의 9개)가 있다. 비록 마들룽이 예측한 전자 구성은 그러한 경우에도 적어도 지상 상태에 가깝다.

한 무기화학 교과서는 마들룽 규칙을 본질적으로 대략적인 경험적 규칙으로 기술하고 있지만,[5] 토마스-에 근거한 이론적 정당성이 있다.다수의 전자 양자-기계 시스템으로서의 원자의 페르미 모델.[6]

d-블록의 예외

발란스 d-subshell은 발란스 s-subshell로부터 하나의 전자(팔라듐 2개의 경우)를 "빌린다".

특별한 예외는 로렌슘 Lr인데, 여기서 마들룽 규칙에 의해 예측된 6d 전자는 7p 전자로 대체된다: 규칙은 [Rn] 5f14 6d1 7s를2 예측하지만, 측정된 구성은 [Rn] 5f14 7s2 7p이다1.

원자 24CR 29CU 41Nb 42모 44루 45RH 46피디 47AG 78PT 79Au 103Lr
코어 전자 [아] [아] [Kr] [Kr] [Kr] [Kr] [Kr] [Kr] [Xe] 4f14 [Xe] 4f14 [Rn] 5f14
마들룽 규칙 3d4 4s2 3d9 4s2 4d3 5s2 4d4 5s2 4d6 5s2 4d7 5s2 4d8 5s2 4d9 5s2 5d8 6s2 5d9 6s2 6d1 7s2
실험적인 3d5 4s1 3d10 4s1 4d4 5s1 4d5 5s1 4d7 5s1 4d8 5s1 4d10 4d10 5s1 5d9 6s1 5d10 6s1 7시2 7분1

예를 들어, 구리 Cu에서는 마들룽 규칙에 따라 3d 서브셸(n + l = 4 + 0 = 4)보다 먼저 4s 서브셸(n + l = 3 + 2 = 5)을 점유한다. 그 다음 규칙은 전자 구성을 1s 2s22 2p6 3s2 3p69 3d2 4s로 예측하는데, 여기서 [Ar] 3d9 4s는2 선행 고귀한 가스인 아르곤의 구성을 나타낸다. 그러나 구리 원자의 측정된 전자 구성은 [Ar] 3d10 4s이다1. 3d 서브쉘을 채움으로써 구리는 더 낮은 에너지 상태에 있을 수 있다.

f-블록의 예외

발란스 d-subshell은 종종 발란스 f-subshell에서 하나의 전자(토륨 2개의 전자)를 "빌린다"고 한다. 예를 들어 우라늄 U에서는 마들룽 규칙에 따라 5f 하위 쉘(n + l = 5 + 3 = 8)이 6d 하위 쉘(n + l = 6 + 2 = 8)보다 먼저 점유된다. 그런 다음, [Rn]이 선행 고귀한 가스인 라돈의 구성을 나타내는 전자 구성 [Rn] 5f4 7s를2 예측한다. 그러나 우라늄 원자의 측정된 전자 구성은 [Rn] 5f3 6d1 7s이다2.

원자 57라 58CE 64Gd 89Ac 90TH 91파 92U 93Np 96CM
코어 전자 [Xe] [Xe] [Xe] [Rn] [Rn] [Rn] [Rn] [Rn] [Rn]
마들룽 규칙 4f1 6s2 4f2 6s2 4f8 6s2 5f1 7s2 5f2 7s2 5f3 7s2 5f4 7s2 5f5 7s2 5f8 7s2
실험적인 5d1 6s2 4f1 5d1 6s2 4f7 5d1 6s2 6d1 7s2 6d2 7s2 5f2 6d1 7s2 5f3 6d1 7s2 5f4 6d1 7s2 5f7 6d1 7s2

이러한 예외는 모두 화학과는 그다지 관련이 없는데, 에너지 차이가 상당히 작고[7] 가까운 원자의 존재가 선호되는 구성을 바꿀 수 있기 때문이다.[8] 주기율표는 그것들을 무시하고 이상적인 구성을 따른다.[9] 그것들은 정전기적 반발 효과의 결과로 발생한다;[7][8] 원자가 양극 이온화되면, 대부분의 이상 징후는 사라진다.[7]

위의 예외는 8s 셸이 완성되는 원소 120까지가 유일할 것으로 예측된다. 원소 121은 g-블록 시작 시 예상 5g 전자가 8p(로렌슘과 유사)로 전달되는 예외여야 한다. 이후, 소스는 예측된 구성에 동의하지 않지만, 매우 강한 상대론적 효과 때문에 마델룽의 120이 넘는 지배로부터 예상되는 구성을 보여주는 요소가 더 이상 많지 않을 것으로 예상된다.[10] 일반적인 생각 두 8s요소 있은 후에도 5g토마토의 화학 활동,~에 이어7d 순으로 지방, 그리고 그때로 8펜스가 내려서 하지만 대부분 예방하는 데, 상대성 이론을 제외하곤"스플릿"은8p 껍질 속으로 들어간 속도로 안정 부분(8p1/2는 행동하는 같은 여분의 덮개 껍질과 함께 8s와 천천히 물에 빠져에 핵심 across 5g 및 6f 시리즈)와 불안정한 부분 (9p와3/2 거의 동일한1/2 에너지를 갖는 8p) 그리고 8s 셸이 7d 원소의 커버링 s-셸과 같이 9s 셸로 대체된다는 것.[10][11]

역사

새로운 양자 이론의 aufbau 원리

구 양자론에서는 각운동량(s-와 p-subshell)이 낮은 궤도는 핵에 가까워진다.

이 원리는 그 이름을 과학자의 이름을 따서 짓기 보다는 독일어인 아우프바우프린시프에서 따온 것이다. 1920년대 초 닐스 보어(Niels Bohr)와 볼프강 파울리에 의해 공식화되었다. 이것은 양자역학을 전자의 성질에 초기에 적용한 것으로, 화학적 성질을 물리적 용어로 설명했다. 각각의 추가된 전자는 원자핵의 양전하와 핵에 묶인 다른 전자의 음전하로 생성된 전기장의 영향을 받는다. 수소에서는 동일한 주 양자수 n을 가진 서브셸 사이에 에너지 차이가 없지만, 다른 원자의 외부 전자에는 해당되지 않는다.

양자역학 이전의 옛 양자론에서 전자는 고전적인 타원 궤도를 차지하도록 되어 있었다. 각운동량이 가장 높은 궤도는 내전자 바깥의 '순환궤도'이지만, 각운동량(s와 p-subshell)이 낮은 궤도는 하위 껍질 편심도가 높아 핵에 더 가까이 다가가 평균적으로 덜 강하게 차폐된 핵전하를 느낀다.

n + l 에너지 순서 규칙

각 행이 n + l의 하나의 값에 해당하는 주기율표(n과 l의 값이 각각 원수와 방위 양자수에 해당하는 경우)는 1928년에 찰스 자넷에 의해 제안되었고, 1930년에 그는 ato의 분석에 의해 결정된 원자 지상 상태에 대한 지식을 바탕으로 이 패턴의 양자적 기초를 명시하였다.마이크 스펙트럼 이 표를 좌판이라고 부르기 시작했다. 자넷은 원소의 실제 n + l 값 중 일부가 그의 에너지 순서 규칙과 일치하지 않았기 때문에 "조정"했고, 관련된 불일치는 측정 오류에서 발생한 것이 틀림없다고 판단했다. 예외인 모든 원소의 경우 정규화된 구성이 저 에너지 흥분 상태여서 화학 결합 에너지의 범위 내에 있지만, 이 경우 실제 값은 정확하고 n + l 에너지 순서 규칙은 완벽한 적합보다는 근사치로 판명되었다.

1936년 독일의 물리학자 에르윈 마델룽은 이를 원자 하위껍질 채우기 순서에 대한 경험적 규칙으로 제안했고, 따라서 대부분의 영어 출처는 마델룽 규칙을 가리킨다. 마들룽은 1926년에 이르면 이런 패턴을 알고 있었을 것이다.[12] 1945년 William Wiswesser는 함수의[13] 값을 증가시키기 위해 하위껍질을 채울 것을 제안했다.

1962년 러시아의 농업 화학자 V.M. 클레흐코프스키가 통계적 토머스–에 근거한 n+l 합계의 중요성에 대한 최초의 이론적 설명을 제안했다.원자의 페르미 모델.[14] 따라서 많은 프랑스어 및 러시아어 출처는 클렉코프스키 규정을 참조한다.[15] 1979년 D. 판 웡은 마들룽 규칙의 두 번째 부분(같은 값 n + l를 가진 두 개의 하위 껍질에 대해 n 채우기 값이 작은 것이 먼저라는 이론적 정당성을 제공했다.[14]

최근 몇 년 동안 중립 원자의 하위 껍질 채우기 순서가 항상 주어진 원자의 전자를 추가하거나 제거하는 순서와 일치하지 않는다는 점에 주목해 왔다. 예를 들어 주기율표의 네 번째 행에서 마들룽 규칙은 4s 하위 껍질이 3d 이전에 점유되었음을 나타낸다. 따라서 K에 대한 중성 원자 접지 상태 구성은 [Ar] 4s1, Ca는 [Ar] 4s2, Sc는 [Ar] 4s2 3d1 등이다. 단, 전자를 제거하여 스칸듐 원자가 이온화되는 경우(만 해당), 구성이 다른데, Sc는 [Ar] 4s2 3d1, Sc는+ [Ar] 4s1 3d1, Sc는2+ [Ar] 3d이다1. 하위 껍질 에너지와 그 질서는 핵 전하량에 따라 달라진다; 4s는 19개의 양성자를 가진 K의 마들룽 규칙에 따라 3d보다 낮지만, Sc에서는2+ 3d가 21개의 양성자를 가지고 있다. 마들룽 규칙은 중립 원자에 대해서만 사용되어야 한다. 중성 원자의 경우에도 d-블록과 f-블록에는 위와 같이 예외가 있다.

이 관점을 뒷받침할 충분한 실험 증거가 있을 뿐만 아니라, 4s 전자가 항상 우선적으로 이온화된다는 점을 감안할 때, 이것과 다른 전이 금속에서 전자의 이온화 순서에 대한 설명을 더욱 쉽게 한다.[16]

참고 항목

참조

  1. ^ Cottingham, W. N.; Greenwood, D. A. (1986). "Chapter 5: Ground state properties of nuclei: the shell model". An introduction to nuclear physics. Cambridge University Press. ISBN 0-521-31960-9.
  2. ^ McLaughlin, R. (1964). "4s, 3d, What?". Journal of Chemical Education. 60 (7): 562. doi:10.1021/ed060p562.
  3. ^ "Electron Configuration". WyzAnt.
  4. ^ Miessler, Gary L.; Tarr, Donald A. (1998). Inorganic Chemistry (2nd ed.). Prentice Hall. p. 38. ISBN 0-13-841891-8.
  5. ^ a b Jolly, William L. (1984). Modern Inorganic Chemistry (1st ed.). McGraw-Hill. pp. 10–12. ISBN 0-07-032760-2.
  6. ^ Wong, D. Pan (1979). "Theoretical justification of Madelung's rule". Journal of Chemical Education. 56 (11): 714. Bibcode:1979JChEd..56..714W. doi:10.1021/ed056p714.
  7. ^ a b c Jørgensen, Christian (1973). "The Loose Connection between Electron Configuration and the Chemical Behavior of the Heavy Elements (Transuranics)". Angewandte Chemie International Edition. 12 (1): 12–19. doi:10.1002/anie.197300121.
  8. ^ a b Feynman, Richard; Leighton, Robert B.; Sands, Matthew (1964). "19. The Hydrogen Atom and The Periodic Table". The Feynman Lectures on Physics. 3. Addison–Wesley. ISBN 0-201-02115-3.
  9. ^ Jensen, William B. (2009). "Misapplying the Periodic Law" (PDF). Journal of Chemical Education. 86 (10): 1186. Bibcode:2009JChEd..86.1186J. doi:10.1021/ed086p1186. Retrieved 16 May 2020.
  10. ^ a b Fricke, Burkhard (1975). Superheavy elements: a prediction of their chemical and physical properties. Recent Impact of Physics on Inorganic Chemistry. Structure and Bonding. 21. pp. 89–144. doi:10.1007/BFb0116498. ISBN 978-3-540-07109-9. Retrieved 4 October 2013.
  11. ^ Pyykkö, Pekka (2016). Is the Periodic Table all right ("PT OK")? (PDF). Nobel Symposium NS160 – Chemistry and Physics of Heavy and Superheavy Elements.
  12. ^ Goudsmit, S. A.; Richards, Paul I. (1964). "The Order of Electron Shells in Ionized Atoms" (PDF). Proc. Natl. Acad. Sci. 51 (4): 664–671 (with correction on p 906). Bibcode:1964PNAS...51..664G. doi:10.1073/pnas.51.4.664. PMC 300183. PMID 16591167.
  13. ^ Wiswesser, William J. (July 1945). "The Periodic System and Atomic Structure I. An Elementary Physical Approach". Journal of Chemical Education. 22 (7): 314–322. Bibcode:1945JChEd..22..314W. doi:10.1021/ed022p314. Retrieved 5 September 2020.
  14. ^ a b Wong, D. Pan (1979). "Theoretical justification of Madelung's rule". J. Chem. Educ. 56 (11): 714–718. Bibcode:1979JChEd..56..714W. doi:10.1021/ed056p714.
  15. ^ Sakho, Ibrahima (2019). Introduction to Quantum Mechanics 1: Thermal Radiation and Experimental Facts Regarding the Quantization of Matter. Wiley. p. 115. ISBN 978-1786304872. Retrieved 11 April 2021.
  16. ^ Scerri, Eric (7 November 2013). "The Trouble With the Aufbau Principle". Education in Chemistry. Vol. 50 no. 6. Royal Society of Chemistry. pp. 24–26.

추가 읽기

외부 링크