자기 양자수
Magnetic quantum number원자 물리학에서, 자기 양자수 m은l 전자의 고유한 양자 상태를 설명하는 네 개의 양자수 중 하나이다.자기 양자 번호는 서브셸 내에서 이용 가능한 궤도를 구별하고, 우주에서의 궤도 방향의 방위성분을 계산하는 데 사용됩니다.특정 서브셸(s, p, d 또는 f 등)의 전자는 θ(0, 1, 2, 또는 3)의 값으로 정의됩니다.m의l 값은 0을 포함하여 - to ~+ , 。따라서 s, p, d 및 f 서브셸은 각각 1, 3, 5, 7개의 궤도를 포함하며 m 값은 각각 0, ±1, ±2, ±3 범위 내에 있습니다.이러한 궤도 각각은 최대 2개의 전자(반대 스핀 포함)를 수용할 수 있어 주기율표의 기초를 형성합니다.
파생
원자의 에너지 상태와 관련된 일련의 양자수가 있다.4개의 양자 n(\ n 및 s는 파동함수 또는 궤도라고 불리는 원자에서 단일 전자의 완전한 양자 상태를 나타냅니다.하나의 전자를 가진 원자의 파동함수에 대한 슈뢰딩거 방정식은 분리 가능한 편미분 방정식이다.(이는 헬륨 원자 또는 서로 상호작용하는 전자를 가진 다른 원자의 경우는 해당되지 않으며, 이 원자는 보다[1] 정교한 용해 방법을 필요로 한다.)즉, 구면 좌표로 표현되는 파동 함수는 반지름, 결속(또는 극)[2] 각도 및 방위각의 세 가지 함수의 곱으로 나눌 수 있습니다.
의 미분방정식은 F() ) \^{\lambda = Ae의 은 라디안 (360) 도수만큼 다르기 때문에 풀 수 .l F의 는 실제 지수와 마찬가지로 임의로 큰displaystyle \와 함께 증가하지 않습니다. 계수 \는 i i의 정수 배수로 양자화해야 하며, 상상의 지수 \를 생성해야 합니다[3]} 。이 정수는 자기 양자수입니다.같은 상수가 colatitude 방정식에서도 나타난다.서 m 2 ( \ { m { \ } } values values 2 2 ( \ { m _ { \ ) display display thenumber number number number number ( \ number number number number number number number number number number number number number number number number number number number number number number number number number number number ){ P의 모든 솔루션을 허용합니다.
| 양자수의 관계 | |||
|---|---|---|---|
| 궤도 | 가치 | 값 수({ m_ | 서브셸당 전자 수 |
| s | 1 | 2 | |
| p | 3 | 6 | |
| d | 5 | 10 | |
| f | 7 | 14 | |
| g | 9 | 18 | |
각운동량의 구성요소로서
이 분석에서 극좌표에 사용되는 축은 임의로 선택됩니다.m {\ m은 일반적으로 {\ z 방향 또는 양자화 축으로 불리는 임의 선택 방향으로 각운동량을 투영하는 것을 말합니다.z {\ {\ z 방향의 각운동량 크기는 다음 [4]공식으로 표시됩니다.
- z { L_ } \ 。
이는 원자 전자의 총 궤도 L의 성분으로, 크기는 다음과 같은 식으로 부껍질의 방위 양자수(\와 관련이 있다.
- 1 + ) 。{ L {\+ 。
여기서는 축소된 플랑크 상수입니다. 인 경우 0 \ 이며 인 경우 L=\)\를 각도(로 측정할 수 없습니다.이러한 특성은 오토 스턴과 발터 게라크의 [5]스턴-게라크 실험에서 처음 입증되었다.
어떤 파동의 에너지도 그 주파수에 플랑크 상수를 곱한 것이다.그 파장은 퀀텀이라고 불리는 에너지의 입자 모양의 패킷을 보여준다.각 양자 상태의 양자 수에 대한 공식은 플랑크의 감소된 상수를 사용합니다. 플랑크는 특정 또는 이산 또는 양자화된 에너지 [4]수준만 허용합니다.
자기장의 영향
m(\ m은 각운동량 벡터의 방향을 느슨하게 나타냅니다.자기 m({ m은 전자가 자기장 내에 있는 경우에만 영향을 줍니다. 이 값이 없으면 mm})의 서로 다른 임의의 값에 대응하는 모든 구면 고조파가 같기 때문입니다.자기 양자수는 외부 자기장에 의한 원자 궤도의 에너지 이동을 결정합니다(제만 효과). 그래서 자기 양자수라는 이름이 붙습니다.그러나 원자궤도에서 전자의 실제 자기 쌍극자 모멘트는 전자 각운동량뿐만 아니라 스핀 양자수로 표현되는 전자 스핀으로부터도 발생한다.
각 전자는 자기장에 자기 모멘트가 있기 때문에 벡터 {\을를) 자기장과 평행하게 만드는 경향이 있는 토크를 받게 됩니다.이 현상을 라모르 세차라고 합니다.
「 」를 참조해 주세요.
레퍼런스
- ^ "Helium atom". 2010-07-20.
- ^ "Hydrogen Schrodinger Equation". hyperphysics.phy-astr.gsu.edu.
- ^ "Hydrogen Schrodinger Equation". hyperphysics.phy-astr.gsu.edu.
- ^ a b c Herzberg, Gerhard (1950). Molecular Spectra and Molecular Structure (2 ed.). D van Nostrand Company. pp. 17–18.
- ^ "Spectroscopy: angular momentum quantum number". Encyclopædia Britannica.
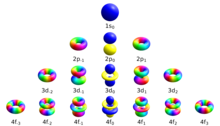
 가지고 있습니다.방위각 성분의
가지고 있습니다.방위각 성분의  수직축을 중심으로 m회 반복되는 색상 구배로 볼 수 있습니다.
수직축을 중심으로 m회 반복되는 색상 구배로 볼 수 있습니다.




 미분방정식은 F
미분방정식은 F


 i
i












 이 벡터의 총 크기보다 작습니다.
이 벡터의 총 크기보다 작습니다.






 각도(
각도(

