자기장

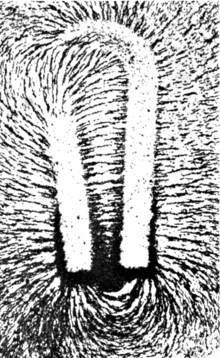
기사 정보
전자기학
전기 자기 역사 교재
정전학 전하 쿨롱의 법칙 컨덕터 전하 밀도 유전율 전기 쌍극자 모멘트 전기장 전위 전기 플럭스/전위 정전 방전 가우스의 법칙 인덕션 절연체 편광 밀도 정전기 삼각전기
자기 정전기 앙페르의 법칙 비오트-사바르 법칙 가우스의 자기 법칙 자기장 자속 자기 쌍극자 모멘트 투과성 자기 스칼라 퍼텐셜 자화 자력 자기 벡터 퍼텐셜 오른손 법칙
전기역학 로렌츠 힘의 법칙 전자 유도 패러데이의 법칙 렌츠의 법칙 변위 전류 맥스웰 방정식 전자기장 전자기 펄스. 전자파 복사 맥스웰 텐서 포인팅 벡터 리에나르비셰르트 퍼텐셜 제피멘코의 방정식 와전류 런던 방정식 전자기장에 대한 수학적 설명
전기 네트워크 교류 캐패시턴스 직류 전류 전기 분해 전류 밀도 줄 가열 기전력 임피던스 인덕턴스 옴의 법칙 병렬 회로 저항 공명 공동 직렬 회로 전압 도파관
공변량 공식 전자기 텐서 (표준 – 에너지 텐서) 사류 전자파 4전위
과학자 암페르 바이오트 쿨롱 데이비 아인슈타인 패러데이 피조 가우스 헤비사이드 핸리다. 헤르츠 홉킨슨 제피멘코 줄 렌츠 리에나루 로렌츠 맥스웰 노이만 외르스테드 옴 포인팅 리치 사바토 가수. 스타인메츠 테슬라 톰슨 볼타 웨버 비헤르트 포아송
v t

자기장은 움직이는 전하, 전류 ^{[1]: ch1 [2]}및 자성 물질에 대한 자기 영향을 설명하는 벡터장이다.자기장 내 이동전하는 자신의 속도와 자기장에 ^{[1]: ch13 [3]: 278} 수직인 힘을 받는다.영구 자석의 자기장은 철과 같은 강자성 물질을 끌어당겨 다른 자석을 끌어당기거나 밀어냅니다.또한, 위치에 따라 변화하는 자기장은 외부 원자 전자의 움직임에 영향을 줌으로써 비자성 물질의 범위에 힘을 가할 것이다.자기장은 자화된 물질을 둘러싸고 전자석에 사용되는 전류와 시간에 따라 변화하는 전기장에 의해 생성됩니다.자기장의 세기와 방향은 위치에 따라 다를 수 있기 때문에, 벡터장이라고 불리는 공간의 각 점에 벡터를 할당하는 함수에 의해 수학적으로 설명된다.

전자기학에서 "자기장"이라는 용어는 기호 B와 H로 나타나는 서로 다르지만 밀접하게 연관된 두 개의 벡터장에 사용됩니다.국제 단위계에서 자기장 강도인 H는 SI 기준 단위(암페어/^{[4]: 22} 미터)로 측정됩니다.B(자속 밀도)는 테슬라(SI 기준 단위: 암페어당 ^{[4]: 21} 킬로그램²) 단위로 측정되며, 이는 암페어당 미터당 뉴턴과 동일합니다.H와 B는 자화를 설명하는 방식이 다릅니다.진공상태에서는 진공투과성을 $통해{\displaystyle \mathbf{}B{}_{}}$ / ${\displaystyle {\mu \mathrm{}}_{}}$ ${\displaystyle 0\mathbf{}}$ $=$ H ${\displaystyle \mathbf${$B$} /\$mu _${0$}=\mathbf${H$\}\}$$$} 두 필드가 관련되지만, 자화물질에서는 각 점에서의 자화에 따라 항이 다르다.

자기장은 전하 이동과 기본 양자 ^{[5][1]: ch1} 특성인 스핀과 관련된 소립자의 고유 자기 모멘트에 의해 생성됩니다.자기장과 전기장은 서로 연관되어 있고 둘 다 자연의 네 가지 기본 힘 중 하나인 전자기력의 구성요소입니다.

자기장은 현대 기술, 특히 전기 공학 및 전기 기계학에서 사용됩니다.회전 자기장은 전기 모터와 발전기 모두에 사용됩니다.변압기 등의 전기장치에서의 자기장 상호작용을 개념화하여 자기회로로서 조사한다.자기력은 홀 효과를 통해 물질의 전하 캐리어에 대한 정보를 제공합니다.지구는 태양풍으로부터 지구의 오존층을 보호하고 나침반을 이용한 항해에 중요한 자기장을 만들어낸다.

묘사

전하에 가해지는 힘은 위치, 속도 및 방향에 따라 달라집니다. ^{[1]: ch1} 이 힘을 설명하기 위해 두 개의 벡터장이 사용됩니다.첫 번째는 전장으로, 정지 전하에 작용하는 힘을 설명하고 운동으로부터 독립된 힘의 성분을 제공합니다.반대로 자기장은 하전 ^{[1]: ch13} 입자의 속도와 방향에 비례하는 힘의 성분을 나타냅니다.자기장은 로렌츠 힘의 법칙에 의해 정의되며, 각 순간 전하 운동과 그것이 경험하는 힘 모두에 수직입니다.

B와 ^{[note 1]}H로 쓰여진 "자기장"이라고 불리는 두 개의 서로 다르지만 밀접하게 관련된 벡터장이 있습니다.이 분야들의 가장 좋은 이름들과 이 분야들이 무엇을 나타내는지에 대한 정확한 해석은 오랜 논쟁의 주제가 되어 왔지만, 기초 물리학이 어떻게 ^[6]작용하는지에 대해서는 폭넓은 합의가 있다.역사적으로, "자기장"이라는 용어는 B를 다른 용어로 사용하면서 H를 위해 남겨져 있었지만, 최근의 많은 교과서들은 "자기장"이라는 용어를 H와 함께 ^{[note 2]}또는 H를 대신해서 B를 묘사하기 위해 사용합니다.둘 다 다른 이름이 많이 있습니다(사이드바 참조).

B의 대체[7] 이름
속속 밀밀 자기[8] 유도 ★★★★★★★★★★★★★★★★★★

임의의 지점의 자기장 벡터 B는 로렌츠 힘의 법칙에서 사용될 때 그 지점에서 ^{[9][10]: 204} 하전 입자에 가해지는 힘을 정확하게 예측하는 벡터로 정의할 수 있습니다.

여기서 F는 입자에 대한 힘, q는 입자의 전하, v는 입자의 속도, ×는 교차곱이다.전하에 가해지는 힘의 방향은 오른손 법칙으로 알려진 니모닉에 의해 결정될 수 있습니다(그림 ^{[note 3]}참조).오른손을 사용하여 엄지손가락은 전류 방향을 가리키고 손가락은 자기장 방향을 가리키면 전하에 가해지는 힘은 손바닥에서 바깥쪽으로 향합니다.음전하를 띤 입자에 가해지는 힘은 반대 방향입니다.속도와 전하가 모두 반전되면 힘의 방향은 동일하게 유지됩니다.따라서 자기장 측정만으로는 오른쪽으로 이동하는 양의 전하가 있는지 왼쪽으로 이동하는 음의 전하가 있는지를 구별할 수 없습니다(두 경우 모두 동일한 전류를 생성합니다).한편, 전기장과 결합된 자기장은 이러한 자기장을 구별할 수 있습니다. 아래의 홀 효과를 참조하십시오.

로렌츠 방정식의 첫 번째 항은 정전학 이론에서 나온 것으로, 전기장 E의 전하 q 입자가 전기력을 경험한다고 말합니다.

두 번째 항은 ^[10]자기력입니다.

교차곱의 정의를 사용하여 자력은 스칼라 ^{[9]: 357} 방정식으로도 쓸 수 있습니다.

여기서_magnetic F, v, B는 각각의 벡터의 스칼라 크기이고 θ는 입자의 속도와 자기장 사이의 각도이다.벡터 B는 로렌츠 힘의 법칙이 하전 입자의 움직임을 정확하게 묘사하기 위해 필요한 벡터장으로 정의됩니다.바꿔 ^{[9]: 173–4} 말하면

[T]he 명령어 "이러한 장소에서 벡터 B의 방향과 크기를 측정한다"는 것은 다음과 같은 연산을 요구한다.이미 알려진 전하 q의 입자를 취합니다. 정지 상태에서 q에 가해지는 힘을 측정하여 E를 결정합니다.그런 다음 속도가 v일 때 입자에 가해지는 힘을 측정한다; 다른 방향으로 v를 반복한다.이제 로렌츠 힘의 법칙을 이 모든 결과에 적합하게 만드는 B를 찾습니다. 즉, 해당 지점의 자기장이 바로 그것입니다.

B 필드는 자기 쌍극자의 토크 m으로도 정의할 수 있습니다.^{[11]: 174}

SI 단위로 B는 테슬라(기호:T).^{[note 4]} B는 가우스(Gauss: G) 단위로 측정된다.(변환량은 1 T = 10000 G)^[12][13]1나노테슬라(nanotesla)는 1 감마(기호: ^[13]θ)에 해당합니다.

할 수

H의 대체[7] 이름
자기장[8] 강도 ★★★ ★★★★

자기 H 필드는 다음과 같이 ^{[10]: 269 [11]: 192 [1]: ch36} 정의됩니다.

$여기$서 ${\displaystyle {\mu \mathrm{}}_{}}$ 0$(\$ _${0})$은 진공 투과율, M은 자화 벡터입니다.진공상태에서 B와 H는 서로 비례한다.재료 내부에서는 서로 다르다(자성 재료 내부 및 외부 H 및 B 참조).H 필드는 SI ^[14]단위로 미터당 암페어(A/m) 및 CGS ^{[12][9]: 286} 단위로 외스트(Oe) 단위로 측정된다.

★★★

국소 자기장을 측정하는 데 사용되는 기기는 자력계라고 알려져 있습니다.자력계의 중요한 종류에는 다양한 자기장만을 측정하는 유도 자력계(또는 서치 코일 자력계), 회전 코일 자력계, 홀 효과 자력계, NMR 자력계, SQUID 자력계 및 플럭스게이트 자력계의 사용이 포함됩니다.멀리 있는 천체들의 자기장은 지역 하전 입자에 대한 영향을 통해 측정된다.예를 들어, 전자는 전기장선 주위를 나선형으로 도는 싱크로트론 방사선을 발생시켜 전파에서 검출할 수 있습니다.자기장 측정의 정밀도는 중력 프로브 B가 5 aT(5×10⁻¹⁸ T)^[15]에서 달성했습니다.

시각화

필드는 각 지점에서 필드의 방향을 따르는 일련의 자기장 선으로 시각화할 수 있습니다.라인은 다수의 지점(또는 공간의 모든 지점)에서 자기장의 강도와 방향을 측정하여 구성할 수 있습니다.그런 다음 각 위치를 자기장의 강도에 비례하는 크기로 국소 자기장의 방향을 가리키는 화살표(벡터라고 함)로 표시합니다.이 화살표를 연결하면 일련의 자기장 선이 형성됩니다.어느 지점에서의 자기장의 방향은 인근 필드선의 방향과 평행하며, 필드선의 국소 밀도는 그 강도에 비례할 수 있다.자기장 라인은 연속적인 분포를 나타내며 분해능이 다르면 선이 더 많거나 더 적다는 점에서 유체 흐름의 유선화와 같습니다.

자기장 선을 표현으로 사용하는 이점은 표면을 통과하는 자기장 선의 수와 같은 간단한 개념을 사용하여 많은 자기 법칙(및 전자파)을 완전하고 간결하게 설명할 수 있다는 것입니다.이러한 개념은 수학적 형태로 빠르게 "번역"될 수 있습니다.예를 들어, 주어진 표면을 통과하는 계자선의 수는 ^{[9]: 237} 자기장의 표면 적분이다.

다양한 현상이 마치 자기장 선이 물리적 현상인 것처럼 자기장 선을 "표시"합니다.예를 들어, 자기장에 배치된 철 줄들은 "필드 라인"^{[note 5]}에 해당하는 라인을 형성합니다.자기장 "선"은 또한 플라즈마 입자 쌍극자 상호작용이 지구 자기장의 국소 방향과 일치하는 가시적인 빛의 줄을 만드는 극성 오로라에 시각적으로 표시됩니다.

필드 선은 자력을 시각화하는 정성적 도구로 사용할 수 있습니다.철이나 플라즈마 등의 강자성 물질에서 자력은 필드 라인이 길이를 따라 장력(고무 밴드 등)을 가하고 인접한 필드 라인에서 그 길이에 수직인 압력을 가한다고 상상함으로써 이해할 수 있다."달리" 자석의 극은 많은 필드 라인에 의해 연결되어 있기 때문에 끌어당기고, "좋아요" 극은 필드 라인이 서로 만나지는 않지만 서로 밀면서 평행하게 움직이기 때문에 밀어냅니다.

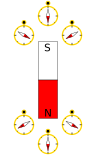
영구 자석은 고유의 영구 자기장을 생성하는 물체입니다.그것들은 자화된 철과 니켈과 같은 강자성 물질로 만들어졌고 그들은 북극과 남극을 모두 가지고 있다.

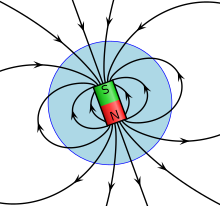
영구 자석의 자기장은 특히 자석 근처에서는 매우 복잡할 수 있습니다.작은^{[note 6]} 직선 자석의 자기장은 자석의 강도에 비례합니다(자기 쌍극자 모멘트 m이라고 함).방정식은 단순하지 않고 자석과의 거리 및 자석의 방향에 따라 달라집니다.단순 자석의 경우, 자석의 남쪽에서 북극으로 그려진 선의 방향으로 m 점을 찍습니다.막대 자석을 뒤집는 것은 m을 180도 회전시키는 것과 같습니다.

큰 자석의 자기장은 각각 고유한 m을 가진 쌍극자라고 불리는 많은 수의 작은 자석의 집합으로 모델링함으로써 얻을 수 있습니다.자석에 의해 생성되는 자기장은 이러한 쌍극자의 순자기장입니다. 자석에 가해지는 순자기력은 개별 쌍극자에 가해지는 힘을 합한 결과입니다.

이 쌍극자의 성질에 대한 두 가지 단순화된 모델이 있었다.이 두 모델은 H와 B라는 두 개의 다른 자기장을 생성합니다.그러나 재료 밖에서는 두 가지가 (곱셈 상수와) 동일하기 때문에 대부분의 경우 구별을 무시할 수 있다.이는 전류에 의한 자기장과 같이 자성 물질에 의해 발생하지 않는 자기장에 특히 해당된다.

실제 자기 모델은 이들 모델보다 복잡합니다. 두 모델 모두 재료가 자성을 띠는 이유를 완전히 설명하지 못합니다.단극 모형은 실험적인 지원을 하지 않는다.암페어 모델은 물질의 자기 모멘트를 일부 설명하지만 전부는 아닙니다.암페어 모델이 예측한 것처럼, 원자 내 전자의 움직임은 전자의 궤도 자기 쌍극자 모멘트에 연결되며, 이러한 궤도 모멘트는 거시적 수준에서 볼 수 있는 자력에 기여합니다.하지만, 전자의 움직임은 고전적이지 않고, 전자의 스핀 자기 모멘트(어느 모델에서도 설명되지 않음) 또한 자석의 총 모멘트에 중요한 기여를 합니다.

역사적으로, 초기 물리학 교과서는 두 자석 사이의 힘과 토크를 전하 사이의 쿨롱 힘과 같은 방식으로 서로 밀어내거나 끌어당기는 자극 때문에 모델링했습니다.미시적 수준에서, 이 모델은 실험적인 증거와 모순되며, 자성의 극 모델은 ^{[10]: 204} 더 이상 개념을 도입하는 전형적인 방법이 아닙니다.하지만, 수학적인 ^[16]단순함 때문에 그것은 여전히 강자성의 거시적 모델로 사용된다.

이 모델에서 자기 H장은 각 극의 표면에 퍼진 가상의 자기장에 의해 생성됩니다.이들 자기전하는 사실상 자화장 M과 관련이 있다.따라서 H장은 양전하로 시작하여 음전하로 끝나는 전기장 E와 유사합니다.따라서 북극 근처에서는 모든 H-필드 선이 북극(자석 내부 또는 외부)에서 멀어지는 반면 남극 근처에서는 모든 H-필드 선이 남극(자석 내부 또는 외부)을 가리킵니다.또한 북극은 H장 방향으로 힘을 느끼는 반면 남극의 힘은 H장과 반대입니다.

소자성 쌍극자 m은 m = q_m d가 되도록 소거리 벡터 d로 분리된_m 극강도 q의 마주보는 2개의 자극에 의해 형성된다.자성체 내부와 외부의 자기장 H를 정확하게 예측하는데, 특히 H가 영구 자석 내부의 자기장 M과 반대라는 사실을 예측한다.

이는 자기 전하 밀도의 가상 개념에 기초하기 때문에 극 모델은 한계가 있다.자극은 전하처럼 서로 떨어져 존재할 수 없으며 항상 남북 쌍으로 발생합니다.자화물체가 반으로 나뉘면 각 조각의 표면에 새로운 극이 나타나기 때문에 각각 한 쌍의 상극이 생긴다.자극 모델은 전류에 의해 생성되는 자성을 설명하지 않으며 각 운동량과 자기 사이의 고유한 연관성도 설명하지 않습니다.

극 모형은 일반적으로 자기 전하를 입자의 물리적 특성이 아닌 수학적 추상화로 취급합니다.하지만, 자기 단극은 물리적으로 하나의 자극(북극 또는 남극)만을 가진 가상의 입자(또는 입자 클래스)입니다.다시 말해, 그것은 전하와 유사한 "자기 전하"를 가질 것이다.자기장 라인은 자기 단극에서 시작하거나 끝나기 때문에 존재한다면 자기장 라인은 시작도 종료도 하지 않는다는 규칙에 예외를 둘 수 있습니다.대통합 이론과 같은 몇몇 이론들은 자기 단극의 존재를 예측해 왔지만, 지금까지 관찰된 것은 하나도 없다.

루프

암페어가 개발한 모델에서 모든 자석을 구성하는 기본 자기 쌍극자는 전류 I의 충분히 작은 암페리안 루프입니다.이 루프의 쌍극자 모멘트는 m = IA입니다.여기서 A는 루프의 면적입니다.

이 자기 쌍극자는 자기 B장을 생성합니다.

그림에는 자기 쌍극자의 자기장이 나타나 있습니다.외부에서는 이상 자기 쌍극자가 동일 강도의 이상 전기 쌍극자와 동일하다.전기 다이폴과는 달리 자기 다이폴은 전류 I 및 면적 a를 갖는 전류 루프로서 적절히 모델화된다.이러한 전류 루프의 자기 모멘트는 다음과 같습니다.

여기서 m의 방향은 루프 면적과 수직이며 오른쪽 규칙을 사용하여 전류 방향에 따라 달라집니다.이상적인 자기 쌍극자는 a면적이 0으로 감소하고 그 전류 I가 무한대로 증가하여 곱 m = Ia가 유한한 실제 자기 쌍극자로 모델링된다.이 모델은 자화에 의한 아인슈타인 드 하스 효과의 기초가 되는 각운동량과 자기모멘트 사이의 관계를 명확히 하고, 그 역방향인 바넷 효과 또는 ^[17]회전에 의한 자화의 기초가 된다.예를 들어 루프를 같은 방향으로 더 빨리 회전시키면 전류가 증가하므로 자기 모멘트가 증가합니다.

과의

사이의 힘

두 개의 작은 자석 사이의 힘을 지정하는 것은 매우 복잡합니다. 왜냐하면 두 자석의 강도와 방향, 그리고 서로 상대적인 거리와 방향에 따라 다르기 때문입니다.힘은 특히 자기 토크에 의한 자석의 회전에 민감합니다.각 자석에 가해지는 힘은 자석의 모멘트와 다른 자석의 자기장에^{[note 7]} 따라 달라집니다.

자석 간의 힘을 이해하려면 위에 제시된 자극 모델을 검토하는 것이 유용합니다.이 모델에서는 한 자석의 H장이 두 번째 자석의 양쪽 극을 밀고 당깁니다.두 번째 자석의 양쪽 극에서 이 H장이 동일할 경우 반대 극에 대한 힘은 반대이기 때문에 이 자석에 대한 순 힘은 없습니다.그러나 첫 번째 자석의 자기장이 균일하지 않은 경우(예를 들어 극 중 하나 근처의 H) 두 번째 자석의 각 극은 다른 자기장을 보고 다른 힘을 받습니다.이 두 힘의 차이는 자석이 자기장이 증가하는 방향으로 이동하며 순 토크를 발생시킬 수도 있습니다.

이는 자석이 더 높은 자기장의 영역으로 끌어당기는(또는 자석의 방향에 따라 밀어내는) 일반적인 규칙의 구체적인 예입니다.영구 자석 또는 전류에 의해 발생하는 모든 불균일한 자기장은 이와 같은 방식으로 작은 자석에 힘을 가합니다.

암페리안 루프 모델의 세부 사항은 서로 다르고 복잡하지만 동일한 결과를 낳습니다. 즉, 자기 쌍극자가 더 높은 자기장의 영역으로 유인/반발합니다.수학적으로 자기장 B에 의한 자기모멘트 m을 갖는 작은 자석에 대한 힘은 다음과 같습니다.^{[18]: Eq. 11.42}

여기서 구배θ는 단위 거리당 m·B의 변화량이며, 방향은 m·B의 최대 증가량이다.도트곱 m · B = mBcos (θ) (여기서 m과 B는 m과 B 벡터의 크기를 나타내고 θ는 그 사이의 각도)m이 B와 같은 방향일 경우 도트 곱은 양의 값이고 경사점은 자석을 더 높은 B 필드 영역(더 엄밀하게는 더 큰 m · B)으로 끌어당깁니다.이 방정식은 크기가 0인 자석에 대해서만 엄격히 유효하지만 너무 크지 않은 자석에는 종종 좋은 근사치가 됩니다.큰 자석의 자기력은 자석을 각각 m을 가진 작은 영역으로 나눈 다음 이 작은 영역 각각에 대한 힘을 합산함으로써 결정됩니다.

영구 자석의 자기 토크

서로 다른 두 개의 자석의 두 개의 같은 극을 서로 가까이 두고 한쪽 자석을 회전시키면 바로 회전하여 첫 번째 자석에 맞춥니다.이 예에서는 고정 자석의 자기장이 자석에 자유롭게 회전할 수 있는 자기 토크를 생성합니다.이 자기 토크 θ는 자석의 극을 자기장 라인에 맞추는 경향이 있습니다.그러므로 나침반은 지구의 자기장과 정렬하기 위해 회전한다.

극 모형의 관점에서, 동일한 H를 경험하는 두 개의 동등하고 반대되는 자기 전하도 동등하고 반대되는 힘을 경험합니다.이러한 등하력 및 반대력은 서로 다른 위치에 있기 때문에, 이 힘은 이들 사이의 거리(힘에 수직)에 비례하는 토크를 생성합니다.극강도에 극간 거리를 곱한 m의 정의는 μ = μm H sin δ로₀ 이어진다. 여기서₀ μ는 진공 투과성이라고 하는 상수이며, μ는⁻⁷ 4µ×10 V·s/(A·m)이고, μ는 H와 m 사이의 각도이다.

수학적으로 작은 자석의 토크 θ는 인가된 자기장과 자석의 자기 모멘트 m에 모두 비례합니다.

여기서 ×은 벡터 교차곱을 나타냅니다.이 방정식은 위에 포함된 모든 질적 정보를 포함합니다.m이 자기장과 같은 방향이면 같은 방향의 벡터 2개에 대해 교차곱이 0이므로 자석에 토크가 없습니다.또한 다른 모든 방향은 자기장 방향으로 비틀리는 토크를 느낀다.

전류와의 상호작용

전하의 전류는 자기장을 발생시키고 자기 B장에 의해 힘을 느낀다.

이동 전하 및 전류에 의한 자기장

움직이는 모든 하전 입자는 자기장을 생성한다.전자와 같은 이동점 전하는 ^[19]입자의 전하, 속도 및 가속도에 따라 복잡하지만 잘 알려진 자기장을 생성합니다.

자기장 선은 와이어 길이와 같은 원통형 전류 전달 도체 주위에 동심원 모양으로 형성됩니다.이러한 자기장의 방향은 "오른쪽 그립 규칙"을 사용하여 결정할 수 있습니다(오른쪽 그림 참조).자기장의 강도는 와이어로부터의 거리에 따라 감소합니다(무한 길이의 와이어의 경우 강도는 거리에 반비례합니다).

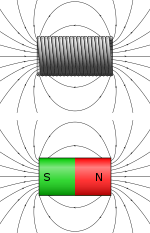
통전선을 루프에 구부리면 루프 내부의 자기장이 집중되어 외부에서는 약해집니다.와이어를 여러 개의 촘촘한 루프에 구부려 코일 또는 "솔레노이드"를 형성하면 이 효과가 향상됩니다.철심 주위에 형성된 장치는 전자석으로 작용하여 강하고 잘 제어된 자기장을 발생시킬 수 있다.무한장 원통형 전자석은 내부에 균일한 자기장을 가지며 외부에는 자기장이 없다.유한 길이 전자석은 코일을 흐르는 전류에 의해 강도와 극성이 결정되는 균일한 영구 자석에 의해 생성된 것과 유사한 자기장을 생성합니다.

정상 전류 I(전하가 축적되거나 어느 지점에서 ^{[note 8]}고갈되지 않는 일정한 전하 흐름)에 의해 발생하는 자기장은 Biot-Savart ^{[20]: 224} 법칙에 의해 설명됩니다.

여기서 적분은 전류 I와 같은 의미의 벡터 선 소자이고₀, μ는 자기 상수이고, r은 dθ의 위치와 자기장이 계산되는 위치 사이의 거리이고, rθ는 r의 방향의 단위 벡터이다.예를 들어, 충분히 긴 직선 와이어의 경우 다음과 같이 됩니다.여기서 r = r. 방향은 오른쪽 ^{[20]: 225} 규칙에 따라 와이어에 수직인 원에 접선합니다.

$현재$의 I$(\displaystyle$ I$)$를 B필드와 연관짓는 조금 더 일반적인^{[21][note 9]} 방법은 Ampér의 법칙을 사용하는 것입니다.

여기서 라인 적분은 임의의 루프 위에 $있고{\displaystyle {}_{}}$ ${\displaystyle {\text{I\_}}_{}}${\$displaystyle$ I_${\text{enc}}}$는 해당 루프로 둘러싸인 전류입니다.Amper의 법칙은 항상 정상 전류에 유효하며 무한 와이어 또는 무한 솔레노이드와 같은 특정 고대칭 상황에서 B 필드를 계산하는 데 사용할 수 있습니다.

시간에 따라 변하는 전기장을 설명하는 변형된 형태에서, Ampér의 법칙은 전기와 자성을 설명하는 4개의 Maxwell 방정식 중 하나입니다.

이동 전하 및 전류에 대한 강제력

하전 입자에 가해지는 힘

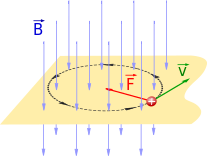
B장 내에서 이동하는 하전입자는 자기장과 수직인 속도의 성분인 자기장의 강도와 비례하는 횡력을 경험한다.이 힘은 로렌츠 힘이라고 알려져 있고, 다음과 같이 주어진다.

여기서 F는 힘, q는 입자의 전하, v는 입자의 순간 속도, B는 자기장(테슬라 단위)이다.

로렌츠 힘은 입자의 속도와 입자를 만든 자기장에 항상 수직입니다.하전 입자가 정적 자기장 내에서 움직일 때 나선축이 자기장과 평행하고 입자의 속도가 일정하게 유지되는 나선 경로를 추적한다.자력은 항상 운동에 수직이기 때문에 자기장은 고립된 ^[22][23]전하에는 작용하지 않습니다.자기장 변화에 의해 발생하는 전계를 통해서만 간접적으로 작동할 수 있습니다.흔히 자기력이 비소자성 쌍극자 또는 다른 힘에 의해 움직임이 제약되는 하전입자에 작용한다고 주장하지만, 이러한 경우 작업은 자기장에 의해 편향된 전하의 전기력에 의해 수행되기 때문에 이는 옳지^[24] 않다.

통전선에 가해지는 힘

전류 반송 와이어는 이동 전하의 집합이기 때문에 전류 반송 와이어에 가해지는 힘은 예상대로 이동 전하의 힘과 유사합니다.통전선은 자기장의 존재 하에서 힘을 느낀다.거시 전류에 대한 로렌츠 힘은 종종 라플라스 힘이라고 불립니다.길이 θ, 단면 A, 전류 i에 의한 전하 q의 도체를 생각해 보자.이 도체를 도체 내 전하 속도에 따라 각도 θ를 만드는 규모 B의 자기장에 배치할 경우, 1회 전하 q에 가해지는 힘은

N자, 고소?은 도체력이다.제가 거기 nqvA 정도씩 생겨나고 있다.

H와 B의 관계

전체의 현재를 다루는 공식은 자기장에 above 파생된 정확하다.자기 재료를 자기장 속에 놓여지는 것은 어려울 수 있다 계산하기 위한 자국의 바인딩 된 전류를 생성합니다.(이 바인딩 된 전류 원자 크기의 전류 루프의 합과 그 내용을 만든다 전자 같은 아원자 입자의 스핀 때문이다.).그 H-field로 혜택 위에서 정의되지만, 어떻게 먼저 자화의 개념을 소개하도록 도와 주는지 보기 위해 이 바인딩 된 현재를 고려하다.

자화

그 자화 벡터장 M얼마나 강하게 재료의 지역이 자성을 나타냅니다.그것은 그 지역의 단위 부피당 순수 자기 쌍극자 모멘트로 정의된다.일정한 자석의 자화를 제공해 물질을 자석의 부피로 나눈 자기 모멘트 m이내 거리로 동등한 상수입니다.이후 자기 모멘트의 SI단위는 A⋅m2, 자화 M의 SI단위 m당은 H-field와 동일한 암페어다.

영역의 자화 M장은 해당 영역의 평균 자기 쌍극자 모멘트 방향을 가리킵니다.따라서 자화계 선은 자석 남극 부근에서 시작하여 자석 북극 부근에서 끝납니다(자석 외부에는 존재하지 않습니다).

Amperian 루프 모델에서 자화는 많은 작은 Amperian 루프를 결합하여 결합 전류라고 불리는 결과 전류를 형성하기 때문입니다.그러면 이 결합 전류가 자석으로 인한 자기 B장의 원천이 됩니다.자기 쌍극자의 정의에 따라 자화장은 암페어의 ^[25]법칙과 유사한 법칙을 따릅니다.

여기서 적분은 닫힌 루프 위의 선 적분이고_b I는 닫힌 루프로 둘러싸인 결합 전류입니다.

자극 모델에서 자화는 자극에서 시작하여 자극에서 끝납니다.따라서 특정 영역이 순 양의 "자기 극 강도"(북극에 해당)를 갖는다면, 그 영역은 떠나는 것보다 들어오는 자화장 선이 더 많습니다.이는 수학적으로 다음과 같습니다.

여기서 적분은 닫힌 표면 S 위의 닫힌 표면 적분이고_M q는 S로 둘러싸인 "자기 전하"(자속 단위)이다. (닫힌 표면은 필드 선이 빠져나갈 수 있도록 구멍이 없는 영역을 완전히 둘러싸고 있다.)마이너스 부호는 자화장이 남쪽에서 북쪽으로 이동하기 때문에 발생합니다.

H-필드 및 자성 재료

SI 단위에서 H 필드는 다음과 같이 B 필드와 관련됩니다.

H장의 관점에서 암페어의 법칙은

여기서_f I는 루프로 둘러싸인 '자유 전류'를 나타내므로 H의 라인 적분은 결합된 ^[26]전류에 전혀 의존하지 않습니다.

이 방정식의 미분 등가물에 대해서는 맥스웰 방정식을 참조한다.암페어의 법칙은 경계 조건으로 이어진다.

여기서_f K는 표면 자유 전류 밀도이며, 단위 $n^(\displaystyle$\hat$\mathbf {n}})$은 중간 2에서 중간 ^[27]1까지의 방향을 가리킵니다.

마찬가지로 닫힌 표면에서 H의 표면 적분은 자유 전류와 독립적이며 닫힌 표면 내에서 "자기 전하"를 선택한다.

자유 전류에 의존하지 않습니다.

따라서 H 필드는 두 개의 독립된 부분으로^{[note 10]} 분리할 수 있다.

여기서₀ H는 자유 전류만으로 인한 인가 자기장이고_d H는 결합 전류로만 인한 소자장이다.

따라서 자기 H장은 결합 전류를 "자기 전하"의 관점에서 재계수합니다.H 필드 라인은 "자유 전류" 주위로만 루프되며, 자기 B 필드와는 달리 자극 근처에서 시작되고 끝납니다.

자기

대부분의 재료는 적용된 B장에 반응하여 자체 자화 M을 생성하며, 따라서 자체 B장을 생성한다.일반적으로 응답은 약하며 자기장이 적용될 때만 존재합니다.자기라는 용어는 물질이 적용된 자기장에 대해 미시적 수준에서 어떻게 반응하는지를 나타내며 물질의 자기 위상을 분류하는 데 사용됩니다.재료는 자기 거동에 따라 다음과 같은 그룹으로 나뉩니다.

• 반자성^[28] 재료는 자기장에 반하는 자화를 일으킨다.
• 상사성^[28] 재료는 인가된 자기장과 같은 방향으로 자화를 일으킨다.
• 강자성 재료 및 밀접하게 관련된 강자성 재료 및 반강자성^[29][30] 재료는 두 필드 간의 복잡한 관계에 있는 인가된 B장과는 무관하게 자화를 가질 수 있다.
• 초전도체(및 강자성 초전도체)^[31][32]는 임계 온도 및 자기장 미만의 완벽한 전도성을 특징으로 하는 물질입니다.또한 이들은 매우 자기적이며 낮은 임계 자기장 아래에 있는 완벽한 반자석일 수 있습니다.초전도체는 종종 B에 대한 M의 복잡한 이력 의존성을 보이는 광범위한 온도와 자기장을 가지고 있다.

상사성 및 반자성의 경우, 자화 M은 종종 다음과 같이 인가된 자기장에 비례합니다.

여기서 μ는 투과성이라고 하는 물질 의존적인 파라미터입니다.경우에 따라서는 투과성이 2등급 텐서일 수 있으므로 H는 B와 같은 방향을 가리키지 않는다.B와 H 사이의 이러한 관계는 구성 방정식의 예입니다.그러나 초전도체와 강자석은 더 복잡한 B-H 관계를 가지고 있습니다. 자기 이력서를 참조하십시오.

저장된 에너지

에너지는 변화하는 자기장이 만들어내는 전기장에 대항하기 위해 그리고 자기장 내에 있는 물질의 자화를 변화시키기 위해 모두 자기장을 생성하기 위해 필요합니다.비분산 재료는 자기장이 파괴될 때 이 같은 에너지가 방출되어 에너지를 자기장에 축적된 것으로 모델링할 수 있다.

선형, 비연속 재료(예를 들어 B = μ가 주파수에 의존하지 않는 μH)의 경우 에너지 밀도는 다음과 같습니다.

주위에 자성물질이 없을 경우 μ를 μ로₀ 치환할 수 있다.그러나 비선형 재료에는 위의 방정식을 사용할 수 없습니다. 아래에 제시된 보다 일반적인 식을 사용해야 합니다.

일반적으로 자기장 δB의 작은 변화를 일으키기 위해 필요한 단위 부피 δW당 증분 작업량은 다음과 같다.

일단 H와 B의 관계가 알려지면, 이 방정식은 주어진 자기 상태에 도달하기 위해 필요한 작업을 결정하기 위해 사용됩니다.강자석과 초전도체와 같은 이력 재료의 경우, 필요한 작업은 자기장이 어떻게 만들어지는지에 달려 있다.그러나 선형 비산포 재료의 경우 일반 방정식은 위에 제시된 보다 단순한 에너지 밀도 방정식으로 직접 연결됩니다.

맥스웰

모든 벡터장과 마찬가지로, 자기장은 그 원천과 관련된 두 가지 중요한 수학적 특성을 가지고 있다. (B의 원천은 전류와 변화하는 전기장이다.)이 두 가지 성질은 전기장의 두 가지 성질과 함께 맥스웰 방정식을 구성합니다.맥스웰 방정식은 로렌츠 힘의 법칙과 함께 전기와 자기 모두를 포함한 고전 전기 역학의 완전한 설명을 형성합니다.

첫 번째 특성은 벡터장 A의 발산이며, 이것은 A가 주어진 지점에서 바깥쪽으로 어떻게 "흐르는"지를 나타낸다.위에서 설명한 바와 같이 B필드 라인은 한 포인트에서 시작하거나 종료하지 않고 완전한 루프를 형성합니다.이것은 수학적으로 B의 발산도가 0이라고 말하는 것과 같다. (이러한 벡터장을 솔레노이드 벡터장이라고 한다.)이 특성은 자기에 대한 가우스의 법칙이라고 불리며 분리된 자극이나 자기 단극이 없다는 진술과 같습니다.

두 번째 수학적 특성은 컬이라고 불리며, θ × A는 A가 주어진 점 주위를 어떻게 휘거나 "순환"하는지를 나타낸다.컬의 결과를 "순환원"이라고 합니다.B와 E의 컬 방정식은 각각 Ampere-Maxwell 방정식과 패러데이의 법칙이라고 불립니다.

이렇게 생성된 B 필드의 중요한 특성 중 하나는 시작도 끝도 없는 자기 B 필드 라인(수학적으로 B는 솔레노이드 벡터 필드)입니다. 필드 라인은 무한대까지만 확장되거나 닫힌 곡선을 형성하기 위해 감싸이거나 끝도 없는(혼돈할 수 있음)^[33] 경로를 따를 수 있습니다.자기장 선은 북극 근처 자석에서 나와 남극 근처로 들어가지만, 자석 B장 선 내부에서는 자석을 통해 남극에서 ^{[note 11]}북극으로 돌아갑니다.B필드 라인이 자석에 들어간 경우, 다른 장소에 남겨야 합니다.단점을 가질 수 없습니다.

좀 더 형식적으로 말하면, 어떤 영역에 들어가는 모든 자기장 라인도 그 영역을 떠나야 하기 때문에, 그 영역에 들어가는 필드 라인의 ^{[note 12]}"수"를 출구 수에서 빼면 동일한 0이 됩니다.수학적으로 이것은 자기에 대한 가우스의 법칙과 같습니다.

여기서 적분은 닫힌 표면S 위의 표면 적분입니다(닫힌 표면은 필드 선이 빠져나가지 않도록 구멍이 없는 영역을 완전히 둘러싸는 표면입니다).dA는 바깥쪽을 가리키기 때문에 적분의 도트 곱은 B필드 포인팅의 경우 양수이고 B필드 포인팅의 경우 음수입니다.

전도 코일을 통과하는 자석과 같은 변화된 자기장은 전계를 생성합니다(따라서 이러한 코일에 전류를 구동하는 경향이 있습니다).이것은 패러데이의 법칙으로 알려져 있고 많은 전기 발전기와 전기 모터의 기초를 형성합니다.수학적으로 패러데이의 법칙은 다음과 같다.

$여기$서$$E(\$displaystyle {E})$는 기전력(또는 닫힌 루프 주변에서 발생하는 전압)이고 δ는 자속입니다. 즉, 면적에 해당 면적을 곱한 자기장의 곱입니다. (이러한 자속의 정의는 B를 종종 자속 밀도라고 합니다.)^{[34]: 210} 음의 부호는 코일의 변화하는 자기장에 의해 발생하는 전류가 이를 유도한 자기장의 변화에 반하는 자기장을 발생시킨다는 사실을 나타냅니다.이 현상은 렌즈의 법칙으로 알려져 있다.패러데이의 법칙의 이 적분 공식은 약간^{[note 13]} 다른 조건에서 적용되는 미분 형식으로 변환될 수 있습니다.

맥스웰의

변화하는 자기장이 전계를 생성하는 방식과 유사하게, 변화하는 전계는 자기장을 생성합니다.이 사실은 암페어의 법칙에 대한 맥스웰의 수정으로 알려져 있으며, 위와 같이 암페어의 법칙에 대한 부가 용어로 적용된다.이 추가 항은 전기 흐름의 시간 변화율에 비례하며 위의 패러데이의 법칙과 유사하지만 다른 양의 정수를 전면에 두고 있습니다(영역을 통과하는 전기 흐름은 전기장의 수직 부분을 곱한 면적에 비례합니다).

보정항을 포함한 완전한 법칙을 맥스웰-앰퍼 방정식이라고 한다.효과가 너무 작아서 적분 형식이 사용되는 대부분의 경우 무시될 수 있기 때문에 일반적으로 적분 형식으로 제공되지 않습니다.

맥스웰 용어는 전자파의 생성과 전파에 매우 중요하다.패러데이의 유도 법칙과 함께 Maxwell의 법칙에 대한 수정은 서로 변화하는 전기장과 자기장이 어떻게 상호작용하여 서로를 지탱하고 빛과 같은 전자파를 형성하는지 설명합니다: 변화하는 전기장은 변화하는 자기장을 생성하고, 다시 변화하는 전기장을 생성합니다.그러나 이것들은 보통 아래에 제시된 이 방정식의 미분 형식을 사용하여 설명된다.

여기서 J는 완전한 현미경 전류 밀도입니다.

위에서 설명한 바와 같이 재료는 인가된 전기 E장과 인가된 자기 B장에 반응하여 자체적인 "바인드" 전하와 전류 분포를 생성하지만 E와 B에 기여하지만 계산이 어렵다.이 문제를 피하기 위해 H 및 D 필드를 사용하여 자유 전류 밀도_f J의 관점에서 맥스웰 방정식을 재인수합니다.

이러한 방정식은 원래의 방정식보다 더 일반적이지 않습니다(물질의 "바인드" 전하와 전류가 알려진 경우).그것들은 또한 E와 D의 관계뿐만 아니라 B와 H의 관계로도 보완되어야 한다.한편, 이러한 양들 사이의 단순한 관계에서 이 형태의 맥스웰 방정식은 결합 전하와 전류를 계산할 필요성을 회피할 수 있습니다.

과

특수상대성이론에 따르면 전자기력을 별도의 전기 및 자기 구성요소로 분할하는 것은 기본이 아니라 관측 기준 프레임에 따라 달라집니다.한 관찰자가 인지하는 전기력은 다른 관찰자에 의해 자력 또는 전기력과 자기력의 혼합으로 인식될 수 있다.

형식적으로 특수상대성이론은 전자기 텐서라고 불리는 2등급 텐서로 전기장과 자기장을 결합한다.참조 프레임을 변경하면 이러한 구성요소가 혼합됩니다.이는 특수상대성이론이 시공간에, 질량, 운동량,^[35] 에너지를 4개의 운동량으로 혼합하는 방식과 유사하다.마찬가지로, 자기장에 저장된 에너지는 전자기 스트레스-에너지 텐서의 전기장에 저장된 에너지와 혼합된다.

벡터

양자역학 및 상대성 이론과 같은 고급 주제에서는 종종 전기장과 자기장의 관점에서보다 전기역학의 잠재적 공식으로 작업하는 것이 더 쉽습니다.이 표현에서 자기 벡터 전위 A와 전기 스칼라 전위 θ는 다음과 같이 정의된다.

벡터 퍼텐셜 A는 θ가 단위 전하당 일반화 퍼텐셜 에너지로 해석되는 것과 마찬가지로^[36] 단위 전하당 일반화 퍼텐셜 모멘텀으로 해석될 수 있다.

맥스웰 방정식은 퍼텐셜로 표현될 때 특별한 상대성 이론과 거의 힘을 ^[37]들이지 않고 일치하는 형태로 주조될 수 있습니다.상대성 이론에서 A는 θ와 함께 입자의 운동량과 에너지를 결합하는 4모멘텀과 유사한 4전위를 형성한다.전자기 텐서 대신 4개의 전위를 사용하면 훨씬 간단하다는 장점이 있으며 양자 역학과 함께 작동하도록 쉽게 수정할 수 있습니다.

현대 물리학에서 전자기장은 고전적인 장이 아니라 양자장으로 이해된다. 전자기장은 각 지점에서 세 개의 수의 벡터가 아니라 각 지점에서 세 개의 양자 연산자의 벡터로 표현된다.전자기 상호작용에 대한 가장 정확한 현대적 설명은 양자전기역학(QED)^[38]으로, 입자물리학의 표준모형으로 알려진 보다 완전한 이론에 통합된다.

QED에서 하전 입자(및 그 반입자) 사이의 전자파 상호작용의 크기는 섭동 이론을 사용하여 계산된다.이러한 다소 복잡한 공식은 가상 광자가 교환되는 파인만 도표로서 주목할 만한 그림 표현을 만들어냅니다.

QED의 예측은 매우 높은 정확도로 실험과 일치합니다. 현재 약 10개⁻¹²(및 실험 오차에 의해 제한됨). 자세한 내용은 QED의 정밀 테스트를 참조하십시오.이것은 QED를 지금까지 구성된 가장 정확한 물리 이론 중 하나로 만듭니다.

이 기사의 모든 방정식은 고전적 근사치로, 여기서 언급된 양자 설명보다 정확도가 낮습니다.그러나, 대부분의 일상적인 상황에서, 두 이론 사이의 차이는 무시할 수 있다.

및

지구의 자기장은 외핵의 액체 철 합금의 대류에 의해 생성됩니다.다이너모 프로세스에서 이 움직임은 전류가 ^[39]전류에 작용하는 전기장과 자기장을 생성하는 피드백 프로세스를 구동합니다.

지구 표면의 장은 거대한 막대 자석이 지구 중심에 위치하여 지구의 회전 축에서 약 11° 기울어진 것과 거의 동일합니다(그림 ^[40]참조).자석 나침반 바늘의 북극은 대략 북쪽을 가리키며, 북극을 향합니다.하지만, 자극이 반대쪽으로 끌리기 때문에, 북극은 사실 지자기장의 남극이다.이러한 용어 혼동은 자석의 극이 가리키는 ^[41]지리적 방향에 의해 정의되기 때문에 발생합니다.

지구의 자기장은 일정하지 않다. 자기장의 세기와 극의 위치는 다양하다.^[42]게다가 극은 지자기 반전이라고 불리는 과정에서 주기적으로 방향을 반전시킨다.가장 최근의 반전은 78만년 ^[43]전에 일어났다.

★★★★★★★★★★★★★★★★」

회전 자기장은 교류 모터 작동의 핵심 원리입니다.이러한 필드에서의 영구 자석은 외부 필드와의 정렬을 유지하도록 회전한다.이 효과는 Nikola Tesla에 의해 개념화되었고 나중에 그와 다른 사람들의 초기 교류 전기 모터에 사용되었습니다.

자기 토크는 전기 모터를 구동하는 데 사용됩니다.하나의 간단한 모터 설계에서 자석은 자유자재로 회전하는 축에 고정되며 전자석 배열로부터 자기장을 받는다.각 전자석을 통해 연속적으로 전류를 전환함으로써 그 자기장의 극성을 회전자 옆에 극과 같이 반전시킴으로써 그 토크가 축으로 전달된다.

교류전류의 위상차가 90도인 2개의 직교코일을 사용하여 회전자기장을 구성할 수 있다.그러나 실제로는 이러한 시스템은 전류가 동일하지 않은 3선 배치를 통해 공급됩니다.

이러한 부등식은 도체 크기의 표준화에 심각한 문제를 일으키기 때문에 이를 극복하기 위해 3개의 전류가 동일하고 위상차가 120도인 3상 시스템을 사용한다.이 경우 상호 기하학적 각도가 120도인 3개의 유사한 코일이 회전 자기장을 생성합니다.3상 시스템이 전기 모터에 이용되는 회전장을 만드는 능력은 3상 시스템이 세계 전력 공급 시스템을 지배하는 주요 이유 중 하나입니다.

동기 모터는 DC 전압으로 공급되는 로터 권선을 사용하여 기계의 들뜸을 제어하고 유도 모터는 다코일 스테이터의 회전 자기장에 이어 단락 로터(자석 대신)를 사용합니다.로터의 단락 회전은 스테이터의 회전장에 와전류를 발생시키고, 이 전류는 로터를 로렌츠 힘에 의해 이동합니다.

1882년, 니콜라 테슬라는 회전 자기장의 개념을 확인했어요.1885년, 갈릴레오 페라리스는 독립적으로 그 개념을 연구했다.1888년 테슬라는 그의 업적으로 미국 특허 381,968을 취득했다.또한 1888년에 페라리스는 토리노에 있는 왕립 과학 아카데미에 논문을 통해 그의 연구를 발표했습니다.

★★★★

가로 자기장에 배치된 전류 전달 도체의 전하 캐리어는 측면 로렌츠 힘을 경험합니다. 그러면 전류와 자기장에 수직인 방향으로 전하 분리가 발생합니다.그 방향의 결과 전압은 인가된 자기장에 비례합니다.이를 홀 효과라고 합니다.

홀 효과는 자기장의 크기를 측정하는 데 자주 사용됩니다.또한 반도체(음전자 또는 양공)와 같은 물질에서 지배적인 전하 캐리어의 신호를 찾는 데도 사용됩니다.

H의 중요한 용도는 선형 재료 내부의 B = μH인 자기 회로에 있다.여기서 μ는 재료의 자기투과율이다.이 결과는 옴의 법칙 J = δE와 형태가 유사합니다. 여기서 J는 전류 밀도, δ는 전도도, E는 전계입니다.이 비유를 확장하면 거시 옴의 법칙(I = VΩR)에 대응하는 것은 다음과 같습니다.

여기서 $\phi \mathrm{}$ $=$ $\int$ B$d\mathrm{}$ $d\mathbf{}$ A$${\$textstyle \Phi$ =\$int \mathbf {B}$ \$cdot \mathrm {d}$ \$mathbf {A} }$는 회로의 자속이며, $F$ $=$ $h\mathrm{}$ H $\cdot$ $d\mathit{}${\ {\$textstyle$ F$=\int$ \$mathbf${H} \mathbf {$HCD}$ \mathbf {H} \m} \mathbf {D}는 회로의 자속입니다.여기서_m 저항 R은 플럭스에 대한 저항과 성질이 유사한 양이다.이 유추를 사용하면 회로 이론의 모든 사용 가능한 기술을 사용하여 복잡한 자기장 기하학의 자속을 계산하는 것이 간단합니다.

대대 largest

이 섹션은 업데이트해야 합니다. 최근의 이벤트나 새로운 정보를 반영하기 위해서, 이 문서를 갱신해 주세요. 마지막 업데이트: 2018년 10월(2021년 7월)

2018년 10월 현재, 실험실 밖에서 거시적으로 생성되는 최대 자기장은 2.8 kT이다(러시아 사로프 VNIEF, 1998).^[44][45]2018년 10월 현재, 거시적 부피 이상의 실험실에서 생성된 최대 자기장은 2018년 ^[45]도쿄 대학 연구진에 의해 1.2 kT였다.실험실에서 생성되는 가장 큰 자기장은 RHIC와 같은 입자 가속기에서 발생하며, 중이온 충돌은 10T에 ^[46][47]이른다¹⁴.마그네타는 0.1~100GT(10~^[48]10T¹¹) 범위의⁸ 자연 발생 물체 중 알려진 가장 강한 자기장을 가집니다.

★★★

★★★★★★

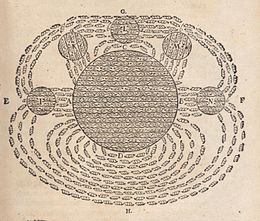
자석과 자석의 성질이 고대 사회에 알려진 반면, 1269년 프랑스 학자 페트루스 페레그리누스 드 마리쿠르가 쇠바늘을 이용해 구형 자석의 표면에 자기장을 지도화하면서 자기장 연구가 시작되었다.그는 두 지점에서 교차하는 자기장선에 주목하면서 지구의 극과 비슷하게 그 점들을 "극"이라고 명명했다.그는 또한 자석이 아무리 ^{[49][note 14]}잘게 썰어도 항상 북극과 남극을 모두 가지고 있다는 원리를 분명히 했다.

거의 3세기 후, 콜체스터의 윌리엄 길버트는 페트루스 페레그리누스의 작품을 복제했고, 지구가 ^{[50]: 34} 자석이라는 것을 처음으로 분명히 말했다.1600년에 출판된, 길버트의 작품, De Magnete는 과학으로서의 자성을 확립하는데 도움을 주었다.

1750년, 존 미첼은 자기극이 샤를 오귀스틴[50]^{: 56} 드 쿨롱의 역제곱 법칙에 따라 끌어당기고 밀어낸다는 것을 1785년에 실험적으로 증명했고 북극과 남극은 ^{[50]: 59} 분리될 수 없다고 분명히 말했다.극 사이의 이 힘을 바탕으로, 시메온 데니스 포아송 (1781–1840)은 1824년에 ^{[50]: 64} 그가 제시한 최초의 성공적인 자기장 모델을 만들었습니다.이 모델에서 자기 H장은 자극에 의해 생성되며, 자기장은 작은 쌍의 남북 자극에 의해 생성된다.

1820년에 세 가지 발견이 이 자성의 기초에 도전장을 던졌다.Hans Christian örsted는 전류가 흐르는 와이어가 원형 ^{[note 15][51]}자기장으로 둘러싸여 있다는 것을 증명했습니다.André-Marie Amperre는 전류가 같은 방향으로 흐르면 서로 끌어당기고 반대 방향으로 ^{[50]: 87 [52]}흐르면 밀어낸다는 것을 보여주었다.마지막으로, 장 밥티스트 비오(Jean-Baptiste Biot)와 펠릭스 사바르(Félix Savart)는 전류가 흐르는 길고 곧은 와이어가 작은 자석에 가한 힘에 대한 경험적 결과를 발표했는데, 그 힘은 와이어에서 ^{[53][50]: 86} 자석까지의 수직 거리에 반비례한다고 판단했습니다.라플레이스는 나중에 라플레이스가 ^[55]그의 연구 결과를 발표하지 않았기 때문에 비오트-사바트 법칙으로 알려지게 된 ^[53][54]와이어의 미분 작용에 기초하여 힘의 법칙을 추론했다.

이러한 실험들을 확장하면서, Ampére는 1825년에 그의 성공적인 자기 모델을 발표했다.이 책에서 그는 자석에 대한^{[50]: 88} 전류의 등가성을 보여주었고, 포아송의 ^{[note 16]}모델에서 자기 전하의 쌍극자 대신 전류의 순환이 지속적으로 흐르기 때문이라고 제안했다.또한 Ampére는 두 전류 사이의 힘을 설명하는 Ampér의 힘 법칙과 일정한 전류에 의해 발생하는 자기장을 정확하게 설명하는 Ampér의 법칙을 모두 도출했습니다.또한 이 연구에서 Ampere는 전기와 ^{[50]: 88–92} 자기 사이의 관계를 설명하기 위해 전기역학이라는 용어를 도입했습니다.

1831년, 마이클 패러데이는 변화하는 자기장이 현재 패러데이의 ^{[50]: 189–192} 유도 법칙으로 알려진 것을 공식화하면서 주위를 둘러싼 전장을 발생시킨다는 것을 발견했을 때 전자기 유도를 발견했습니다.나중에, 프란츠 에른스트 노이만은 자기장의 움직이는 전도체에 대해 유도가 암페르의 힘의 ^{[50]: 222} 법칙의 결과라는 것을 증명했다.그 과정에서, 그는 자기 벡터 전위를 도입했는데, 이것은 나중에 ^{[50]: 225} 패러데이가 제안한 기본 메커니즘과 동등하다는 것을 보여주었다.

1850년, 당시 윌리엄 톰슨으로 알려진 켈빈 경은 현재 H와 B를 가리키는 두 개의 자기장을 구별했다.전자는 푸아송의 모델에, 후자는 암페르의 모델과 ^{[50]: 224} 귀납에 적용되었습니다.또한 H와 B가 어떻게 관련되어 있는지 도출하여 ^{[50]: 245 [56]}투과성이라는 용어를 만들었습니다.

1861년과 1865년 사이에, 제임스 클락 맥스웰은 모든 고전 전기와 자성을 설명하고 통합한 맥스웰 방정식을 개발하고 발표했다.이 방정식의 첫 번째 세트는 1861년에 "힘의 물리적 선에 대하여"라는 제목의 논문에서 발표되었습니다.이 방정식은 유효하지만 불완전했다.맥스웰은 1865년 후반의 논문 '전자장의 동적 이론'에서 그의 방정식 세트를 완성했고 빛이 전자파라는 사실을 증명했다.하인리히 헤르츠는 1887년과 1888년에 실험적으로 ^[57][58]이 사실을 확인하는 논문을 발표했다.

발전

1887년, 테슬라는 교류로 작동하는 유도 모터를 개발했다.모터는 다상 전류를 사용하여 모터를 회전시키기 위해 회전 자기장을 생성했습니다(1882년에 ^[59][60][61]테슬라가 고안했다고 주장한 원리).테슬라는 1888년 ^[62][63]5월에 전기 모터에 대한 특허를 받았다.1885년 갈릴레오 페라리스는 독립적으로 회전 자기장을 연구했고 1888년 ^[64]3월 테슬라가 특허를 받기 불과 두 달 전 토리노 왕립과학원에 논문을 발표했다.

20세기는 고전 전기역학이 이미 특수 상대성 이론과 일치하고, 고전 전기역학을 양자역학으로 확장시켰다는 것을 보여주었다.상대성을 확립한 1905년의 그의 논문에서 알버트 아인슈타인은 전기장과 자기장이 모두 다른 기준 프레임에서 바라본 동일한 현상의 일부라는 것을 보여주었다.마침내, 양자 역학의 새로운 분야가 전기 역학과 결합되어 양자 전기 역학을 형성했고, 이것은 전자장 에너지가 광자의 형태로 양자화된다는 개념을 처음으로 공식화했다.

「」도 .

★★★★

• 자기유체역학 – 전기전도 유체의 역학 연구
• 자기 이력 – 강자성에 적용
• 자성 나노 입자 – 수십 개의 원자 폭의 초소형 자성 입자
• 자기 재연결 – 태양 플레어와 오로라를 일으키는 효과
• SI 전자 장치 – 전자기에 사용되는 공통 장치
• 매그니튜드 순서(자기장) – 최소 자기장부터 최대 검출까지의 자기장 소스 및 측정 장치 목록
• 계속 ★★★★★★
• 이펙트

★★★

• 자기 헬리시티 – 자기장이 자신을 감싸는 정도

프로그램

• 다이너모 이론 – 지구 자기장 생성을 위한 제안된 메커니즘
• 헬름홀츠 코일 – 거의 균일한 자기장 영역을 생성하기 위한 장치
• 자기장 보기 필름 – 영역의 자기장을 보기 위해 사용되는 필름
• 자기권총 – 목표물의 자기장을 검출하는 어뢰 또는 해군 기뢰 장치
• 맥스웰 코일 – 거의 일정한 자기장을 대량으로 생성하는 장치
• 별의 자기장 – 별의 자기장에 대한 설명
• 텔트론 튜브 – 전자 빔을 표시하는 데 사용되는 장치로 이동 전하에서 전기장과 자기장의 영향을 보여줍니다.

읽기 ★★★★★★★★★★★★★★」

( )

• Wikimedia Commons의 자기장 관련 미디어
• 크로웰, B. "전자성"
• Nave, R. '자기장'하이퍼 물리
• 자기장, 자기장.theory.uwinnipeg.ca 를 참조해 주세요.
• 호들리, 릭, "자기장은 어떻게 생겼나?" 2005년 7월 17일