필드 라인

양전하(왼쪽), 음전하(가운데) 및 전하되지 않은 물체(오른쪽)에 의해 생성되는 전기장을 나타내는 필드 라인.

필드 라인은 벡터 필드를 시각화하기 위한 그래픽 비주얼 보조 도구입니다.이것은 길이를 ^[1]^[2]따라 각 점에서 필드 벡터에 접하는 가상의 방향선으로 구성됩니다.인접한 필드 라인의 대표 집합을 보여주는 다이어그램은 과학 및 수학 문헌에서 벡터 필드를 묘사하는 일반적인 방법입니다. 이를 필드 라인 다이어그램이라고 합니다.그것들은 많은 다른 유형들 중에서 전기장, 자기장, 그리고 중력장을 보여주기 위해 사용된다.유체역학에서 유체 흐름의 속도장을 나타내는 필드 라인을 유선이라고 합니다.

정의 및 설명

왼쪽 그림은 두 개의 동일한 양의 전하의 전계선을 나타냅니다.오른쪽 그림은 반대쪽 부호의 두 전하의 전계선을 보여줍니다.

벡터 필드는 공간의 각 점에서 방향과 크기를 정의합니다.그 벡터 필드의 필드선은 각 포인트에서 ^[3]^[2]^[1]필드 벡터에 접선함으로써 벡터 필드의 방향을 따르는 공간을 통과하는 선을 추적함으로써 구성될 수 있다.필드선은 보통 방향선 세그먼트로 표시되며, 화살표는 벡터 필드의 방향을 나타냅니다.2차원 필드선은 평면 곡선이며 대부분의 필드선 다이어그램은 이 유형입니다.벡터장이 0이 아닌 유한한 각 점에서 벡터장은 고유한 방향을 가지므로 필드 선은 절대 교차할 수 없습니다. 따라서 벡터장이 0이 아닌 유한한 ^[3]^[2]각 지점을 통과하는 필드 선은 정확히 1개입니다.필드가 0 또는 무한인 점에는 필드 선이 없습니다. 필드 선에서 방향을 정의할 수는 없지만 필드 선의 끝점이 될 수 있기 때문입니다.

모든 영역에 무한대의 포인트가 있으므로 무한대의 필드 선을 그릴 수 있지만 필드 선 다이어그램에는 제한된 수만 표시할 수 있습니다.따라서 어떤 필드 라인이 표시되는지는 그림을 그리는 사람 또는 컴퓨터 프로그램에 의해 결정되며, 단일 벡터 필드는 다른 필드 라인 세트로 표시될 수 있습니다.필드 라인 다이어그램은 그려진 필드 라인 사이의 필드에 대한 정보를 제공하지 않기 때문에 벡터 필드의 불완전한 기술일 수 밖에 없으며, 몇 개의 라인을 표시할지에 따라 다이어그램이 얼마나 유용한 정보를 제공하는지가 결정됩니다.

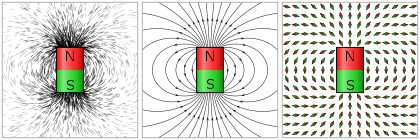
개별 필드 라인은 벡터 필드의 방향을 표시하지만 크기는 표시하지 않습니다.또한 필드의 크기를 나타내기 위해 필드 선 다이어그램이 그려지고 각 선이 동일한 양의 플럭스를 나타내도록 합니다.그런 다음 임의의 위치에서 필드 선의 밀도(단위 수직 영역당 필드 선의 수)는 해당 지점의 벡터 필드의 크기에 비례합니다.인접 필드 선이 수렴되는 영역(더 가까워지는 영역)은 필드가 해당 방향으로 더 강해지고 있음을 나타냅니다.

0이 아닌 발산이 있는 벡터 필드에서는 필드 라인은 양의 발산점(소스)에서 시작하여 음의 발산점(싱크)에서 끝나거나 무한대로 확장됩니다.예를 들어, 전계선은 양전하로 시작하여 음전하로 끝납니다.자기장과 같이 발산성이 없는 필드(솔레노이드)에서는 필드 라인은 끝점이 없습니다. 닫힌 루프이거나 ^[4]^[5]끝없는 필드입니다.

물리학에서 필드 라인의 도면은 방사형 고조파의 힘장과 반대로 선원과 싱크가 물리적 의미를 갖는 경우에 주로 유용하다.예를 들어, Gauss의 법칙은 전장이 양전하로 공급되고 음전하로 흡수되며, 따라서 전장선은 양전하로 시작하여 음전하로 끝난다.중력장은 원천이 없고 질량으로 가라앉고 다른 곳에서도 없습니다. 중력장 선은 무한대에서 나와 질량으로 끝납니다.자기장에는 소스나 싱크(자기장에 대한 가우스의 법칙)가 없기 때문에, 자기장 라인은 시작이나 끝이 없습니다. 즉, 닫힌 루프만 형성하거나, 양방향으로 무한대로 확장하거나, 자신을 교차하지 않고 무한히 지속할 수 있습니다.그러나 위에서 설명한 바와 같이 필드가 0인 점과 필드 라인의 방향이 정의되지 않기 때문에 필드 라인으로 교차할 수 없는 점 주변에서 특별한 상황이 발생할 수 있습니다.예를 들어 이 상황은 두 개의 동일한 양의 전기점 전하 사이의 중간에서 발생합니다.거기서 자기장이 사라지고 전하에서 축방향으로 오는 선이 끝납니다.동시에 중간점을 통과하는 횡단면에서는 무한대의 필드선이 방사상으로 분기한다.끝과 시작 선의 동시 존재는 포인트에서 필드의 ^[5]발산 없는 특성을 보존합니다.

필드 선 밀도가 필드 크기에 비례하도록 의도된 이러한 유형의 도면의 경우 3차원을 모두 나타내는 것이 중요합니다.예를 들어, 단일 절연 지점 전하에서 발생하는 전계를 생각해 보십시오.이 경우 전계선은 3차원 공간에서 모든 방향으로 균일하게 전하에서 나오는 직선입니다.즉 $1/r^{2}$ 밀도는 $1/r^{2}$ / $1/r^{2}$ 2(\ $displaystyle 1$ /r $^{2$ 에 비례하며, 이 경우 쿨롱의 법칙과 일치하는 올바른 결과입니다.그러나 이 설정의 전계선이 2차원 평면에 그려진 경우 2차원 밀도는 $1/r$ 1/ $r에$ 이 상황에 ^[6] $맞지$ 않는 결과가 됩니다.

건설

필드 라인 구축

벡터 $\mathbf {F} (\mathbf {x} )$ F $)(\displaystyle \mathbf {F}(\mathbf$ {x $})$ 와 $\mathbf {F} (\mathbf {x} )$ $\mathbf {x} _{\text{0}}$ x 0(\ $displaystyle$ $\mathbf {x}_$ ${\text{0})$ 이 주어지면 필드 라인은 해당 점 $($ 0 $)$ 에서 필드 벡터를 구함으로써 반복적으로 구성할 수 있습니다 $.$ 이 점에서의 단위 접선 벡터는 $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ ( $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ 0 ) $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ / $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ ( $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ ) \ $displaystyle \mathbf {x} _{\text{0}}$ / \ $mathbf {F}$ (\ $mathbf {x} _{\text{0}}})$ 입니다 $\mathbf {F} (\mathbf {x} _{\text{0}})/|\mathbf {F} (\mathbf {x} _{\text{0}})|$ 새로운 점의 방향을 따라 $단거리$ d ${\displaystyle$ ds $}$ 를 이동합니다 $ds$ .

\displaystyle \mathbf {x} _{\text{1}}=\mathbf {x} _{\text{0}}+{\mathbf {F}(\mathbf {x} _{\text{0}) \over \mathbf {F} (\mathbf {x} _{\text{0}}) }ds}

그런 다음 해당

\mathbf {F} (\mathbf {x} _{\text{1}})

F

\mathbf {F} (\mathbf {x} _{\text{1}})

1)의

\mathbf {F} (\mathbf {x} _{\text{1}})

필드(\displaystyle

\mathbf {F}(\text{1}})

를

\mathbf {F} (\mathbf {x} _{\text{1}})

찾고

\mathbf {F} (\mathbf {x} _{\text{2}})

지점

\mathbf {F} (\mathbf {x} _{\text{2}})

(

)

방향

으로 거리

(\displaystyle

\mathbf {F}(\displaystyle

ds

})

를

ds

\mathbf {F} (\mathbf {x} _{\text{2}})

이동합니다.각

\mathbf {x} _{\text{i}}

(\

에서

\mathbf {x} _{\text{i}}

다음 점을 찾을 수 있습니다.

\mathbf {x} _{\text{i+1}=\mathbf {x} + {\mathbf {F} (\text{i}) \over \mathbf {F} (\mathbf {x} _{x} _{\texti}) } ds

이 과정을 반복하고 점을 연결하면 필드 라인을 원하는 만큼 확장할 수 있습니다.각 직선 세그먼트는 실제로 시작점에서 길이를 따라 필드에 접하지 않기 때문에 실제 필드 라인에 대한 근사치일 뿐입니다.그러나

\displaystyle

ds에 충분한

작은

값을 사용하여 더 많은 짧은 단계를 수행함으로써 필드 라인을 원하는 만큼 가깝게 근사할 수 있습니다.필드 라인은 음의

-ds

스텝 -

-ds

s

\displaystyle

-ds를

-ds

사용하여 반대 방향으로 각 스텝을

\mathbf {x} _{\text{0}}

으로써 x 0

(\

과

\mathbf {x} _{\text{0}}

반대 방향으로 확장할 수 있습니다.

예

자석의 영역을 묘사하는 다른 방법들.

벡터 필드가 속도 필드를 나타내는 경우 필드 라인은 흐름의 스트림 라인을 따릅니다.아마도 필드 라인에 의해 묘사되는 벡터장의 가장 친숙한 예는 자석에서 나오는 필드 라인을 사용하여 종종 묘사되는 자기장일 것이다.

발산 및 컬

필드 라인을 사용하여 벡터 미적분으로부터 익숙한 양을 추적할 수 있습니다.

필드 라인의 밀도가 필드의 크기에 비례하도록 선이 그려진 경우 필드 라인을 통해 분산을 쉽게 볼 수 있습니다(위 참조).이 경우 분산은 필드 라인의 시작과 종료로 간주될 수 있습니다.벡터장이 하나 이상의 선원에 대한 방사형 역제곱 법칙장의 결과인 경우, 이는 선원 밖에서 그러한 필드의 확산이 0이라는 사실에 해당합니다.솔레노이드 벡터장(즉, 어디에서나 발산이 0인 벡터장)에서 필드선은 시작도 끝도 없이 닫힌 루프를 형성하거나 양방향으로 무한대로 흐릅니다.벡터 필드가 일부 영역에서 양의 발산일 경우 해당 영역의 점부터 시작하는 필드 선이 있습니다.벡터 필드가 일부 영역에서 음의 발산일 경우 해당 영역의 포인트에서 끝나는 필드 선이 있습니다.
켈빈-스토크스 정리는 제로 컬이 있는 벡터장의 필드 라인(즉, 중력장이나 정전장 등 보수적인 벡터장)은 닫힌 루프가 될 수 없다는 것을 보여준다.즉, 필드 라인이 닫힌 루프를 형성할 때 항상 컬이 존재합니다.필드 라인의 나선 모양과 같은 다른 상황에서도 존재할 수 있습니다.

물리적 중요성

무작위로 떨어뜨리면(여기 쉐이커와 같이), 철제 줄들이 자기장 선을 대략적으로 나타내도록 배열됩니다.자기장은 유리 표면 아래에 있는 영구 자석에 의해 생성됩니다.

필드 라인은 "단순한" 수학적 구조이지만, 상황에 따라서는 물리적 의미를 갖습니다.유체역학에서, 일정한 흐름의 속도장 선(유선형)은 유체의 입자의 경로를 나타냅니다.플라즈마 물리학의 맥락에서, 같은 전계선상에 있는 전자나 이온은 강하게 상호작용하는 반면, 일반적으로 다른 전계선상에 있는 입자는 상호작용하지 않는다.이것은 자기장에서 철필링의 입자가 보이는 것과 같은 거동입니다.

사진 속 철제 줄들은 서로 다른 필드 라인에 맞춰져 있는 것처럼 보이지만 상황은 더 복잡하다.2단계 프로세스로 시각화하기 쉽습니다. 첫째, 줄 바꿈이 자기장 전체에 균일하게 퍼져 있지만 모두 자기장 방향으로 정렬됩니다.그런 다음 줄의 축척과 강자성 특성에 따라 필드를 양쪽으로 감쇠시켜 우리가 ^{[citation needed]}보는 선 사이에 겉으로 보이는 공간을 만듭니다.물론 여기에 설명된 두 단계는 평형이 달성될 때까지 동시에 발생합니다.필링의 고유 자성은 필드를 변경하기 때문에 필링에 의해 나타나는 선은 원래 자기장의 필드 라인의 근사치일 뿐입니다.자기장은 연속적이며 이산적인 선을 가지고 있지 않습니다.

「」를 참조해 주세요.

강제 필드(물리학)
줄리아 세트의 필드 라인
외부 광선 - Douady 필드 라인 -만델브로트 집합 또는 채워진 줄리아 집합의 허버드 전위
힘의 선
벡터 필드

레퍼런스

^ ^a ^b Tou, Stephen (2011). Visualization of Fields and Applications in Engineering. John Wiley and Sons. p. 64. ISBN 9780470978467.
^ ^a ^b ^c Durrant, Alan (1996). Vectors in Physics and Engineering. CRC Press. pp. 129–130. ISBN 9780412627101.
^ ^a ^b Haus, Herman A.; Mechior, James R. (1998). "Section 2.7: Visualization of Fields and the Divergence and Curl". Electromagnetic fields and energy. Hypermedia Teaching Facility, Massachusetts Institute of Technology. Retrieved 9 November 2019.
^ Lieberherr, Martin (6 July 2010). "The magnetic field lines of a helical coil are not simple loops". American Journal of Physics. 78 (11): 1117–1119. Bibcode:2010AmJPh..78.1117L. doi:10.1119/1.3471233.
^ ^a ^b Zilberti, Luca (25 April 2017). "The Misconception of Closed Magnetic Flux Lines". IEEE Magnetics Letters. 8: 1–5. doi:10.1109/LMAG.2017.2698038. S2CID 39584751 – via Zenodo (https://zenodo.org/record/4518772#.YCJU_WhKjIU). {{cite journal}}:외부 링크 via=(도움말)
^ A. 울프, S. J. 밴 훅, E. R.몇 주, 전계선 다이어그램이 Am을 사용할 수 없습니다.J. Phys., Vol. 64, No. 6. (1996), 714–724 DOI 10.119/1.18237페이지

추가 정보

Griffiths, David J. (1998). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 65–67 and 232. ISBN 978-0-13-805326-0.

외부 링크

선택한 전하 쌍의 전계선을 보여주는 인터랙티브 Java 애플릿 Wolfgang Bauer에 의해 웨이백 머신에 보관된 2011-08-13
Massachusetts Institute of Technology 코스의 "Visualization of Fields and the Divergence and Curl" 코스 노트.

[Tou-1] Tou, Stephen (2011). Visualization of Fields and Applications in Engineering. John Wiley and Sons. p. 64. ISBN 9780470978467.

[Durrant-2] Durrant, Alan (1996). Vectors in Physics and Engineering. CRC Press. pp. 129–130. ISBN 9780412627101.

[Haus-3] Haus, Herman A.; Mechior, James R. (1998). "Section 2.7: Visualization of Fields and the Divergence and Curl". Electromagnetic fields and energy. Hypermedia Teaching Facility, Massachusetts Institute of Technology. Retrieved 9 November 2019.

[lieb-4] Lieberherr, Martin (6 July 2010). "The magnetic field lines of a helical coil are not simple loops". American Journal of Physics. 78 (11): 1117–1119. Bibcode:2010AmJPh..78.1117L. doi:10.1119/1.3471233.

[:0-5] Zilberti, Luca (25 April 2017). "The Misconception of Closed Magnetic Flux Lines". IEEE Magnetics Letters. 8: 1–5. doi:10.1109/LMAG.2017.2698038. S2CID 39584751 – via Zenodo (https://zenodo.org/record/4518772#.YCJU_WhKjIU). {{cite journal}}:외부 링크 via=(도움말)

[6] A. 울프, S. J. 밴 훅, E. R.몇 주, 전계선 다이어그램이 Am을 사용할 수 없습니다.J. Phys., Vol. 64, No. 6. (1996), 714–724 DOI 10.119/1.18237페이지

[1]

[2]

[3]

[4]

[5]

[6]

Search

필드 라인

네임스페이스

더

목차

정의 및 설명

건설

예

발산 및 컬

물리적 중요성

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

필드 라인

정의 및 설명

건설

예

발산 및 컬

물리적 중요성

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.