쿨롱의 법칙

쿨롱의 역제곱 법칙 또는 간단히 쿨롱의 법칙은 정지해 있는 두 전기로 대전된 입자 사이의 힘의 양을 계산하는 물리학의 실험 법칙입니다^[1]. 이 전기력을 일반적으로 정전기력 또는 쿨롱기력이라고 합니다.^[2] 이 법칙은 일찍이 알려져 있었지만, 1785년 프랑스 물리학자 샤를 오귀스트 드 쿨롱에 의해 처음 발표되었습니다. 쿨롱의 법칙은 입자의 전하량에 대한 의미 있는 논의를 가능하게 했기 ^[1]때문에 전자기학 이론의 발전에 필수적이었고 아마도 그 출발점일 것입니다.^[3]

이 법칙은 두 점전하 사이의 인력 또는 반발하는 정전기력의 크기, 즉 절대값은 전하의 크기의 곱에 정비례하고 두 점전하 사이의 거리 제곱에 반비례한다고 말합니다.^[4] 쿨롱은 비슷한 전기 전하를 가진 물체가 반발한다는 사실을 발견했습니다.

따라서 이 세 가지 테스트에서 동일한 종류의 전기로 전기가 공급된 두 공이 서로 작용하는 반발력은 거리의 제곱의 반비례를 따릅니다.^[5]

쿨롱은 또한 역제곱 법칙에 따라 반대로 대전된 물체가 끌어당긴다는 것을 보여주었습니다.

F =k_{\text{e}}{\frac { q_{1}  q_{2} }{r^{2}}}

여기서 $k$ 는_e 상수, $q$ 와₁ $q$ 는₂ 각각의 전하량, 스칼라 r은 전하 사이의 거리입니다.

힘은 두 전하를 연결하는 직선을 따라 있습니다. 전하들이 같은 부호를 가지면 전하들 사이의 정전기적 힘이 밀어내고, 다른 부호를 가지면 전하들 사이의 힘이 끌어당깁니다.

역제곱 법칙인 이 법칙은 아이작 뉴턴의 만유인력 역제곱 법칙과 비슷하지만, 중력은 항상 물체를 끌어당기는 힘을 만드는 반면, 정전기적 힘은 전하를 끌어당기거나 밀어내는 힘을 만듭니다. 또한, 중력은 정전기력보다 훨씬 약합니다.^[2] 쿨롱의 법칙은 가우스의 법칙을 유도하는 데 사용될 수 있고, 그 반대의 경우도 가능합니다. 정지한 단일 점전하의 경우 두 법칙이 동등하여 같은 물리법칙을 다른 방법으로 표현합니다.^[6] 이 법은 광범위하게 테스트되었으며 관찰 결과 10m에서⁻¹⁶ 10m⁸ 사이의 규모에 대한 법이 유지되었습니다.^[6]

역사

지중해 주변의 고대 문화는 호박의 막대와 같은 특정한 물체가 깃털이나 종이 조각과 같은 가벼운 물체를 끌어당기기 위해 고양이의 털로 문지를 수 있다는 것을 알고 있었습니다. Miletus의 Thales는 기원전 600년경에 정전기에 대한 최초의 기록을 세웠는데,^[7] 그 때 그는 마찰이 호박 조각이 작은 물체를 끌어당길 수 있다는 것을 알아차렸습니다.^[8]^[9]

1600년에 영국의 과학자 윌리엄 길버트는 전기와 자기를 주의 깊게 연구하여, 석재 효과와 호박을 문지르면서 발생하는 정전기를 구별했습니다.^[8] 그는 문지른 후 작은 물체를 끌어당기는 성질을 가리키기 위해 그리스어로 호박을 뜻하는 ἤλεκτρον(electron)에서 유래한 네오 라틴어 "electricus"를 만들었습니다. 이 연관성은 1646년 토마스 브라운의 "Pseudodoxia Epidemica"에 처음으로 인쇄된 영어 단어 "electric"과 "electric"을 탄생시켰습니다.^[11]

18세기의 초기 연구자들은 전기력이 거리에 따라 중력처럼 감소한다고 의심했습니다. (거리의 역제곱으로) 다니엘 베르누이와^[12] 알레산드로 볼타는 축전기의 판 사이의 힘을 측정했습니다. 그리고 1758년에 역제곱 법칙을 가정한 프란츠 아에피누스.^[13]

영국의 조셉 프리스틀리는 전기로 대전된 구체에 대한 실험을 바탕으로 전기력이 뉴턴의 만유인력의 법칙과 유사한 역제곱 법칙을 따른다고 최초로 제안했습니다. 그러나 그는 이에 대해 일반화하거나 자세히 설명하지 않았습니다.^[14] 1767년, 그는 전하들 사이의 힘이 거리의 역제곱에 따라 달라진다고 추측했습니다.^[15]^[16]

1769년, 스코틀랜드의 물리학자 존 로비슨은 그의 측정에 따르면, 같은 부호의 전하를 가진 두 구 사이의 반발력이 $x$ 와^−2.06 달라진다고 발표했습니다.^[17]

1770년대 초 영국의 헨리 캐번디시에 의해 거리와 전하 모두에서 전하를 띤 물체들 사이의 힘의 의존성이 이미 발견되었지만 발표되지는 않았습니다.^[18] 캐번디시는 "따라서 전기 인력과 반발력은 2 + 1/50과 2 - 1/50 사이의 거리의 일부 힘과 반대여야 한다는 결론을 내릴 수 있으며, 역 중복 비율과 전혀 다르다고 생각할 이유가 없습니다."라고 썼습니다.

마침내 1785년, 프랑스 물리학자 샤를 오귀스트 드 쿨롱은 전기와 자기에 대한 그의 첫 세 가지 보고서를 발표하고 그의 법칙을 진술했습니다. 이 출판물은 전자기학 이론의 발전에 필수적이었습니다.^[4] 그는 비틀림 균형을 이용해 하전 입자의 반발력과 인력을 연구했고, 두 점전하 사이의 전기력의 크기는 전하의 곱에 정비례하고, 두 점전하 사이의 거리의 제곱에 반비례한다는 사실을 밝혀냈습니다.

토션 밸런스는 중간에서 가는 섬유에 의해 매달린 바로 구성됩니다. 섬유는 매우 약한 비틀림 스프링 역할을 합니다. 쿨롱의 실험에서 비틀림 균형은 금속으로 코팅된 볼이 한쪽 끝에 부착되어 실크 실에 의해 매달린 절연봉이었습니다. 공은 알려진 정전기 전하로 대전되었고, 같은 극성의 두 번째 대전된 공이 그 근처에 왔습니다. 충전된 두 개의 공은 서로를 밀어내고 섬유를 일정 각도로 비틀어 기기의 눈금에서 읽을 수 있습니다. 쿨롱은 주어진 각도를 통해 섬유를 비틀 때 어느 정도의 힘이 필요한지 알 수 있었고, 공 사이의 힘을 계산하여 자신의 역제곱 비례 법칙을 도출할 수 있었습니다.

스칼라 형식

쿨롱의 법칙은 간단한 수학적 표현으로 말할 수 있습니다. 스칼라 형태는 두 점전하 $q$ 와₁ $q 2$ 사이의 $정전기력$ F 벡터의 크기를 제공하지만 방향은 제공하지 않습니다. $r$ 이 전하 사이의 거리라면 힘의 크기는

\mathbf {F}  ={\frac { q_{1}q_{2} }{4\pi \varepsilon _{0}r^{2}}},

여기

서 ε는 전기 상수입니다. 생성물

qq

가₁₂ 양수이면 두 전하 사이의 힘이 반발하고, 생성물이 음수이면 두 전하 사이의 힘이 매력적입니다.^[19]

벡터형태

이미지에서 벡터

F

는₁

q

가₁ 경험한 힘이고, 벡터

F

는₂

q

가₂ 경험한 힘입니다.

qq 12

>

0일

때 힘은 (이미지와 같이) 반발력이고

qq 12

<

0일

때 힘은 (이미지와 반대) 매력적입니다. 힘의 크기는 항상 같습니다.

벡터 형태의 쿨롱의 법칙은 전하가 경험하는 ${\textstyle \mathbf {F} _{1}}$ 정전기력 ${\textstyle \mathbf {F} _{1}}$ ${\textstyle \mathbf {F} _{1}}$ ${\$ 위치 r $\mathbf {r} _{1}$ ${\$ 다른 전하 근처에서, $q_{1}$ 1 ${\$ $q_{2}$ $q_{2}$ ${\$ 위치 $\mathbf {r} _{2}$ ${\displaystyle$ \ $mathbf$ {r $}_{2},$ 진공에서의 값은 다음과^[20] 같습니다.

\mathbf {F} _{1}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{\frac {\mathbf {r} _{1}-\mathbf {r} _{2}}{ \mathbf {r} _{1}-\mathbf {r} _{2} ^{3}}}={\frac {q_{1}q_{2}}{4\pi \varepsilon _{0}}}{\frac {\mathbf {\hat {r}} _{12}}{ \mathbf {r} _{12} ^{2}}}

${\textstyle {\boldsymbol {r}}_{12}={\boldsymbol {r}}_{1}-{\boldsymbol {r}}_{2}}$ 서 r ${\textstyle {\boldsymbol {r}}_{12}={\boldsymbol {r}}_{1}-{\boldsymbol {r}}_{2}}$ = r ${\textstyle {\boldsymbol {r}}_{12}={\boldsymbol {r}}_{1}-{\boldsymbol {r}}_{2}}$ - r 2 {\textstyle {\boldsymbol {r}_{12} = {\boldsymbol {r}_{1}-{\boldsymbol {r}_{2}는 전하 사이의 벡터 거리이며, ${\textstyle {\widehat {\mathbf {r} }}_{12}={\frac {\mathbf {r} _{12}}{ \mathbf {r} _{12} }}}$ a unit vector pointing from ${\textstyle q_{2}}$ to ${\textstyle q_{1}}$ , and $\varepsilon _{0}$ the electric constant. 여기서 벡터 표기는 ${\textstyle \mathbf {\hat {r}} _{12}}$ ${\textstyle \mathbf {\hat {r}} _{12}}$ ${\$ 를 ${\textstyle \mathbf {\hat {r}} _{12}}$ 사용합니다.

쿨롱 법칙의 벡터 형태는 단순히 단위 벡터 ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ ${\$ 에 의해 주어진 방향을 가진 법칙의 스칼라 정의이며 ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ 충전 $q_{2}$ 2 ${\$ 에서 충전 $q_{1}$ $q_{1}$ ${\$ 까지의 $q_{2}$ 라인과 평행합니다 $q_{1}$ ^[21] 두 전하가 동일한 부호(전하와 같은)를 가진 경우 제품 $q_{1}q_{2}$ 1 $q_{1}q_{2}$ $q_{1}q_{2}$ ${\$ 가 양수이고 $q_{1}q_{2}$ $q_{1}$ $q_{1}$ ${\$ 에 대한 힘의 방향은 $q_{1}$ ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ ${\$ 전하가 서로 밀어냅니다 ${\textstyle {\widehat {\mathbf {r} }}_{12}}$ 전하가 반대 부호를 갖는 경우 제품 $q_{1}q_{2}$ $q_{1}q_{2}$ $q_{1}q_{2}$ 2 ${\$ 는 음이고 $q_{1}q_{2}$ $q_{1}$ 1 ${\$ 의 힘 ${\textstyle -{\hat {\mathbf {r} }}_{12}}$ 은 $q_{1}$ ${\textstyle -{\hat {\mathbf {r} }}_{12}}$ - r ${\textstyle -{\hat {\mathbf {r} }}_{12}}$ ${\textstyle -{\hat {\mathbf {r} }}_{12}}$ ${\$ 전하가 서로 끌어당깁니다.

뉴턴의 제3법칙에 따라 $q_{2}$ 2 {\textstyle \ $mathbf {F}_{2}$ 가 경험하는 정전기력 F ${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$ $q_{2}$ 는 ${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$ ${\textstyle \mathbf {F} _{2}}$ = ${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$ - F ${\textstyle \mathbf {F} _{2}=-\mathbf {F} _{1}}$ ${\textstyle$ \mathbf {F}_{2}=-\mathbf {F}_{1}입니다.

이산 전하의 체계

중첩의 법칙은 쿨롱의 법칙을 임의의 수의 점전하를 포함하도록 확장할 수 있게 해줍니다. 점전하 시스템으로 인해 점전하에 작용하는 힘은 단순히 각각의 전하로 인해 해당 점전하에 단독으로 작용하는 개별 힘의 벡터 덧셈입니다. 결과적인 힘 벡터는 그 점 전하를 제거한 상태에서 전기장 벡터와 평행합니다.

진공에서 ${\textstyle \mathbf {r} }$ ${\textstyle N}$ 의 ${\textstyle N}$ {\ $textstyle$ N $}$ 개의 ${\textstyle N}$ 이산 전하로 인해 ${\textstyle \mathbf {r} }$ r {\ $textstyle$ \ $mathbf$ { $r}$ 의 작은 $전하$ q {\ $displaystyle$ q ${\textstyle \mathbf {F} }$ }에 ${\textstyle \mathbf {F} }$ F {\ $textstyle \mathbf$ { $F}$ 를 가합니다^[20] ${\textstyle \mathbf {r} }$

\mathbf {F}(\mathbf {r})={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{N}q_{\i}{\frac {\mathbf {r} -\mathbf {r}_{i}}{\mathbf {r} -\mathbf {r}_{i}^{3}}={q \over 4\pi \varepsilon _{0}}\sum _{i=1}^{n}q_{\hat {\mathbf {R}}}_{i}\over \mathbf {R}_{i}

여기서 $q_{i}$ ${\$ 및 ${\textstyle \mathbf {r} _{i}}$ ${\$ _ ${i}$ 는 ${\textstyle \mathbf {r} _{i}}$ 각각 i번째 전하의 크기와 위치입니다. ${\textstyle {\hat {\mathbf {R} }}_{i}}$ is a unit vector in the direction of ${\textstyle \mathbf {R} _{i}=\mathbf {r} -\mathbf {r} _{i}}$ , a vector pointing from charges $q_{i}$ to $q$ .^[21]

연속전하분포

이 경우 선형 중첩의 원리도 사용됩니다. 연속적인 전하분포의 경우, 전하를 포함하는 영역에 대한 적분은 무한합과 같으며, 공간의 각 무한소 요소를 $dq$ 를 띤 $q$ $dq$ 로 취급합니다 $dq$ 전하의 분포는 일반적으로 선형, 표면 또는 체적입니다.

λ $\lambda (\mathbf {r} ')$ r $')$ ${\$ displaystyle \lambda(\mathbf {r $}')}$ 가 위치 r' {\displaystyle \mathbf {r} '}에서 단위 길이당 전하를 제공하고 d ℓ ' {\displaystyle d\ell '}이 길이의 무한소 요소인 선형 전하 분포의 경우,

dq'=\lambda(\mathbf {r'})\,d\ell '

σ $r')$ ${\$ displaystyle \sigma(\mathbf {r}')}가 위치 r' {\displaystyle \mathbf {r} '}의 단위 면적당 전하를 제공하고 dA' {\displaystyle dA'}가 면적의 무한소 요소인 표면 전하 분포의 경우,

dq'=\sigma(\mathbf {r'})\,dA'

ρ $\rho (\mathbf {r} ')$ r $')$ ${\$ displaystyle \rho(\mathbf {r $}')}$ 가 위치 r' {\displaystyle \mathbf {r} '}의 단위 부피당 전하를 제공하고 dV' {\displaystyle dV'}가 볼륨의 무한소 요소인 볼륨 전하 분포의 경우,

dq'=\rho({\boldsymbol {r'})\,dV'

진공에서 ${\boldsymbol {r}}$ ${\boldsymbol {r}}$ ${\$ 의 $q$ 작은 테스트 전하 $q$ $q$ 에 대한 힘은 전하 분포에 대한 적분으로 제공됩니다.

\mathbf {F}(\mathbf {r})={\frac {q}{4\pi \varepsilon _{0}}\int dq'{\frac {\mathbf {r} -\mathbf {r'}{ \mathbf {r} -\mathbf {r'}^{3}

쿨롱 법칙의 "continu 전하" 버전은 $|\mathbf {r} -\mathbf {r'} |=0$ r - $|\mathbf {r} -\mathbf {r'} |=0$ ' = 0 ${\displaystyle$ \mathbf {r} -\mathbf {r'} = $|\mathbf {r} -\mathbf {r'} |=0$ 위치에 적용하면 안 됩니다. 왜냐하면 그 위치는 하전 입자의 위치와 직접적으로 겹치기 때문입니다. 전자 또는 양성자)는 전기장 또는 전위를 고전적으로 분석할 수 있는 유효한 위치가 아닙니다. 전하는 현실에서 항상 이산적이며, "continu 전하" 가정은 $|\mathbf {r} -\mathbf {r'} |=0$ r - $|\mathbf {r} -\mathbf {r'} |=0$ ' = $0 {\$ displaystyle \mathbf {r} -\mathbf {r'} = 0}을(를) $|\mathbf {r} -\mathbf {r'} |=0$ 할 수 없도록 되어 있는 근사치에 불과합니다.

쿨롱 상수

쿨롱 상수는 쿨롱의 법칙과 관련 공식에 나타나는 비례성 인자입니다. $k_{\text{e}}$ ${\$ 로 표시되며 $k_{\text{e}}$ 이를 전기력 상수 또는^[23] 정전 상수라고도 하며, 따라서 첨자 'e'입니다. 쿨롱 상수는 ${\textstyle k_{\text{e}}={\frac {1}{4\pi \varepsilon _{0}}}}$ = ${\textstyle k_{\text{e}}={\frac {1}{4\pi \varepsilon _{0}}}}$ π ε 0 {\textstyle k_ ${\text$ {e}} = ${\$ frac {1}{4\pi \varepsilon _{0}}}에 의해 제공됩니다. 상수 $\varepsilon _{0}$ ε 0 ${\displaystyle \varepsilon$ _{0}}은 진공 전기 유전율(전기 상수라고도 함)입니다. 전하가 잠기는 물질의 무차원 상대 유전율인 $\varepsilon _{r}$ ε r ${\displaystyle \varepsilon$ _{r}} 또는 제품 ε a = ε 0 ε r {\ $displaystyle \varepsilon$ _{a}=\varepsilon _{0}\varepsilon _{r}, 이는 "물질의 절대 유전율"이라고 불리며 여전히 전기 공학에서 사용됩니다.

2019년 SI 기준 단위의 재정의 ^[25]^[26]이후 CODATA 2018 권장값에서 계산한 쿨롱 상수는^[27]

k_{\text{e}}=8.987\,551\,792\,3\,(14)\times 10^{9}\ \mathrm {N{\cdot }m^{2}{\cdot }C^{-2}} .

한계

쿨롱의 역제곱 법칙의 유효성을 위해서는 다음 세 가지 조건이 충족되어야 합니다.^[28]

전하가 구형 대칭 분포(예: 점전하 또는 하전된 금속 구)를 가져야 합니다.
전하가 겹쳐서는 안 됩니다(예: 서로 다른 점 전하여야 합니다).
가속되지 않는 기준 프레임에 대해서는 전하가 정지되어 있어야 합니다.

이 중 마지막은 정전기 근사치로 알려져 있습니다. 운동이 일어나면 아인슈타인의 상대성 이론을 고려해야 하고, 그 결과 두 물체에 생성되는 힘을 변화시키는 추가적인 요소가 도입됩니다. 이 추가적인 힘의 부분을 자기력이라고 하며, 자기장으로 설명합니다. 느린 운동의 경우 자기력은 최소이며 쿨롱의 법칙은 여전히 거의 정확한 것으로 간주될 수 있지만 전하들이 서로 관련하여 더 빠르게 움직일 때는 완전한 전기 역학 규칙(자기력을 포함하는)을 고려해야 합니다.

전기장

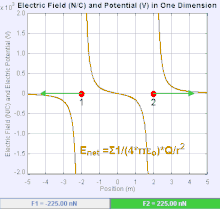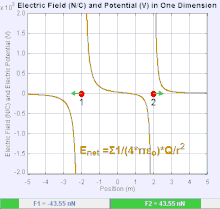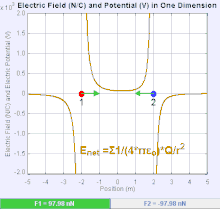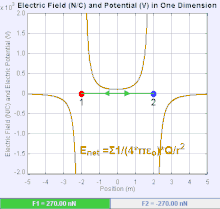
전기장은 단위 시험 전하가 경험하는 쿨롱 힘을 공간의 각 점과 연관시키는 벡터장입니다.^[20] 전하 ${\textstyle q_{t}}$ ${\textstyle q_{t}}$ 에 대한 쿨롱 힘 F ${\textstyle \mathbf {F}$ 의 세기와 방향은 ${\textstyle \mathbf {F} =q_{t}\mathbf {E} }$ = ${\textstyle \mathbf {F} =q_{t}\mathbf {E} }$ ${\textstyle \mathbf {F} =q_{t}\mathbf {E} }$ ${\textstyle \mathbf$ {F} = q_{t}\mathbf {E}와 같은 다른 전하에 의해 설정된 전기장 ${\textstyle \mathbf {E} }$ ${\textstyle \mathbf {E}$ 에 따라 달라집니다. 가장 단순한 경우, 필드는 단일 소스 포인트 전하에 의해서만 생성되는 것으로 간주됩니다. 더 일반적으로, 그 장은 중첩의 원리에 의해 전체에 기여하는 전하의 분포에 의해 생성될 수 있습니다.

양의 소스 포인트 전하 ${\textstyle q}$ ${\textstyle q}$ 에 의해 필드가 생성되는 경우 ${\textstyle q}$ 전기장의 방향은 그로부터 방사상 바깥쪽으로 향하는 선을 따라, 즉 필드에 배치된 경우 양의 ${\textstyle q_{t}}$ ${\textstyle q_{t}}$ 전하 ${\textstyle q_{t}}$ {\ $textstyle q_{$ t}가 이동하는 ${\textstyle q_{t}}$ 방향을 가리킵니다. 음의 점 소스 전하의 경우 방향은 방사상 안쪽입니다.

전기장 $E$ 의 크기는 쿨롱의 법칙으로부터 유도될 수 있습니다. 점전하 중 하나를 소스로 선택하고, 다른 하나를 테스트 전하로 선택함으로써 진공에서 한 점전하 Q가 일정 거리에서 생성하는 $전기장$ E의 크기는 다음과 같습니다.

\mathbf {E} = k_{\text{e}}{\frac {q}{r^{2}}

${\textstyle \mathbf {r} _{i}}$ ${\$ 에 $q_{i}$ 위치한 전하 $q_{i}$ ${\$ 의 계 N은 중첩에 의해 크기와 방향이 전기장을 생성합니다 ${\textstyle \mathbf {r} _{i}}$ .

\mathbf {E}(\mathbf {r})={1 \over 4\pi \varepsilon _{0}}\sum _{i=1}^{N}q_{\frac {\mathbf {r} -\mathbf {r} _{i}} {\mathbf {r} -\mathbf {r} _{i} ^{3}

원자력

쿨롱의 법칙은 원자 내에서도 성립하며, 양전하를 띤 원자핵과 음전하를 띤 전자들 사이의 힘을 정확하게 설명합니다. 이 단순한 법칙은 또한 원자를 결합하여 분자를 형성하는 힘과 원자와 분자를 결합하여 고체와 액체를 형성하는 힘을 정확하게 설명합니다. 일반적으로 이온 사이의 거리가 멀수록 인력의 힘과 결합 에너지가 0에 가까워지고 이온 결합은 덜 유리합니다. 반대 전하의 크기가 증가할수록 에너지가 증가하고 이온 결합이 더 유리합니다.

가우스의 법칙과의 관계

쿨롱의 법칙으로부터 가우스의 법칙 도출

가우스의 법칙은 쿨롱의 법칙과 전기장이 중첩 원리를 따른다는 가정으로부터 유도될 수 있는데, 이것은 결과적인 필드가 각 입자에 의해 생성된 필드의 벡터 합(또는 전하가 공간 영역에 분포되어 있는 경우 적분)이라는 것입니다.

증명개요

쿨롱의 법칙에 따르면 정지점 전하에 의한 전기장은 다음과 같습니다.

\mathbf {E}(\mathbf {r})={\frac {q}{4\pi \varepsilon _{0}}{\frac {\mathbf {e}_{r}}{r^{2}

어디에

$e$ 는_r 방사 단위 벡터입니다.
$r$ 은 반지름, $r$ ,
$ε$ 는 전기 상수이고,
$q$ 는 원점에 위치한 것으로 추정되는 입자의 전하입니다.

쿨롱의 법칙에서 나온 표현을 사용하여, 우리는 적분을 사용하여 공간의 $서로$ 다른 점에서 무한소 전하에 의한 $r$ 에서의 장의 합을 구하고, 다음을 제공함으로써 $r$ 에서의 전체 장의 합을 구합니다.

\mathbf {E}(\mathbf {r})={\frac {1}{4\pi \varepsilon _{0}}\int {\frac {\rho(\mathbf {s})(\mathbf {r} -\mathbf {s}}{\mathbf {r} -\mathbf {s}^{3}}\,d^{3}\mathbf {s

여기

서 ρ은 전하 밀도입니다. r에 대하여 이 방정식의 양변의 미분을 취하면, 다음과 같은 정리를^[29] 이용할 수 있습니다.

\nabla \cdot {\frac {\mathbf {r} }{ \mathbf {r}  ^{3}}}=-\nabla ^{2}{\frac {1}{ \mathbf {r}  }}=4\pi \delta (\mathbf {r} )

여기서δ(r)은 디랙 델타 함수이며, 결과는

\nabla \cdot \mathbf {E}(\mathbf {r})={\frac {1}{\varepsilon _{0}}\int \rho(\mathbf {s})\,\delta(\mathbf {r} -\mathbf {s})\,d^{3}\mathbf {s

Dirac 델타 함수의 "시프팅 특성"을 사용하여, 우리는 다음에 도달합니다.

\nabla \cdot \mathbf {E}(\mathbf {r})={\frac {\rho(\mathbf {r})}{\varepsilon _{0}}

그것은 가우스의 법칙의 차등적인 형태입니다, 원하는 대로 말입니다.

쿨롱의 법칙은 정지전하에만 적용되므로, 이 유도만으로 이동전하에 대해 가우스의 법칙이 성립할 것으로 기대할 이유는 없습니다. 사실, 가우스의 법칙은 움직이는 전하에 대해 성립하며, 이 점에서 가우스의 법칙은 쿨롱의 법칙보다 더 일반적입니다.

가우스의 법칙으로부터 쿨롱의 법칙 도출

엄밀하게 말하면, 쿨롱의 $법칙$ 은 E의 컬에 관한 어떠한 정보도 제공하지 않기 때문에(헬름홀츠 분해와 패러데이 법칙 참조), 가우스의 법칙만으로는 쿨롱의 법칙을 유도할 수 없습니다. 그러나 점전하로부터의 전기장이 구형 대칭이라고 가정하면 쿨롱의 법칙은 가우스의 법칙으로부터 증명될 수 있습니다. (이 가정은 쿨롱의 법칙 자체와 마찬가지로 전하가 정지해 있으면 정확히 사실이고, 전하가 운동하고 있으면 거의 사실입니다.)

증명개요

가우스 법칙의 적분 형태에 있는 $S$ 를 점전하 $Q$ 를 중심으로 하는 반지름 $r$ 의 구면으로 하면, 우리는

\point _{S}\mathbf {E} \cdot d\mathbf {A} = {\frac {Q} {\varepsilon _{0}

구면 대칭의 가정에 의해, 적분은 적분에서 제거될 수 있는 상수입니다. 결과는.

4\pir^{2}{\hat {\mathbf {r}}}\cdot \mathbf {E}(\mathbf {r})={\frac {Q}{\varepsilon _{0}}

여기서 r

̂는 전하로부터 방사상으로 떨어진 곳을 가리키는 단위 벡터입니다. 다시 구면 대칭에 의해,

E

는 반지름 방향을 가리키고, 그래서 우리는

\mathbf {E}(\mathbf {r})={\frac {Q}{4\pi \varepsilon _{0}}{\frac {\hat {\mathbf {r}}}{r^{2}

이것은 본질적으로 쿨롱의 법칙과 동등합니다. 따라서 쿨롱의 법칙에서 전기장의 역제곱 법칙 의존성은 가우스의 법칙을 따릅니다.

상대성이론

특수 상대성 이론에 의해 자기장은 전기장에 의해 발생하는 힘의 변환으로 보일 수 있기 때문에, 쿨롱의 법칙은 움직이는 전하에 의해 발생하는 자기장의 형태에 대한 통찰력을 얻는 데 사용될 수 있습니다. 입자의 역사에 가속도가 포함되지 않을 때, 쿨롱의 법칙은 위에서 보여준 맥스웰 방정식을 푸는 데 있어 대칭 논쟁에 의해 뒷받침되는 고유한 관성 프레임의 모든 시험 입자에 대해 가정될 수 있습니다. 쿨롱의 법칙은 같은 형태의 움직이는 시험 입자로 확장될 수 있습니다. 이 가정은 쿨롱의 법칙과 달리 고정된 테스트 전하에 국한되지 않는 로렌츠 힘 법칙에 의해 뒷받침됩니다. 전하가 관측자의 불변성을 고려할 때, 따라서 균일하게 움직이는 점전하의 전기장과 자기장은 쿨롱의 법칙에 의해 주어진 기준틀에서 시험 전하에 대한 4개의 힘의 로런츠 변환에 의해 유도될 수 있고, 로런츠 힘의 형태로 주어진 정의에 의해 자기장과 전기장을 귀속시킬 수 있습니다.^[30] 따라서 균일하게 움직이는 점전하에 대한 필드는 다음과 같습니다.^[31]

\mathbf {E} = {\frac {q}{4\pi \epsilon _{0}r^{3}}{\frac {1-\beta ^{2}\sin ^{2}\theta )^{3/2}}\mathbf {r}

\mathbf {B} ={\frac {q}{4\pi \epsilon _{0}r^{3}}{\frac {1-\beta ^{2}\sin ^{2}\theta )^{3/2}}{\frac {\mathbf {v} \times \mathbf {r} }{c^{2}} ={\frac {\mathbf {v} \times \mathbf {E} } {c^{2}}

여기서

q

{\

displaystyle q

}는

q

점 소스의 전하,

\mathbf {r}

{\displaystyle

\

mathbf

{r

}은

점

\mathbf {r}

소스에서 공간의 점까지의 위치 벡터,

\mathbf {v}

{\

displaystyle \mathbf {v}

은

\mathbf {v}

하전 입자의 속도 벡터,

\beta

{\displaystyl

}

는 하전 입자의 속도를

빛

의

\beta

도와

\mathbf {v}

θ의 속도로 나눈 비율

{\

displaystyle \theta}는 r {\displaystyle \mathbf {r}과 v {\displaystyle \mathbf {v} 사이의 각도입니다.

이러한 형태의 해결책은 특수 상대성 이론의 틀에서와 같이 뉴턴의 제3법칙을 따를 필요가 없습니다(그러나 상대론적 에너지 운동량 보존을 위반하지 않는 한).^[32] 전기장에 대한 표현은 점전하의 비상대론적 속도에 대한 쿨롱 법칙으로 줄어들고 비상대론적 한계(대략 $β$ ≪ 1 {\ $displaystyle \beta$ \ll 1})의 자기장을 전류에 적용하여 Biot-Savart 법칙을 얻을 수 있습니다. 지연된 시간으로 표현하면, 이 해들은 리나드 해에 의해 주어진 맥스웰 방정식의 일반적인 해와도 일치합니다.특정한 적용 범위 내에서 쿨롱 법칙의 유효성으로 인해 비처트 포텐셜. 또한 정지 전하에 대한 가우스 법칙에 대한 구형 대칭은 문제의 속도 방향 지정에 의한 대칭의 깨짐으로 인해 움직이는 전하에 대해 유효하지 않습니다. 맥스웰 방정식과의 일치는 위의 두 방정식에 대해서도 수동으로 확인할 수 있습니다.^[33]

쿨롱 퍼텐셜

양자장이론

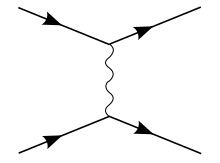
쿨롱 퍼텐셜은 연속체 상태(E > 0)를 인정하며, 전자-양성자 산란과 수소 원자를 나타내는 이산 결합 상태를 설명합니다.^[34] 또한 두 대전 입자 사이의 비상대론적 한계 내에서 다음과 같이 유도할 수 있습니다.

비 relat ${\textstyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )}$ 양자역학에서 산란 ${\textstyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )}$ A ${\textstyle {\mathcal {A}}(|\mathbf {p} \rangle \to |\mathbf {p} '\rangle )}$ (p ⟩ → p' ⟩) ${\textstyle {\mathcal {$ A}}( $\mathbf {p$ } $\rangle$ \ $to \$ mathbf {p} '\rangle )}는 다음과 같습니다.

{\mathcal {A}}( \mathbf {p} \rangle \ to \mathbf {p} '\rangle )-1=2\pi \ delta (E_{p}-E_{p'})(-i)\int d^{3}\mathbf {r} \,V(\mathbf {r})e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r}

이는 다음과 비교됩니다.

\int {\frac {d^{3}k}{(2\pi )^{3}}}e^{ikr_{0}}\langle p',k S p,k\rangle

여기서는 서로 흩어지는 두 개의 전자에 대한 (연결된) S-행렬 엔트리를 살펴보는데, 하나는 "고정된" 운동량을 전위의 근원으로 취급하고, 다른 하나는 전위에서 흩어지는 것입니다.

$m_{0}\gg |\mathbf {p} |$ 행렬 요소를 계산하기 위해 파인만 규칙을 사용하여 m 0 ≫ p {\ $displaystyle m_{0$ }\gg $\mathbf$ {p}인 비상대론적 한계를 얻습니다.

\langle p',k S p,k\rangle  _{conn}=-i{\frac {e^{2}}{ \mathbf {p} -\mathbf {p} ' ^{2}-i\varepsilon }}(2m)^{2}\delta (E_{p,k}-E_{p',k})(2\pi )^{4}\delta (\mathbf {p} -\mathbf {p} ')

QM 산란과 비교하면 QM과 비교하여 QFT에서 운동량 고유 상태의 정규화가 다르기 때문에 $(2m)^{2}$ $(2m)^{2}$ ( $(2m)^{2}$ $(2m)^{2}$ ${\$ 를 폐기하고 다음을 얻어야 합니다.

\int V(\mathbf {r} )e^{-i(\mathbf {p} -\mathbf {p} ')\mathbf {r} }d^{3}\mathbf {r} ={\frac {e^{2}}{ \mathbf {p} -\mathbf {p} ' ^{2}-i\varepsilon }}

여기서 푸리에가 양쪽을 변환하고 적분을 풀고

\varepsilon \to 0

에

\varepsilon \to 0

ε → 0

{\

displaystyle \varepsilon \to 0}을 취하면 산출됩니다.

V(r)={\frac {e^{2}}{4\pi r}}

쿨롱 퍼텐셜로.^[35]

그러나 쿨롱 문제에 대한 고전적인 Born 유도의 동등한 결과는 엄격하게 우연적인 것으로 생각됩니다.^[36]^[37]

쿨롱 퍼텐셜과 그 유도는 유카와 퍼텐셜의 특별한 경우로 볼 수 있는데, 교환된 보손(광자)이 정지 질량을 갖지 않는 경우입니다.^[34]

쿨롱의 법칙을 검증하기 위한 간단한 실험

간단한 실험으로 쿨롱의 법칙을 검증할 수 있습니다. 길이 l $l$ 의 무시할 수 있는 질량 $l$ $m$ 의 두 $q$ 줄에 매달려 있는 질량 $m$ {\displaystyle m}과 $m$ 동일한 부호의 전하 $q$ {\ $displaystyle$ q $}$ 의 작은 구체 두 개를 생각해 보십시오 $l$ 각 구에 작용하는 힘은 무게 $mg$ ${\displaystyle mg$ 로프 장력 $\mathbf {T}$ ${\$ 전기력 $\mathbf {T}$ $\mathbf {F}$ ${\$ 의 세 가지입니다 $\mathbf {F}$ 평형 상태에서:

\mathbf {T} \sin \theta _{1}=\mathbf {F} _{1}

(1)

그리고.

\mathbf {T} \cos \theta _{1}=mg

(2)

(1)을 (2)로 나누기:

{\frac {\sin \theta _{1}}{\cos \theta _{1}}={\frac {F_{1}}{mg}\rightarrow F_{1}=mg\tan \theta _{1}

(3)

$\mathbf {L} _{1}$ $\mathbf {L} _{1}$ ${\$ $displaystyle \mathbf {L}$ $_$ ${1}}$ 을 $\mathbf {L} _{1}$ 전하를 띤 구들 사이의 거리라고 하자; 쿨롱의 $법칙$ 이 옳다고 가정하면 $\mathbf {F} _{1}$ $\mathbf {F} _{1}$ 사이의 반발력은 $\mathbf {F} _{1}$ 과 같습니다 $.$

F_{1}={\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}

(Coulomb's law)

그래서:

{\frac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}=mg\tan \theta _{1}

(4)

이제 구들 중 하나를 방출하고 그것을 대전된 구와 접촉시키면, 그들 각각은 전하 ${\textstyle {\frac {q}{2}}}$ ${\textstyle {\frac {q}{2}}}$ {\ $textstyle {\frac$ { $q}{2}}$ 를 얻습니다 ${\textstyle {\frac {q}{2}}}$ 평형 상태에서, 전하 사이의 거리는 ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ < ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ 1 ${\$ <\ $mathbf {L} _{1}$ 이며 ${\textstyle \mathbf {L} _{2}<\mathbf {L} _{1}}$ , 전하 사이의 반발력은 다음과 같습니다.

F_{2}={\frac {{({\frac {q}{2}})}^{2}}{4\pi \varepsilon _{0}L_{2}^{2}}}={\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}

(5)

우리는 $\mathbf {F} _{2}=mg\tan \theta _{2}$ $\mathbf {F} _{2}=mg\tan \theta _{2}$ = $\mathbf {F} _{2}=mg\tan \theta _{2}$ $\mathbf {F} _{2}=mg\tan \theta _{2}$ ⁡ θ 2 {\displaystyle \mathbf {F} _{2} = mg\tan \theta _{2} 및 다음과 같은 것을 알고 있습니다.

{\frac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}=mg\tan \theta _{2}

(4)를 (5)로 나누면 다음을 얻을 수 있습니다.

{\frac {\left({\cfrac {q^{2}}{4\pi \varepsilon _{0}L_{1}^{2}}}\right)}{\left({\cfrac {\frac {q^{2}}{4}}{4\pi \varepsilon _{0}L_{2}^{2}}}\right)}}={\frac {mg\tan \theta _{1}}{mg\tan \theta _{2}}}\Rightarrow 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}={\frac {\tan \theta _{1}}{\tan \theta _{2}}}

(6)

각도 $\theta _{1}$ θ 1 ${\displaystyle \theta$ _{ $\theta _{2}$ }} $\theta _{2}$ 및 θ 2 ${\displaystyle$ $\$ theta _{2}와 $전하$ L 1 ${\displaystyle \$ $\mathbf {L} _{2}$ { $}$ _{1}과 L 2 ${\displaystyle$ \mathbf {L} _{2}를 측정하면 실험 오차를 고려할 때 동일성이 참인지 확인할 수 있습니다. 실제로는 각도를 측정하기 어려울 수 있으므로 로프의 길이가 충분히 크다면 각도는 다음과 같은 근사를 할 수 있을 정도로 작습니다.

\tan \theta \approx \sin \theta ={\frac {L}{2}}{\ell }}={\frac {L}{2\ell }}\오른쪽 화살표 {\frac {\tan \theta _{1}}{\tan \theta _{2}}\approx {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}

(7)

이 근사를 사용하면 (6) 관계는 훨씬 단순한 표현이 됩니다.

{\frac {\frac {L_{1}}{2\ell }}{\frac {L_{2}}{2\ell }}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx 4{\left({\frac {L_{2}}{L_{1}}}\right)}^{2}\Rightarrow {\frac {L_{1}}{L_{2}}}\approx {\sqrt[{3}]{4}}

(8)

이런 식으로, 검증은 전하 사이의 거리를 측정하고, 나눗셈이 이론적인 값에 근사하는지 확인하는 것으로 제한됩니다.

참고 항목

비오-사바르트 법칙
다윈 라그랑지안
전자기력
가우스의 법칙
영상 전하의 방법
분자 모델링
비슷한 구조를 사용하지만 전하 대신 질량을 사용하는 뉴턴의 만유인력 법칙
정적 힘과 가상 입자 교환
카시미르 효과

참고문헌

^ ^a ^b Huray, Paul G. (2010). Maxwell's equations. Hoboken, New Jersey: Wiley. pp. 8, 57. ISBN 978-0-470-54991-9. OCLC 739118459.
^ ^a ^b Halliday, David; Resnick, Robert; Walker, Jearl (2013). Fundamentals of Physics. John Wiley & Sons. pp. 609, 611. ISBN 9781118230718.
^ Roller, Duane; Roller, D. H. D. (1954). The development of the concept of electric charge: Electricity from the Greeks to Coulomb. Cambridge, Massachusetts: Harvard University Press. p. 79.
^ ^a ^b Coulomb (1785). "Premier mémoire sur l'électricité et le magnétisme" [First dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 569–577.
^ Coulomb (1785). "Second mémoire sur l'électricité et le magnétisme" [Second dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 578–611. Il résulte donc de ces trois essais, que l'action répulsive que les deux balles électrifées de la même nature d'électricité exercent l'une sur l'autre, suit la raison inverse du carré des distances.
^ ^a ^b Purcell, Edward M. (21 January 2013). Electricity and magnetism (3rd ed.). Cambridge. ISBN 9781107014022.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)
^ Cork, C.R. (2015). "Conductive fibres for electronic textiles". Electronic Textiles: 3–20. doi:10.1016/B978-0-08-100201-8.00002-3. ISBN 9780081002018.
^ ^a ^b Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. p. 50. ISBN 978-981-02-4471-2.
^ Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. pp. 6–7. ISBN 978-0-444-51258-1.
^ Baigrie, Brian (2007). Electricity and Magnetism: A Historical Perspective. Greenwood Press. pp. 7–8. ISBN 978-0-313-33358-3.
^ Chalmers, Gordon (1937). "The Lodestone and the Understanding of Matter in Seventeenth Century England". Philosophy of Science. 4 (1): 75–95. doi:10.1086/286445. S2CID 121067746.
^ Socin, Abel (1760). Acta Helvetica Physico-Mathematico-Anatomico-Botanico-Medica (in Latin). Vol. 4. Basileae. pp. 224–25.
^ Heilbron, J.L. (1979). Electricity in the 17th and 18th Centuries: A Study of Early Modern Physics. Los Angeles, California: University of California Press. pp. 460–462 and 464 (including footnote 44). ISBN 978-0486406886.
^ Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. pp. 144–56. ISBN 978-0-271-01662-7.
^ Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. London, England. p. 732.
^ Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. Wiley. ISBN 978-0-7803-5384-8.
^ Robison, John (1822). Murray, John (ed.). A System of Mechanical Philosophy. Vol. 4. London, England: Printed for J. Murray.
^ Maxwell, James Clerk, ed. (1967) [1879]. "Experiments on Electricity: Experimental determination of the law of electric force.". The Electrical Researches of the Honourable Henry Cavendish... (1st ed.). Cambridge, England: Cambridge University Press. pp. 104–113.
^ "Coulomb's law". Hyperphysics.
^ ^a ^b ^c Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. Addison-Wesley. ISBN 9780201021158.
^ ^a ^b ^c Fitzpatrick, Richard (2006-02-02). "Coulomb's law". University of Texas.
^ "Charged rods". PhysicsLab.org.
^ Walker, Jearl; Halliday, David; Resnick, Robert (2014). Fundamentals of physics (10th ed.). Hoboken, NJ: Wiley. p. 614. ISBN 9781118230732. OCLC 950235056.
^ Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, p. 15, ISBN 978-92-822-2272-0
^ BIPM statement: Information for users about the proposed revision of the SI (PDF)
^ "Decision CIPM/105-13 (October 2016)". 이 날은 미터 대회의 144주년이 되는 날입니다.
^ $k$ = 1 / ( $4$ πε)에서 파생 –
^ Discussion on physics teaching innovation: Taking Coulomb's law as an example. CRC Press. 2015-07-28. pp. 465–468. doi:10.1201/b18636-105. ISBN 978-0-429-22704-2. {{cite book}}: work= 무시됨(도움말)
^ Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.
^ Rosser, W. G. V. (1968). Classical Electromagnetism via Relativity. pp. 29–42. doi:10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4.
^ Heaviside, Oliver (1894). Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge.
^ Griffiths, David J. (1999). Introduction to electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. p. 517. ISBN 0-13-805326-X. OCLC 40251748.
^ Purcell, Edward (2011-09-22). Electricity and Magnetism. Cambridge University Press. doi:10.1017/cbo9781139005043. ISBN 978-1-107-01360-5.
^ ^a ^b Griffiths, David J. (16 August 2018). Introduction to quantum mechanics (Third ed.). Cambridge, United Kingdom. ISBN 978-1-107-18963-8.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)
^ "Quantum Field Theory I + II" (PDF). Institute for Theoretical Physics, Heidelberg University.
^ Baym, Gordon (2018). Lectures on quantum mechanics. Boca Raton. ISBN 978-0-429-49926-5. OCLC 1028553174.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)
^ Gould, Robert J. (21 July 2020). Electromagnetic processes. Princeton, N.J. ISBN 978-0-691-21584-6. OCLC 1176566442.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

외부 링크

쿨롱의 프로젝트 PHYSNET에 관한 법칙
전기와 원자 - 온라인 교과서의 한 장
쿨롱의 법칙을 가르치는 미로 게임 - Molecular Workbench 소프트웨어를 통해 만들어진 게임
전하, 분극, 전기력, 쿨롱의 법칙 월터 르윈, 8.02 전기와 자기, 2002년 봄: 강의 1 (영상) MIT 오픈코스웨어. 라이센스: 크리에이티브 커먼즈 속성-비상업적-공유 동일.

[:0-1] Huray, Paul G. (2010). Maxwell's equations. Hoboken, New Jersey: Wiley. pp. 8, 57. ISBN 978-0-470-54991-9. OCLC 739118459.

[halliday-2] Halliday, David; Resnick, Robert; Walker, Jearl (2013). Fundamentals of Physics. John Wiley & Sons. pp. 609, 611. ISBN 9781118230718.

[3] Roller, Duane; Roller, D. H. D. (1954). The development of the concept of electric charge: Electricity from the Greeks to Coulomb. Cambridge, Massachusetts: Harvard University Press. p. 79.

[1785a-4] Coulomb (1785). "Premier mémoire sur l'électricité et le magnétisme" [First dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 569–577.

[1785b-5] Coulomb (1785). "Second mémoire sur l'électricité et le magnétisme" [Second dissertation on electricity and magnetism]. Histoire de l'Académie Royale des Sciences [History of the Royal Academy of Sciences] (in French). pp. 578–611. Il résulte donc de ces trois essais, que l'action répulsive que les deux balles électrifées de la même nature d'électricité exercent l'une sur l'autre, suit la raison inverse du carré des distances.

[Purcell-6] Purcell, Edward M. (21 January 2013). Electricity and magnetism (3rd ed.). Cambridge. ISBN 9781107014022.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

[7] Cork, C.R. (2015). "Conductive fibres for electronic textiles". Electronic Textiles: 3–20. doi:10.1016/B978-0-08-100201-8.00002-3. ISBN 9780081002018.

[stewart-8] Stewart, Joseph (2001). Intermediate Electromagnetic Theory. World Scientific. p. 50. ISBN 978-981-02-4471-2.

[9] Simpson, Brian (2003). Electrical Stimulation and the Relief of Pain. Elsevier Health Sciences. pp. 6–7. ISBN 978-0-444-51258-1.

[10] Baigrie, Brian (2007). Electricity and Magnetism: A Historical Perspective. Greenwood Press. pp. 7–8. ISBN 978-0-313-33358-3.

[11] Chalmers, Gordon (1937). "The Lodestone and the Understanding of Matter in Seventeenth Century England". Philosophy of Science. 4 (1): 75–95. doi:10.1086/286445. S2CID 121067746.

[12] Socin, Abel (1760). Acta Helvetica Physico-Mathematico-Anatomico-Botanico-Medica (in Latin). Vol. 4. Basileae. pp. 224–25.

[13] Heilbron, J.L. (1979). Electricity in the 17th and 18th Centuries: A Study of Early Modern Physics. Los Angeles, California: University of California Press. pp. 460–462 and 464 (including footnote 44). ISBN 978-0486406886.

[14] Schofield, Robert E. (1997). The Enlightenment of Joseph Priestley: A Study of his Life and Work from 1733 to 1773. University Park: Pennsylvania State University Press. pp. 144–56. ISBN 978-0-271-01662-7.

[15] Priestley, Joseph (1767). The History and Present State of Electricity, with Original Experiments. London, England. p. 732.

[16] Elliott, Robert S. (1999). Electromagnetics: History, Theory, and Applications. Wiley. ISBN 978-0-7803-5384-8.

[17] Robison, John (1822). Murray, John (ed.). A System of Mechanical Philosophy. Vol. 4. London, England: Printed for J. Murray.

[18] Maxwell, James Clerk, ed. (1967) [1879]. "Experiments on Electricity: Experimental determination of the law of electric force.". The Electrical Researches of the Honourable Henry Cavendish... (1st ed.). Cambridge, England: Cambridge University Press. pp. 104–113.

[19] "Coulomb's law". Hyperphysics.

[:1-20] Feynman, Richard P. (1970). The Feynman Lectures on Physics Vol II. Addison-Wesley. ISBN 9780201021158.

[uTexas-21] Fitzpatrick, Richard (2006-02-02). "Coulomb's law". University of Texas.

[22] "Charged rods". PhysicsLab.org.

[23] Walker, Jearl; Halliday, David; Resnick, Robert (2014). Fundamentals of physics (10th ed.). Hoboken, NJ: Wiley. p. 614. ISBN 9781118230732. OCLC 950235056.

[24] Le Système international d’unités [The International System of Units] (PDF) (in French and English) (9th ed.), International Bureau of Weights and Measures, 2019, p. 15, ISBN 978-92-822-2272-0

[SI-statement-25] BIPM statement: Information for users about the proposed revision of the SI (PDF)

[26] "Decision CIPM/105-13 (October 2016)". 이 날은 미터 대회의 144주년이 되는 날입니다.

[ke-27] $k$ = 1 / ( $4$ πε)에서 파생 –

[28] Discussion on physics teaching innovation: Taking Coulomb's law as an example. CRC Press. 2015-07-28. pp. 465–468. doi:10.1201/b18636-105. ISBN 978-0-429-22704-2. {{cite book}}: work= 무시됨(도움말)

[29] Griffiths, David J. (2013). Introduction to Electrodynamics (4th ed.). Prentice Hall. p. 50.

[30] Rosser, W. G. V. (1968). Classical Electromagnetism via Relativity. pp. 29–42. doi:10.1007/978-1-4899-6559-2. ISBN 978-1-4899-6258-4.

[31] Heaviside, Oliver (1894). Electromagnetic waves, the propagation of potential, and the electromagnetic effects of a moving charge.

[32] Griffiths, David J. (1999). Introduction to electrodynamics (3rd ed.). Upper Saddle River, NJ: Prentice Hall. p. 517. ISBN 0-13-805326-X. OCLC 40251748.

[33] Purcell, Edward (2011-09-22). Electricity and Magnetism. Cambridge University Press. doi:10.1017/cbo9781139005043. ISBN 978-1-107-01360-5.

[griffiths-34] Griffiths, David J. (16 August 2018). Introduction to quantum mechanics (Third ed.). Cambridge, United Kingdom. ISBN 978-1-107-18963-8.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

[35] "Quantum Field Theory I + II" (PDF). Institute for Theoretical Physics, Heidelberg University.

[36] Baym, Gordon (2018). Lectures on quantum mechanics. Boca Raton. ISBN 978-0-429-49926-5. OCLC 1028553174.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

[37] Gould, Robert J. (21 July 2020). Electromagnetic processes. Princeton, N.J. ISBN 978-0-691-21584-6. OCLC 1176566442.{{cite book}}: CS1 maint: 위치 누락 게시자(링크)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[23]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

Search