전자 유도

좌측 솔레노이드에 교류 전류가 흐르면서 변화하는 자기장이 생성됩니다.이 장은 전자기 유도에 의해 우측 와이어 루프에 전류가 흐르게 합니다.

전자기 또는 자기 유도는 변화하는 자기장에서 전기 도체에 걸쳐 기전력을 발생시키는 것입니다.

마이클 패러데이는 일반적으로 1831년에 유도를 발견한 것으로 알려져 있으며, 제임스 클러크 맥스웰은 그것을 패러데이의 유도의 법칙이라고 수학적으로 묘사했다.렌츠의 법칙은 유도장의 방향을 설명한다.패러데이의 법칙은 나중에 맥스웰-파라데이 방정식으로 일반화되었는데, 이는 그의 전자기 이론에서 맥스웰 방정식 4개 중 하나이다.

전자기 유도는 인덕터 및 변압기와 같은 전기 부품과 전기 모터 및 발전기와 같은 장치를 포함하여 많은 응용 분야를 찾아냈다.

역사

와이어 코일 사이의 유도를 보여주는 패러데이의 실험:액체 배터리(오른쪽)는 작은 코일(A)을 통해 흐르는 전류를 공급하여 자기장을 생성합니다.코일이 정지해 있으면 전류가 유도되지 않습니다.그러나 작은 코일이 큰 코일(B) 안이나 밖으로 이동하면 큰 코일을 통과하는 자속이 변화하여 전류계(G)^[1]에 의해 검출되는 전류를 유도한다.

패러데이의 철제 링 장치 다이어그램입니다.좌측 코일의 자속 변화는 우측 ^[2]코일에 전류를 유도합니다.

전자기 유도는 1831년 ^[3]^[4]마이클 패러데이에 의해 발견되었다.그것은 1832년 ^[5]^[6]조셉 헨리에 의해 독립적으로 발견되었다.

패러데이의 첫 번째 실험 시연 (1831년 8월 29일)에서, 그는 철 고리 또는 "토러스"^{[citation needed]}의 반대쪽 면에 두 개의 와이어를 감쌌다.전자석에 대한 그의 이해에 기초하여, 그는 전류가 하나의 와이어로 흐르기 시작할 때, 일종의 파동이 링을 통과하여 반대편에 전기적 효과를 일으킬 것이라고 예상했습니다.그는 한 전선을 전류계에 꽂고, 다른 전선을 배터리에 연결하는 것을 지켜보았다.그는 와이어를 배터리에 연결했을 때와 분리했을 때 과도 전류를 보았는데, 이를 ^[7]"전기의 파동"이라고 불렀습니다.이 유도는 배터리 연결 및 ^[2]분리 시 발생하는 자속 변화 때문입니다.두 달 안에 패러데이는 몇 가지 전자기 유도의 다른 징후를 발견했다.예를 들어, 막대 자석을 와이어 코일에 빠르게 넣고 꺼낼 때 과도 전류를 보고 슬라이딩 전기 리드("파라데이의 디스크")^[8]로 막대 자석 근처에서 구리 디스크를 회전시켜 안정적인(DC) 전류를 생성했습니다.

패러데이는 힘의 선이라고 불리는 개념을 사용하여 전자기 유도를 설명했다.하지만, 그 당시 과학자들은 그의 이론적인 생각들이 수학적으로 ^[9]공식화되지 않았다는 이유로 널리 거부하였다.예외는 제임스 클럭 맥스웰이었는데, 그는 패러데이의 아이디어를 그의 양적 전자기 ^[9]^[10]^[11]이론의 기초로 사용했다.맥스웰 모형에서, 전자기 유도의 시간 변화 양상은 미분 방정식으로 표현되는데, 올리버 헤비사이드는 패러데이의 원래 공식과 약간 다르고 운동 EMF를 설명하지 않음에도 불구하고 패러데이의 법칙이라고 언급했다. 헤비사이드의 버전은 다음과 같은 형식이다.오늘날 맥스웰 방정식으로 알려진 방정식 그룹에서 n화되었습니다.

1834년 하인리히 렌츠는 그의 이름을 딴 법을 제정하여 "회로를 통과하는 플럭스"를 묘사했다.렌츠의 법칙은 유도된 EMF와 전자기 유도에 따른 전류의 방향을 제시합니다.

이론.

패러데이의 유도 법칙과 렌츠의 법칙

솔레노이드

전류가 일정하게 흐르는 솔레노이드의 종단면입니다.자기장 라인은 화살표와 함께 표시됩니다.자속은 '필드 라인의 밀도'에 해당합니다.따라서 자속은 솔레노이드 중앙에서 가장 밀도가 높고 솔레노이드 바깥쪽에서 가장 약합니다.

패러데이의 유도 법칙은 와이어 루프로 둘러싸인 공간 영역을 통해 자속 δ를_B 활용합니다.자속은 표면 ^[12]적분으로 정의됩니다.

\displaystyle \Phi _{\mathrm {B} =\int _{\Sigma}\mathbf {B} \cdot d\mathbf {A} \,}

여기서 dA는 와이어 루프로 둘러싸인 표면 δ의 요소이고, B는 자기장입니다.도트곱B·dA는 극소량의 자속에 해당합니다.좀 더 시각적으로 보면 와이어 루프를 통과하는 자속은 루프를 통과하는 자기장 라인의 수에 비례합니다.

표면을 통과하는 플럭스가 변화하면 패러데이의 유도 법칙에 따르면 와이어 루프가 기전력(EMF)^{[note 1]}을 획득합니다.이 법칙의 가장 일반적인 버전은 폐쇄 회로에서 유도 기전력이 ^[16]^[17]회로에 둘러싸인 자속의 변화율과 동일하다는 것입니다.

{\mathcal {E}}=-{\frac {d\Phi_{\mathrm {B}}}}{dt}},

{\mathcal {E}}

서 E

(\

는

{\mathcal {E}}

EMF이고 δ는_B 자속입니다.기전력의 방향은 유도 전류가 ^[18]생성된 변화에 반하는 방향으로 흐른다는 렌츠의 법칙에 의해 결정됩니다.이것은 앞의 방정식의 음수 부호 때문이다.생성된 EMF를 증가시키기 위해 공통적인 접근법은 N개의 동일한 선회로 구성된 와이어의 단단히 감긴 코일을 생성하여 플럭스 링크를 이용하는 것입니다. 각 코일은 동일한 자속을 통과합니다.그 결과 EMF는 1개의 ^[19]^[20]와이어의 N배가 됩니다.

{\mathcal {E}}=-N{\frac {d\Phi_{\mathrm {B}}}{dt}

와이어 루프 표면을 통과하는 자속의 변화를 통해 EMF를 생성하는 방법은 여러 가지가 있습니다.

자기장 B가 변화한다(예: 교류 자기장 또는 B장이 강한 막대 자석을 향해 와이어 루프를 이동한다).
와이어 루프가 변형되어 표면 δ가 변화한다.
표면 dA의 방향 변경(예: 와이어 루프를 회전시켜 고정 자기장으로),
상기의 임의의 조합

맥스웰 패러데이 방정식

일반적으로 표면 δ를 둘러싼 와이어 루프 내의 ${\mathcal {E}}$ E $(\$ 와 ${\mathcal {E}}$ 와이어 내의 전계 E의 관계는 다음과 같습니다.

{\mathcal {E}}=\point _{\mathbf {E}\cdot d'boldsymbol {\ell}

여기서 dθ는 표면 δ의 윤곽 요소이며, 이를 플럭스의 정의와 결합한다.

\displaystyle \Phi _{\mathrm {B} =\int _{\Sigma}\mathbf {B} \cdot d\mathbf {A} \,}

우리는 맥스웰-패러데이 방정식의 적분 형식을 쓸 수 있다

\point \Sigma }\mathbf {E}\cdot d"bold symbol {ell }=-{\frac {d}{dt}}{\int _ {\Sigma }\mathbf {B}}\cdot d\mathbf {A}}}

그것은 네 개의 맥스웰 방정식 중 하나이며, 따라서 고전 전자기학의 이론에서 기본적인 역할을 한다.

패러데이의 법칙과 상대성 이론

패러데이의 법칙은 두 가지 다른 현상을 설명합니다: 움직이는 와이어의 자력에 의해 생성되는 운동 EMF(로렌츠 힘 참조)와 변화하는 자기장에 의해 발생하는 변압기 EMF(맥스웰-파라데이 방정식의 미분 형태에 의해)입니다.제임스 클러크 맥스웰은 ^[21]^[22]1861년에 분리된 물리적 현상에 관심을 끌었다.이것은 물리학의 독특한 예로서, 그러한 두 ^[23]가지 다른 현상을 설명하기 위해 그러한 기본 법칙이 어디에서 호출되는지에 대한 것으로 여겨진다.

알버트 아인슈타인은 두 상황이 모두 도체와 자석 사이의 상대적인 움직임과 일치한다는 것을 알아챘고, 결과는 어떤 것이 움직이고 있는지에 영향을 받지 않았다.이것은 그가 특수 상대성 이론을 ^[24]발전시키도록 이끈 주요한 길들 중 하나였다.

적용들

전자기 유도의 원리는 다음을 포함한 많은 장치 및 시스템에 적용됩니다.

발전기

일정한 크기의 반경 외향 포인팅 자기장 B에서 각속도θ로 회전하는 직사각형 와이어 루프.회로는 브러시가 상부 및 하부 디스크와 슬라이딩 접촉하여 완성되며, 이들 디스크에는 전도성 림이 있습니다.이것은 드럼 제너레이터의 간이 버전입니다.

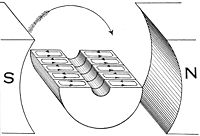
회로의 상대적인 움직임과 자기장에 의한 패러데이의 유도 법칙에 의해 발생하는 EMF는 발전기의 기초가 되는 현상이다.영구 자석이 도체에 대해 상대적으로 이동하거나 그 반대로 이동하면 기전력이 생성됩니다.와이어가 전기 부하를 통해 연결되면 전류가 흐르고, 따라서 전기 에너지가 생성되어 운동의 기계적 에너지가 전기 에너지로 변환됩니다.예를 들어 드럼 제너레이터는 우측 하단의 그림에 기초하고 있습니다.이 아이디어의 다른 구현은 오른쪽에 단순화된 형태로 표시된 패러데이의 디스크입니다.

패러데이의 디스크 예에서는 디스크가 디스크에 수직인 균일한 자기장에서 회전하여 로렌츠 힘에 의해 레이디얼 암에 전류가 흐릅니다.이 전류를 구동하기 위해서는 기계적인 작업이 필요하다.생성된 전류가 전도 림에 흐르면 이 전류에 의해 Ampér의 회로 법칙(그림에 "유도 B"로 표시됨)을 통해 자기장이 생성됩니다.따라서 림은 디스크의 회전에 저항하는 전자석이 됩니다(렌즈의 법칙의 예).그림의 반대쪽에서는 회전 암에서 림의 반대쪽을 통해 하단 브러시로 리턴 전류가 흐릅니다.이 리턴 전류에 의해 유도되는 B 전계는 인가된 B 전계에 반대하여 회로의 반대쪽을 통과하는 플럭스를 감소시키는 경향이 있으며, 회전에 의한 플럭스의 증가에 반대합니다.그림의 가까운 쪽에서는 리턴 전류가 회전 암에서 림의 가까운 쪽을 통해 하단 브러시로 흐릅니다.유도된 B 필드는 회로의 이쪽에서 플럭스를 증가시켜 회전으로 인한 플럭스의 감소에 반대합니다.이러한 반작용력에도 불구하고 디스크를 계속 움직이는 데 필요한 에너지는 발생하는 전기 에너지와 정확히 동일합니다(마찰, 줄 가열 및 기타 비효율성으로 인해 낭비되는 에너지).이 동작은 기계적 에너지를 전기에너지로 변환하는 모든 발전기에 공통적입니다.

변압기

와이어 루프의 전류가 변화하면 변화하는 전류에 의해 변화하는 자기장이 생성됩니다.이 자기장에 도달한 두 번째 와이어는 결합 자속 dΩ/d_B t의 변화로서 이 자기장의 변화를 경험합니다.따라서 유도 EMF 또는 변압기 EMF라고 하는 두 번째 루프에 기전력이 설정됩니다. 이 루프의 양끝이 전기 부하를 통해 연결되면 전류가 흐릅니다.

전류 클램프

전류 클램프는 분할 코어가 있는 변압기의 한 종류로, 와이어 또는 코일에 분리하여 클립하여 전류를 측정하거나 반대로 전압을 유도할 수 있습니다.기존 기기와 달리 클램프는 도체와 전기적으로 접촉하거나 클램프를 부착하는 동안 도체를 분리할 필요가 없습니다.

자기 유량계

패러데이의 법칙은 전기 전도성 액체와 슬러리의 흐름을 측정하는 데 사용됩니다.이런 기구들은 자기 유량계라고 불린다.속도 v로 이동하는 전도성 액체로 인해 자기장 B에서 발생하는 유도 전압 δ는 다음과 같이 구한다.

{E}}=-B\ell v,

여기서 θ는 자기 유량계의 전극 간 거리입니다.

와전류

일정한 자기장을 통과하는 전기 도체 또는 변화하는 자기장 내의 정지 도체는 와전류라고 불리는 유도에 의해 유도되는 원형 전류를 가집니다.와전류는 자기장에 수직인 평면에서 닫힌 루프 형태로 흐릅니다.와전류 브레이크 및 유도 가열 시스템에 유용합니다.그러나 변압기, AC 모터 및 발전기의 금속 자기 코어에서 유도되는 와전류는 금속 저항의 열로서 에너지(코어 손실이라고 함)를 소산하기 때문에 바람직하지 않습니다.이러한 장치의 코어는 와전류를 줄이기 위해 여러 가지 방법을 사용합니다.

저주파 교류 전자석 및 변압기의 코어는 고체 금속 대신 비전도성 코팅으로 분리된 적층이라고 불리는 금속 판의 스택으로 만들어지는 경우가 많습니다.이러한 얇은 판은 아래 설명과 같이 바람직하지 않은 기생 와전류를 감소시킵니다.
고주파에서 사용되는 인덕터 및 변압기는 종종 페라이트나 철분말과 같은 비전도성 자성 재료로 만들어진 자성 코어를 수지 바인더와 함께 가지고 있습니다.

전자석 적층

와전류는 고체금속질량이 자기장에서 회전할 때 발생하는데, 그 이유는 금속의 외부가 내측보다 자기력선을 많이 절단하기 때문이다.따라서 유도기전력이 균일하지 않기 때문이다.이는 전위가 가장 큰 점과 가장 작은 점 사이에 전류를 발생시키는 경향이 있다.와전류는 상당한 양의 에너지를 소비하며 종종 유해한 ^[25]온도 상승을 일으킵니다.

이 예에서는 와전류의 세분화를 나타내기 위해 5개의 적층판 또는 플레이트만을 나타내고 있습니다.실제 사용 시 라미네이션 또는 펀칭 횟수는 40~66인치(16~26cm)이며 와전류 손실을 약 1%까지 감소시킵니다.단열재로 플레이트를 분리할 수 있지만 전압이 너무 낮아 플레이트의 자연 녹/산화물 코팅이 라미네이션 ^[25]사이를 흐르는 전류를 방지하기에 충분합니다.

CD 플레이어에 사용되는 DC 모터에서 직경 약 20mm의 로터입니다.기생 유도 손실을 제한하는 데 사용되는 전자석 극 조각의 라미네이션에 주목하십시오.

도체 내 기생 유도

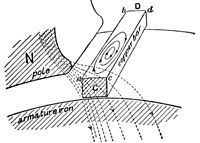
이 그림에서는 회전 전기자의 고체 구리봉 도체가 계자 자석의 극편 N의 선단 바로 아래를 통과하고 있습니다.동봉에 걸쳐 힘의 선이 불균일하게 분포되어 있는 것에 주의해 주세요.자기장은 구리 막대의 왼쪽 가장자리(a,b)에 더 집중되어 있고, 오른쪽 가장자리(c,d)에 더 약합니다.막대의 두 가장자리가 동일한 속도로 이동하므로 막대에 걸친 전계 강도의 차이가 구리 ^[25]막대에 소용돌이 또는 전류 에지를 생성합니다.

전기 모터, 발전기 및 변압기와 같은 고전류 전력 주파수 장치는 여러 개의 작은 도체를 병렬로 사용하여 대형 고체 도체 내에 형성될 수 있는 와류 흐름을 분해합니다.같은 원리가 전력 주파수보다 높은 변압기, 예를 들어 스위치 모드 전원 공급기에 사용되는 변압기 및 무선 수신기의 중간 주파수 결합 변압기에 적용됩니다.

「」를 참조해 주세요.

레퍼런스

메모들

^ EMF는 와이어를 절단하여 개방 회로를 생성하고 전압계를 리드에 연결하여 측정하는 전압입니다.수학적으로 E $(\$ { $E})$ 는 ${\mathcal {E}}$ 와이어 ^[13]^[14]^[15]루프를 한 바퀴 도는 단위 전하에서 사용 가능한 에너지로 정의됩니다.

레퍼런스

^ Poyser, A. W. (1892). Magnetism and Electricity: A Manual for Students in Advanced Classes. London and New York: Longmans, Green, & Co. p. 285.
^ ^a ^b Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.
^ Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 978-0-13-241326-8.
^ "Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2013-12-13. Retrieved 2006-11-30.
^ Errede, Steven (2007). "A Brief History of The Development of Classical Electrodynamics" (PDF).
^ "Electromagnetism". Smithsonian Institution Archives.
^ 마이클 패러데이, L. 피어스 윌리엄스, 페이지 182-3
^ 마이클 패러데이, L. 피어스 윌리엄스, 페이지 191-5
^ ^a ^b 마이클 패러데이, L. 피어스 윌리엄스, 페이지 510
^ Maxwell, James Cluck(1904), 전기와 자성에 관한 논문, Vol.II, 제3판옥스퍼드 대학 출판부, 178-9페이지와 189페이지.
^ "아카이브 전기:마이클 패러데이, 공학 및 기술 연구소.
^ Good, R. H. (1999). Classical Electromagnetism. Saunders College Publishing. p. 107. ISBN 0-03-022353-9.
^ Feynman, R. P.; Leighton, R. B.; Sands, M. L. (2006). The Feynman Lectures on Physics, Volume 2. Pearson/Addison-Wesley. p. 17-2. ISBN 0-8053-9049-9.
^ Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.
^ Tipler, P. A.; Mosca, G. (2003). Physics for Scientists and Engineers (5th ed.). W.H. Freeman. p. 795. ISBN 978-0716708100.
^ Jordan, E.; Balmain, K. G. (1968). Electromagnetic Waves and Radiating Systems (2nd ed.). Prentice-Hall. p. 100. ISBN 9780132499958.
^ Hayt, W. (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. p. 312. ISBN 0-07-027406-1.
^ Schmitt, R. (2002). Electromagnetics Explained. Newnes. p. 75. ISBN 9780750674034.
^ Whelan, P. M.; Hodgeson, M. J. (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.
^ Nave, C. R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 2011-08-29.
^ Maxwell, J. C. (1861). "On physical lines of force". Philosophical Magazine. 90 (139): 11–23. doi:10.1080/14786446108643033.
^ Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 301–303. ISBN 0-13-805326-X. 이 글에서 "페러데이의 법칙"이라고 부르는 EMF와 관련된 법칙은 그리피스에 의해 "범용 플럭스 규칙"이라고 불립니다.그는 이 기사에서 "맥스웰-페러데이 방정식"이라고 부르는 것을 언급하기 위해 "페러데이의 법칙"이라는 용어를 사용합니다.
^ "플럭스 규칙"은 파인만이 EMF와 관련된 자속의 법칙을 언급하기 위해 사용하는 용어입니다.
^ Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper" (PDF). Annalen der Physik. 17 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.

번역자
^ ^a ^b ^c 이미지와 참조 텍스트는 공개 도메인북에서 가져온 것입니다.Hawkins 전기 가이드, 1권, 19장:Theo Copyright 1917 by Theo., 270–273쪽, 전기자의 이론.Audel & Co, 미국 인쇄

추가 정보

Maxwell, James Cluck (1881), 전기와 자성에 관한 논문, Vol. II, 제3장, §530, 페이지 178영국 옥스포드: Clarendon Press.ISBN 0-486-60637-6.

외부 링크

[16] EMF는 와이어를 절단하여 개방 회로를 생성하고 전압계를 리드에 연결하여 측정하는 전압입니다.수학적으로 E $(\$ { $E})$ 는 ${\mathcal {E}}$ 와이어 ^[13]^[14]^[15]루프를 한 바퀴 도는 단위 전하에서 사용 가능한 에너지로 정의됩니다.

[1] Poyser, A. W. (1892). Magnetism and Electricity: A Manual for Students in Advanced Classes. London and New York: Longmans, Green, & Co. p. 285.

[Giancoli-2] Giancoli, Douglas C. (1998). Physics: Principles with Applications (Fifth ed.). pp. 623–624.

[3] Ulaby, Fawwaz (2007). Fundamentals of applied electromagnetics (5th ed.). Pearson:Prentice Hall. p. 255. ISBN 978-0-13-241326-8.

[4] "Joseph Henry". Distinguished Members Gallery, National Academy of Sciences. Archived from the original on 2013-12-13. Retrieved 2006-11-30.

[5] Errede, Steven (2007). "A Brief History of The Development of Classical Electrodynamics" (PDF).

[6] "Electromagnetism". Smithsonian Institution Archives.

[7] 마이클 패러데이, L. 피어스 윌리엄스, 페이지 182-3

[8] 마이클 패러데이, L. 피어스 윌리엄스, 페이지 191-5

[Williams510-9] 마이클 패러데이, L. 피어스 윌리엄스, 페이지 510

[10] Maxwell, James Cluck(1904), 전기와 자성에 관한 논문, Vol.II, 제3판옥스퍼드 대학 출판부, 178-9페이지와 189페이지.

[IEEUK-11] "아카이브 전기:마이클 패러데이, 공학 및 기술 연구소.

[12] Good, R. H. (1999). Classical Electromagnetism. Saunders College Publishing. p. 107. ISBN 0-03-022353-9.

[Feynman-13] Feynman, R. P.; Leighton, R. B.; Sands, M. L. (2006). The Feynman Lectures on Physics, Volume 2. Pearson/Addison-Wesley. p. 17-2. ISBN 0-8053-9049-9.

[Griffiths2-14] Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 301–303. ISBN 0-13-805326-X.

[15] Tipler, P. A.; Mosca, G. (2003). Physics for Scientists and Engineers (5th ed.). W.H. Freeman. p. 795. ISBN 978-0716708100.

[Jordan_&_Balmain_(1968)-17] Jordan, E.; Balmain, K. G. (1968). Electromagnetic Waves and Radiating Systems (2nd ed.). Prentice-Hall. p. 100. ISBN 9780132499958.

[Hayt_(1989)-18] Hayt, W. (1989). Engineering Electromagnetics (5th ed.). McGraw-Hill. p. 312. ISBN 0-07-027406-1.

[19] Schmitt, R. (2002). Electromagnetics Explained. Newnes. p. 75. ISBN 9780750674034.

[20] Whelan, P. M.; Hodgeson, M. J. (1978). Essential Principles of Physics (2nd ed.). John Murray. ISBN 0-7195-3382-1.

[21] Nave, C. R. "Faraday's Law". HyperPhysics. Georgia State University. Retrieved 2011-08-29.

[22] Maxwell, J. C. (1861). "On physical lines of force". Philosophical Magazine. 90 (139): 11–23. doi:10.1080/14786446108643033.

[Griffiths1-23] Griffiths, D. J. (1999). Introduction to Electrodynamics (3rd ed.). Prentice Hall. pp. 301–303. ISBN 0-13-805326-X. 이 글에서 "페러데이의 법칙"이라고 부르는 EMF와 관련된 법칙은 그리피스에 의해 "범용 플럭스 규칙"이라고 불립니다.그는 이 기사에서 "맥스웰-페러데이 방정식"이라고 부르는 것을 언급하기 위해 "페러데이의 법칙"이라는 용어를 사용합니다.

[Feynman2-24] "플럭스 규칙"은 파인만이 EMF와 관련된 자속의 법칙을 언급하기 위해 사용하는 용어입니다.

[25] Einstein, A. (1905). "Zur Elektrodynamik bewegter Körper" (PDF). Annalen der Physik. 17 (10): 891–921. Bibcode:1905AnP...322..891E. doi:10.1002/andp.19053221004.

번역자

[Imagesand-26] 이미지와 참조 텍스트는 공개 도메인북에서 가져온 것입니다.Hawkins 전기 가이드, 1권, 19장:Theo Copyright 1917 by Theo., 270–273쪽, 전기자의 이론.Audel & Co, 미국 인쇄

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[note 1]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[13]

[14]

[15]

Search

전자 유도

네임스페이스

더

목차

역사