반자성

열분해 탄소는 상온 물질 중 가장 큰 반자성 상수 중 하나를 가지고 있다.여기서 열분해탄소시트는 네오디뮴 자석의 강한 자기장으로부터의 반발에 의해 부상한다.

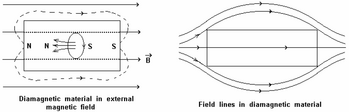
반자성 재료는 자기장에 의해 반발되며, 인가된 자기장이 반대 방향으로 유도 자기장을 생성해 반발력을 일으킨다.반면 상사성 재료와 강자성 재료는 자기장에 의해 흡인된다.반자성은 모든 물질에서 발생하는 양자역학적 효과이다. 반자성이 자성에 대한 유일한 기여일 때, 그 물질은 반자성이라고 불린다.상사성 및 강자성 물질에서는 재료 중의 자성 쌍극자의 흡인력에 의해 약한 반자력을 극복한다.반자성 물질의 자기 투과율은 진공 투과율₀ μ보다 낮다.대부분의 물질에서 반자성은 민감한 실험실 기구로만 감지할 수 있는 약한 효과이지만, 초전도체는 자기장을 내부로부터 완전히 밀어내기 때문에 강한 반자성 역할을 한다.

자기장에서의 반자성 물질 상호작용.

반자성은 안톤 브루그만스가 1778년 비스무트가 ^[1]자기장에 의해 물리치는 것을 관찰했을 때 처음 발견되었다.1845년, 마이클 패러데이는 그것이 물질의 특성이라는 것을 증명했고 모든 물질이 적용된 자기장에 반응한다는 결론을 내렸습니다.윌리엄 휴웰의 제안으로 패러데이는 처음에 이 현상을 반자성(diamagnetic, 즉 diamagnetic,^[2]^[3] 혹은 diamagnetic이라는 접두사)이라고 불렀고, 나중에 반자성으로 바꾸었다.

간단한 경험칙은 입자(원자, 이온 또는 분자)가 상사성인지 ^[4]반자성인지를 결정하기 위해 화학에서 사용됩니다.입자의 모든 전자가 쌍으로 되어 있다면 이 입자로 이루어진 물질은 반자성이고, 짝이 없는 전자를 가지고 있다면 물질은 상사성입니다.

자재

눈에 띄는 반자성^[5] 물질

재료.	【×10_m⁻⁵(SI 유닛)】
초전도체	−10⁵
열분해 탄소	−40.9
비스무트	−16.6
네온	−6.74
수성.	−2.9
실버	−2.6
탄소(다이아몬드)	−2.1
이끌다	−1.8
카본(그래파이트)	−1.6
구리	−1.0
물.	−0.91

반자성은 모든 물질의 특성이며 항상 자기장에 대한 물질의 반응에 약한 기여를 합니다.하지만, 다른 형태의 자기(강자성 또는 상사성)는 너무 강해서, 한 물질에 여러 가지 다른 형태의 자성이 존재할 때, 반자성의 기여는 보통 무시할 수 있습니다.반자성 거동이 가장 강한 영향을 미치는 물질을 반자성 물질 또는 반자성 물질이라고 합니다.반자성 물질은 일반적으로 어떤 사람들이 비자성 물질로 생각하는 물질로 물, 나무, 석유와 일부 플라스틱과 같은 대부분의 유기 화합물, 구리를 포함한 많은 금속, 특히 수은, 금, 비스무트와 같은 많은 핵심 전자를 가진 무거운 금속을 포함합니다.다양한 분자 조각의 자화율 값은 파스칼 상수라고 불립니다.

반자성 재료는 물 또는 수성 재료와 마찬가지로 1보다 작거나 같은 상대적인 투과성을 가지며, 따라서 감수성은 δ_v = μ_v - 1로 정의되므로 0보다 작거나 같다.이것은 반자성 물질이 자기장에 의해 거부된다는 것을 의미합니다.그러나 반자성은 매우 약한 특성이기 때문에 일상생활에서는 그 효과를 볼 수 없다.예를 들어 물과 같은 반자석의 자화율은 θ_v = -9⁻⁶.05×10이다.가장 강한 반자성 물질은 비스무트이며_v, θ = -1.66×10이지만⁻⁴ 열분해 탄소는 한 평면에서 θ_v = -4.00×10의⁻⁴ 감수성을 가질 수 있다.그럼에도 불구하고, 이 값들은 파라자넷과 강자석에 의해 나타나는 자기보다 훨씬 작은 크기이다.θ는_v 인가된 자기장에 대한 내부 자기장의 비율에서 도출되므로 무차원 값이다.

드물게 반자성 기여가 상사성 기여보다 강할 수 있습니다.이는 0 미만의 자기 감수성을 가지지만(따라서 정의상 반자성 물질) X선 자기 원형 이색성으로 주의 깊게 측정했을 때 강한 반자성 ^[6]기여에 의해 극복되는 매우 약한 상사성 기여가 있는 금의 경우이다.

초전도체

통상 전도율(왼쪽)에서 초전도율(오른쪽)로의 이행.전이 시, 초전도체는 자기장을 방출하고 완벽한 반자석으로 작용합니다.

초전도체는 마이스너 ^[7]효과로 인해 (얇은 표면층을 제외한) 모든 자기장을 방출하기 때문에 완벽한 반자성체(θ_v = -1)로 간주될 수 있다.

데모

곡면수면

강력한 자석(예: 슈퍼 마그넷)이 물층(자석의 지름에 비해 얇은 것)으로 덮여 있으면 자석의 장은 물을 상당히 밀어냅니다.이로 인해 수면에 약간의 보조개가 생기는데,^[8]^[9] 이 보조개는 수면에 반사되어 보일 수 있습니다.

공중부양

살아있는 개구리가 Nimegen High Field Magnet Laboratory의 ^[10]약 16테슬라 자기장에서 비터 솔레노이드의 직경 32mm(1.26인치)의 수직 보어 안에서 떠다니고 있습니다.

반자성은 자기장 내에서 안정적인 평형 상태에서 전력 소비 없이 부상할 수 있다.언쇼의 정리는 정적 자기 부상 가능성을 배제하는 것 같다.하지만, 언쇼의 정리는 강자석과 파라자넷과 같은 긍정적인 감수성을 가진 물체에만 적용된다.이것들은 자유 공간에 존재하지 않는 필드 최대값에 끌린다.반자성(부정 모멘트를 유도하는)은 필드 최소값에 끌리며 빈 공간에 필드 최소값이 있을 수 있습니다.

희토류 영구자석 등 자기장 내에서 비정상적으로 강한 반자성 재료인 열분해 흑연 박편을 안정적으로 띄울 수 있다.이것은 실온에서 모든 컴포넌트에서 실행할 수 있기 때문에 시각적으로 효과적이고 비교적 편리한 반자성 시연입니다.

네덜란드의 Radboud University Nijmegen은 물과 다른 물질들이 성공적으로 부유하는 실험을 수행했다.가장 장관을 이루는 것은 살아있는 개구리(그림 참조)가 ^[11]떠다니는 것이었다.

2009년 9월, 캘리포니아 패서디나에 있는 NASA의 제트 추진 연구소는 ^[13]쥐가 개구리보다 생물학적으로 인간과 더 가깝기 때문에 중요한 진전인 초전도 ^[12]자석을 사용하여 성공적으로 쥐를 띄웠다고 발표했다.JPL은 뼈와 근육량에 미치는 미중력의 영향에 관한 실험을 수행하기를 희망한다고 말했다.

단백질 결정의 성장을 연구하는 최근의 실험은 강력한 자석을 사용하여 지구의 ^[14]중력에 대항하는 방식으로 성장을 가능하게 하는 기술로 이어졌다.

비스무트판과 영구 ^[15]자석을 부유시키는 몇 개의 영구 자석으로 간단한 시연용 수제 장치를 구성할 수 있다.

이론.

물질의 전자는 일반적으로 저항이 0인 궤도에 안착하며 전류 루프와 같은 역할을 합니다.따라서 반자성 효과는 일반적으로 일반적이라고 생각할 수 있습니다. 왜냐하면 인가된 자기장은 기본적으로 완벽한 반자성인 초전도체와 유사한 방식으로 이러한 루프에서 변화를 반대하는 전류를 생성하기 때문입니다.그러나 전자는 양성자의 전하에 의해 궤도상에 고정되고 파울리 배타 원리에 의해 더욱 구속되기 때문에, 많은 물질들은 반자성을 나타내지만, 일반적으로 적용된 장에는 거의 반응하지 않는다.

Bohr-Van Leeuwen 정리는 순수하게 고전적인 체계에서는 반자성이나 상사성이 있을 수 없다는 것을 증명한다.그러나, 반자성에 대한 랑게뱅의 고전 이론은 ^[16]양자 이론과 같은 예측을 제공한다.고전 이론은 다음과 같다.

랑게뱅 반자성

Paul Langevin의 반자성 이론(1905)^[17]은 닫힌 껍데기를 가진 원자를 포함하는 물질에 적용된다(유전체 참조).전하와 질량을 가진 전자에 적용되는 강도의 장은 주파수 = / $2$ 의m Larmor 세차운동을 일으킨다.단위 시간당 회전수는 $/2µ$ 이므로 전자가 있는 원자의 전류는 (SI 단위)^[16]입니다.

I=-{\frac {Ze^{2}B}{4\pi m}}.

전류 루프의 자기 모멘트는 전류에 루프 면적을 곱한 값과 같습니다.필드가 축과 정렬되어 있다고 가정합니다.평균 루프 영역은 $\scriptstyle \pi \left\langle \rho ^{2}\right\rangle$ ⟨ $\scriptstyle \pi \left\langle \rho ^{2}\right\rangle$ 2 ${\$ \ $displaystyle \ pi$ \ $left$ \ $langle ^$ {2} $\ right$ \ $rangle$ 로 지정할 수 있습니다.여기서 $\scriptstyle \left\langle \rho ^{2}\right\rangle$ 2 ${\$ \ $displaystyle$ \ $scriptstyle$ \ $left$ \ $langle ^$ { 2 } \ $right$ \ $rangle }$ 는 $\scriptstyle \left\langle\rho^2\right\rangle$ 직각 전자의 평균 제곱 거리입니다.따라서 자기 모멘트는

\mu =-{\frac {Ze^{2}B}{4m}}\langle \rho ^{2}\rangle .

전하 분포가 구면 대칭이면 좌표 분포가 독립적이고 동일한 분포라고 가정할 수 있습니다.다음으로, $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ x 2 $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ y 2 $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ z $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ 3 $\scriptstyle \left\langle x^{2}\right\rangle \;=\;\left\langle y^{2}\right\rangle \;=\;\left\langle z^{2}\right\rangle \;=\;{\frac {1}{3}}\left\langle r^{2}\right\rangle$ r 2 $⟩$ \ $displaystyle$ \ $scriptstyle \$ left \ $scriptle x ^$ {2} \ $right$ \ rangle \ ; = \ ; \ $left$ \ $right$ \ $rangle z =$ { 2 ; \ right } \ rangle z $=$ { 2 ; \ $rangle$ $^{2}\right\rangle }$ 은 $\scriptstyle \left\langle r^2 \right\rangle$ 핵에서 전자의 평균 제곱 거리입니다.따라서 $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ 2 $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ x 2 + $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ y 2 $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ 3 $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ $\scriptstyle \left\langle \rho ^{2}\right\rangle \;=\;\left\langle x^{2}\right\rangle \;+\;\left\langle y^{2}\right\rangle \;=\;{\frac {2}{3}}\left\langle r^{2}\right\rangle$ \ $display style \ left$ \ $rho ^ {$ 2} \ $right$ \ $rangle$ \ ; = \ ; \ $right$ \ $rangle$ x $^$ { $2}$ \ $right$ \ rangle \ ; + + \ $rangle$ \ rangle \ $rangle$ \ $rangle$ \ ^ 2 $}$ nit 부피, SI 단위에서의^[18] 부피 반자성 자화율은

\chi = frac {{0}n\mu } {B} =-{\frac {{0} e^{2}Zn}{6m} \langle r^{2}\rangle .

원자에서 랑게뱅 감수성은 Van Vleck 상사성 감수성과 같은 크기이다.

금속제

Langevin 이론은 또한 국부화되지 않은 전자들도 있기 때문에 금속에 대한 완전한 그림은 아니다.자유 전자 가스의 반자성을 설명하는 이론은 레프 ^[19]란다우의 이름을 딴 란다우 반자성이라고 불리며, 대신 로렌츠 힘에 의해 전자의 궤적이 휘어질 때 형성되는 약한 반작용장을 고려한다.그러나 란다우 반자성은 파울리 상사성(Pauli paramagnetism)과 대조되어야 하며, 이는 비국재화 전자 ^[20]^[21]스핀의 편광과 관련된 효과이다.3D 시스템의 벌크 케이스와 낮은 자기장의 경우, (용적) 반자성 자화율은 SI 단위로 다음과 같은 Landau 양자화를 사용하여 계산할 수 있습니다.

{\displaystyle \chi =-\mu _{0}{\frac {e^{2}}}{12\pi ^{2}m\hbar}}}{\displayrt {2mE_{\rm {F}}}}}},

$E_{\rm {F}}$ 서 E F $(\$ 는 $E_{\rm {F}}$ 페르미 에너지입니다. $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ 는 - ${\textstyle -1/3}$ $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ 2 g ( $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ F ) / $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ { $displaystyle$ $-\mu _{\rm {B}}^{2}g (E_$ ${\$ $rm$ {F $})$ /3 $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ 에 $-\mu _{0}\mu _{\rm {B}}^{2}g(E_{\rm {F}})/3$ 상당하며 $,$ $\mu _{\rm {B}}=e\hbar /2m$ 서 $\mu _{\rm {B}}=e\hbar /2m$ - ${\textstyle -1/3}$ / $\mu _{\rm {B}}=e\hbar /2m$ 폴리아자기율 $\mu _{\rm {B}}=e\hbar /2m$ $/$ m입니다. $ystyle$ g $(E)}$ 는 $g(E)$ 상태의 밀도(볼륨당 에너지당 상태 수)입니다.이 공식은 운반체의 스핀 축퇴(스핀 electrons 전자)를 고려합니다.

도프 반도체의 경우, 란다우와 파울리 감수성 사이의 비율은 진공 상태의 전자 질량과 다른 전하 캐리어의 유효 질량에 의해 변화하여 반자성 기여가 증가할 수 있습니다.여기에 제시된 공식은 대량에만 적용됩니다. 양자 점과 같은 제한된 시스템에서는 양자 ^[22]^[23]구속에 의해 설명이 변경됩니다.또한 강한 자기장의 경우, 비국재화 전자의 감수성은 전계 강도의 함수로서 진동한다.이것은 De Haas-Van Alphen 효과라고도 알려져 있으며, 또한 란다우에 의해 이론적으로 처음 기술되었다.

「」를 참조해 주세요.

반강자성
자기화학
모세 효과
반자성 부등식 – 함수의 도함수와 공변 도함수의 도함수에 관련된 수학적 부등식

레퍼런스

^ Gerald Küstler (2007). "Diamagnetic Levitation – Historical Milestones". Rev. Roum. Sci. Techn. – Électrotechn. Et Énerg. 52, 3: 265–282.
^ Jackson, Roland (21 July 2014). "John Tyndall and the Early History of Diamagnetism". Annals of Science. 72 (4): 435–489. doi:10.1080/00033790.2014.929743. PMC 4524391. PMID 26221835.
^ "diamagnetic, adj. and n". OED Online. Oxford University Press. June 2017.
^ "Magnetic Properties". Chemistry LibreTexts. 2 October 2013. Retrieved 21 January 2020.
^ Nave, Carl L. "Magnetic Properties of Solids". Hyper Physics. Retrieved 9 November 2008.
^ Motohiro Suzuki, Naomi Kawamura, Hayato Miyagawa, Jose S. Garitaonandia, Yoshiyuki Yamamoto, and Hidenobu Hori (24 January 2012). "Measurement of a Pauli and Orbital Paramagnetic State in Bulk Gold Using X-Ray Magnetic Circular Dichroism Spectroscopy". Physical Review Letters. 108 (4): 047201. Bibcode:2012PhRvL.108d7201S. doi:10.1103/PhysRevLett.108.047201. PMID 22400883.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)
^ Poole, Jr., Charles P. (2007). Superconductivity (2nd ed.). Amsterdam: Academic Press. p. 23. ISBN 9780080550480.
^ Beatty, Bill (2005). "Neodymium supermagnets: Some demonstrations—Diamagnetic water". Science Hobbyist. Retrieved 26 September 2011.
^ Quit007 (2011). "Diamagnetism Gallery". DeviantART. Retrieved 26 September 2011.
^ "Diamagnetic Levitation". High Field Laboratory. Radboud University Nijmegen. 2011. Retrieved 26 September 2020.
^ "The Real Levitation". High Field Laboratory. Radboud University Nijmegen. 2011. Retrieved 26 September 2011.
^ Liu, Yuanming; Zhu, Da-Ming; Strayer, Donald M.; Israelsson, Ulf E. (2010). "Magnetic levitation of large water droplets and mice". Advances in Space Research. 45 (1): 208–213. Bibcode:2010AdSpR..45..208L. doi:10.1016/j.asr.2009.08.033.
^ Choi, Charles Q. (9 September 2009). "Mice levitated in lab". Live Science. Retrieved 26 September 2011.
^ Kleiner, Kurt (10 August 2007). "Magnetic gravity trick grows perfect crystals". New Scientist. Retrieved 26 September 2011.
^ "Fun with diamagnetic levitation". ForceField. 2 December 2008. Archived from the original on 12 February 2008. Retrieved 26 September 2011.
^ ^a ^b Kittel, Charles (1986). Introduction to Solid State Physics (6th ed.). John Wiley & Sons. pp. 299–302. ISBN 978-0-471-87474-4.
^ Langevin, Paul (1905). "Sur la théorie du magnétisme". Journal de Physique Théorique et Appliquée (in French). 4 (1): 678–693. doi:10.1051/jphystap:019050040067800. ISSN 0368-3893.
^ Kittel, Charles (2005). "Chapter 14: Diamagnetism and Paramagnetism". Introduction to Solid State Physics (8 ed.). John Wiley & Sons. ISBN 978-0471415268.
^ 란다우, L.D. "Diamagnetismus der metalle." Zeitschrift für Physik A 하드론과 핵 64.9(1930): 629-637.
^ Chang, M. C. "Diamagnetism and paramagnetism" (PDF). NTNU lecture notes. Retrieved 24 February 2011.
^ Drakos, Nikos; Moore, Ross; Young, Peter (2002). "Landau diamagnetism". Electrons in a magnetic field. Retrieved 27 November 2012.
^ Lévy, L.P.; Reich, D.H.; Pfeiffer, L.; West, K. (1993). "Aharonov-Bohm ballistic billiards". Physica B: Condensed Matter. 189 (1–4): 204–209. Bibcode:1993PhyB..189..204L. doi:10.1016/0921-4526(93)90161-x.
^ Richter, Klaus; Ullmo, Denis; Jalabert, Rodolfo A. (1996). "Orbital magnetism in the ballistic regime: geometrical effects". Physics Reports. 276 (1): 1–83. arXiv:cond-mat/9609201. Bibcode:1996PhR...276....1R. doi:10.1016/0370-1573(96)00010-5. S2CID 119330207.

외부 링크

[1] Gerald Küstler (2007). "Diamagnetic Levitation – Historical Milestones". Rev. Roum. Sci. Techn. – Électrotechn. Et Énerg. 52, 3: 265–282.

[2] Jackson, Roland (21 July 2014). "John Tyndall and the Early History of Diamagnetism". Annals of Science. 72 (4): 435–489. doi:10.1080/00033790.2014.929743. PMC 4524391. PMID 26221835.

[3] "diamagnetic, adj. and n". OED Online. Oxford University Press. June 2017.

[4] "Magnetic Properties". Chemistry LibreTexts. 2 October 2013. Retrieved 21 January 2020.

[hyper-5] Nave, Carl L. "Magnetic Properties of Solids". Hyper Physics. Retrieved 9 November 2008.

[6] Motohiro Suzuki, Naomi Kawamura, Hayato Miyagawa, Jose S. Garitaonandia, Yoshiyuki Yamamoto, and Hidenobu Hori (24 January 2012). "Measurement of a Pauli and Orbital Paramagnetic State in Bulk Gold Using X-Ray Magnetic Circular Dichroism Spectroscopy". Physical Review Letters. 108 (4): 047201. Bibcode:2012PhRvL.108d7201S. doi:10.1103/PhysRevLett.108.047201. PMID 22400883.{{cite journal}}: CS1 maint: 여러 이름: 작성자 목록(링크)

[7] Poole, Jr., Charles P. (2007). Superconductivity (2nd ed.). Amsterdam: Academic Press. p. 23. ISBN 9780080550480.

[8] Beatty, Bill (2005). "Neodymium supermagnets: Some demonstrations—Diamagnetic water". Science Hobbyist. Retrieved 26 September 2011.

[9] Quit007 (2011). "Diamagnetism Gallery". DeviantART. Retrieved 26 September 2011.

[10] "Diamagnetic Levitation". High Field Laboratory. Radboud University Nijmegen. 2011. Retrieved 26 September 2020.

[11] "The Real Levitation". High Field Laboratory. Radboud University Nijmegen. 2011. Retrieved 26 September 2011.

[12] Liu, Yuanming; Zhu, Da-Ming; Strayer, Donald M.; Israelsson, Ulf E. (2010). "Magnetic levitation of large water droplets and mice". Advances in Space Research. 45 (1): 208–213. Bibcode:2010AdSpR..45..208L. doi:10.1016/j.asr.2009.08.033.

[13] Choi, Charles Q. (9 September 2009). "Mice levitated in lab". Live Science. Retrieved 26 September 2011.

[14] Kleiner, Kurt (10 August 2007). "Magnetic gravity trick grows perfect crystals". New Scientist. Retrieved 26 September 2011.

[15] "Fun with diamagnetic levitation". ForceField. 2 December 2008. Archived from the original on 12 February 2008. Retrieved 26 September 2011.

[Kittel-16] Kittel, Charles (1986). Introduction to Solid State Physics (6th ed.). John Wiley & Sons. pp. 299–302. ISBN 978-0-471-87474-4.

[17] Langevin, Paul (1905). "Sur la théorie du magnétisme". Journal de Physique Théorique et Appliquée (in French). 4 (1): 678–693. doi:10.1051/jphystap:019050040067800. ISSN 0368-3893.

[18] Kittel, Charles (2005). "Chapter 14: Diamagnetism and Paramagnetism". Introduction to Solid State Physics (8 ed.). John Wiley & Sons. ISBN 978-0471415268.

[19] 란다우, L.D. "Diamagnetismus der metalle." Zeitschrift für Physik A 하드론과 핵 64.9(1930): 629-637.

[ntnu-20] Chang, M. C. "Diamagnetism and paramagnetism" (PDF). NTNU lecture notes. Retrieved 24 February 2011.

[21] Drakos, Nikos; Moore, Ross; Young, Peter (2002). "Landau diamagnetism". Electrons in a magnetic field. Retrieved 27 November 2012.

[22] Lévy, L.P.; Reich, D.H.; Pfeiffer, L.; West, K. (1993). "Aharonov-Bohm ballistic billiards". Physica B: Condensed Matter. 189 (1–4): 204–209. Bibcode:1993PhyB..189..204L. doi:10.1016/0921-4526(93)90161-x.

[23] Richter, Klaus; Ullmo, Denis; Jalabert, Rodolfo A. (1996). "Orbital magnetism in the ballistic regime: geometrical effects". Physics Reports. 276 (1): 1–83. arXiv:cond-mat/9609201. Bibcode:1996PhR...276....1R. doi:10.1016/0370-1573(96)00010-5. S2CID 119330207.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[13]

[12]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

Search

반자성

네임스페이스

더

목차

자재

초전도체

데모

곡면수면

공중부양

이론.

랑게뱅 반자성

금속제

「」를 참조해 주세요.

레퍼런스

외부 링크

Search

반자성

자재

초전도체

데모

곡면수면

공중부양

이론.

랑게뱅 반자성

금속제

「 」를 참조해 주세요.

레퍼런스

외부 링크

「」를 참조해 주세요.