스핀 글라스

스핀 글라스(상단)의 무작위 스핀 구조와 순서가 지정된 페로마그넷(하단)의 개략적 표현

유리(아모르퍼스 SiO₂)

쿼츠 (크리스탈린 SiO₂)

강자석과 비교한 스핀 유리의 자기 장애는 석영(오른쪽)에 비해 유리(왼쪽)의 위치 장애와 유사하다.

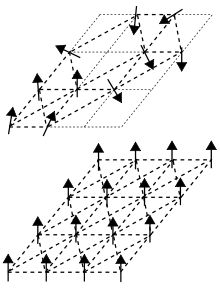
응축물리학에서 스핀 글라스는 '냉동온도' Tf라는 온도에서 스핀을 얼릴 때의 협동행동 외에 무작위성이 특징인 자기 상태를 말한다.^[1] 자석 회전은 대략 3차원 공간에서 남북 자석 극의 방향이다. 강자성 고형분에서는 원자의 자석이 모두 같은 방향으로 정렬된다. 강자석과 대비되는 스핀 글라스는 스핀들이 일반 패턴과 무작위로 정렬되거나 정렬되지 않고 커플링 역시 무작위로 정렬되는 "분해된" 자기 상태를 의미한다.^[1]

유리(glass)라는 용어는 스피닝 글라스의 자성 장애와 기존의 화학적 글라스의 위치 장애(positional disorder)와 예를 들어 창문 글라스의 위치 장애(positional disorder)를 비유한 데서 유래한다. 유리창이나 어떤 비정형 고형물에서 원자 결합 구조는 매우 불규칙하다. 대조적으로 결정체는 원자 결합의 균일한 패턴을 가진다. 강자성 고형물에서 자석 회전은 모두 같은 방향으로 정렬된다; 이것은 결정체의 격자 기반 구조와 유사하다.

스핀 글라스에 들어 있는 개별 원자 결합은 대략 같은 수의 강자성 결합(이웃이 같은 방향을 갖는 경우)과 반자성 결합(이웃이 정확히 반대 방향을 갖는 경우:북극과 남극이 180도 뒤집히는 경우)의 혼합물이다. 정렬된 원자 자석과 정렬되지 않은 원자 자석의 이러한 패턴은 좌절된 상호작용이라고 알려진 것을 만들어낸다. 즉, 규칙적으로 완전히 정렬된 고체에서 볼 수 있는 것과 비교하여 원자 결합의 기하학적 구조를 왜곡하는 것이다. 그들은 또한 원자의 둘 이상의 기하학적 배치가 안정된 상황을 만들 수도 있다.

스핀 글라스와 그 안에서 발생하는 복잡한 내부 구조는 가장 낮은 에너지 구성(직렬하고 강자성) 이외의 안정된 구성에서 "고정"되기 때문에 "측정 가능한"이라고 불린다. 이 구조들의 수학적인 복잡성은 컴퓨터 과학에서 물리학, 화학, 재료 과학 및 인공 신경 네트워크에 응용하여 실험적으로 또는 시뮬레이션에서 연구하기 어렵지만 보람이 있다.

자기행동

그것은 다른 자기계와 스핀글라스를 구별하는 시간 의존성이다.

스핀 글라스 전환 온도 T 이상으로_c 스핀 글라스는 전형적인 자기 행동(파라마그네틱스 등)을 보인다.^{[note 1]}

샘플이 전환 온도로 냉각될 때 자기장을 적용하면 샘플의 자기화는 퀴리법에서 설명한 대로 증가한다. T에_c 도달하면 샘플은 스핀 글라스가 되고 더 냉각되면 자화에는 거의 변화가 없다. 이것을 현장 냉각 자화라고 한다.

외부 자기장이 제거되면 스핀 글라스의 자기화는 재탄성 자화라고 알려진 더 낮은 값으로 급격히 떨어진다.

그런 다음 자기화는 0(또는 원래 값의 일부 작은 부분—이것은 알려지지 않은 상태로 남아 있음)에 가까워질 때 천천히 분해된다. 이 붕괴는 비우량적이며 어떤 단순한 기능도 자기화 대 시간의 곡선에 적절하게 적합할 수 없다.^[2] 이 느린 부패는 유리잔 돌리기에 특이하다. 일 순서에 대한 실험 측정 결과 계측기 소음 수준 이상의 지속적인 변화가 나타났다.^[2]

스핀 안경은 강자성 물질에서 외부 자기장이 제거된 후 자기화가 리마넌트 값으로 무한정 유지된다는 점에서 강자성 물질과 다르다. 파라자성 물질은 외부 자기장이 제거된 후 자기화가 재탄생되지 않고 빠르게 0으로 떨어진다는 점에서 스핀글라스와는 차이가 있다. 붕괴는 빠르고 기하급수적이다.^{[citation needed]}

외부 자기장이 없는 상태에서 T이하로_c 시료를 냉각시키고 스핀 글라스 위상으로 전환한 후 자기장을 적용하면, 제로필드 냉각 자화라고 하는 값으로 초기증가가 빠르게 일어난다. 그리고 나서 필드 냉각 자석화 쪽으로 천천히 상승 드리프트가 발생한다.

놀랍게도 시간의 두 가지 복잡한 함수(영역 냉각 및 재냉 자화)의 합은 상수, 즉 자기장 냉각 값이며, 따라서 둘 다 최소한 아주 작은 외부장의 한계에서는 시간과 함께 동일한 기능 형태를 공유한다.^[3]

에드워즈-앤더슨 모델

$이$ 모델에서는 스핀을 d $d$ 차원 $d$ 격자에 배열하고 Ising 모델과 유사한 가장 가까운 인접 상호 작용만 한다. 이 모델은 임계 온도에 대해 정확히 해결할 수 있으며 유리 위상은 저온에서 존재하는 것으로 관찰된다.^[4] 이 스핀 시스템에 대한 해밀턴인은 다음과 같은 방법으로 주어진다.

H=-\sum _{\langle ij\angle }J_{ij}S_{i}S_{j}

여기서 $S_{i}$ ${\$ 는 $격자점$ i $i$ 에서 스핀 하프 입자에 대한 Pauli 스핀 행렬을 가리킨다 $S_{i}$ $i$ $J_{ij}$ $J_{ij}$ ${\$ $displaystyle J_{ij}$ 의 음수 값은 $i$ {\ $displaystyle i$ $}$ 와 $i$ j $}$ 에서 스핀들 사이의 반자성 교호작용을 나타낸다 $J_{ij}$ $j$ 합계는 격자 위의 모든 가장 가까운 이웃 위치에 걸쳐 있다. 스핀-스핀 상호작용의 자기성을 나타내는 $J_{ij}$ 변수 $J_{ij}$ $J_{ij}$ ${\$ 를 본드 또는 링크 변수라고 한다.

이 시스템의 파티션 기능을 결정하려면 자유 에너지 f [ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ = $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ - $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ Z $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ [ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ $f\left[J_{ij}\right]=-{\frac {1}{\beta }}\ln {\mathcal {Z}}\left[J_{ij}\right]$ [Ji j ] {\ $displaystyle f\left[]$ 의 평균을 구해야 한다. $J_{ij}\오른쪽]=-{\frac {1}{\beta }}}\ln {\mathcal {Z}\왼쪽[]$ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ${ij}\오른쪽]$ 여기서 Z ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ [ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ = ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ ( ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ - ${\mathcal {Z}}\left[J_{ij}\right]=\operatorname {Tr} _{S}\left(e^{-\beta H}\right)$ $){\$ $J_{ij}$ ${ij}\right]=\operatorname {Tr} _{S}\left($ e^{-\ $beta$ H $}\right$ J $J_{ij}$ $J_{ij}$ ${\$ 의 가능한 모든 값에 대해 $J_{ij}$ $J_{ij}$ $J_{ij}$ ${\$ 의 값 분포는 평균 $J_{0}$ $J_{0}$ ${\$ 과 $J_{0}$ 분산 $J^{2}$ ${\$ :

P(J_{ij}}={\sqrt {\frac {N}{2\pi J^{2}}:\exp \{-{\frac {N}{2}{\frac}{N}{2}}}}{\frac}{2}}}{2}}}}}}}}J^{2}}}\왼쪽(J_{ij}-{\frac {J_{0}}}{{N}}\오른쪽)^{2}\오른쪽\}.

복제 방법을 사용하여 자유 에너지를 일정 온도 이하로 해결하면 시스템의 스핀 글라스 위상(또는 유리 위상)이라는 새로운 자기 위상이 존재하는 것으로 확인되며, 이는 스피 간의 2점 상관 함수의 비반사 값과 $m=0$ 함께 사라지는 $m=0$ m = $m=0$ ${\displaystym$ m= $0}$ 이(가) 특징이다.ns 동일한 격자점(lattice point)에서 두 개의 다른 복제본에서:

q=\sum _{i=1}^{{N}S_{i}^{\alpha }S_{i}^{\beta }\neq 0,

여기서 $\alpha ,\beta$ , $\alpha ,\beta$ $\property ,\properties$ 은 $\alpha ,\beta$ (는) 복제본 색인이다. 따라서 유리 스핀 위상 전환에 대한 강자성의 순서 매개변수는 $q$ $q$ 이고 $q$ 유리를 스핀하는 파라마그네틱의 순서 매개변수는 다시 $q$ $q$ 이다 $q$ 따라서 3개의 자기 위상을 설명하는 새로운 순서 매개변수는 $m$ $m$ 과 $m$ $q$ ${\displaysty q}$ 로 구성된다 $q$

복제본 대칭의 가정 하에서 평균 필드 자유 에너지는 다음과 같은 표현으로 주어진다.^[4]

{\begin{aligned}\beta f={}&-{\frac {\beta ^{2}J^{2}}{4}}(1-q)^{2}+{\frac {\beta J_{0}m^{2}}{2}}\\&-\int \exp \left(-{\frac {z^{2}}{2}}\right)\log \left(2\cosh \left(\beta Jz+\beta J_{0}m\right)\right)\,\mathrm {d} z.\end{정렬}}

셔링턴-키크패트릭 모델

스핀 안경은 특이한 실험 특성 외에도 광범위한 이론적, 계산적 조사의 대상이다. 스핀 안경에 대한 초기 이론 연구의 상당 부분은 시스템의 파티션 함수의 복제본을 바탕으로 한 평균장 이론의 형태를 다루었다.

스핀 글라스의 중요하고 정확하게 해결할 수 있는 모델은 1975년 데이비드 셔링턴과 스콧 커크패트릭에 의해 소개되었다. 그것은 긴 거리 좌절 페로, 그리고 반자성 커플링을 가진 이싱 모델이다. 그것은 자기화 및 복잡한 비전기적 평형 상태를 설명하는 스핀 안경의 평균 필드 근사치에 해당한다.

Edwards-Anderson(EA) 모델과 달리, 시스템에서 2-spin 상호작용만 고려되지만, 각 상호작용의 범위는 잠재적으로 무한할 수 있다(격자 크기 순서에 따라). 따라서, 우리는 어떤 두 개의 스핀도 강자성 또는 반자성 결합과 연결될 수 있고 이것들의 분포는 Edwards-Anderson 모델의 경우와 같이 정확히 주어진다. SK용 해밀턴 모델은 EA 모델과 매우 유사하다.

H=-\sum _{i<j}J_{ij}S_{i}S_{j}

여기서 $J_{ij},S_{i},S_{j}$ $J_{ij},S_{i},S_{j}$ , $J_{ij},S_{i},S_{j}$ $J_{ij},S_{i},S_{j}$ , S $J_{ij},S_{i},S_{j}$ ${\$ 는 EA 모델과 같은 의미를 갖는다 $J_{ij},S_{i},S_{j}$ . 셰링턴, 커크패트릭 등의 초기 시도 끝에 이 모델의 평형 해법은 1979년 조르지오 파리시에 의해 복제 방법으로 발견되었다. M. M. Mezard, G. Parisi, M.A. Virasoro 등에 의한 파리 솔루션 해석의 후속 작업은 인간성 파괴, 초경량성 및 비자위성으로 특징지어지는 유리 같은 저온 단계의 복잡한 성격을 재확립시켰다. 추가적인 발전으로 충치법이 생겨나 복제본이 없는 저온 국면을 연구할 수 있게 되었다. 프란체스코 게라와 미셸 탈라그랜드의 작품에서 파리 해법에 대한 엄격한 증거가 제공되었다.^[5]

레플리카 평균장 이론의 형식주의는 신경망 연구에도 적용되어, 훈련 알고리즘(백프로파게이션 등)을 설계하거나 구현할 필요 없이 단순한 신경망 아키텍처의 저장 용량 등의 속성 계산을 가능하게 했다.^[6]

인접 회전 장치 사이의 커플링이 가우스 분포를 따르는 가우스 모델처럼 단거리 좌절 상호작용과 장애를 가진 보다 현실적인 스핀 글라스 모델도 특히 몬테카를로 시뮬레이션을 사용하여 광범위하게 연구되었다. 이 모델들은 날카로운 위상 전환에 따른 스핀 글라스 위상을 보여준다.

스핀 유리 이론은 응축 물질 물리학에서의 관련성 외에도 신경 네트워크 이론, 컴퓨터 과학, 이론 생물학, econophysics 등에 응용하는 등 강력한 학제 간 특성을 획득했다.

무한범위 모델

무한 범위 모델은 Sherrington-Kirkpatrick 모델의 일반화로서, $r\leq N$ $r$ 의 스핀 상호작용뿐만 아니라 r ${\displaystyle r\leq$ N $}$ 및 N $N$ 이 $r$ $r \leq N$ $N$ ( $가$ $r\leq N$ 스핀의 총 수입니다. SK 모델과 비슷한 에드워즈-앤더슨 모델과 달리 인터랙션 범위는 여전히 무한하다. 이 모델의 해밀턴인은 다음과 같이 설명된다.

H=-\sum _{i_{1}<\cdots <i_{r}J_{1}{1}\dots i_{r}}{r}S_{1}{1}}\cdots S_{i_{r}}}}}

여기서 $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ … $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ r $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ , $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ , $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ … $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ r ${\$ }\ $dots i_{r}, S_{i_{1},\dots ,S_{i_{r}}}}}$ 는 EA 모델과 비슷한 의미를 갖는다 $J_{i_{1}\dots i_{r}},S_{i_{1}},\dots ,S_{i_{r}}$ . 이 모델의 $r\to \infty$ → $r\to \infty$ $r\to \fty$ 한계는 $r\to \infty$ 랜덤 에너지 모델이라고 알려져 있다. 이 한계에서, 특정 상태에 존재하는 스핀 글라스의 확률은 오직 그 상태의 에너지에 의존하고 그 상태의 개별적인 스핀 구성에 의존하지 않는다는 것을 알 수 있다. 격자 전체에 걸친 자기 결합의 가우스 분포는 일반적으로 이 모델을 해결하기 위해 가정된다. 다른 어떤 분포도 중심 한계 정리의 결과로서 동일한 결과를 제공할 것으로 예상된다. ${\frac {J_{0}}{N}}$ ${\frac {J_{0}}{N}}$ 함수는 ${\frac {J_{0}}{N}}$ 평균 J 0 ${\frac {J_{0}}{N}}$ {\ $displaystyle {\frac {J_{0}{N}$ 및 분산 ${\frac {J_{0}}{N}}$ J ${\frac {J^{2}}{N}}$ {\ $displaystyle {\frac{$ 을 ${\frac {J^{2}}{N}}$ 를) 사용하여 다음과 같이 제공된다.

P\left(J_{i_{1}\cdots i_{r}\오른쪽)={\\sqrt{\n^{{N-1}{J^{2}\pi r!}}}\exp \left\{-{\frac{N^{r-1}{J^{2}r!}}}\좌(J_{i_{1}\cdots i_{r}-{\frac {J_{0}r!}}{2N^{r-1}\오른쪽)\오른쪽\}}

이 시스템의 순서 매개변수는 SK 모델과 동일한 두 개의 다른 복제본에서 동일한 사이트 $q$ ${\displaystyle q$ 에 있는 스핀들 간의 2점 스핀 상관 관계와 $자기화$ m ${\displaystyle$ m $}$ 에 $m$ 의해 제공된다. 이 무한 범위 모델은 1-Replica Symmetry Breaking뿐만 아니라 $복제본$ 대칭성을 가정하여 $q$ m $m$ 및 $m$ $q$ $q$ 측면에서 자유 에너지를^[4] 위해 명시적으로 해결할 수 있다.^[4]

{\displaystyle{\begin{정렬}\beta f={}&,{\frac{1}{4}}\beta ^{2}J^{2}q^{r}-{\frac{1}{2}}r\beta ^{2}J^{2}q^{r}-{\frac{1}{4}}\beta ^{2}J^{2}+{\frac{1}{2}}\beta J_{0}rm^{r}+{\frac{1}{4{\sqrt{2\pi}}}}r\beta ^{2}J^{2}q^{r-1}+{}\\&, \int\exp \left(-{\frac{1}{2}}{2}z^ \right)\log \left(2\cosh \left(\beta Jz{\sqrt{{\frac{1}{2}}rq^{r-1}}}와{.\frac{1}}{2}}\beta J_{0}rm^{r-1}\오른쪽)\,\\mathrm {d}z\end}}}

비전기적 동작 및 응용 프로그램

열역학 시스템은 시스템의 어떤 (균형) 인스턴스라도 주어지면 결국 가능한 (균형) 상태(동일한 에너지의)를 모두 방문하게 될 때 에고딕적이다. 스핀 글라스 시스템의 한 가지 특징은 동결 온도 $T_{\text{f}}$ f ${\$ 이하에서 인스턴스가 "비에너지" 상태 집합에 갇힌다는 것이다. 즉, 시스템은 여러 상태 사이에서 변동할 수 있지만 동등한 에너지의 다른 상태로 전환할 수 없다. 직관적으로, 시스템이 계층적으로 질서 정연한 에너지 경관의 깊은 미니마에서 벗어날 수 없다고 말할 수 있다; 미니마 사이의 거리는 매우 높은 에너지 장벽과 함께 초경량계에 의해 주어진다.^{[note 2]} 참여 비율은 주어진 인스턴스(instance)에서 접근할 수 있는 상태 수, 즉 지상 상태에 참여하는 상태의 수는 다음과 같다. 스핀글라스의 에고다이컬한 측면은 2021년 노벨물리학상 절반을 조르지오 파리에게 수여하는 데 큰 도움이 됐다.^[7]^[8]^[9]

구리의 묽은 망간과 같은 물리적 시스템의 경우, 일반적으로 동결 온도는 30 켈빈(-240 °C) 정도로 낮기 때문에, 스핀 글라스 자력은 일상생활에서 응용하지 않고 실제로 존재하는 것으로 보인다. 그러나 비에너지 상태와 험난한 에너지 환경은 컴퓨터 과학 최적화 및 유전학 상의 많은 문제뿐만 아니라 홉필드 네트워크를 포함한 특정 신경 네트워크의 행동을 이해하는 데 상당히 유용하다.

자가 유도 스핀 글라스

2020년 라드부드 대학과 웁살라 대학의 물리학 연구자들은 네오디뮴의 원자 구조에서 자기 유도 스핀 글라스로 알려진 행동을 관찰했다고 발표했다. 한 연구자는 "...우리는 터널링 현미경을 스캔하는 전문가다. 개별 원자의 구조를 볼 수 있게 하고, 원자의 북극과 남극을 해결할 수 있다. 이런 고정밀 영상화의 발달로 네오디뮴에서 그 행동을 발견할 수 있었는데, 그 이유는 자기 구조의 믿을 수 없을 정도로 작은 변화를 해결할 수 있었기 때문이다." 네오디뮴은 주기율표 원소에서 이전에는 볼 수 없었던 복잡한 자기 방식으로 작용한다.^[10]^[11]

현장의 역사

1960년대 초반부터 1980년대 후반까지 스핀안경의 역사에 대한 자세한 설명은 Philip W. Anderson의 Physics Today 인기 기사에서 찾아볼 수 있다.^[12]^[13]^[14]^[15]^[16]^[17]^[18]

참고 항목

메모들

^ $T_{c}$ $T_{c}$ ${\$ 는 이른바 "냉동 온도" $T_{f}$ $T_{f}$ ${\$ 와 동일하다 $T_{c}$ .
^ 에너지 경관의 계층적 장애는 한 문장으로 특징지어질 수 있는데, 이 풍경 속에는 아직 더 깊은(랜덤) 계곡 내에 (랜덤) 계곡이 있고... 등이 있다.

참조

^ Jump up to: ^a ^b Mydosh, J A (1993). Spin Glasses: An Experimental Introduction. London, Washington DC: Taylor & Francis. p. 3. ISBN 0748400389. 9780748400386.
^ Jump up to: ^a ^b Joy, P A; Kumar, P S Anil; Date, S K (7 October 1998). "The relationship between field-cooled and zero-field-cooled susceptibilities of some ordered magnetic systems". J. Phys.: Condens. Matter. 10 (48): 11049–11054. Bibcode:1998JPCM...1011049J. doi:10.1088/0953-8984/10/48/024.
^ Nordblad, P; Lundgren, L; Sandlund, L (February 1986). "A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses". Journal of Magnetism and Magnetic Materials. 54–57 (1): 185–186. Bibcode:1986JMMM...54..185N. doi:10.1016/0304-8853(86)90543-3.
^ Jump up to: ^a ^b ^c ^d Nishimori, Hidetoshi (2001). Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press. p. 243. ISBN 9780198509400.
^ Michel Talagrand, Spin Glass의 평균 필드 모델 I: 기본 예(2010)
^ Gardner, E; Deridda, B (7 January 1988). "Optimal storage properties of neural network models" (PDF). J. Phys. A. 21 (1): 271. Bibcode:1988JPhA...21..271G. doi:10.1088/0305-4470/21/1/031.
^ "Trio of scientists win Nobel prize for physics for climate work". the Guardian. October 5, 2021.
^ https://www.nobelprize.org/uploads/2021/10/popular-physicsprize2021.pdf
^ https://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf
^ Umut Kamber; Anders Bergman; Andreas Eich; Diana Iuşan; Manuel Steinbrecher; Nadine Hauptmann; Lars Nordström; Mikhail I. Katsnelson; Daniel Wegner; Olle Eriksson; Alexander A. Khajetoorians (May 29, 2020). "Self-induced spin glass state in elemental and crystalline neodymium". Retrieved 29 May 2020. Cite 매거진 요구 사항 magazine= (도움말)
^ Radboud University Nijmegen (May 28, 2020). "New 'Whirling' State of Matter Discovered: Self-Induced Spin Glass". Retrieved 29 May 2020.
^ Philip W. Anderson (1988). "Spin Glass I: A Scaling Law Rescued" (PDF). Physics Today. 41 (1): 9–11. Bibcode:1988PhT....41a...9A. doi:10.1063/1.2811268.
^ Philip W. Anderson (1988). "Spin Glass II: Is There a Phase Transition?" (PDF). Physics Today. 41 (3): 9. Bibcode:1988PhT....41c...9A. doi:10.1063/1.2811336.
^ Philip W. Anderson (1988). "Spin Glass III: Theory Raises its Head" (PDF). Physics Today. 41 (6): 9–11. Bibcode:1988PhT....41f...9A. doi:10.1063/1.2811440.
^ Philip W. Anderson (1988). "Spin Glass IV: Glimmerings of Trouble" (PDF). Physics Today. 41 (9): 9–11. Bibcode:1988PhT....41i...9A. doi:10.1063/1.881135.
^ Philip W. Anderson (1989). "Spin Glass V: Real Power Brought to Bear" (PDF). Physics Today. 42 (7): 9–11. Bibcode:1989PhT....42g...9A. doi:10.1063/1.2811073.
^ Philip W. Anderson (1989). "Spin Glass VI: Spin Glass As Cornucopia" (PDF). Physics Today. 42 (9): 9–11. Bibcode:1989PhT....42i...9A. doi:10.1063/1.2811137.
^ Philip W. Anderson (1990). "Spin Glass VII: Spin Glass as Paradigm" (PDF). Physics Today. 43 (3): 9–11. Bibcode:1990PhT....43c...9A. doi:10.1063/1.2810479.

문학

Edwards, S.F.; Anderson, P.W. (1975), "Theory of spin glasses", Journal of Physics F: Metal Physics, 5 (5): 965–974, Bibcode:1975JPhF....5..965E, doi:10.1088/0305-4608/5/5/017. ShieldSquare 캡차
Sherrington, David; Kirkpatrick, Scott (1975), "Solvable model of a spin-glass", Physical Review Letters, 35 (26): 1792–1796, Bibcode:1975PhRvL..35.1792S, doi:10.1103/PhysRevLett.35.1792. Papercore 요약 http://papercore.org/Sherrington1975
Nordblad, P.; Lundgren, L.; Sandlund, L. (1986), "A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses", Journal of Magnetism and Magnetic Materials, 54: 185–186, Bibcode:1986JMMM...54..185N, doi:10.1016/0304-8853(86)90543-3.
Binder, K.; Young, A. P. (1986), "Spin glasses: Experimental facts, theoretical concepts, and open questions", Reviews of Modern Physics, 58 (4): 801–976, Bibcode:1986RvMP...58..801B, doi:10.1103/RevModPhys.58.801.
Bryngelson, Joseph D.; Wolynes, Peter G. (1987), "Spin glasses and the statistical mechanics of protein folding", Proceedings of the National Academy of Sciences, 84 (21): 7524–7528, Bibcode:1987PNAS...84.7524B, doi:10.1073/pnas.84.21.7524, PMC 299331, PMID 3478708.
Fischer, K. H.; Hertz, J. A. (1991), Spin Glasses, Cambridge University Press.
Mezard, Marc; Parisi, Giorgio; Virasoro, Miguel Angel (1987), Spin glass theory and beyond, Singapore: World Scientific, ISBN 978-9971-5-0115-0.
Mydosh, J. A. (1995), Spin Glasses, Taylor & Francis.
Parisi, G. (1980), "The order parameter for spin glasses: a function on the interval 0-1" (PDF), J. Phys. A: Math. Gen., 13 (3): 1101–1112, Bibcode:1980JPhA...13.1101P, doi:10.1088/0305-4470/13/3/042 Papercore 요약 http://papercore.org/Parisi1980.
Talagrand, Michel (2000), "Replica symmetry breaking and exponential inequalities for the Sherrington–Kirkpatrick model", Annals of Probability, 28 (3): 1018–1062, doi:10.1214/aop/1019160325, JSTOR 2652978.
Guerra, F.; Toninelli, F. L. (2002), "The thermodynamic limit in mean field spin glass models", Communications in Mathematical Physics, 230 (1): 71–79, arXiv:cond-mat/0204280, Bibcode:2002CMaPh.230...71G, doi:10.1007/s00220-002-0699-y, S2CID 16833848
Aminov, T. G.; Novotortsev, V. N. (2014), "Spin Glasses in Cu_0.5Fe_0.5Cr₂S₄ - Based Solid Solutions", Inorganic Materials, 50 (13): 1343–00, doi:10.1134/s0020168514130020, ISSN 0020-1685, S2CID 96777069

외부 링크

[2] $T_{c}$ $T_{c}$ ${\$ 는 이른바 "냉동 온도" $T_{f}$ $T_{f}$ ${\$ 와 동일하다 $T_{c}$ .

[8] 에너지 경관의 계층적 장애는 한 문장으로 특징지어질 수 있는데, 이 풍경 속에는 아직 더 깊은(랜덤) 계곡 내에 (랜덤) 계곡이 있고... 등이 있다.

[:0-1] Jump up to: ^a ^b Mydosh, J A (1993). Spin Glasses: An Experimental Introduction. London, Washington DC: Taylor & Francis. p. 3. ISBN 0748400389. 9780748400386.

[JPhys-3] Jump up to: ^a ^b Joy, P A; Kumar, P S Anil; Date, S K (7 October 1998). "The relationship between field-cooled and zero-field-cooled susceptibilities of some ordered magnetic systems". J. Phys.: Condens. Matter. 10 (48): 11049–11054. Bibcode:1998JPCM...1011049J. doi:10.1088/0953-8984/10/48/024.

[Nordblad-4] Nordblad, P; Lundgren, L; Sandlund, L (February 1986). "A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses". Journal of Magnetism and Magnetic Materials. 54–57 (1): 185–186. Bibcode:1986JMMM...54..185N. doi:10.1016/0304-8853(86)90543-3.

[nishimori-5] Jump up to: ^a ^b ^c ^d Nishimori, Hidetoshi (2001). Statistical Physics of Spin Glasses and Information Processing: An Introduction. Oxford: Oxford University Press. p. 243. ISBN 9780198509400.

[6] Michel Talagrand, Spin Glass의 평균 필드 모델 I: 기본 예(2010)

[Gardner-7] Gardner, E; Deridda, B (7 January 1988). "Optimal storage properties of neural network models" (PDF). J. Phys. A. 21 (1): 271. Bibcode:1988JPhA...21..271G. doi:10.1088/0305-4470/21/1/031.

[9] "Trio of scientists win Nobel prize for physics for climate work". the Guardian. October 5, 2021.

[10] ttps://www.nobelprize.org/uploads/2021/10/popular-physicsprize2021.pdf

[11] ttps://www.nobelprize.org/uploads/2021/10/sciback_fy_en_21.pdf

[sciencemag-12] Umut Kamber; Anders Bergman; Andreas Eich; Diana Iuşan; Manuel Steinbrecher; Nadine Hauptmann; Lars Nordström; Mikhail I. Katsnelson; Daniel Wegner; Olle Eriksson; Alexander A. Khajetoorians (May 29, 2020). "Self-induced spin glass state in elemental and crystalline neodymium". Retrieved 29 May 2020. Cite 매거진 요구 사항 magazine= (도움말)

[scitechdaily-13] Radboud University Nijmegen (May 28, 2020). "New 'Whirling' State of Matter Discovered: Self-Induced Spin Glass". Retrieved 29 May 2020.

[14] Philip W. Anderson (1988). "Spin Glass I: A Scaling Law Rescued" (PDF). Physics Today. 41 (1): 9–11. Bibcode:1988PhT....41a...9A. doi:10.1063/1.2811268.

[15] Philip W. Anderson (1988). "Spin Glass II: Is There a Phase Transition?" (PDF). Physics Today. 41 (3): 9. Bibcode:1988PhT....41c...9A. doi:10.1063/1.2811336.

[16] Philip W. Anderson (1988). "Spin Glass III: Theory Raises its Head" (PDF). Physics Today. 41 (6): 9–11. Bibcode:1988PhT....41f...9A. doi:10.1063/1.2811440.

[17] Philip W. Anderson (1988). "Spin Glass IV: Glimmerings of Trouble" (PDF). Physics Today. 41 (9): 9–11. Bibcode:1988PhT....41i...9A. doi:10.1063/1.881135.

[18] Philip W. Anderson (1989). "Spin Glass V: Real Power Brought to Bear" (PDF). Physics Today. 42 (7): 9–11. Bibcode:1989PhT....42g...9A. doi:10.1063/1.2811073.

[19] Philip W. Anderson (1989). "Spin Glass VI: Spin Glass As Cornucopia" (PDF). Physics Today. 42 (9): 9–11. Bibcode:1989PhT....42i...9A. doi:10.1063/1.2811137.

[20] Philip W. Anderson (1990). "Spin Glass VII: Spin Glass as Paradigm" (PDF). Physics Today. 43 (3): 9–11. Bibcode:1990PhT....43c...9A. doi:10.1063/1.2810479.

[1]

[note 1]

[2]

[3]

[4]

[5]

[6]

[note 2]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

show 권한통제
일반	통합 권한 파일(독일)
국립도서관	프랑스. (데이터) 미국 일본.
기타	주제용어의 면면적용 마이크로소프트 어학

Search