줄리아 세트

(4차원) Julia의 4차원 함수에 대한 3차원 슬라이스

복소역학에서 수학의 한 분야인 줄리아 집합과 파투 집합은 함수에서 정의된 두 개의 상보 집합이다.비공식적으로 함수의 Fatou 집합은 함수의 반복 하에서는 인근의 모든 값이 유사하게 동작하는 속성을 가진 값으로 구성되며, Julia 집합은 임의로 작은 섭동이 반복된 함수 값의 시퀀스에 급격한 변화를 일으킬 수 있는 값으로 구성됩니다.따라서 Fatou 집합에서 함수의 동작은 "정규"인 반면, Julia 집합에서는 "혼돈"인 것입니다.

함수 f의 Julia 세트는 일반적으로 J $\operatorname {J} (f),$ ( $\operatorname {J} (f),$ ) $\operatorname {J} (f),$ , {\ $displaystyle$ \ $operatorname {J}$ ( $f$ Fatou 세트는 F $\operatorname {F} (f).$ ( $\operatorname {F} (f).$ ) . $\operatorname {F$ ( $f)$ 로 $\operatorname {F} (f).$ 됩니다.이 세트들은 $\operatorname {F} (f).$ ^[a] 20세기 초에 복소역학 연구를 시작한 프랑스의 수학자 가스통^[1] 줄리아와 피에르^[2] 파투의 이름을 따서 지어졌다 $.$

형식적 정의

f $f(z)$ $)$ { $displaystyle$ f $(z)}$ 를 $f(z)$ 리만 구에서 그 자체로의 부정수 정칙함수라고 $f(z)$ .이러한 $f(z)$ f $)$ { $displaystyle$ f $(z)}$ 는 $f(z)$ $p(z)$ 정확히 비표준 복소 유리 함수, 즉 $f(z)=p(z)/q(z)$ $= p$ / $f(z)=p(z)/q(z)$ q( $)$ { $displaystyle$ f $($ $z)=$ p $(z)/q(z)}$ 이며 $f(z)=p(z)/q(z)$ , $p(z)$ 서 p $)$ { $displaystyle$ p( $z)}$ $q(z)$ q( $z)$ 는 $q(z)$ 복소 다항식이다.p와 q는 공통의 루트가 없고, 적어도 1개의 루트가 1보다 크다고 가정합니다.다음으로 f $f(z)$ ( $f(z)$ )({ $displaystyle f($ z)})에 $f(z)$ 의해 불변으로 $F_{1},...,F_{r}$ F r $F_{1},...,F_{r}$ {{ $1},$ ..., $F_{r}$ 의 $F_{1},...,F_{r}$ 열린 $F_{1},...,F_{r}$ $F_{1},...,F_{r}$ $F_{1},...,F_{r}$ ..., ..., F_{r}은 다음과 같이 한정되어 있습니다.

$F_{i}$ 의 $F_{i}$ 조합은 평면 내에 밀집되어 $있습니다.$
$f(z)$ f $f(z)$ ( $f(z)$ ) $f(z)$ { $displaystyle$ f $(z)}$ 는 $f(z)$ 각 $F_{i}$ $F_{i}$ { $displaystyle$ F_ ${i$ 에서 규칙적이고 동일하게 동작합니다.

마지막 문장은 $(\$ 의 $F_{i}$ 점에 의해 생성된 반복 시퀀스의 끝부분이 정확히 동일한 집합, 즉 유한 사이클이거나 동심원에 놓여 있는 원형 또는 고리 모양의 집합의 유한 사이클임을 의미한다.첫 번째 경우에는 사이클이 끌어당기고 두 번째 경우에는 사이클이 중립입니다.

이들 $F_{i}$ $(\$ $displaystyle$ $F_{i})$ 는 $F_{i}$ f $z$ 의 Fatou 도메인이며, 이들의 결합은 f $)$ 의 f $displaystyle \operatorname {F})$ 의 $\operatorname {F} (f)$ f(\ $displaystyle$ f $(z$ ))의 Fatou $\operatorname {F} (f)$ F $\operatorname {F} (f)$ displaystyle f(f)입니다. 각 f( $f(z)$ $f(z)$ 는 최소 $f(z)$ 의 임계점을 포함합니다. $p(z)$ $f'(z)=0$ ( $f'(z)=0$ ) $f'(z)=0$ { $displaystyle$ f' ( z ) = $0$ , $f(z)=\infty$ f $f(z)=\infty$ ( z ) $=$ f ( $z$ ) = \ $infty$ } (분자 $p(z)$ p ( $p(z)$ $)$ 의 $q(z)$ 가 분모 $q(z)$ ( $q(z)$ z $q(z)$ 의 도수보다 적어도2 이상 큰 경우, a ( $xisplaystyle p$ (z ) = \ infty } 입니다 $f(z)=\infty$ $.$ 일부 $c$ 에 대해 $tyle f(z)=1/g($ z $f(z)=1/g(z)+c$ )+c}이고 이 조건을 만족하는 $g(z)$ 함수 $g(z)$ z $)\display$ g $(z)}$ 이다 $g(z)$ .

$\operatorname {F} (f)$ $\operatorname {F} (f)$ ( $){$ $displaystyle \operatorname { F$ } ( f )의 $\operatorname {F} (f)$ 보수는 f $f(z)$ ( $f(z)$ )의 Julia $\operatorname {J} (f)$ J $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ ){ $displaystyle$ $\operatorname$ { $J}$ ( $f)$ 입니다 $\operatorname {J} (f)$ .모든 임계점이 주기적인 것이 아니라 주기적인 J의 경우, $\operatorname {J} (f)$ 인 J. $나 {J}(f)}$ 이 $\operatorname {J} (f)$ (가) 전부입니다.그렇지 않은 경우 J $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ f ) { $displaystyle$ \ $operatorname {J} ($ f)}은 $\operatorname {J} (f)$ 아무 곳에서도 밀도가 높은 집합(내부 포인트가 없음) 및 셀 수 없는 집합(실수와 같은 카디널리티)입니다.처럼 F⁡(f){\displaystyle \operatorname{F}(f)}, J⁡(f)((f)}고정 f(z){\displaystyle f(z)}에 의해, 그리고 이것이 반복을 격퇴하고 있다, 모든 w에 대한 neighbourho에 그 f(w)을 f(z)−, z− w{\displaystyle f(z)-f(w)>z-w}의미 남아 있지 않다.고정됩니다의z ( $\operatorname {J} (f)$ $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ ) \ $displaystyle \operatorname {J}$ ( $f)$ $\operatorname {J} (f)$ ）。즉 $f(z)$ 줄리아 세트에서 f $)$ { $displaystyle f($ z $f(z)$ )}가 무질서하게 $f(z)$ 합니다.Julia 집합에는 반복 순서가 유한한 점이 있지만, 그러한 점의 수는 셀 수 있는 수 밖에 없습니다(그리고 그것들은 Julia 집합의 극히 작은 부분을 구성합니다.이 집합 외부의 점에 의해 생성된 시퀀스는 결정론적 혼돈이라고 불리는 현상으로 무질서하게 동작합니다.

Fatou 집합과 Julia 집합은 합리적인 지도라고 알려진 합리적인 함수를 반복하는 것에 대한 광범위한 연구가 있었다.예를 들어, 합리적인 지도의 파투 집합은 0,^[3] 1, 2 또는 무한히 많은 성분을 가지고 있는 것으로 알려져 있습니다.합리적 지도의 파투 집합의 각 구성요소는 4개의 다른 클래스 ^[4]중 하나로 분류될 수 있습니다.

Julia 집합에 대한 동등한 설명

$\operatorname {J} (f)$ $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ ) { $displaystyle \operatorname {J}$ ( $f)}$ 는 $\operatorname {J} (f)$ f에서 완전히 불변하는 최소 3개의 점을 포함하는 최소 닫힌 집합입니다.
$\operatorname {J} (f)$ J $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ ) { $displaystyle \operatorname {J}$ ( $f)}$ 는 $\operatorname {J} (f)$ 일련의 반복 주기점 폐쇄입니다.
최대 $\;z\in X\;,$ 의 점 z $\;z\in X\;,$ X $,$ {\ $displaystyle \;z\in$ X $\;}$ 를 $\;z\in X\;,$ 제외한 모든 점에서 줄리아 세트는 완전한 후방 궤도 $\bigcup _{n}f^{-n}(z).$ ) $\bigcup _{n}f^{-n}(z).$ - $\bigcup _{n}f^{-n}(z).$ ( $\bigcup _{n}f^{-n}(z).$ ) $\bigcup _{n}f^{-n}(z).$ . { $displaystyle \big cup$ _ ${n}f^{-n}(z)$ 의 한계점 세트입니다(아래 참조). $\bigcup _{n}f^{-n}(z).$
f가 전체 함수인 $\operatorname {J} (f)$ J $\operatorname {J} (f)$ ( $\operatorname {J} (f)$ ) { $displaystyle \operatorname {J}(f)}$ 은 $\operatorname {J} (f)$ 반복 시 무한대로 수렴하는 점 집합의 경계입니다.
f가 다항식인 경우 $\operatorname {J} (f)$ $\operatorname {J} (f)$ δ ( $\operatorname {J} (f)$ ) { $displaystyle \operatorname {J}(f)}$ 은 $\operatorname {J} (f)$ 채워진 줄리아 집합의 경계이다. 즉, f의 반복 아래 궤도가 경계를 유지하는 점들이다.

Julia 집합과 Fatou 집합의 속성

Julia 집합과 Fatou 집합 f는 모두 완전 불변함수 f:^[5]

f^{-1}(\operatorname {J}(f))=f(\operatorname {J}(f))=\operatorname {J}(f),

f^{-1}(\operatorname {F}(f))=f(\operatorname {F}(f))=\operatorname {F}(f).

예

f $f(z)=z^{2}$ $=$ $f(z)=z^{2}$ 2 $({$ $displaystyle$ f $(z$ )= $z^{2})$ 의 $f(z)=z^{2}$ $f(z)=z^{2}$ , 줄리아 집합은 단위 원이며, 이에 대해 두 배의 각도로 반복이 주어진다( $2\pi$ 인수가 $2µ의$ 분수가 아닌 점에서 혼돈한 연산 $).$ 파투 도메인은 원의 내부와 외부 두 가지이며, 각각 0과 ,로 반복됩니다.

$g(z)=z^{2}-2$ $=$ $g(z)=z^{2}-2$ - $g(z)=z^{2}-2$ ({ $displaystyle$ g $(z$ )= $z^{2}-2)$ 의 경우 줄리아 $g(z)=z^{2}-2$ 집합은 -2와 2 사이의 선분입니다.Fatou 도메인이 하나 있습니다.선분 상에 없는 점들은 )을 향해 반복됩니다.(도메인의 이동과 축척을 제외하고 이 반복은 단위 $간격$ 의 $→$ ( $x$ - $x\to 4(x-{\tfrac {\,1\,}{2}})^{2}$ ) 2 $x\to 4(x-{\tfrac {\,1\,}{2}})^{2}$ ( $x$ - {\ $tfrac {$ , 1 , {2 $}})^2}$ 에 $x\to 4(x-{\tfrac {\,1\,}{2}})^{2}$ $x\to 4(x-{\tfrac {\,1\,}{2}})^{2}$ 합니다.이것은, 카오스 시스템의 예로서 일반적으로 사용되고 있습니다).

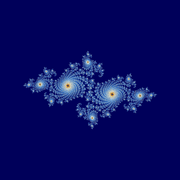
함수 f와 g는 z $z^{2}+c$ + $z^{2}+c$ {\ $displaystyle$ z $^{2}+c$ $z^{2}+c$ 입니다.여기서 c는 복소수입니다.이러한 반복을 위해 줄리아 집합은 일반적으로 단순한 곡선이 아니라 프랙탈이며, c의 일부 값에는 놀라운 형태를 취할 수 있다.아래 그림을 참조하십시오.

Julia는 f : z → z-1에³ 대해 Newton의 방법과 관련된 유리 함수에 대해 설정(흰색).세 가지 매력자(f의 세 뿌리)에 따라 빨강, 초록, 파랑 톤으로 설정된 파투의 색채.

일부 함수 f(z)의 경우 Julia 집합은 단순한 곡선이 아니라 프랙탈이라고 미리 말할 수 있다.이는 합리적인 함수의 반복에 대해 다음과 같은 결과가 나왔기 때문입니다.

정리.각 Fatou 도메인은 동일한 경계를 가지며, 결과적으로 Julia ^{[citation needed]}집합입니다.

즉, Julia 집합의 각 점이 각 Fatou 도메인에 대한 누적 지점임을 의미합니다.따라서 Fatou 도메인이 세 개 이상인 경우 Julia 집합의 각 점은 세 개 이상의 서로 다른 열린 집합의 점이 무한히 가까워야 하며, 이는 Julia 집합이 단순한 곡선이 될 수 없음을 의미합니다.예를 들어, 이 현상은 f(z)가 방정식 P $\;P(z):=z^{n}-1=0~:~n>2\;$ : $\;P(z):=z^{n}-1=0~:~n>2\;$ $\;P(z):=z^{n}-1=0~:~n>2\;$ n - $=$ $\;P(z):=z^{n}-1=0~:~n>2\;$ : $\;P(z):=z^{n}-1=0~:~n>2\;$ > 2 {\ $displaystyle \;P(z):=z^{n$ }-1 $=0~:~n>$ 2 $\;P(z):=z^{n}-1=0~:~n>2\;$ 를 풀기 위한 뉴턴 반복일 때 발생합니다.

f(z)=z-{\frac {P(z)}{P'(z)}={n}\;}{nz^{n-1}}~

오른쪽 이미지는 대/소문자 n = 3을 나타냅니다.

이차 다항식

매우 인기 있는 복잡한 동적 시스템은 합리적인 지도의 특별한 경우인 복잡한 2차 다항식의 패밀리에 의해 주어진다.이러한 2차 다항식은 다음과 같이 표현될 수 있다.

f_{c}(z)=z^{2}+c~,

여기서 c는 복잡한 파라미터입니다.;0{\displaystyle R>0}가 충분히 R2− R≥ c.{\displaystyle R^{2}-R\geq c. 이 체계는 잠수정을}(예를 들어, c는 맨들 브로트 집합에서, 그리고 ≤ 2,{\displaystyle c(2}그래서 우리는 단순히 R=2.{\displaystyle R=2~을 방치할 것 c 있다.})그리고 그 가득 찬 줄리아 세트 큰 일부 R을 정하다.(의주어지는 복잡한 평면

\displaystyle K(f_{c})=\left\{z\in \mathbb {C} :\forall n\in \mathbb {N}, f_{c}^{n}(z) \leq R\right\}~,}

$f_{c}^{n}(z)$ 서 f c $f_{c}^{n}(z)$ ( $f_{c}^{n}(z)$ z $f_{c}^{n}(z)$ ) { $displaystyle f_{c}^{n}(z)$ 은 $f_{c}^{n}(z)$ f $f_{c}(z).$ ) $f_{c}(z).$ . {display $f_{c}(z)$ 의 n번째 반복입니다.} 이 $f_{c}(z).$ 함수의 $J(f_{c})$ 집합 $J(f_{c})$ ( f $c$ ) { $displaystyle$ J ( $f$ _ $J(f_{c})$ { $c$ ) } 이 $K(f_{c})$ ( $f$ c ) \ $displaystyle$ K ( $f$ _ { c $K(f_{c})$ ) $K(f_{c})$ } 의 $K(f_{c})$ 입니다 $.$

Julia는 z $z^{2}+0.7885\,e^{ia},$ + $z^{2}+0.7885\,e^{ia},$ . $z^{2}+0.7885\,e^{ia},$ $z^{2}+0.7885\,e^{ia},$ $,$ {\ $displaystyle$ z $^{2}+0.7885,e^{ia}}$ 로 $z^{2}+0.7885\,e^{ia},$ 설정합니다. 여기서 a 범위는 0 ~ $2\pi$ $†$ {\ $displaystyle$ 2 $\pi}$ 입니다.
줄리아의 비디오는 왼쪽으로 설정되어 있다.
f, $c$ = $1$ - ,에_c 대해 설정된 채워진 줄리아. 여기서 θ는 황금 비율입니다.
f, $c$ = ( $126$ $- 2)$ + ( $126 - 1$ ) $i$ = $-0.4$ + $0.6i$ 로 설정된_c Julia
Julia는 $f$ 로 설정, $c =$ 0. $285$ + 0i_c
Julia는 $f$ 로 설정, $c =$ 0 $.285$ + 0.01i_c
Julia는 $f$ 로 설정_c, c $= 0.45$ + $0$ .1428i
Julia가 f, $c$ = $-0.70176 - 0.3842i$ 로 설정됨_c
Julia가 f, $c$ = $-0.835 - 0.2321i$ 로 설정됨_c
Julia는 f로_c $설정$ , c $= -0$ .8 + 0 $.ggi$
Julia는 $f$ , vc = $-0.7269 + 0.199i$ 로 설정_c
Julia는 f, $c$ = $-0.8i$ 로 설정_c
100 × 100 그리드에 배치되어 각 이미지의 중심이 세트의 값과 복잡한 평면의 동일한 위치에 대응하도록 Julia 세트의 컬렉션.이렇게 배치하면 전체 이미지가 만델브로 세트를 묘사한 사진 모자이크와 비슷합니다.

2차 다항식의 매개변수 평면, 즉 가능한 c 값의 평면은 유명한 만델브로트 집합을 발생시킵니다.실제로 Mandelbrot 집합은 J $J(f_{c})$ c $)\displaystyle$ J $(f_{c}}$ 가 $J(f_{c})$ 연결되도록 $J(f_{c})$ c 집합으로 정의됩니다.Mandelbrot 집합 외부의 파라미터의 경우 Julia 집합은 칸토어 공간입니다. 이 경우 Fatou 먼지라고도 합니다.

대부분의 경우, Julia의 c 세트는 c의 충분히 작은 동네에 있는 Mandelbrot 세트와 비슷합니다.이것은 특히 임계점이 사전 주기적인 매개변수 c와 같은 이른바 미시우레비츠 매개변수에 적용된다.예:

c = i에서, 앞발의 짧은 앞발가락인 Julia 세트는 가지치기 번개처럼 보입니다.
긴 뾰족한 꼬리의 끝인 c = -2에서 Julia 세트는 직선 세그먼트입니다.

즉, Julia $J(f_{c})$ J ( $J(f_{c})$ c $J(f_{c})$ ) $J(f_{c})$ { $displaystyle$ J ( $f$ _ { c ) $J(f_{c})$ }는 $J(f_{c})$ 미시우레비츠 포인트 주변에서 ^[6]국소적으로 유사합니다.

일반화

Julia와 Fatou 세트의 정의는 이미지가 영역을 포함하는 특정 지도의 경우로 쉽게 넘어갑니다. 가장 주목할 만한 것은 초월적 자형 함수 및 Adam Epstein의 유한 유형 지도입니다.

줄리아 집합은 또한 여러 복잡한 변수의 역학 연구에서 일반적으로 정의됩니다.

유사 코드

다음 의사 코드의 실장은 각 프랙탈의 함수를 하드 코드화합니다.보다 동적이고 재사용 가능한 코드를 위해 복잡한 숫자 연산을 구현하는 것을 고려해 보십시오.

일반 줄리아 세트에 대한 의사 코드

f(z)=z^{2}+c

R = 탈출하다 반지름  # R**2 - R > = sqrt (cx**2 + cy**2)를 선택하도록 R > 0 을 선택합니다.  위해서 각각 화소 (x, y) 에 그 화면., 하다:    {     zx = 스케일이 있는 x 조정하다 의 화소 #(-R과 R 사이의 스케일)        # zx는 z의 실제 부분을 나타냅니다.     zy = 스케일이 있는 y 조정하다 의 화소 #(-R과 R 사이의 스케일)        # zy는 z의 가상 부분을 나타냅니다.      반복 = 0     max_displaces(최대_displaces) = 1000        하는 동안에 (zx * zx + zy * zy < > R**2  그리고.  반복 < > max_displaces(최대_displaces))      {         xtemp = zx * zx - zy * zy         zy = 2 * zx * zy  + 사이          zx = xtemp + cx              반복 = 반복 + 1      }        한다면 (반복 == max_displaces(최대_displaces))         돌아가다 블랙입니다.;     또 다른         돌아가다 반복; }

다중 줄리아 세트용 의사 코드

f(z)=z^{n}+c

R = 탈출하다 반지름 # R**n - R > = sqrt (cx**2 + cy**2)가 되도록 R > 0 을 선택합니다.  위해서 각각 화소 (x, y) 에 그 화면., 하다: {     zx = 스케일이 있는 x 조정하다 의 화소 #(-R과 R 사이의 스케일)     zy = 스케일이 있는 y 조정하다 의 화소 #(-R과 R 사이의 스케일)        반복 = 0     max_displaces(최대_displaces) = 1000        하는 동안에 (zx * zx + zy * zy < > R**2  그리고.  반복 < > max_displaces(최대_displaces))      {         xtmp = (zx * zx + zy * zy) ^ (n / 2) * 왜냐하면(n * atan2(zy, zx)) + cx;      zy = (zx * zx + zy * zy) ^ (n / 2) * 죄(n * atan2(zy, zx)) + 사이;      zx = xtmp;              반복 = 반복 + 1     }      한다면 (반복 == max_displaces(최대_displaces))         돌아가다 블랙입니다.;     또 다른         돌아가다 반복; }

잠재적 함수와 실제 반복 횟수

f $f(z)=z^{2}$ $f(z)=z^{2}$ $f(z)=z^{2}$ 2 $({$ f $(z$ )= $z^{2})$ 에 $f(z)=z^{2}$ 대해 $f(z)=z^{2}$ 된 Julia는 단위 원이며, 외부 Fatou 도메인에서 전위함수 θ(z)는 θ(z) = log z로 정의된다.이 함수의 등전위선은 동심원입니다. $|f(z)|=|z|^{2}$ $|f(z)|=|z|^{2}$ $|f(z)|=|z|^{2}$ 2 $({$ f $(z)$ = $z$ ^{ $2})$ 로 $|f(z)|=|z|^{2}$ 지정하면 다음과 같습니다.

{\displaystyle \varphi (z)=\lim _{k\to \infty }{\frac {\log z_{k}}{2^{k}}},

$z_{k}$ 서 z k $(\$ 는 $z_{k}$ z에 의해 생성된 반복 시퀀스입니다.보다 일반적인 $f(z)=z^{2}+c$ f ( $f(z)=z^{2}+c$ ) $|\psi (f(z))|=|\psi (z)|^{2}$ $f(z)=z^{2}+c$ 2 + $f(z)=z^{2}+c$ (\ $displaystyle$ f $(z$ )= $z^{2}+c$ 의 경우, 줄리아 집합이 연결되어 있는 경우(즉, c가 만델브로 집합에 속해 있는 경우), 외부 파투 도메인과 외부 단위 원의 외부 사이에 생체 동형 지도 $|\psi (f(z))|=|\psi (z)|^{2}$ 가 존재하는 것으로 증명되었다 $|\psi (f(z))|=|\psi (z)|^{2}$ $|\psi (f(z))|=|\psi (z)|^{2}$ ) $|\psi (f(z))|=|\psi (z)|^{2}$ (\ $displaystyle \psi (f(z))$ = \ $psi (z)$ ^{ $2$ ^[7] 즉, 이 대응관계로 정의되는 외부 파투 영역에서의 전위함수는 다음과 같다.

\varphi (z)=\lim _{k\to\infty}{\frac {\log z_{k}}{2^{k}}}.

이 공식은 Julia 집합이 연결되어 있지 않은 경우에도 의미가 있습니다.따라서 모든 c에 대해 이 공식에 의해 by를 포함하는 Fatou 도메인에서 잠재적 함수를 정의할 수 있습니다.θ가 임계점 및 고정점인 일반 유리함수 f(z)에 대해, 즉 분자의 도수 m이 분모의 도수 n보다 적어도 2 큰 경우, θ를 포함하는 파투 도메인상의 퍼텐셜 함수를 다음과 같이 정의한다.

{\displaystyle \varphi (z)=\lim _{k\to \infty}{\frac {\log z_{k}}{d^{k}}},

여기서 d = m - n은 유리함수의 ^[8]정도이다.

N이 매우 큰 수(예를¹⁰⁰ 들어 10)이고 k가 z $|z_{k}|>N$ > $|z_{k}|>N$ {\ $displaystyle$ z_ ${k}$ > $N$ 과 같은 첫 번째 반복 수인 경우 다음과 같이 됩니다.

{\frac z_{k} {d^{k}} = frac {\log(N)} {d^{\nu(z)}}

$)$ { $style \nu (z$ 의 경우, 이는 실제 반복 번호로 간주되어야 하며, 다음과 같은 값이 있습니다.

\displaystyle \nu(z)=k-{\frac {log(\log z_{k} /\log(N)}},

여기서 마지막 번호는 [0, 1)]의 간격입니다.

순서 r의 유한 유인 사이클에 대한 반복의 경우, z $z^{*}$ {\ {\ $displaystyle$ z $^{*}}$ 가 $z^{*}$ 사이클의 $f(f(...f(z^{*})))=z^{*}$ 이라면 $f(f(...f(z^{*})))=z^{*}$ ( $f(f(...f(z^{*})))=z^{*}$ . $f(f(...f(z^{*})))=z^{*}$ f ( $f(f(...f(z^{*})))=z^{*}$ $f(f(...f(z^{*})))=z^{*}$ $f(f(...f(z^{*})))=z^{*}$ $=$ z $f(f(...f(z^{*})))=z^{*}$ ${\displaystyle$ f ( $f$ ( ... $f$ ( z ^{*})} $f(f(...f(z^{*})))=z^{*}$ (r-fold composition)) 및 숫자이다.

\alpha = specfrac {1} {\left (f(\cdots f(z))}/dz)_{z=z^{*}\right }}\qquad (>1)

사이클의 매력입니다.w가 z ${\({$ z $^{*}})$ 에 $z^{*}$ 매우 가까운 점이고 w times가 반복된 경우 다음과 같이 표시됩니다.

{\displaystyle \alpha =\lim _{k\to\infty}{\frac {w-z^{*}}{w'-z^{*}}}}.

$|z_{kr}-z^{*}|\alpha ^{k}$ z $|z_{kr}-z^{*}|\alpha ^{k}$ - $|z_{kr}-z^{*}|\alpha ^{k}$ k {\ $displaystyle z_{kr}-z^{*}$ \ $alpha$ ^{ $k}$ 는 $|z_{kr}-z^{*}|\alpha ^{k}$ k와 거의 독립적이다.Fatou 도메인상의 잠재적인 함수는 다음과 같이 정의합니다.

\displaystyle \varphi (z)=\lim _{k\to \infty }{\frac {1}{(z_{kr}-z^{*} \alpha ^{k}}}}.}

θ가 매우 작은 숫자이고 k가 $|z_{k}-z^{*}|<\epsilon$ k - z $|z_{k}-z^{*}|<\epsilon$ < { $style z_{k$ }- $z^{*} <\epsilon$ $|z_{k}-z^{*}|<\epsilon$ 과 $|z_{k}-z^{*}|<\epsilon$ 첫 번째 반복 숫자일 경우 다음과 같이 됩니다.

(\displaystyle \varphi (z)=parfrac {1}{\varepsilon \alpha ^{\nu (z)}})}

$)$ { $style \nu (z$ 의 경우, 이는 실제 반복 번호로 간주되어야 하며, 다음과 같은 값이 있습니다.

\displaystyle \nu(z)=k-{\frac {log(\varepsilon / z_{k}-z^{*})}{\log(\alpha)}}}

만약 흡인력이 θ이고, 사이클이 초매력임을 의미하며, 사이클의 점 중 하나가 임계점임을 의미한다면, 우리는 α를 다음과 같이 치환해야 한다.

\alpha =\lim _{k\to\infty}{\frac {\log w'-z^{*}}{\log w-z^{*}}}

여기서 w'는 r회 반복되며, "(z)"의 공식은 다음과 같습니다.

\displaystyle \varphi (z)=\lim _{k\to \infty }{\frac {log(1/z_{kr}-z^{*}}}{\alpha ^{k}}}}.}

이제 실제 반복 횟수는 다음과 같습니다.

\displaystyle \nu(z)=k-{\frac {log(\log z_{k}-z^{*}/\log(\varepsilon)}}}, {\log(\alpha)}},}

착색에는 0부터 H-1까지 번호가 매겨진 H 색(예를 들어, H = 500)의 주기적 배율이 있어야 한다. $\nu (z)$ $\nu (z)$ ( $\nu (z)$ ) $\nu (z)$ \ $displaystyle \ nu$ ( $z$ )에 $\nu (z)$ 사진의 색 농도를 결정하는 고정 실수를 곱하여 이 수 모듈로 H의 정수 부분을 취합니다.

잠재적 기능의 정의와 우리의 착색 방법은 사이클이 매력적이라는 것을 전제로 한다. 즉, 중립이 아니다.주기가 중립이면 파투 도메인을 자연스러운 방법으로 색칠할 수 없습니다.반복의 종점이 회전 운동이기 때문에 예를 들어 반복에 의해 고정된 사이클에서 최소 거리로 색을 칠할 수 있다.

필드 라인

무한대로 반복하기 위한 등전위선

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

-

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

3 /

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

) (

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

-

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

2 /

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

)

{\frac {(1-z^{3}/6)}{(z-z^{2}/2)^{2}}}+c

+ c { \ display \

frac

{ ( 1 - z^ {

3

} /

6

} { ( z -

z^

{

2}

/

2)^{2}}

+

c

} 형식의 반복을 위한 필드 라인

각 Fatou 도메인(중립이 아님)에는 서로 직교하는 두 개의 라인 시스템, 즉 등전위 라인(전위 함수 또는 실제 반복 수)과 필드 라인이 있습니다.

Fatou 도메인을 반복 $\nu (z)$ 에 따라 색칠하면(앞 섹션에서 정의한 실제 반복 번호 $\nu (z)$ ( $\nu (z)$ $)\displaystyle \nu (z$ 가 아님), 반복 대역은 등전위선의 경로를 나타냅니다.반복이 δ에 대한 경우(통상적인 $반복$ $z^{2}+c$ + $c의$ 외부 Fatou $도메인$ 의 경우와 마찬가지로, 반복 시퀀스의 마지막 지점이 x축(첫 번째 그림) 위 또는 아래에 있으므로 색상을 변경함으로써 필드 라인의 경로를 쉽게 표시할 수 있지만, 이 경우(더 자세한 내용)정확하게: Fatou 도메인이 매우 매력적일 때) 적어도 여기서 설명하는 방법으로는 필드 라인을 일관되게 그릴 수 없습니다.이 경우 필드 라인을 외부 광선이라고도 합니다.

z가 매력적인 Fatou 도메인의 포인트가 되도록 합시다.z를 여러 번 반복하면 반복 시퀀스의 끝은 유한 사이클 C이고, 파투 도메인은 (정의상) 반복 시퀀스가 C로 수렴하는 점들의 집합이다.필드 라인은 C의 포인트와 C의 포인트로 반복되는 (무한 개수의) 포인트로부터 발행됩니다.그리고 그들은 줄리아 집합에서 끝납니다. 혼돈적이지 않은 점(즉, 유한한 사이클을 생성함)으로요.r을 사이클 C의 순서(포인트 수)로 하고 z $z^{*}$ {\(\ $displaystyle$ z $^{*})$ 를 $z^{*}$ C의 포인트로 $z^{*}$ . $f(f(\dots f(z^{*})))=z^{*}$ ( $f(f(\dots f(z^{*})))=z^{*}$ ( $f(f(\dots f(z^{*})))=z^{*}$ $f(f(\dots f(z^{*})))=z^{*}$ ) $f(f(\dots f(z^{*})))=z^{*}$ $f(f(\dots f(z^{*})))=z^{*}$ $∗$ ( \ $displaystyle$ f ( $f$ ( \ $displaystyle$ f ( z ^ { * ) ) = z $^$ { * } $f(f(\dots f(z^{*})))=z^{*}$ （ r - fold composition ） = r - f-fold composition ） = z^{*}}}}이 있고, 복소수α를 다음과 같이 정의한다.

\displaystyle \alpha =(d(f(\displaystyle f(z))))/dz)_{z=z^{*}}.}

C의 점이 $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ i $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ , … $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ , $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ ( $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ $z_{i},i=1,\dots ,r(z_{1}=z^{*})$ z ${\$ ) { $displaystyle$ z $_$ ${$ i } , $i$ = 1 $,\$ displays , $r$ ( $z_{1$ } = $z$ 인 경우, α는 r $f'(z_{i})$ f $f'(z_{i})$ i $f'(z_{i})$ ) { $displaystyle$ f $'(z_i)$ 의 곱입니다.순환의 진짜 번호 1/α이다, 우리들의 인수 사이클이도super-attracting, 1<>.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output .sfra 의미한다 중립적 입장이다.C.num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}1/ α<>∞. $z^{*}$ ${\$ { \ $displaystyle$ z $^$ { * } is $z^{*}$ $f(f(\dots f(z)))$ ( $f(f(\dots f(z)))$ ( $z$ ) $f(f(\dots f(z)))$ } { $displaystyle$ $f(f(\dots f(z)))$ f ( \ $f(f(\dots f(z)))$ $z$ $f(f(\dots f(z)))$ f ( z ) $f(f(\dots f(z)))$ } $f(f(\dots f(z)))$ , , , f f $f(f(\dots f(z)))$ f $($ ( $f$ ( $z$ ) $f(f(\dots f(z)))$ α $f(f(\dots f(z)))$ ( β β β β β)))) ))))))) )) ) of of))))) ))))))) β β β β ( )))))) ))))))))))))))))))))))))))) $(\displaystyle \alpha$ = \ $alpha$ e $^{\alpha$ i}) $\alpha =|\alpha |e^{\beta i}$

위해 Fatou도메인에 색깔에는 반복 zk({\displaystyle z_{k}(k=0,1,2,\dots{0}일 경우 ,z_ =z)의 순서 설정} 때 zk− z∗<>ϵ{\displaystyle z_{k}-z^{*}<>\epsilon}을 막고, 우리는 수에 따라 요점 zcolour 적은 수의 ε 선택했다. k(또는실제 반복 횟수(매끄러운 착색 방식을 선호할 경우)를 지정합니다.z $z_{k}-z^{*}$ { $display style$ z $^$ { * } $z^{*}$ $z^{*}$ an an an an an an an { $display style$ z $^$ { * } $z^{*}$ $z_{k}-z^{*}$ {\ if display {\ from from from display $z_{k}-z^{*}$ display { $display style$ z _ { $k$ }- $z^$ { * }}}}} $z_{k}-z^{*}$ satisfies satisfies satisfies satisfies satisfies satisfies satisfies satisfies satisfies if if if if if if if if if if if if that that that that if if if that that that that if if if if if if from from from if if if if if if if from from if if if if if if

\displaystyle \psi -k\displays = \theta \mod \pi .,}

반복 대역을 필드 라인 방향으로 통과시키면(및 사이클에서 멀어져), 반복수 $\psi -k\beta \mod \pi$ 는 1 증가하고, 숫자 θ는 $\psi -k\beta \mod \pi$ })는 $\psi -k\beta \mod \pi$ 필드 라인을 따라 일정해진다.

z^{2}+c

2

z^{2}+c

+

z^{2}+c

\

displaystyle

z

^{2}

+

c

}

z^{2}+c

의 반복을 위한 필드 라인의 그림

A colouring of the field lines of the Fatou domain means that we colour the spaces between pairs of field lines: we choose a number of regularly situated directions issuing from $z^{*}$ , and in each of these directions we choose two directions around this direction.한 쌍의 두 필드 라인이 줄리아 세트의 동일한 포인트로 끝나지 않을 수 있으므로, 우리의 컬러 필드 라인은 줄리아 세트를 향해 (끝없이) 갈 수 있습니다.필드 라인의 중심선까지의 거리에 따라 색을 칠할 수 있으며, 이 색상과 일반 색상을 혼합할 수 있습니다.그런 사진들은 매우 장식적이다(두 번째 사진).

색칠된 필드선(두 필드선 사이의 영역)은 반복 대역에 의해 분할되며, 이러한 부분은 단위 사각형과 일대일 대응에 놓일 수 있다.한쪽 좌표는 경계 필드선 중 하나로부터의 거리이고, 다른 한쪽 좌표는 경계 필드선 내부로부터의 거리(계산)이다.(이 숫자는 실제 반복 번호의 비반복 부분)따라서, 필드 라인(세 번째 사진)에 화상을 넣을 수 있습니다.

줄리아 세트 플롯

내부 각도 0인 경우 내부 2진 분해

방법:

Julia 세트의 거리 추정 방법(DEM/J)
Inverse Repeating Method(IIM; 역반복방식)

역방향(Inverse) 반복(IIM) 사용

랜덤 IIM을 사용하여 생성된 Julia 세트 그림

MIIM을 사용하여 생성된 Julia 세트 그림

위에서 설명한 바와 같이 Julia 세트는 (본질적으로) 모든 점의 사전 이미지 세트의 한계점 집합으로 찾을 수 있습니다.그래서 우리는 주어진 함수의 줄리아 집합을 다음과 같이 표시할 수 있습니다.Julia 세트에 있는 것으로 알고 있는 임의의 점(예: 역주기점)부터 시작하여 f의 높은 반복 $f^{n}$ z의 모든 사전 이미지를 $계산$ 하십시오. f $^{n})$ 아래에서 $f^{n}$ z의 모든 사전 이미지를 계산합니다.

불행히도 반복된 사전 이미지의 수가 기하급수적으로 증가함에 따라 계산상으로는 이 작업을 수행할 수 없습니다.다만, 반복 기능 시스템의 「랜덤 게임」과 같은 방법으로 이 방법을 조정할 수 있습니다.즉, 각 단계에서 f의 역이미지 중 하나를 무작위로 선택합니다.

예를 들어, 2차 다항식_c f의 경우, 역방향 반복은 다음과 같이 설명된다.

(\displaystyle z_{n-1}=sqrt {z_{n}-c}).}

각 단계에서 2개의 제곱근 중 하나를 랜덤으로 선택한다.

Julia 세트의 특정 부분은 역 Julia 알고리즘으로 접근하기가 매우 어렵습니다.따라서 더 나은 이미지를 만들려면 IIM/J(MIIM/J라고 함)를 수정하거나 다른 방법을 사용해야 합니다.

DEM/J 사용

$f_{c}(z)=z^{2}+c$ c $f_{c}(z)=z^{2}+c$ ( $f_{c}(z)=z^{2}+c$ ) $=$ $f_{c}(z)=z^{2}+c$ 2 + $f_{c}(z)=z^{2}+c$ {\ $displaystyle$ f_ ${c$ }(z)= $z^{2}+c}$ 에 $f_{c}(z)=z^{2}+c$ 설정된 줄리아 이미지
$c=-0.74543+0.11301*i$
$c=-0.75+0.11*i$
$c=-0.1+0.651*i$
거리 추정에 의해 그려진 줄리아 세트. 반복은 1 $1-z^{2}+z^{5}/(2+4z)+c$ - $1-z^{2}+z^{5}/(2+4z)+c$ 2 + $1-z^{2}+z^{5}/(2+4z)+c$ 5 $1-z^{2}+z^{5}/(2+4z)+c$ / ( $1-z^{2}+z^{5}/(2+4z)+c$ + $1-z^{2}+z^{5}/(2+4z)+c$ ) + $1-z^{2}+z^{5}/(2+4z)+c$ $1-z^{2}+z^{5}/(2+4z)+c$ $1-z^{2}+z^{5}/(2+4z)+c$ 이다.
거리 추정을 이용한 줄리아 세트의 3차원 렌더링

Julia 세트는 무한히 얇기 때문에 픽셀에서 거꾸로 반복하여 효과적으로 그릴 수 없습니다.무한히 많은 시작점을 조사하는 것은 비현실적이기 때문에 단편적으로 보일 것입니다.반복 횟수는 Julia 세트 근처에서 크게 변경되므로 부분적인 해결책은 가장 가까운 색상 등고선에서 세트의 윤곽을 암시하는 것이지만 세트가 흐려 보이는 경향이 있습니다.

Julia 세트를 흑백으로 그리는 더 좋은 방법은 세트로부터 픽셀(DEM)의 거리를 추정하고 세트에 가까운 모든 픽셀에 색을 입히는 것입니다.거리 추정 공식은 잠재적 함수 δ(z)에 대한 공식에서 도출된다.【(z)】의 등전위선이 가까이 있으면 $|\varphi '(z)|$ $|\varphi '(z)|$ $\delta (z)=\varphi (z)/|\varphi '(z)|$ $)】({displaystyle$ \ $varphi '(z)})$ 가 $|\varphi '(z)|$ 크고, 반대로 $\delta (z)=\varphi (z)/|\varphi '(z)|$ 의 등전위선은 $=【($ )】(z) 【(z $/vari)】$ 의 등전위선이다.이 공식에서 찾은 값(최대 상수 인자)은 z가 Julia ^[8]집합을 향해 수렴하는 실제 거리로 수렴하는 것으로 입증되었습니다.

우리는 f(z)가 합리적이라고 가정한다. 즉, $f(z)=p(z)/q(z)$ $=$ $f(z)=p(z)/q(z)$ / $f(z)=p(z)/q(z)$ q( $)$ { $display style$ f $(z$ )= $p(z)/q(z)}$ 여기서 $f(z)=p(z)/q(z)$ p(z)와 q(z)는 각각 m과 n도의 복소 다항식이며, 우리는 θ(z)에 대해 위의 식들의 도함수를 구해야 한다.또한 z $($ 만 $z_{k}$ 다르므로 z k $($ {k})에 $z_{k}$ $z'_{k}$ $z_{k}$ ${\$ { $display style$ z $'_{$ $k$ }의 $z'_{k}$ $z_{k}$ $z'_{k}$ 를 계산해야 합니다. $그러나$ z k $z_{k}=f(f(\cdots f(z)))$ ( $z_{k}=f(f(\cdots f(z)))$ $f$ ( $z_{k}=f(f(\cdots f(z)))$ ) $z_{k}=f(f(\cdots f(z)))$ ) { $displaystyle z_{$ $k}$ $= f$ ( \ $cdots$ f ( $z$ ) } $z_{k}=f(f(\cdots f(z)))$ （ k $f'(z_{k})$ - f ( \ cdots f ( $z$ $)$ $f'(z_{k})$ $z'_{k}$ $z'_{k}$ $z'_{k}$ $f'(z_{k})$ of of $f'(z_{k})$ of $f'(z_{k})$ of of of $z'_{k}$ of $f'(z_{k})$ of of $z'_{k+1}=f'(z_{k})z'_{k}$ of of of of of $of$ of $z'_{k+1}=f'(z_{k})z'_{k}$ of but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but but $yle$ z $'_{k+1}=f'(z_{k})z'_{k$ z $z'_{0}=1$ $=$ ${style$ z $'_{0$ }= $1$ }부터 $z'_{0}=1$ 합니다(다음 $z_{k+1}=f(z_{k})$ z $z_{k+1}=f(z_{k})$ + $1$ $z_{k+1}=f(z_{k})$ f ( $z_{k+1}=f(z_{k})$ k $z_{k+1}=f(z_{k})$ ) { $style z_{k}$ = $f(z_{k}).$

θ에 대한 반복(더 정확히는 m $n$ n + $2일$ $때$ , 그래서 θ가 초매력 고정점일 때), 우리는 다음을 가진다.

\varphi '(z) =\lim _{k\to \infty }{\frac {z'_{k}}{z_{k} d^{k}}}

( $d$ $= m$ - $n$ ) 결과:

\displaystyle \varphi(z)=\varphi '(z)=\lim _{k\to \infty }\log z_{k} / z'_{k} .,

z $z^{*}$ δ(\ $displaystyle$ z $^{*})$ $z^{*}$ 을 $z^{*}$ 포함하며 차수가 r인 유한 유인 사이클(초매력적이지 않음)을 향해 반복하기 위해, 다음과 같이 한다.

\displaystyle \varphi '(z) =\lim _{k\to \infty }z'_{kr} /(z_{kr}-z^{*}^{2}\alpha ^{k}),,}

결과적으로:

\displaystyle \varphi(z)=\varphi '(z)=\lim_{k\to\infty}z_{kr}-z^{*}/z'_{kr}.,}

초매력 사이클의 경우 공식은 다음과 같습니다.

\displaystyle (z)=\lim _{k\to \infty }\log z_{kr}-z^{*}^{2}/z'_{kr} .,

이 수치는 반복이 정지했을 때 계산됩니다.거리 추정은 사이클의 인력과 무관합니다.이는 "도 무한대"의 초월 함수(예: sin(z) 및 tan(z))에 대한 의미를 갖는다.

경계 그리기 외에 거리 함수를 제3차원으로 도입하여 입체 프랙탈 풍경을 만들 수 있다.

「」를 참조해 주세요.

메모들

^ 표기법에 대해서:수학의 다른 분야에서는 J $\operatorname {J} (f),$ ( $\operatorname {J} (f),$ ) , ${\displaystyle$ \ $operatorname$ { $J$ } ( $f),}$ $\operatorname {J} (f),$ 은 $\operatorname {J} (f),$ 매끄러운 다양체 사이의 실수값 $매핑$ f의 야코비 행렬을 나타낼 수도 있습니다.

레퍼런스

^ Gaston Julia(1918) "Mémoire sur l'iteration des fonctions rationnelles", 저널 de Mathématiques Pures et Appliées, vol. 8, 47-245페이지.
^ Pierre Fatou(1917) "수르 레 대체 비율넬", Comptes Rendus de l'l Academie des Sciences de Paris, vol. 164, 806–808 및 vol. 165, 992–995.
^ Beardon, 유리함수의 반복, 정리 5.6.2.
^ Beardon, 유리함수의 반복, 정리 7.1.1.
^ Beardon, 유리함수의 반복, 정리 3.2.4.
^ Tan Lei, "만델브로 집합과 줄리아 집합의 유사성", 수학 물리학에서의 커뮤니케이션 134(1990), 페이지 587–617.
^ Douady, Adrien; Hubbard, John H. (1984). "Etude dynamique des polynômes complexes". Prépublications mathémathiques d'Orsay. 2; "[op.cit.]". 4. 1985. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
^ ^a ^b Peitgen, Heinz-Otto; Richter Peter (1986). The Beauty of Fractals. Heidelberg: Springer-Verlag. ISBN 0-387-15851-0.

참고 문헌

Carleson, Lennart; Gamelin, Theodore W. (1993). Complex Dynamics. Springer.
Douady, Adrien; Hubbard, John H. (1984). "Etude dynamique des polynômes complexes". Prépublications mathémathiques d'Orsay. 2; "[op.cit.]". 4. 1985. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)
Milnor, J.W. (2006) [1990]. Dynamics in One Complex Variable. Annals of Mathematics Studies. Vol. 160 (Third ed.). Princeton University Press;
에 처음 등장했습니다.
Bogomolny, Alexander. "Mandelbrot Set and Indexing of Julia Sets". cut-the-knot. Algebra curriculum.
Demidov, Evgeny (2003). "The Mandelbrot and Julia sets' anatomy".
Beardon, Alan F. (1991). Iteration of Rational Functions. Springer. ISBN 0-387-95151-2.

외부 링크

"Julia set", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
Weisstein, Eric W. "Julia Set". MathWorld.
Bourke, Paul. "Julia set fractal (2D)" (personal site).
Sawyer, Jamie (6 April 2007). "Julia sets" (blog).
McGoodwin, Michael. "Julia jewels: An exploration of Julia sets" (personal site).
Pringle, Lucy. "Crop circle Julia Set" (personal site).
Greig, Josh. "Interactive Julia Set Applet". Archived from the original on 2012-03-26.
Joyce, David E. "Julia and Mandelbrot set explorer" (academic personal site). Clark University.
"A simple program to generate Julia sets". liazardie.com. Archived from the original on 2011-03-17. – Windows, 370 kB
"A collection of applets". SourceForge. – 애플릿 중 하나가 반복 기능 시스템을 통해 Julia 세트를 렌더링할 수 있습니다.
"Julia meets HTML5". Google Labs. Archived from the original on 2011-02-18. HTML5 Fractal generator for your browser
"Julia". r-project.org. GNU R Package. 25 November 2014. generate Julia or Mandelbrot set at a given region and resolution
"Julia sets". – 줄리아 세트의 시각적 설명.
"FractalTS". github.io. – Mandelbrot, Burning ship 및 해당 Julia 세트 발전기.
"Julia set images, online rendering". finengin.net.

[1] 표기법에 대해서:수학의 다른 분야에서는 J $\operatorname {J} (f),$ ( $\operatorname {J} (f),$ ) , ${\displaystyle$ \ $operatorname$ { $J$ } ( $f),}$ $\operatorname {J} (f),$ 은 $\operatorname {J} (f),$ 매끄러운 다양체 사이의 실수값 $매핑$ f의 야코비 행렬을 나타낼 수도 있습니다.

[2] Gaston Julia(1918) "Mémoire sur l'iteration des fonctions rationnelles", 저널 de Mathématiques Pures et Appliées, vol. 8, 47-245페이지.

[3] Pierre Fatou(1917) "수르 레 대체 비율넬", Comptes Rendus de l'l Academie des Sciences de Paris, vol. 164, 806–808 및 vol. 165, 992–995.

[4] Beardon, 유리함수의 반복, 정리 5.6.2.

[5] Beardon, 유리함수의 반복, 정리 7.1.1.

[6] Beardon, 유리함수의 반복, 정리 3.2.4.

[7] Tan Lei, "만델브로 집합과 줄리아 집합의 유사성", 수학 물리학에서의 커뮤니케이션 134(1990), 페이지 587–617.

[8] Douady, Adrien; Hubbard, John H. (1984). "Etude dynamique des polynômes complexes". Prépublications mathémathiques d'Orsay. 2; "[op.cit.]". 4. 1985. {{cite journal}}:Cite 저널 요구 사항 journal=(도움말)

[Peitgen1986-9] Peitgen, Heinz-Otto; Richter Peter (1986). The Beauty of Fractals. Heidelberg: Springer-Verlag. ISBN 0-387-15851-0.

[a]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

v t 프랙탈
특성.	프랙탈 치수 아수아드 박스 카운트 히구치 상관 관계 하우스도르프 포장. 토폴로지 재귀 자기유사성
반복 함수 시스템.	반슬리 양치류 칸토어 집합 코흐 눈꽃 멩거 스펀지 시에르핀스키 카펫 시에르핀스키 삼각형 아폴로 개스킷 피보나치어 프랙탈 아프리카 공간 채우기 곡선 블랑망주 곡선 드람 곡선 민코프스키 용곡선 힐베르트 곡선 코흐 곡선 레비 C 곡선 무어 곡선 페아노 곡선 시에르핀스키 곡선 Z차 곡선 스트링 T-제곱 n플레이크 빅섹 프랙탈 헥사플레이크 고스퍼 곡선 피타고라스나무 바이어스트라스 함수
이상한 매력자	다분할계
L계	프랙탈 캐노피 공간 채우기 곡선 H 트리
이스케이프 타임 프랙탈	불타는 배 프랙탈 줄리아 세트 가득 찬 뉴턴 프랙탈 두아디토끼 랴푸노프 프랙탈 만델브로트 집합 미시우레비치 점 멀티봇 세트 뉴턴 프랙탈 트리콘 만델박스 만델구
렌더링 기술	버드하브 궤도 트랩 피커버 줄기
랜덤 프랙탈	브라운 운동 갈색나무 브라운 모터 프랙탈 풍경 레비 비행 침투 이론 자기 회피 보행
사람	마이클 반즐리 게오르크 칸토르 빌 고스퍼 펠릭스 하우스도르프 데스몬드 폴 헨리 개스톤 줄리아 헬게 폰 코흐 폴 레비 알렉산드르 랴푸노프 브누아 만델브로 하미드 나데리 예가네 루이스 프라이 리처드슨 바츠와프 시에르핀스키
다른.	"영국 해안은 얼마나 깁니다?" 해안선의 역설 하우스도르프 차원에 따른 프랙탈 목록 프랙탈의 아름다움 (1986년 책) 프랙탈 아트 혼돈: 새로운 과학 만들기 (1987년 책) 자연의 프랙탈 기하학 (1982년 책) 만화경 카오스 이론

Search

줄리아 세트

네임스페이스

더

목차

형식적 정의

Julia 집합에 대한 동등한 설명

Julia 집합과 Fatou 집합의 속성

예

이차 다항식

일반화

유사 코드

일반 줄리아 세트에 대한 의사 코드

다중 줄리아 세트용 의사 코드

잠재적 함수와 실제 반복 횟수

필드 라인

줄리아 세트 플롯

역방향(Inverse) 반복(IIM) 사용

DEM/J 사용

「」를 참조해 주세요.

메모들

레퍼런스

참고 문헌

외부 링크

Search

줄리아 세트

형식적 정의

Julia 집합에 대한 동등한 설명

Julia 집합과 Fatou 집합의 속성

예

이차 다항식

일반화

유사 코드

일반 줄리아 세트에 대한 의사 코드

다중 줄리아 세트용 의사 코드

잠재적 함수와 실제 반복 횟수

필드 라인

줄리아 세트 플롯

역방향(Inverse) 반복(IIM) 사용

DEM/J 사용

「 」를 참조해 주세요.

메모들

레퍼런스

참고 문헌

외부 링크

「」를 참조해 주세요.