안장점

수학에서 안장점 또는 미니맥스점은^[1] 직교 방향의 기울기(미분)가 모두 0(임계점)인 함수 그래프 표면의 점이지만 함수의 ^[2]국소 극점은 아닙니다.안장점의 예로는 한 축 방향(피크 사이)을 따라 상대 최소값이 있고 교차 축을 따라 상대 최대값이 있는 임계점이 있는 경우를 들 수 있습니다.단, 안장점이 이 형태일 필요는 없습니다.예를 들어 $함수{\displaystyle }$f (${\displaystyle x}$ ,${\displaystyle y}$ ) $=$ ${\displaystyle {x\mathrm{}}^{}}$2 + ${\displaystyle {}^{}}$ ${\displaystyle {3\mathrm{}}^{}}$ ${\$ f$(x,y$)=$x^{2}+y^{3$}}}은$($는${\displaystyle )}$ 상대 최대값도 상대 최소값도 아니므로 $안장점$인 ($, 0)$에 임계점이${\displaystyle }$있지만 $y(\displaystyle$y$$) $방향$에는 상대 최대값 또는 상대 최소값이 없습니다.

이 이름은 2차원의 원형 예가 한 방향으로 굽은 표면이고 다른 방향으로 굽은 표면이라는 점에서 유래되었으며, 이는 지형 안장을 형성하는 두 봉우리 사이의 승마용 안장 또는 산길과 유사합니다.등고선의 경우 2차원의 새들 점이 해당 점에서 교차하는 한 쌍의 선이 있는 등고선 맵을 생성합니다.안장점의 높이가 이러한 지도에 사용된 정수 배수와 일치하지 않을 가능성이 높기 때문에 실제 무기 측량 지도에서는 이러한 교차가 드물다.대신 새들 점은 새들 점으로부터 접근하거나 멀어지는 네 가지 등고선 세트의 중간에 공백으로 나타납니다.기본 안장점의 경우, 이러한 세트는 쌍으로 발생하며, 대향하는 높은 쌍과 대향하는 낮은 쌍이 직교 방향으로 배치됩니다.임계 등고선은 일반적으로 직교할 필요가 없습니다.

수학 토론

두 실변수의 실수값 함수 F(x,y)의 주어진 정지점이 안장점인지 확인하는 간단한 기준은 그 지점에서 함수의 헤시안 행렬을 계산하는 것이다: 만약 헤시안 행렬이 무한하다면, 그 점은 안장점이다.예를 들어$,{\displaystyle }$ 함수 $z{\displaystyle }$ $=$ ${\displaystyle {}^{}{2\mathrm{}}^{}}$ - ${\displaystyle {}^{}}$ (${\displaystyle x}$,${\displaystyle y}$$$,${\displaystyle z}$ )$$$=$ (${\displaystyle 0}$ ,${\displaystyle 0}$, $)$ ($x , y$$$, z )의 헤시안 행렬은 행렬이다$.$

$(\displaystyle {bmatrix} 2&0&-2\end {bmatrix})$

그건 불확실하죠.따라서 이 점이 안장점입니다.이 기준은 충분한 조건만 제시합니다.${\displaystyle \mathrm{예}}$를 들어$,{\displaystyle }$ 점${\displaystyle }$(${\displaystyle 0,}$ ${\displaystyle 0,}$ 0$)$ {{$displaystyle$$(0,0,0$)}은$$ z ${\displaystyle =}$ ${\displaystyle {}^{}{4\mathrm{}}^{}}$ - ${\displaystyle {y\mathrm{}}^{}}$4,$${\$displaystyle$ z$=x^{4}-y^{4}}}$의 새들 점이지만, 이 함수의 헤시안 행렬은 무한 행렬이 아닙니다.

가장 일반적인 용어로 매끄러운 함수(그래프가 곡선, 표면 또는 하이퍼서페이스)를 위한 안장점은 그 점 근방의 곡선/표면 등이 그 점에서의 접선 공간의 어느 쪽에도 완전히 있지 않은 정지점이다.

1차원 영역에서 안장점은 정지점인 동시에 변곡점인 점을 말한다.변곡점이기 때문에 국소적인 극단점이 아닙니다.

안장면

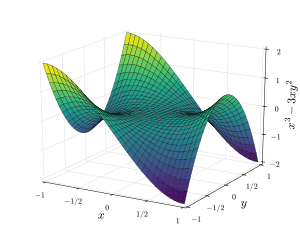
안장면은 하나 이상의 안장점을 포함하는 평활면이다.

유클리드 공간에서의 2차원 안장 표면의 고전적인 예로는 2차 표면, 쌍곡선 $포물면{\displaystyle }$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ ${\displaystyle {}^{}}$ - ${\displaystyle {y\mathrm{}}^{}}$2(\$displaystyle z=x^{2}-y^{$2})$$ (종종 "안장 표면" 또는 "표준 안장 표면"이라고 함) 및 한 시트의 쌍곡선이 있다.프링글스 감자칩이나 바삭바삭한 것은 쌍곡선 포물결 모양의 일상적인 예이다.

새들 표면은 양의 가우스 곡률을 갖는 볼록/엘리틱 표면과 구별되는 음의 가우스 곡률을 가진다.전형적인 3차 안장 표면은 원숭이 ^[3]안장이다.

예

연속공간에 정의된 2인용 제로섬 게임에서 평형점은 안장점이 된다.

2차 선형 자율 시스템의 경우 특성 방정식이 하나의 양의 실제 고유값과 하나의 음의 실제 고유값을 갖는 ^[4]경우 임계점은 안장점이 됩니다.

등식 구속조건이 적용되는 최적화에서 1차 조건은 라그랑지안의 안장점을 나타낸다.

기타 용도

동적 시스템에서, 동적도가 미분 가능한 지도 f에 의해 주어지는 경우, 점은 θ의 미분(여기서 n은 점의 주기)이 점에서 계산될 때 (복잡한) 단위 원에 고유값이 없는 경우에만 쌍곡선이 됩니다.안장점은 안정적이고 불안정한 다양체가 0이 아닌 차원을 갖는 쌍곡선 주기점입니다.

행렬의 안장점은 열에서 가장 큰 요소인 동시에 행에서 가장 작은 요소인 요소입니다.

「 」를 참조해 주세요.

• 새들 포인트 방법은 적분 근사법에 대한 라플라스 방법의 확장입니다.
• 익스트림
• 파생 검정
• 쌍곡 평형점
• 미니맥스 정리
• 최대-최소 부등식
• 몽키안장
• 산악 패스 정리

레퍼런스

인용문

원천

추가 정보

• Hilbert, David; Cohn-Vossen, Stephan (1952). Geometry and the Imagination (2nd ed.). Chelsea. ISBN 0-8284-1087-9.

외부 링크

• Wikimedia Commons의 Saddle Point 관련 미디어