열역학적 온도
Thermodynamic temperature| 열역학 |
|---|
 |
열역학적 온도는 열역학에서 운동 이론이나 통계 역학과 구별되는 양이다.열역학 온도 판독치 0은 열역학 제3법칙에서 특히 중요합니다.관례상 측정단위가 켈빈(단위기호: K)인 온도계 켈빈으로 보고된다.비교를 위해, 295 K의 온도는 21.85 °C 및 71.33 °F와 같습니다.
열역학적 온도의 영점인 절대 영점에서는 물질의 입자 성분은 최소한의 움직임을 가지며 차가워질 [1][2]수 없습니다.절대 영(0 K)은 -273.15°C 및 -459.67°F와 정확하게 동일합니다.절대 0에 있는 물질은 전달 가능한 평균 운동 에너지가 남아 있지 않고 유일하게 남아있는 입자 운동은 제로 포인트 [3]에너지라고 불리는 퍼베이시브 양자 역학 현상 때문이다.예를 들어, 절대 영점이었던 액체 헬륨 용기 안의 원자들이 여전히 영점 에너지 때문에 약간 흔들릴지라도, 이론적으로 완벽한 열 엔진은 작동 유체 중 하나로 헬륨과 같은 순수한 운동 에너지 (열 에너지)를 다른 작동 유체에 전달하지 못하고 열역학적 작용이 없다.uld가 발생합니다.
온도는 일반적으로 물질의 부피나 압력(게이 러삭의 법칙 참조), 또는 방출된 흑체 방사선의 파장과 같은 물질의 다른 물리적 특성과의 상호 관계를 과학적으로 조사할 때 절대적인 용어로 표현된다.절대 온도는 화학 반응 속도를 계산할 때도 유용합니다(아레니우스 방정식 참조).게다가 절대 온도는 일반적으로 극저온학 및 초전도 같은 관련 현상에 사용됩니다. 예를 들어 다음과 같습니다. "편리하게도 탄탈의 전이 온도(Tc) 4.4924 켈빈은 헬륨의 끓는점 4.221 K보다 약간 높습니다."
개요
SI(International System of Units)는 열역학적 온도를 측정하기 위한 켈빈 척도와 척도를 따라 특정 값에 대한 측정 단위 켈빈(단위 기호: K)을 지정합니다.켈빈은 또한 다음과 같은 사용 예에 따라 온도 간격(두 온도 사이의 간격 또는 차이)을 나타내는 데 사용됩니다. "60/40 주석/납 납땜은 비공정성이며 고화 시 5 켈빈 범위에 걸쳐 플라스틱입니다.섭씨 1도의 온도 간격은 1켈빈과 같다.
켈빈의 크기는 열역학적 온도의 기초가 되는 매우 물리적 특성인 원자 입자 운동의 운동 에너지와 관련하여 2019년에 재정의되었다.재정의는 볼츠만 상수를 정확히 1.380649×10−23 줄/켈빈(J/K)[4]으로 고정했습니다.볼츠만 상수에 대한 복합 측정 단위도 종종 J·K로−1 표시되는데, 이는 곱셈 점(·)과 켈빈 기호 뒤에 이어지는 -1 지수 때문에 추상적으로 보일 수 있다.하지만, 이것은 단지 같은 척도를 나타내는 또 다른 수학적 구문일 뿐이다: 켈빈 당 줄(운동 에너지를 포함한 에너지의 SI 단위).
어떤 물질에 온도를 주입하는 특성은 볼츠만 상수에 따라 열에너지가 특정 가스의 압력과 온도에 어떻게 정확하게 정의된 변화를 일으키는지와 관련된 이상적인 가스 법칙을 조사함으로써 쉽게 이해할 수 있습니다.이것은 헬륨과 아르곤과 같은 단원자 기체가 물질에서 일어날 수 있는 가능한 움직임의 특정한 부분집합에서만 움직이는 완벽한 탄성과 구형의 당구공처럼 운동적으로 작용하기 때문입니다: 그것은 세 가지의 변환 자유도를 포함합니다.변환 자유도는 3D 공간의 X, Y 및 Z 축을 따라 당구공과 같은 익숙한 움직임입니다(아래 그림 1 참조).그렇기 때문에 귀한 가스는 모두 원자당 동일한 비열 용량을 가지며 그 값이 모든 가스 중에서 가장 낮은 것입니다.
그러나 분자(화학적으로 결합된 두 개 이상의 원자)는 내부 구조를 가지고 있기 때문에 추가적인 내부 자유도를 가지고 있으며(아래 그림 3 참조), 이는 분자가 단원자 가스보다 주어진 온도 상승에 대해 더 많은 열에너지를 흡수하도록 한다.열에너지는 사용 가능한 모든 자유도에서 생성됩니다. 이는 등분할 정리에 따르기 때문에 사용 가능한 모든 내부 자유도는 세 개의 외부 자유도와 동일한 온도를 가집니다.그러나 모든 기체에 압력을 가하는 성질은 기체 입자가 용기로부터 나오는 단위 면적당 순 힘이며 원자와 분자의 세 가지 변환 [5]자유도에서 발생하는 운동에너지의 함수이다.
볼츠만 상수를 다른 규칙 제정과 함께 특정 값으로 고정하는 것은 열역학 온도의 단위 간격인 켈빈의 크기를 귀한 가스의 평균 운동 거동으로 정확하게 설정하는 효과를 가져왔다.또한 열역학 온도 척도의 시작점인 절대 0은 표본에 0 평균 운동 에너지가 남아 있는 점으로 재확인되었다. 남은 입자 운동은 0점 에너지로 인한 무작위 진동을 구성하는 점뿐이다.
랭킨 스케일
역사상 많은 온도 척도가 존재했지만 열역학적 온도를 측정하는 척도는 두 가지뿐이며 절대 영점이 영점(0)입니다.켈빈 척도와 랭킨 척도가 있습니다.
거의 항상 국제 단위계를 사용하여 현대적인 측정이 이루어지는 과학 세계 전체에서 열역학적 온도는 켈빈 척도를 사용하여 측정됩니다.랭킨 척도는 미국의 영어 엔지니어링 유닛의 일부이며 특정 엔지니어링 분야, 특히 레거시 레퍼런스 저작물에 사용됩니다.랭킨 눈금은 화씨(기호: °F)와 같은 크기의 랭킨도(기호: °R)를 단위로 사용합니다.
랭킨 1도의 단위 증분은 정확히 1 켈빈보다 크기가 1.8배 작으므로 켈빈 척도의 특정 온도를 랭킨 척도로 변환하고 랭킨 척도의 온도에서 켈빈 척도로 변환하려면 "영점"에 대해 °R / 1.8 = K가 된다.물 얼음의 ing 지점(0°C 및 273.15K)은 491.67°R이다.
온도 간격(스팬 또는 두 온도 간의 차이)을 변환하려면 앞서 설명한 것과 동일한 공식을 사용합니다. 예를 들어, 5 켈빈의 범위는 랭킨의 9도 범위와 정확하게 동일합니다.
켈빈의 현대적 재정의
1954년부터 2019년까지 65년 동안 SI 베이스 유닛의 재정의 기간 동안 1 켈빈의 온도 간격은 다음과 같이 정의되었다.1/273.16 물의 삼중점과 절대 영점 사이의 차이.1954년 국제측량국(프랑스어 약자 BIPM으로 알려진)의 결의안 및 이후 결의안 및 간행물은 물의 삼중점을 정확히 273.16K로 정의했으며, 이전 협약(즉, 0°C는 오랫동안 t로 정의됨) 때문에 이를 수용하는 것이 "일반 관행"임을 인정했다.물의 녹는점과 물의 삼중점이 오랫동안 구별하기 어려울 정도로 0.01°C에 가까운 것으로 실험적으로 결정되었다.) 섭씨 척도와 켈빈 척도의 차이는 273.15 켈빈으로 인정된다. 즉, 0°C는 273.15 [6]켈빈과 같다.이후 분해능뿐만 아니라 이것의 순효과는 두 가지였다. 1) 절대 0을 정확히 0K로 정의했고 2) 비엔나 표준 평균 해양수라고 불리는 특수 동위원소 제어수의 삼중점은 정확히 273.16 켈빈과 0.01 °C로 정의했다.앞서 언급한 분해능의 한 가지 효과는 물의 녹는점이 273.15 켈빈과 0 °C에 매우 가깝지만 정의값이 아니며 보다 정밀한 측정을 통해 정제되어야 한다는 것이었다.
1954년 BIPM 표준은 물의 동위원소 시료 간 동위원소 변화로 인한 불확실성 내에서 물의 동결점과 3배 지점 주변의 온도를 잘 설정했지만, 3배 지점과 절대 0점 사이의 중간 값뿐만 아니라 실온과 그 이상의 추정 값도 경험해야 했다.개별 실험실의 장치 및 절차를 통해 결정됩니다.이러한 단점은 1990년 국제 온도 척도(ITS-90)에 의해 해결되었습니다. ITS-90은 13.8033 K에서 1,357.77 K까지 13개의 추가 지점을 정의했지만, ITS-90은 정의상으로는 금속 샘플의 용융점 또는 동결점에 따라 추정된 값 중 8개가 남아 있기 때문에 몇 가지 문제가 있었습니다.녹거나 결빙점이 영향을 받지 않도록 순수하게 흐릅니다(보통 우울함).
2019년 SI 베이스 유닛의 재정의는 SI 베이스 유닛을 정의하는 마지막 물리적 아티팩트(프랑스에 위치한 금고에 세 개의 중첩된 벨 항아리 아래에 보관된 백금/이리듐 실린더)인 킬로그램에서 SI 시스템의 정의적 기초의 상당 부분을 분리하기 위한 것이었다.baltzmann 상수를 포함한 4개의 물리 상수를 확실하게 고정해야 했습니다.
볼츠만 상수를 정밀하게 정의된 값으로 할당하는 것은 가장 정밀하게 측정되는 것을 제외하고는 현대 온도계에 실질적인 영향을 미치지 않았다.재정의 전 물의 삼중점은 정확히 273.16K와 0.01°C였고 볼츠만 상수는 1.38064903(51)×10−23 J/K로 실험적으로 결정되었다. 여기서 "(51)은 두 개의 최하위 자릿수(03)의 불확실성을 나타내며 표준 불확도 [7]037ppm과 같다.이후 볼츠만 상수를 정확히 1.380649×10−23 J/K로 정의함으로써 0.37ppm의 불확실성이 물의 삼중점으로 전달되었고, 이는 실험적으로 결정된 273.1600 ±0.0001 K(0.0100 ±0.0001 °C)의 값이 되었다.SI 재정의 후 물의 3중점이 273.16K에 매우 근접하게 된 것은 우연이 아니었다. 볼츠만 상수의 최종 값은 물의 3중점을 핵심 기준 [8]온도로 사용한 아르곤과 헬륨에 대한 현명한 실험을 통해 부분적으로 결정되었다.[9]
2019년 재정의에도 불구하고, 물 3중점 셀은 273.16K와 0.01°C에서 매우 정밀한 교정 기준으로서 현대 온도계에서 계속 기능한다.또한 물의 3중점은 ITS-90으로 구성된 14개의 보정점 중 하나로 남아 있으며, 이는 수소 3중점(13.8033K)에서 열역학 온도의 거의 100배 범위인 구리 응고점(1357.77K)에 걸쳐 있다.
온도, 운동, 전도 및 열 에너지의 관계

운동에너지의 성질, 반향운동, 온도
물질의 부피(통계적으로 유의한 입자의 양)의 열역학적 온도는 변환 운동으로 알려진 특정 입자 운동의 평균 운동 에너지에 정비례합니다.공간의 세 X, Y 및 Z 축 치수의 이러한 단순한 움직임은 입자가 세 개의 공간 자유도로 움직인다는 것을 의미합니다.이 운동 에너지의 특정한 형태는 때때로 운동 온도라고 불린다.변환 운동은 열에너지의 한 형태일 뿐이며, 기체의 온도뿐만 아니라 압력과 부피의 대부분을 제공합니다.가스의 온도, 압력 및 부피 간의 관계는 이상적인 가스 법칙의 공식 pV = nRT로 정의되며 가스 법칙에 구체화됩니다.
세 가지 변환 자유도에서만 발생하는 운동 에너지는 물질의 열역학적 온도를 구성하지만, 그림 3에서 볼 수 있듯이 분자는 결합 길이, 결합 각도, 회전의 세 가지 범주로 분류되는 다른 자유도를 가질 수 있다.세 가지 추가 범주가 모두 모든 분자에 대해 반드시 이용 가능한 것은 아니며, 세 가지 모두를 경험할 수 있는 분자의 경우에도 일부는 특정 온도 이하로 "동결"될 수 있습니다.그럼에도 불구하고, 특정 조건 하에서 분자가 이용할 수 있는 모든 자유도는 물질의 특정 열 용량에 기여합니다. 즉, 물질의 특정 양을 1 켈빈 또는 섭씨 1도 상승시키는 데 필요한 열(운동 에너지)의 양을 증가시킵니다.
운동 에너지, 질량 및 속도의 관계는 E = 1/2mv라는2 [10]공식으로k 주어진다.따라서 질량이 1단위로 움직이는 입자는 질량이 4배지만 속도는 절반인 입자와 운동 에너지와 온도가 정확히 같다.
기체 내 원자 또는 분자의 통계적으로 유의한 집합에서 변환 운동의 운동 에너지가 가스의 압력과 부피에 기여하는 정도는 볼츠만 상수(기호: kB)에 의해 확립된 열역학적 온도의 비례 함수이다.볼츠만 상수는 또한 기체의 열역학적 온도를 개별 입자의 변환 운동 평균 운동 에너지와 다음과 같이 관련짓습니다.
- 는 각 입자의 평균 운동 에너지(J)입니다.
- kB = 1.380649×10−23 J/K
- T는 물질 부피의 열역학 온도(K)이다.
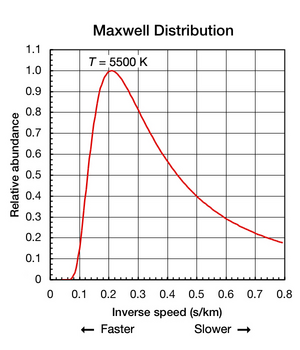
볼츠만 상수가 입자의 표본에서 평균 운동 에너지를 찾는데 유용한 반면, 중요한 것은 물질이 분리되고 열역학적 평형 상태에 있을 때조차도 개별 원자와 분자의 이동 운동이 일어나는 것입니다.다양한 속도(위 그림 1의 애니메이션을 참조하십시오.어느 순간이라도 이 범위 내에서 주어진 속도로 이동하는 입자의 비율은 맥스웰-볼츠만 분포에 의해 설명되는 확률에 의해 결정됩니다.그림 2의 그래프는 5500K 헬륨 원자의 속도 분포를 나타낸다.가장 가능성이 높은 속도는 4.780km/s(0.2092초/km)입니다.하지만, 어떤 특정한 비율의 원자는 어떤 순간에 더 빠르게 움직이는 반면, 어떤 원자는 상대적으로 더 느리게 움직인다; 어떤 원자는 순간적으로 가상의 정지 상태에 있다(오른쪽 x 축에서 벗어남).이 그래프는 x축에 역속도를 사용하므로 아래 그림 5의 곡선과 쉽게 비교할 수 있다.두 그래프에서 x축의 0은 무한 온도를 나타냅니다.또한 두 그래프의 x축과 y축은 비례적으로 조정됩니다.
번역 동작의 고속화
번역 운동을 직접 감지하려면 매우 특별한 실험 장비가 필요하지만, 액체 속에 떠 있는 작은 입자와 원자 또는 분자의 충돌로 인해 일반 현미경으로 볼 수 있는 브라운 운동이 발생한다.소립자의 병진운동은 매우 빠르고[11] 직접 관찰하기 위해서는 절대영도에 가까운 온도가 필요하다.예를 들어, NIST의 과학자들이 1994년에 700nK (10억분의 1 켈빈)의 기록적인 저온에 도달했을 때, 그들은 광학 격자 레이저 장비를 사용하여 단열적으로 세슘 원자를 냉각시켰다.그리고 나서 그들은 끼임 레이저를 끄고 온도를 [12]계산하기 위해 초당 7mm의 원자 속도를 직접 측정했다.다음 각주에 [13]병진운동의 속도 및 속도를 계산하기 위한 공식이 제시되어 있다.
운동 온도에 의한 원자 움직임을 상상하는 것은 어렵지 않으며, 그러한 움직임과 제로점 에너지에 의한 움직임을 구별하는 것은 어렵지 않다.왼쪽의 그림 2.5와 같이 절대 0에 매우 가까운 원자를 가진 다음과 같은 가정적인 사고 실험을 생각해 보자.광학 현미경의 최대 배율인 400배율로 설정된 일반적인 광학 현미경을 통해 들여다본다고 상상해 보십시오.이러한 현미경은 일반적으로 직경이 0.4mm가 넘는 시야를 제공한다.시야의 중심에는 어두운 배경에 비추고 빛나는 단일 부상 아르곤 원자(Argon은 공기의 약 0.93%로 구성됨)가 있습니다.만약 이 아르곤 원자는 beyond-record-setting 절대 zero,[14]의 일반화 캘빈의one-trillionth에 수직이고 오른쪽을 향해 시야의 범위가로 이동하고 있었습니다. 이 여행 거리에 대한 thi의 끝에 있는 마침표의 너비와 같다 139초가 이미지의 중심에서 200-micron 진드기에 마크로 이사를 해야 것이다.ss최신 컴퓨터 모니터에 접속할 수 있습니다.아르곤 원자가 천천히 움직이면 제로점 에너지에 의한 위치 지터는 광학 현미경의 200나노미터(0.0002mm) 해상도보다 훨씬 작아집니다.중요한 것은 원자의 초당 14.43미크론의 이동 속도가 절대 0이 아니기 때문에 원자의 모든 운동 에너지를 구성한다는 것입니다.만약 원자가 정확히 절대 0에 있다면, 0점 에너지로 인해 감지할 수 없는 밀림은 원자를 아주 약간만 방황하게 만들겠지만, 원자는 평균적으로 시야 내의 같은 지점에 영구적으로 위치하게 될 것이다.이것은 모터가 꺼진 보트가 현재 비교적 고요하고 바람이 없는 바닷물에서 약간 흔들리는 것과 유사하다. 비록 보트가 무작위로 왔다 갔다 하지만, 그것은 오랜 기간 동안 같은 지점에 머무르며 물 속을 나아가지 못한다.따라서, 정확히 절대 0에 있는 원자는 "움직이지 않을 것"은 아니지만, 통계적으로 유의한 원자의 집합은 다른 원자 집합으로 전달될 수 있는 0의 순 운동 에너지를 가질 것이다.이것은 두 번째 원자 집합의 운동 온도에 관계없이, 그들 역시 제로 포인트 에너지의 효과를 경험하기 때문입니다.통계 역학의 결과와 열역학의 특성입니다.
분자의 내부 운동과 내부 에너지

위에서 언급했듯이, 물질의 운동 온도에 흡수되는 세 가지 변환 자유도 외에 분자가 흔들릴 수 있는 다른 방법이 있다.오른쪽 애니메이션에서 볼 수 있듯이, 분자는 복잡한 물체입니다; 그들은 원자의 집단이고 열 교반으로 인해 세 가지 다른 방식으로 내부 화학 결합을 변형시킬 수 있습니다: 회전, 결합 길이, 결합 각도 움직임; 이것들은 모두 내부 자유도입니다.이것은 분자를 헬륨과 아르곤과 같은 단원자 물질과 구별하게 만들며, 헬륨과 아르곤은 오직 세 가지의 변환 자유도를 가지고 있다.운동 에너지는 분자 내부의 자유도에 저장되며, 분자 내부의 온도를 제공한다.이러한 움직임을 "내부"라고 부르지만, 분자의 외부 부분은 정지해 있는 물 풍선의 꿈틀거림처럼 여전히 움직인다.이것은 각각의 분자 충돌에 따른 내부 운동과 변환 운동 사이의 운동에너지의 양방향 교환을 가능하게 한다.따라서 분자로부터 내부 에너지가 제거됨에 따라 분자 운동 온도(번역 운동의 운동 에너지)와 내부 온도가 동일한 비율로 동시에 감소한다.이 현상은 균등분할정리에 의해 설명되며, 균등분할정리는 입자가 이용할 수 있는 모든 활성자유도에 대해 입자운동의 운동에너지가 균등하게 분포한다는 것을 말한다.분자의 내부 온도는 보통 운동 온도와 같기 때문에, 그 구별은 보통 연소, 고체의 승화, 부분 진공에서의 뜨거운 가스의 확산과 같은 비국소 열역학적 평형(LTE) 현상에 대한 상세한 연구에만 관심이 있습니다.
분자 내부에 저장된 운동 에너지는 물질이 주어진 온도에서 더 많은 열에너지를 포함하고 주어진 온도 상승을 위해 추가적인 내부 에너지를 흡수하도록 합니다.이것은, 주어진 순간에, 내부 운동으로 묶인 어떤 운동 에너지도 분자의 이동 [15]운동에 기여하는 같은 순간에 있지 않기 때문입니다.이 여분의 운동 에너지는 단순히 주어진 온도 상승을 위해 물질이 흡수하는 내부 에너지의 양을 증가시킨다.이 특성은 물질의 비열 용량으로 알려져 있습니다.
다른 분자는 온도가 증가할 때마다 내부 에너지를 흡수합니다. 즉, 분자의 비열 용량이 다릅니다.높은 비열 용량은 부분적으로 특정 물질의 분자가 다른 물질보다 내부 자유도를 더 많이 가지고 있기 때문에 발생합니다.예를 들어, 이원자 분자인 상온 질소는 5개의 활성 자유도를 가지고 있습니다. 즉, 3개의 활성 자유도는 변환 운동과 2개의 내부 회전 자유도로 구성됩니다.당연히 등분할 정리에 따라 질소는 단원자 [16]가스와 마찬가지로 몰당 비열용량(특정 분자 수)의 5/3를 갖는다.또 다른 예는 가솔린입니다(표 참조).휘발유는 각 분자가 평균 21개의 원자로 구성되어 내부 자유도가 높기 때문에 약간의 온도 변화만으로 몰당 많은 양의 열에너지를 흡수할 수 있습니다.더 크고 복잡한 분자도 수십 개의 내부 자유도를 가질 수 있습니다.
열에너지의 확산: 엔트로피, 포논, 이동 전도 전자
열전도는 시스템의 뜨거운 부분에서 차가운 부분으로 열에너지가 확산되는 것입니다.시스템은 단일 벌크 엔티티 또는 여러 개의 이산 벌크 엔티티 중 하나일 수 있다.이 문맥에서 벌크란 통계적으로 유의한 입자의 양(미소한 양일 수 있음)을 의미합니다.고립된 시스템 내에서 열에너지가 확산될 때마다 시스템 내 온도차가 감소합니다(그리고 엔트로피가 증가합니다).
한 가지 특별한 열전도 메커니즘은 입자의 운동인 입자의 운동이 충돌로 입자에서 입자로 운동량을 전달할 때 발생합니다.기체에 있어서 이러한 변환운동은 그림 1과 같은 성질이다.이 애니메이션에서 볼 수 있듯이 연속적인 충돌에 의해 기체의 부피 전체에 운동량(열)이 확산될 뿐만 아니라 분자 또는 원자 전체가 새로운 영역으로 나아가 운동 에너지를 가져올 수 있다.따라서 온도 차이는 기체 전체에 걸쳐 매우 빠르게 균일해집니다. 특히 가벼운 원자나 분자의 경우, 대류는 이 과정을 훨씬 [17]더 빠르게 가속화합니다.
그러나 고체에서의 변환 운동은 포논의 형태를 취한다(오른쪽 그림 4 참조).포논은 제한된 양자화된 파동 패킷으로 특정 물질의 음속으로 이동합니다.고체 내에서 포논이 상호작용하는 방식에 따라 열전도율을 포함한 다양한 특성이 결정됩니다.전기 절연 고형물의 경우 포논 기반의 열전도는 일반적으로 비효율적이며[18] 이러한 고형물은 단열재(유리, 플라스틱, 고무, 세라믹 및 암석)로 간주됩니다.이것은 고체에서는 원자와 분자가 이웃에 대해 제자리에 잠겨 자유롭게 돌아다닐 수 없기 때문입니다.
그러나 금속은 포논 기반의 열전도에만 국한되지 않습니다.열 에너지는 분자와 분자의 직접적인 충돌 대신 매우 가벼운 이동 전도 전자를 통해 전달되기 때문에 금속을 통해 매우 빠르게 전달됩니다.이것이 금속의 열전도율과 전기전도율 [19]사이에 거의 완벽한 상관관계가 있는 이유입니다.전도 전자는 금속이 비국재화(특정 원자에 얽매이지 않음)되고 제로점 에너지의 영향으로 인해 일종의 양자 가스처럼 행동하기 때문에 금속에 비상한 전도성을 주입한다(ZPE에 대한 자세한 내용은 아래 주 1 참조).또한 전자는 정지 질량만으로 비교적 가볍다.양성자의 1/1/1입니다.이는 총을 쏘는 소총과 비교했을 때 .22 쇼트 탄환(29개 또는 1.88g)과 거의 같은 비율이다.아이작 뉴턴이 운동의 제3법칙으로 썼듯이
법칙 3: 모든 힘은 쌍으로 발생하며, 이 두 힘은 크기가 같고 방향이 반대입니다.
하지만 총알은 같은 힘을 가할 때 소총보다 더 빨리 가속한다.운동 에너지가 속도의 제곱에 따라 증가하기 때문에, 비록 둘 다 팽창하는 추진제 가스로부터 같은 힘을 경험하더라도, 거의 모든 운동 에너지가 소총이 아닌 탄환에 들어갑니다.마찬가지로, 그것들은 훨씬 덜 크기 때문에, 열에너지는 이동 전도 전자에 의해 쉽게 전달된다.게다가 그것들은 비국재적이고 매우 빠르기 때문에 운동열 에너지는 풍부한 전도 전자를 가진 금속을 통해 매우 빠르게 전도됩니다.
열에너지의 확산 : 흑체방사

열복사는 원자의 다양한 진동 운동에서 발생하는 충돌의 부산물이다.이러한 충돌은 원자의 전자가 열 광자를 방출하게 만든다.광자는 전하가 가속될 때마다 방출됩니다(두 원자의 전자 구름이 충돌할 때 발생하는 현상).심지어 내부 온도가 절대 0보다 큰 개별 분자들도 원자로부터 흑체 방사선을 방출한다.평형상태의 물질의 부피에서 흑체 광자는 플랑크 곡선이라고 불리는 벨 곡선 모양의 스펙트럼에서 파장 범위에 걸쳐 방출된다(오른쪽 그림 5 참조).플랑크 곡선의 꼭대기(피크 방사 파장)는 흑체의 온도에 따라 전자기 스펙트럼의 특정 부분에 위치합니다.극저온에서 물질은 긴 전파 파장을 방출하는 반면 극저온에서는 짧은 감마선을 생성한다(일반 온도 표 참조).
흑체 복사는 광자가 주변 원자에 흡수되면서 그 과정에서 운동량을 전달하면서 물질 전체에 열에너지를 확산시킨다.흑체 광자는 또한 물질로부터 쉽게 빠져나와 주변 환경에 흡수될 수 있습니다. 그 과정에서 운동 에너지가 손실됩니다.
Stefan-Boltzmann 법칙에 따라 흑체 방사선의 강도는 절대 온도의 네 번째 거듭제곱으로 증가한다.따라서 824K(빛나는 칙칙한 빨간색에 조금 못 미치는)의 흑체는 296K(실온)의 60배의 복사 전력을 방출합니다.그래서 멀리서도 뜨거운 물체의 복사열을 쉽게 느낄 수 있다.백열등에서 볼 수 있는 것과 같은 고온에서는 흑체 복사가 열에너지가 시스템을 빠져나가는 주요 메커니즘이 될 수 있습니다.
열역학 온도표
절대 0부터 절대 고온까지 열역학 온도 척도의 전체 범위와 그 사이의 몇 가지 주목할 점이 아래 표에 나와 있습니다.
| 켈빈 | 피크 방사율 파장[20] 흑체 광자 | |
| 절대 제로 (정의에 따라 정의됨) | 0 K | ∞ [3] |
| 가장 낮은 측정값 온도 [21] | 450 pK | 6,400 km |
| 1밀리켈빈 (정의에 따라 정의됨) | 0.001 K | 2.897 77 m (라디오, FM 대역)[22] |
| 우주 마이크로파 백그라운드 방사선 | 2.725 K | 1.063mm(피크 파장) |
| 물의 삼점 | 273.16 K | 10.6083 µm (장파장 I.R.) |
| ISO 1 표준 온도 정밀 도량형용 (정의상 정확히 20°C) | 293.15 K | 9.88495 µm (장파장 I.R.) |
| 백열등[A] | 2500 K[B] | 1.16 µm (근적외선)[C] |
| 태양의 가시[C][23] 표면 | 5778 K | 501.5 nm (녹색등) |
| 번개의 채널. | 28,000K | 100 nm (원 자외선) |
| 태양핵 | 16 MK | 0.18 nm(X선) |
| 열핵 폭발 (피크 온도)[24] | 350 MK | 8.3 × 10−3 nm (감마선) |
| Sandia 국립 연구소' Z머신[D][25] | 2 GK | 1.4 × 10−3 nm (감마선) |
| 고질량 별의 마지막[26] 날 핵 | 3 GK | 1 × 10−3 nm (감마선) |
| 쌍성 중성자별 시스템을 병합하는 중 | 350 GK | 8 × 10−6 nm (감마선) |
| 감마선 폭발 전구체[28] | 1 TK | 3 × 10−6 nm (감마선) |
| CERN의 양성자와 핵충돌[29] | 10 TK | 3 × 10−7 nm (감마선) |
| Universe 5.391 × 10초−44 빅뱅 이후 | 1.417 × 1032 K | 1.616 × 10−26 nm (플랭크 주파수)[30] |
상열 변화
입자 운동의 운동 에너지는 물질 내 총 열 에너지에 기여하는 한 가지에 불과하고, 또 다른 것은 상전이이며, 이것은 물질이 냉각될 때 형성될 수 있는 분자 결합의 잠재적 에너지입니다(예: 응축 및 동결).상전이에 필요한 열에너지를 잠열이라고 합니다.이 현상은 반대 방향으로 생각하면 더 쉽게 파악할 수 있습니다. 잠열은 화학 결합을 끊는 데 필요한 에너지입니다(예: 증발 및 용해 중).거의 모든 사람이 상전이의 영향을 잘 알고 있습니다. 예를 들어, 100°C에서 증기를 뿜으면 헤어 드라이어의 100°C 공기보다 훨씬 빠르게 심한 화상을 입을 수 있습니다.이는 수증기가 응축되면서 피부에 있는 액체 상태의 물로 다량의 잠열이 방출되기 때문이다.
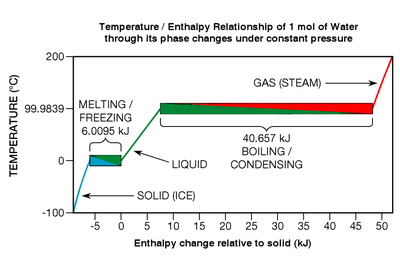
상전이 중에 열에너지가 해방되거나 흡수되더라도 순수한 화학 원소, 화합물 및 공정 합금은 어떠한 온도 변화도 보이지 않습니다(아래 그림 7 참조).한 가지 특정 유형의 상전이를 고려해 보십시오. 바로 용해입니다.고체가 녹을 때, 결정 격자 화학 결합은 분해됩니다; 그 물질은 더 질서 있는 상태로 알려진 상태에서 덜 질서 있는 상태로 이행하고 있습니다.그림 7은 파란색에서 녹색으로 향하는 왼쪽 하단 상자 안에서 얼음이 녹는 모습을 보여준다.
특정 열역학 지점인 녹는점(물의 경우 넓은 압력 범위에 걸쳐 0°C)에서 모든 원자 또는 분자는 평균적으로 격자에서 벗어나지 않고 화학 결합을 견딜 수 있는 최대 에너지 임계값에 도달합니다.화학적 결합은 모두 아니면 아무것도 아닌 힘이다: 그것들은 단단하게 유지되거나 끊어진다; 중간 상태는 없다.결과적으로, 물질이 녹는점에 있을 때, 추가된 열에너지의 모든 줄들은 원자나 [31]분자의 특정 양의 결합을 끊고, 그것들을 정확히 같은 온도의 액체로 변환합니다; 운동 에너지는 번역 운동에 추가되지 않습니다(그것이 물질의 온도를 주는 것입니다).그 효과는 팝콘과 비슷합니다: 특정 온도에서 추가적인 열에너지는 전환이 완료될 때까지 알맹이를 더 뜨겁게 만들 수 없습니다.(액체의 동결과 같이) 프로세스가 역방향일 경우 물질에서 열에너지를 제거해야 한다.
상기와 같이 상전이에 필요한 열에너지를 잠열이라고 합니다.녹는 것과 얼리는 것의 특정한 경우, 그것은 융합의 엔탈피 또는 융합의 열이라고 불립니다.결정 격자의 분자 결합이 강할 경우, 물과 대부분의 금속 [32]원소의 경우 일반적으로 몰당 6~30kJ의 범위에서 융해 열이 상대적으로 클 수 있다.물질이 (분자 결합을 형성하는 경향이 거의 없는) 단원자 가스 중 하나일 경우, 핵융합 열은 [33]몰당 0.021 ~ 2.3 kJ로 더 약하다.상대적으로 말하면, 상전이란 정말로 에너지적인 사건일 수 있습니다.0°C에서 얼음을 0°C에서 물에 완전히 녹이려면 동일한 액체 물 덩어리의 온도를 섭씨 1도 상승시키는 데 필요한 열 에너지의 약 80배를 추가해야 한다.금속의 비율은 훨씬 더 크며, 일반적으로 400배에서 1200배 [34]사이입니다.그리고 끓는 상전이 냉동보다 훨씬 더 강력합니다.예를 들어 물을 완전히 끓이거나 증발시키는 데 필요한 에너지(기화 엔탈피로 알려진 것)는 1도 [35]상승에 필요한 에너지의 약 540배입니다.
물의 상당한 증발 엔탈피는 수증기가 응축될 정도로 피부가 빨리 탈 수 있는 이유이다(위의 그림 7에서 빨간색에서 녹색으로 향함).반대로 액체 상태의 물이 증발하면서 피부가 시원해지는 이유다(상대습도에 따라 습구온도 이하에서 일어나는 과정이다.물의 고에너지 증발 엔탈피는 또한 왜 태양 전지 덮개가 난방비를 줄이는데 매우 효과적인지에 대한 기초가 되는 중요한 요소이다: 그것들은 증발을 방지한다.예를 들어, 1.29m 깊이의 수영장에서 불과 20mm의 물이 증발하면 물은 섭씨 8.4도(15.1°F)로 냉각됩니다.
내부 에너지
전도 전자를 포함한 모든 입자 운동 및 내부 에너지의 총합과 위상 변화의 잠재적 에너지, 그리고 0점[3] 에너지는 물질의 내부 에너지를 구성합니다.
절대 영점에서의 내부 에너지
물질이 냉각됨에 따라, 다른 형태의 내부 에너지와 그 관련 효과는 동시에 크기가 감소합니다: 물질이 덜 질서 있는 상태에서 더 질서 있는 상태로 변화함에 따라 사용 가능한 상 전이의 잠열이 방출됩니다; 원자와 분자의 이동 운동이 감소합니다(운동 온도 감소).분자의 내부운동은 감소한다(내부온도는 감소한다). 전도전자(물질이 전기전도체일 경우)는 다소 느리게 이동한다. 그리고 흑체 복사의 피크 방사 파장은 증가한다(광자의 에너지는 감소한다).물질의 입자가 가능한 한 가깝게 정지하고 ZPE에 의해 유도되는 양자역학적 움직임만 유지하면 물질의 온도는 절대영도(T=0)가 된다.

절대 0은 열역학적 온도가 0인 점이며 물질의 입자 성분이 최소의 움직임을 갖는 점이지만 절대 0은 물질이 반드시 내부 에너지를 0으로 포함하는 지점이 아닙니다. 내부 에너지가 무엇을 의미하는지 매우 정밀해야 합니다.종종 물질에서 발생할 수 있는 모든 위상 변화는 절대 0에 도달할 때까지 발생합니다.하지만 항상 그렇지는 않다.특히 T = 0 헬륨은 실압에서 액체 상태로 유지되며(오른쪽 그림 9), 결정화하려면 25bar(2.5MPa) 이상의 압력을 받아야 한다.헬륨의 핵융합 열(헬륨 얼음을 녹이는 데 필요한 에너지)이 너무 낮아서(몰당 21줄에 불과) 0점 에너지의 운동 유발 효과가 더 낮은 압력에서 얼지 않도록 하기에 충분하기 때문이다.
또 다른 문제는 많은 고체가 결정 구조를 매우 높은 압력(최대 수백만 바 또는 수백 기가파스칼)에서 보다 콤팩트한 배열로 변경한다는 것입니다.이러한 현상을 고체-고체상 전이라고 하며, 결정 격자가 열역학적으로 유리한 소형 격자로 변화함에 따라 잠열이 방출됩니다.
위의 복잡성은 T = 0 물질의 내부 에너지에 관한 다소 번거로운 포괄적 문구를 만든다.그러나 압력에 관계없이 절대 영점에서는 가장 가까운 배열(왼쪽 위 그림 8 참조)을 가진 가장 낮은 에너지 결정 격자를 가진 모든 고체는 최소 내부 에너지를 포함하며, 항상 존재하는 0점 [3] [37]에너지의 배경 때문에 그 에너지만 유지한다고 말할 수 있다.또한 일정한 압력에서 주어진 물질에 대해 절대 0은 엔탈피(내부 에너지, 압력 및 부피를 고려한 [38]작업 전위의 측정)가 가장 낮은 지점이라고 말할 수 있다.마지막으로, 모든 T = 0 물질은 0의 운동 열에너지를 [3] [13]포함하고 있다고 말하는 것은 항상 사실이다.
열역학적 온도의 실용적 응용
열역학적 온도는 과학자들뿐만 아니라 가스와 관련된 많은 분야의 일반인들에게도 유용할 수 있습니다.절대적인 용어로 변수를 표현하고 Gay-Lussac의 온도/압력 비례 법칙을 적용함으로써 일상적인 문제에 대한 해결책은 간단합니다. 예를 들어, 온도 변화가 자동차 타이어 내부의 압력에 어떻게 영향을 미치는지 계산하는 것입니다.타이어의 냉간[39] 게이지 압력이 200kPa이면 절대 압력은 300kPa입니다.[40][41]실온(타이어 용어로 차가운)은 296 K입니다.타이어 온도가 20°C(20kelvins) 더 높을 경우 용액은 316K/296K = 6.8% 더 높은 열역학 온도 및 절대 압력, 즉 게이지 압력 220kPa의 절대 압력으로 계산됩니다.
이상기체의 법칙과의 관계
열역학적 온도는 이상적인 가스 법칙과 그 결과와 밀접하게 관련되어 있습니다.그것은 열역학 제2법칙과도 연관될 수 있다.열역학적 온도는 특별한 특성을 가지며, 특히 이상적인 열 엔진의 효율성을 고려함으로써 (일부 일정한 승수까지) 고유하게 정의된 것으로 볼 수 있다.따라서 두 온도1 T와2 T의 비율2 T/T는1 모든 절대 척도에서 동일합니다.
엄밀히 말하면, 시스템의 온도는 열평형 상태에 있을 때만 명확하게 정의됩니다.현미경으로 보면, 개별 입자간의 열량이 상쇄되면 물질은 열평형 상태에 있다.물리적 현상에 대한 다양한 관측에서 도출된 많은 가능한 온도 척도가 있습니다.
대략적으로 말하면, 온도 차이는 두 시스템 간의 열 방향을 결정하며, 결합된 에너지가 가능한 가장 낮은 상태로 최대한 분산되도록 합니다.우리는 이 분포를 "엔트로피"라고 부릅니다.온도와 엔트로피의 관계를 더 잘 이해하려면 Carnot 열 엔진에 설명된 열, 작업 및 온도 간의 관계를 고려하십시오.엔진은 가스 충전 피스톤을 통해 고온 열원 T와H 저온 열 싱크 T 사이의C 온도 구배를 유도하여 열을 작업으로 변환합니다.사이클당 수행되는 작업은 고온 소스로부터 엔진이 차지하는 열H q와 엔진에서 발생하는 폐열의 합인 qC < [42]0인 순열과 같은 크기입니다.엔진의 효율은 시스템에 가해지는 열로 나눈 작업입니다.
Carnot의 정리는 동일한 열 저장고 사이에서 작동하는 모든 가역 엔진은 동등하게 효율적이라는 것입니다.따라서 온도1 T와 온도2 T 사이에서 작동하는 모든 가역 열 엔진은 동일한 효율성을 가져야 합니다. 즉, 효율은 온도의 함수입니다.
또한 온도1 T와3 T 사이에서 작동하는 가역 열 엔진은 T와 다른 (중간) 온도2 T 사이1, 그리고 T와3 T 사이의2 두 번째 사이클로 구성된 것과 동일한 효율성을 가져야 합니다.그렇지 않을 경우 에너지(q의 형태)가 낭비되거나 획득되어 사이클이 컴포넌트 사이클로 분할될 때마다 전체적인 효율이 달라집니다.분명히 사이클은 작은 사이클의 수에 관계없이 구성할 수 있습니다.
수학적으로 Q, Q23, Q를 이해하면1
그러나 첫 번째 함수는 T의2 함수가 아니기 때문에, 최종 두 함수의 곱은 변수로 T를 제거해야2 한다.따라서 함수 f를 다음과 같이 정의하는 방법밖에 없습니다.
즉, 교환되는 열의 비율은 각 열이 발생하는 온도의 함수이다.We can choose any monotonic function for our ; it is a matter of convenience and convention that we choose 다음으로 하나의 고정 기준 온도(즉 물의 3중점)를 선택하여 열역학적 온도 척도를 설정합니다.
이러한 정의는 이상적인 기체 유도 정의와 일치합니다. 또한 열역학적 온도의 정의는 T와C T의 관점에서H 카르노 효율을 나타낼 수 있게 하며, 따라서 (완전한) 카르노 사이클이 등방성이라는 것을 도출합니다.
이를 효율성에 대한 첫 번째 공식에 대입하면 온도와 관련하여 다음과 같은 관계가 생성됩니다.
T = 0의 경우C 효율이 100%이고 T < 0의 경우C 효율이 100% 이상 된다는 점에 유의하십시오. 이는 비현실적입니다.방정식 (4)의 오른쪽과 중간 부분에서 1을 빼면 C q - TH (\{q_가 됩니다. 등
이 방정식의 일반화는 정리이며, 다음과 같이 정의된 상태 S, 어떻게 그 상태에 도달했는지에 의존하지 않는 함수)의 존재를 제안한다.
| (5) |
여기서 첨자는 가역 프로세스에서의 열 전달을 나타냅니다. S S는 앞에서 설명한 시스템의 엔트로피이며, 모든 사이클에서 S S의 는 0입니다(상태 기능에 필요).식 5는 엔트로피와 열의 관점에서 온도에 대한 대체 정의를 얻기 위해 재배열할 수 있습니다(논리 루프를 피하기 위해 먼저 통계 역학을 통해 엔트로피를 정의해야 합니다).
S S가 에너지 E E의 S S인 정용량 시스템의 경우 와 열역학적 T(\ T는 다음과 같습니다.
역사
1702–1703: 기욤 아몬톤스 (1663–1705)는 절대 0을 특징으로 하는 기본(열역학) 온도 척도의 존재를 추론한 최초의 연구자로 그를 신뢰하기 위해 사용될 수 있는 두 개의 논문을 발표했다.그는 당시 사용하던 공기 온도계를 개선하기 위해 노력하던 중 이 사실을 발견했다.그의 J-튜브 온도계는 온도계의 감지 부분 안에 갇힌 고정된 공기 덩어리에 의해 지탱되는 수은 기둥으로 구성되었다.열역학적 관점에서 그의 온도계는 일정한 압력 하에서 가스의 부피/온도 관계에 의존했다.물의 끓는점과 얼음의 녹는점에 대한 그의 측정은 그의 온도계 안에 갇힌 공기의 질량이나 공기가 지탱하는 수은의 무게와 상관없이 얼음 지점의 공기 부피의 감소는 항상 같은 비율이라는 것을 보여주었다.이러한 관찰을 통해 그는 충분한 온도 저하가 공기량을 0으로 감소시킬 것이라고 단언했다.사실, 그의 계산 결과 절대 0은 -240°C에 해당하며, 이는 실제 값인 -273.15°C보다 33.15도만 부족한 수치입니다.절대 온도와 절대 압력 사이의 일대일 관계에 대한 아몬톤의 발견은 한 세기 후에 다시 발견되었고 조셉 루이스 게이-루삭에 의해 과학계에서 널리 알려졌습니다.오늘날, 이 열역학의 원리는 일반적으로 게이-루삭의 법칙으로 알려져 있지만 아몬톤의 법칙으로도 알려져 있습니다.
1742: 앤더스 셀시우스 (1701–1744)는 현대의 셀시우스 온도 척도의 "뒤로" 버전을 만들었다.셀시스의 원래 척도에서 0은 물의 끓는점을 나타내고 100은 얼음의 녹는점을 나타냅니다.온도계에 대한 두 개의 지속적 도에 대한 그의 논문에서, 그는 얼음의 녹는점이 압력에 의해 효과적으로 영향을 받지 않는다는 것을 보여주는 그의 실험을 이야기했다.그는 또한 물의 끓는점이 대기압의 함수로서 어떻게 변화하는지 놀라운 정밀도로 알아냈다.그는 평균 해수면에서의 평균 기압에서 온도 척도(물의 비등점) 0을 보정할 것을 제안했다.
1744년: 앤더스 셀시우스의 죽음과 동시에, 유명한 식물학자 칼 린네 (1707–1778)는 0이 얼음의 녹는점을 나타내고 100이 물의 끓는점을 나타내는 그의 첫 번째 온도계를 받자마자 셀시우스의 눈금을 효과적으로[44] 뒤집었다.그의 온실에서 사용하기 위해 맞춤 제작된 린네우스 온도계는 그 당시 스웨덴의 과학 기구 제조사 다니엘 에크스트롬에 의해 만들어졌다.이후 204년 동안 전 세계 과학 및 온도 측정 커뮤니티에서는 이 척도를 섭씨 척도라고 불렀습니다.섭씨 눈금의 온도는 종종 단순히 도 또는 더 큰 특이성이 필요한 경우 도로 보고되었다.이 척도의 온도 값 기호는 °C였다(수년간 여러 형식으로).센티그라드라는 용어는 각도 측정 단위(직각의 100분의 1)의 프랑스어 이름이기도 하고 다른 언어에서도 비슷한 의미를 가지고 있기 때문에, "센티시멀 도"라는 용어는 국제 표준 기구(International Bureau of Weights)와 같은 매우 정확하고 모호하지 않은 언어가 요구되었을 때 사용되었습니다.nd 측정(Bureau international des poids et mesure)(BIPM).제9회 CGPM(체중 및 측정에 관한 일반회의(Confrence généale des poids et mesure))와 CIPM(Comité international des poids et mesure)은 [46]1948년에 공식적으로[45] 섭씨(기호: °C)를 채택했다.
1777: 그의 책 피로메트리에서 (베를린:Haude & Spener, 1779)는 죽기 4개월 전에 완성되었고, Johann Heinrich Lambert (1728–1777)는 때때로 Joseph Lambert로 잘못 불리며, 고정된 가스 부피의 압력/온도 관계에 기초한 절대 온도 척도를 제안했다.이것은 기욤 아몬톤스가 75년 전에 발견한 일정한 압력 하에서 가스의 부피와 온도 관계와는 다릅니다.램버트는 절대 0이 단순한 직선 외삽이 0 가스 압력에 도달한 지점이며 -270°C와 동일하다고 밝혔다.
Circa 1787: 85년 전 기욤 아몽톤의 연구에도 불구하고, 자크 알렉상드르 세사르 샤를(1746–1823)은 종종 일정한 압력 하에서 가스의 부피가 절대 온도에 비례한다는 것을 발견했지만 발표하지는 않았다.그가 만든 공식은1 V/T1 = V2/T입니다2.
1802: Joseph Louis Gay-Lussac (1778–1850)은 일정한 압력 하에서 가스의 부피가 절대(열역학) 온도와 선형으로 어떻게 변화하는지를 설명하는 연구 결과를 발표했습니다.이 행동은 찰스의 법칙이라고 불리며 가스 법칙 중 하나이다.이 공식은 얼음의 녹는점에 상대적인 가스 팽창 계수에 273을 사용한 최초의 공식입니다(절대 0이 -273°C와 동일함을 나타냄).
1848년: 켈빈 경으로도 알려진 윌리엄 톰슨(1824–1907)은 그의 논문 "절대 온도 측정 척도에 대하여"에서 무한 추위가 영점이고 그 단위 증가에 섭씨도를 사용하는 척도의 필요성에 대해 썼다.Gay-Lussac과 마찬가지로, Thomson은 절대 0이 당시의 공기 온도계에서 -273°C에 해당한다고 계산했습니다.이 절대 척도는 오늘날 켈빈 열역학 온도 척도로 알려져 있습니다.주목할 점은 Thomson의 값 -273은 실제로 0.00366에서 도출되었으며, 이는 빙점에 대한 섭씨당 가스의 허용 팽창 계수였습니다.유효 자릿수 5자리까지 표현되는 -0.00366의 역수는 -273.22°C로, 실제 값인 -273.15°C에 상당히 가깝다.
1859: 맥콘 랭킨(1820–1872)은 윌리엄 톰슨과 비슷하지만 단위 증분에 화씨도를 사용한 열역학 온도 척도를 제안했다.이 절대 척도는 오늘날 랭킨 열역학 온도 척도로 알려져 있습니다.
1877–1884: 루드비히 볼츠만(1844–1906)은 입자 역학과 흑체 복사가 수행하는 역할을 이해함으로써 열역학에 큰 기여를 했다.그의 이름은 오늘날 열역학에서 사용되는 공식들 중 몇 개에 붙여졌다.
1930년대 전후: 얼음의 녹는점과 물의 끓는점에 세심하게 보정된 가스 온도 측정 실험 결과 절대 영도는 -273.15°C에 해당합니다.
1948년: 제9차 CGPM(Conférence Généale des Poids et Mesures, 중량 및 측정에 관한 총회라고도 함)의 결의안 3은 물의 삼중점을 정확히 0.01°C로 고정했다.이때, 삼중점은 여전히 동등한 켈빈 값에 대한 공식적인 정의가 없었고, 결의안은 "나중에 고정될 것"이라고 선언했다.1930년대에 측정된 절대 영점 값이 정말로 -273.15°C이면 물의 삼중점(0.01°C)은 273.16K에 해당한다. 또한 CIPM(Comité International des poids et mesures, 국제 가중치 및 CGPM 측정 위원회라고도 공식적으로 알려져 있다.)섭씨와 섭씨 온도 척도에 대한 sius. [46]
1954년: 제10차 CGPM의 해상도 3은 물의 3중점을 상부 정의점으로 선택하고(절대 0에 대한 변화가 없음), 정확하게 273.16 켈빈(당시 실제로 273.16 켈빈으로 표기)의 온도를 할당함으로써 켈빈 척도를 현대적으로 정의했다.이것은 9번째 CGPM의 해결법 3과 함께 절대 영점을 정확히 0 켈빈과 -273.15°C로 정의하는 효과가 있었다.
1967/1968: 제13차 CGPM의 결의안 3은 열역학적 온도 켈빈(기호 K)의 단위 증가량을 절대도, 기호 °K로 변경했다.또한 제13차 CGPM은 단위증가의 크기를 보다 명확하게 규정하는 것이 유용하다고 판단하여 결의안 4에서 "열역학 온도의 단위인 켈빈은 물의 3중점 열역학 온도의 1/273.16이다"라고 결정했다.
2005년: CIPM(Comité International des Poids et Mesures, International Committee for Measures)은 물의 삼중점 온도를 기술하기 위해 켈빈 열역학 온도 척도의 정의는 p로 정의된 동위원소 조성을 가진 물을 지칭할 것이라고 단언했다.비엔나 표준 평균 해양수의 공칭 사양과 상당히 동일해야 한다.
2019년 : 2018년 11월, 제26차 도량형총회(CGPM)는 Kelvin의 정의를 Boltzmann 상수(단위 J/K)를 1.380649×10으로−23 수정하여 변경하였다.이 변경(및 SI 단위 정의의 기타 변경)은 미터 협약 144주년인 2019년 5월 20일에 발효되었다.
「 」를 참조해 주세요.
메모들
- 다음 주에서는 1.85487(14)×10과43 같이 수치적 동등성이 간결한 형태로 나타나는 경우, 괄호 사이의 두 자릿수는 유의한 두 자릿수의 1-µ(1 표준 편차, 68% 신뢰 수준)에서 불확실성을 나타낸다.
- ^ 랭킨, W. J. M., "증기 엔진 및 기타 원동기에 대한 설명서", 리처드 그리핀과 회사, 런던 (1859), 페이지 306-307.
- ^ 윌리엄 톰슨, 제1대 켈빈 남작, "히트", 아담과 찰스 블랙, 에든버러(1880), 페이지 39.
- ^ a b c d e 과학자들은 절대 영도에 가까운 온도를 달성하고 있지만, 완전히 영도의 상태에 이르지는 못한다.그러나 과학자들이 물질에서 모든 운동열 에너지를 제거할 수 있다고 해도 양자역학 제로포인트 에너지(ZPE)는 절대 제거할 수 없는 입자 운동을 일으킨다.브리태니커 백과사전은 제로포인트 에너지를 "분자가 절대 0도 온도에서도 유지하는 진동 에너지"로 정의한다.ZPE는 자연의 기본 입자 사이의 진공에 있는 모든 퍼베이시브 에너지장의 결과입니다. 이것은 카시미르 효과와 다른 현상의 원인이 됩니다.제로 포인트 에너지 및 제로 포인트 필드를 참조하십시오.헬륨의 보스-아인슈타인 응축수에 대한 ZPE의 영향에 대한 자세한 내용은 Alberta 대학 물리학부의 웨이백 기계에서 보관된 고체 헬륨 2008-02-12를 참조하십시오.
절대 영점(T=0)은 0 분자 운동의 상태는 아니지만, 0 온도의 점이며 볼츠만 상수에 따라 0 입자 운동 에너지와 0 운동 속도의 점이기도 하다.원자가 어떻게 운동 속도가 0인 동시에 ZPE에 의해 진동할 수 있는지를 이해하기 위해, 다음의 사고 실험을 고려하세요: 무중력 상태에서 두 개의 T=0 헬륨 원자는 조심스럽게 배치되고 그들 사이에 평균 620 pm의 간격이 있는 것으로 관찰됩니다(원자 지름 10의 간격).ZPE로 인해 고정 위치에 대해 서로 밀리게 되므로 이는 "평균"의 분리입니다.그런 다음 원자 하나에 정확히 83요코켈빈(1 yK = 1×10−24 K)의 운동 킥이 주어진다.이것은 이 원자의 속도 벡터를 다른 원자에게 향하게 하는 방식으로 이루어집니다.83yK의 운동 에너지가 있는 상태에서 공통 바리센터를 통과하는 620pm 간격은 719pm/s의 속도로 닫히고 0.862초 후에 충돌한다.이것은 위의 그림 1과 같은 속도입니다.운동 킥이 주어지기 전에, T=0 원자는 ZPE에 의해 밀리고 있음에도 불구하고 그 상태와 상대적인 방향에서 무한히 지속할 수 있기 때문에 운동 에너지와 운동 속도가 0이었다.T=0에서는 다른 시스템으로의 전달에 사용할 수 있는 운동에너지가 없다.볼츠만 상수와 그 관련 공식은 입자 역학과 속도 벡터의 영역을 설명하는 반면, ZPE는 양자 역학의 수학에 의해 기술된 방식으로 입자를 밀어내는 에너지장이다.가스의 원자 및 분자 충돌에서 ZPE는 카오스 정도, 즉 예측 불가능성을 발생시켜 역학을 반발시킨다. 즉, 특정 충돌 후 ZPE에 의해 유발되는 입자 운동이 더 적을 수 있다.ZPE의 이러한 무작위 특성은 T>0K 가스의 부피 양(통계적으로 유의한 입자 양)의 압력이나 부피 모두에 영향을 미치지 않는 이유이다.그러나 T=0 응축 물질(예: 고체 및 액체)에서 ZPE는 원자가 완전히 정지해 있는 원자간 밀림을 일으킨다.ZPE가 물질에 미치는 실제 영향은 열역학 시스템에 따라 달라질 수 있습니다(예를 들어, ZPE에 의해 헬륨은 최소 25bar 또는 2.5MPa의 압력이 가해지지 않는 한 동결되지 않습니다). ZPE는 열에너지의 형태로 물질의 내부 에너지를 계산할 때 적절히 포함될 수 있습니다.
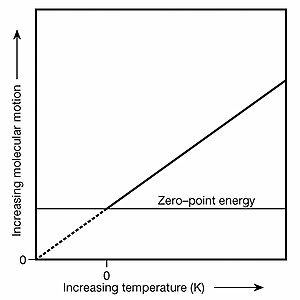
또한 절대 0은 열역학 및 그 방정식이 "계"(복수의 입자와 평균으로 모델링된 장) 간의 열 에너지 교환을 다루기 때문에 열역학 및 그 방정식이 기초되는 기준선으로 작용한다.따라서 절대 0에 있는 시스템 내에서 ZPE에 의해 유도되는 입자 운동을 조사할 수 있지만 이러한 시스템으로부터의 열에너지의 순유출은 결코 있을 수 없다.또한 흑체 복사의 피크 방사 파장은 절대 0에서 무한대로 변화한다. 실제로 피크는 더 이상 존재하지 않으며 흑체 광자는 더 이상 탈출할 수 없다.그러나 ZPE로 인해 가상 광자는 여전히 T=0에서 방출됩니다.이러한 광자는 가로채고 관찰할 수 없기 때문에 "가상"이라고 불립니다.게다가 이 제로 포인트 방사선은, 독자적인 제로 포인트 스펙트럼을 가지고 있다.그러나 T=0 시스템이 0점 방사선을 방출하더라도 주변 환경이 T=0보다 높은 온도일 경우 열이 내부로 유입되고 주변 환경이 T=0일 경우 내부와 외부 모두에서 동일한 ZP 방사선의 플럭스가 발생하기 때문에 이러한 시스템으로부터의 순열류 Q가 발생할 수 없다.ZPE 유도 광자의 자발적 방출과 함께 T=0에도 유사한 Q 평형이 존재한다(이 문맥에서는 자극 방출이라고 더 적절하게 불린다).오른쪽 상단의 그래프는 절대 0과 0점 에너지의 관계를 보여줍니다.또한 이 그래프는 제로점 에너지가 어떻게 그 이름을 얻었는지 이해하는 데 도움이 됩니다. 즉, 제로점 에너지가 제로점 켈빈점에 유지되는 진동 에너지 물질입니다.판데르발스 힘을 포함한 고전적인 열역학 연산을 통한 고전적인 전자기 영점 방사선 스펙트럼의 도출, 다니엘 C.Cole, Physical Review A, 42(1990) 1847.
- ^ CODATA 값: 볼츠만 상수.상수, 단위 및 불확실성에 대한 NIST 참조.미국 국립 표준 기술 연구소
- ^ 조지아 주립 대학교, 하이퍼 물리 프로젝트, "Equipartition of Energy"
- ^ "SI brochure, section 2.1.1.5". International Bureau of Weights and Measures. Archived from the original on 26 September 2007. Retrieved 9 May 2008.
- ^ Newell, D B; Cabiati, F; Fischer, J; Fujii, K; Karshenboim, S G; Margolis, H S; de Mirandés, E; Mohr, P J; Nez, F; Pachucki, K; Quinn, T J; Taylor, B N; Wang, M; Wood, B M; Zhang, Z; et al. (Committee on Data for Science and Technology (CODATA) Task Group on Fundamental Constants) (29 January 2018). "The CODATA 2017 values of h, e, k, and NA for the revision of the SI". Metrologia. 55 (1): L13–L16. Bibcode:2018Metro..55L..13N. doi:10.1088/1681-7575/aa950a.
- ^ "SI Redefinition – Kelvin: Boltzmann Constant". National Institute of Standards and Technology. Archived from the original on 1 July 2020. Retrieved 13 Dec 2020.
- ^ "Accoustic Thermometry". National Institute of Standards and Technology. Archived from the original on 23 September 2020. Retrieved 13 Dec 2020.
- ^ 약 30GK 미만의 비상대론적 온도에서 고전 역학은 입자의 속도를 계산하기에 충분하다.30 GK에서 개별 중성자(중성자별의 구성 성분과 이 범위의 온도를 가진 우주에서 몇 안 되는 물질 중 하나)는 1.0042µ(감마 또는 로렌츠 인자)를 갖는다.따라서 운동 에너지의 고전적인 뉴턴 공식은 30 GK 미만의 온도에서 0.5퍼센트 미만의 오차를 보인다.
- ^ 짝수실-온도 공기는 평균 분자 변환 속도(벡터 절연 속도가 아님)가 1822km/시이다.1입방밀리미터에 대략 2.42×10개씩16 모여 있는 것을 고려하면 분자 크기의 물질치고는 비교적 빠른 속도이다.전제 조건:습한 공기의 평균 분자량 = 28.838 g/g 및 T = 296.15 K. 가정 주요 변수:평균 해수면 위의 고도 194m(인간 거주지의 전 세계 중위 고도), 실내 온도 23°C, 이슬점 9°C(상대 습도 40.85%), 해수면 760mmHg(101.325kPa)-보정 기압.
- ^ 인용: 광학 격자에서 700nK까지 세슘 단열 냉각, A. Kastberg 등, Physical Review Letters 74, No. 9, 1995년 2월 27일, 페이지 1542.주목할 점은 나트륨 원자의 보스-아인슈타인 응축액에서 450pK의 기록적인 저온 온도(A. E. Leanhardt et al.에 의해 달성됨)이다.평균 벡터 절연 원자 속도 0.4mm/s, 평균 원자 속도 0.7mm/s에 해당한다.
- ^ a b 원자와 분자의 변환 운동 속도는 열역학 온도에 따라 다음과 같이 계산됩니다.어디서...
- ~ {\는 m/s 단위의 변환 입자 움직임의 벡터 평균 속도입니다.
- kB(볼츠만 상수) = 1.380649×10−23 J/K
- T는 켈빈 단위의 열역학 온도입니다.
- m은 물질의 분자량(kg/g)이다.
서 s 는 m/s 단위의 변환 입자 운동 속도입니다 .물질의 구성 입자의 이동 운동의 평균 에너지는 속도가 아닌 평균 속도와 관련이 있습니다.따라서 운동에너지의 고전적인 공식에서 s~(\를 v로 하면 Ek = 1µ2m µv는2 E = 3/2kT와B 정확히mean 동일한 값을 생성한다(운동 에너지의 특성, 번역 운동 및 온도 섹션 참조).볼츠만 상수와 그 관련 공식은 절대 0이 입자 움직임의 제로 운동 에너지와 제로 운동 속도 양쪽의 점이라는 것을 증명한다 (위 참고 1 참조). - ^ 부엌 알루미늄 박 두 장(0.04 mm)이 적도에서 지구 주변 거리에 있는 것과 같이 1 켈빈의 1조분의 1은 1 켈빈이다.
- ^ 분자의 내부 자유도는 분자의 외부 표면을 진동시키고 전체적인 회전 운동을 발생시킬 수 있습니다(그렇지 않으면 정지해 있는 물 풍선의 흔들림이나 회전과 비슷합니다).만약 한 분자가 용기의 벽에 충돌하면서 하나의 분자를 조사한다면, 분자의 내부 자유도에서 전달되는 운동 에너지의 일부는 충돌 순간 동안 그것의 번역 운동에 건설적으로 추가될 수 있고 여분의 운동 에너지는 용기의 벽으로 전달될 것이다.이는 컨테이너의 평균 압력에 추가적인 국소적인 임펄스 같은 기여를 유도할 것입니다.그러나 분자의 내부 운동은 무작위이기 때문에 용기의 벽이나 다른 분자와 충돌할 때 파괴적으로 번역 운동을 방해할 확률이 동일합니다.가스의 부피 양에 걸쳐 평균화된 분자의 내부 열 운동은 가스의 온도, 압력 또는 부피에 전혀 영향을 미치지 않습니다.분자의 내부 자유도는 단순히 운동 에너지가 저장되는 추가 장소를 제공한다.이것이 바로 분자 기반 가스가 단원자 가스보다 더 큰 특정 내부 용량을 갖는 이유입니다(여기서 주어진 온도 상승을 달성하기 위해 추가적인 내부 에너지가 추가되어야 한다.
- ^ 일정한 압력으로 측정할 경우 서로 다른 양의 작업을 수행해야 하므로 일정 부피로 측정할 때.질소의 CH(100kPa, 20°C)는v 20.8J–1 mol–1 K 대 12.4717J–1 mol–1 K인 단원자 가스와 같다.인용: W.H. 프리먼의 물리화학, Part 3: 변화 (PDF 형식 422 kB), 연습 21.20b, 787페이지.또한 조지아 주립 대학의 몰 특정 가스 가열도 있습니다.
- ^ 가스의 부피 전체에 걸쳐 열에너지가 균등해지는 속도는 매우 빠릅니다.그러나 가스는 고형물에 비해 밀도가 매우 낮기 때문에 가스를 통과하는 열유속(면적당 열출력)은 상대적으로 낮습니다.이것이 다중 창문의 데드 에어 스페이스가 단열성을 갖는 이유입니다.
- ^ 다이아몬드는 주목할 만한 예외이다.매우 양자화된 포논 진동 모드는 단단한 결정 격자에서 발생합니다.따라서 다이아몬드는 비열용량이 매우 낮을 뿐만 아니라 열전도율도 매우 높습니다.
- ^ 7:1 전도율 범위에서 상관관계는 752(WµmµK−1−1)/(MSµcm), θ = 81이다.Ag, Cu, Au, Al, Ca, Be, Mg, Rh, Ir, Zn, Co, Ni, Os, Fe, Pa, Pt, Sn 데이터에 근거한 값과 표준 편차.인용:CRC Handbook of Chemistry and Physics, 제1회 학생판 및 Web Elements 홈페이지 링크의 데이터.
- ^ 인용된 방출 파장은 평형 상태의 진짜 흑체를 위한 것이다.이 표에서는 태양만이 자격이 있다.CODATA 권장값 2.897771955…×10mkK−3 빈 변위법 상수 b에 사용.
- ^ 2003년 MIT의 연구진은 나트륨(Na)23 원자의 보스-아인슈타인 응축수(BEC)에서 450 ±80 pK의 아레코드 저온 온도를 달성했다. 인용:냉각 보스-아인슈타인 응축수 500 피코켈빈 이하, A. E. Leanhardt et al., Science 301, 2003년 9월 12일, 1515페이지.원자의 열속도는 평균 0.4mm/s였다.주목할 만한 것은 이 기록의 최대 방출 흑체 파장 6400km가 대략 지구의 반지름이라는 점이다.
- ^ 2 .897 77m의 피크 방사 파장은 103.456MHz의 주파수입니다.
- ^ 측정은 2002년에 이루어졌으며 ±3 켈빈의 불확실성을 가지고 있다.1989년 측정에서 5777 ± 2.5 K의 값이 나왔다. 인용:태양의 개요(헬싱키 대학 물리학과 이론물리학부의 태양물리학 1장 강의 노트).종이 다운로드 (252 kB PDF 2014-08-23 Wayback Machine에서 보관)
- ^ 350MK 값은 텔러-울람 구성의 열핵 무기에서 최대 핵융합 연료 온도(일반적으로 "수소 폭탄"으로 알려져 있음)이다.가젯식 핵분열 폭탄 코어(일반적으로 "원자 폭탄"으로 알려져 있음)의 최고 온도는 50 ~ 100 MK 범위이다. 인용:핵무기 FAQ, 고온에서의 3.2.5 문제관련 웹 페이지 링크.참조된 모든 데이터는 공개적으로 이용 가능한 출처에서 수집되었다.
- ^ 물질의 대량에 대한 최고 온도는 핵융합 물리학 실험에서 사용된 펄스 동력 기계에 의해 달성되었습니다."벌크량"이라는 용어는 입자 가속기의 충돌과 구별되는데, 이때 높은 "온도"는 주어진 순간에 두 개의 아원자 입자 또는 원자핵의 잔해에만 적용됩니다.>2 GK의 온도는 "shot Z1137" 동안 약 10나노초 동안 달성되었습니다.실제로 플라즈마 내 철 및 망간 이온은 3ns(ns 112~115) 동안 평균 3.58±0.41GK(309±35keV)였다.인용:2 × 109 Kelvin 이상의 자기 유체 역학적으로 불안정한 Z 핀치에서의 이온 점성 가열, M. G. Haines 등, Physical Review Letters 96, 7호, id. 075003.Sandia의 보도 자료 링크.2006-07-02 Wayback Machine에서 아카이브 완료
- ^ Hertzsprung-Russell 다이어그램에서 주계열을 떠나 황-32 → 아르곤-36 → 칼슘-40 → 티타늄-44 → 크롬-48 → 철-56 니켈로 실리콘-28을 녹이는 알파 과정을 시작한 후(하루 지속됨) 고질량 별의 중심 온도 .수열을 끝낸 지 몇 분 만에 이 별은 II형 초신성으로 폭발합니다.인용:별의 진화: '빛나는 이웃의 삶과 죽음' (미시건 대학의 아서 홀랜드와 마크 윌리엄스 지음)웹 사이트에 링크합니다.자세한 내용은 여기를 참조해 주세요.아카이브 2011-08-14는 Wayback Machine에 있으며, NASA의 별에 대한 간결한 논문은 여기에 있습니다.2015년 7월 20일 Wayback Machine에서 보관
- ^ (감마선 폭발을 발생시키는) 쌍성 중성자 별 시스템의 병합 중 30 MeV(350 GK)의 피크 내부 온도를 예측한 컴퓨터 모델에 기초한다 .모델의 중성자별은 각각 1.2와 1.6 태양질량이었고, 지름은 약 20km였으며, 완전히 합쳐지기 전 마지막 몇 밀리초 동안 약 390Hz의 속도로 중심(공통 질량 중심) 주위를 돌고 있었다.350 GK 부분은 두 쌍의 개발 중인 공통 코어에 위치한 작은 볼륨으로 약 5ms의 시간 범위에 걸쳐 약 1에서 7km까지 다양했습니다.G4 음표(피아노에서 28번째 흰색 건반)와 같은 주파수로 서로를 공전하는 상상할 수 없는 밀도의 두 개의 도시 크기의 물체를 상상해 보세요.350GK에서 중성자의 평균 진동속도는 빛의 30%, 상대론적 질량(m)은 휴지질량(m0)보다 5% 크다는 점도 주목할 만하다.인용:Oechslin, R.;Janka, H.- T.(2006년)."중성자 별 합병에서 토러스 장치 구성과well-localized 짧은 감마선 폭발".왕립 천문 학회 월간 알리는 안내문.368(4):1489–1499. arXiv:astro-ph/0507099v2.Bibcode:2006MNRAS.368.1489O. doi:10.1111/j.1365-2966.2006.10238.x. S2CID 15036056.그 연구읜 브라우저 기반의 요약, 여기를 클릭합니다.
- ^ New Scientist:8극단: 우주에서 가장 뜨거운 2011년 3월 7일, "이 과정의 세부 사항은 현재 알려지지 않았지만, 그것은 1조 켈빈(초) 정도의 어떤 것으로 가열된 상대론적 입자들의 불덩어리를 포함해야 한다"고 말했다.
- ^ 인용: 물리학자들은 입자를 어떻게 연구하나요? CERN이 웨이백 머신에 2007-10-11을 아카이브했습니다.
- ^ Planck 주파수는 1.854 87(14) × 10Hz43(플랑크 시간의 역수)입니다.플랑크 주파수의 광자는 하나의 플랑크 길이의 파장을 가지고 있다.1.416 79(11) × 1032 K의 플랑크 온도는 계산된 b/T = 2max.045 31(16) × 10−26 nm의 파장과 같다.그러나 실제 피크 방사 파장은 플랑크 길이 1.616 24(12) × 10−26 nm로 양자화된다.
- ^ 물의 융합 엔탈피(0°C, 101.325kPa)는 분자당 0.062284eV에 해당하므로 0°C 물 얼음에 열 에너지 1줄씩을 추가하면 1.0021×1020 물 분자가 결정 격자에서 이탈하여 액체가 된다.
- ^ 물의 융해 엔탈피는 6.0095 kJ−1 mol−1 K(0°C, 101.325 kPa)이다.인용:용수 구조와 과학, 용수 특성, 용융 엔탈피(0°C, 101.325kPa)(런던 사우스 뱅크 대학).웹 사이트에 링크합니다.융접 엔탈피가 6~30J−1 mol−1 K 범위에 포함되지 않는 유일한 금속은 (높은 쪽에 있는) 다음과 같다.Ta, W, Re, 그리고 (낮은 면에는) Ga, In, Hg, Tl, Pb 및 Np. 인용:웹 요소의 홈 페이지에 대한 링크입니다.
- ^ 제논 값 인용:이 링크는 WebElements의 제논 데이터(사용 가능한 값의 범위는 2.3~3.1kJ/mol)에 대한 링크입니다.또 0.021kJ/mol에 불과한 헬륨의 핵융합열은 결합력이 약해 25기압 이상의 압력을 받지 않는 한 0점 에너지가 헬륨의 동결을 막는다는 점도 주목할 만하다.
- ^ CRC Handbook of Chemistry and Physics, 제1회 학생판 및 웹 요소.
- ^ HO2 비열 용량, Cp = 0.075327 kJ−1 mol−1 K(25°C), 융접 엔탈피 = 6.0095 kJ/mol(0°C, 101.140 kPa)증발 엔탈피(표준) = 40.657 kJ/mol(100°C).인용:물 구조와 과학, 물의 특성(런던 사우스 뱅크 대학).웹 사이트에 링크합니다.
- ^ 이동 전도 전자는 비국재화(즉, 특정 원자에 결합되지 않음)되며, 제로점 에너지의 영향으로 인해 양자 가스의 일종처럼 행동합니다.따라서 절대 영점에서도 전도 전자는 여전히 약 16.6×10m/s의 페르미 속도로 원자 사이를 이동한다.운동 열 에너지는 이 속도를 더하고 또한 비국재화된 전자가 핵으로부터 더 멀리 이동하도록 합니다.
- ^ 다른 어떤 결정 구조도 최밀 충전 장치의 패킹 밀도를 74.048% 초과할 수 없습니다.이 밀도를 가진 자연에서 발견된 두 개의 규칙적인 결정 격자는 육각형 밀착(HCP)과 면 중심 입방체(FCC)입니다.이러한 규칙적인 격자는 가능한 가장 낮은 에너지 상태에 있습니다.다이아몬드는 FCC 결정 격자로 가장 가깝게 채워진 구조입니다.적절한 결정성 화합물은 일반적으로 크기가 다른 원자로 구성되지만 분자 수준에서 고려했을 때 가장 근접하게 채워진 구조로 간주될 수 있다.이러한 화합물 중 하나가 마그네슘 알루미늄 스피넬(MgAlO24)로 알려진 일반적인 광물입니다.면 중심의 입방체 결정 격자를 가지며 압력의 변화는 낮은 에너지 상태의 격자를 만들 수 없습니다.
- ^ 진공상태에서 동결될 수 있는 자연발생 화학원소 92개 중 거의 절반도 가장 가까운 결정격자를 가지고 있다.이 세트에는 베릴륨, 오스뮴, 네온 및 이리듐(헬륨 제외)이 포함되므로 내부 에너지(기호:U. 엔탈피(공식:H = U + pV), 내부 에너지는 분석의 성격에 따라 다른 열 에너지 소스(특히 ZPE)를 제외할 수 있다.따라서 완벽한 진공상태에서 모든 T = 0 최접촉 충전물질은 분석의 성질에 따라 엔탈피가 최소화되거나 0이 된다.화학 열역학에서의 Legendre Transforms 사용, 로버트 A.알베티, 순수한 사과.화학, 73 (2001) 1349.
- ^ 대기압과 관련하여 측정된 압력의 맥락에서 "gage" 대 "gauge" 철자와 관련하여 선호하는 철자는 국가별로, 심지어 산업별로도 다르다.또한 두 철자 모두 특정 산업 또는 국가 내에서 자주 사용됩니다.영국 영어권 국가의 산업에서는 일반적으로 압력 측정기와 구별하기 위해 "게이지 압력"이라는 철자를 사용합니다. 영국의 압력 측정기는 압력 게이지로 표기합니다.같은 이유로 미국의 대형 압력 변환기 및 계측 제조업체 중 많은 수가 압력 게이지라고 하는 계측기와 구별하기 위해 공식 문서에 스펠링 게이지 압력(여기서 사용되는 규칙)을 사용합니다.(Honeywell-Sensotec의 FAQ 페이지와 Fluke Corporation의 제품 검색 페이지를 참조하십시오).
- ^ 압력 또한 절대적인 조건이어야 합니다.게이지 압력이 0kPa인 타이어 안의 공기도 뜨거워지면 팽창합니다.엔지니어들이 온도를 보정할 때 절대 압력 측면에서 작업해야 한다는 것을 간과하는 것은 드문 일이 아닙니다.예를 들어, 항공기 타이어의 주요 제조업체는 공식에서 게이지 압력을 사용한 온도 보상 타이어 공기압에 관한 문서를 발행했다.그러나 관련된 높은 게이지 압력(180psi; 12.4bar; 1.24MPa)은 오차가 매우 작다는 것을 의미합니다.게이지 압력이 일반적으로 약 2bar(200kPa)인 저압 자동차 타이어의 경우 절대 압력으로 조정하지 못하면 상당한 오류가 발생합니다.참조 문서:항공기 타이어 정격(155kB PDF, 여기).
- ^ 여기서는 하나의 표준 대기의 101.325 kPa 값 대신 100 kPa의 차이가 사용됩니다.1982년 국제순수응용화학연합(IUPAC)은 물질의 물리적 특성을 규정하기 위해 표준 압력(대기압)을 정확히 100kPa( 750 750.062 Torr)로 정의할 것을 권고했다.이는 대략적인 수치일 뿐만 아니라 매우 실질적인 효과가 있었다. 비교적 적은 수의 사람들이 해수면에서 살고 일하며, 100kPa는 약 112m의 고도에서 평균 압력에 해당하며, 이는 인간 거주지의 전 세계 중앙 고도 194m에 가깝다.특히 저압 또는 고정밀 작업의 경우 실제 대기압을 측정해야 합니다.인용:IUPAC.org, 골드북, 표준 압력
- ^ a b 를 클릭합니다Planck, M. (1945). Treatise on Thermodynamics. Dover Publications. p. §90 & §137.
eqs.(39), (40), & (65)
. - ^ 를 클릭합니다Fermi, E. (1956). Thermodynamics. Dover Publications (still in print). p. 48.
eq.(64)
. - ^ 온도 측정의 간단한 역사 및 웁살라 대학교(스웨덴), 린네우스의 온도계
- ^ bipm.org
- ^ a b 옥스포드 영어 사전(OED)에 따르면, "셀시우스의 온도계"라는 용어는 적어도 1797년부터 사용되었다고 합니다.또한, "섭씨 또는 섭씨 온도계"라는 용어는 적어도 1850년 초에 특정 유형의 온도계를 언급하면서 다시 사용되었다.또한 OED는 1928년 기온 보고를 인용했다. "내 고도는 약 5,800m였고 온도는 섭씨 28도였다."하지만, 사전은 단어나 용어의 가장 이른 사용을 찾기 위해 노력하며 과학의 역사를 통해 사용된 용어와 관련하여 유용한 자료가 아니다.박사의 여러 글에 따르면온도 측정 초기부터 21세기까지의 온도 척도(영문: PDF 형식 150kB), 온도(2판/1990/Academic Press / 012566817), BIPM(1988–2004)의 책임자 테리 퀸 CBE FRS는 온도 측정기 초기부터 21세기까지의 온도 척도(영문: PDF 형식 150kB) 및 온도(2판/1990/아카데믹 프레스/012566817), 온도 측정기)에 의해 사용되지 않은 온도 측정기와 관련된 용어가 포함되어 있다.1948년 CIPM과 CGPM이 이 용어를 채택할 때까지 mmunity.BIPM은 그 이전에는 섭씨도가 산발적이고 비과학적인 용도로 사용되고 있다는 사실조차 알지 못했다.12권으로 구성된 1933년판 OED에는 섭씨라는 단어가 기재되어 있지 않았다(그러나 온도 측정의 맥락에서 섭씨와 섭씨 모두 기재되어 있었다).1948년 셀시우스 채택은 세 가지 목적을 달성했다.
- 모든 일반적인 온도 척도에는 켈빈, 섭씨, 화씨, 레아우무르, 랭킨과 같은 가까운 관계자의 이름을 따서 단위 이름을 붙입니다.
- 섭씨 척도를 현대적 형태로 만든 린네의 중요한 공헌에도 불구하고, 셀시스의 이름은 C로 시작되었기 때문에 명백한 선택이었다.따라서, 수 세기 동안 섭씨라는 명칭과 관련하여 사용되었던 기호 °C는 계속 사용될 수 있으며 동시에 새로운 명칭과 직관적인 연관성을 물려받을 수 있다.
- 새로운 이름은 섭씨라는 용어의 모호함을 제거하여 각도 측정 단위를 나타내는 프랑스어 이름만을 지칭할 수 있게 되었습니다.
외부 링크
- 제로 포인트 에너지와 제로 포인트 필드.다양한 양자 효과에 대한 자세한 설명이 있는 웹 사이트입니다.Calphysics Institute의 Bernard Haisch가 작성했습니다.
















 각 입자의 평균 운동 에너지(
각 입자의 평균 운동 에너지(




 사이클당 수행되는 작업입니다.따라서 효율은 qH / q에만C 의존합니다.
사이클당 수행되는 작업입니다.따라서 효율은 qH / q에만C 의존합니다.














 정용량 시스템의 경우
정용량 시스템의 경우  열역학적
열역학적 










 m/s 단위의 변환 입자 움직임의 벡터 평균 속도입니다.
m/s 단위의 변환 입자 움직임의 벡터 평균 속도입니다.
 m/s 단위의 변환 입자 운동 속도입니다 .물질의 구성 입자의 이동 운동의 평균 에너지는 속도가 아닌 평균 속도와 관련이 있습니다.따라서 운동에너지의 고전적인 공식에서 s
m/s 단위의 변환 입자 운동 속도입니다 .물질의 구성 입자의 이동 운동의 평균 에너지는 속도가 아닌 평균 속도와 관련이 있습니다.따라서 운동에너지의 고전적인 공식에서 s


