양자 유한 오토마톤

양자 컴퓨팅에서 양자 유한 오토마타(QFA) 또는 양자 상태 기계는 확률론적 오토마타 또는 마르코프 결정 과정의 양자 유사체이다.그것들은 실제 양자 컴퓨터의 수학적 추상화를 제공한다.1회 측정 및 다회 측정 오토마타 등 여러 유형의 오토마타를 정의할 수 있습니다.양자 유한 오토마타는 또한 유한형 서브시프트의 양자화 또는 마르코프 사슬의 양자화로 이해될 수 있다.QFA는 다시 기하학적 유한 오토마타 또는 위상 유한 오토마타의 특수한 경우이다.

오토마타는 유한한 $\Sigma$ 의 $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ ( $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ 0 , $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ 1, $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , , $),$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ ( \ $displaystyle$ \ $display$ style $\Sigma$ $=$ ( \ $display$ style _ { $0$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , \ $cdots$ , \ $cdots$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , \ { $\sigma _{i}$ k $\sigma _{i}$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ $\Sigma$ )를 $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ 수신하여 $동작합니다.$ $(\displaystyle$ \ $operatorname$ {Pr $}(\sigma))$ 는 $\operatorname {Pr}(\sigma )$ 자동이 허용 상태에 있을 가능성을 나타냅니다.즉, 자동이 문자열을 수락했는지 거부했는지 여부를 나타냅니다.

QFA에 의해 받아들여진 언어는 결정론적 유한 오토마타의 정규 언어가 아니며 확률론적 유한 오토마타의 확률적 언어도 아니다.이러한 양자 언어에 대한 연구는 여전히 활발한 연구 분야로 남아 있다.

비공식적인 설명

양자 유한 오토마타를 이해하기 위한 간단하고 직관적인 방법이 있습니다.하나는 결정론적 유한 오토마타(DFA)의 그래프 이론적 해석으로 시작한다.DFA는 유향 그래프로 나타낼 수 있으며, 상태는 그래프 내의 노드로, 화살표는 상태 천이를 나타냅니다.각 화살표는 특정 상태와 입력 기호가 주어진 화살표가 다음 상태를 가리키도록 가능한 입력 기호로 라벨링됩니다.이러한 그래프를 표현하는 한 가지 방법은 입력 기호별로 하나의 행렬을 갖는 인접 행렬 세트를 사용하는 것이다.이 경우 가능한 DFA 상태 목록은 열 벡터로 작성됩니다.소정의 입력 심볼에 대해서, 인접 행렬은, 소정의 상태(상태 벡터내의 행)가 어떻게 다음 상태로 이행하는지를 나타냅니다.상태 천이는 행렬 곱셈에 의해 주어집니다.

각 입력 기호가 다른 전이를 일으킬 수 있기 때문에 가능한 각 입력 기호에 대해 고유한 인접 행렬이 필요합니다.인접 매트릭스의 엔트리는 0과 1이어야 합니다.매트릭스 내의 임의의 컬럼에 대해 0이 아닌 엔트리는 1개뿐입니다.이것은 다음(고유한) 상태 천이를 나타내는 엔트리입니다.마찬가지로 시스템 상태는 컬럼벡터이며, 1개의 엔트리만0이 아닙니다.이 엔트리는 시스템의 현재 상태에 대응합니다. $\Sigma$ { $displaystyle$ \ $Sigma }$ 는 $\Sigma$ 입력 기호 세트를 나타냅니다.특정 입력 $\alpha \in \Sigma$ $\alpha \in \Sigma$ \ $display$ \ $displaystyle \ alpha$ \ $in$ \ Sigma $\alpha \in \Sigma$ 에 대해 DFA가 다음 상태로 진화하는 것을 나타내는 인접 매트릭스로서 $U_{\alpha }$ α { \ $displaystyle$ U _ { \ $alpha }$ 라고 $U_{\alpha }$ $U_{\alpha }$ 합니다.세트 $\{U_{\alpha }|\alpha \in \Sigma \}$ { $\{U_{\alpha }|\alpha \in \Sigma \}$ $\{U_{\alpha }|\alpha \in \Sigma \}$ α $\{U_{\alpha }|\alpha \in \Sigma \}$ δ $\{U_{\alpha }|\alpha \in \Sigma \}$ $}$ { $displaystyle$ \{ $U_{\alpha } \alpha \in \Sigma$ \}는 $\{U_{\alpha }|\alpha \in \Sigma \}$ DFA의 상태 전이 함수를 완전히 기술합니다.Q는 DFA의 가능한 상태 세트를 나타냅니다.Q에 N개의 상태가 있는 경우, 각 $U_{\alpha }$ Uα $(\$ {\alpha $U_{\alpha }$ })는 $U_{\alpha }$ N차원이다.초기 $q_{0}\in Q$ $q_{0}\in Q$ 0 $q_{0}\in Q$ ${$ $displaystyle q$ _ { $0$ } \ $in$ Q $q_{0}\in Q$ }는 q'번째 행에 있는₀ 열 벡터에 대응합니다 $q_{0}\in Q$ .일반 상태 q는 q'번째 행에 1이 있는 열 벡터이다.표기법을 남용함으로써 q와₀ q도 이 두 벡터를 나타냅니다.그런 다음 입력 테이프에서 입력 $\alpha \beta \gamma \cdots$ β $\alpha \beta \gamma \cdots$ β β $\alpha \beta \gamma \cdots$ β $q=\cdots U_{\gamma }U_{\beta }U_{\alpha }q_{0}.$ $\alpha \beta \gamma \cdots$ β U $q=\cdots U_{\gamma }U_{\beta }U_{\alpha }q_{0}.$ 0 . ${\displaystyle$ $\alpha \beta \gamma \cdots$ q $=$ \ $cdots$ U_ ${\gamma$ } $U_{\beta }_{\$ alpha $\alpha \beta \gamma \cdots$ $}$ 를 읽으면 DFA의 상태가 표시됩니다. $q=\cdots U_{\gamma }U_{\beta }U_{\alpha }q_{0}.$ 상태 천이는 일반 행렬 곱셈(즉, $U_{\alpha }$ 에 $Uα를$ 곱한₀ $값$ 으로 나타납니다.적용 순서는 선형대수의 표준 표기법을 따르기 때문에 '불규칙'이다.

선형 연산자와 벡터의 관점에서 위의 DFA 설명은 상태 벡터 q를 어떤 일반 벡터로 대체하고 $\{U_{\alpha }\}$ { $\{U_{\alpha }\}$ α $}$ {displaystyle \{ $U_{\$ alpha $\{U_{\alpha }\}$ }\}을 $\{U_{\alpha }\}$ (를) 일부 일반 연산자에 의해 대체함으로써 일반화가 거의 요구됩니다.QFA는 기본적으로 q를 확률 진폭으로 대체하고 { $\{U_{\alpha }\}$ α $\{U_{\alpha }\}$ \{ $U_{\$ alpha $\{U_{\alpha }\}$ }\})을 $\{U_{\alpha }\}$ 유니터리 행렬로 대체합니다.다른 유사한 일반화도 명확해진다: 벡터 q는 다양체상의 어떤 분포가 될 수 있다; 전이 행렬의 집합은 다양체의 자기동형이 된다; 이것은 위상 유한 오토마톤을 정의한다.마찬가지로, 행렬은 동질 공간의 자기동형으로서 받아들여질 수 있다.이것은 기하학적 유한 오토마톤을 정의한다.

QFA에 대한 공식적인 설명으로 넘어가기 전에 언급하고 이해해야 할 두 가지 중요한 일반화가 있습니다.첫 번째는 비결정론적 유한 오토마톤(NFA)입니다.이 경우 벡터 q는 0이 아닌 여러 엔트리를 가질 수 있는 벡터로 대체됩니다.그런 다음 이러한 벡터는 Q의 멱집합 요소를 나타냅니다. 이는 Q의 표시기 함수일 뿐입니다.마찬가지로 상태 전이 $\{U_{\alpha }\}$ { $\{U_{\alpha }\}$ α $\{U_{\alpha }\}$ }(\ $displaystyle$ \{ $U_{\$ alpha $\{U_{\alpha }\}$ }\})는 $\{U_{\alpha }\}$ 특정 열에 0이 아닌 엔트리를 여러 개 포함할 수 있도록 정의됩니다.마찬가지로 성분별 행렬 곱셈 중에 실행되는 곱셈 연산은 부울 연산 및/또는 연산으로 대체되어야 하며, 이는 특성 2의 링으로 동작하도록 해야 한다.

잘 알려진 정리에 따르면 각 DFA에 대해 동등한 NFA가 존재하며, 그 반대도 마찬가지입니다.이는 DFA와 NFA가 인식할 수 있는 언어 집합이 동일하다는 것을 의미합니다.이것들은 정규 언어입니다.QFA에 대한 일반화에서는 인식된 언어 집합이 다릅니다.이 세트를 설명하는 것은 QFA 이론에서 가장 중요한 연구 문제 중 하나입니다.

즉시 밝혀져야 할 또 다른 일반화는 전이 행렬에 확률 행렬을 사용하고 상태에 확률 벡터를 사용하는 것이다. 이것은 확률론적 유한 오토마톤을 제공한다.상태 벡터가 확률로 해석되기 위해서는 상태 벡터의 엔트리가 실수, 양의 값, 합계가 1이어야 합니다.전이행렬은 이 속성을 보존해야 합니다.이것이 확률적이어야 하는 이유입니다.각 상태 벡터는 심플렉스의 점을 지정하는 것으로 상상되어야 한다. 따라서, 이것은 심플렉스가 다양체이고 확률 행렬이 심플렉스의 선형 자기 형태인 위상 자동화이다.각각의 전환은 (본질적으로) 이전과 독립적이기 때문에(우리가 받아들여진 언어와 거부된 언어 사이의 차이를 무시한다면), PFA는 본질적으로 마르코프 사슬의 한 종류가 된다.

반면 QFA에서 매니폴드는 복소 투영 $\mathbb {C} P^{N}$ $\mathbb {C} P^{N}$ P $(\$ P $^{N$ 이며, 전이 행렬은 유니터리 행렬이다. $\mathbb {C} P^{N}$ $\mathbb {C} P^{N}$ N $(\$ 의 ${\mathbb {C}}P^{N}$ 각 점은 양자역학적 확률 진폭 또는 순수 상태에 해당하며, 단일 행렬은 시스템의 시간 진화를 지배하는 것으로 간주할 수 있습니다(슈뢰딩거 그림 참조).순수 상태에서 혼합 상태로의 일반화는 간단해야 합니다.혼합 상태는 $\mathbb {C} P^{N}$ C $\mathbb {C} P^{N}$ N $(\displaystyle \mathbb {C}$ P $^{N$ 에서의 측정 이론 확률 분포입니다.

고려해야 할 중요한 점은 언어를 입력하는 동안 다양성에 나타나는 분포입니다.자동화가 언어를 인식하는 데 있어서 '효율적'이 되기 위해서는, 그 분포가 '가능한 한 균일한' 것이어야 한다.이러한 균일성에 대한 요구는 최대 엔트로피 방법의 기본 원리입니다. 즉, 이들은 단순히 자동화의 선명하고 콤팩트한 작동을 보장합니다.즉, 숨겨진 마르코프 모델을 훈련하는 데 사용되는 기계 학습 방법은 QFA에도 일반화됩니다. 즉, Viterbi 알고리즘과 Forward-Backward 알고리즘은 QFA에 쉽게 일반화됩니다.

QFA 연구는 1997년^[1] 콘닥스와 와트러스의 연구에서 대중화되었고, 이후 무어와 크러치펠트에 ^[2]의해 1971년 이온 바이아누에 의해 ^[3]^[4]기술되었다.

1회 측정 오토마타

Measure-Once 오토마타는 크리스 무어와 제임스 P에 의해 도입되었습니다. 크러치필드.^[2]그것들은 다음과 같이 공식적으로 정의될 수 있다.

일반 유한 오토마톤과 마찬가지로 양자 오토마톤은 $N$ $(\displaystyle$ N $)$ 상태 $N$ 큐비트 $|\psi \rangle$ (\ $displaystyle$ \ $psi \rangle$ 로 표현되는 N $(\$ $displaystyle$ N $)$ $N$ 큐비트 $|\psi \rangle \in \mathbb {C} P^{N}$ $|\psi \rangle \in \mathbb {C} P^{N}$ 로 $간주$ 됩니다 $.$ $aystyle \psi \rangle \in \mathbb {C} P^{N}$ 은 $|\psi \rangle \in {\mathbb {C}}P^{N}$ N{\ $displaystyle$ $\Vert \cdot \Vert$ N $}$ 차원 $N$ 복소 투영 $N$ 의 요소이며, Fubini-Study 메트릭인 내부곱 $\Vert \cdot \Vert$ ‖ $display$ \ \ $displaystyle$ \ $Vert$ \ $cdot$ \ Vert $}$ 를 $\Vert \cdot \Vert$ 운반합니다.

상태 전이, 전이 행렬 또는 de Bruijn 그래프는 N $N\times N$ × $(\display style$ N\ $times$ N $)$ 단위 $U_{\alpha }$ $U_{\alpha }$ α(\ $displaystyle$ $U_{\alpha$ $\alpha \in \Sigma$ $U_{\alpha }$ $N\times N$ 으로 표시되며, 각 $\alpha \in \Sigma$ $\alpha \in \Sigma$ $\alpha$ display $\alpha \in \Sigma$ display \ display \ $displaystyle$ \alpha \ $in$ \Sigma $}$ 에 대해 하나의 단위 행렬이 $입력$ 됩니다. $\alpha$ 유니터리 매트릭스에서는 자동화가 $|\psi \rangle$ 상태에서 $|\psi ^{\prime }\rangle$ 상태로 이행하는 것을 $나타냅니다$ $.{$ $displaystyle$ $|\psi \rangle$ \ $psi$ \rangle $|\psi \rangle$ $|\psi ^{\prime }\rangle$ $。$

\displaystyle \psi ^{\prime }\rangle = U_{\alpha } \psi \rangle }

따라서 트리플 $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ N $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ { $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ α $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ α δ $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ δ δ } $（$ \ $displaystyle$ （ \ $mathbb$ { $C$ } $P^{ N$ } , \ $Sigma$ , \ ; \ $vert$ \ ; \ alpha \ $in$ \ Sigma \ $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ } )은 $(\mathbb {C} P^{N},\Sigma ,\{U_{\alpha }\;\vert \;\alpha \in \Sigma \})$ 퀀텀을 형성한다.

자동의 허용 상태는 N $N\times N$ × $N\times N$ (\ $displaystyle$ N $\times$ N $)$ 투영 $N\times N$ $P$ (\ $displaystyle$ P $P$ 에 의해 주어지며 $,$ N(\ $displaystyle$ N $)$ 차원 양자 $N$ 상태 $|\psi \rangle$ ${\$ $|\psi \rangle$ { $displaystyle \$ $psi \rangle }$ 일 $|\psi \rangle$ 때 $|\psi \rangle$ ⟩ ⟩ $|\psi \rangle$ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ ⟩ $displaydisplaydisplaydisplaydisplaydisplaydisplay$

\displaystyle \psi P \psi \rangle = \Vert P \psi \rangle \Vert ^{2}}

스테이트 머신이 소정의 $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ $=$ ( $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ , 1, $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ $displaystyle$ \ $display$ = ( \ $displaystyle$ _ ${ 0$ , \ $displaystyle$ _ { 0 , \ $cdots$ , \ { k $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ } )를 $\sigma =(\sigma _{0},\sigma _{1},\cdots ,\sigma _{k})$ 받아들일 확률은 다음과 같습니다.

\operatorname {Pr}(\displaystyle)=\Vert PU_{\sigma_{k}}\cdots U_{\sigma_{1}}U_{\sigma _{0}} \psi \rangle \Vert ^{2}

여기서 벡터 $({style\psi\rangle})$ 는 $|\psi \rangle$ 오토마톤의 초기 상태, 즉 오토마톤이 문자열 입력을 받기 전의 상태를 나타내는 것으로 이해된다.빈 문자열 $"\displaystyle \varnothing"$ 은 $\varnothing$ 유닛 매트릭스일 뿐이므로

\operatorname {Pr}(\varnothing)=\Vert P \psi \rangle \Vert ^{2}

초기 상태가 허용 상태가 될 확률입니다.

${\$ {\ {\ {\ {\ {\ {\ ${\$ {\ {\ {\ {\ {\ {\ {\ （ \ $display$ $|\psi \rangle$ $style$ $\psi$ $\rangle$ $\sigma$ $）$ {\ $|\psi \rangle$ of $\sigma$ {\ ${\$ of of the of {\ of of of of of의 순서가 거꾸로 되므로 단순히 $|\psi \rangle$ 글자의 순서를 유지하기 위해 Hermitian 전치 상태의 오른쪽 액션을 사용하여 QFA를 정의하는 것은 드문 일이 아닙니다.똑같아요.

정규언어는 양자 유한오토마톤에 의해 확률 ${displaystyle$ $p$ $}$ 로 $p$ $\sigma$ 받아들여진다.예를 들어, 그 $언어$ 의 모든 $\sigma$ ${\$ {\displaystyle \sigma $}($ 및 주어진 고정 초기상태 $|\psi \rangle$ {\ $displaystyle$ \ $psi$ $|\psi \rangle$ \ $rangle$ $|\psi \rangle$ $p<\operatorname {Pr} (\sigma )$ 에 대해 p $p<\operatorname {Pr} (\sigma )$ $p<\operatorname {Pr} (\sigma )$ （ $p<\operatorname {Pr} (\sigma )$ （ \ $displaystyle ）$ ） $。$

예

상태 전이표에 의해 주어진 고전적인 결정론적 유한 오토마톤을 고려한다.

**상태 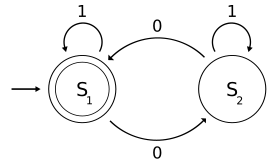전환 테이블**
입력 주	1	0
S₁.	S₁.	S₂.
S₂.	S₂.	S₁.

상태도

양자 상태는 bra-ket 표기로 벡터이다.

\psi \rangle =a_{1}\rangle +a_{2} S_{2}\rangle =a_{1}\a_{2}\end{bmatrix}

$a_{1},a_{2}$ $a_{1},a_{2}$ $({$ 는 $a_{1},a_{2}$ 다음과 같이 정규화되어 있습니다.

{bmatrix}a_{1}^{*}\;a_{2}^{*}\end{bmatrix}{\displaystyle {bmatrix}a_{1}\end{bmatrix}=a_{1}+a_{2}}^{*}a_{2}=1

유니터리 전이 행렬은

\displaystyle U_{0}=\begin{bmatrix}0&1&0\end{bmatrix}}

그리고.

({displaystyle U_{1}=begin{bmatrix}1&0&1&end{bmatrix})

$S_{1}$ 1 $(\$ 을 $S_{1}$ 수용 상태로 $S_{1}$ 하면 투영 매트릭스는

P=begin{bmatrix}1&0\\0&0\end{bmatrix}

쉽게 알 수 있듯이 초기 상태가 순수 $|S_{1}\rangle$ $|S_{1}\rangle$ 1 ${\$ \ $displaystyle S_{1$ } \ $rangle$ } $|S_{2}\rangle$ $|S_{2}\rangle$ 2 ${\$ \ $displaystyle S_{2}$ \ $rangle$ 인 경우 기계의 작동 결과는 기존의 결정론적 유한 상태 기계와 완전히 동일합니다.특히, 이러한 초기 상태에 대해 확률 1과 함께 이 자동화에 의해 받아들여지는 언어가 있으며, 이는 고전적인 DFA의 정규 언어와 동일하며 정규식으로 주어진다.

({displaystyle (1^{*}0)^{*})^{*},\!}

비클래식 $동작$ 은 1 $({displaystyle$ $a_{2}$ {1})과 2({ $displaystyle$ a_ ${2})$ 가 $a_{2}$ 모두 0이 아닌 경우에 발생합니다. $U_{0}$ $U_{0}$ 0 $(\$ $U_{1}$ U $U_{1}$ (\ $displaystyle U_{1})$ 이 $U_{1}$ 단순하지 않은 경우 보다 미묘한 동작이 발생합니다. 예를 들어, de Rham 곡선은 가능한 모든 유한 이진 문자열 집합에 작용하는 양자 유한 상태 기계의 예입니다.

측정 다량 오토마타

Measure-many automata는 Kondacs와 Watrus에 ^[1]의해 1997년에 도입되었습니다.일반적인 프레임워크는 하나의 투영 대신 각 문자를 읽은 후에 수행되는 투영 또는 양자 측정이 있다는 점을 제외하고 한번 측정 자동화와 유사합니다.정식 정의는 다음과 같습니다.

Hilbert ${\mathcal {H}}_{Q}$ ${\mathcal {H}}_{Q}$ Q $(\$ style $\mathcal$ {H}} $_{Q})$ 는 ${\mathcal {H}}_{Q}$ 세 개의 직교 부분 공간으로 분해됩니다.

{\mathcal {H}}_{Q}={\text{accept}}\oplus {\text{reject}}\oplus {\mathcal {H}}_{\text{non-halting}}}

문헌에서 이러한 직교 부분 공간은 보통 힐베르트 ${\mathcal {H}}_{Q}$ ${\mathcal {H}}_{Q}$ 에 대한 직교 기저 벡터 $집합$ Q $(\$ Q ${\mathcal {H}}_{Q}$ 로 $Q$ 공식화된다. 이 기저 벡터 집합은 $Q_{\text{acc}}\subset Q$ $Q_{\text{acc}}\subset Q$ ${\mathcal {H}}_{Q}$ acc $Q_{\text{acc}}\subset Q$ Q(\ $displaystyle Q_{$ text}_acc $})$ $Q_{\text{rej}}\subset Q$ $Qsubset$ 으로 $Q_{\text{acc}}\subset Q$ 나뉜다. $(\displaystyle Q_{\text{rej}}\subset$ Q $Q_{\text{rej}}\subset Q$ 는 다음과 같습니다.

{H}_{\text{accept}}=\operatorname {span}\{q\rangle: q\rangle\in Q_{\text{acc}}\}

$acc$ \ $displaystyle$ P _ { \ $text$ { $P_{\text{acc}}$ acc $P_{\text{acc}}$ } 、 $P_{\text{non}}$ $P_{\text{rej}}$ \ $displaystyle$ P $_$ { \ $text$ { rej $P_{\text{rej}}$ } 、 $P_{\text{non}}$ $non$ \ $displaystyle$ P _ { \ $text$ { $non$ } 。각각각각 서브스페이스에 투영됩니다.

(\displaystyle P_{\text{acc}):{\mathcal {H}}_{Q} ~ {\text{accept}}

기타 등등.입력 문자열의 해석은 다음과 같이 진행됩니다.오토마톤은 $({displaystyle\psi\rangle$ 상태라고 생각합니다. $({displaystyle\alpha$ 를읽으면 오토마톤이 상태가 됩니다.

\displaystyle \psi ^{\prime }\rangle = U_{\alpha } \psi \rangle }

이 때 투영 $연산자$ P{\ $displaystyle$ P $P$ 를 ${\mathcal {H}}_{\text{accept}}$ 사용하여 $ψ$ ${\$ $|\psi ^{\prime }\rangle$ \ $displaystyle \psi ^$ { $\ prime }$ \ $rangle$ $|\psi ^{\prime }\rangle$ the the ${\mathcal {H}}_{\text{reject}}$ at at ${\mathcal {H}}_{\text{reject}}$ at ${\mathcal {H}}_{\text{accept}}$ { ${$ { { { { { at ${\mathcal {H}}_{\text{accept}}$ at at at at { { { at at at $at$ at { { { at at { { { { { { { { { { { { { { { $({displaystyle {H}}_{\text{reject}}}$ ${\mathcal {H}}_{\text{non-halting}}$ H $(\$ 붕괴 확률은 다음과 같습니다.

\displaystyle \operatorname {Pr} _{\text{acc} =\Vert P_{\text{acc} ^{\prime}\rangle \Vert ^{2}}

"수용" 부분 공간에 대해, 그리고 다른 두 공간에 대해서도 유사하게.

파형 함수가 "승인" 또는 "거부" 하위 공간으로 축소된 경우 추가 처리가 중지됩니다.그렇지 않으면 다음 문자를 입력에서 읽고 P $P_{\text{non}}$ {\ $display style$ P_ ${\text{non$ 고유 $P_{\text{non}}$ 에 적용됩니다. 문자열 전체를 읽을 때까지 처리를 계속하거나 기계가 정지합니다.대부분의 경우 문자열의 왼쪽 및 오른쪽 끝 마크 역할을 하기 위해 알파벳에 추가 기호 ${\(\displaystyle \kappa)$ 와 $\kappa$ $가 인접해 있습니다.

문헌에서 measure-many automaton은 종종 태플 $(Q;\Sigma ;\delta ;q_{0};Q_{\text{acc}};Q_{\text{rej}})$ ; $(Q;\Sigma ;\delta ;q_{0};Q_{\text{acc}};Q_{\text{rej}})$ ; $(Q;\Sigma ;\delta ;q_{0};Q_{\text{acc}};Q_{\text{rej}})$ 0 ; $(Q;\Sigma ;\delta ;q_{0};Q_{\text{acc}};Q_{\text{rej}})$ acc ; $(Q;\Sigma ;\delta ;q_{0};Q_{\text{acc}};Q_{\text{rej}})$ $)\displaystyle(Q;\Sigma$ ;\ $delta ;q_{0})$ 로 표시된다. $Q_{\text{acc}};$ $Q_{\text{rej$ 여기서 Q $(\displaystyle$ Q $),$ $,(\displaystyle \Sigma),$ $Q_{\text{acc}}$ $\Sigma$ $acc(\$ displaystyle $Q_{\text{acc}})$ 및 $Q_{\text{acc}}$ $Q_{\text{rej}}$ $(\$ 는 $Q_{\text{rej}}$ 위와 같이 정의됩니다.초기 상태는 $|\psi \rangle =|q_{0}\rangle$ ⟩ $|\psi \rangle =|q_{0}\rangle$ $|\psi \rangle =|q_{0}\rangle$ 0 $⟩$ { $displaystyle \psi \rangle =q_{0}\rangle$ 로 표시됩니다.유니터리 변환은 맵 $\delta$ { $displaystyle \rangle$ 로 표시됩니다.

\displaystyle \displaystyle:Q\times \Sigma \times Q\to \mathbb {C} }

하도록

\displaystyle U_{\alpha }q_{1}\rangle =\sum _{q_{2}\in Q}\delta (q_{1},\alpha,q_{2}q_rangle }

양자 컴퓨팅과의 관계

2019년 현재 대부분의 양자컴퓨터는 1회 측정 유한 오토마타의 구현으로, 이를 프로그래밍하기 위한 소프트웨어 $|\psi \rangle$ 은 $§$ { $displaystyle \psi \rangle$ $측정$ P {\ $displaystyle$ P}, Unitary $P$ $U_{\alpha }$ $U_{\alpha }$ {\ $displaystyle$ U_ ${\alpha$ 의 상태 준비 상태를 공개하고 있습니다.h 제어된 NOT 게이트, Hadamard 변환 및 기타 양자 논리 게이트를 프로그래머에게 직접 전달합니다.

실제 양자 컴퓨터와 위에 제시된 이론적 프레임워크의 주요 차이점은 초기 상태 준비가 결코 점처럼 순수한 상태를 초래할 수 없으며, 또한 단일 연산자를 정확하게 적용할 수 없다는 것입니다.따라서 초기 상태는 혼합 상태로 간주해야 합니다.

\displaystyle \rho =\int p(x) \psi _{x}\rangle dx}

원하는 초기 순수 상태에 $|\psi \rangle$ 한 초기 상태를 준비하는 기계의 능력을 특징짓는 $p(x)$ 일부 확률 $p(x)$ p $p(x)$ ) { $displaystyle p(x$ 이 상태는 안정적이지 않지만 시간이 지남에 따라 일정량의 양자 디코일런스가 발생한다.정밀한 측정도 불가능하며 대신 측정 프로세스를 설명하기 위해 양의 측정 시스템 값 측도를 사용합니다.마지막으로, 각각의 단일 변환은 날카롭게 정의된 단일 양자 논리 게이트가 아니라 혼합물이다.

U_{\alpha,\rho}=\int p_{\alpha}(x)U_{\alpha,x}module

기계가 원하는 $U_{\alpha }$ $(\$ displaystyle U_ ${\alpha }}$ 에 얼마나 잘 영향을 미칠 수 있는지를 기술하는 $p_{\alpha }(x)$ $p_{\alpha }(x)$ $p_{\alpha }(x)$ pα $x$ )(\ $displaystyle U_{\alpha$ 에 대해 설명합니다.

이러한 효과의 결과, 상태의 실제 시간 진화는 무한정밀 순점으로 간주할 수 없고, 임의로 날카로운 변환의 시퀀스에 의해 동작할 수 없으며, 보다 정확하게는 변환만을 상태에 연결하는 에르고드 프로세스, 또는 시간이 지남에 따라 상태를 스멀링하는 혼합 프로세스로 간주할 수 있다.

푸시다운 오토마톤 또는 스택머신과 양자 유사점은 없습니다.이것은 복제 금지 정리 때문입니다.기계의 현재 상태를 복사하여 나중에 참조하기 위해 스택에 푸시하고 다시 되돌릴 방법이 없습니다.

기하학적 일반화

위의 구성들은 양자 유한 자동화의 개념이 임의의 위상 공간에 어떻게 일반화 될 수 있는지를 보여준다. $\mathbb {C} P^{N}$ 를 들어, $\mathbb {C} P^{N}$ P N $(\displaystyle \mathbb {C}$ $P^{N$ 을 대체하기 위해 일부 (N차원) 리만 대칭 공간을 사용할 수 있습니다. 유니터리 행렬 대신 리만 다양체의 등각성, 또는 더 일반적으로 주어진 위상 공간에 적합한 열린 함수 집합을 사용합니다.초기 상태는 공간의 한 점으로 간주할 수 있습니다.수락 상태의 집합은 토폴로지 공간의 임의의 서브셋으로 간주할 수 있습니다.그리고 동형사상에 의한 반복 후에 점이 수용 집합과 교차할 경우 이 위상 자동화에 의해 형식 언어가 받아들여진다고 말한다.하지만 물론 이것은 M 오토매틱의 표준 정의에 지나지 않습니다.위상 자동의 거동은 위상 역학 분야에서 연구된다.

양자 자동화는 2진수 결과를 갖는 대신(반복된 지점이 최종 집합 안에 있는지 여부에 관계없이) 확률을 갖는다는 점에서 위상 자동화와 다르다.양자확률은 어떤 최종상태 P에 투영된 초기상태의 (제곱) 즉, $\mathbf {Pr} =\vert \langle P\vert \psi \rangle \vert ^{2}$ r $=$ P $\mathbf {Pr} =\vert \langle P\vert \psi \rangle \vert ^{2}$ $displaystyle \mathbf {Pr}$ =\ $vert \part$ \psi \rangle \ $vert$ $^{2})$ 이다. 그러나 이 확률진폭은 $\vert P\rangle$ PVert 지점 $\vert P\rangle$ 의 거리의 매우 단순한 $함수$ 이다 $\vert P\rangle$ $ngle }$ 과 $\vert P\rangle$ ( $)$ C P $\mathbb {C} P^{N}$ 의 점 $\vert \psi \rangle$ θ $\vert \psi \rangle$ {\ $displaystyle \vert \psi \rangle}({$ $displaystyle \mathbb {C} P^{N$ 을 Fubini-Study 메트릭에 의해 지정된 거리 메트릭으로 지정합니다.요약하자면, 받아들여지는 언어의 양자 확률은 메트릭으로 해석될 수 있으며, 최초 상태와 최종 상태 사이의 메트릭 거리가 0일 경우 수용 확률이 단일성이 되고, 그렇지 않을 경우 수용 확률이 0이 아닌 경우 수용 확률이 1 미만이다.따라서 양자 유한 오토마톤은 기하학적 오토마톤 또는 미터법 오토마톤의 특수한 경우일 뿐이며, $\mathbb {C} P^{N}$ 서 C P $(\displaystyle$ \ $mathbb$ { $C} P^{N$ })은 일부 미터법으로 일반화되며, 확률 측도는 해당 공간에 대한 미터법의 단순한 함수로 대체된다.

「」를 참조해 주세요.

양자 마르코프 연쇄

메모들

^ ^a ^b Kondacs, A.; Watrous, J. (1997), "On the power of quantum finite state automata", Proceedings of the 38th Annual Symposium on Foundations of Computer Science, pp. 66–75
^ ^a ^b C. Moore, J. Crutchfield, "Quantum automata and quantum grammars", 이론 컴퓨터 과학, 237(2000) 페이지 275-306.
^ I. Bainau, "시스템의 유기적 수퍼카테고리와 질적 역학", 수학 생물물리학 회보, 33페이지 339-354.
^ I. Baianu, "범주, 함수와 양자 자동 이론"(1971년).제4차 세계 대전의회 LMPS, 1971년 8월~9월

[Kondacs-1] Kondacs, A.; Watrous, J. (1997), "On the power of quantum finite state automata", Proceedings of the 38th Annual Symposium on Foundations of Computer Science, pp. 66–75

[Moore-2] C. Moore, J. Crutchfield, "Quantum automata and quantum grammars", 이론 컴퓨터 과학, 237(2000) 페이지 275-306.

[3] I. Bainau, "시스템의 유기적 수퍼카테고리와 질적 역학", 수학 생물물리학 회보, 33페이지 339-354.

[4] I. Baianu, "범주, 함수와 양자 자동 이론"(1971년).제4차 세계 대전의회 LMPS, 1971년 8월~9월

[1]

[2]

[3]

[4]

Search

양자 유한 오토마톤

네임스페이스

더

목차

비공식적인 설명

1회 측정 오토마타

예

측정 다량 오토마타

양자 컴퓨팅과의 관계

기하학적 일반화

「」를 참조해 주세요.

메모들

Search

양자 유한 오토마톤

비공식적인 설명

1회 측정 오토마타

예

측정 다량 오토마타

양자 컴퓨팅과의 관계

기하학적 일반화

「 」를 참조해 주세요.

메모들

「」를 참조해 주세요.