가산기(전자제품)

가산기 또는 ^[1]여름은 숫자를 더하는 디지털 회로입니다.많은 컴퓨터 및 기타 종류의 프로세서애드더는 산술 논리 유닛(ALU)에 사용됩니다.프로세서의 다른 부분에서도 사용되며 주소, 테이블 인덱스, 증분 및 감소 연산자 및 이와 유사한 연산을 계산하기 위해 사용됩니다.

가산기는 이진 코드화된 10진수나 초과-3과 같은 많은 숫자 표현에 대해 구성할 수 있지만, 가장 일반적인 가산기는 이진수로 작동합니다.음수를 나타내기 위해 2의 보 또는 1의 보를 사용하는 경우, 덧셈기를 덧셈기-감산기로 수정하는 것은 간단하다.다른 부호화된 숫자 표현에서는 기본 덧셈기에 대한 더 많은 논리가 필요합니다.

바이너리 가산기

반 가산기

반 가산 로직 다이어그램

반감기 작동 중

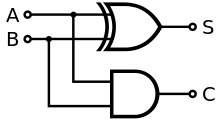
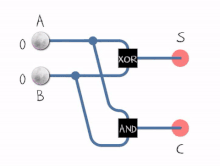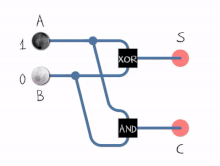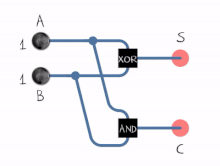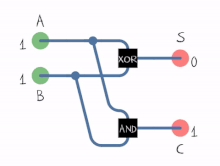
하프 가산기는 2개의 단일 이진수 A와 B를 더합니다.출력은 합(S)과 반송(C)의 두 가지입니다.반송 신호는 여러 자리 추가의 다음 자리까지 오버플로를 나타냅니다.합계의 값은 2C + S입니다.오른쪽 그림에 표시된 가장 단순한 하프 가산기 설계에는 S를 위한 XOR 게이트와 C를 위한 AND 게이트가 포함되어 있습니다.합계(이 경우 S)의 부울 로직은 A'B + AB인 반면 반송(C)은 AB입니다.반송 출력을 결합하기 위해 OR 게이트를 추가하면 두 개의 하프 가산기를 결합하여 완전한 ^[2]가산기를 만들 수 있습니다.하프 가산기는 2개의 입력 비트를 더하고 반 가산기의 두 출력인 반송파 및 합계를 생성합니다.하프 가산기의 입력 변수는 Augend 및 addend 비트라고 불립니다.출력 변수는 합계와 자리올림수입니다.반 가산기에 대한 진실 표는 다음과 같습니다.

입력		출력
A	B	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

NAND 게이트만 사용하는 하프 가산기.

풀 가산기

풀 가산기의 논리도.

완전 추가 작동 중.완전 가산기는 입력의 1s 수를 이진수로 나타냅니다.

블록 측면에 C와_out C가 그려진_in 1비트 풀 가산기의 개략도 기호로 멀티비트 가산기에서의 사용을 강조합니다.

9개의 NAND 게이트에서 조립된 풀가더.

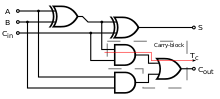
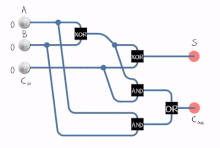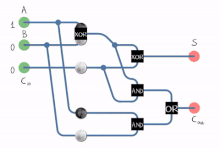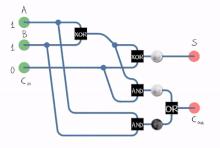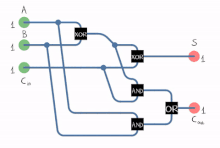
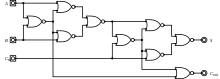
풀 가산기를 사용하면 이진수가 추가되고 입력 및 출력된 값이 계산됩니다.1비트 풀 가산기는 A, B 및 C로_in 쓰여지는 경우가 많은3개의 1비트 번호를 추가합니다.A와 B는 오퍼랜드이며_in, C는 앞의 그다지 중요하지 않은 ^[3]스테이지에서 가져온 비트입니다.풀 가산기는 보통 8, 16, 32 등의 비트 이진수를 추가하는 캐스케이드 가산기의 컴포넌트입니다.이 회로는 2비트 출력을 생성합니다.출력 반송 및 합계는 일반적으로 신호_out C 및 S로 표시됩니다. 여기서 합계는 2C_out + S입니다.

풀 가산기는 커스텀 트랜지스터 레벨 회로 또는 다른 게이트로 구성되는 등 다양한 방법으로 구현될 수 있습니다.하나의 구현 예는 S = A c_in B c_out C 및 C = (A ( B_in) + (C ( B)입니다.

본 실시형태에서는 실행출력 전 최종 OR 게이트는 결과 로직을 변경하지 않고 XOR 게이트로 대체될 수 있다.회로가 칩당 하나의 게이트 유형만 포함하는 단순한 집적회로 칩을 사용하여 구현되는 경우 두 가지 유형의 게이트만 사용하는 것이 편리합니다.

NOR 완전 가산기

또, A, B를 1개의 하프 가산기의 입력에 접속한 후, 그 합계 출력 S를 2개의 하프 가산기의 입력의 1개_in, C를 다른 입력으로 하고, 최종적으로 2개의 하프 가산기의 반송 출력을 AN 또는 A 게이트에 접속하는 것으로 풀 가산기를 구성할 수 있다.후반 가산기의 합계 출력은 풀 가산기의 최종 합계 출력(S)이며, OR 게이트의 출력은 최종 반송 출력(C_out)입니다.풀 가산기의 임계 경로는 양쪽 XOR 게이트를 통과하여 합계 비트s로 끝납니다.XOR 게이트를 완료하는 데 1개의 지연이 걸린다고 가정하면, 풀 가산기의 임계 경로에 의해 부과되는 지연은 다음과 같습니다.

\displaystyle T_{\text{FA}=2\cdot T_{\text{X}OR}}=2D}

반송의 임계 경로는 가산기의 1개의 XOR 게이트를 통과하고 반송 블록의 2개의 게이트(AND 및 OR)를 통과합니다.따라서 AND 또는 OR 게이트가 완료하는 데 1개의 지연이 걸리는 경우 지연은 다음과 같습니다.

T_{\text{c}}}=T_{\text{X}OR}}+T_{\text{AND}}+T_{\text{OR}}=D+D+D=3D

전체 가산기는 9개의 ^[4]NAND 게이트를 사용하여 구현할 수 있습니다.

전체 덧셈에 대한 진실 표는 다음과 같습니다.

입력			출력
A	B	C_에	C_나가.	S
0	0	0	0	0
0	0	1	0	1
0	1	0	0	1
0	1	1	1	0
1	0	0	0	1
1	0	1	1	0
1	1	0	1	0
1	1	1	1	1

전체 가산기의 모든 입력을 반전시키면 ^[5]캐리어를 반전시킬 필요가 없으므로 고속 리플 캐리어 가산기 설계에 사용할 수 있는 모든 출력도 반전됩니다.

CMOS에서의^[5] 단일 트랜지스터 반송 지연을 수반하는 반전 출력의 풀 가산기

여러 비트를 지원하는 애드

리플 캐리어 가산기

논리 블록 다이어그램이 표시된 4비트 가산기

10진수 4자리 리플 반송 가산기.FA = 완전 가산기, HA = 반 가산기.

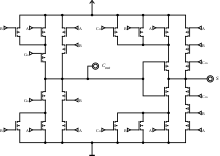
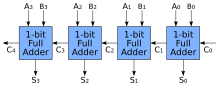
N비트 번호를 추가하기 위해 여러 개의 풀애더를 사용하여 논리회선을 작성할 수 있습니다.각 풀 가산기는 이전 가산기의 C인_out C를_in 입력한다.이러한 종류의 가산기를 리플 캐리 가산기(RCA)라고 부릅니다.각 비트가 다음 풀 가산기로 "리플"되기 때문입니다.첫 번째(그리고 첫 번째) 완전 가산기는 (C = 0이라는 가정_in 하에) 절반 가산기로 대체할 수 있습니다.이전 가산기(Cout n-1)의 출력이 다음 가산기(Cin)에 입력으로 전달되었습니다.

리플 캐리어 가산기의 레이아웃은 간단하기 때문에 설계 시간이 빠릅니다.단, 각 풀 가산기는 이전의 풀 가산기에서 캐리어 비트가 계산될 때까지 대기해야 하므로 리플 캐리어 가산기는 비교적 느립니다.게이트 지연은 전체 가산기 회로를 검사하여 쉽게 계산할 수 있습니다.각 완전 가산기에는 3가지 수준의 논리가 필요합니다.32비트 리플 캐리어 가산기에는 32개의 풀 가산기가 있기 때문에 임계 패스(크리티컬 케이스) 지연은 3(입력에서 제1 가산기로 반송) + 31 × 2(후기 가산기로 반송 전파용) = 65 게이트 ^[6]지연입니다.n비트 캐리 리플 가산기의 최악의 지연에 대한 일반적인 방정식은 다음과 같습니다.합계와 캐리 비트를 모두 고려합니다.

\displaystyle T_{\text{CRA}}(n)=T_{\text{\text}HA}}+(n-1)\cdot T_{\text{c}}}+T_{\text{s}}}=T_{\text{\text}FA}}+(n-1)\cdot T_{c}=3D+(n-1)\cdot 2D=(2n+1)\cdot D.}

교대로 반송 극성과 최적화된 AND-OR-Invert 게이트를 갖춘 설계는 약 2배의 속도를 ^[7]^[5]낼 수 있습니다.

4비트 가산기(carry lookahead 포함)

이월 예측 가산기

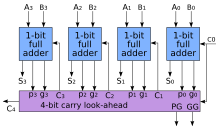
계산 시간을 줄이기 위해 엔지니어들은 자리올림수 예측 가산기(CLA)를 사용하여 두 개의 이진수를 더하는 더 빠른 방법을 고안했습니다.각 비트 위치에 대해 2개의 신호(P 및 G)를 생성하여 동작합니다.이는 캐리(최소1개의 입력은 1)가 덜 중요한 비트 위치에서 전파되는지(둘 다 입력이 1) 또는 해당 비트 위치에서 차단되는지(둘 다 입력이 0) 여부에 따라 결정됩니다.대부분의 경우 P는 단순히 반 가산기의 합계 출력이고 G는 동일한 가산기의 반송 출력입니다.P, G가 생성된 후 비트 위치별 캐리어가 작성된다.일부 고급 캐리어어헤드 아키텍처는 맨체스터 캐리어 체인, 브렌트-쿵 애더(BKA)^[8] 및 Kogge-Stone 애더(^[9]^[10]KSA)

다른 일부 멀티비트 가산기 아키텍처는 가산기를 블록으로 나눕니다.계산 시간을 최적화하기 위해 회로의 전파 지연에 따라 이들 블록의 길이를 변경할 수 있습니다.이러한 블록 기반 가산기에는 각 비트가 아닌 각 블록의 P 및 G 값을 결정하는 반송 건너뛰기(또는 반송 바이패스) 가산기, 합계를 생성하고 가능한 반송 입력(0 또는 1) 중 하나의 값을 블록에 전달하는 반송 선택 가산기가 포함되어 있으며, 반송 비트가 kn일 때 멀티플렉서를 사용하여 적절한 결과를 선택합니다.소유합니다.

64비트 가산기

여러 개의 자리올림수 예측 가산기를 결합하면 더 큰 가산기를 만들 수 있습니다.이것은 여러 레벨에서 사용하여 더 큰 추가기를 만들 수 있습니다.예를 들어, 다음 가산기는 64비트 가산기로, 2레벨의 선행 캐리어 유닛을 갖춘4개의 16비트 CLA를 사용합니다.

다른 가산기 설계에는 자리올림 선택 가산기, 조건부 합계 가산기, 자리올림 건너뛰기 가산기 및 자리올림-완전 가산기가 포함됩니다.

캐리어 저장 추가기

가산회로가 3개 이상의 수의 합계를 산출하는 경우에는 반송 결과를 전파하지 않는 것이 유리하다.대신 3개의 입력 가산기가 사용되며 합계와 자리올림이라는2개의 결과가 생성됩니다.합계와 반송파는 반송 신호의 전파를 기다릴 필요 없이 후속 3자리 가산기의 두 가지 입력으로 공급될 수 있습니다.그러나 모든 덧셈 단계 후에는 최종 합계와 결과를 얻기 위해 기존의 덧셈기(리플 캐리 또는 룩어헤드 등)를 사용해야 합니다.

3:2 압축기

전체 가산기는 3:2 손실 압축기로 볼 수 있습니다. 즉, 3개의 1비트 입력을 합산하여 결과를 단일 2비트 숫자로 반환합니다. 즉, 8개의 입력 값을 4개의 출력 값에 매핑합니다.따라서 예를 들어, 101의 이진수 입력은 1 + 0 + 1 = 10(16진수 2)의 출력이 됩니다.실행은 결과 중 하나의 비트를 나타내며, 합계는 0비트를 나타냅니다.마찬가지로, 2:2 손실 압축기로서 하프 가산기를 사용하여 4개의 가능한 입력을 3개의 가능한 출력으로 압축할 수 있습니다.

이러한 압축기를 사용하여 3개 이상의 덧셈의 합계를 가속화할 수 있습니다.덧셈이 정확히 3인 경우 레이아웃은 반송 저장 가산기로 알려져 있습니다.추가가 4개 이상일 경우 압축기 층이 여러 개 필요하며 회로에는 다양한 설계가 가능합니다.가장 일반적인 것은 Dadda 및 Wallace 트리입니다.이러한 종류의 회로는 멀티플라이어에 가장 많이 사용되며, 이러한 회로를 다다 및 월러스 멀티플라이어라고도 합니다.

양자 가산기

양자 완전 가산기, 토폴리와 CNOT 게이트 사용.B 출력을 복원하기 위해 계산 해제가 필요하지 않은 경우 이 그림에서 점으로 둘러싸인 CNOT 게이트웨이를 생략할 수 있습니다.

Topfoli와 CNOT 양자 로직 게이트만을 사용하여 양자 풀 ^[11]^[12]가산기를 생성할 수 있습니다.동일한 회로를 기존의 가역 계산에도 사용할 수 있습니다.

양자 푸리에 변환은 회로 복잡도가 낮기 때문에 수를 더하는 ^[13]^[14]데도 효율적으로 사용할 수 있다.

아날로그 주소

바이너리 가산기와 마찬가지로 2개의 입력 전류를 조합하면 이들 전류가 효과적으로 추가됩니다.하드웨어의 제약 내에서 비이진 신호(즉 베이스가 2보다 큰 것)를 합산하여 합계를 계산할 수 있다."서밍 앰프"^[15]라고도 하는 이 기술은 추가 회로의 트랜지스터 수를 줄이는 데 사용할 수 있습니다.

「」를 참조해 주세요.

이진수 승수
감산기
전자 믹서 - 아날로그 신호 추가용

레퍼런스

^ Singh, Ajay Kumar (2010). Digital VLSI Design. Prentice Hall India. p. 321. ISBN 9788120341876 – via Google Books.
^ Lancaster, Geoffrey A. (2004). Excel HSC Software Design and Development. Pascal Press. p. 180. ISBN 978-1-74125175-3.
^ Mano, M. Morris (1979). Digital Logic and Computer Design. Prentice-Hall. pp. 119–123. ISBN 978-0-13-214510-7.
^ Teja, Ravi (2021-04-15), Half Adder and Full Adder Circuits, retrieved 2021-07-27
^ ^a ^b ^c Fischer, P. "Einfache Schaltungsblöcke" (PDF). Universität Heidelberg. Archived from the original (PDF) on 2021-09-05. Retrieved 2021-09-05.
^ Satpathy, Pinaki (2016). Design and Implementation of Carry Select Adder Using T-Spice. Anchor Academic Publishing. p. 22. ISBN 978-3-96067058-2.
^ Burgess, Neil (2011). Fast Ripple-Carry Adders in Standard-Cell CMOS VLSI. 20th IEEE Symposium on Computer Arithmetic. pp. 103–111.
^ Brent, Richard Peirce; Kung, Hsiang Te (March 1982). "A Regular Layout for Parallel Adders". IEEE Transactions on Computers. C-31 (3): 260–264. doi:10.1109/TC.1982.1675982. ISSN 0018-9340. S2CID 17348212. Archived from the original on September 24, 2017.
^ Kogge, Peter Michael; Stone, Harold S. (August 1973). "A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations". IEEE Transactions on Computers. C-22 (8): 786–793. doi:10.1109/TC.1973.5009159. S2CID 206619926.
^ Reynders, Nele; Dehaene, Wim (2015). Ultra-Low-Voltage Design of Energy-Efficient Digital Circuits. Analog Circuits and Signal Processing Series. Analog Circuits And Signal Processing (ACSP) (1 ed.). Cham, Switzerland: Springer International Publishing AG Switzerland. doi:10.1007/978-3-319-16136-5. ISBN 978-3-319-16135-8. ISSN 1872-082X. LCCN 2015935431.
^ Feynman, Richard P. (1986). "Quantum mechanical computers". Foundations of Physics. Springer Science and Business Media LLC. 16 (6): 507–531. Bibcode:1986FoPh...16..507F. doi:10.1007/bf01886518. ISSN 0015-9018. S2CID 122076550.
^ "Code example: Quantum full adder". QuTech (Delft University of Technology (TU Delft) and the Netherlands Organisation for Applied Scientific Research (TNO)).
^ Draper, Thomas G. (7 Aug 2000). "Addition on a Quantum Computer". arXiv:quant-ph/0008033.
^ Ruiz-Perez, Lidia; Juan Carlos, Garcia-Escartin (2 May 2017). "Quantum arithmetic with the quantum Fourier transform". Quantum Information Processing. 16 (6): 152. arXiv:1411.5949v2. Bibcode:2017QuIP...16..152R. doi:10.1007/s11128-017-1603-1. S2CID 10948948.
^ https://www.electronics-tutorials.ws/opamp/opamp_4.html

추가 정보

Liu, Tso-Kai; Hohulin, Keith R.; Shiau, Lih-Er; Muroga, Saburo (January 1974). "Optimal One-Bit Full-Adders with Different Types of Gates". IEEE Transactions on Computers. Bell Laboratories: IEEE. C-23 (1): 63–70. doi:10.1109/T-C.1974.223778. ISSN 0018-9340. S2CID 7746693.
Lai, Hung Chi; Muroga, Saburo (September 1979). "Minimum Binary Parallel Adders with NOR (NAND) Gates". IEEE Transactions on Computers. IEEE. C-28 (9): 648–659. doi:10.1109/TC.1979.1675433. S2CID 23026844.
Mead, Carver; Conway, Lynn (1980) [December 1979]. Introduction to VLSI Systems (1 ed.). Reading, MA, USA: Addison-Wesley. Bibcode:1980aw...book.....M. ISBN 978-0-20104358-7. Retrieved 2018-05-12.
Davio, Marc; Dechamps, Jean-Pierre; Thayse, André (1983). Digital Systems, with algorithm implementation (1 ed.). Philips Research Laboratory, Brussels, Belgium: John Wiley & Sons, a Wiley-Interscience Publication. ISBN 978-0-471-10413-1. LCCN 82-2710.

외부 링크

산술 모듈용 하드웨어 알고리즘은 그림과 함께 몇 가지 가산기 레이아웃에 대한 설명을 포함합니다.
8비트 완전 가산기 및 감산기: 학습 목적으로만 JavaScript에 내장된 인터랙티브 완전 가산기의 데모입니다.
인터랙티브 풀 가산기 시뮬레이션(Java 필요), Teahlab의 온라인 회로 시뮬레이터로 구성된 인터랙티브 풀 가산기 회로.
인터랙티브 하프 가산기 시뮬레이션(Java 필요), Teahlab의 회로 시뮬레이터로 구축된 하프 가산기 회로.
Verilog에 내장된 4비트 풀 가산기 시뮬레이션과 함께 제공되는 리플 캐리 풀 가산기 비디오 튜토리얼
Shirriff, Ken (November 2020). "Reverse-engineering the carry-lookahead circuit in the Intel 8008 processor".

[1] Singh, Ajay Kumar (2010). Digital VLSI Design. Prentice Hall India. p. 321. ISBN 9788120341876 – via Google Books.

[Lancaster_2004-2] Lancaster, Geoffrey A. (2004). Excel HSC Software Design and Development. Pascal Press. p. 180. ISBN 978-1-74125175-3.

[Mano_1979-3] Mano, M. Morris (1979). Digital Logic and Computer Design. Prentice-Hall. pp. 119–123. ISBN 978-0-13-214510-7.

[4] Teja, Ravi (2021-04-15), Half Adder and Full Adder Circuits, retrieved 2021-07-27

[Fischer-5] Fischer, P. "Einfache Schaltungsblöcke" (PDF). Universität Heidelberg. Archived from the original (PDF) on 2021-09-05. Retrieved 2021-09-05.

[Adder-6] Satpathy, Pinaki (2016). Design and Implementation of Carry Select Adder Using T-Spice. Anchor Academic Publishing. p. 22. ISBN 978-3-96067058-2.

[Burgess_2011-7] Burgess, Neil (2011). Fast Ripple-Carry Adders in Standard-Cell CMOS VLSI. 20th IEEE Symposium on Computer Arithmetic. pp. 103–111.

[Brent-Kung_1982-8] Brent, Richard Peirce; Kung, Hsiang Te (March 1982). "A Regular Layout for Parallel Adders". IEEE Transactions on Computers. C-31 (3): 260–264. doi:10.1109/TC.1982.1675982. ISSN 0018-9340. S2CID 17348212. Archived from the original on September 24, 2017.

[Kogge-Stone_1973-9] Kogge, Peter Michael; Stone, Harold S. (August 1973). "A Parallel Algorithm for the Efficient Solution of a General Class of Recurrence Equations". IEEE Transactions on Computers. C-22 (8): 786–793. doi:10.1109/TC.1973.5009159. S2CID 206619926.

[ULVD_2015-10] Reynders, Nele; Dehaene, Wim (2015). Ultra-Low-Voltage Design of Energy-Efficient Digital Circuits. Analog Circuits and Signal Processing Series. Analog Circuits And Signal Processing (ACSP) (1 ed.). Cham, Switzerland: Springer International Publishing AG Switzerland. doi:10.1007/978-3-319-16136-5. ISBN 978-3-319-16135-8. ISSN 1872-082X. LCCN 2015935431.

[11] Feynman, Richard P. (1986). "Quantum mechanical computers". Foundations of Physics. Springer Science and Business Media LLC. 16 (6): 507–531. Bibcode:1986FoPh...16..507F. doi:10.1007/bf01886518. ISSN 0015-9018. S2CID 122076550.

[12] "Code example: Quantum full adder". QuTech (Delft University of Technology (TU Delft) and the Netherlands Organisation for Applied Scientific Research (TNO)).

[13] Draper, Thomas G. (7 Aug 2000). "Addition on a Quantum Computer". arXiv:quant-ph/0008033.

[14] Ruiz-Perez, Lidia; Juan Carlos, Garcia-Escartin (2 May 2017). "Quantum arithmetic with the quantum Fourier transform". Quantum Information Processing. 16 (6): 152. arXiv:1411.5949v2. Bibcode:2017QuIP...16..152R. doi:10.1007/s11128-017-1603-1. S2CID 10948948.

[15] ttps://www.electronics-tutorials.ws/opamp/opamp_4.html

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

Search

가산기(전자제품)

네임스페이스

더

목차

바이너리 가산기

반 가산기

풀 가산기

여러 비트를 지원하는 애드

리플 캐리어 가산기

이월 예측 가산기

캐리어 저장 추가기

3:2 압축기

양자 가산기

아날로그 주소

「」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

Search

가산기(전자제품)

바이너리 가산기

반 가산기

풀 가산기

여러 비트를 지원하는 애드

리플 캐리어 가산기

이월 예측 가산기

캐리어 저장 추가기

3:2 압축기

양자 가산기

아날로그 주소

「 」를 참조해 주세요.

레퍼런스

추가 정보

외부 링크

「」를 참조해 주세요.