5개 한계 튜닝

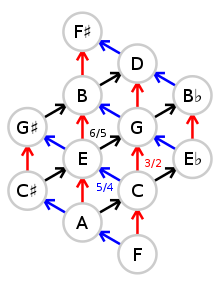
5 한계 튜닝, 5 한계 튜닝 또는 5-프리미트 튜닝(5-odd-limit tuning과 혼동되지 않음)은 주어진 참조 노트(기본 노트)의 주파수에 2, 3, 5의 정수 파워 제품(5- 이하로 제한된 프라임 번호)을 곱하여 각 음의 주파수를 얻는 모든 악기를 튜닝하는 시스템이다. 2⁻³/3¹/5¹ = 15/8로.

2의 힘은 옥타브에 의한 인터뷰 움직임을 나타낸다. 3의 힘은 완벽한 5분의 1의 간격(더하기 1 옥타브, 1/2을 곱하여 제거할⁻¹ 수 있음)에 의한 움직임을 나타낸다. 5의 힘은 3분의 1의 간격을 나타낸다(더하기 2 옥타브, 1/4을⁻² 곱하여 분리 가능). 따라서, 5 한계 튜닝은 전적으로 3개의 기본 순 튜닝 간격(옥타브, 3/5), 3/5의 스택으로 구성된다. 조화에 대한 인식은 고조파 계열의 낮은 숫자와 관련이 있는 것으로 보이며, 5 한계 튜닝은 3개의 가장 낮은 프리타임에 의존하므로 5 한계 튜닝은 매우 자음적인 하모니를 생산할 수 있어야 한다. 따라서 5제한 조정은 억양을 얻기 위한 방법으로 간주된다.

프라임의 (비제로 정수) 동력은 다른 프라임의 동력과 같기 때문에 사용 가능한 간격, 피치 클래스, 피치 클래스, 피치, 키 중심, 화음 및 변조의 수는 제한되지 않는다. 따라서 사용 가능한 간격은 3차원 격자(하나 차원 또는 한 방향)에서 무한히 연장될 수 있다. 각 전성기에 대해 옥타브를 무시하면 두 방향으로 무한 확장되는 피치 클래스(노트명)의 2차원 격자로 볼 수 있다.

그러나 음향기기를 위해 설계된 대부분의 튜닝 시스템은 실용적인 이유로 전체 투구수를 제한한다. 또한 각 옥타브에 동일한 수의 피치를 갖는 것이 일반적이며(그러나 항상 그렇게 되는 것은 아님), 고정된 피치 클래스 세트의 옥타브 트랜지션을 나타낸다. 그 경우 튜닝 시스템은 옥타브 당 일정 수의 투구수를 옥타브 반복 스케일로도 생각할 수 있다.

특정 5 한계 튜닝 시스템에서 피치의 주파수는 튜닝 시스템에 대해 선택한 고정 기준 피치의 주파수(예: A440, A442, A432, C256 등)에 피치 등급과 옥타브를 결정하기 위한 2의 힘을 어느 정도 조합하여 곱하여 얻을 수 있다.

예를 들어, 기본 노트가 C256인 5 한계 튜닝 시스템이 있다면(초당 256 사이클을 가지고 있고 우리는 그것을 C라고 부르기로 결정했다는 의미_C), f = 256Hz 또는 "C의 주파수는 256Hz와 같다". 이 C 위에 E를 정의하는 몇 가지 방법이 있다. 3분의 1을 사용하면 1인자 5가 올라가고 2인자가 내려가고, 5분의 1은 주파수 비율이 5/4가 되거나, 5분의 1을 사용하면 3인자 4가 올라가고 6인자 2가 내려가는 81/64가 될 수 있다. 주파수는 다음과 같이 된다.

${\displaystyle f_{E}=5^{1}\cdot 3^{0}\cdot 2^{-2}\cdot f_{C}={5 \over 4}\cdot 256\\\\\mathrm {Hz} =320\mathrmatrmatrm {Hz}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

또는

${\displaystyle f_{E}=5^{0}\cdot 3^{4}\cdot 2^{-6}\cdot f_{C}={81 \over 64}\cdot 256\\\\\mathrm {Hz} = 324\mathrmatrmatrm {Hz}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}$

이음계

우리 자신을 7개의 피치 클래스(옥타브당 7노트)로 제한한다고 가정하면, 5-리미트 튜닝을 사용하여 익숙한 이음계 스케일을 여러 가지 방법으로 튜닝할 수 있는데, 이 모든 것이 대부분의 트라이애드를 이상적으로 튜닝하고 자음 및 안정되게 만들지만, 일부 트라이애드는 안정성이 떨어지는 인터벌릭 구성으로 남겨둔다.

주어진 척도의 두드러진 음은 주파수가 상대적으로 작은 정수의 비율을 형성하도록 조정된다. 예를 들어 G장조의 키에서 노트 G 대 D(완벽한 5번째)의 빈도 비율은 3/2인 반면, G 대 C의 빈도수는 2/3(내림차순 5번째) 또는 4/3(완벽한 4번째)이 상승하고, 주요 3번째 G 대 B의 빈도수는 5/4이다.

단지 이음계 척도는 다음과 같이 도출될 수 있다. C장조의 키를 상상하면, 부지배적 뿌리 F와 지배적 뿌리 G가 양쪽에 있는 강장근 C에서 5분의 1(3:2) 떨어져 있고, 화음 FAS, CEG, GBD가 단지 주요 3중(주파수 비율 4:5:6)이라고 주장한다고 가정하자.

톤	이름	C		D		E		F		G		A		B		C
	비율	1/1		9/8		5/4		4/3		3/2		5/3		15/8		2/1
	내추럴	24		27		30		32		36		40		45		48
	센트	0		204		386		498		702		884		1088		1200
스텝	간격		T		t		s		T		t		T		s
	비율		9/8		10/9		16/15		9/8		10/9		9/8		16/15
	센트 스텝		204		182		112		204		182		204		112

이것은 프톨레마이오스의 강렬한 디아토닉 스케일로 알려져 있다. 여기서 "Natural"로 향하는 행은 (위 행에 분모의 lcm를 곱하여) 자연수의 공통 목록을 사용하여 이 모든 비율을 표현한다. 즉, 고조파 계열 내에서 이 1 옥타브 스케일 형상이 가장 낮은 것은 고조파 24~48 옥타브에서 발견된 24개 고조파 중 7개 부분집합으로 나타난다.

3장 3분의 3이 정확하다(5:4), 3단 3분의 3이 예상대로 정확하다(6:5) 그러나 D에서 F까지는 반음절 또는 피타고라스 마이너 3분의 3(하강 3단 3단, 완전 5단, 옥타브 조정)으로, 방금 튜닝한 (6:5) 단음절보다 좁은 구음 쉼표다.

결과적으로 우리는 EGB와 ACE가 단지 사소한 트라이애드일 뿐(10:12:15)인 척도를 얻지만, DFA 트라이애드는 우리가 예상할 수 있는 사소한 모양이나 소리를 가지고 있지 않다(27:32:40). 게다가, BDF 3중창은 우리가 6:5 마이너 3분의 2를 쌓음으로써 얻을 수 있는 감소된 3중창(25:30:36)이 아니다. 대신 다음과 같이 된다.^[1][2]

기본적인 단계별 척도 간격은 다음과 같이 나타난다는 것을 알 수 있다.

• s = 16:15 (세미톤)
• t = 10:9(최소 톤)
• T = 9:8(주요 톤)

더 큰 간격을 형성하기 위해 조합될 수 있는 것(다른 것 중):

• Ts = 6:5(소수 3위)
• Tt = 5:4(주요 3번째)
• Tts = 4:3(완벽한 4번째)
• TTts = 3:2(완벽한 5번째)
• TTTts 2:1 (옥타브)

또 다른 방법은 다음과 같다. A 마이너의 상대적인 마이너 키를 생각하고 D, A, E를 5분의 1의 척수로 사용하면서, 우리는 코드 DFA, ACE, EGB가 마이너 트라이애드일 뿐이라고 주장할 수 있다(10:12:15).

톤	이름	A		B		C		D		E		F		G		A
	비율	1/1		9/8		6/5		4/3		3/2		8/5		9/5		2/1
	내추럴	120		135		144		160		180		192		216		240
	센트	0		204		316		498		702		814		1018		1200
스텝	간격		T		s		t		T		s		T		t
	비율		9/8		16/15		10/9		9/8		16/15		9/8		10/9
	센트 스텝		204		112		182		204		112		204		182

초기 척도와 대조해 보면, 다섯 쌍의 연속 노트에서 단계 비율은 그대로 유지되지만, 하나의 노트인 D와 단계인 C-D와 D-E는 그 비율을 바꾸었다.

3대 3은 아직 5:4이고, 3대 3은 아직 6:5이고, 4대 3은 32:27인데, DF는 32:27이 아니라 지금은 BD라는 점을 제외하면 말이다. FAS와 CEG는 여전히 주요 트라이애드(4:5:6), GBD는 현재(108:135:160), BDF는 현재(135:160:192)에 불과하다.

D를 낮추는 대신 A를 올리는 등의 다른 가능성도 있지만, 각 조정은 다른 것을 깨뜨린다.

7개의 투구로 제한하면 구성에서 7개의 이온성 트라이애드를 메이저(4:5:6)로, 마이너(10:12:15)로, 축소(25:30:36)로 모두 얻는 것은 분명 불가능하다.

그것은 원하는 하모니를 조화롭게 실행하기 위해 투구수를 늘려야 한다는 것을 보여준다.

12음계

5-리미트 튜닝으로 12톤 스케일을 만들기 위해, 우리는 15개의 적절한 억양이 담긴 테이블을 만드는 것으로 시작한다.

요인	1⁄9	1⁄3	1	3⁄1	9⁄1
5⁄1	D− 10/9 182[3]	A 5/3 884	E 5/4 386	B 15/8 1088	F♯+ 45/32 590[3]	주석을 달다 비율 센트
1	B♭− 16/9 996[3]	F 4/3 498	C 1 0	G 3/2 702	D 9/8 204	주석을 달다 비율 센트
1⁄5	G♭− 64/45 610[3]	D♭− 16/15 112[3]	A♭ 8/5 814	E♭ 6/5 316	B♭ 9/5 1018	주석을 달다 비율 센트

첫 번째 행과 첫 번째 열에 나열된 요인은 각각 3과 5의 힘이다(예: ½9 = 3⁻²) 색상은 음조가 거의 동일한 음조의 음조의 쌍을 나타낸다. 비율은 모두 이 도표(이 척도의 기본 참고)의 중심에서 C에 상대적으로 표현된다. 두 단계로 계산된다.

1. 표의 각 셀에 대해 해당 인자를 곱하여 기준 비율을 구한다. 예를 들어, 왼쪽 하단 셀의 기본 비율은 1/9 · 1/5 = 1/45이다.
2. 그런 다음 기준 비율은 C에서 시작하는 옥타브 범위(1/1 ~ 2/1) 내에 이를 가져오는 데 필요한 만큼 큰 2의 음 또는 양의 힘으로 곱한다. 예를 들어 왼쪽 아래 셀(1/45)의 기본 비율에⁶ 2를 곱하고 결과 비율은 64/45로 1/1과 2/1 사이의 숫자다.

두 번째 단계에서 사용된 2의 힘은 오름차순 또는 내림차순 옥타브로 해석될 수 있다는 점에 유의하십시오. 예를 들어, 음의 주파수를 2로⁶ 곱하면 음을 6옥타브 증가시킨다. 또한 표의 각 행은 5분의 1의 순서(오른쪽 끝), 각 열은 3분의 1의 순서(위쪽 끝)로 간주할 수 있다. 예를 들어, 표의 첫 번째 줄에는 D와 A에서 오름차순 5번째가 있고, A에서 E로 내려가는 옥타브에 이은 또 다른 하나가 있다. 이것은 동일한 비율을 계산하기 위한 대안이지만 동등한 방법을 제안한다. 예를 들어, C에서 시작하여 한 셀을 왼쪽으로 이동하고 한 셀을 위쪽으로 이동하여 A(5/3 비율)를 얻을 수 있으며, 이는 1/5(2/3)씩 하강하고 1/3(5/4)만큼 상승하는 것을 의미한다.

${\displaystyle {1 \over 1}\cdot {2 \over 3}\cdot {5 \over 4}={10 \over 12}={5 \over 6}}}}}$

이 값이 C보다 낮으므로 원하는 비율 범위(1/1 2/1의 취지)내에서 끝내려면 한 옥타브 위로 이동해야 한다.

${\displaystyle {5 \over 6}\cdot {2 \over 1}={10 \over 6}={5 \over 3}.}$

12음 음계는 극음 음표 두 개당 한 개의 음표를 제거하여 얻는다. C 기반 피타고라스에도 유효하고 1/4 콤마는 하나의 척도를 의미한다는 관습에 따라 G according 제거의 공통점이 있는 최소 세 가지 방법으로 이 작업을 수행할 수 있다. 강장제 C보다 반 옥타브 가까이 낮은 5분의 1 옥타브라는 점에 유의하십시오. 강장제의 비율은 분자와 척도 내에서 모든 음조의 분모에서 가장 큰 값을 가지며, 이 값을 최소로 조화시키지 않는다. 모든 이유로 피해야 한다.
우리가 운용적으로 여기서 대칭 척도 1이라고 하는 첫 번째 전략은 테이블의 왼쪽 위와 오른쪽 아래 모서리에 있는 톤을 제거하기 위한 선택으로 구성된다. 대칭 척도 2로 표시된 두 번째 것은 두 번째 행의 첫 번째 셀과 마지막 셀("1"로 표시됨)에 있는 노트를 폐기하는 것으로 구성된다. 비대칭 척도로 표시된 세 번째 열은 첫 번째 열("1/9"로 표시됨)을 폐기하는 것으로 구성된다. 결과 12톤 눈금은 다음과 같다.

대칭 척도 1
요인	1⁄9	1⁄3	1	3	9
5		A 5/3	E 5/4	B 15/8	F♯+ 45/32
1	B♭− 16/9	F 4/3	C 1	G 3/2	D 9/8
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5

대칭 척도 2
요인	1⁄9	1⁄3	1	3	9
5	D− 10/9	A 5/3	E 5/4	B 15/8	F♯+ 45/32
1		F 4/3	C 1	G 3/2
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5	B♭ 9/5

비대칭척도
요인	1⁄9	1⁄3	1	3	9
5		A 5/3	E 5/4	B 15/8	F♯+ 45/32
1		F 4/3	C 1	G 3/2	D 9/8
1⁄5		D♭− 16/15	A♭ 8/5	E♭ 6/5	B♭ 9/5

제1저울과 제2저울에서 B♭과 D는 정확히 서로 역행하는 것이다. 이것은 세 번째 것에 대한 사실이 아니다. 이 두 음계가 대칭으로 간주되는 이유다(G♭ 제거는 다른 튜닝 시스템으로 생산되는 음계를 포함하여 12 톤 음계를 모두 약간 비대칭으로 만든다).

비대칭 시스템은 설계상 가장 "정당한" 비율(더 작은 숫자를 포함하는 비율), 9개의 순수 5분의 1(인자 3/2) 및 8개의 순수 3분의 1(인자 5/4)을 가질 수 있지만, 또한 6개의 순수한 마이너 3분의 1(인자 6/5)을 가질 수 있는 장점이 있다. 단, 2개의 불순 5분의 1(예: D to A는 3/2가 아닌 40/27), 3개의 불순 소 3분의 1(예: D to F는 6/5가 아닌 32/27)이 들어 있어 사실상 좁은 키 범위까지 변조를 제한한다. 강장제 C의 화음, 지배성 G, 부지배성 F는 물론 D♭, A♭, E♭과 부성음 Fm, Cm, gm, Am, Bm, Em도 순수하지만 Dm은 아니다.

비대칭 체계의 단점은 대칭 체계의 경우 12개가 아닌 14개의 늑대를 생산한다는 것이다.

첫 번째 대칭 척도의 B♭는 다른 척도의 B♭와 싱토닉 쉼표로 다른 척도의 B♭와 21센트를 초과한다. 균등 강화 척도에서는 모든 스텝을 동일한 주파수 비율로 만들어 차이를 없앤다.

로그 척도에 주파수 인자 2/1(파란색), 3/2(녹색), 5/4(갈색)를 쌓아서 만든 비대칭 척도

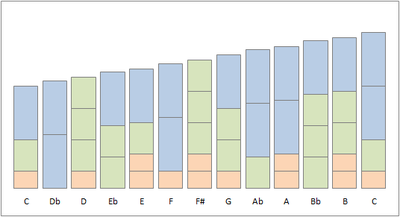
비대칭 축척의 구성은 그림에 그래픽으로 나타나 있다. 각 블록은 2/1, 3/2 및 5/4의 구성 주파수 비율의 센트 높이를 가진다. 반복적인 패턴을 인식할 수 있다. 예를 들어, 5/4 블록과 3/2 블록을 2/1 블록으로 교체하여 다음 노트를 만드는 경우가 많으며, 이는 16/15의 비율을 나타낸다.

2/1, 3/2 및 5/4 대신 주파수 요인 2, 3 및 5를 사용하여 작성된 유사한 이미지는 여기를 참조하십시오.

적정 비율

이러한 척도를 만드는 데 사용되는 정의 비율은 다른 척도의 구간의 일치도를 평가하기 위한 참조로 사용될 수 있다(예를 들어, 이 비교 표 참조). 그러나 5제한 조정만이 억양을 얻을 수 있는 유일한 방법은 아니다. 짝수 "정당한" 비율의 구간만 구성하거나, 동일한 성질의 등가물에 더 가까운 값을 사용하여 교대로 구성할 수 있다. 예를 들어, 7 한계 튜닝은 때때로 작은 7번째(7/4)와 그 반대인 주요 2번째(8/7)에 대해 더 많은 자음 간격을 얻기 위해 사용된다. 이러한 기준 비율의 목록은 다음과 같이 제공되며, 이를 순수 또는 엄밀히 말하면 단순한 구간 또는 비율이라고 할 수 있다.

간격명	짧다	수 반의	5음 튜닝				7회전 튜닝	17음 튜닝
			대칭척도		비대칭척도
			N. 1	N. 2	표준	확장됨
완벽한 일치	P1	0	1/1	1/1	1/1	1/1	1/1	1/1
마이너초	m2	1	16/15	16/15	16/15	16/15	15/14	14/13
주요2길	M2	2	9/8	10/9	9/8	9/8	8/7	8/7
마이너 세 번째	m3	3	6/5	6/5	6/5	6/5	6/5	6/5
메이저 3	M3	4	5/4	5/4	5/4	5/4	5/4	5/4
퍼펙트 네 번째	P4	5	4/3	4/3	4/3	4/3	4/3	4/3
증강4길	A4	6	45/32	45/32	45/32	25/18	7/5	2012년 7월 5일 또는 17일
감소된 5번째	d5	6	64/45	64/45	64/45	36/25	10/7	10/7 또는 24/17
퍼펙트 파이브	P5	7	3/2	3/2	3/2	3/2	3/2	3/2
마이너 6	m6	8	8/5	8/5	8/5	8/5	8/5	8/5
6번 소령	M6	9	5/3	5/3	5/3	5/3	5/3	5/3
마이너 7	m7	10	16/9	9/5	9/5	9/5	7/4	7/4
7장조	M7	11	15/8	15/8	15/8	15/8	15/8	13/7
퍼펙트 옥타브	P8	12	2/1	2/1	2/1	2/1	2/1	2/1

노란색으로 강조 표시된 셀은 같은 행에 있는 비색상 셀의 간격보다 더 공정한 간격을 나타낸다. 청록색으로 강조 표시된 것은 더 공평한 비율을 나타낸다.

삼중수소 45/32와 64/45의 비율(증가 4번째 및 감소 5번째)은 엄격하게 정의되는 모든 맥락에서 볼 수 있는 것은 아니지만 위에서 언급한 5개 한계 조정 척도에서 가능한 가장 정당하다. 확장된 비대칭 5 한계 척도(아래 참조)는 삼중수소(25/18 및 36/25) 모두에 대해 약간 더 정의로운 비율을 제공하는데, 이 순도 또한 논란의 여지가 있다. 7 한계 조정은 7/5(약 582.512 센트, 일명 패리티트리톤)와 10/7(약 617.488 센트)의 가능한 가장 적절한 비율을 허용한다. 이 비율은 17/12(약 603.000센트)와 24/17(약 597.000센트)보다 자음성이 높지만, 같은 성질의 600.000센트에 가까워서 후자 역시 상당히 흔하다.

위에서 언급한 7/4 간격 (약 968.826 센트)은 음악 이론의 역사 전반에 걸쳐 논쟁거리가 되어왔다. 음악 이론의 역사에서 그것은 같은 성질의 7번째보다 31 센트 더 평평하다.

구간의 크기

위의 표는 기본 노트 C에 대한 각 톤의 주파수 비율만 보여준다. 단, 12개의 음표 각각에서 시작하여 간격을 형성할 수 있다. 따라서 각 구간 유형별로 12개의 구간(단독 12개, 세미톤 12개, 세미톤 2개로 구성된 12개 구간, 세미톤으로 구성된 12개 구간 등)을 정의할 수 있다.

5 한계 튜닝에서는 유니언과 옥타브를 제외한 각 간격 타입의 크기가 각각 서너 가지씩 다르다. 이것은 억양을 찾는데 지불된 가격이다. 오른쪽과 아래의 표는 "대칭 척도"에 대한 주파수 비율과 대략적인 크기를 센트로 보여준다. "대칭 척도 1"에 대한 유사한 표들이 여기와 여기에 발표된다. 간격 이름은 표준 단축 형식으로 주어진다. 예를 들어, C에서 G까지의 간격의 크기는 완벽한 5번째(P5)인 C행의 7번째 열에서 찾을 수 있다. 위에서 정의한 순수한 간격은 굵은 글꼴로 표시된다(위에서 설명한 바와 같이 A4의 경우 45/32 5 590 센트의 정당한 억양비를 순수하다고 보지 않는다).

색상 코드는 시공표의 기준 크기에서 벗어나는 구간을 구분하여 편차의 양을 표시한다. 늑대의 간격은 검은색으로 표시되어 있다.^[4]

배율 전체에 걸쳐 간격 크기가 다른 이유는 배율을 형성하는 투구 간격이 일정하지 않기 때문이다. 즉, 12개의 주석에 대한 구성에 의해 정의된 빈도는 4개의 다른 의미(즉, 인접 주 간 간격)를 결정한다. 예를 들어,

• ${\displaystyle S_{1}={5 \over 4}\div {6 \over 5}={25 \over 24}\ 약 70.672\\hbox{cents}}}}}}$
  ("E♭과 E 사이의 just" 증강된 일치)
• ${\displaystyle S_{2}={9 \over 8}\div {16 \over 15}={135 \over 128}\약 92.179\{\hbox{cents}}}}}}}$
  (DR과 D의 일치성 증대)
• ${\displaystyle S_{3}={16 \over 15}\ 약 111.731\[\hbox{cents}}}}$
  ("C와 D 사이의 "단순" 초)
• ${\displaystyle S_{4}={9 \over 5}\div {5 \over 3}={27 \over 25}\ 약 133.238\{\hbox{cents}}}}}}}}$
  (A와 B 사이의 최소값)

반대로, 균등하게 강화한 색도 눈금에서는, 정의상 12개의 투구는 균등하게 간격을 두고, 모든 세미톤은 정확한 크기를 가지고 있다.

• ${\displaystyle S_{E}={\sqrt[{12}]{2}}=100.000\{\hbox{cents}}.}$

따라서 주어진 유형의 모든 구간은 크기가 동일하다(예: 모든 주요 3분의 1은 크기가 같고, 5분의 1은 모두 크기가 같다). 이 경우에 지불되는 가격은, 물론, 합성과 옥타브에 대한 것 외에는, 어느 것도 정당하게 튜닝되고 완벽하게 자음된 것은 없다는 것이다.

5 한계 조정은 순수한 간격의 수를 최대화하기 위해 설계되었지만, 이 시스템에서도 몇 개의 간격은 현저하게 불순하다(예를 들어, 그림에서 볼 수 있듯이, 144개 간격 중 60개가 시공 표에 나타난 정당한 삽입된 기준 크기에서 19.6센트 이상 차이가 난다). 또한, 5 한계 튜닝은 피타고라스 튜닝에 관해서 훨씬 더 많은 늑대 간격을 산출하는데, 이것은 단지 억양 튜닝으로 3 한계로 간주할 수 있다. 즉, 피타고라스 튜닝이 늑대 간격 2개(5분의 1과 4분의 1)만을 결정하는 반면, 5제한 대칭 척도는 그 중 12개를 생성하며, 비대칭 척도는 14를 생성한다. 그것은 또한 비록 그들은 완전히 conditions[4]가 되기 늑대 간격을 만나지 못하는 사실은 25,3/3가량 되었으며, 3개의 대형/6오렌지 색으로 표에 표시한 다음 해당하는 순수한 비율에서 가감(1동조의 쉼표, 즉, 81/80하거나 벗어나는(비율 40/27, 32/27, 27/16(또는 G−, E♭−, A+[3])점은 중요하다. 에 대해 21.5센트)는 불협화음으로 분명히 인식될 수 있을 정도로 크다.^[5]

분명히 우리가 순수하고 자음적인 간격을 늘리려고 할수록 나머지 것은 보상에 의해 불순하고 불협화음이 된다. 일부 주요 초(M2)와 부 7초(m7)는 이 규칙의 유일한 예외를 나타낸다. 표에서 볼 수 있듯이 오렌지로 표시된 것은 크기가 해당 기준 크기(9/8 및 9/5)보다 81/80이 좁더라도 순수(10/9 및 16/9)이다.

다른 튜닝 시스템과 비교하려면 이 표도 참조하십시오.

콤마스

다른 튜닝 시스템에서는 쉼표를 두 종류의 세미톤(직교와 색도, 마이너 초, m2 또는 증강된 일치, A1)의 차이와 동일한 분 간격으로 정의할 수 있다. 그러나 이 경우 4가지 다른 종류의 세미콘(A1, S와₁ S₂, 2m2, S와₃ S₄)이 생산되며, 12가지 다른 쉼표는 크기 차이(센트)로 정의하거나 비율과 동등하게 비율을 나타낼 수 있다. 이 중 오름차순 6개(비율이 1/1보다 크고 센트(센트)의 양수)를 선택한다.

쉼표명	등가정의		크기
	의미심장한 기질에서.	5제한 조정 (축척도)	비율	센트
디아스키마 (DS)	${\displaystyle {m2} \over A1}$ 6분의 1의 비율로	${\displaystyle {S_{3} \over S_{2}}={{16 \over 15}\div {135 \over 128}}}}}$	${\displaystyle {2048 \over 2025}}$	$19번.6~}$
싱토닉 쉼표(SC)	${\displaystyle {{}LD} \over {DS}={{GD} {LD} 이상$	${\displaystyle {S_{2} \over S_{1}}={135 \over 128}\div {25 \over 24}}}}$	${\displaystyle {81\\80}}$	$21.5.~}$
		${\displaystyle {S_{4} \over S_{3}}}={{27 \over 25}\div {16 \over 15}}}}}$
소다이스(LD)	${\displaystyle {m2} \over A1}$ 4분의 1의 비율로	${\displaystyle {S_{3} \over S_{1}}={{16 \over 15}\div {25 \over 24}}}}$	${\displaystyle {display\\125}$	$(\displaystyle 41.1)~}$
		${\displaystyle {S_{4} \over S_{2}}={{27 \over 25}\div {135 \over 128}}}}}$
더 큰 다이즈(GD)	${\displaystyle {m2} \over A1}$ 1/3로 1을 의미했다.	${\displaystyle {S_{4} \over S_{1}}={{27 \over 25}\div {25 \over 24}}}}$	${\displaystyle {648 \{625}}}$	$62.6 디스플레이 스타일~}$

나머지 6개 비율은 이것과 정반대여서 폐기되며, 따라서 길이가 정확히 같지만 반대 방향(즉, 하강 방향, 1/1 미만의 비율, 센트 단위의 마이너스 크기)이다. 우리는 4가지 다른 크기의 쉼표를 얻는다: 디아스키마, 작은 다이시스, 싱토닉 콤마, 큰 다이시스. S₁(Just A1)와 S₃(Just m2)는 이 12음계 척도에서 가장 자주 발생하는 의미(위 표 참조)이므로 이들 사이의 비율로 정의되는 덜 다이스가 가장 자주 관측되는 쉼표다.

싱토닉 콤마도 5 한계 튜닝으로 주음(크기 9/8인 M2)과 부음(크기 10/9인 M2)의 비율로 정의된다. 다른 튜닝 시스템에서는 이온과 크로마틱 세미톤 사이의 비율(m2/A1)으로 정의할 수 없지만, 이는 싱토닉 기질 연속체(한 가지 템포도 포함)의 어떤 튜닝 시스템에서도 완벽한 5분의 1을 튜닝하는 데 사용되는 중요한 기준 값이다.

감소된 초

위에서 언급한 세 가지 쉼표, 즉 디아시스마, 다이스마, 대 다이시스(diaschisma), 즉 디아시스(diisma), 대 다이시스는 감소된 두 번째의 정의를 충족하며, 이는 디아소닉과 색색 세미톤(또는 그 주파수 비율 사이의 등가)의 크기 차이인 것이다.

반대로, 싱토닉 콤마는 두 색의 반음계₂(S와₁ S) 사이의 센트 차이 또는 두 개의 이음계 반음계(S와₄ S₃) 사이의 차이 중 하나로 정의되며, 감소된 초로 간주할 수 없다.

12음계 확장

위의 표는 3과 5의 저전력만을 사용하여 기본 비율을 만든다. 그러나 5² = 25, 5⁻² = 1/25, 3³ = 27 또는 3⁻³ = 1/27과 같이 동일한 숫자의 높은 양과 음의 힘을 사용하면 쉽게 확장할 수 있다. 이 기본 비율을 조합하면 25, 35 또는 그 이상의 투구를 가진 척도를 얻을 수 있다.

예를 들어 다음과 같이 각 방향으로 행을 추가하면 35개의 투구를 얻을 수 있다.

요인		1/9	1/3	1	3	9
125	주석을 달다 비율 센트	A♯ 125/72 955.0[3]	E♯ 125/96 457.0	B♯ 125/64 1158.9	F+ 375/256 660.9[3]	C+ 1125/1024 162.9[3]
25	주석을 달다 비율 센트	F♯ 25/18 568.7[3]	C♯ 25/24 70.7	G♯ 25/16 772.6	D♯ 75/64 274.6	A♯+ 225/128 976.5[3]
5	주석을 달다 비율 센트	D− 10/9 182.4	A 5/3 884.4	E 5/4 386.3	B 15/8 1088.3	F♯+ 45/32 590.2
1	주석을 달다 비율 센트	B♭− 16/9 996.1	F 4/3 498.0	C 1/1 0.0	G 3/2 702.0	D 9/8 203.9
1/5	주석을 달다 비율 센트	G♭− 64/45 609.8	D♭− 16/15 111.7	A♭ 8/5 813.7	E♭ 6/5 315.6	B♭ 9/5 1017.6
1/25	주석을 달다 비율 센트	E− 256/225 223.5[3]	B− 128/75 925.4[3]	F♭ 32/25 427.4	C♭ 48/25 1129.3	G♭ 36/25 631.3
1/125	주석을 달다 비율 센트	C− 2048/1125 1037.1[3]	G− 512/375 539.1[3]	D− 128/125 41.1[3]	A을 192/125 743.0	E 144/125 245.0

(위의 비대칭 눈금에서와 같이) 왼쪽 열(1/9)을 제거하는 경우도 있으므로 투구 수가 적은 비대칭 테이블을 만든다. 위에서 설명한 제한적인 5 한계 튜닝(C 대 G³- = 64/45)과 관련하여 감소된 5번째(C-G³ = 36/25)에 대해 정의 비율이 산출된다는 점에 유의하십시오.^[6]

역사

아마도 서양에서 이론화된 최초의 튜닝 시스템인 피타고라스 튜닝에서,^[7] 유일한 높은 자음 간격은 완벽한 5번째와 그것의 반전, 완벽한 4번째였다. 피타고라스 제3장조(81:64)와 소제3장조(32:27)는 불협화음이었고, 이로 인해 음악가들이 트라이애드와 화음을 사용할 수 없게 되어 수세기 동안 비교적 단순한 질감의 음악을 쓸 수밖에 없었다. 중세 말기에, 음악가들은 일부 음의 음을 약간 조절함으로써 피타고라스 3분의 1이 자음으로 만들어질 수 있다는 것을 깨달았다. 예를 들어, 동기화 쉼표(81:80)를 줄이면 E, C-E(주요 3번째), E-G(소수 3번째)의 주파수가 정의가 된다. 즉, C-E는 의 정당한 억양비로 좁혀진다.

${\displaystyle {81\over 64}\cdot {80\over 81}={1\cdot 5}{4\cdot 1.}={5\cdot 4}}}$

그리고 동시에 E-G는 정의로운 비율의

${\displaystyle {32 \over 27}\cdot {81 \over 80}={{2\cdot 3} {1\cdot 5}={6 \over 5}}}}}}}$

단점은 5번째 A-E와 E-B는 E를 납작하게 함으로써 피타고라스 늑대의 5번째와 거의 같이 불협화음이 된다는 것이다. 그러나 다섯 번째 C-G는 자음 상태를 유지하는데, 이는 E만 평탄화되었기 때문이다(C-E * E-G = 5/4 * 6/5 = 3/2). C-E와 함께 C-major triad(C-E-G)를 생산할 수 있다.

이러한 간단한 근거를 일반화함으로써, 16세기 후반에 지오세포 자를리노는 최초로 정당하게 삽입된 7음계(다이아토닉) 척도를 만들었는데, 여기에는 순수하게 완벽한 5분의 2(3:2), 순수하게 큰 3분의 1 및 순수하게 작은 3분의 1이 포함되어 있었다.

F → A → C → E → G → B → D

이것은 단지 3분의 1(M3, 비율 5:4)과 3분의 1(m3, 비율 6:5)의 순서인데, F:

F + M3 + M3 + M3 + M3 + M3 + M3 + M3 + M3

M3 + m3 = P5(완벽한 5번째), 즉 5/4 * 6/5 = 3/2이므로, 이는 단지 억양만으로 5 한계에서 얻은 이음계 척도와 정확히 동일하므로 12음(색채) 척도에 사용되는 구성표의 하위 집합으로 볼 수 있다.

A	→	E	→	B
↑		↑		↑
F	→	C	→	G	→	D

여기서 두 행 모두 5분의 1만 배열하고 F-A, C-E, G-B는 3분의 1만 배열한다.

M3		M3		M3
+		+		+
F	+	P5	+	P5	+	P5

참고 항목

• 음계의 수학
• 마이크로톤 음악
• 마이크로튜너
• 피타고라스 간격
• 세미톤
• 단지 억양만으로 된 5-한계의 간격 목록
• 평균 구간 목록
• 음악 간격 목록
• 피치 간격 목록
• 풀톤 스케일
• 정수
• 헥사니
• 전자 튜너
• 조화와 불협화음

메모들

외부 링크

• 미국의 예술: 미국 작곡가의 억양을 이용한 미세 톤/정당한 억양 작품
• 크리살리스 재단 – 저스트 억양: 두 가지 정의
• 단테 로사티의 21톤 저스트 억양 기타
• 막 억양 마크 노비츠키
• Just Intonation by Kyle Gann의 설명
• Ubuweb의 Tellus Audio Cassette Magazine 프로젝트 아카이브에 게시된 Just Intonation Network 웹에서 편집한 저스트 인턴테이션 작품 선택
• 중세 음악 예술 재단
• 음악 경개 – 저스트 억양
• 저스트 억양이 왜 그렇게 좋게 들리는가?
• 윌슨 아카이브스
• 바르비에리, 파트리치오. Enharmonic 악기와 음악, 1470–1900. (2008) 라티나, 일 르반테
• 22 노트 인도 악기 소리 12개가 포함된 억양 키보드 소프트웨어 Libreria Editrice
• Plainsthound Music Edition – JI 음악과 연구, 헬름홀츠-엘리스 JI 피치 표기법 정보