이중슬릿 실험

현대 물리학에서 이중 슬릿 실험은 빛과 물질이 파동과 입자 모두에 대해 겉보기에는 불일치하는 고전적 정의를 만족시킬 수 있다는 것을 보여주며, 이는 양자 역학의 근본적인 확률론적 성격에 대한 증거로 여겨집니다.이런 종류의 실험은 1801년 토마스 영에 의해 가시광선의 파동 거동의 증명으로서 처음 수행되었습니다.^[1]그 당시에는 빛이 파동이나 입자로 구성되어 있다고 생각되었습니다.현대 물리학의 시작과 함께, 약 백 년 후에, 빛이 사실 파동과 입자의 특성을 둘 다 보여줄 수 있다는 것을 깨달았습니다.1927년 데이비슨과 저머, 그리고 독립적으로 조지 파젯 톰슨과 알렉산더 레이드는 전자가 같은 행동을 보인다는 것을 증명했고, 나중에 원자와 분자로 확장되었습니다.^[2][3][4]토마스 영의 빛에 대한 실험은 양자역학과 파동-입자 이중성의 개념이 발달하기 훨씬 전부터 고전물리학의 일부였습니다.그는 이것이 크리스티안 하위헌스의 빛에 대한 파동 이론이 옳았음을 증명한다고 믿었고, 그의 실험은 때때로 영의 실험^[5] 또는 영의 틈으로 언급됩니다.^[6]

이 실험은 파동을 두 개의 별개의 파동(일반적으로 파동은 많은 광자로 구성되어 있으며 개별 광자의 파동 특성과 혼동하지 않기 위해 파면이라고 더 잘 지칭됨)으로 분할되는 일반적인 "이중 경로" 실험에 속합니다.두 파동의 경로 길이가 변경되면 위상이 이동하여 간섭 패턴이 생성됩니다.또 다른 버전은 마하-젠더 간섭계로 빔을 쪼개는 빔 스플리터로 빔을 분리합니다.

에 관한 일련의 기사들 중 일부
양자역학
${\displaystyle i\hbar {\frac {\partial }{\partial t}} \psi(t)\rangle = {\hat {H} \psi(t)\rangle }$ 슈뢰딩거 방정식
서론 용어집 역사
배경 고전역학 구 양자론 브라켓 표기법 해밀토니안 방해다
펀더멘털 상보성 비간섭성 얽힘 에너지 준위 측정. 비국소성 양자수 주 중첩 대칭성 터널링 불확정성 파동함수 붕괴
실험 벨 부등식 데이비슨-게르메르 더블슬릿 엘리츠르-바이드만 프랑크-헤르츠 레게트-가르그 부등식 마흐젠더 포퍼 퀀텀 지우개 지연선택 슈뢰딩거고양이 스턴-게를라흐 휠러의 지연 선택
제형 개요 하이젠베르크 상호작용 매트릭스 위상 공간 슈뢰딩거 이력 합계(경로 적분)
방정식 디랙 클라인고든 파울리 릿드버그 슈뢰딩거
해석 베이지안 일관된 이력 코펜하겐 드브로이-봄이 앙상블 숨김 변수 현지의 초결정론 다세계 대물붕괴 양자 논리학 관계형 거래 폰 노이만-위그너
고급주제 상대론적 양자역학 양자장론 양자정보과학 양자 컴퓨팅 양자 혼돈 EPR 역설 밀도행렬 산포론 양자 통계역학 양자기계학습
사이언티스트 아하로노프 벨 벳더 블래킷 블로흐 봄이 보어 태어난 보스 드브로이 콤프턴 디랙 데이비슨 데비 에렌페스트 아인슈타인 에버렛 포크 페르미 파인만 글라우버 구츠윌러 하이젠베르크 힐베르트 조던 크레이머즈 파울리 새끼 양 란다우 라우에 모즐리 밀리칸 오네스 플랑크 라비 라만 릿드버그 슈뢰딩거 시몬스 소머펠트 폰 노이만 웨일 빈 위그너 지만 자일링거
v t

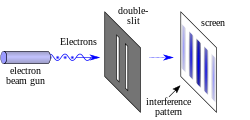
이 실험의 기본 버전에서 레이저 빔과 같은 간섭성 광원은 두 개의 평행한 슬릿으로 뚫린 플레이트를 비추고, 슬릿을 통과한 빛은 플레이트 뒤의 스크린에서 관찰됩니다.^[7][8]빛의 파동성은 두 개의 슬릿을 통과하는 빛의 파동을 방해하여 화면에 밝고 어두운 띠를 생성합니다. 이는 빛이 고전적인 입자로 구성되어 있다면 예상할 수 없었던 결과입니다.^[7][9]그러나 개별 입자(파도가 아닌)와 같이 항상 스크린에서 빛이 흡수되는 점이 발견됩니다. 간섭 패턴은 스크린에 도달하는 이러한 입자의 밀도 변화를 통해 나타납니다.^[10]또한 슬릿에 검출기가 포함된 실험 버전에서는 검출된 광자가 하나의 슬릿(고전 입자처럼)을 통과하고 두 개의 슬릿(파동처럼)을 통과하지 않는다는 것을 발견했습니다.^{[11][12][13][14][15]}그러나 이러한 실험은 입자가 어떤 슬릿을 통과하는지 감지하면 간섭 패턴이 형성되지 않는다는 것을 보여줍니다.이러한 결과는 파동-입자 이중성의 원리를 보여줍니다.^[16][17]

전자와 같은 다른 원자 규모의 실체들은 이중 슬릿을 향해 발사될 때 같은 행동을 보이는 것으로 밝혀졌습니다.^[8]또한 개별 이산 충격의 감지는 본질적으로 확률적인 것으로 관찰되며, 이는 고전 역학을 사용하면 설명할 수 없습니다.^[8]

이 실험은 전자와 광자보다 훨씬 큰 물체로 이루어질 수 있지만, 크기가 커질수록 더 어려워집니다.이중 슬릿 실험이 수행된 가장 큰 개체는 각각 2000개의 원자로 구성된 분자(총 질량은 25,000개의 원자 질량 단위)였습니다.^[18]

이중 슬릿 실험(및 그 변형)은 양자역학의 중심 퍼즐을 표현하는 명확성으로 고전이 되었습니다.실험 결과를 예측하는 관찰자의 능력에 대한 근본적인 한계를 보여주기 때문에, 리처드 파인만은 이것을 "어떤 고전적인 방법으로 설명하는 것은 불가능하고, 양자역학의 핵심을 가지고 있는 현상"이라고 불렀습니다.실제로는 양자역학의 유일한 신비를 담고 있습니다."^[8]

개요

빛이 일반 입자나 고전 입자로 엄격히 구성되어 있고, 이 입자들이 슬릿을 통해 직선으로 발사되어 반대편 스크린을 타격할 수 있다면, 우리는 슬릿의 크기와 모양에 상응하는 패턴을 볼 수 있을 것입니다.그런데 이 '단일 슬릿 실험'이 실제로 이뤄지면 화면 위 패턴은 빛이 퍼지는 회절 패턴입니다.슬릿이 작을수록 퍼짐의 각도가 커집니다.이미지의 맨 위 부분은 빨간색 레이저가 슬릿을 비추고 두 개의 희미한 측면 밴드를 주의 깊게 보면 패턴의 중앙 부분을 보여줍니다.더 세련된 장치로 더 많은 밴드를 볼 수 있습니다.회절은 슬릿에서 나오는 빛의 파동이 간섭한 결과로 패턴을 설명합니다.

한 개가 두 개의 평행한 슬릿을 비추면 두 개의 슬릿에서 나오는 빛이 다시 간섭하게 됩니다.여기서 간섭은 일련의 빛과 어두운 띠가 번갈아 나타나는 더 뚜렷한 패턴입니다.밴드의 폭은 조명광의 주파수의 성질입니다.^[19] (오른쪽 아래 사진 참조)

토마스 영(1773–1829)이 이 현상을 처음 증명했을 때, 파면의 가감 간섭에 의해 밝기의 분포가 설명될 수 있기 때문에 빛은 파동으로 구성되어 있음을 나타냅니다.^[8]1800년대 초에 수행된 영의 실험은 빛의 파동 이론을 이해하는 데 결정적인 역할을 했고, 17세기와 18세기에 받아들여졌던 빛 전파의 모델이었던 아이작 뉴턴이 제안한 빛의 분자 이론을 물리쳤습니다.

그러나 나중에 광전 효과가 발견된 것은 다른 상황에서 빛이 마치 이산 입자로 구성된 것처럼 행동할 수 있다는 것을 보여주었습니다.이 모순적으로 보이는 발견들은 고전 물리학을 넘어서 빛의 양자적 성질을 고려하는 것을 필요하게 했습니다.

파인만은 모든 양자역학은 이 단일 실험의 결과를 통해 신중하게 생각하는 것으로부터 얻을 수 있다고 말하는 것을 좋아했습니다.^[20]또한 (사고 실험으로) 검출기를 각 슬릿 앞에 배치하면 간섭 패턴이 사라질 것이라고 제안했습니다.^[21]

Englert-Greenberger 이중성 관계는 양자 역학의 맥락에서 이중 슬릿 간섭의 수학에 대한 상세한 처리를 제공합니다.

저강도 이중슬릿 실험은 G. I.에 의해 처음 수행되었습니다. 1909년 테일러(^[22]Taylor)는 광자 방출/흡수 사건이 대부분 비중첩될 때까지 입사광의 수준을 줄임으로써 발생했습니다. 슬릿 간섭 실험은 1961년 튀빙겐 대학의 클라우스 욘손이 일관성 있는 전자 빔과 다중 슬릿으로 수행할 때까지 빛 이외의 다른 것으로 수행되지 않았습니다.^[23][24]1974년 이탈리아의 물리학자 피에르 조르지오 메리, 지안 프랑코 미시롤리, 줄리오 포치는 일관성 있는 소스와 쌍프리즘 빔 스플리터의 단일 전자를 사용하여 양자 이론에 의해 예측된 간섭 패턴 축적의 통계적 특성을 보여주는 관련 실험을 수행했습니다.^[25][26]2002년, 이 실험의 단일 전자 버전은 Physics World의 독자들에 의해 "가장 아름다운 실험"으로 선정되었습니다.^[27]그 이후로 많은 관련 실험들이 발표되었는데 약간의 논란이 있었습니다.^[28]

2012년에 Stefano Frabboni와 동료들은 단일 전자를 나노 제작된 슬릿(폭 약 100 nm)에 보냈고, 단일 전자 탐지기로 전송된 전자를 탐지함으로써 이중 슬릿 간섭 패턴의 축적을 보여줄 수 있었습니다.^[29]간섭 간섭과 관련된 많은 관련 실험들이 수행되어 왔습니다; 그것들은 현대 전자 회절, 현미경 그리고 고해상도 이미징의 기초입니다.^[30][31]

2018년 마르코 지암마르치(Marco Giammarchi)가 이끄는 그룹에 의해 코모(Como)의 라파엘 페라굿(Rafael Ferragut)의 양전자 실험실(L-NESS, Politecnico di Milano)에서 반물질에 대한 단일 입자 간섭이 입증되었습니다.^[32]

실험의 변형

개별 입자로부터의 간섭

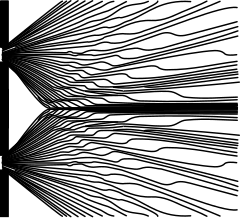
이 실험의 중요한 버전은 단일 입자 검출을 포함합니다.이중 슬릿 장치를 통해 일관성 있는 입자를 한 번에 하나씩 보내면 예상대로 단일 입자가 화면에 흰색 점으로 표시됩니다.그러나 놀랍게도, 이 입자들이 하나씩 쌓이게 할 때 간섭 패턴이 나타납니다(아래 그림 참조).

이는 모든 물질이 파동과 입자 특성을 모두 나타내는 파동-입자 이중성을 보여줍니다.입자는 단일 위치에서 단일 펄스로 측정되는 반면 파동의 모듈러스 제곱은 화면의 특정 위치에서 입자를 감지할 확률을 설명하여 통계적 간섭 패턴을 제공합니다.^[34]This phenomenon has been shown to occur with photons,^[35] electrons,^[36] atoms, and even some molecules: with buckminsterfullerene (C
₆₀) in 2001,^{[37][38][39][40]} with 2 molecules of 430 atoms (C
₆₀(C
₁₂F
₂₅)
₁₀ and C
₁₆₈H
₉₄F
₁₅₂O
₈N
₄S
₄) in 2011,^[41] and with molecules of up to 2000 atoms in 2019.^[42]

마하젠더 간섭계

마하-젠더 간섭계는 이중 슬릿 실험의 단순화된 버전으로 볼 수 있습니다.간섭계에서 광자는 두 개의 슬릿 후에 자유 공간을 통해 전파하고 확장된 스크린의 어떤 위치에도 부딪히는 대신 두 개의 경로를 통해서만 전파하고 두 개의 개별 광검출기에 부딪힐 수 있습니다.이를 통해 미분 방정식이 아닌 차원 2의 간단한 선형 대수를 통해 설명할 수 있습니다.

레이저에 의해 방출된 광자는 첫 번째 빔 스플리터에 부딪혀 두 개의 가능한 경로 사이에 중첩됩니다.두 번째 빔 스플리터에서는 이러한 경로가 간섭하여 광자가 확률 1로 오른쪽의 광검출기에 부딪히고 확률 0으로 아래의 광검출기에 부딪히게 합니다.광자가 빔 스플리터 사이의 경로 중 하나에 확실히 있다면 어떤 일이 일어날지 고려하는 것은 흥미로운 일입니다.이것은 경로 중 하나를 차단함으로써 달성될 수도 있고, 거기에 광자의 존재를 감지함으로써 동등하게 달성될 수도 있습니다.두 경우 모두 경로 간에 더 이상 간섭이 발생하지 않으며 두 광검출기 모두 확률 1/2로 타격을 받습니다.이로부터 광자가 첫 번째 빔 스플리터 이후에 이런저런 경로를 밟는 것이 아니라 두 경로의 진정한 양자 중첩에 있다는 결론을 내릴 수 있습니다.^[43]

"어느 방향" 실험과 상호보완성의 원리

잘 알려진 사고 실험은 입자 검출기가 어떤 슬릿을 광자가 통과하는지 보여주는 슬릿에 위치하면 간섭 패턴이 사라질 것이라고 예측합니다.^[8]이 양방향 실험은 광자가 입자나 파동처럼 행동할 수 있지만 동시에 둘 다 관찰할 수 없다는 보완성 원리를 보여줍니다.^[44][45][46]양자역학의 역사에서 이 사고 실험의 중요성에도 불구하고(예를 들어 아인슈타인의 이 실험에 대한 논의 참조), 이 실험의 기술적으로 실현 가능한 실현은 1970년대까지 제안되지 않았습니다.^[47](포톤을 흡수하지 않으면 광자를 검출할 수 없기 때문에 교과서적 사고 실험의 순진한 구현은 불가능합니다.)현재 다양한 보완성 측면을 설명하기 위한 여러 실험이 수행되고 있습니다.^[48]

1987년에^[49][50] 수행된 한 실험은 간섭을 완전히 파괴하지 않고 입자가 어떤 경로를 택했는지에 대한 부분적인 정보를 얻을 수 있다는 결과를 보여주었습니다.이러한 "파형 입자 트레이드 오프"는 간섭 패턴의 가시성과 어느 방향 경로의 구별 가능성과 관련된 불평등의 형태를 갖습니다.^[51]

지연 선택 및 양자 지우개 변형

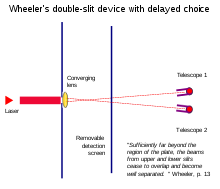
Wheeler의 지연 선택 실험은 입자가 슬릿을 통과한 후 "어떤 경로" 정보를 추출하는 것이 슬릿에서의 이전 행동을 소급적으로 변화시키는 것처럼 보일 수 있음을 보여줍니다.

양자 지우개 실험은 "어떤 경로" 정보를 지우거나 영구적으로 사용할 수 없게 함으로써 파동 동작을 복원할 수 있음을 보여줍니다.

양자 지우개 현상에 대한 간단한 집에서 직접 하는 삽화는 Scientific American의 한 기사에 실렸습니다.^[52]각 슬릿의 축이 서로 직교하도록 편광자를 설정하면 간섭 패턴이 제거됩니다.편광자는 각 빔에 어떤 경로 정보를 도입하는 것으로 간주될 수 있습니다.다른 편광자에 대해 45°의 축을 가진 세 번째 편광자를 디텍터 앞에 도입하면 이 정보가 "지워져" 간섭 패턴이 다시 나타날 수 있습니다.이는 빛을 고전파로 간주하고 원형 ^{[52]: 91} 편광기와 단일 광자를 사용할 때도 설명할 수 있습니다.^{[53]: 6} 얽힌 광자 쌍을 사용한 편광기의 구현은 고전적인 설명이 없습니다.^[53]

약계측

연구자들은 2012년에 발표된 매우 공개된 실험에서 각 입자가 입자에 의해 생성된 간섭 패턴에 전혀 악영향을 미치지 않고 걸어온 경로를 확인했다고 주장했습니다.^[54]이를 위해, 그들은 화면으로 들어오는 입자들이 점과 같은 정보원이 아니라 두 개의 세기의 최대치를 가진 정보원에서 나오는 것이라는 설정을 사용했습니다.그러나 Svensson과^[55] 같은 논평가들은 사실 이 이중 슬릿 실험의 변형에서 수행된 약한 측정과 하이젠베르크 불확정성 원리 사이에는 충돌이 없다고 지적했습니다.약한 측정 후 선택은 각 개별 입자에 대해 동시에 위치 및 운동량 측정을 허용하지 않고 다른 위치에 도달한 입자의 평균 궤적을 측정할 수 있습니다.다시 말해, 실험자들은 전체 궤적에 대한 통계 지도를 만들고 있었습니다.^[55]

기타변주

1967년, Pleegor와 Mandel은 광원으로서 두 개의 별개의 레이저를 사용하여 두 소스 간섭을 증명했습니다.^[56][57]

한 번에 하나의 슬릿만 열린 이중 슬릿 시스템에서 검출된 광자가 어느 슬릿에서 나올 수 있을 정도의 경로 차이라면 간섭이 관찰된다는 것이 실험적으로 1972년에 입증되었습니다.^[58][59]실험 조건은 시스템의 광자 밀도가 균일도보다 훨씬 적을 정도였습니다.

1991년, Carnal과 Mlynek는 금박의 마이크로미터 크기의 슬릿을 통과하는 준안정 헬륨 원자로 고전적인 영의 이중 슬릿 실험을 수행했습니다.^[60][61]

1999년 버키볼 분자(각각 60개의 탄소 원자로 구성됨)를 사용하여 회절 격자를 사용하는 양자 간섭 실험이 성공적으로 수행되었습니다.^[37][62]버키볼은 전자 현미경에서 볼 수 있을 만큼 충분히 큽니다(직경이 약 0.7 nm로 양성자보다 거의 50만 배 큽니다).

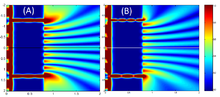
2002년에는 전자장 방출원을 이용하여 이중슬릿 실험을 시연했습니다.이 실험에서 바늘 꼭지점에 가까이 위치한 두 개의 방출 부위에서 일관성 있는 전자파가 방출되었고, 이는 이중 슬릿의 역할을 하여 진공에서 파동을 두 개의 일관성 있는 전자파로 분열시켰습니다.그러면 두 전자파 사이의 간섭 패턴을 관찰할 수 있습니다.^[63]2017년, 연구원들은 빛으로 유도된 전계 전자 방출기를 사용하여 이중 슬릿 실험을 수행했습니다.이 기술을 사용하면 10 나노미터 규모로 배출 지점을 광학적으로 선택할 수 있습니다.연구자들은 두 개의 배출물(슬릿) 중 하나를 선택적으로 비활성화(폐쇄)함으로써 간섭 패턴이 사라졌음을 보여줄 수 있었습니다.^[64]

2005년 E. R. Eliel은 두 개의 서브 파장 슬릿에 의해 천공된 얇은 금속 스크린의 광학적 투과에 대한 실험적이고 이론적인 연구를 발표했습니다.입사광 빔의 파장의 함수에 따라 원장 이중 슬릿 패턴의 전체 세기가 감소 또는 향상되는 것으로 나타남.^[65]

2012년, 네브래스카-링컨 대학의 연구원들은 Richard Feynman에 의해 설명된 것처럼 두 개의 슬릿의 전송과 단일 전자 탐지 사건의 모니터링을 제어할 수 있는 새로운 장비를 사용하여 전자에 대한 이중 슬릿 실험을 수행했습니다.전자는 전자총에 의해 발사되어 폭 62nm×4μm의 1~2개의 슬릿을 통과했습니다.^[66]

2013년에는 각각 810개의 원자(총 질량이 10,000개가 넘는 원자 질량 단위)로 구성된 분자를 대상으로 회절 격자를 이용한 양자 간섭 실험을 성공적으로 수행했습니다.^[3][4]이 기록은 2019년에 2000 원자(25,000 amu)로 증가했습니다.^[18]

유체역학 파일럿파 유사체

이중 슬릿을 통한 단일 입자 간섭을 포함하여 양자 역학 시스템의 다양한 측면을 재현할 수 있는 유체역학적 유사체가 개발되었습니다.^[67]액체 표면을 따라 튕겨 나가는 실리콘 오일 방울로, 자체 파동장과 공명하는 상호작용을 통해 스스로 추진합니다.이 방울은 튕길 때마다 액체를 부드럽게 풀어줍니다.동시에 과거의 바운스로 인한 파문이 진로에 영향을 미칩니다.이 물방울이 파일럿 파동이라고 알려진 것을 형성하는 자신의 잔물결과 상호작용함으로써 이전에는 기본 입자에 특이한 것으로 여겨졌던 행동을 나타내게 됩니다. 여기에는 기본 입자가 측정될 때까지 특정한 위치 없이 파도처럼 공간을 통해 퍼져 있다는 증거로 관습적으로 받아들여지는 행동도 포함됩니다.^[68][69]

이 유체역학 파일럿 파동 시스템을 통해 모방된 행동에는 양자 단일 입자 회절,^[70] 터널링, 양자화된 궤도, 궤도 레벨 분할, 스핀 및 다중 모드 통계가 포함됩니다.불확실성 관계와 배제 원칙을 추론하는 것도 가능합니다.이 시스템의 다양한 기능을 설명하는 동영상을 이용할 수 있습니다.(외부 링크 참조).

그러나 중첩에 두 개 이상의 입자를 포함하는 더 복잡한 시스템은 그러한 단순하고 고전적으로 직관적인 설명을 수용할 수 없습니다.^[71]따라서, 얽힘의 유체역학적 유사체는 개발되지 않았습니다.^[67]그럼에도 불구하고 광학식 아날로그는 가능합니다.^[72]

시간에 맞춰 이중슬릿 실험

2023년, 인듐 주석 산화물(ITO)로 코팅된 스크린에 펌프 레이저 펄스를 조사하여 간섭 패턴을 시간에 따라 재현하는 실험이 보고되었습니다.약 200 펨토초 동안 투명에서 반사성으로 변경하는 것은 ITO 스크린에 부딪히는 후속 프로브 레이저 빔이 시간에 따른 슬릿으로 광학 특성의 일시적인 변화를 보고 그 중 두 개는 각각의 주파수 성분에 파괴적으로 또는 건설적으로 위상 차이가 누적되는 이중 슬릿으로 결과를 나타내는 것입니다.간섭무늬로^[73][74][75]전형적인 파도에서도 비슷한 결과가 나왔습니다.^[73][75]

고전파광학 공식

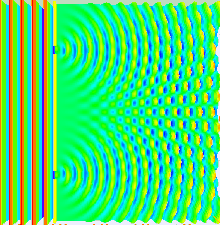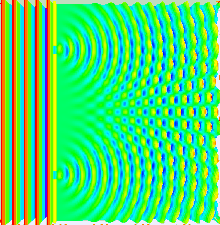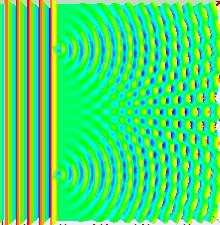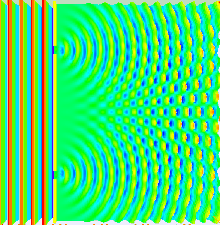
빛의 행동의 대부분은 고전파 이론을 사용하여 모델링할 수 있습니다.Huygens-Fresnel 원칙은 그러한 모델 중 하나입니다. 파면의 각 지점이 2차 웨이블릿을 생성하고, 이후 지점에서 발생하는 교란은 해당 지점의 개별 웨이블릿의 기여를 합산하여 찾을 수 있습니다.이 합산은 위상과 개별 웨이블릿의 진폭을 고려해야 합니다.오직 빛의 장의 세기만 측정할 수 있습니다. 이는 진폭의 제곱에 비례합니다.

이중 슬릿 실험에서 두 개의 슬릿은 단일 레이저의 준단색광에 의해 조명됩니다.슬릿의 폭이 충분히 작으면(레이저 광의 파장보다 훨씬 작음) 슬릿은 빛을 원통형 파장으로 회절시킵니다.이 두 원통형 파면은 중첩되며, 따라서 결합된 파면의 어떤 지점에서든 진폭, 그리고 강도는 두 파면의 크기와 위상 모두에 따라 달라집니다.두 파동 사이의 위상 차이는 두 파동이 이동한 거리의 차이에 의해 결정됩니다.

슬릿(멀린 필드)의 분리에 비해 시야 거리가 큰 경우에는 오른쪽 아래 그림에 표시된 지오메트리를 사용하여 위상 차이를 확인할 수 있습니다.각도 θ로 이동하는 두 파동 사이의 경로 차이는 다음과 같습니다.

${\displaystyle d\sin \theta \approx d\theta}$

d는 두 슬릿 사이의 거리입니다.두 파동이 위상에 있을 때, 즉 경로 차이가 파장의 정수, 즉 합산 진폭과 같으므로 합산 강도가 최대이고, 반위상에 있을 때, 즉 경로 차이가 파장의 반, 1.5 파장 등과 같다면,그러면 두 파동이 취소되고 합산된 강도는 0이 됩니다.이 효과를 간섭이라고 합니다.간섭무늬 최대치는 각도에 따라 발생합니다.

${\displaystyle ~d\theta _{n}=n\lambda ,~n=0,1,2,\ldots }$

여기서 λ는 빛의 파장입니다.가장자리의 각 간격, θ은 다음과 같이 주어집니다.

${\displaystyle \theta _{f}\approx \lambda /d}$

슬릿으로부터 z 거리에 있는 프린지의 간격은 다음과 같이 주어집니다.

${\displaystyle ~w=z\theta _{f}=z\lambda /d}$

예를 들어 두 개의 슬릿을 0.5mm(d) 분리하고 0.6μm 파장 레이저(λ)로 비추면 1m(z) 거리에서 가장자리 간격이 1.2mm가 됩니다.

만약 슬릿 b의 폭이 파장에 비해 현저하다면, 프라운호퍼 회절 방정식은 회절광의 세기를 다음과 같이 결정하기 위해 필요합니다.^[76]

${\displaystyle {\begin{aligned}I(\theta)&\propto \cos ^{2}\left[{\frac {\pid\sin \theta}{\lambda}}\right]~\mathrm {sinc}^{2}\left[{\frac {\pi b\sin \theta}{\lambda}}\right]\end{aligned}}$

여기서 sinc 함수는 x ≠ 0의 경우 sinc(x) = sin(x)/x, sinc(0) = 1로 정의됩니다.

이는 위의 그림에 나타나 있는데, 첫 번째 패턴은 이 식에서 sinc 함수에 의해 주어진 단일 슬릿의 회절 패턴이고, 두 번째 그림은 두 개의 슬릿에서 회절된 빛의 결합된 세기를 나타내고, 여기서 코스 함수는 미세한 구조를 나타내고,그리고 더 거친 구조는 sinc 함수에 의해 설명된 것과 같이 개별 슬릿에 의한 회절을 나타냅니다.

근거리장에 대한 유사한 계산은 관찰면이 슬릿이 위치한 평면에 가까워질수록 각 슬릿과 관련된 회절 패턴의 크기가 감소하여 간섭이 발생하는 면적이 감소함을 의미하는 프레넬 회절 방정식을 적용하여 할 수 있으며,그리고 두 회절 패턴이 겹치지 않을 때 완전히 사라질 수도 있습니다.^[77]

경로-적분 공식

이중 슬릿 실험은 파인만이 제공하는 양자역학의 경로 적분 공식을 설명할 수 있습니다.^[78]경로 적분 공식은 가능한 모든 궤적에 대한 합으로 시스템에 대한 단일 고유 궤적의 고전적 개념을 대체합니다.기능적 통합을 사용하여 궤적을 함께 추가합니다.

각 경로는 동일한 가능성이 있는 것으로 간주되므로 동일한 양을 제공합니다.그러나 경로를 따라 주어진 지점에서 이 기여의 단계는 경로를 따라 작용에 의해 결정됩니다.

다음으로 이 모든 기여를 합산하고 최종 결과의 크기를 제곱하여 입자 위치에 대한 확률 분포를 얻습니다.

확률을 계산할 때 항상 그렇듯이, 다음을 적용하여 결과를 정규화해야 합니다.

결과의 확률 분포는 각 경로를 따라 작용에 비례하여 전파되는 파동의 원점에서 최종 지점까지의 모든 경로에 걸쳐 중첩 표준의 정규화된 제곱입니다.서로 다른 경로에 따른 누적 작용의 차이(따라서 기여의 상대적인 단계)는 이중 슬릿 실험에서 관측된 간섭 패턴을 생성합니다.파인만은 그의 공식화는 단지 수학적인 설명일 뿐, 우리가 측정할 수 있는 실제 과정을 설명하려는 시도는 아니라고 강조했습니다.

실험의 해석

슈뢰딩거의 고양이 사고 실험과 마찬가지로 이중 슬릿 실험은 양자역학의 다양한 해석 사이의 차이점과 유사성을 강조하기 위해 종종 사용됩니다.

코펜하겐 해석

코펜하겐 해석은 닐스 보어, 베르너 하이젠베르크, 막스 보른 등의 연구에서 비롯된 양자역학의 의미에 대한 견해의 모음입니다."코펜하겐 해석"이라는 용어는 1950년대에 Heisenberg가 1925년에서 1927년 사이에 개발된 아이디어를 언급하기 위해 만든 것으로 보입니다.^{[79][80][81][82]}따라서 그 해석이 무엇을 의미하는지에 대한 명확한 역사적 진술은 없습니다.코펜하겐 해석의 여러 버전에서 공통적으로 나타나는 특징은 양자역학이 본질적으로 불확정적이라는 생각과 보른 규칙을 사용하여 확률을 계산한다는 것, 그리고 보어의 원리를 포함합니다.모든 물체를 동시에 관찰하거나 측정할 수 없는 특정 쌍의 보완적인 특성을 가지고 있다는 것을 의미합니다.^[83]게다가 대상을 '관찰'하거나 '측정'하는 행위는 돌이킬 수 없고, 그 측정 결과에 따라 그 어떤 진실도 대상에게 귀속될 수 없습니다.특정 실험은 입자 거동(특정 슬릿 통과) 또는 파동 거동(간섭)을 입증할 수 있지만 둘 다 동시에 입증할 수는 없습니다.^{[84][85]: 167 [86]}코펜하겐 유형의 해석은 양자 기술이 물리학자들의 개인적인 믿음과 다른 임의적인 정신적 요인으로부터 독립적이라는 점에서 객관적이라고 주장합니다.^{[85]: 85–90}

가장 기본적인 이중 슬릿 실험의 결과인 간섭 패턴 관찰은 두 개의 슬릿 각각에서 스크린으로 가는 두 경로의 파동 간섭으로 설명됩니다.^[8]단일 입자 결과는 파동이 확률 분포를 만들기 위해 제곱한 확률 진폭임을 보여줍니다.^[8]입자는 이산적이고 동일하며, 전체 간섭 패턴을 형성하기 위해서는 많은 입자가 필요합니다.^[8]일부 양방향 실험의 결과는 보완성에 대한 관찰로 설명됩니다. 슬릿을 모니터링하기 위해 실험을 수정하면 간섭 패턴이 억제됩니다.^{[87][88]: 155} 다른 방향의 실험에서는 분석에서 보완성에 대해 언급하지 않습니다.^[89]

관계해석

카를로 로벨리가 처음 제안한 양자역학의 관계적 해석에 따르면 이중 슬릿 실험과 같은 관측은 관측자(측정 장치)와 관측 대상(물리적으로 상호 작용하는) 사이의 상호 작용에서 구체적으로 도출되는 것이지,^[90] 대상이 가지고 있는 어떤 절대적인 속성이 아닙니다.전자의 경우, 처음에 특정 슬릿에서 "관측"된다면, 관찰자-입자(광자-전자) 상호작용은 전자의 위치에 대한 정보를 포함합니다.이로 인해 화면에서 입자의 최종 위치가 부분적으로 제한됩니다.만약 그것이 특정한 슬릿이 아니라 스크린에서 "관찰"된다면, 상호작용의 일부로서 "어떤 경로" 정보가 없기 때문에, 스크린에서 전자의 "관찰" 위치는 엄격하게 확률 함수에 의해 결정됩니다.이것은 각각의 개별 전자가 두 개의 슬릿을 통과한 것처럼 화면에 나타나는 결과적인 패턴을 동일하게 만듭니다.^{[citation needed]}

다세계 해석

코펜하겐과 마찬가지로 다세계 해석에는 여러 가지 변형이 있습니다.통합 주제는 물리적 현실이 파동 함수와 동일시되고, 이 파동 함수는 항상 붕괴 없이 슈뢰딩거 방정식을 따라 단위적으로 진화한다는 것입니다.^[91][92]결과적으로, 오직 간섭을 통해서만 상호작용하는 많은 평행 우주들이 있습니다.데이비드 도이치는 이중 슬릿 실험을 이해하는 방법은 각 우주에서 입자가 특정한 슬릿을 통해 이동하지만 운동은 다른 우주의 입자와의 간섭에 영향을 받는다는 것이라고 주장합니다.이렇게 하면 관측 가능한 가장자리가 생성됩니다.^[93]다중세계 해석의 또 다른 옹호자인 데이비드 월리스는 이중슬릿 실험의 친숙한 설정에서 두 경로는 충분히 분리되어 있지 않아 평행우주의 관점에서 설명할 수 없다고 말합니다.^[94]

드브로이-봄이론

양자역학에 대한 표준적인 이해의 대안인 드브로이-봄 이론은 입자들이 항상 정확한 위치를 가지고 있으며, 그들의 속도는 파동함수에 의해 정의된다고 말합니다.따라서 이중 슬릿 실험에서 하나의 입자가 하나의 특정 슬릿을 통해 이동하는 반면, 그것에 영향을 미치는 소위 "파일럿 웨이브"는 두 개의 슬릿을 통해 이동할 것입니다.두 개의 슬릿 드브로이-봄 궤적은 크리스 드우드니가 버크벡 칼리지(런던)에서 크리스 필리피디스, 바질 힐리와 함께 작업하면서 처음 계산했습니다.^[95]드브로이-봄 이론은 표준 양자역학과 동일한 통계 결과를 생성하지만 입자를 안내하는 임시 양자 전위를 통해 복잡성을 추가함으로써 많은 개념적 어려움을 해소합니다.^[96]

모델은 슈뢰딩거 방정식과 많은 면에서 유사하지만, 상대론적인 경우에^[97] 실패하고 양자장 이론에서 입자 생성 또는 소멸과 같은 특징을 설명하지 않는 것으로 알려져 있습니다.노벨상 수상자인 베르너 하이젠베르크,^[98] 앤서니 제임스 레게트^[99], 로저 펜로즈^[100] 경과 같은 많은 작가들은 새로운 것을 추가하지 않았다고 비판했습니다.

예를 들어, Ryszard Horodecki의 3파 가설과^[101][102] 드브로이 및 콤프턴 파동의 다른 복잡한 조합과 같은 이러한 유형의 접근 방식의 더 복잡한 변형이 나타났습니다.^{[103][104][105]}현재까지 이것들이 유용하다는 증거는 없습니다.

참고 항목

참고문헌

추가열람

• Al-Khalili, Jim (2003). Quantum: A Guide for the Perplexed. London: Weidenfeld & Nicolson. ISBN 978-0-297-84305-4.
• Ananthaswamy, Anil (2018). Through Two Doors at Once: The Elegant Experiment That Captures the Enigma of Our Quantum Reality. Dutton/Penguin. ISBN 978-1-101-98609-7.
• Feynman, Richard P. (1988). QED: The Strange Theory of Light and Matter. Princeton University Press. ISBN 978-0-691-02417-2.
• Frank, Philipp (1957). Philosophy of Science. Prentice-Hall.
• French, A.P.; Taylor, Edwin F. (1978). An Introduction to Quantum Physics. Norton. ISBN 978-0-393-09106-9.
• Greene, Brian (2000). The Elegant Universe. Vintage. ISBN 978-0-375-70811-4.
• Greene, Brian (2005). The Fabric of the Cosmos. Vintage. ISBN 978-0-375-72720-7.
• Gribbin, John (1999). Q is for Quantum: Particle Physics from A to Z. Weidenfeld & Nicolson. ISBN 978-0-7538-0685-2.
• Hey, Tony (2003). The New Quantum Universe. Cambridge University Press. Bibcode:2003nqu..book.....H. ISBN 978-0-521-56457-1.
• Sears, Francis Weston (1949). Optics. Addison Wesley.
• Tipler, Paul (2004). Physics for Scientists and Engineers: Electricity, Magnetism, Light, and Elementary Modern Physics (5th ed.). W. H. Freeman. ISBN 978-0-7167-0810-0.

외부 링크

• MIT의 Walter Lewin의 이중 슬릿 간섭 강의

인터랙티브 애니메이션

• 하위헌스와 간섭

단일 입자 실험

• Merli, Missiroli, Pozzi의 첫 번째 단일 전자 실험에서 나온 영화 및 기타 정보가 포함된 웹사이트.
• 단일 전자 사건을 보여주는 영화는 이중 슬릿 실험에서 간섭 패턴을 형성하기 위해 축적됩니다.내레이션이 있는 여러 버전(파일 크기 = 3.6~10.4MB)(무비 길이 = 1m 8s)
• 무료보기 영상 '전자파가 마이크로코스모스를 공개하다' 베가 사이언스 트러스트 제공 토노무라 아키라의 왕실 기관 담론
• Tonomura 동영상에 대한 배경 정보와 동영상 링크를 제공하는 Hitachi 웹사이트

유체역학적 아날로그

• "매크로 물체에 대해 단일 입자 간섭 관찰"
• 파일럿파 유체역학:보충 비디오
• 웜홀을 통해:Yves Couder. 실리콘 액적을 통한 파동/입자 이중성 설명

컴퓨터 시뮬레이션

• 영의 이중슬릿 간섭에 대한 자바 시연
• 양자 입자의 수, 입자의 주파수 및 슬릿 분리를 독립적으로 변화시킬 수 있는 Mathematica Player에서 실행되는 시뮬레이션