부분순서세트
Partially ordered set| 타동사 이항 관계 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
수학, 특히 순서 이론에서 부분 순서 집합(역시 포셋)은 집합 원소의 순서, 순서 또는 배열의 직관적인 개념을 공식화하고 일반화한다. 포셋은 세트 내의 특정 요소 쌍에 대해 요소 중 하나가 순서에서 다른 요소보다 선행한다는 것을 나타내는 이진 관계와 함께 집합으로 구성된다. 관계 자체를 '부분적 질서'라고 한다.
"부분 순서"와 "부분 순서 집합"이라는 이름의 부분적인 단어는 모든 요소 쌍이 비교할 필요가 없다는 뜻으로 사용된다. 즉, 어떤 요소도 포셋에서 다른 요소보다 선행하지 않는 요소 쌍이 있을 수 있다. 따라서 부분 주문은 모든 쌍이 유사한 총 주문을 일반화한다.
비공식적 정의
부분 순서는 비교의 개념을 정의한다. x와 y의 두 요소는 서로에 대한 네 가지 상호 배타적 관계에 서 있을 수 있다: x < y 또는 x = y 또는 x > y 또는 x와 y는 비교할 수 없다.[1][2]
부분 순서가 있는 세트를 부분 순서 집합(포셋이라고도 함)이라고 한다. 다른 종류의 질서가 의미하는 것이 없는 것이 분명한 한, 순서 집합이라는 용어도 가끔 사용된다. 특히, 완전히 순서가 정해진 세트는 "순서된 세트"라고도 할 수 있으며, 특히 이러한 구조물이 포셋보다 더 일반적인 영역에서는 더욱 그러하다.
포셋은 주문 관계를 그린 하세 다이어그램을 통해 시각화할 수 있다.[3]
부분오더관계
부분 순서 관계는 전이적 관계와 비대칭 관계인 동질적 관계다.[4] 부분 순서 관계에 대한 두 가지 일반적인 하위 정의가 있는데, 반사적 부분 순서 관계와 불변적인 부분 순서 관계를 위해 각각 "비강제"와 "강제"라고도 한다. 두 가지 정의는 일대일 대응으로 넣을 수 있기 때문에 엄격한 부분 순서가 있을 때마다 그에 상응하는 고유한 비강제 부분 순서가 있고, 그 반대의 경우도 있다. 부분 순서라는 용어는 일반적으로 엄격하지 않은 부분 순서 관계를 가리킨다.
비강제 부분순서
반사적, 약한 [4]또는 엄격하지 않은 부분 순서는[5] 반사적, 비대칭적, 전이적인 세트 에 대한 동종 관계 ≤이다. 즉, 모든 , , , 에 대해 다음을 충족해야 한다.
- 반사성: a 즉 모든 요소는 그 자체와 관련되어 있다.
- 대칭: 와 = = b b및 두 개의 뚜렷한 요소가 서로 선행되지 않는다.
- transitivity: 만약 와 가 , c{\ b c 그 .
비강제 부분 순서는 대칭 사전 순서라고도 한다.
엄격한 부분 순서
불능, 강함 [4]또는 엄격한 부분 순서는 불능, 전이성 및 비대칭인 설정된 에 있는 동종 관계 <>이다. 즉, 모든 ,b, : 에 대해 다음과 같은 조건을 만족한다.
- 불변성 a 즉 어떤 도 그 자체와 되지 않음
- Transitability: < 와 b <가 있으면, 그 은< {\ 그
- 비대칭: < 가 있다면, b< 이 아니다
불굴의성과 전이성이 함께 비대칭성을 암시한다. 또한 비대칭성은 불변성을 내포하고 있다. 즉, 타동적 관계는 그것이 불변적인 경우에만 비대칭이다.[6] 따라서 불변성과 비대칭성(두 가지 모두 제외)을 생략해도 그 정의는 같다.
엄격한 부분 주문은 엄격한 사전 주문으로도 알려져 있다.
엄격하고 엄격하지 않은 부분 주문 관계의 대응
세트 에 대한 엄격하고 엄격하지 않은 부분 주문은 밀접하게 관련되어 있다. Anon-strict 부분 순서 ≤{\displaystyle \leq}엄격한 부분 순서에 ≤ a입니다;{\displaystyle a\leq.}그 말은 엄격한 부분 순서 집합<>형식의 모든 관계를 제거하여;:)≤ ∖ Δ P{\displaystyle<>\;:=\ \leq)\setminus)\Delta_{P}}이Δ P:={(p, 변환될 수 있습니다.p) :pin 에 있는 ID관계와 {\ 및 은 집합 감산을 나타낸다. 반대로 P의 엄격한 부분 순서 <는 그 형태의 모든 관계를 결합하여 엄격하지 않은 부분 순서로 변환될 수 있다. 즉, Δ P < p}\는 엄격하지 않은 부분 순서다. 따라서 이(가) 엄격하지 않은 부분 순서라면 그에 상응하는 엄격한 부분 순서 <는 다음이 주는 불손한 커널이다.
이중주문
The dual (or opposite) of a partial order relation is defined by letting be the converse relation of , i.e. if and only if . 엄격하지 않은 부분 순서의 이중은 엄격하지 않은 부분 순서,[7] 엄격한 부분 순서의 이중은 엄격한 부분 순서다. 관계의 이중은 원래의 관계다.
표기법
우리는 P{P\displaystyle}에≤{\displaystyle \leq}은non-strict 부분 순서 관계3-tuple(P, ≤,<>){\displaystyle(P,\leq ,<.)},[8],<, 많은 것은 P{P\displaystyle}의 자세한 내용은 재귀적이지 않은 커널에{\displaystyle<>}은 관련된 엄격한 부분 순서 관계 poset 생각할 수 있다. ≤{\displayst 은(는) 의 이중이고 > 은는) < 의 이중이다
집합의 네 가지 부분 순서 관계 ,< ,,> }}} 중 어느 하나라도 다른 세 가지를 고유하게 결정한다. 따라서 표기법의 문제로서 은(P , ) {\leq (P < ) {\ (P을를) 쓰고, 다른 관계가 적절하게 정의되었다고 가정할 수 있다. 엄격하지 않은 부분 순서 {\을(를) 통해 정의하는 것이 가장 일반적이다. 일부 저자는 또는[9] displaystyle }과 같은 ≤ {\과(와) 다른 기호를 사용하여[10] 전체 주문과 부분 순서를 구분한다.
부분 주문을 언급할 때 을를) > 의 보완으로 삼으면 안 된다 관계는>≤{\displaystyle \leq}의≤{\displaystyle \leq}의 정원의 하위 집합,지만 을은 재귀적이지 않은 커널의{\displaystyle>}은 그 반대;만약에 만약{\displaystyle \leq}≤{\displaystyle>}≤{\displaystyle \leq}의 정원과 같습니다.는 답은al order.[a]
예
수학에서 발생하는 양성의 표준 예는 다음과 같다.
- 표준보다 작거나 동등한 관계 ≤에 의해 정렬된, 또는 일반적으로 완전히 정렬된 순서는 엄격하지 않은 부분 순서다.
- 실제 P , 에서 보통보다 작은 관계 <는 엄격한 부분 순서이며, . 에서 보통보다 큰 관계 <>도 마찬가지다
- 정의상 모든 엄격한 약한 질서는 엄격한 부분적인 질서가 된다.
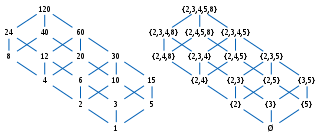
- 포함 순서가 지정된 집합(전원 집합)의 하위 집합 집합 집합(그림 1 참조) 이와 유사하게, 시퀀스 집합은 하위 문자열로, 문자열 집합은 하위 문자열로 정렬한다.
- 구분 가능성의 관계를 갖춘 자연수 집합.
- 도달 가능성으로 정렬된 방향 아세클릭 그래프의 꼭지점 세트.
- 포함에 의해 정렬된 벡터 공간의 하위 스페이스 세트.
- 부분 순서가 정해진 P의 경우, P의 모든 원소를 포함하는 시퀀스 공간, 여기서 시퀀스 a는 의 모든 항목이 b의 해당 항목보다 앞에 있으면 시퀀스 b보다 선행한다. Formally, if and only if for all ; that is, a componentwise order.
- 세트 X와 부분 순서가 지정된 세트 P의 경우, X에서 P까지의 모든 기능을 포함하는 함수 공간. 여기서 f ≤ g는 모든 x )에 대해 f() ≤ g(x) if와 if g)인 에만 해당된다
- 울타리, 순서 관계의 교대로 정의된 부분 순서 집합 a < b > c < d ...
- 특수 상대성 및 대부분의 경우 [b]일반 상대성에서의 사건 집합, 여기서 두 사건의 경우 X와 Y, X ≤ Y는 Y가 미래 X의 라이트 콘에 있는 경우에만 해당된다. 사건 Y는 X가 Y인 경우에만 인과적으로 영향을 받을 수 있다.
부분적으로 주문된 세트의 친숙한 예로는 족보 후손이 주문한 사람들의 집합이다. 어떤 한 쌍의 사람들은 후예-앵커 관계를 맺지만, 다른 한 쌍의 사람들은 비할 데 없이 다른 한 쌍의 후손도 아니다.
부분적으로 주문된 세트의 데카르트 제품 주문
강도를 높이기 위해(즉, 쌍의 감소) 부분적으로 주문한 두 세트의 데카르트 제품에서 가능한 부분 주문 중 세 가지는 다음과 같다(그림 3-5 참조).
- 사전 순서: (a, b) ≤ (c, d) (a = c 및 b ≤ d)인 경우,
- 제품 주문: (a, b) ≤ (c, d) ≤ c와 b ≤ d인 경우;
- 해당 엄격한 명령의 직접 생산물의 반사적 폐쇄: (a, b) ≤ (c, d) if (a, b, b < d) 또는 (a = c, b = d)
세 가지 모두 세트가 넘는 데카르트 제품에 대해 유사하게 정의될 수 있다.
동일한 영역에 걸쳐 순서가 지정된 벡터 공간에 적용되며, 결과는 각 경우에 순서가 지정된 벡터 공간에도 적용된다.
전체 주문 세트의 데카르트 제품에 대한 주문도 참조하십시오.
부분 순서의 집합 합계
두 개의 (분리된) 포셋을 결합하는 또 다른 방법은 다음과 같은 경우에만 기초 집합 ZX와 Y의 조합에 정의된 서수 합[11](또는 선형 합), [12]Z = X ⊕ Y이다.
- a, b ∈X b가 있는 X 또는
- a, b ∈Y with b or
- X와 B의 Y
만약 두 개의 양자가 잘 정렬되어 있다면, 그들의 서수 합도 잘 정렬되어 있다.[13]
직렬-병렬 부분 순서는 서수 합 연산(이 맥락에서 직렬 구성이라고 함)과 또 다른 연산인 병렬 구성에서 형성된다. 병렬 구성은 부분적으로 정렬된 두 세트의 분리 결합이며, 한 세트의 요소와 다른 세트의 요소 간의 순서 관계가 없다.
파생 개념
The examples use the poset consisting of the set of all subsets of a three-element set ordered by set inclusion (see Fig.1).
- a는 b일 때 b와 관련이 있다. 관계가 대칭적일 필요는 없기 때문에 b도 a와 관련이 있음을 의미하지는 않는다. 예를 들어 { } \{은(는 { {\\{과(와) 관련이 있지만 그 반대의 경우는 아니다.
- a와 b는 ≤ b 또는 b ≤ a와 비교할 수 있다. 그렇지 않으면 비할 데 없는 것이다. 를 들어 { x} 과) { x ,, z 과와) { } {\은(와) 같지 않다.
- 전체 순서 또는 선형 순서는 모든 원소 쌍이 비교 가능한 부분 순서, 즉 삼분법을 유지하는 것이다. 예를 들어, 표준 순서가 있는 자연수.
- 체인은 완전히 순서가 정해진 포셋의 하위 집합이다. 예를 들어 {{{ { , y, 은(는) 체인이다.
- 반제(反制)는 두 개의 뚜렷한 원소가 비교할 수 없는 포셋의 부분집합이다. 예를 들어 단골격의 집합{ { { z
- 요소 a는 ≤ b와 {\neq 예를 들어 {x{\이가){ 보다 완전히 작으면 b 원소보다 작다고 한다.
- 한 요소면서 다른 원소 b, a⋖ b(또는<>:b) 쓴로 적용되는 경우 엄정한 b이상 세번째 요소 c그들 사이에 맞고 공식적으로:둘 다 ≤ b와 ≠ b{a\neq b\displaystyle}사실과 ≤ c≤ b는 ≠ c≠ b와 함께 각 c에 거짓이다.{\displaystyle a\neq c\neq. b이다.} 적은 엄명<>를 사용한다고 한다.;, 관계 a ⋖ b는 "a < b는 되지만 어떤 c에 대해서도 < c < b는 아니다"로 동등하게 바꾸어 말할 수 있다. 예를 들어 { 은(는) x 이(가) 포함되지만{ y 은(는)에 포함되지 않는다.
아르테마
포셋 , 에는 다음과 같은 몇 가지 개념의 "가장 위대한" 및 "최소한" 요소가 있다.
- 최대 요소 및 최소 요소: An element is a greatest element if for every element An element is a least element if for every element A poset can only have one greatest or least element. 실행 예제에서는 집합{ 이(가) 가장 큰 요소이고 이(가) 가장 작은 요소다.
- 최대 요소 및 최소 요소: P 은(는) a >와 같은 요소 a이(가) 없는 경우 최대 요소다 유사하게 m m은는) . a>과 같은 요소 P{\ P}이(가) 없는 경우 최소 요소다. 포셋이 가장 큰 원소를 가지고 있는 경우에는 고유한 최대 원소여야 하지만, 그렇지 않으면 최대 원소가 둘 이상 있을 수 있고, 마찬가지로 최소 원소 및 최소 원소에 대해서도 유사하다. 실행 예제에서{ 및은(는) 최대적이고 최소적인 요소다. 이러한 요소를 제거하면 3개의 최대 원소와 3개의 최소 원소가 있다(그림.6 참조).
- 상한 및 하한: P의 부분 집합 A의 경우, P의 요소 x는 각 요소 a의 in x인 경우 A의 상한이다. 특히 x는 A의 상한이 되기 위해 A에 있을 필요는 없다. 마찬가지로 P의 원소 x는 각 원소 a의 for x인 경우 A의 하한이다. P의 가장 큰 요소는 P 자체의 상한이며, 최소 요소는 P의 하한이다. 이 예제에서{ 집합은{ { y 요소의 집합에 대한 상한 값이다.
또 다른 예로, 1은 다른 모든 원소를 나누기 때문에 최소 원소라고 할 수 있는 양의 정수를 고려한다. 반면에 이 양수에는 최대 원소가 없다(어떤 정수의 배수인 포지셋에 0을 포함하더라도 최대 원소가 될 수 있다; 그림.7 참조). 이 부분적으로 주문한 세트는 최대 요소조차 가지고 있지 않은데, 그 이유는 어떤 g도 그것과 구별되는 2g과 같이 나누기 때문에 g는 최대 요소가 아니기 때문이다. 숫자 1이 1보다 큰 원소의 순서에 따라 구별되는 점을 유지하면서 1을 제외한다면, 결과 포셋은 최소 요소를 가지지 않지만, 프라임 수는 최소 요소다. 이 포셋에서 60은 하위 집합{ ,,5, 의 상한(최소 상한은 아님)이며, 하한은 없다(1은 포셋에 없기 때문에). 반면에 2는 2의 하위 집합 중 하한이다. 상한이 없다.
부분적으로 정렬된 집합 간의 매핑
부분적으로 정렬된 두 세트(S, ≤)와 (T, ≼)[c]가 있을 경우, f: → 은(는) x,y S , S y {\ x y이(가) f(x) ≼ f(y)를 의미하는 경우 주문 보존 또는 모노톤 또는 동위원소라고 한다. (U, ≲)도 부분적으로 주문한 세트인 경우, : → 및 : → U 은(는) 주문 보존 방식으로 구성 g f도 주문 보존이 된다. 함수 : → T is called order-reflecting if for all f(x) ≼ f(y) implies If is both order-preserving and order-reflecting, then it is called an order-embedding of (S, ≤) into (T, ≼). In the latter case, is necessarily injective, since implies and in turn according to the antisymmetry of If an order-embedding S와 T가 존재하는 두 포지션 사이에 S가 T에 내장될 수 있다고 말한다. 주문-임베딩 : → T 은(는) 비주사적이며, 순서 이형성이라고 하며, 부분 순서(S, ≤), (T, ≼)는 이형성이라고 한다. 이소모르프 주문은 구조적으로 유사한 하세 다이어그램을 가지고 있다(그림.8 참조). 주문 보존 맵 : → 및 : → U 은(는) g f f}과 g {\이(가) 각각 S와 T에서 ID 기능을 산출하고, 그 다음 S와 T는 순서가 이질성인 것이다.[14]
예를 들어 : N →( N) 에서 자연수 집합(disibility에 의해 정렬됨)에서 자연수 집합(set conclusion에 의해 정렬됨)까지를 지정하면 각 숫자를 소수점 집합으로 정의할 수 있다. It is order-preserving: if divides then each prime divisor of is also a prime divisor of However, it is neither injective (since it maps both 12 and 6 to ) nor order-reflecting (since 12 does 나누지 않음 6). 대신 각 번호를 기본 전력 분배기 집합에 입력하면\ {mathb 에서 {\mathb {P}(\mathb {로 순서를 보존하고 순서를 반영하며, 따라서 주문-embedding을 정의하는 맵 N→ P() It is not an order-isomorphism (since it, for instance, does not map any number to the set ), but it can be made one by restricting its codomain to Fig.9 shows a subset of and its isomorphic image under 그러한 질서 이형성을 동력 집합으로 구성하는 것은 분배 격자라 불리는 광범위한 부분적 질서에 일반화할 수 있다. "Birkhoff의 표현 정리"를 참조하라.
부분주문수
OEIS의 시퀀스 A001035는 n개의 라벨 부착 요소 집합에 대한 부분 주문 수를 제공한다.
| 엘레멘츠 | 아무거나 | 타동사 | 반사적 | 대칭 | 프리오더 | 부분순서 | 총예약자 | 총순번 | 등가관계 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 1 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 |
| 2 | 16 | 13 | 4 | 8 | 4 | 3 | 3 | 2 | 2 |
| 3 | 512 | 171 | 64 | 64 | 29 | 19 | 13 | 6 | 5 |
| 4 | 65,536 | 3,994 | 4,096 | 1,024 | 355 | 219 | 75 | 24 | 15 |
| n | 2n2 | 2n2−n | 2n(n+1)/2 | n! | |||||
| OEIS | A002416 | A006905 | A053763 | A006125 | A000798 | A001035 | A000670 | A000142 | A000110 |
S(n, k)는 두 번째 종류의 스털링 숫자를 가리킨다는 점에 유의한다.
엄격한 부분 주문 건수는 부분 주문 건수와 같다.
이등형성까지만 카운트를 하면 시퀀스 1, 1, 2, 5, 16, 63, 318, ...(OEIS의 시퀀스 A000112)를 얻는다.
선형연장
A partial order on a set is an extension of another partial order on provided that for all elements whenever it is also the case that y . 선형 확장은 선형(즉, 전체) 순서이기도 한 확장이다. 전형적인 예로, 완전 주문 세트의 사전 순서는 그들의 제품 주문의 선형 확장이다. 모든 부분 순서는 전체 순서(주문-확장 원리)로 확장할 수 있다.[15]
컴퓨터 과학에서 부분 순서의 선형 확장을 찾는 알고리즘(지시된 AC 반복 그래프의 도달 가능성 순서로 표현됨)을 위상학적 정렬이라고 한다.
방향 시계열 그래프
엄격한 부분 순서는 지시된 반복 그래프(DAG)에 직접 해당된다. 의 각 요소를 노드로 하고 의 각 요소를 에지로 하여 그래프를 구성하면 모든 엄격한 부분 순서가 DAG이며, DAG의 전이적 폐쇄는 엄격한 부분 순서일 뿐만 아니라 DAG 자체도 된다. 대조적으로 엄격하지 않은 부분 순서는 모든 노드에서 자체 루프를 가지므로 DAG가 아니다.
범주론에서
Every poset (and every preordered set) may be considered as a category where, for objects and there is at most one morphism from to More explicitly, let hom(x, y) = {(x, y)} if x ≤ y (and otherwise the empty set) and 그러한 범주를 양태라고 부르기도 한다.
포셋은 이형성인 경우에만 서로 동등하다. 포셋에서 가장 작은 원소가 존재한다면 초기 원소가 되고, 가장 큰 원소가 존재한다면 단자 물체가 된다. 또한 모든 사전 주문 세트는 포셋과 동등하다. 마지막으로, 포셋의 모든 하위 범주는 이소모르피즘-폐쇄된다.
위상학적 공간의 부분 순서
If is a partially ordered set that has also been given the structure of a topological space, then it is customary to assume that is a closed subset of the topological product space Under this assumption partial order relations are well behaved at limits in the sense that if and and for all then [16]
간격
poset P의 간격은 p의 부분집합 I이며, 어떤 x와 y의 속성과 P의 어떤 z에 대해서도, x z z y y의 경우, z도 I에 있다(이 정의는 실수의 간격 정의를 일반화한다).
≤ b의 경우, 닫힌 간격[a, b]은 ≤ x ≤ b(즉, ≤ x 및 x ≤ b)를 만족하는 원소 x의 집합이다. 그것은 적어도 a와 b 원소를 포함하고 있다.
해당 엄격한 관계 "<를 사용하여, 열린 간격(a, b)은 < x < b (즉, a < x와 x < b))를 만족하는 요소 x의 집합이다. 열린 간격은 < b>라도 비어 있을 수 있다. 예를 들어, 1 < 2와 같은 정수 I가 없기 때문에 정수의 개방 간격(1, 2)은 비어 있다.
반쯤 열린 간격[a, b)과 (a, b]은 유사하게 정의된다.
때때로 정의가 a > b를 허용하도록 확장되기도 하는데, 이 경우 간격이 비어 있다.
, P 이(가) 있는 경우 ⊆ [a, b]와 같은 간격 I. 구간표기법으로 나타낼 수 있는 모든 구간은 분명히 경계를 이루지만, 그 역은 사실이 아니다. 예를 들어 P = (0, 1) ∪ (1, 2) ∪ (2, 3)을 실수의 하위 포셋으로 한다. 부분집합(1, 2)은 경계간격이지만, P에는 최소나 우월성이 없으므로 P의 요소를 이용한 구간 표기법으로 표기할 수 없다.
포셋은 모든 경계 구간이 유한할 경우 국소적으로 유한하다고 불린다. 예를 들어, 정수는 자연적인 순서에 따라 국소적으로 유한하다. 데카르트 제품 × mathb {N} \ {N}}의 사전 순서는 국소적으로 유한하지 않다. 구간 표기법을 사용하여 속성 "a는 b로 덮인다"는 것을[ ={ . 로 동등하게 바꾸어 사용할 수 있다.
부분 순서에서 간격의 이 개념은 구간 순서라고 알려진 부분 순서의 특정 종류와 혼동해서는 안 된다.
참고 항목
- 항이마트로이드(antimatroid)는 양자리보다 더 많은 순서의 일반적 패밀리를 허용하는 집합의 순서의 공식화.
- 인과 집합, 양자 중력에 대한 양전자 기반 접근법
- 비교가능성
- 부분순서완료
- 지시된 세트 – 두 요소가 항상 일부 제3 원소보다 작거나 같은 사전 순서를 사용하여 설정
- 그라데트 포셋
- 발생 대수
- 격자 – 최소 상한과 최대 하한을 갖는 부분 순서
- 국소 유한양행
- 뫼비우스는 양자에 대해 기능한다.
- 중첩 집합 집합 집합
- 폴리토프 주문
- 순서필드
- 순서군
- 순서가 지정된 벡터 공간 – 부분 순서의 벡터 공간
- Poset 토폴로지, 어떤 Poset에서든 정의할 수 있는 위상학적 공간의 일종
- Scott 연속성 – 두 부분 주문 사이의 함수 연속성.
- 세미라티체
- 세미오더
- 확률적 우세
- 엄격한 미약한 순서 – "b"와 "b"의 관계가 타동적인 엄격한 부분 순서 "<".
- 총 주문 – 모든 요소가 유사한 주문
- 트리 – 세트포함 데이터 구조
- Zorn의 보조정리 – 선택의 공리와 동등한 수학적 명제
메모들
인용구
- ^ "Finite posets". Sage 9.2.beta2 Reference Manual: Combinatorics. Retrieved 5 January 2022.
compare_elements(x, y): Compare x and y in the poset. If x<y, return -1. If x=y, return 0. If x>y, return 1. If x and y are not comparable, return None.
- ^ Chen, Peter; Ding, Guoli; Seiden, Steve. "On Poset Merging" (PDF): 2. Retrieved 5 January 2022.
A comparison between two elements s, t in S returns one of three distinct values, namely s≤t, s>t or s t.
Cite 저널은 필요로 한다.journal=(도움말) - ^ Merrifield, Richard E.; Simmons, Howard E. (1989). Topological Methods in Chemistry. New York: John Wiley & Sons. pp. 28. ISBN 0-471-83817-9. Retrieved 27 July 2012.
A partially ordered set is conveniently represented by a Hasse diagram...
- ^ a b c Wallis, W. D. (14 March 2013). A Beginner's Guide to Discrete Mathematics. Springer Science & Business Media. p. 100. ISBN 978-1-4757-3826-1.
- ^ Simovici, Dan A. & Djeraba, Chabane (2008). "Partially Ordered Sets". Mathematical Tools for Data Mining: Set Theory, Partial Orders, Combinatorics. Springer. ISBN 9781848002012.
- ^ Flaška, V.; Ježek, J.; Kepka, T.; Kortelainen, J. (2007). Transitive Closures of Binary Relations I. Prague: School of Mathematics - Physics Charles University. p. 1. 보조정리 1.1(iv) 이 출처는 비대칭 관계를 "엄격한 대칭성"이라고 한다.
- ^ 데이비 & 프리스틀리(2002년), 페이지 14-15.
- ^ Avigad, Jeremy; Lewis, Robert Y.; van Doorn, Floris (29 March 2021). "13.2. More on Orderings". Logic and Proof (Release 3.18.4 ed.). Retrieved 24 July 2021.
So we can think of every partial order as really being a pair, consisting of a weak partial order and an associated strict one.
- ^ Rounds, William C. (7 March 2002). "Lectures slides" (PDF). EECS 203: DISCRETE MATHEMATICS. Retrieved 23 July 2021.
- ^ Kwong, Harris (25 April 2018). "7.4: Partial and Total Ordering". A Spiral Workbook for Discrete Mathematics. Retrieved 23 July 2021.
- ^ Neggers, J.; Kim, Hee Sik (1998), "4.2 Product Order and Lexicographic Order", Basic Posets, World Scientific, pp. 62–63, ISBN 9789810235895
- ^ 데이비 & 프리스틀리(2002년), 페이지 17–18.
- ^ P. R. Halmos (1974). Naive Set Theory. Springer. p. 82. ISBN 978-1-4757-1645-0.
- ^ 데이비 & 프리스틀리(2002년), 페이지 23–24.
- ^ Jech, Thomas (2008) [1973]. The Axiom of Choice. Dover Publications. ISBN 978-0-486-46624-8.
- ^ Ward, L. E. Jr (1954). "Partially Ordered Topological Spaces". Proceedings of the American Mathematical Society. 5 (1): 144–161. doi:10.1090/S0002-9939-1954-0063016-5. hdl:10338.dmlcz/101379.
참조
- Davey, B. A.; Priestley, H. A. (2002). Introduction to Lattices and Order (2nd ed.). New York: Cambridge University Press. ISBN 978-0-521-78451-1.
- Deshpande, Jayant V. (1968). "On Continuity of a Partial Order". Proceedings of the American Mathematical Society. 19 (2): 383–386. doi:10.1090/S0002-9939-1968-0236071-7.
- Schmidt, Gunther (2010). Relational Mathematics. Encyclopedia of Mathematics and its Applications. 132. Cambridge University Press. ISBN 978-0-521-76268-7.
- Bernd Schröder (11 May 2016). Ordered Sets: An Introduction with Connections from Combinatorics to Topology. Birkhäuser. ISBN 978-3-319-29788-0.
- Stanley, Richard P. (1997). Enumerative Combinatorics 1. Cambridge Studies in Advanced Mathematics. 49. Cambridge University Press. ISBN 0-521-66351-2.
외부 링크
| 위키미디어 커먼즈에는 하세 다이어그램과 관련된 미디어가 있다. |















 (가)
(가)


 그렇지 않다
그렇지 않다






 있다면, b
있다면, b
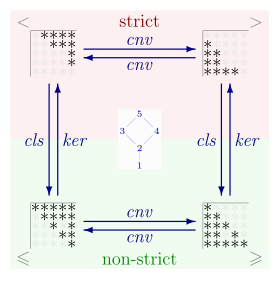



 엄격하지 않은 부분 순서다. 따라서
엄격하지 않은 부분 순서다. 따라서  (가) 엄격하지 않은 부분 순서라면 그에 상응하는 엄격한 부분 순서 <는 다음이 주는
(가) 엄격하지 않은 부분 순서라면 그에 상응하는 엄격한 부분 순서 <는 다음이 주는 










































 (가) f(x) ≼ f(y)를 의미하는
(가) f(x) ≼ f(y)를 의미하는









 (는) g
(는) g 
















 확장
확장









![{\displaystyle [a,b]=\{a,b\}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c22504982538e7e532e76ad1ebfafd8abd6bb8f2)

