파스칼의 삼각형

수학에서 파스칼의 삼각형은 확률론, 조합론, 대수학에서 발생하는 이항 계수의 삼각형 배열입니다. 서양 세계의 많은 곳에서는 프랑스 수학자 블레즈 파스칼의 이름을 따서 지어졌지만, 다른 수학자들은 그보다 몇 세기 앞서 페르시아, ^[1]인도,^[2] 중국, 독일, 이탈리아에서 그것을 연구했습니다.^[3]

파스칼 삼각형의 행은 일반적으로 맨 위(0번째 행)에 n = 0 ${\$displaystyle n = 0} 행으로 시작하여 열거됩니다. 각 행의 항목은 $k$ = ${\$displaystyle k = 0}으로 시작하는 왼쪽부터 번호가 매겨지며 일반적으로 인접 행의 숫자에 대해 엇갈립니다. 삼각형은 다음과 같은 방법으로 구성할 수 있습니다. 0행(맨 위 행)에는 고유한 0이 아닌 항목 1이 있습니다. 각 후속 행의 각 항목은 빈 항목을 0으로 처리하여 위와 왼쪽에 숫자를 더하고 오른쪽에 숫자를 더하여 구성됩니다. 예를 들어 1행(또는 다른 행)의 초기 수는 1(0과 1의 합)인 반면 3행의 숫자 1과 3은 4행의 숫자 4를 생성하기 위해 추가됩니다.

공식

파스칼 삼각형의 $n$ ${\displaystyle n}$번째 행과 $k$ ${\displaystyle k}$번째 열에 있는 항목은$$(${\displaystyle \genfrac{}{}{0ex}{}{n}{}}$ k${\displaystyle )}$ ${\displaystyle {n \choose$ k$}$라고 표시됩니다$.$ 예를 들어, 맨 위 행의 0이 아닌 고유한 항목은$$(${\displaystyle \genfrac{}{}{0ex}{}{0}{})}$ = ${\displaystyle 1}$ ${\displaystyle${0 \choose 0} = 1}입니다. 이 표기법을 사용하면, 전항의 구성은 다음과 같이 기재할 수 있습니다.

${\displaystyle (n}$ ${\displaystyle \genfrac{}{}{0ex}{}{k}{}}$) =${\displaystyle }$(n$-$ 1 k - 1 ) + (n - 1 k ) {\displaystyle {n \cho${\displaystyle o}$se k} = {n-1 \choose k-1} + {n-1 \choose k}},

음이 아닌 정수 $n{\displaystyle }$ ${\displaystyle$ n$}$ 및$$ 임의의 정수 $0{\displaystyle \mathrm{}}$ ${\displaystyle \le }$ ${\displaystyle k}$ ${\displaystyle \le }$ ${\displaystyle n}$ ${\displaystyle 0\leq k\leq$ n$}$에 대하여$.$^[4] 이항 계수에 대한 이러한 반복을 파스칼의 법칙이라고 합니다.

역사

파스칼의 삼각형을 이루는 수들의 패턴은 파스칼 시대 이전에 잘 알려져 있었습니다. 이슬람 세계에서 페르시아 수학자 알카라지 (953–1029)는 이항 계수의 첫 번째 공식과 파스칼의 삼각형에 대한 첫 번째 설명을 포함한 지금은 잃어버린 책을 썼습니다.^[5][6][7] 이 삼각형은 후에 또 다른 페르시아 수학자인 오마르 카얌(1048–1131)에 의해 반복되었습니다. 따라서 이 삼각형은 이란에서는 카얌 삼각형(مثلث خیام)이라고도 불립니다. 이항 정리를 포함하여 삼각형과 관련된 여러 정리들이 알려져 있었습니다. Khayyam은 n번째 근을 이항팽창에 기초하여, 따라서 이항계수에 기초하여 찾는 방법을 사용했습니다.^[1]

파스칼의 삼각형은 중국 수학자 자셴(1010–1070)의 연구 결과로 11세기 초에 중국에서 알려졌습니다. 13세기 동안, 양희(1238–1298)가 삼각형을 제시했고 그래서 그것은 중국에서 아직도 양희의 삼각형(杨辉三角; 楊輝三角)으로 알려져 있습니다.

유럽에서는 파스칼의 삼각형이 요르다누스 드 네모어 산술(13세기)에 처음 등장했습니다.^[10] 이항 계수는 14세기 초에 Gersonides가 곱셈 공식을 사용하여 계산했습니다.^[11] 페트루스 아피아누스 (1495–1552)는 1527년에 사업 계산에 관한 그의 책의 전면에 삼각형을 출판했습니다.^[12] Michael Stifel은 1544년에 삼각형의 한 부분(각 행의 두 번째 열부터 중간 열까지)을 출판하여 그것을 도형 숫자의 표로 묘사했습니다.^[11] 이탈리아에서 파스칼의 삼각형은 1556년에 삼각형의 여섯 줄을 발표한 이탈리아 대수학자 니콜 ò 폰타나 타르탈리아 (1500–1577)의 이름을 따서 타르탈리아의 삼각형이라고 불립니다. 제롤라모 카르다노도 1570년 삼각형과 삼각형을 구성하는 덧셈과 곱셈 규칙을 발표했습니다.^[11]

파스칼의 삼각형 산술은 1665년 사후에 출판되었습니다.^[13] 여기서 파스칼은 당시 삼각형에 대해 알고 있던 몇 가지 결과를 수집하여 확률 이론의 문제를 해결하는 데 사용했습니다. 이 삼각형은 나중에 피에르 레이몽 드 몽모트에 의해 파스칼의 이름을 따서 "Table de M. Pascal pourles combinisons" (프랑스어: 파스칼의 조합표)라고 불렀고, 아브라함 드 모이브르 (1730)는 "Triangulum 산술 PASCALIANUM" (라틴어: 파스칼의 산술 삼각형)이라고 불렀고, 현대 서양식 이름의 기초가 된 것입니다.^[14]

이항 전개

파스칼의 삼각형은 이항 전개에서 발생하는 계수를 결정합니다. 예를 들어, 확장을 고려합니다.

$2$$}=x^{2}+2xy+y^{2}=\mathbf {1} x^{2}y^{0}+\mathbf {2} x^{1}y^{1}+\mathbf {1} x^{0}y^{2}}$.

계수는 파스칼 삼각형의 ${\displaystyle 두}$ 번째 행에 있는 숫자입니다:$$(${\displaystyle \genfrac{}{}{0ex}{}{20}{})}$ = 1 ${\$$displaystyle {2 \choose$ 0}=$1},$ (${\displaystyle 21}$) = 2 {\displaystyle {2 \choose 1}=2}, (22) = 1 {\displaystyle {2 \choose 2}=1}.

일반적으로 $x{\displaystyle }$+ ${\displaystyle y}$ ${\displaystyle$ x$+y}$와 같은 이항이 n ${\displaystyle n}$의 양의 정수 전력으로 상승하면$$ 다음과 같이 됩니다$.$

${\displaystyle (x+y)^{n}=\sum _{k=0}^{n}a_{k}x^{n-k}y^{k}=a_{0}x^{n}+a_{1$$}x^{n-1}y+a_{2$$}x^{n-2}y^{2}+\ldots +a_{n-1}xy^{n-1}+a_{n}y^{n}}$,

여기서$$ 이 $확장$에서 계수$$ak {\$display$ a_${k}$는 정확히 파스칼 $삼각형$의 $n행{\displaystyle }$ ${\display$ n$}$ 위의 숫자입니다. 다시 말해,

${\displaystyle {}_{}{k}_{}}$ =${\displaystyle }$(n$k$ ) {\displaystyle a${\displaystyle {\_}_{}}${k} = {n \choose k}}.

이것이 이항 정리입니다.

파스칼 삼각형의 전체 오른쪽 대각선은 ${\displaystyle {이러한}^{}}$ 이항 전개에서$$ $y{\displaystyle {}^{}}$ ${\$의 계수에 해당하고 다음 대각선은 x $y{\displaystyle }$ -${\displaystyle 1^{}}$ ${\$의 계수에 해당합니다$$.

이항 정리가 파스칼의 삼각형의 단순한 구성과 어떻게 연관되는지를 알아보기 위해, $($${\displaystyle x}$+ ${\displaystyle y{}^{}}$) ${\displaystyle {\mathrm{n}}^{}}$+ 1 ${\displaystyle (x+y)^{n+1}}$의 팽창 계수를 (${\displaystyle \mathrm{x}}$ +${\displaystyle }$1${\displaystyle {}^{}}$ ${\displaystyle n^{}}${\$displaystyle (x+1)^{n}$의 해당 계수로 계산하는 문제를 고려합니다(간단성을 위해 ${\displaystyle \mathrm{설정}}$ $y$ = 1$${\displaystyle y = 1}). 그렇다면

${\displaystyle (\mathrm{x}}$+ 1${\displaystyle {}^{})}$ ${\displaystyle n}$ = ${\displaystyle \sum }$ ${\displaystyle k_{}}$ = 0$$ x {\displaystyle (x+1)^${\displaystyle \{}$n} =\sum${\displaystyle }$_{k=0}^{n}a_{k}x^{k}}.

지금이다

${\displaystyle (x+1)^{n+1}=(x+1)(x+1)^{n}=x(x+1)^{n}+(x+1)^{n}=\sum _{i=0}^{n}a_{i}x^{i+1}+\sum _{i=0}^{n}a_{i}x^{i}.}$

두 가지 요약은 다음과 같이 재구성할 수 있습니다.

${\displaystyle {\begin{aligned}\sum _{k=0}^{n}a_{k}x^{k+1}+\sum _{k=0}^{n}a_{k}x^{k}&=\sum _{k=1}^{n+1}a_{k-1}x^{k}+\sum _{k=0}^{n}a_{k}x^{k}\\[4pt]&=\sum _{k=1}^{n}a_{k-1}x^{k}+\sum _{k=1}^{n}a_{k}x^{k}+a_{0}x^{0}+a_{n}x^{n+1}\\[4pt]&=\sum _{k=1}^{n}(a_{k-1}+a_{k})x^{k}+a_{0}x^{0}+a_{n}x^{n+1}\\[4pt]&=\sum _{k=1}^{n}(a_{k-1}+a_{k})x^{k}+x^{0}+x^{n+1}\end{aligned}}}$

(다항식을 거듭제곱으로 올리는 방법 때문에 a ${\displaystyle 0_{}}$ = a${\displaystyle {}_{}}$= $1$ {\displaystyle a_{0} = a_{n} = 1}).

이제 다항식${\displaystyle }$(${\displaystyle x}$+ ${\displaystyle 1{}^{}}$ ${\displaystyle n^{}}$+ 1 ${\$${\displaystyle 1}$$)^{n+1}$에 대한 식을${\displaystyle }$(${\displaystyle x}$+ 1${\displaystyle {}^{}}$ n ${\$의 계수로$$ 표현합니다($$이것들은 ${\displaystyle {ak}_{}}$ ${\$). 위의 선으로 표현하고자 할 때 필요한 것입니다. 왼쪽 위에서 오른쪽 아래로 가는 대각선의 모든 $항들$은 x$${\$displaystyle$x}의 같은 거듭제곱에 해당하며$,$ ${\displaystyle$ a$}$ - $항들$은 다항식${\displaystyle }$(${\displaystyle \mathrm{x}}$+ 1${\displaystyle {}^{}}$ ${\displaystyle n^{}}$ ${\$+ 1$)^{n}$의 계수임을 기억하십시오$.$ ${\displaystyle {그리고}^{}}{\displaystyle }$(${\displaystyle x}$+ ${\displaystyle 1{}^{}}$ n${\displaystyle {}^{}}$+ ${\displaystyle 1^{}}$ ${\$의 계수를 결정하고 있습니다$.$ Now, for any given ${\displaystyle 0<k<n+1}$, the coefficient of the ${\displaystyle x^{k}}$ term in the polynomial ${\displaystyle (x+1)^{n+1}}$ is equal to ${\displaystyle a_{k-1}+a_{k}}$. 이것은 실제로 파스칼의 삼각형을 일렬로 구성하는 간단한 규칙입니다.

이 주장을 (수학적 귀납법에 의한) 이항 정리의 증명으로 바꾸는 것은 어렵지 않습니다.

$({\displaystyle a^{}}$+ b${\displaystyle {}^{}}$) n = ${\displaystyle b}$ ${\displaystyle n^{}}$($b$+ 1$$) n {\displaystyle (a + b)^{n} = b^{n}\left ({\frac {a}{b}}+1\right)$^{n$ 일반적인 경우의 확장에서는 계수가 동일합니다.

$이항{\displaystyle }$ 정리의 흥미로운 결과는 변수 x {\$displaystyle$ x$}$와 y {\$displaystyle y}$를 모두 1로$$ 설정함으로써 얻어집니다$.$ 이 경우$,$ ${\displaystyle {우리}^{}}$는 (${\displaystyle 1}$+${\displaystyle {}^{}}$1) n =$$ n {\displaystyle (1 + 1)^{n} = 2^{n} 이므로,

${\displaystyle \sum _{k=0}^{n}{n \선택 k}={n \선택 0}+{n \선택 1}+\cdots +{n \선택 n-1}+{n \선택 n}=2^{n}}$

즉, 파스칼 삼각형의 $n{\displaystyle }$ ${\displaystyle$ $n$$}$행에$$ 있는 항목의 $합$은 n ${\displaystyle$ n$}$번째$$ 거듭제곱 2입니다. 이는$n{\displaystyle }$ {\$displaystyle n}$ - 요소$$ 집합의 부분 집합(전원 집합의 기수)이 ${\displaystyle {2n}^{}}$ ${\$ 2$^{n}}$이라는 문장과 동일하며$,$ 이는 부분 집합의 수가 가능한 길이 각각의 조합의 합이라는 것을 관찰하면 알 수 있습니다. $범위$는 0 ~ n ${\displaystyle$ n$}$입니다$.$

조합

파스칼의 삼각형의 두 번째 유용한 응용은 조합의 계산에 있습니다. 예를 들어, 한 번에$$ $k{\displaystyle }$ ${\displaystyle k}$개를 취한 $n{\displaystyle }$ ${\displaystyle$ n$}$개$$ 항목의 조합 수는 다음 식으로 알 수 있습니다.

${\displaystyle \mathbf {C} (n$$}{k!(n-k)!$$}}}$.

하지만 이것은 파스칼의 삼각형 세포에 대한 공식이기도 합니다. 계산을 수행하는 것이 아니라 단순히 삼각형에서 적절한 엔트리를 조회할 수 있습니다. 첫 번째 행과 첫 번째 행에 번호가 0인 경우, 답은 $n{\displaystyle }${\$display n}$ 행의 $입력$ k ${\display k}$에 있습니다$.$ 예를 들어, 8개의 작업을 채워야 하지만 10개의 후보가 있다고 가정하면, 선택 위원회는 10개 중에서 8개를 선택하는 방법이 몇 가지인지 알고 싶어합니다. 정답은 10행의 8번 입력, 즉 45번 입력, 즉 10번 선택 8번 입력, 45번 입력입니다.

이항 분포 및 컨볼루션에 대한 관계

${\displaystyle {2n}^{}}$ ${\displaystyle 2^{n}}$로 나누면 p$$= ${\displaystyle \frac{12}{}}$ ${\$displaystyle p = {\frac {1}{2}}인 대칭인 경우 파스칼 $삼각형$의 $n$ ${\displaystyle$ n$}$행은 이항 분포가 됩니다. 중심 극한 정리에 의해, $이{\displaystyle }$ 분포는 n ${\displaystyle n}$이(가) 증가함에 따라 정규 분포에 접근합니다. 이는 조합 공식에 관련된 요인에 스털링 공식을 적용해도 알 수 있습니다.

이는 두 가지 방식으로 이산 컨볼루션의 운영과 관련이 있습니다. ${\displaystyle \mathrm{첫째}}$, 다항식 곱셈은 이산 컨볼루션에 정확히 해당하므로 시퀀스를${\displaystyle }$반복적으로${\displaystyle \{\dots ,}$ ${\displaystyle 0,}$ ${\displaystyle 0,}$ 1${\displaystyle ,}$ 1${\displaystyle ,0,}$ 0$$$,$ …} {\$displaystyle \{\ldots,$ 0,$0, 1,$1, 0, 0, \$ldots \}$ 자체로 $x{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle x+1}$의 거듭제곱에$$해당하므로 삼각형의 행을 생성합니다${\displaystyle .}$ 둘째, 랜덤 변수에 대한 분포 함수를 반복적으로 변환하는 것은 해당 변수의 독립적인 사본 n개에 대한 분포 함수를 계산하는 것과 일치합니다. 이는 바로 중심 극한 정리가 적용되는 상황이므로 한계에서 정규 분포가 발생합니다. (어떤 것의 컨볼루션을 반복적으로 자체적으로 취하는 동작을 컨볼루션 파워라고 합니다.)

패턴 및 속성

파스칼의 삼각형은 많은 성질을 가지고 있고 많은 패턴의 수를 포함하고 있습니다.

행

• 단일 행의 요소의 합은 앞에 있는 행의 합의 두 배입니다. 예를 들어, 0행(가장 위 행)은 1의 값을 가지며, 1행은 2의 값을 가지며, 2행은 4의 값을 갖습니다. 이것은 한 줄에 있는 모든 항목이 다음 줄에 있는 두 개의 항목을 생성하기 때문입니다. 하나는 왼쪽, 하나는 오른쪽입니다. 행 $n{\displaystyle }$ ${\displaystyle n}$의 요소의 합은 $2{\displaystyle {\mathrm{}}^{}}$ ${\displaystyle n^{}}$ ${\$ 2$^{n}}$과 같습니다$$$.$
• 각 행의 원소들의 곱을 취하면, 생성물들의 수열(OEIS의 수열 A001142)은 자연 로그의 밑, e와 관련이 있습니다.^[16][17] 구체적으로, define the sequence ${\displaystyle s_{n}}$ for all ${\displaystyle n\geq 0}$ as follows: ${\displaystyle s_{n}=\prod _{k=0}^{n}{n \choose k}=\prod _{k=0}^{n}{\frac {n!$$}{k!(n-k)!$$}}}$
  그렇다면 연속적인 행 제품의 비율은.
  $${\displaystyle {\frac {s_{n+1}}{s_{n}}}={\frac {\displaystyle (n+1)!^{n+2}\prod _{k=0}^{n+1}{\frac {1}{k!^{2}}}{\display style n!^{n+1}\prod _{k=0}^{n}{\frac {1}{k!^{2}}}}}={\frac {(n+1)^{n}}{n!}}}$$

  
  그리고 이 비율들의 비율은
  $${\displaystyle {\frac {s_{n+1}\cdot s_{n-1}}{s_{n}^{2}}}=\left({\frac {n+1}{n}}\right)^{n},~n\geq 1.}$$

  
  위 식의 우변은 $e{\displaystyle }$ ${\displaystyle e}$의 한계 정의 형식을 취합니다.
  $${\displaystyle e=\lim_{n\to \infty}\left(1+{\frac {1}{n}}\right)^{n}}$$

  
  .
• $π${\$displaystyle$ \pi}는$$Nilakanta 무한급수를 사용하여 파스칼의 삼각형에서 찾을 수 있습니다.
  $${\displaystyle \pi =3+\sum _{n=1}^{\infty }(-1)^{n+1}{\frac {2n+1 \choose 1}{{2n+1 \choose 2}{2n+2 \choose 2}}}}$$

  
• $그런$ 다음 ${\displaystyle$ n$}$ 행은$$ 모든 ${\displaystyle$ a$}$에 대해 숫자 ${\displaystyle {}_{}^{}}$ 및 ${\$로 표시됩니다$.$ 임의 베이스로의 확장을 참조하십시오.
• 파스칼의 삼각형에 있는 숫자들 중 일부는 로자니치의 삼각형에 있는 숫자들과 관련이 있습니다.
• n행 원소의 제곱의 합은 2n행의 중간 원소와 같습니다. 예를 들어 1 + 4 + 6 + 4 + 1 = 70입니다. 일반적인 형태:
  $${\displaystyle \sum _{k=0}^{n}{n \선택 k}^{2}={2n \선택 n}}$$

  
• n이 짝수인 어떤 행에서도 왼쪽 두 자리를 뺀 중간 항은 카탈로니아 숫자, 구체적으로 (n/2 + 1)번째 카탈로니아 숫자와 같습니다. 예를 들어, 4행에서, 3번째 카탈로니아 숫자인 6 - 1 = 5와 4/2 + 1 = 3입니다.
• p가 소수인 행 p에서 1을 제외한 행의 모든 항은 p의 배수입니다. 이것은 ${\displaystyle 쉽게}$ 증명될 수 있는데, $만약$ $p$∈ P$displaystyle$p\$in \mathbb$ {P}이면 p는 1과 그 자신에 대한 인자를 저장하지 않기 때문입니다. 삼각형의 모든 입력은 정수이므로 정의에 따라${\displaystyle }$(${\displaystyle p}$- k${\displaystyle )!}$ ${\displaystyle ($p - k$)!$$}$$그리고$ $k{\displaystyle !}$ ${\displaystyle$ k$!}$는 p${\displaystyle !}$ ${\displaystyle p!}$의 인자입니다$.$ 그러나 p 자체가 분모에 나타날 수 있는 가능한 방법은 없으므로 p(또는 그 중 일부 배수)는 분자에 남겨져야 하므로 전체 항목은 p의 배수가 됩니다.
• 패리티: n행의 홀수 항을 계산하려면 n을 이진법으로 변환합니다. x를 이진 표현에서 1의 개수라고 합니다. 그러면 홀수 항의 개수는 2개가^x 됩니다. 이 숫자들은 굴드 수열의 값입니다.^[19]
• n ≥ 0인 2행 - 1행의 모든 항목이 홀수입니다.
• 극성: 파스칼 삼각형의 한 행의 원소를 교대로 더하고 뺄 때 결과는 0입니다. 예를 들어 6행은 1, 6, 15, 20, 15, 6, 1이므로 공식은 1 - 6 + 15 - 20 + 15 - 6 + 1 = 0입니다.

대각선

파스칼의 삼각형의 대각선은 다음과 같은 수의 단순화를 포함합니다.

• 왼쪽 가장자리와 오른쪽 가장자리를 따라 가는 대각선은 1의 대각선만 포함합니다.
• 모서리 대각선 옆의 대각선은 자연수를 순서대로 포함합니다. 1차원 단순 숫자는 선분이 숫자 선을 따라 다음 정수로 확장됨에 따라 1씩 증가합니다.
• 안쪽으로 이동하면 다음 대각선 쌍에는 삼각형 숫자가 순서대로 포함됩니다.
• 대각선의 다음 쌍은 정사면체 숫자를 순서대로 포함하고, 다음 쌍은 오각형 숫자를 제공합니다.

${\displaystyle {\begin{aligned}P_{0}(n)&=P_{d}(0)=1,\\P_{d}(n)&=P_{d}(n-1)+P_{d-1}(n)\\&=\sum _{i=0}^{n}P_{d-1}(i)=\sum _{i=0}^{d}P_{i}(n-1).\end{align}}}$

삼각형의 대칭성은 n차원^th 수가 n차원^th 수와 같다는 것을 의미합니다.

재귀를 포함하지 않는 대안 공식은

여기서 n은^(d) 상승 요인입니다.

함수 P의 기하학적 의미는 모든 d에 대하여 P(1) = 1입니다. P(1) = 1에 해당하는 첫 번째 점 아래에 추가 점을 두어 d차원 삼각형(3차원 삼각형은 정사면체)을 구합니다. 이 점들을 파스칼 삼각형의 숫자 배치와 유사한 방식으로 배치합니다. P_d(x)를 구하려면 대상 모양을 구성하는 총 x개의 점이 있어야 합니다. 그러면_d P(x)는 모양에 있는 총 점의 수와 같습니다. 0차원 삼각형은 점이고 1차원 삼각형은 단순히 선이므로 P(x) = 1이고 자연수의 수열인 P(x) = x입니다. 각_{d − 1} 층의 점 수는 P(x)에 해당합니다.

행 또는 대각선을 자체적으로 계산

다른 요소나 인수를 계산하지 않고 모든 요소를 행 또는 대각선으로 계산하는 간단한 알고리즘이 있습니다.

To compute row ${\displaystyle n}$ with the elements ${\displaystyle {\tbinom {n}{0}},{\tbinom {n}{1}},\ldots ,{\tbinom {n}{n}}}$, begin with ${\displaystyle {\tbinom {n}{0}}=1}$. For each subsequent element, 값은 이전 값에 분자와 분모가 천천히 변하는 분수를 곱하여 결정됩니다.

${\displaystyle {n \choose k}={n \choose k-1}\times {\frac {n+1-k}{k}}.$

For example, to calculate row 5, the fractions are ${\displaystyle {\tfrac {5}{1}}}$, ${\displaystyle {\tfrac {4}{2}}}$, ${\displaystyle {\tfrac {3}{3}}}$, ${\displaystyle {\tfrac {2}{4}}}$ and ${\displaystyle {\tfrac {1}{5}}}$, and hence the elements are ${\displaystyle {\tbinom {5}{0}}=1}$, ${\displaystyle {\tbinom {5}{1}}=1\times {\tfrac {5}{1}}=5}$, ${\displaystyle {\tbinom {5}{2}}=5\times {\tfrac {4}{2}}=10}$, etc. (나머지 원소들은 대칭성에 의해 가장 쉽게 얻어집니다.)

요소$({\displaystyle n\genfrac{}{}{0ex}{}{}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{0}{}),}$(${\displaystyle n\genfrac{}{}{0ex}{}{}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{}}{}),}$(${\displaystyle n\genfrac{}{}{0ex}{}{}{}}$+ ${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{}}{}),\dots ,}$ ${\displaystyle {\tbinom {n}{0},$ {\$tbinom {n+1}, {\tbinom {n+2},\dots,$$}$다시$$(${\displaystyle n}$ ${\displaystyle \genfrac{}{}{0ex}{}{0}{})}$ $=$ ${\displaystyle 1}${\displaystyle {\tbinom {n}{0}}}$=$1}로 시작하여 특정 분수의 곱으로 후속 요소를 얻습니다.

${\displaystyle {n+k \choose k}={n+k-1}\times {\frac {n+k}{k}}.$

For example, to calculate the diagonal beginning at ${\displaystyle {\tbinom {5}{0}}}$, the fractions are ${\displaystyle {\tfrac {6}{1}},{\tfrac {7}{2}},{\tfrac {8}{3}},\ldots }$, and the elements are ${\displaystyle (\genfrac{}{}{0ex}{}{5}{0})=1,(\genfrac{}{}{0ex}{}{6}{1})=1\times \frac{6}{1}=6,}$${\displaystyle (\genfrac{}{}{0ex}{}{72}{})}$ = ${\displaystyle 6\times }$ $72$ = 21 {\displaystyle {\tbinom {5${\displaystyle \}}${0}}=1,{\tbinom {6${\displaystyle \}}${1}}=1\transition {\tfrac {6${\displaystyle \}}${1}}=6,{\tbinom {${\displaystyle 7}$}{2}=6\transition {\tfrac {7${\displaystyle \}}${2}}=21} 등입니다. 대칭적으로 이러한 요소는${\displaystyle }$(${\displaystyle \genfrac{}{}{0ex}{}{55}{}),}$(${\displaystyle \genfrac{}{}{0ex}{}{65}{}),}$(${\displaystyle \genfrac{}{}{0ex}{}{75}{})}$ ${\$}, ${\tbinom {7}{5}}$등과 같습니다.

전체적인 패턴 및 속성

• 파스칼의 삼각형에서 홀수만 색칠하여 얻은 패턴은 시에르핀스키 삼각형으로 알려진 프랙탈과 매우 유사합니다. 이러한 유사성은 더 많은 행이 고려될수록 점점 더 정확해집니다. 한계에서 행의 수가 무한대에 가까워질수록 고정된 둘레를 가정한 시에르핀스키 삼각형이 생성됩니다. 좀 더 일반적으로 숫자는 3, 4 등의 배수 여부에 따라 색을 다르게 칠할 수 있습니다. 그 결과 다른 유사한 패턴이 나타납니다.

검정 숫자의 비율이 n이 증가함에 따라 0이 되는 경향이 있으므로 n이 무한대인 경향이 있으므로 홀수 이항 계수의 비율이 0이 되는 경향이 있습니다.^[21]

• 격자의 삼각형 부분(아래 이미지와 같이)에서 주어진 노드에서 삼각형의 맨 위 노드까지의 최단 격자 경로의 수는 파스칼 삼각형의 해당 항목입니다. 삼각형 모양의 플링코 게임 보드에서 이 배포판은 다양한 경품을 받을 확률을 제공해야 합니다.

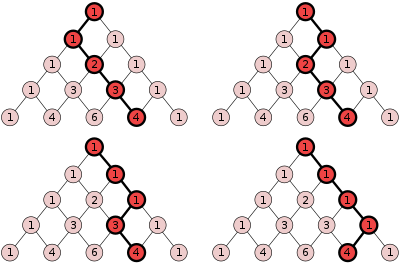
• 파스칼 삼각형의 행이 왼쪽으로 정당화되면 대각선 밴드(아래 색상 코드)는 피보나치 수에 합됩니다.

1
1	1
1	2	1
1	3	3	1
1	4	6	4	1
1	5	10	10	5	1
1	6	15	20	15	6	1
1	7	21	35	35	21	7	1

행렬 지수로서의 구성

인자에 의한 단순한 구성으로 인해 행렬 지수의 관점에서 파스칼의 삼각형을 매우 기본적으로 표현할 수 있습니다. 파스칼의 삼각형은 아각형에 1, 2, 3, 4, ... 순서를 가지고 다른 모든 곳에 0을 갖는 행렬의 지수입니다.

단순화를 이용한 클리포드 대수의 구축

각 n-심플렉스의 요소에 레이블을 지정하는 것은 기하 대수에서 행렬이 아닌 형태로 사용되는 클리퍼드 대수의 기본 요소와 일치합니다. 회전과 같은 기하학적 연산을 인식하면 대수학 연산을 찾을 수 있습니다. 파스칼 삼각형의 각 행 n이 (n-1)-심플렉스에 해당하는 것처럼, 아래에 설명된 것처럼, n차원 기하 대수학에서 명명된 기저 형태의 수를 정의하기도 합니다. 이항 정리는 파스칼의 삼각형이 제공하는 기하학적 관계를 증명하는 데 사용될 수 있습니다.^[22] 이와 같은 증명은 모든 1의 첫 번째 열은 무시되어야 하는 반면 대수학에서는 실수 R ${\$에 대응하며 기본은 1입니다.

다각형의 기하학적 구조와의 관계

이 섹션에서는 출처를 인용하지 않습니다. 신뢰할 수 있는 출처에 인용을 추가하여 이 섹션을 개선하는 데 도움을 주세요. 출처가 없는 자료는 이의를 제기하여 제거할 수 있습니다. (2016년 10월) (이 템플릿 메시지를 제거하는 방법과 시기에 대해 알아봅니다.)

파스칼의 삼각형은 다각형(예: 삼각형, 사면체, 정사각형 또는 정육면체) 내의 요소 수(예: 모서리 및 모서리)에 대한 룩업 테이블로 사용할 수 있습니다.

단순화 요소의 수

우선 파스칼의 삼각형의 세 번째 선부터 생각해 보자, 값은 1, 3, 3, 1입니다. 2차원 삼각형은 1개의 2차원 요소(그 자체), 3개의 1차원 요소(선 또는 모서리), 3개의 0차원 요소(수직 또는 모서리)를 가지고 있습니다. 최종 숫자 (1)의 의미는 설명하기가 더 어렵습니다(그러나 아래 참조). 우리의 예로 계속해서, 정사면체는 1개의 3차원 요소(자체), 4개의 2차원 요소(얼굴), 6개의 1차원 요소(가장자리) 및 4개의 0차원 요소(수직)를 가지고 있습니다. 마지막 1을 다시 더하면 이 값들은 삼각형의 네 번째 행(1, 4, 6, 4, 1)에 해당합니다. 선 1은 점에 해당하고 선 2는 선분(다이어드)에 해당합니다. 이 패턴은 임의의 고차원 초사면체(심플체라고 함)까지 계속됩니다.

이 패턴이 존재하는 이유를 이해하기 위해서는 먼저 (n - 1)-심플렉스로부터 n-심플렉스를 구축하는 과정은 단순히 새로운 정점을 후자에 추가하는 것으로 구성되며, 이 새로운 정점이 원래의 심플렉스의 공간 밖에 있도록 위치하고 모든 원래의 정점에 연결하는 것으로 구성된다는 것을 이해해야 합니다. 예를 들어, 삼각형에서 사면체를 만드는 경우를 생각해 보십시오. 그 중 후자의 요소는 파스칼 삼각형의 3행으로 열거됩니다. 즉, 1개의 면, 3개의 모서리, 3개의 꼭짓점. 삼각형에서 사면체를 만들려면 삼각형의 평면 위에 새로운 꼭짓점을 놓고 이 꼭짓점을 원래 삼각형의 세 꼭짓점에 모두 연결합니다.

정사면체에서 주어진 차원의 원소의 수는 이제 두 개의 수의 합이 됩니다: 먼저 원래 삼각형에서 발견된 원소의 수에 새로운 원소의 수를 더한 수인데, 각각의 원소는 원래 삼각형에서 한 차원이 적은 원소를 기반으로 만들어집니다. 따라서 사면체에서 세포(다면체 요소)의 수는 + = 1, 면의 수는 + = 4, 모서리의 수는 + = 6, 새로운 정점의 수는 + = 4입니다. 주어진 차원의 원소의 수를 한 차원 아래의 원소의 수에 합하여 다음의 상위 심플렉스에서 발견되는 전자의 수에 도달하는 이 과정은 파스칼의 삼각형 행에 인접한 두 개의 수를 합하여 아래의 수를 산출하는 과정과 같습니다. 따라서 파스칼 삼각형의 한 행에 있는 최종 숫자 (1)의 의미는 다음 행으로 표현되는 다음 높은 심플렉스를 산출하기 위해 해당 행으로 표현되는 심플렉스에 추가되는 새로운 정점을 나타내는 것으로 이해됩니다. 이 새로운 꼭짓점은 원래 심플렉스의 모든 원소에 연결되어 새로운 심플렉스에서 한 차원 높은 새로운 원소를 산출하는데, 이것이 파스칼의 삼각형에서 볼 수 있는 것과 동일한 것으로 밝혀진 패턴의 기원입니다.

하이퍼큐브의 원소 수

삼각형과 달리 사각형과 관련해서도 비슷한 패턴이 관찰됩니다. 패턴을 찾으려면 (x + 1)^{row number} 대신 (x + 2)의 계수를 입력하는 파스칼 삼각형과 유사한 것을 구성해야 합니다.^{row number} 몇 가지 방법이 있습니다. 더 간단한 것은 0행 = 1행 = 1, 2행으로 시작하는 것입니다. 다음 규칙에 따라 아날로그 삼각형을 구성합니다.

${\displaystyle {n \choose k}=2\times {n-1 \choose k-1}+{n-1 \choose k}}$

즉, 파스칼 삼각형의 규칙에 따라 한 쌍의 숫자를 선택하되, 더하기 전에 왼쪽 숫자를 두 배로 선택합니다. 결과적으로 다음과 같습니다.

${\displaystyle {\text{matrix}}{\text{ 1}}\{\text{ 1}}\quad {\text{ 2}}\{\text{ 1}}\quad {\text{ 4}\text{ 1}\text{ 1}\text{ 6}\text{ 12}\text{ 8}\text{ 1}\text{ 1}\text{ 8}\text{ 1}\text{ }\text{ }\text{ }\text{ 24}\text{ 32}\text{ 16}\text{ 1}\text{ 10}\text{ }\text{ 40}\text{ }\text{ }\text{ } 80}\quad {\text{ 80}}\quad {\text{ 32}\{\text{ 1}}\quad {\text{ 12}\quad {\text{ 60}\quad 160\text 240\quad 192\quad {\text{ 64}\{\text{ 1}\text{ 1}\text{ 14}\text{ 84}\quad 280\quad 672\quad 448\quad 128\end{ matrix}}$

이 삼각형을 만드는 다른 방법은 파스칼의 삼각형에서 시작해서 각 원소에 2를^k 곱하는 것인데, k는 주어진 수의 행에 있는 위치입니다. 예를 들어, 파스칼의 삼각형 4행의 두 번째 값은 6입니다. (1의 기울기는 각 행의 0번째 항목에 해당합니다.) 아날로그 삼각형에서 해당 위치에 있는 값을 얻으려면 6에 2 = 6 × 2 = 6 × 4 = 24를 곱합니다. 이제 아날로그 삼각형이 구성되었으니, 임의의 차원의 정육면체(하이퍼큐브라고 함)를 구성하는 임의의 차원의 요소의 수는 파스칼의 삼각형과 유사한 방식으로 표에서 읽을 수 있습니다. 예를 들어, 2차원 정육면체(사각형)의 2차원 요소의 수는 1이고, 1차원 요소(변 또는 선)의 수는 4이며, 0차원 요소(점 또는 꼭짓점)의 수는 4입니다. 이것은 표의 두 번째 행(1, 4, 4)과 일치합니다. 정육면체는 1개의 정육면체, 6개의 면, 12개의 모서리, 8개의 꼭짓점으로 아날로그 삼각형의 다음 선(1, 6, 12, 8)에 해당합니다. 이 패턴은 무한정 계속됩니다.

이 패턴이 존재하는 이유를 이해하려면, 먼저 (n - 1)-큐브로부터 n-큐브의 구성은 단순히 원래 도형을 복제하여 원래 도형의 공간과 직교하는 거리(정규 n-큐브의 경우, 모서리 길이)를 변위함으로써 수행된다는 것을 인식해야 합니다. 그런 다음 새 그림의 각 꼭짓점을 원본의 해당 꼭짓점에 연결합니다. 이 초기 복제 과정은 n-큐브의 차원 요소를 열거하기 위해, 합을 맞추기 전에 파스칼 삼각형의 이 아날로그 행에 있는 한 쌍의 숫자 중 첫 번째 숫자를 두 배로 늘려야 하는 이유입니다. 따라서 초기 배가는 다음 상위 n-큐브에서 찾을 수 있는 "원래" 요소의 수를 산출하며, 이전과 마찬가지로 새로운 요소는 하나의 더 적은 차원(꼭짓점의 모서리, 모서리의 면 등)의 요소를 기반으로 구축됩니다. 다시, 행의 마지막 수는 다음으로 높은 n-큐브를 생성하기 위해 추가될 새로운 정점의 수를 나타냅니다.

이 삼각형에서 행 m의 원소들의 합은^m 3과 같습니다. 다시 4행의 요소를 예로 사용하려면 1 + 8 + 24 + 32 + 16 = 81, 이는 34 = 81 {\display 3^{4}= 81}과 같습니다.

정육면체의 꼭짓점을 거리별로 세는 방법

파스칼 삼각형의 각 행은 n차원 정육면체의 고정된 꼭짓점에서 각 거리에 있는 꼭짓점의 개수를 제공합니다. 예를 들어, 3차원에서 세 번째 행(1 3 31)은 일반적인 3차원 정육면체에 해당합니다. 즉, V에서 0 떨어진 곳에 하나의 정점이 있고(즉, V 자체), 1 떨어진 곳에 세 개의 정점이 있으며, √2에 세 개의 정점이 있고, √3에 하나의 정점이 있습니다(V 반대쪽 정점). 두 번째 행은 정사각형에 해당하는 반면, 숫자가 큰 행은 각 차원에서 하이퍼큐브에 해당합니다.

sin(x)/ⁿ⁺¹x의 푸리에 변환

앞에서 설명했듯이 (x + 1)ⁿ의 계수는 삼각형의 n번째 행입니다. 이제 (x - 1)ⁿ의 계수는 부호가 +1에서 -1로 번갈아 가며 다시 돌아온다는 점을 제외하고는 동일합니다. 적절한 정규화 후 sin(x)/ⁿ⁺¹x의 푸리에 변환에서도 동일한 패턴의 숫자가 발생합니다. 좀 더 정확하게 말하면, n이 짝수이면 변환의 실수 부분을 취하고, n이 홀수이면 허수 부분을 취합니다. 그러면 그 결과 값(적절하게 정규화됨)이 교대하는 부호가 있는 삼각형의 n번째 행에 의해 제공되는 계단 함수가 됩니다.^[23] 예를 들어, 다음과 같은 결과가 발생하는 단계 함수의 값입니다.

${\displaystyle {\mathfrak {Re}}\left({\text{푸리에}\left[{\frac {\sin(x)^{5}}{x}\right]\right]}$

삼각형의 네 번째 행을 교대로 기호로 구성합니다. 이는 다음과 같은 기본 결과를 일반화한 것입니다(전기 공학에서 자주 사용됨).

${\displaystyle {\mathfrak {Re}}\left({\text{푸리에}\left[{\frac {\sin(x)^{1}}{x}\right]\right]}$

박스카 기능입니다.^[24] 삼각형의 대응하는 행은 숫자 1로 구성된 0행입니다.

n이 2 또는 3 mod 4와 합동이면 부호는 -1로 시작합니다. 실제로 (정규화된) 첫 번째 항의 순서는 i의 거듭제곱에 해당하며, i는 복잡한 평면에서 단위 원과 축의 교차점을 중심으로 순환합니다.

확장

파스칼의 삼각형은 정점에서 1보다 위로 위로 확장되어 가산 성질을 보존할 수 있지만, 그렇게 하는 방법은 여러 가지가 있습니다.^[25]

더 높은 차원으로

파스칼의 삼각형은 차원의 일반화가 더 높습니다. 3차원 버전은 파스칼의 피라미드 또는 파스칼의 사면체로 알려져 있고, 일반적인 버전은 파스칼의 단순한 것으로 알려져 있습니다.

복소수로

요인 함수가 $z$로 정의되면!${\displaystyle }$=${\displaystyle }$γ (z $+$ 1) ${\displaystyle$ z!$=$\$Gamma$$($$)},$ 파스칼의 삼각형은 정수를 넘어 C {\displaystyle \mathbb {C}로 확장될 수 있습니다. 왜냐하면 $γ$(z + 1) {\displaystyle \Gamma(z+1)}는 전체 복소 평면과 동형이기 때문입니다.

임의의 베이스로

아이작 뉴턴은 파스칼의 삼각형에서 끈으로 여겨지는 첫 다섯 줄이 11의 거듭제곱이라는 것을 관찰했습니다. 그는 후속 행들도 11의 거듭제곱을 생성한다고 증거 없이 주장했습니다.^[27] 1964년 로버트 L. 박사. Morton은 각 $행$ n ${\displaystyle n}$을 라디칼 $a$ ${\displaystyle$ a$}$ 숫자로 읽을 수 있다는 보다 일반화된 주장을 제시했습니다. 여기서 ${\displaystyle {}_{}^{}}$ → ∞ $11$ n ${\displaystyle \lim_{n$\to $\infty }11_{$a}^{n}은 삼각형의 가상적인 말단 행 또는 한계이며 행은 그 부분 곱입니다. 그는 $n행$ ${\displaystyle n}$의 항목을$$자릿값 숫자로 직접 해석할 때$$(${\displaystyle \mathrm{a}}$+ 1${\displaystyle {}^{}}$ n = ${\displaystyle 11}$ {\displaystyle (a + 1)^{n} = 11_{a}^{n}의 이항 확장에 해당한다는 것을 증명했습니다. 그 이후로 더 엄격한 증명이 개발되었습니다. 이 해석 뒤에 숨겨진 원리를 더 잘 이해하기 위해, 다음은 이항형에 대해 기억해야 할 몇 가지 사항입니다.

• A radix ${\displaystyle a}$ numeral in positional notation (e.g. ${\displaystyle 14641_{a}}$) is a univariate polynomial in the variable ${\displaystyle a}$, where the degree of the variable of the ${\displaystyle i}$th term (starting with ${\displaystyle i=0}$) is ${\displaystyle i}$. 예를 들어, ${\displaystyle {14641}_{}}$ ${\displaystyle a_{}}$ = 1 ⋅ ${\displaystyle a}$ 4 + 4 ⋅ a 3 + 6 ⋅ a 2 + 4 ⋅ a 1 + 1 ⋅ a 0 {\displaystyle 14641_{a}=1\cdot a^{4}+4\cdot a^{3}+6\cdot a^{2}+4\cdot a^{1}+1\cdot a^{0}입니다.
• 행은$$(${\displaystyle a}$+ ${\displaystyle b{}^{}}$) n ${\displaystyle (a$+ $b)^{n}}$의 이항 전개에 해당합니다$.$ $b$ = ${\displaystyle 1}$ ${\$displaystyle b= 1}을(를) 설정하면 $전개$에서$$b {\$displaystyle$ b$}$를 제거할 수 있습니다. 이제 확장은 위에서 설명한 ^[31][32]것처럼 ${\display$ a$}$ 숫자의$$ 라디칼 확장 $형태$를 나타냅니다. Thus, when the entries of the row are concatenated and read in radix ${\displaystyle a}$ they form the numerical equivalent of ${\displaystyle (a+1)^{n}=11_{a}^{n}}$. If ${\displaystyle c=a+1}$ for ${\displaystyle c<0}$, then the theorem holds for ${\displaystyle a=\{c-1,}$${\displaystyle -(c}$+ ${\displaystyle 1}$) ${\displaystyle \}}$ ${\displaystyle \mathrm{mod}}$ ${\displaystyle 2}$ ${\displaystyle c}$ ${\displaystyle$=\{$c-1,-(c+1)\}\;\mathrm {mod} \;2c}$ 홀수 $값$이 n ${\displaystyle$ n$}$인 경우 음의 행 곱이 생성됩니다.

행의 반지름(변수 ${\displaystyle a$을 1과 10으로 설정하면, $행$n {\$displaystyle$ n$}$은 각각 ${\displaystyle {제품}^{}}$ ${\displaystyle {}_{}^{}}$ n = 2$${\$displaystyle 11_{1}^{n$}= 2^{$n}}$ 및 11 10 n = 11 n {\displaystyle 11_{10}^{n}= 11^{n}이 됩니다. 예를 들어, 행 곱 n(1 + 1 n$)$ n = 11 n {\displaystyle n^{n}\left(1+{\frac {1}{n}\right)를 산출하는 = ${\$displaystyle a=n}을 생각해 보십시오.$^{n$}$=$11_{n$}^{n$ $11{\displaystyle }$ ${\displaystyle {}_{}^{}}$ ${\$$displaystyle 11_{n}^{n}}$ 행 {\displaystyle n$}$의 항목을 $연결$하여 11 n {\displaystyle n}의 숫자 표현을 구성합니다$.$ 위의 이미지에서 12번째 행은 곱을 나타냅니다.

${\displaystyle 11_{12}^{12}=1:10:56:164:353:560:650:560:353:164:56:10:1_{12}=27433a9699701_{12}}$

${\displaystyle \mathrm{반지름}}$ 12 {\$displaystyle$12$}$에서 복합 숫자(":"로 delim)를 사용합니다$.$ $k$ = n${\displaystyle }$-$$ {\$displaystyle$ k = n-1}부터 k = 1 {\$displaystyle$ k = 1}까지의 숫자는 이 행 항목이 12 {\displaystyle 12} 이상의 값으로 계산되므로 복합입니다. 숫자를 정규화하려면 첫 번째 복합 항목의 접두사, 즉, 계수의 접두사$({\displaystyle n\genfrac{}{}{0ex}{}{}{}}$ ${\displaystyle \genfrac{}{}{0ex}{}{\mathrm{n}}{}}$- 1${\displaystyle \genfrac{}{}{0ex}{}{}{}}$) ${\$를 가장 왼쪽 자리까지 제거하고, 제거된 접두사를 바로 왼쪽에 있는 항목과 합하여 ${\displaystyle \mathrm{radix-12}}$ ${\displaystyle 12}$ 산술을$$ 사용하여 왼쪽으로 진행합니다. 가장 왼쪽에 도착할 때까지. 이 특정 예에서 정규화된 문자열은 모든 $n{\displaystyle }$ ${\displaystyle n}$에 대해 ${\displaystyle 01}$ ${\displaystyle 01}$로 끝납니다$.$ > ${\displaystyle$ n$> 2$에 대해 $가장$ 왼쪽 자리는 2 ${\displaystyle$ $2$$}$이며 이는 ${\displaystyle {엔트리}_{}}$ $k$ = ${\$$displaystyle$k= 1}에서 10 $n$ {\displaystyle 10_{$n}$ 중 1 ${\displaystyle 1}$을 운반함으로써 얻어집니다. 따라서 정규화된 값 ${\displaystyle {}_{}^{}}$ ${\$의 길이는 행 길이 $n{\displaystyle }$+ ${\displaystyle 1}$ ${\displaystyle n+1}$과 같습니다$.$ $1{\displaystyle }$$.$ n {\$displaystyle$ $1$$.1_{$n}^{$n}}$의 적분 부분은 n ${\displaystyle$ n$}($소수점이 이동한 왼쪽 자리 수)가 행 길이보다 한 자리 적기 때문에 정확히 한 자리 수를 포함합니다$$. 아래는 정규화된 $1{\displaystyle {.11}_{}^{}}$ ${\displaystyle {1234}_{}^{}}$ ${\displaystyle {1234}_{}^{}}${\$displaystyle 1.1_{1234}^{1234}}$의 값입니다$.$ 복합 숫자는 10으로 표시된 ${\displaystyle 1234}$ ${\displaystyle 1234}$ 잔기이기$$ 때문에 값에 남아 있습니다.

${\displaystyle 1.1_{1234}^{1234}=2.885:2:35:977:696:\overbrace {\ldots } ^{\text{1227 digits}}:0:1_{1234}=2.717181235\ldots _{10}}$

참고 항목

참고문헌

외부 링크

• "Pascal triangle", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Weisstein, Eric W. "Pascal's triangle". MathWorld.
• 일곱 제곱 곱하기의 구법 도표 (1303년, 파스칼의 삼각형의 첫 아홉 줄을 묘사한 추시제의 서원위치엔에서)
• 산술 삼각형에 관한 파스칼의 논문 (Pascal 논문의 페이지 이미지, 1654; 요약)