영대칭 그래프

Zero-symmetric graph
18-vertex zero-symmetric graph
정점 18개와 가장자리 27개로 구성된 가장 작은 제로 대칭 그래프
Truncated cuboctahedron
0대칭 다면체인 잘린 큐옥타헤드론
자동화에 의해 정의된 그래프 패밀리
거리 변환의 → 거리 규칙의 ← 매우 규칙적인.
↓
대칭(대칭 변환) ← t-변환, t ≥ 2 꼬불꼬불한
↓
(연결된 경우)
정점 및 에지 변환 		→ 가장자리-변환적이고 규칙적인 → 가장자리-변환성
↓ ↓ ↓
정점 변환의 → 정칙의 → (양립할 경우)
복엽의
↑
케이리 그래프 ← 무궤도적 비대칭의

그래프 이론의 수학적 분야에서, 제로 대칭 그래프는 각각의 꼭지점이 정확히 세 개의 입사 모서리를 가지고 있고, 각각의 두 꼭지점에 대해 다른 정점에 대해 하나의 정점을 취하는 고유한 대칭성이 있는 연결된 그래프다.이러한 그래프는 정점-변환 그래프일 수는 없지만 에지-변환 그래프는 될 수 없다. 대칭의 수는 정점의 수와 같으며, 모든 에지를 다른 에지로 가져가기에는 너무 적다.[1]

두 개의 에지 궤도를 갖는 가장 작은 제로 대칭 그래프

이 종류의 그래프의 이름은 R. M. 포스터가 H. S. M. Coxeter에게 보낸 1966년 편지에서 만들었다.[2]그룹 이론의 맥락에서, 제로 대칭 그래프는 대칭 그룹의 그래픽 정규 표현이라고도 불린다.[3]

예

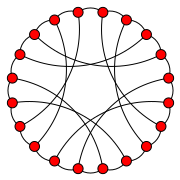
가장 작은 영대칭 그래프는 18개의 정점을 가진 비계획 그래프다.[4]LCF 표기법은 [5,-5]9이다.

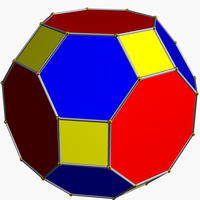
평면 그래프 중에서 잘린 칸막이와 잘린 이코사이드스크립트 그래프도 0대칭이다.[5]

이 예들은 모두 초당적인 그래프들이다.그러나 쌍방향 그래프가 아닌 제로대칭 그래프의 더 큰 예가 존재한다.[6]

이러한 예는 세 가지 다른 대칭 등급(궤도)의 가장자리를 가지고 있다.단, 가장자리 궤도가 두 개뿐인 제로 대칭 그래프가 존재한다.그러한 그래프의 가장 작은 크기는 20개의 정점을 가지며, LCF 표기법 [6,6,-6,-6]5[7]이다.

특성.

모든 유한 제로 대칭 그래프는 케이리 그래프로서, 입방 정점 변환 그래프를 더 일반적으로 유지하지 않으며 제로 대칭 그래프에 관한 결합체 열거 작업의 해결에 도움이 되는 속성이다.최대 1280 정점에 97687개의 제로 대칭 그래프가 있다.이러한 그래프는 동일한 정점 수에서 입방체 Cayley 그래프의 89%와 연결된 모든 정점 변환 입방 그래프의 88%를 형성한다.[8]

수학의 미해결 문제:

모든 유한한 제로대칭 그래프는 해밀턴 사이클을 포함하고 있는가?

(수학에서 더 풀리지 않은 문제)

알려진 모든 유한 연결 제로 대칭 그래프는 해밀턴 사이클을 포함하지만, 모든 유한 연결 제로 대칭 그래프가 반드시 해밀턴 그래프인지는 알 수 없다.[9]이것은 (알려진 5개의 예외를 제외하고, 제로 대칭이 없는) 모든 유한 연결 정점 변환 그래프와 모든 유한한 케이슬리 그래프는 해밀턴 그래프라는 로바스 추측의 특별한 경우다.

참고 항목

  • 반대칭 그래프, 두 에지 사이에 대칭이 있지만 두 꼭지점 사이에 대칭이 없는 그래프(제로대칭 그래프의 정의에서 에지와 정점의 역할 반전)

참조

  1. ^ Coxeter, Harold Scott MacDonald; Frucht, Roberto; Powers, David L. (1981), Zero-symmetric graphs, Academic Press, Inc. [Harcourt Brace Jovanovich, Publishers], New York-London, ISBN 0-12-194580-4, MR 0658666
  2. ^ 콕시터, 프루히트 & 파워스(1981), 페이지 ix.
  3. ^ Lauri, Josef; Scapellato, Raffaele (2003), Topics in Graph Automorphisms and Reconstruction, London Mathematical Society Student Texts, Cambridge University Press, p. 66, ISBN 9780521529037.
  4. ^ Coxeter, Frucht & Powers(1981), 그림 1.1, 페이지 5.
  5. ^ Coxeter, Frucht & Powers (1981), 75 페이지와 80 페이지.
  6. ^ 콕시터, 프루히트 & 파워스(1981), 페이지 55.
  7. ^ Conder, Marston D. E.; Pisanski, Tomaž; Žitnik, Arjana (2017), "Vertex-transitive graphs and their arc-types", Ars Mathematica Contemporanea, 12 (2): 383–413, arXiv:1505.02029, doi:10.26493/1855-3974.1146.f96, MR 3646702
  8. ^ Potočnik, Primož; Spiga, Pablo; Verret, Gabriel (2013), "Cubic vertex-transitive graphs on up to 1280 vertices", Journal of Symbolic Computation, 50: 465–477, arXiv:1201.5317, doi:10.1016/j.jsc.2012.09.002, MR 2996891.
  9. ^ 콕시터, 프루히트 & 파워스(1981), 페이지 10.