뫼비우스 변환
Möbius transformation기하학과 복소해석학에서 복소평면의 뫼비우스 변환은 다음 형태의 유리함수입니다.
기하학적으로 뫼비우스 변환은 먼저 평면에서 단위 구로 역 입체 사영을 적용하고 구를 공간의 새로운 위치와 방향으로 이동 및 회전한 다음 입체 사영을 적용하여 구에서 다시 평면으로 매핑함으로써 얻을 수 있습니다.[1] 이러한 변환은 각도를 보존하고 모든 직선을 선이나 원에 매핑하며 모든 원을 선이나 원에 매핑합니다.
뫼비우스 변환은 복잡한 사영선의 사영 변환입니다. 이들은 뫼비우스 군이라고 불리는 군을 형성하는데, 이 군은 사영 선형 군 PGL(2, C)입니다. 하위 그룹과 함께 수학 및 물리학 분야에서 수많은 응용 프로그램을 가지고 있습니다.
뫼비우스 기하학과 그 변환은 이 경우를 다른 분야에 비해 다양한 차원으로 일반화합니다.
뫼비우스 변환은 아우구스트 페르디난트 뫼비우스를 기리기 위해 명명된 것으로, 호모그래피, 선형 분수 변환, 쌍선형 변환, 스핀 변환(상대성 이론에서)의 한 예입니다.[2]
개요
뫼비우스 변환은 된 복소 평면 C^= ∪ { ∞ } displaystyle {\mathbb {C}}}=\mathbb {C} \cup \{\infty \}}(즉, 무한대의 점으로 증강된 복소 평면)에서 정의됩니다.
입체 사영은 를 구와 동일시하며, 이를 리만 구라고 합니다. C 는 복소 사영선 로 생각할 수 있습니다 뫼비우스 변환은 정확하게 리만 구에서 그 자체로의 주관적 등각 지도, 즉 복잡한 다양체로서의 리만 구의 자기 동형화이며, 또는 다양체로서의 CP { {1}의자기 동형화입니다. 따라서 모든 뫼비우스 변환들의 집합은 구성 아래의 군을 형성합니다. 이 그룹을 뫼비우스 그룹이라고 하며, 때로는 ^) C라고 합니다.
뫼비우스 그룹은 쌍곡 3-공간의 방향 보존 등각의 그룹과 동형이므로 쌍곡 3-매니폴드를 연구할 때 중요한 역할을 합니다.
물리학에서 로렌츠 군의 항등원 성분은 뫼비우스 군이 리만 구에 작용하는 것과 같은 방식으로 천구에 작용합니다. 사실 이 두 군은 동형입니다. 상대론적 속도로 가속하는 관측자는 지구 근처에서 볼 수 있는 별자리의 패턴이 무한소 뫼비우스 변환에 따라 연속적으로 변환되는 것을 보게 될 것입니다. 이 관측은 종종 트위스터 이론의 출발점으로 여겨집니다.
뫼비우스 군의 특정 부분군은 단순히 연결된 다른 리만 곡면(복소수 평면과 쌍곡 평면)의 자기 형태론 군을 형성합니다. 이처럼 뫼비우스 변환은 리만 표면 이론에서 중요한 역할을 합니다. 모든 리만 표면의 기본 군은 뫼비우스 군의 이산 부분군입니다(복시안 군과 클라이니아 군 참조). 뫼비우스 군의 특히 중요한 이산 부분군은 모듈러 군이며, 모듈러 형태, 타원 곡선 및 펠리안 방정식 이론의 중심입니다.
뫼비우스 변환은 차원 n > 2의 공간에서 n-구에서 n-구로의 주관적 등각 방향 보존 맵으로 더 일반적으로 정의될 수 있습니다. 이러한 변환은 도메인의 컨포멀 매핑의 가장 일반적인 형태입니다. 리우빌의 정리에 따르면 뫼비우스 변환은 번역, 유사성, 직교 변환 및 반전의 구성으로 표현될 수 있습니다.
정의.
뫼비우스 변환의 일반적인 형태는 다음과 같습니다.
c ≠ 0인 경우, 이 정의는 다음과 같이 정의함으로써 리만 구 전체로 확장됩니다.
c = 0이면, 다음을 정의합니다.
따라서 뫼비우스 변환은 항상 리만 구에서 리만 구로 가는 주관적 홀로포밍 함수입니다.
모든 뫼비우스 변환들의 집합은 구성 아래 집단을 형성합니다. 이 군은 합성과 반전이 복소형 지도인 복소형 다양체의 구조를 부여받을 수 있습니다. 뫼비우스 군은 복소 리 군입니다. 군은 일반적으로 오토 ^)displaystyle \operatorname {Aut}({\widehat {\mathbb {C}}})으로 표시되며, 리만 구의 오토모피즘 군입니다.
ad = bc인 경우 위에서 정의된 유리 함수는 상수입니다(c = d = 0이 아닌 경우, 정의되지 않은 경우).
고정점
모든 비 항등식 뫼비우스 변환은 리만 구에 두 개의 고정점γ 1 γ 2displaystyle 1},\gamma_{2}를 가지고 있습니다. 여기서 고정된 점은 다중으로 계산됩니다. 포물선 변환은 고정된 점이 일치하는 것입니다. 이 고정된 점들 중 하나 또는 둘 다 무한대의 점일 수 있습니다.
고정점 결정
변환의 고정점은
c = 0일 때 2차 방정식은 선형 방정식으로 퇴화되고 변환은 선형입니다. 이것은 고정된 점 중 하나가 무한대의 점이라는 상황에 해당합니다. ≠ d가 유한할 때 두 번째 고정점은 다음과 같이 주어집니다.
이 경우 변환은 번역, 회전 및 확장으로 구성된 단순 변환이 됩니다.
c = 0이고 a = d인 경우 두 고정점은 무한대이며 뫼비우스 변환은 순수 번역에 해당합니다.
위상 증명
위상적으로, (비 항등식) 뫼비우스 변환이 2개의 점(복수성)을 고정한다는 사실은 구면의 오일러 특성이 2인 것과 일치합니다.
첫째, 투영 선형 그룹 PGL(2, K)은 급격하게 3-경향적입니다. - 구별되는 점의 순서 3배에 대해 뫼비우스가 변환하는 것과 동일한 대수적 증명(본질적으로 그룹이 3차원인 것처럼 차원 계산)에 의해 하나의 삼중을 다른 삼중으로 취하는 고유한 맵이 있습니다. 따라서 최소 3개의 점을 고정하는 모든 지도가 항등식입니다.
다음으로, ( C 로 뫼비우스 군을 식별하면 모든 뫼비우스 함수가 항등원성임을 알 수 있습니다. 실제로, 일반 선형 그룹의 구성원은 가우스-조단 제거에 의해 동일성 맵으로 축소될 수 있으며, 이는 투영 선형 그룹이 경로 연결되어 동일성 맵에 대한 호모토피를 제공한다는 것을 보여줍니다. The Lefschetz–호프 정리(Hopf theorem)는 유한 개의 고정점이 있는 지도의 고정점의 지수(이 맥락에서 다중성)의 합은 지도의 레프셰츠 수와 같으며, 이 경우 단순히 오일러 특성인 상동성 그룹에 대한 항등식 지도의 흔적입니다.
반면 실제 투영 선의 투영 선형 그룹인 PGL(2, R)은 점을 고정할 필요가 없습니다. 예를 들어(+ x)/(- ) + x) / (1 - x 에는 (실제) 고정점이 없습니다. 복잡한 변환으로 ±i를 고정합니다. 반면 지도 2x는 0과 ∞의 두 점을 고정합니다. 이는 원의 오일러 특성(실사영선)이 0이라는 사실과 일치하며, 따라서 레프셰츠 고정점 정리는 최소 0점 이상을 고정해야 하지만 그 이상일 가능성이 있다고만 말합니다.
노멀폼
뫼비우스 변환은 또한 소위 정상 형태로 고정된 점의 관점에서 작성되기도 합니다. 우리는 먼저 두 개의 뚜렷한 고정점이 있는 비포물선 사례를 처리합니다.
포물선이 아닌 경우:
포물선이 아닌 모든 변환은 확장/회전, 즉 형태의 변환에 결합됩니다.
f에 서로 다른 고정점(γ, γ)이 있는 경우 변환 - 1 gfg^{-1}}은 0과 ∞에 고정점이 있으므로입니다. -1(z) ={\gfg^{-1}(z) = kz}. 그런 다음 변환 f에 대한 고정점 방정식을 쓸 수 있습니다.
다음을 위한 풀이 포브(행렬 형태):
위 식을 통해 고정점에서 f 의 도함수를 계산할 수 있습니다.
고정된 점들의 순서가 주어지면, 우리는 f 의 승수들 중 하나(k)를 특성 상수 off로 구별할 수 있습니다. 고정된 점의 순서를 반대로 하면 특성 상수에 대한 역승수를 취하는 것과 같습니다.
록소드로믹 변환의 경우, k > 1일 때마다 γ이 반발 고정점이고, γ이 매력적인 고정점이라고 말합니다. k < 1의 경우 역할이 반대입니다.
포물선 경우:
포물선의 경우 고정된 점 γ가 하나만 존재합니다. 그 지점을 ∞로 보내는 변환은
여기서 β를 번역 길이라고 합니다. 포물선 변환에 대한 고정점 공식은 다음과 같습니다.
(행렬 형태의) f에 대한 풀이는 다음을 제공합니다.
β는 포물선 변환의 경우 항상 1인 f의 특성 상수가 아닙니다. 위 식을 통해 다음과 같이 계산할 수 있습니다.
변환의 극점
∞ = - dc {\textstylez_{\infty} =-{\frac {d}{c}}는 H {\displaystyle {\mathfrak {H}}의 극으로 불리는데, 이 점은 H {\displaystyle {\mathfrak {H}} 아래에서 무한대의 점으로 변환됩니다.
역극 ∞ = ctextstyle Z_{\infty} = {\frac {a}{c}}는 무한대의 점이 변환되는 지점입니다. 두 극의 중간 지점은 항상 두 고정 지점의 중간 지점과 동일합니다.
이 네 개의 점은 변환의 특징적인 평행사변형이라고도 불리는 평행사변형의 꼭짓점입니다.
변환 은 두 개의 고정 점 γ γ 및 pole z ∞displaystyle z_{\infty}}로 지정할 수 있습니다.
이를 통해γ 1, γ \gamma_1},\gamma_{2}가 주어진 와 ∞ {\displaystyle infty}} 간의 변환 공식을 도출할 수 있습니다.
마지막 식은 행렬의 (상호) 고유값 비율λ 1 λ 2 1}}{\lambda _{2}} 중 하나와 일치합니다.
단순 뫼비우스 변환 및 구성
뫼비우스 변환은 단순 변환의 시퀀스로 구성될 수 있습니다.
다음과 같은 간단한 변환도 뫼비우스 변환입니다.
- = + b(a = 1 c = 0 d = 1) {\displaystyle fz) = zquad(a = 1 c = 0 d = 1)}는 번역입니다.
- =(b = 0 c = 0 d = 1) {\displaystyle fz) = quad(b = 0 c = 0 d = 1)}는 호모티와 회전의 조합입니다. = a = 1}이면회전이고, ∈ {\style a\ \mathbb {R}이면 동형 사상입니다.
- ( ) = / (a = 0 b = 1 c = 1 d = 0) {\displaystyle fz) = 1quad(a = 0 b = 1 c = 1 d = 0)} (실축에sion 및 반사)
단순 변환의 구성
≠ 0인 c\n 0 다음을 입력합니다.
- ) = z+ d / c {\displaystyle f_{1(z) = z + quad } (d/c로 번역)
- 2) = 1/ {\displaystyle f_{2(z) = 1 quad } (실축에rsion 및 반사)
- 3) = c - ad c 2 z {\displaystyle f_{3(z) = {\frac {bc-ad}{c^{2quad } (동형 및 회전)
- ) = z+ a / c {\displaystyle f_{4(z) = z+quad } (a/c로 번역)
그런 다음 이 함수를 구성하여 다음과 같이 표시할 수 있습니다.
이러한 분해는 뫼비우스 변환의 많은 특성을 명확하게 합니다.
기본 속성
뫼비우스 변환은 일련의 단순한 변환과 같습니다. 구성은 뫼비우스 변환의 많은 특성을 명확하게 합니다.
역변환 공식
역 뫼비우스 변환의 존재와 그것의 명시적인 공식은 더 단순한 변환의 역함수의 구성에 의해 쉽게 도출됩니다. 즉i, 각i g가 f의 역이 되도록4 함수 g1, g2, g3, g를 정의합니다. 그러면 구성이.
각도와 일반화된 원의 보존
이러한 분해로부터, 우리는 뫼비우스 변환이 원 반전의 모든 사소한 특성을 수행한다는 것을 알 수 있습니다. 예를 들어, 각도 보존은 각도를 보존하는 확장과 등각선(번역, 반사, 회전)이기 때문에 원 반전이 각도를 보존한다는 것을 증명하기 위해 축소됩니다.
또한 뫼비우스 변환은 일반화된 원과 일반화된 원을 매핑하는데, 이는 원 반전이 이러한 특성을 가지고 있기 때문입니다. 일반화된 원은 원 또는 선이며, 후자는 무한대의 점을 통과하는 원으로 간주됩니다. 뫼비우스 변환이 반드시 원을 원에, 선을 선에 매핑하는 것은 아니며, 두 개를 혼합할 수 있습니다. 원을 다른 원에 매핑하더라도 반드시 첫 번째 원의 중심을 두 번째 원의 중심에 매핑할 필요는 없습니다.
교차비율보존
교차 비율은 뫼비우스 변환 하에서 불변입니다. 즉, 뫼비우스 변환이 4개의 서로 다른 점 1 z 를 의 서로 다른 점 w , w 4 {\displaystyle 를 매핑하면,
점 중 하나가 무한대에 있는 점인 경우 교차 비율은 제한을 사용하여 정의해야 합니다. 예를 들어, 1, 2 ∞ 2}, {3infty}의 교차 비율은 다음과 같습니다.
네 개의 다른 점들의 교차비는 선이나 원이 그들을 통과하는 경우에만 실제입니다. 이것은 뫼비우스 변환이 일반화된 원을 보존한다는 것을 보여주는 또 다른 방법입니다.
공액
일반화된 원 D가1 z와2 z를 통과하고 두 점 a와 b에서 C를 절단하는 경우 (z1, z; a, b), (z, z2; a, b)는 조화 교차비(즉, 그들의 교차비는 -1)일 때, 두 점 z와1 z는2 일반화된 원 C에 대해 켤레입니다. 이 속성은 원 D의 선택에 의존하지 않습니다. 이 속성은 선 또는 원에 대해 대칭이라고도 합니다.[3][4]
두 점 z, z는∗ 선에 대해 대칭인 경우 선에 대해 공액입니다. 두 점은 원에 대해 공역을 하면 원에 대해 공역을 합니다.
점∗ z는 L이 점 z에서0 e에iθ 기초하여 벡터에 의해 결정되는 선일 때 z에 켤레입니다. 이것은 명시적으로 다음과 같이 나타낼 수 있습니다.
C가 z를0 중심으로 하는 반지름 r의 원일 때, 점 z는∗ z에 켤레입니다. 이것은 명시적으로 다음과 같이 나타낼 수 있습니다.
뫼비우스 변환은 일반화된 원과 교차 비율을 보존하기 때문에 결합도 보존합니다.
투영 행렬 표현
뫼비우스 군과 PGL 간의 동형
복소 사영선 CP에1 대한 PGL(2, C)의 자연 작용은 정확히 리만 구에 대한 뫼비우스 군의 자연 작용입니다.
복소 사영선과 리만 구면의 대응
여기서 사영선 CP와1 리만 구는 다음과 같이 식별됩니다.
여기서 [z:z]는 CP의 동차 좌표이며, 점 [1:0]은 리만 구의 점 ∞에 해당합니다. 뫼비우스 변환과 관련된 많은 계산은 동차 좌표를 사용함으로써 단순화될 수 있습니다. 왜냐하면 ∞를 다루는 경우의 구별이 필요하지 않기 때문입니다.
복소 사영선에 대한 PGL(2, C)의 작용
모든 가역적 복소수 2×2 행렬
결과는 그러므로
위의 항등식을 이용하면 리만 구 위의 다음과 같은 점에 해당합니다.
리만 구면에서 뫼비우스 변환과 동치
위 행렬은 그것의 행렬식 ad - bc가 0이 아닌 경우에만 가역적이기 때문에, 이것은 복잡한 사영선에서 PGL(2, C)의 작용과 함께 뫼비우스 변환 그룹의 작용의 식별을 유도합니다. 이 식별에서 위 행렬 는 뫼비우스 변환 ↦ az + b + . {\ z to cz+d}}에 해당합니다.
식별은H {\{\ {와 0이 아닌 스칼라λ displaystyle \lambda }의 곱셈이 PGL(2, C)의 요소를 변경하지 않으며, 이 곱셈이 모든 행렬에λ \lambda,이는 해당 뫼비우스 변환을 변경하지 않습니다.
기타그룹
임의의 필드 K에 대하여, 사영 선형 자기 동형의 그룹 PGL(2, K)을 부분 선형 변환의 그룹과 유사하게 식별할 수 있습니다. 이것은 예를 들어 광학에서 실제 선의 호모그래피와 그 응용에 대한 연구에 널리 사용됩니다.
를 행렬식의 제곱근으로 나누면 행렬식 1을 얻을 수 있습니다. 이것은± 를 커널로 하는 특수 선형 그룹 SL(2, C)에서 PGL(2, C)로 주관적 그룹 동형을 유도합니다.
이를 통해 뫼비우스 군이 3차원 복소 리 군(또는 6차원 리얼 리 군)이며, 이는 반단순하고 비콤팩트한 군이며, SL(2,C)이 PSL(2,C)의 이중 피복임을 알 수 있습니다. SL(2, C)은 단순히 연결되어 있기 때문에 뫼비우스 군의 보편 피복이며, 뫼비우스 군의 기본 군은 Z입니다2.
변환을 3점으로 지정
리만 구면에 세 개의 구별점 z1, 3{\집합과 두 번째 구별점 3 집합이 주어지면 j = 1, 2, 3 {\displaystyle j=1, 2, 3}에 대해 j = j f(z_{j})= w_{j}}를 갖는 뫼비우스 변환 ( 가 정확히 하나 존재합니다. (즉, 리만 구에 대한 뫼비우스 군의 작용은 급격하게 3-일시적입니다.) 점 집합에서 f f를 결정하는 몇 가지 방법이 있습니다.
0, 1, ,로 먼저 매핑
뫼비우스 변환을 쉽게 확인할 수 있습니다.
행렬이 있는
1, z {\ ∞, 0, 1 {\infty,}를 매핑합니다. 중 ∞ {\infty}인 경우, 다음 의 것으로부터 {\{\에 대한 적절한 공식을 구합니다. 먼저 모든 엔트리를 zj 로 나눈 다음 z →∞ {\{j}\toinfty}를 취합니다
If is similarly defined to map to then the matrix which maps ~ 가 됩니다.
∞ } {\displaystyle \{0, 1,\infty \}(순서화되지 않은 집합)의 안정기는 하모닉 그룹으로 알려진 하위 그룹입니다.
명시적 행렬식
방정식이.
표준 쌍곡선의 방정식과 같습니다.
-평면에서. The problem of constructing a Möbius transformation mapping a triple to another triple is thus equivalent to finding the coefficients c, d} 점( 을 지나는 쌍곡선의 ab,c 명시적인 방정식은 행렬식을 평가함으로써 찾을 수 있습니다.
첫 번째 줄을 따라 라플라스 확장을 통해. 그 결과 행렬식이 생성됩니다.
행렬 =(b d ) {\ {H}} = {\begin{pmatrix}a&b\c&d\end{pmatrix}}의 a b d displaystyle c, d입니다. The constructed matrix has determinant equal to which does not resp. j 가 쌍으로 다르므로 뫼비우스 변환이 잘 정의되어 있으면 사라집니다. j{\ wj {\w_} 중 ∞ {\\infty}인 경우, 먼저 4개의 결정 요소를 모두 이 변수로 나눈 다음 변수가 ∞ {\displaystyle \infty}에 가까워질 때 한계를 취합니다.
뫼비우스 군의 부분군
뫼비우스 변환의 계수 a,,, a,, 가 d - = displaystyle ad-bc = 1}인 실수가 필요하면 PSL(2, R)로 표시된 뫼비우스 그룹의 하위 그룹을 얻습니다. 이것은 상위 반평면 H = x + iy : y > 0을 자신에게 매핑하는 뫼비우스 변환의 그룹이며, 모든 생체형(또는 동등하게: 양방향, 등각 및 방향 보존) 맵 H → H의 그룹과 동일합니다. 적절한 메트릭이 도입되면, 상위 반평면은 쌍곡면 H의2 모델이 되고, Poincaré 반평면 모델이 되며, PSL(2, R)은 이 모델에서 H의2 모든 방향 보존 등각의 그룹입니다.
열린 원반 D = z : z < 1 을 자신에게 매핑하는 모든 뫼비우스 변환의 부분군은 모든 형태의 변환으로 구성됩니다.
위의 두 부분군은 모두2 H의 등각군 역할을 하므로 동형입니다. 변환과 결합하여 구체적인 동형이 주어집니다.
또는 ri를 중심으로 반지름이 r인 열린 디스크를 고려합니다. 이 디스크의 Poincaré 디스크 모델은 r이 ∞에 가까워질수록 상위 반평면 모델과 동일합니다.
뫼비우스 군 {M의 최대 콤팩트 부분군은 다음과 같습니다(Tóth 2002).[5]
펠릭스 클라인(Felix Klein)은 뫼비우스 변환의 20면체 그룹을 사용하여 (Klein 1913)의 5차 방정식에 대한 분석적 해결책을 제시했습니다. (Tóth 2002)에 현대적인 설명이 제공됩니다.[6]
뫼비우스 변환의 계수 a, b, c, d가 ad - bc = 1인 정수가 필요한 경우 복잡한 평면의 격자, 타원 함수 및 타원 곡선 연구에서 중요한 PSL(2, R)의 이산 하위 그룹인 모듈 그룹 PSL(2, Z)을 얻습니다. PSL의 이산 부분군(2, R)을 푹시안 군(Fuchsian group)이라고 하며, 이들은 리만 표면 연구에서 중요합니다.
분류

다음 논의에서는 항상 표현 행렬 가 H = - b = \det {\mathfrak {H} = ad-bc = 1}이 되도록 정규화되었다고 가정합니다.
비동일성 뫼비우스 변환은 일반적으로 포물선, 타원형, 쌍곡선 및 록소드로믹의 네 가지 유형으로 분류되며 쌍곡선은 록소드로믹의 하위 클래스입니다. 분류는 대수적 및 기하학적 의미를 모두 가지고 있습니다. 기하학적으로 다른 유형은 아래 그림에서 보여주는 것처럼 복잡한 평면의 다른 변환을 초래합니다.
트레이스 H = + d {\displaystyle \operatorname {tr} {\mathfrak {H}}= a+d}를 보면 4가지 유형을 구분할 수 있습니다. 궤적은 공액 하에서 불변입니다. 즉,
포물선 변환
행렬식 1의 H{\{\로 정의된 비 항등식 뫼비우스 변환은 포물선이라고 합니다. 다음과 같습니다.
에서 주어진 고정점을 갖는 모든 포물선 뫼비우스 변환의 집합은항등식과 함께 부분군을 형성합니다.
특성상수
포물선이 아닌 모든 변환은 두 개의 고정된 점을 가지며 다음과 같은 행렬에 의해 정의됩니다.
타원 변환

이 변환은 그 이실수인 H {\H}}로 표현될 수 있다면 타원형이라고 합니다
변환은 λ = 1이고 λ ≠ ±1인 경우에만 타원형입니다. λ = eiα {\displaystyle \ lambda = e^{i\alpha}} 쓰기, 타원 변환은 다음에 공액됩니다.
특성 상수가 k인 의 H 에 대하여 의 특성 상수는 k입니다n. 따라서 유한한 순서의 모든 뫼비우스 변환은 타원 변환, 즉 정확히 λ이 통합의 뿌리인 경우 또는 동등하게 α가 π의 합리적 배수인 경우입니다. 분수 다중 평균 α = π/2의 가장 단순한 가능성은 tr H = 0 {\displaystyle \operatorname {tr} {\mathfrak {H}}=0}의 고유한 이기도 하며, 이는 기하학적으로 약 2개의 고정점에 대해 180° 회전하는 것과 일치합니다. 이 클래스는 행렬 형태로 표시됩니다.
쌍곡 변환
만약 이 변환이 그 이실수인 H {\ {H}}로 표현될 수 있다면 쌍곡선이라고 합니다
변환은 λ가 실제이고 λ ≠가 ±1인 경우에만 쌍곡선입니다.
록소드로믹 변환
은 H { ^{ {H}}가 [0, 4]에 없으면 loxodromic이라고 합니다. 변환은λ ≠ 1 {\ \n인 경우에만 loxodromic입니다. 1
역사적으로 록스로드롬이나 마름모선에 의한 항해는 일정한 베어링의 경로를 의미합니다. 그 결과 생성된 경로는 로그 나선형으로 록스드로믹 뫼비우스 변환이 만드는 복잡한 평면의 변환과 유사한 형태입니다. 아래의 기하학적 도형을 참조하십시오.
일반구분
| 변신 | 트레이스 제곱 | 승수 | 학급대표 | |
|---|---|---|---|---|
| 원형 | σ = 0 | k = -1 | z ↦-z | |
| 타원형 | 0 ≤ σ < 4 | k = 1 | z ↦ z | |
| 포물선 | σ = 4 | k = 1 | z ↦ z + a | |
| 쌍곡 | 4 < σ < | z ↦ z | ||
| Loxodromic | σ ∈ C \ [0,4] | z ↦ kz | ||
실제 사례와 용어에 대한 주석
실수 위에서는 (계수가 실제여야 하는 경우) 쌍곡선이 아닌 록소드로믹 변환이 없으며 분류는 실제 원뿔의 경우와 같이 타원형, 포물선 및 쌍곡선으로 구성됩니다. 이 용어는 trace의 절대값인 tr /2의 절반을 변환의 편심으로 간주하기 때문입니다 – 차원에 대해 2로 나눈 것이 수정되므로 항등식이 편심도 1을 갖습니다(이 때문에 tr / n은 때때로 trace의 대안으로 사용됩니다). 그리고 절대값은 PSL 작업으로 인해 ±1의 인자까지만 정의된 트레이스에 대해 수정됩니다. 또는 위에서 수행한 것과 같이 이심률 제곱의 절반을 이심률 제곱의 대용으로 사용할 수도 있습니다. 이러한 분류는 실제 이심률과 일치하지만(제곱과 절대값이 다르기 때문에 정확한 이심률 값은 아닙니다) 복잡한 이심률은 아닙니다. SL(2, R)의 요소를 분류하는 데에도 동일한 용어가 사용되며(2중 덮개), 다른 곳에서도 유사한 분류가 사용됩니다. 록소드로믹 변환은 본질적으로 복잡한 현상이며 복잡한 이심률에 해당합니다.
특성상수의 기하학적 해석
다음 그림은 (구면에서 평면으로 입체 변환 후) 포물선이 아닌 경우의 뫼비우스 변환의 두 고정점을 보여줍니다.
특성 상수는 로그로 나타낼 수 있습니다.
타원 변환
ρ = 0이면 고정된 점들은 매력적이지도 않고 반발적이지도 않고 무관심하며, 변환은 타원형이라고 합니다. 이러한 변환은 고정된 두 점을 중심으로 원의 모든 점을 이동하는 경향이 있습니다. 고정된 점들 중 하나가 무한대에 있다면, 이것은 한 점을 중심으로 아핀 회전을 하는 것과 같습니다.
타원형 뫼비우스 변환에 의해 생성된 하나의 모수 부분군을 취하면 연속 변환을 얻어 부분군의 모든 변환이 동일한 두 점을 고정합니다. 다른 모든 점들은 리만 구면의 두 고정점 사이에 내포된 원의 계열을 따라 흐릅니다. 일반적으로 두 고정점은 서로 다른 두 점이 될 수 있습니다.
이것은 중요한 물리적 해석을 가지고 있습니다. 어떤 관측자가 어떤 축을 중심으로 일정한 각속도로 회전한다고 상상해 보세요. 그러면 우리는 두 고정점을 천구의 북극점과 남극점으로 잡을 수 있습니다. 이제 밤하늘의 모양은 고정점 0, ∞ 및 관찰자의 일정한 각속도에 해당하는 숫자 α를 공유하는 타원 변환의 단일 매개변수 하위 그룹에 의해 설명된 방식으로 정확히 연속적으로 변형됩니다.
다음은 평면에 입체 사영된 후에 타원형 뫼비우스 변환이 리만 구에 미치는 영향을 보여주는 몇 가지 그림입니다.
이 그림들은 단일 뫼비우스 변환의 효과를 보여줍니다. 생성되는 1-매개변수 부분군은 그림에서 제안하는 원형 호 계열을 따라 점을 연속적으로 이동합니다.
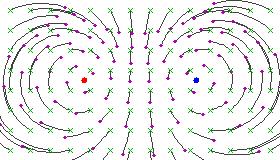
쌍곡 변환
α가 0(또는 2 π의 배수)이면 변환은 쌍곡선이라고 합니다. 이러한 변환은 한 고정점에서 다른 고정점으로 원형 경로를 따라 점을 이동하는 경향이 있습니다.
쌍곡 뫼비우스 변환에 의해 생성된 1-모수 부분군을 취하면 부분군의 모든 변환이 동일한 두 점을 고정하도록 연속 변환을 얻을 수 있습니다. 다른 모든 점들은 첫 번째 고정점에서 벗어나 두 번째 고정점을 향해 원형 호들의 특정 계열을 따라 흐릅니다. 일반적으로 두 고정점은 리만 구면 위의 임의의 두 개의 별개의 점일 수 있습니다.
이것도 중요한 물리적 해석이 있습니다. 관측자가 자신의 천체에 있는 북극 방향으로 (일정한 가속도 크기로) 가속한다고 상상해보세요. 그런 다음 밤하늘의 모양은 고정점 0, ∞를 공유하는 쌍곡 변환의 단일 매개변수 하위 그룹이 설명한 방식으로 정확히 변환되며 실수 ρ는 그의 가속 벡터 크기에 해당합니다. 별들은 남극에서 북극으로 갈수록 경도를 따라 움직이는 것으로 보입니다. (그 경도는 구면에서 평면까지 입체 사영하에서 원형의 호로 나타납니다.)
다음은 (평면에 입체 사영된 후) 리만 구에 쌍곡 뫼비우스 변환이 미치는 영향을 보여주는 몇 가지 그림입니다.
이 그림들은 고정점에 위치한 양전하와 음전하의 필드선과 유사한데, 원형 흐름선은 두 고정점 사이의 일정한 각도에 속하기 때문입니다.
록소드로믹 변환
ρ와 α가 모두 0이 아닌 경우 변환은 록소드로믹이라고 합니다. 이러한 변환은 S자형 경로의 모든 점을 한 고정점에서 다른 고정점으로 이동하는 경향이 있습니다.
"록스로드롬"이라는 단어는 그리스어에서 유래했습니다: "λοξος (록소스), 기울어짐 + οςμ δρό (드로모스), 코스". 일정한 베어링으로 항해할 때 - 만약 여러분이 (예를 들어) 북동쪽 방향을 유지한다면, 결국 여러분은 로그 나선형으로 북극 주위를 항해하게 될 것입니다. 메르카토르 투영법에서 북극과 남극은 무한대로 투영되기 때문에 이러한 코스는 직선입니다. 록스로드롬이 경도의 선에 대해 상대적으로 기울어지는 각도(즉, 기울기, 나선의 "조임")는 k의 인수입니다. 물론 뫼비우스 변환은 북극과 남극만이 아니라 어디에서나 두 개의 고정점을 가질 수 있습니다. 그러나 모든 록소드로믹 변환은 그러한 록소드로믹을 따라 모든 점을 이동하는 변환에 결합될 것입니다.
임의의 록소드로믹 뫼비우스 변환에 의해 생성된 1-모수 부분군을 취하면, 부분군의 모든 변환이 동일한 두 점을 고정하도록 연속 변환을 얻습니다. 다른 모든 점들은 첫 번째 고정점에서 벗어나 두 번째 고정점을 향해 특정 곡선 계열을 따라 흐릅니다. 쌍곡의 경우와 달리, 이 곡선들은 원형의 호가 아니라, 구면에서 평면으로 입체 사영되는 특정 곡선들은 한 고정점을 중심으로 반시계 방향으로 종종 비틀리고 다른 고정점을 중심으로 종종 시계 방향으로 비틀리는 나선형 곡선으로 나타납니다. 일반적으로 두 고정점은 리만 구면 위의 임의의 두 개의 별개의 점일 수 있습니다.
두 고정점이 0, ∞일 때 물리적 해석을 추측할 수 있습니다. 어떤 축을 중심으로 회전하고 (각속도가 일정한) 같은 축을 따라 움직이는 관측자. 고정점 0, ∞ 및 ρ, α가 각각 실제 선형 및 각속도의 크기에 의해 결정되는 록소드로믹 변환의 1-매개변수 부분군에 따라 밤하늘 변환의 모습을 볼 수 있습니다.
입체 사영
이 이미지는 뫼비우스 변환이 리만 구에 입체적으로 투영된 것을 보여줍니다. 특히 구면에 투영될 때 무한대의 고정점이라는 특수한 경우는 임의의 위치에 고정점이 있는 것과 다르지 않게 보입니다.
| 무한대의 한 고정점 | ||
 |  |  |
| 정반대의 고정점 | ||
 |  |  |
| 임의의 위치에 고정된 점 | ||
 |  |  |
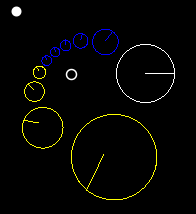
변환 반복
If a transformation has fixed points γ1, γ2, and characteristic constant k, then will have {2}' _{2},k'k^{n}}.
변환을 반복하거나 단계로 나누어 애니메이션화하는 데 사용할 수 있습니다.
이 이미지는 다양한 특성 상수를 사용한 변환에서 연속적으로 반복되는 세 개의 점(적색, 파란색 및 검은색)을 보여줍니다.
 |  |  | |
그리고 이 이미지들은 쌍곡, 타원, 록소드로믹 변환 하에서 원을 변환할 때 어떤 일이 일어나는지 보여줍니다. 타원 및 록소드로믹 이미지에서 α 값은 1/10입니다.
고차원
고차원에서 뫼비우스 변환은 ¯ { n}}의 동형화이며, {R ^{n의 한 점 이며, 이는 구면의 반전과 초평면의 반사의 유한한 구성입니다. 등각기하학에서 리우빌의 정리는 적어도 3차원에서 모든 등각 변환은 뫼비우스 변환이라는 것을 말합니다. 모든 뫼비우스 변환은 형태에 넣을 수 있습니다.
서 ∈ R a,bin \mathbb {R} ^{n}}, α ∈ R {\displaystyle \alpha \in \mathbb {R}, A {\displaystyle A}는 직교 행렬이고, ε {\displaystyle \varepsilon }는 0 또는 2입니다. 뫼비우스 변환의 군은 뫼비우스 군이라고도 합니다.[8]
방향성을 보존하는 뫼비우스 변환들은 뫼비우스 그룹에서 아이덴티티의 연결된 구성 요소를 형성합니다. 차원 n = 2에서, 방향 보존 뫼비우스 변환은 바로 여기서 다루는 리만 구의 지도입니다. 방향을 역전시키는 것들은 이것들로부터 복잡한 접합에 의해 얻어집니다.[9]
변환의 도메인, 즉 ¯{\ mathbb {R} ^{n}}}는 n차원 구 Sn {\displaystyle S^{n}}와 동형입니다. 이 두 공간 사이의 표준 동형은 케일리 변환이며, 그 자체는 + 1 ¯ R^{n1}}의 뫼비우스 변환입니다. 이 식별은 뫼비우스 변환이 의 등각 동형으로도 생각할 수 있음을 의미합니다 n-구면은 뫼비우스 군의 작용과 함께 뫼비우스 기하학이라고 불리는 (클라인의 에를랑겐 프로그램의 의미에서) 기하학적 구조입니다.[10]
적용들
로런츠 변환
로렌츠 그룹과 뫼비우스 그룹의 동형화는 몇몇 저자들에 의해 주목되었습니다: 펠릭스 클라인(Felix Klein, 1893, 1897)[11]이 쌍곡 기하학과 뫼비우스 기하학과 관련된 자동적 함수에 대한 이전 연구에 기초하여, 구스타프 헤르글로츠(Gustav Herglotz, 1909)[12]는 쌍곡 운동(즉, 쌍곡 운동)을 보여주었습니다. 쌍곡 공간의 등각 자기 동형화) 단위 구를 그 자체로 변환하는 것은 로런츠 변환에 해당하며, 이를 통해 헤르글로츠는 하나의 매개 변수 로런츠 변환을 록소드로믹, 타원형, 쌍곡 및 포물선 그룹으로 분류할 수 있었습니다. 다른 작가들로는 에밀 아르틴 (1957),[13] H. S. M. 콕서터 (1965),[14] 로저 펜로즈, 볼프강 린들러 (1984),[15] 트리스탄 니덤 (1997)[16] 그리고 W. M. 올리비아 (2002)가 있습니다.[17]
민코프스키 공간은 실수들의 순서화된 4배의 공간(x0, x, x123, x)으로 이루어진 4차원 실수 좌표 공간 R과4 2차 형식으로 구성됩니다.
특수 상대성 이론에서 용어를 빌려 Q > 0인 점은 시간과 동일한 것으로 간주됩니다. 또한 x0 > 0인 경우 해당 점을 미래 점이라고 합니다. Q < 0인 점을 공간과 같다고 합니다. 널 원뿔 S는 Q = 0인 점들로 구성됩니다. 미래의 널 원뿔 N은 x > 0인 널 원뿔의 점들입니다. 그런 다음 천구는 R의4 원점이 되는 N의+ 광선 모음으로 식별됩니다. 2차 형태 Q를 보존하고 시간 방향을 보존하는 양의 행렬식을 갖는 R에4 대한 선형 변환의 집합은 제한된 로렌츠 그룹 SO+(1, 3)를 형성합니다.
천구의 기하학과 관련하여, 변환의 그룹+ SO(1, 3)는 구의 뫼비우스 변환의 그룹 PSL(2, C)과 동일시됩니다. 각 (x, x, x, x) ∈ R에 에르미트 행렬을 연결합니다.
행렬 X의 행렬식은 Q(x0, x, x1, x2)와 같습니다3. 특수 선형군은 다음을 통해 이러한 행렬의 공간에 작용합니다.
-
(1)
각 A ∈ SL(2, C)에 대하여, 그리고 SL(2, C)의 이 작용은 det A = 1이기 때문에 X의 행렬식을 보존합니다. X의 행렬식은 2차 형식 Q와 동일하므로, SL(2, C)는 로런츠 변환에 의해 작용합니다. 차원적 근거에서 SL(2, C)은 SO(1, 3)의 아이덴티티의 이웃을 커버합니다. SL(2, C)가 연결되어 있기 때문에 제한된 로렌츠 그룹 SO+(1, 3) 전체를 커버합니다. 또한 작용 (1)의 커널은 부분군 {±I}이므로, 몫군으로 전달하면 군 동형 사상이 됩니다.
-
(2)
이제 (x, x, x, x)가 null일 때 행렬 X는 0의 행렬식을 가지므로 복소 켤레를 갖는 복소 2-벡터 ξ의 외부 곱으로 분할됩니다.
-
(3)
2성분 벡터 ξ은 SL(2, C)에 의해 (1)과 호환되는 방식으로 작용합니다. 이제 에르미트 행렬에서의 SL(2, C) 표현의 커널은 {±I}임이 분명합니다.
천체에 대한 PSL(2, C)의 작용도 입체 투영을 사용하여 기하학적으로 설명할 수 있습니다. 먼저 x = 1로 주어진 R의 초평면을 생각해 보자. 천구는 미래의 널콘 N과+ 초평면의 교점의 구 S와+ 식별될 수 있습니다. 이 구의 북극 (1, 0, 0, 1)에서 평면 x = 0으로 입체 사영하는 것은 좌표 (1, x, x, x)와 한 점을 취합니다.
복소좌표 소개
-
(4)
N의 점에 대한 SO(1, 3)의 작용은 초평면 S를 보존하는 것이 아니라 S의 점에 작용한 다음 다시 S의 결과가 되도록 재스케일링하는 것은 구에 대한 SO(1, 3)의 작용을 제공하고 이는 복소 변수 ζ에 대한 작용으로 이어집니다. 사실, 이 작용은 부분적인 선형 변환에 의한 것이지만, 이것은 천구의 이 표현에서 쉽게 볼 수 없습니다. 반대로, ζ 변수의 부분 선형 변환의 경우, 적합한 (유일하게 결정된) 재스케일 후에 N에 대한 고유한 로렌츠 변환으로 넘어갑니다.
동작을 더 명확하게 볼 수 있게 해주는 입체 사영에 대한 더 불변의 설명은 변수 ζ = z:w를 복소 사영선 CP에 대한 한 쌍의 균질 좌표의 비율로 고려하는 것입니다. 입체 사영은 C2 - {0}에서 N으로의+ 변환으로 이어지는데, 이 변환은 실제 스케일링에 대해 2도 동차입니다.
-
(5)
가 ¯ + ¯ = 1. {\displaystyle z{\bar {z}+w{\ {w}}= 1.}인 눈금에 대한 제한은 (4)와 일치합니다. (5)의 구성 요소는 정확하게 외부 제품에서 얻은 것입니다.
요약하면, 제한된 로렌츠 그룹 SO+(1,3)의 작용은 뫼비우스 그룹 PSL(2,C)의 작용과 일치합니다. 이는 다음과 같은 정의에 동기를 부여합니다. 차원 n ≥ 2에서 뫼비우스 군 뫼브(n)는 자신에 대한 원 구 S의 모든 방향 보존 등각선 군입니다. 등각구를 민코프스키 공간 R에서1,n+1 널콘의 미래 지향 광선의 공간으로 구현함으로써, 양의 행렬식을 갖는 로런츠 변환의 제한된 로런츠+ 그룹 SO(1,n+1)를 갖는 뫼브(n)의 동형화가 존재하여 시간의 방향을 보존합니다.
콕서터는 대신 등가 이차 형식 Q 2 3 = x + x + x 32 - x 42로 시작했습니다. {\displaystyle Q(x_{1},\x_{2},\x_{3}\x_{4}) = x_{1}^{2}+x_{2)
그는 {x : Q(x) = -1}가 안정적인 변환을 가진 로렌츠 군을 확인했습니다. 그런 다음 그는 x를 동차 좌표로 해석하고 {x : Q(x) = 0}, 널콘을 {x : Q(x) < 0}의 쌍곡선 공간에 대한 케일리 절대값으로 해석했습니다. 그 다음, 콕서터는 변수들을 소개했습니다.
따라서 로렌츠 불변 사차원은 구ξ2 + η 2 +ζ 2 =에 해당합니다{\displaystyle \xi ^{2}+\eta ^{2}+\zeta ^{2}= 1.} 콕서터는 펠릭스 클라인이 (0, 0, 1)의 입체 사영을 복소 평면 z = ξ + i η 1 - ζ에 적용하여 이 대응에 대해 작성했다고 언급합니다.z={\ 콕서터는 역평면의 원이 쌍곡 공간의 평면을 나타내고 일반적인 호모그래피는 두 개 또는 네 개의 원에 있는 역의 곱이며, 이는 두 개 또는 네 개의 평면에 있는 역의 곱인 일반적인 쌍곡 변위에 해당합니다.
쌍곡선 공간
위에서 본 바와 같이 뫼비우스 군 PSL(2, C)은 민코프스키 공간에 원점, 공간의 방향 및 시간의 방향을 보존하는 등각선의 군으로 작용합니다. 쌍곡 3-공간 H의 모델을 형성하는 양의 빛 원뿔에서 Q = 1이 있는 지점으로 제한하여 뫼비우스 그룹이 H에 방향 보존 등각의 그룹으로 작용한다는 것을 알 수 있습니다. 사실, 뫼비우스 군은 쌍곡 3-공간의 방향 보존 등각들의 군과 같습니다.
푸앵카레 볼 모델을 사용하면, R의3 단위 공을 H와3 동일시하면, 우리는 리만 구를 H의3 "등각 경계"로 생각할3 수 있습니다. H의 모든 방향 보존 등각계는 리만 구에서 뫼비우스 변환을 일으키고, 그 반대의 경우도 마찬가지입니다. 이것은 물리학에서 AdS/CFT 대응 추측으로 이어지는 첫 번째 관찰입니다.
참고 항목
메모들
참고문헌
특정한
- ^ Arnold & Rogness 2008, 정리 1.
- ^ Needham, Tristan (2021). Differential Geometry and Forms; A Mathematical Drama in Five Acts. Princeton University Press. p. 77, footnote 16. ISBN 9780691203690.
- ^ Olsen, John, The Geometry of Mobius Transformations (PDF)
- ^ Weisstein, Eric W. "Symmetric Points". MathWorld.
- ^ Tóth 2002, 섹션 1.2, 회전과 뫼비우스 변환, p. 22.
- ^ Tóth 2002, Section 1.6, 추가 주제: 클라인의 정이십면체 이론, 66쪽.
- ^ Iwaniec, Tadeusz and Martin, Gaven, Liouville 정리, 해석과 위상학, 339–361, World Sci. NJ, River Edge, Public., 1998
- ^ J.B. Wilker (1981) "역기하학", MR0661793
- ^ Berger, Marcel (1987), Geometry II, Springer (Universitext), p. 18.10
- ^ Akivis, Maks; Goldberg, Vladislav (1992), Conformal differential geometry and its generalizations, Wiley-Interscience
- ^ 펠릭스 클라인(Felix Klein, 1893), 니치트-에우클리디스케 지오메트리, 오토그 볼, 괴팅겐;
로버트 프리크 & 펠릭스 클라인(1897), 오토모프 펑크티온 I., 튜브너, 라이프치히 - ^ Herglotz, Gustav (1910) [1909], "Über den vom Standpunkt des Relativitätsprinzips aus als starr zu bezeichnenden Körper" [On bodies that are to be designated as 'rigid' from the relativity principle standpoint], Annalen der Physik (in German), 336 (2): 393–415, Bibcode:1910AnP...336..393H, doi:10.1002/andp.19103360208
- ^ 에밀 아르틴(Emil Artin, 1957) 기하 대수학, 204페이지
- ^ H. S. M. 콕서터(H. S. M. Coxeter) (1967) "로런츠 그룹과 호모그래피의 그룹", L. G. Kovacs & B. H. Neumann (편집자) 1965년 8월 10일-20일 호주 캔버라 국립대학에서 열린 그룹 이론 국제 회의 절차, Gordon and Breach Science Publishers
- ^ Penrose & Rindler 1984, 8-31쪽.
- ^ Needham, Tristan (1997). Visual Complex Analysis (PDF). Oxford: Oxford University Press. pp. 122–124.
- ^ Olivia, Waldyr Muniz (2002). "Appendix B: Möbius transformations and the Lorentz group". Geometric Mechanics. Springer. pp. 195–221. ISBN 3-540-44242-1. MR 1990795.
일반
- Arnold, Douglas N.; Rogness, Jonathan (2008), "Möbius Transformations Revealed" (PDF), Notices of the AMS, 55 (10): 1226–1231
- Beardon, Alan F. (1995), The Geometry of Discrete Groups, New York: Springer-Verlag, ISBN 978-0-387-90788-8
- Hall, G. S. (2004), Symmetries and Curvature Structure in General Relativity, Singapore: World Scientific, ISBN 978-981-02-1051-9 (로렌츠 군의 리 대수의 리 부분대수의 분류는 6장을 참조하십시오.)
- Katok, Svetlana (1992), Fuchsian Groups, Chicago:University of Chicago Press, ISBN 978-0-226-42583-2 2장을 참조하십시오.
- Klein, Felix (1913) [1st German ed. 1884], Lectures on the icosahedron and the solution of equations of the fifth degree, translated by Morrice, George Gavin (2nd ed.), London: Kegan Paul, Trench, Trübner, & Co. 에서 번역한
- Knopp, Konrad (1952), Elements of the Theory of Functions, New York: Dover, ISBN 978-0-486-60154-0 (리만 구, 입체 사영, 뫼비우스 변환에 대한 아름다운 소개는 이 고전 책의 3~5장을 참조하십시오.)
- Mumford, David; Series, Caroline; Wright, David (2002), Indra's Pearls: The Vision of Felix Klein, Cambridge University Press, ISBN 978-0-521-35253-6 (비수학자를 목표로 하며, 다이어그램으로 풍부하게 설명된 이론과 결과에 대한 탁월한 설명을 제공합니다.)
- Needham, Tristan (1997), Visual Complex Analysis, Oxford: Clarendon Press, ISBN 978-0-19-853446-4 (3장에서 뫼비우스 변환에 대한 아름다운 설명을 참조하십시오. 여기에는 결합까지의 분류가 포함됩니다.)
- Penrose, Roger; Rindler, Wolfgang (1984), Spinors and space–time, Volume 1: Two-spinor calculus and relativistic fields, Cambridge University Press, ISBN 978-0-521-24527-2
- Schwerdtfeger, Hans (1979), Geometry of Complex Numbers, Dover, ISBN 978-0-486-63830-0 (뫼비우스 변환에 대한 소개는 2장을 참조하십시오.)
- Tóth, Gábor (2002), Finite Möbius groups, minimal immersions of spheres, and moduli
더보기
- Lawson, M. V. (1998). "The Möbius Inverse Monoid". Journal of Algebra. 200 (2): 428. doi:10.1006/jabr.1997.7242.

















































![{\displaystyle [z_{1}:z_{2}]\ \thicksim {\frac {z_{1}}{z_{2}}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1b4893a9352becf62e6802c31e40598ca194503f)
![{\displaystyle z=[z_{1}:z_{2}]\mapsto w=[w_{1}:w_{2}],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc5b9ee99389d90b99ce1c3d0b682bd9c989a830)

![{\displaystyle w=[w_{1}:w_{2}]=[az_{1}+bz_{2}:cz_{1}+dz_{2}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7aa8217621ca48fbcf416802b515f547ad12dfbb)
![{\displaystyle w=[az_{1}+bz_{2}:cz_{1}+dz_{2}]\thicksim {\frac {az_{1}+bz_{2}}{cz_{1}+dz_{2}}}={\frac {a{\frac {z_{1}}{z_{2}}}+b}{c{\frac {z_{1}}{z_{2}}}+d}}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b68e27c617b076ebcbb2457d95a94b3bb4ce33c1)











































 n. 따라서
n. 따라서