메르카토르 투영법

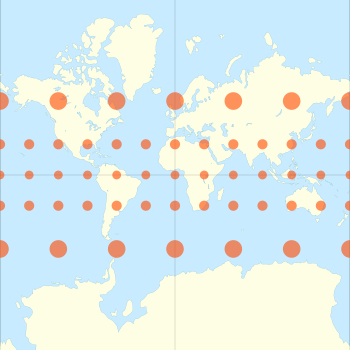
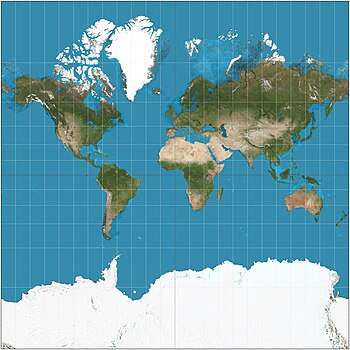
메르카토르 투영법(/mrrkekettrr/)은 1569년 플랑드르 지리학자이자 지도 제작자인 제라르두스 메르카토르가 제시한 원통형 지도 투영법이다.이는 국지적인 방향과 모양을 보존하면서 북쪽을 위아래로, 남쪽을 아래쪽으로 표현하는 것이 독특하기 때문에 항해의 표준 지도 투영법이 되었다.따라서 지도는 적합하다.부작용으로, 메르카토르 투영법은 적도에서 멀리 떨어진 물체의 크기를 팽창시킨다.이 팽창은 적도 부근에서는 매우 작지만 위도가 증가함에 따라 극지방에서는 무한대가 된다.결과적으로, 그린란드와 남극대륙과 같은 육지는 중앙 아프리카와 같은 적도 근처의 육지에 비해 실제보다 훨씬 더 크게 보입니다.

역사

메르카토르의 기원에 대해 약간의 논란이 있다.독일의 박식가 Erhard Etzlaub는 휴대용 주머니 크기의 해시계를 조정할 수 있도록 위도 0°~67°에 걸친 유럽과 아프리카 일부 지역의 축소판 "나침반 지도"(약 10×8cm)를 새겼습니다.이 지도에서 발견된 1511년의 투영도는 1987년 스나이더에^[1] 의해 메르카토르의 투영법과 같은 투영법이라고 진술되었다.하지만, 해시계의 기하학적 구조를 볼 때, 이 지도들은 해시계의 기초인 그노모닉 투영법의 제한적인 경우인 비슷한 중심 원통 투영법에 기초했을지도 모른다.스나이더는 1994년 ^[2]자신의 평가를 "유사 예측"으로 수정했다.

중국의 역사학자 조셉 니덤은 중국이 ^[3]머카토르보다 수백 년 먼저 머카토르 투영법을 개발해 송나라 때 별표에 사용했다고 썼다.그러나 이것은 단순하고 흔한 오인 사례였다.사용 중인 투영법은 등각 투영법이었다.

포르투갈의 수학자이자 우주론자인 페드로 누네스는 처음으로 록소드롬의 수학적 원리와 해양 항해에서의 사용을 설명했다.1537년, 그는 방향의 왜곡을 최소화하기 위한 방법으로 원통형 등거리 투영에 여러 장의 대형 시트로 구성된 항해 지도를 만들 것을 제안했다.만약 이 시트들을 같은 크기로 만들어 조립한다면, 그것들은 메르카토르 투영법에 근접할 것이다.

1569년, 그의 상표명 제라르두스 메르카토르로 알려진 게르하르트 크레머는 가로 202cm, 세로 124cm, 세로 18장으로 인쇄된 거대한 평면구 지도를 출판함으로써 새로운 전망을 발표했다.메르카토르는 "Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata"라는 지도를 "선원 사용을 위해 수정된 새롭고 강화된 지구 기술"이라고 명명했다.이 제목은 지도상의 텍스트 섹션으로 보이는 투영을 사용하는 방법에 대한 정교한 설명과 함께 메르카토르가 정확히 무엇을 달성했는지 이해하고 항해를 돕기 위한 투영을 의도했음을 보여준다.메르카토르는 건축 방법이나 그가 어떻게 그곳에 도착했는지 설명하지 않았다.수년에 걸쳐 여러 가설이 제시되었지만, 어쨌든 페드로 누네스와 메르카토르의 우정과 누네스가 만든 로크소드로믹 테이블에 대한 그의 접근은 그의 노력에 도움을 준 것으로 보인다.

영국의 수학자 에드워드 라이트는 1599년에 투영을 구성하기 위한 최초의 정확한 표를 발표했고, 더 자세히는 1610년에 그의 논문을 "항해의 확실한 오류"라고 불렀다.최초의 수학 공식은 헨리 본드라는 수학자에 의해 1645년경에 발표되었다.그러나 관련된 수학은 1589년 ^[4]경부터 수학자 토마스 해리오트에 의해 개발되었지만 출판되지 않았다.

메르카토르 투영법의 발달은 16세기 항해 지도 제작의 큰 돌파구였다.그러나, 이전의 항법 및 측량 기술은 항법에서의 사용과는 양립할 수 없었기 때문에, 그것은 훨씬 앞선 것이었다.두 가지 주요 문제가 그것의 즉각적인 적용을 막았다: 적절한 정확도로 경도를 결정하는 것의 불가능과 항해에 지리적 방향 대신 자기 방향을 사용했다는 사실.해양 크로노미터가 발명되고 자기편향의 공간 분포가 알려진 18세기 중반이 되어서야 메르카토르 투영법이 항해자들에 의해 완전히 채택될 수 있었다.

이러한 위치 결정 한계에도 불구하고, 메르카토르의 투영법은 메르카토르의 첫 출판 이후 수 세기 동안 많은 세계 지도에서 찾아볼 수 있다.그러나 위치 결정 문제가 크게 해결된 19세기에 이르러서야 세계 지도를 지배하기 시작했다.일단 메르카토르가 상업 및 교육 지도의 일반적인 투영법이 되었을 때, 그것은 대륙의 불균형한 표현과 극지방을 유용하게 보여줄 수 없다는 이유로 지도 제작자들로부터 지속적인 비판을 받았다.

메르카토르의 부적절한 사용에 대한 비판은 19세기 후반과 20세기 초에 메르카토르의 대안으로 직접 선전되는 새로운 발명품들을 낳았다.이러한 압력으로 인해 출판사들은 20세기 동안 프로젝션의 사용을 점차 줄였다.그러나 웹 매핑의 출현으로 웹 메르카토르 투사 형태가 갑자기 부활했습니다.

오늘날 Mercator는 해양 차트, 가끔 세계 지도, 웹 지도 서비스에서 찾을 수 있지만 상업용 지도는 대부분 버려졌고 세계의 벽지도는 많은 대체 투영에서 찾을 수 있습니다.2005년부터 그것에 의존해 온 Google Maps는 여전히 로컬 지역 지도에 그것을 사용하고 있지만, 2017년에 로컬 지역 밖으로 줌 아웃된 지도에 대해서는 데스크톱 플랫폼에서 프로젝션을 삭제했다.다른 많은 온라인 지도 서비스에서는 여전히 Web Mercator를 독점적으로 사용하고 있습니다.

특성.

모든 원통형 투영에서와 마찬가지로 메르카토르의 평행선과 경락은 서로 직각입니다.이를 위해, 적도로부터 거리가 증가함에 따라 증가하는 피할 수 없는 지도의 동-서 연장은 메르카토르 투영에 대응하는 북-남 연장을 동반하므로, 모든 지점에서 동-서 축척이 북-남 축척과 동일하여 등각 지도 투영이다.등각 투영으로 모든 위치의 각도가 유지됩니다.

메르카토르 지도의 선형 축척은 위도에 따라 증가하기 때문에 적도에서 멀리 떨어진 지리적 물체의 크기를 왜곡하고 행성의 전체 기하학적 구조에 대한 왜곡된 인식을 전달한다.북위도 또는 남위도 70° 이상의 위도에서는 극점에서 선형 척도가 무한히 커지기 때문에 메르카토르 투영을 실질적으로 사용할 수 없다.따라서 Mercator 지도는 절대 극지 영역을 완전히 표시할 수 없습니다(지구의 회전 축을 중심으로 한 원통형 투영을 기반으로 하는 한). 다른 용도는 횡단형 Mercator 투영을 참조하십시오).

Mercator 투영법은 일정한 방위각을 가진 모든 선(수학적으로 경맥과 일정한 각도를 이루는 선)을 직선에 매핑합니다.순응성과 직선 마름모꼴이라는 두 가지 특성은 이 투영법을 해양 항해에 독특하게 적합하게 만듭니다. 즉, 코스와 베어링은 풍향 장미 또는 굴절기를 사용하여 측정되며, 지도에서 해당 방향은 평행 자(예: 평행 자)를 사용하여 지점에서 지점으로 쉽게 이동할 수 있습니다.

사이즈의 왜곡

모든 지도 투영에서와 마찬가지로 모양이나 크기는 지구 표면의 실제 배치를 왜곡한 것입니다.

메르카토르 투영법은 적도에서 멀리 떨어진 지역을 과장한다.

크기 왜곡의 예

• 남극대륙은 엄청나게 큰 것으로 보인다.만약 지구 전체가 지도화된다면 남극대륙은 무한히 팽창할 것이다.실제로는 세 번째로 작은 대륙이다.

• 캐나다의 북극 군도 북쪽에 있는 엘즈미어 섬은 호주가 39배 이상 크지만 호주와 거의 같은 크기로 보입니다.캐나다의 북극 군도에 있는 모든 섬들은 적어도 4배는 더 커 보이고, 더 북쪽 섬들은 더 커 보인다.

• 그린란드는 아프리카와 같은 크기로 보이지만 실제로는 아프리카의 면적이 14배나 된다.
  • 그린란드의 실제 면적은 콩고민주공화국의 면적과 맞먹는다.
  • 아프리카는 남아메리카와 거의 같은 크기로 보이지만 실제로는 아프리카가 1.5배 이상 크다.

• 스발바르가 보르네오보다 더 큰 것처럼 보이지만 실제로는 보르네오가 스발바르보다 약 12배 더 크다.

• 알래스카는 호주와 같은 크기인 것처럼 보이지만, 호주는 실제로 호주와 같은 크기이다.4+1/2배의 크기.
  • 알래스카는 또한 지도에서 브라질만큼 많은 지역을 차지하는 반면, 브라질의 면적은 알래스카의 거의 5배이다.

• 마다가스카르와 영국은 거의 같은 크기로 보이는 반면, 마다가스카르는 사실 영국 제도 중 가장 큰 섬보다 두 배 이상 더 크다.
  • 스웨덴은 마다가스카르보다 훨씬 더 큰 것으로 보인다.사실 마다가스카르는 조금 더 크다.

• 러시아는 아프리카 전체 또는 북미보다 더 큰 것으로 보인다.중국과 인접한 미국을 합친 것보다 두 배나 큰 것으로 나타나는데, 실제로는 그 규모가 비슷합니다.
  • 북방 인플레이션은 러시아의 형체를 심하게 왜곡시켜, 러시아의 위도가 중위도에 비해 북에서 남으로 훨씬 더 커 보이고 북극 지역도 크게 확장된다.

비판

국토의 왜곡이 심하기 때문에 일반적인 세계지도에 적합하지 않다는 견해도 있다^[who?].메르카토르 자신은 상대 영역을 나타내기 위해 등면적 사인파 투영법을 사용했다.하지만, 그러한 왜곡에도 불구하고, 메르카토르 투영법은,^[5][6][7][8] 특히 19세기 후반과 20세기 초반에, 이러한 사용에 대한 많은 비판에도 불구하고, 아마도 세계 지도에서 사용되는 가장 일반적인 투영법이었을 것이다.

메르카토르의 매우 일반적인 사용법 때문에, 메르카토르 투영법은 사람들의 ^[9]세계관에 영향을 미쳤다고 여겨져 왔고, 유럽이나 북미에 비해 적도 근처의 나라들이 너무 작다는 것을 보여주기 때문에, 사람들이 그 나라들을 ^[10]덜 중요하게 여기도록 만들었을 것이다.이러한 비판의 결과로, 현대의 지도는 더 이상 세계 지도나 적도에서 멀리 떨어진 지역에 메르카토르 투영법을 사용하지 않으며, 다른 원통 투영법이나 등면적 투영법을 선호한다.그러나 메르카토르 투영법은 여전히 왜곡이 최소인 적도 부근에서 일반적으로 사용됩니다.시간대 지도에서도 자주 볼 수 있습니다.

Arno Peters는 Mercator의 문제를 해결하기 위해 일반적으로 Gall-Peters 프로젝션이라고 불리는 것을 제안하면서 논란을 일으켰고, 1855년부터의 Gall의 작품과 같은 지도 제작자들의 이전 작품들을 참조하지 않고 Mercator의 원래 작품이라고 주장했다.그가 추진한 투영법은 원통형 등면적 투영법의 특정 파라미터화이다.이에 대응하여, 북미 7개 지리적 그룹에 의한 1989년 결의안은 메르카토르와 ^[11]갤-피터를 모두 포함하는 범용 세계 지도에 원통형 투영법을 사용하는 것을 폄하했다.

사용하다

실제로 인쇄된 모든 해양 차트는 항해에 매우 유리한 특성 때문에 메르카토르 투영법에 기초하고 있습니다.온 ^[12]디맨드로 계산된 로컬 영역 지도에 고유하게 유리한 특성 때문에 인터넷에서 호스팅되는 거리 지도 서비스에서도 일반적으로 사용됩니다.메르카토르 투영법은 1960년대 ^[13]판구조론의 수학적 발전에도 중요했다.

해상 항법

Mercator 투영법은 일정한 방향성을 직선 세그먼트로 나타낸다는 독특한 특성 때문에 해양 항해에 사용하도록 설계되었습니다.선박이 일정한 나침반 방향으로 항해할 수 있기 때문에 다른 항로를 항해할 때 자주 필요할 수 있는 어렵고 오류가 발생하기 쉬운 항로 수정을 줄일 수 있기 때문에 해양 항법에서는 럼(rumb, 또는 수학적으로 록소드롬)으로 알려진 이러한 항로가 선호된다.지구 반지름에 비해 거리가 작을 경우, 대원 세그먼트인 기술적으로 가장 짧은 코스와의 차이는 무시할 수 있으며, 거리가 긴 경우에도 일정한 베어링의 단순성이 매력적이다.메르카토르의 관찰대로라면 최단 항로는 도착하지 않지만 반드시 도착한다.항해를 한다는 것은 선원들이 항로를 일정하게 유지하기만 하면 된다는 것을 의미했습니다.항로를 계속 유지하기만 하면 됩니다.항로를 언제 출발할지, 목적지를 알 수 있고, 메르카토르 투영법에서 두 개의 ^{[citation needed]}좌표를 정확하게 보여주는 지도가 있으면 됩니다.

Web Mercator

많은 주요 온라인 거리 지도 서비스(Bing Maps, Google Maps, Mapbox, MapQuest, OpenStreetMap, Yahoo!) 지도 등)는 지도 이미지에^{[citation needed]} Web Mercator 또는 Google Web Mercator라는 변형 Mercator 투영법을 사용합니다.이 투영법은 소규모로 확연한 변동에도 불구하고 대규모(로컬) 지도에 심리스하게 확대/축소할 수 있는 인터랙티브한 세계지도로서 적합하며, 변형 투영법의 적합성에 따라 왜곡이 거의 없습니다.

주요 온라인 거리 지도 서비스의 타일링 시스템은 위도 θ_max = ±85.05113°에서 극지방을 잘라낸 것을 제외하고 세계 대부분의 영역을 단일 사각 이미지로 가장 낮은 줌 수준으로 표시합니다.(아래 참조).이 범위를 벗어난 위도 값은 θ = ±90°^{[citation needed]}에서 분산되지 않는 다른 관계를 사용하여 매핑됩니다.

수학

원통 투영

지구의 표면은 타원형의 회전 타원체로 가장 잘 모델링되지만, 소규모 지도의 경우 타원체는 반지름 a의 구에 의해 근사되며, 여기서 a는 약 6,371 km이다.지구의 이 구면 근사치는 이 섹션에서 지구라고 불리는 반지름 R의 작은 구에 의해 모델링될 수 있습니다.지구본이 지도의 축척을 결정합니다.다양한 원통형 투영법은 지구본에서 적도에서 지구본에 접하는 원통으로 지리적 세부사항을 전송하는 방법을 지정합니다.그런 다음 실린더가 전개되어 평면 ^[14][15]지도를 제공합니다.분율 R/a를 투영법의 대표 분율(RF) 또는 주 척도라고 합니다.예를 들어, 책에 인쇄된 메르카토르 지도는 지구 반지름 2.13cm에 대응하는 적도 폭 13.4cm, RF 약 1/300M(RF를 쓸 때 1,000,000의 약자로 사용됨)인 반면, 메르카토르의 원래 1569 지도는 지구 반지름 315cm에 대응하는 198cm의 폭을 가질 수 있습니다./2000만

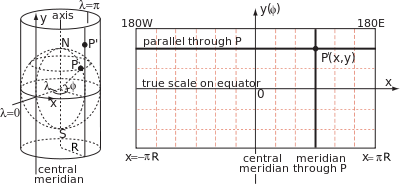
원통형 지도 투영법은 위도θ 및 경도θ의 지리 좌표를 적도상의 원점과 적도를 따른 x축을 가진 지도상의 데카르트 좌표에 연결하는 공식에 의해 규정된다.구조상, 같은 자오선의 모든 점은 x의 일정한 값으로 실린더의 동일한^[a] 발생기에 있지만, 발생기(적도로부터 측정)를 따른 거리 y는 위도 y( of)의 임의^[b] 함수이다.일반적으로 이 기능은 지구 중심에서 실린더까지의 기하학적 투영(화면상의 광선과 같은)을 설명하지 않으며, 이는 원통형 지도를 개념적으로 투영하는 무제한적인 방법 중 하나에 불과합니다.

원기둥은 적도에서 지구본에 접해 있기 때문에 지구본과 원기둥 사이의 스케일 팩터는 적도의 통일성일 뿐 다른 곳은 없습니다.특히, 평행 또는 위도 원의 반지름은 R cos µ이므로 지도에서 해당 평행선은 1/cos µ = sec µ의 계수만큼 늘어나야 한다.이 평행의 스케일 팩터는 일반적으로 k로 표시되며, 자오선의 해당 스케일 ^[16]팩터는 h로 표시됩니다.

스케일 팩터

Mercator 투영도는 투영도가 적합해야 하는 요건에 따라 결정됩니다.이에 대한 의미 중 하나는 "척도 요인의 이방성"으로, 점 척도 요인이 방향과 독립적이므로 투영에 의해 작은 모양이 보존됩니다.즉, 수직 척도 요인 h가 수평 척도 요인 k와 같다는 것을 의미합니다.k = 초이므로 h도 마찬가지입니다.

그래프에는 위도에 따른 이 척도 요인의 변동이 표시됩니다.몇 가지 수치는 다음과 같습니다.

위도 30°에서 스케일 팩터는 k = 초 30° = 1.15이다.

위도 45°에서 스케일 팩터는 k = 초 45° = 1.41이다.

위도 60°에서 스케일 팩터는 k = 초 60° = 2이다.

위도 80°에서 스케일 팩터는 k = 초 80° = 5.76이다.

위도 85°에서 스케일 팩터는 k = 초 85° = 11.5이다.

면적 척도 인수는 평행 및 자오선 척도 hk = 초의² 곱이다.그린란드의 경우, 중위도 위도로 73°를 취하면 hk = 11.7이다.호주의 경우, 중위도 위도 25°를 취하면 hk = 1.2이다.영국의 경우, 중위도 위도 55°를 취하면 hk = 3.04이다.

위도와의 변동은 다음과 같이 여러 막대 눈금으로 표시될 수 있습니다.

투사 고유의 왜곡을 나타내는 고전적인 방법은 티쏘의 인디케이터스를 사용하는 것입니다.Nicolas Tissot은 지도 투영에서 숫자 h와 k로 지정된 한 지점에서 축척 인자가 해당 지점에서 타원을 정의한다는 점에 주목했다.원통 투영의 경우 타원의 축이 경맥 및 ^[16][17][c]평행에 정렬됩니다.메르카토르 투영법(h = k)의 경우, 타원은 해당 위도에 대한 척도 계수 값에 비례하는 반지름을 가진 원으로 퇴화됩니다.이러한 원은 투영된 지도에 크기가 극단적으로 변동하는 형태로 렌더링되어 메르카토르의 축척 변화를 나타냅니다.

메르카토르 투영 변환

파생

위에서 설명한 바와 같이 등방성 조건은 h = k = sec δ임을 의미한다.반지름 R의 지구상에 경도 θ와 위도 θ가 있는 점을 고려합니다.θ가 극소량 dθ만큼 증가하면 지점은 반지름 R의 지구 자오선을 따라 R dθ를 이동하므로 y, dy의 해당 변화는 hR dθ = Rsec δ dθ이어야 한다.따라서 y(sec) = Rsec입니다.마찬가지로 θ를 dθ씩 증가시키면 점 R cos θ dθ가 지구 평행선을 따라 이동하므로 dx = kR cos θ dθ = R dθ가 됩니다.즉, xθ(r) = R. 방정식 적분

$\displaystyle x'(\displayda)=R,\qquad y'(\varphi)=R\sec \varphi ,}$

x(표준₀) = 0 및 y(0) = 0일 때 x(표준)와 y(표준)를 나타냅니다.값 θ는₀ 임의의 중심 자오선의 경도이며, 보통 그리니치 자오선(즉, 0)의 경도입니다.각도 θ와 θ는 라디안으로 표현됩니다.이차 ^[18][19]함수의 적분에 의해

$(\displaystyle x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left [\tan \lefts\frac {pi }{4}}+{\frac {varphi }{2}}\right}\right})}$

예 R = 1인 경우 함수 y(가변)는 θ와 나란히 표시된다: 극에서 무한대인 경향이 있다.선형 Y축 값은 일반적으로 인쇄된 지도에는 표시되지 않습니다. 대신 일부 지도는 오른쪽에 위도 값의 비선형 척도를 표시합니다.대부분의 경우 지도는 선택된 자오선과 평행선의 눈금만을 표시합니다.

역변환

${\displaystyle \displayda _{0}+{\frac {x}{R}},\qquad \varphi =2\tan ^{-1}\left[\exp \display\frac {y}{R}\right]-{\frac },}$

두 번째 방정식의 오른쪽에 있는 식은 구더만 함수를 정의한다. 즉, θ = gd(y/R): 따라서 직접 방정식은 y = R·gd⁻¹(gd)^[18]로 작성될 수 있다.

대체 표현

y(),)에 대한 많은 대체 표현들이 있는데, 모두 기초적인 ^[19]조작에 의해 도출되었다.

${\displaystyle {\frac {R}{2}}\left[{\frac {1+\sin \varphi}}{1-\sin \varphi }}\right]&={R}\ln \left[{\frac {1+\sin \varphi }}\cosvarphi } } } } }=R\ln \left(\sec \varphi +\tan \varphi \right)\\[2ex]&R\tanh ^{-1}\left(\sin \varphi \right)=R\operoname(\varphi \right)R\operatorname {gd}^{-1}(\varphi)\end { aligned}}$

대응하는 반전은 다음과 같습니다.

$\displaystyle \varphi =\sin ^{-1}\left(\tanh {frac {y}{R}\right)=\operatorname {sgn}(y)\sec ^-1}\left(\cosh {R}) {right}$

도 단위로 표시되는 각도의 경우:

$(\displaystyle x=brac {\pi R(\lambda ^{\lambda }-\brada _{0}^{\ln }}{180}}}{{\right], \qquad \ln y=R\ln \left[\t[ 45+{\frac {\varphi }}}{\right}}}}}{{\right}}}}}}\fright.}$

위의 공식은 지구 반지름 R을 기준으로 작성되었다.종종 지도 너비 W = 2µR로 직접 작업하는 것이 편리합니다.예를 들어, 기본 변환 방정식은

${\displaystyle x=barfrac {W}{2\pi }}\left(\displayda -\barfda _{0}\오른쪽),\qquad \brack {W}{2\pi }}}\ln \left[\tfrac {\braphi }{4}}+{\fright}\frac {\fright}\fright}.}$

절단 및 애스펙트

메르카토르 투영법의 좌표 y는 극점에서 무한이 되고 지도는 90도 미만의 위도에서 잘려야 한다.이 작업은 대칭적으로 수행할 필요가 없습니다.Mercator의 원래 지도는 80°N과 66°S에서 잘렸고, 그 결과 유럽 국가들이 지도의 중앙으로 이동했다.그의 지도의 가로 세로 비율은 198/120 = 1.65이다.핀란드 학교 지도책은 약 76°N과 56°S(횡단비 1.97)로 잘렸다.

대부분의 웹 기반 매핑은 가로 세로 비율이 1인 확대 가능한 버전의 Mercator 투영을 사용합니다.이 경우 얻어진 최대 위도는 y = ±W/2 또는 등가 y/R = µ에 해당해야 한다. 역변환 공식 중 하나를 사용하여 해당 위도를 계산할 수 있다.

$\displaystyle \varphi =\tan ^{-1}\left [\sinh \frac {y}{R}\right]=\tan ^{-1}\left [\sinh \pi \right]=\tan ^{-1}\left [ 11.5487\right]=85.05113^{right}.$

소자 형상

각도의 변환이나 축척 변동과 같은 y())와 투영 특성 사이의 관계는 지구상 및 지도상의 해당 작은 요소의 기하학적 구조를 따릅니다.아래 그림은 지구상에서 위도 and과 경도 on의 점 P와 위도 + + and와 경도 + + δ의 근방 점 Q를 보여줍니다.세로줄 PK와 MQ는 길이 Rθθ인 ^[d]경락의 호입니다.수평선 PM과 KQ는 길이 R(cos ))의 평행선의 호이다.투영의 해당 점은 폭 θx 및 높이 θy의 직사각형을 정의합니다.

작은 요소의 경우 각도 PKQ는 대략 직각이기 때문에

$\displaystyle \tan \alpha \approx {R\cos \varphi},\delta \varphi},\qquad \qquad \tan \tan =\frac {\frac x}{\frac y},\frac \frac \fcos \fi},\fcos\fcos \fi},\da},\frac,\da},\da},\delta\d$

앞에서 언급한 지구본에서 실린더까지의 스케일 계수는 다음과 같습니다.

병렬 스케일 계수 $\displaystyle \varphi \;=\;{\frac {P'M'}{PM}}\;\;{\frac {\cos \varphi \,\frac \varphi },$

자오선 스케일 계수 ${\displaystyle h(\varphi)\;=\;{\frac {P'K'}{PK}\;{\frac {\delta \varphi},}}.}$

경맥은 상수 x의 선에 매핑되므로 x = R(θ - θ₀) 및 x = R(라디안)이 있어야 합니다.따라서, 무한히 작은 원소의 한계에서

$\displaystyle \tan \varpi = sec frac {R\sec \varphi }{y'(varphi)}}\tan \alpha \,\qquad k=\sec \varphi \,\qquad h=sec frac {y'(varphi)}{R}}}}.$

메르카토르 투영법의 경우 y'(r) = Rsec δ이므로 h = k, α = β가 된다.h = k라는 사실은 위에서 설명한 척도 인자의 등방성입니다.α = β라는 사실은 지도의 동일 동일 방위각 항행 경로가 지도상의 동일한 일정 그리드 베어링에 매핑된다는 사실을 반영한다.

거리 공식

메르카토르 지도상의 눈금자 거리를 구상의 실제(대원) 거리로 변환하는 것은 적도를 따라 간단하지만 다른 곳은 없습니다.한 가지 문제는 위도에 따른 척도 변화이며, 또 다른 문제는 자오선이나 적도를 제외한 지도상의 직선(점선)이 대원에 해당되지 않는다는 것입니다.

마름모꼴(항행) 거리와 대원(참) 거리의 구별은 메르카토르에 의해 명확하게 이해되었다.(1569 맵의 범례 12 참조).그는 특히 저위도에서 짧은 거리 또는 중간 거리의 코스에 대한 진정한 큰 원 거리에 대한 허용 가능한 근사치라고 강조했다.그는 심지어 "적도 부근에서 측정해야 할 대원 거리가 대원 20도, 스페인 프랑스 부근 15도, 북방 8도, 심지어 10도를 넘지 않을 때는 마름모꼴 선 거리를 사용하는 것이 편리하다"고 말했다.

중간점이 위도 θ에 있는 짧은 선의 눈금자 측정의 경우, 여기서 스케일 팩터는 k = sec θ = 1/cos θ입니다.

실제 거리 = 마름모꼴 거리 ruler 눈금자 거리 × cos rf / RF. (단선)

반지름과 대원둘레가 각각 6,371km와 40,030km일 때 RF 1/300M은 R = 2.12cm, W = 13.34cm이며, 이는 적도의 한 지점에서 3mm의 눈금자 측정값이 약 900km에 해당한다는 것을 의미한다.위도 20°, 40°, 60° 및 80°에 해당하는 거리는 각각 846km, 689km, 450km, 156km이다.

거리가 멀수록 다양한 접근법이 필요합니다.

적도에서

스케일은 적도상의 통일성입니다(비고정 투영의 경우).따라서 적도에서 눈금자 측정을 해석하는 것은 간단합니다.

참 거리 = 눈금자 거리 / RF(표준)

위 모델의 경우 RF = 1/300M일 경우 1cm는 3,000km에 해당합니다.

다른 유사점

다른 모든 병렬에서 스케일 팩터는 초 µ이므로

평행 거리 = 눈금자 거리 × cos δ / RF (표준).

위 모델의 경우 위도 60°에서 1cm는 1,500km에 해당합니다.

평행선은 큰 원이 아니기 때문에 평행선상의 선택된 끝점 사이의 최단 거리가 아닙니다.이 차이는 단거리에서는 작으나 세로분리인 θ가 증가할수록 증가한다.60°에서 평행선의 경도 10°로 분리된 두 지점, A와 B의 경우 평행선을 따른 거리는 대원 거리보다 약 0.5km 더 크다.(평행상의 거리 AB는 (a cos θ)θ이다.화음 AB의 길이는 2(a cos θ) sin θ/2이다.이 화음은 중심에서 2arcsin(cos ) sin ) / 2)과 같은 각도로, A와 B 사이의 대원거리는 2aarcsin(cos ) sin ) / 2)이다.세로 간격이 180°인 극단적인 경우, 평행선을 따른 거리는 평행선 원주의 절반인 10,007.5km이다.반면, 이들 점 사이의 측지선은 중심에서 60°의 각도로 기울어진 극을 통과하는 거대한 원호입니다. 이 원호의 길이는 거대한 원둘레의 6분의 1로, 약 6,672km입니다.차이는 3338km이므로 지도에서 측정한 눈금자 거리는 축척 계수의 위도 변동을 수정한 후에도 상당히 오해의 소지가 있습니다.

자오선에

지도의 자오선은 지구상의 큰 원이지만 연속적인 축척 변동은 눈금자 측정만으로는 자오선의 먼 점 사이의 실제 거리를 산출할 수 없습니다.그러나 Mercator 1569 세계지도(시트 3, 9, 15)와 후속 모든 해도의 경우와 같이 위도를 직접 읽을 수 있는 정확하고 정교한 위도 척도로 지도에 표시된 경우, 두 위도 θ와₁ θ₂ 사이의 자오선 거리는 단순하다.

${\displaystyle m_{12}=a \varphi _{1}-\varphi _{2} .}$

끝점의 위도를 자신 있게 결정할 수 없는 경우 눈금자 거리를 계산하여 대신 찾을 수 있습니다.적도₁ y와₂ y에서 측정한 지도 자오선 끝점의 눈금자 거리를 구면 위의 이러한 점 사이의 실제 거리는 역 메르카토르 공식 중 하나를 사용하여 구면에서의 실제 거리를 구한다.

${\displaystyle m_{12}=a\left \tan ^{-1}\left [\sinh \left frac {y_{1}\right]-\tan ^{-1}\left [\sinh \tan \frac {y_{2}}{R}\right}\right},\right},\,\,$

여기서 R은 지도의 폭 W에서 R = W/2µ로 계산할 수 있다.예를 들어, R = 1인 지도에서 y = 0, 1, 2, 3의 값은 θ = 0°, 50°, 75°, 84°의 위도에 해당하므로 지도에서 1cm의 연속 간격은 지구 상의 위도 간격 50°, 25°, 9° 및 5,180km, 2,80km, 1,000km의 거리에 해당한다.

마름모꼴로

메르카토르 지도에서 경맥에 대한 각도α의 직선은 마름모꼴 선이다.α = δ/2 또는 3µ/2일 때, 마름모는 평행선 중 하나에 해당하며, 오직 하나의 적도는 큰 원이다.α = 0 또는 θ일 때 이는 자오선 대원에 해당한다(지구 주위에서 계속되는 경우).다른 모든 값의 경우 지구상의 극에서 극으로 나선형이 모든 경맥을 같은 각도로 교차하므로 ^[19]큰 원이 아닙니다.이 섹션에서는 이들 중 마지막 사례만 설명합니다.

만약 α가 0도 아니고 θ도 아닌 경우, 위도 θ 사이의 구면상에 있는 극소 럼선의 길이가 초 α θ인 것을 알 수 있다.α는 마름모꼴에서 일정하기 때문에 이 식을 통합하여 지구의 유한 마름모꼴 선에 대해 다음과 같이 나타낼 수 있습니다.

$\displaystyle r_{12}=a\sec \alpha \varphi _{1}-\varphi _{2} =a,\sec \alpha \;\Delta \varphi .}$

다시 한 번, 지도상의 정확한 위도 척도에서 δ를 직접 읽을 수 있는 경우 위도₁ θ와₂ θ를 가진 지도 지점 사이의 마름모꼴 거리는 위와 같이 구한다.이러한 척도가 없는 경우 끝점과 적도 사이의₁ 눈금자 거리 y와₂ y는 역식을 통해 결과를 제공합니다.

${\displaystyle r_{12}=a\sec \alpha \left \tan ^{-1}\frac {y_{1}\right}-\tan ^{-1}\sinh \leftfrac {y_{2}}{R}\right}-\tan }$

이러한 공식은 구체상의 마름모꼴 거리를 나타내며, 이는 보다 정교한 ^[e]계산이 필요한 실제 거리와는 크게 다를 수 있다.

타원체에 대한 일반화

지구가 구상체(회전 타원체)에 의해 모델링될 때, Mercator 투영법이 적합하게 유지되려면 수정되어야 합니다.비고정 버전에^[20] 대한 변환 방정식 및 스케일 계수는 다음과 같습니다.

스케일 팩터는 원통이 적도의 타원체에 접해 있기 때문에 적도의 통일성입니다.스케일 팩터의 타원형 보정은 위도에 따라 증가하지만 1% 미만의 보정인 e보다² 크지는 않습니다(e의 값은² 모든 기준 타원체에 대해 약 0.006입니다).이것은 적도에 매우 가깝다는 점을 제외하고는 눈금의 부정확성보다 훨씬 작습니다.오직 적도 근처의 지역에 대한 정확한 메르카토르 투영만이 타원체 보정을 필요로 할 것이다.

등각 위도가 포함되기 때문에 역수는 반복적으로 해결된다.

「 」를 참조해 주세요.

• 지도 제작
• 중앙 원통형 투영 – 더 왜곡됨. 때로는 Mercator 투영을 구성하는 방법으로 잘못 설명되기도 합니다.
• 컨포멀 맵 투영
• 등각 투영 – 왜곡이 적지만 면적이 동일하지 않음
• Gall-Peters 투영 – 등면적 원통 투영
• 요르단 횡단 메르카토르
• 지도 투영 목록
• 메르카토르 1569 세계지도
• 항해도
• Rumbline 네트워크
• 티쏘인디케트릭스
• 횡단 메르카토르 투영법
• 범용 횡단 메르카토르 좌표계

메모들

레퍼런스

참고 문헌

• 를 클릭합니다Maling, Derek Hylton (1992), Coordinate Systems and Map Projections (second ed.), Pergamon Press, ISBN 0-08-037233-3.
• Monmonier, Mark (2004), Rhumb Lines and Map Wars: A Social History of the Mercator Projection (Hardcover ed.), Chicago: The University of Chicago Press, ISBN 0-226-53431-6
• Olver, F. W.J.; Lozier, D.W.; Boisvert, R.F.; et al., eds. (2010), NIST Handbook of Mathematical Functions, Cambridge University Press
• Osborne, Peter (2013), The Mercator Projections, doi:10.5281/zenodo.35392. (Supplements: Maxima files and Latex code and figures) {{citation}}:외부 링크 postscript=(도움말)CS1 유지보수: 포스트스크립트(링크)
• Snyder, John P (1993), Flattening the Earth: Two Thousand Years of Map Projections, University of Chicago Press, ISBN 0-226-76747-7
• Snyder, John P. (1987), Map Projections – A Working Manual. U.S. Geological Survey Professional Paper 1395, United States Government Printing Office, Washington, D.C. 이 문서는 USGS 페이지에서 다운로드할 수 있습니다.흥미로운 소개 섹션과 함께 대부분의 예상에 대한 자세한 내용을 제공하지만, 첫 번째 원칙에서 어떠한 예상도 도출하지 못합니다.

추가 정보

• Rapp, Richard H (1991), Geometric Geodesy, Part I, Ohio State University Department of Geodetic Science and Surveying, hdl:1811/24333

외부 링크

• Admaiorem Gerardi Mercatoris gloriam – 메르카토르의 1569년 세계지도 고해상도 이미지가 포함되어 있습니다.
• radicalcartography.net의 모든 일반적인 투영 예시와 속성 표.
• Mercator 투영법의 메트릭 변형을 연구하는 대화형 Java 애플릿입니다.
• Web Mercator: 부적합, 부적합(Noel Zinn, Hydrometronics LLC)
• 브리티시컬럼비아 대학의 메르카토르 투영
• Google 지도 좌표