룸 라인

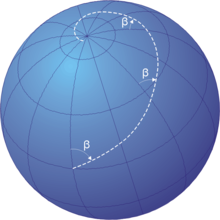
항법에서, 심박선, 심박선, (/rʌm/) 또는 록소드롬은 같은 각도에서 경도의 모든 경맥, 즉 진정한 북쪽에 대해 측정된 일정한 방향을 갖는 경로를 가로지르는 호이다.

소개

지구 표면에 대한 작은 선 코스를 따라가는 것의 효과는 1537년 포르투갈의 수학자 페드로 누네스에 의해 처음 논의되었는데, 그의 해양차트 방어 논문에서 1590년대 토마스 해리엇이 수학적으로 더 발전했다.

구면 표면의 두 점 사이의 최단 거리의 경로인 큰 원과 대조를 이룰 수 있는 것이 바로 이 원은 구면상의 두 점 사이의 최단 거리의 경로다. 큰 원에서는 목적지점까지의 방향성이 일정하게 유지되지 않는다. 큰 원을 따라 차를 몰려면 핸들을 고정시켜 놓지만, 덤불 선을 따라가려면 바퀴를 돌려 극이 가까워질수록 더욱 날카롭게 돌려야 한다. 즉, 큰 원은 국소적으로 지오데틱 곡면성이 0인 "직선"인 반면, 룸 라인은 0이 아닌 지오데틱 곡면성을 가지고 있다.

경도와 위도의 평행 경맥은 각각 교차로 각도가 0°와 90°인 덤불 선의 특별한 경우를 제공한다. 남북 통행로에서는 적도를 따라 동서 통행로에서 하듯이 큰 원과 겹친다.

메르카토르 투영 지도에서, 어떤 루움 선은 직선이다; 지도 가장자리에서 벗어나지 않고 지구상의 어떤 두 지점 사이에 있는 지도에 루움 선을 그릴 수 있다. 그러나 이론적으로 록소드롬은 지도의 오른쪽 가장자리를 넘어 확장될 수 있으며, 그 다음 동일한 경사를 가진 왼쪽 가장자리에서 계속된다(지도가 정확히 경도 360도를 덮고 있다고 가정한다).

경맥을 비스듬히 자르는 굵은 선은 극을 향해 소용돌이치는 록스로믹 곡선이다.^[1] 메르카토르 투영에서는 북극과 남극이 무한대로 발생하므로 절대 나타나지 않는다. 그러나 무한히 높은 지도의 전체 로크소드롬은 두 가장자리 사이에 무한히 많은 선 세그먼트로 구성될 것이다. 입체 투영 지도에서, 록소드롬은 등각형 나선형으로, 중심은 북극 또는 남극이다.

모든 록소드롬은 한 극에서 다른 극으로 소용돌이친다. 극 근처에는 로그 나선형(정확히 입체 투영 위에 있는 것, 이하 참조)에 가깝기 때문에 각 극을 무한히 돌지만 한정된 거리에서 극에 도달한다. 로크소드롬(완벽한 구를 가정)의 극대극 길이는 자오선을 진정한 북쪽으로부터 멀리 떨어진 베어링의 코사인(cosine)으로 나눈 길이다. 록소드롬은 극지방에서 정의되지 않는다.

• 극대극로원경3길
• 
• 
• 

어원 및 역사 설명

록소드롬이라는 단어는 고대 그리스어 οξςς lo lo logos: "oblique" + Δρμοςς dramenn: "to running"에서 유래되었다. rhumb라는 단어는 스페인어 또는 포르투갈어 럼보/루모("코스" 또는 "방향")에서, 그리스어 ῥόμβο rohmbos, ^[2]렘베인에서 유래될 수 있다.

1878년판 《유니버설 정보 백과사전》에서는 록소드롬 선을 다음과 같이 설명하고 있다.^[3]

록소드롬선(Loxodrom curvatureic Line)은 주어진 표면의 곡률선 시스템의 모든 부재를 동일한 각도로 절단하는 곡선이다. 나침반의 같은 지점을 향해 항해하는 배는 모든 경혈을 같은 각도로 자르는 그런 선을 묘사한다. 메르카토르의 투영 (q.v.)에서 록소드로믹 선은 분명히 곧다.^[3]

'엉덩이'라는 용어가 사용되기 시작했을 때 정확한 의미가 없었기 때문에 오해가 생길 수 있다. 이 용어는 "로컬하게"만 적용되고 항해를 위해 선원이 어떤 일을 하던지 의미할 뿐이라는 의미를 내포하고 있는 모든 부정확함을 함축하고 있기 때문에, 그것은 로크소드롬에 그랬던 것처럼 풍력선에도 똑같이 잘 적용되었다. 따라서, 포르톨란이 사용 중일 때 포톨란스의 직선에도 "엉덩이"가 적용되었고, 메르카토르 차트의 직선에도 항상 적용이 가능했다. 단거리에서 포르톨란 "럼스"는 메르카토르 럼스"와 의미 있게 다르지 않지만, 요즘 "럼스"는 수학적으로 정밀한 "록소드롬"과 동의어로서 소급적으로 만들어졌기 때문에 동의어다.

레오 백로가 말한 대로:^[4] "..이 시기의 바다차트에 'Rhumbline'이라는 단어가 잘못 적용되었는데, 이는 록소드롬이 적절한 투영에 도표를 그릴 때만 정확한 항로를 제공하기 때문이다. 측량 조사 결과 초기 차트에서 어떤 투영법도 사용되지 않았으며, 따라서 우리는 '포톨란'이라는 이름을 유지하고 있다."

수학적 설명

반경 1방위각 λ고, 극지방의 각도의 범위 동안 −.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output.sfrac.tion,.mw-parser-output.sfrac .tion{디스플레이:inline-block, vertical-align:-0.5em, font-size:85%;text-align:센터}.mw-parser-output.sfrac .num,.mw-parser-output.sfrac .den{디스플레이:블록, line-height:1em, 마진:00.1em.}.mw-parser-output.sfrac .den{border-top:1px 고체}.mw-parser-output .sr-only{국경:0;클립:rect(0,0,0,0), 높이:1px, 마진:-1px, 오버 플로: 숨어 있었다. 패딩:0;위치:절대, 너비:1px}π/2 ≤ φ ≤ π/2(여기 latitude에 대응하여 정의된), 데카르트 단위 벡터 나는, j, k은 동경 벡터 r를 쓰는 데 사용될 수 있다.

${\displaystyle \mathbf {r} (\lambda ,\varphi )=(\cos {\lambda }\cdot \cos {\varphi })\mathbf {i} +(\sin {\lambda }\cdot \cos {\varphi })\mathbf {j} +(\sin {\varphi })\mathbf {k} \,.}$

구의 방위각 및 극방향에 있는 직교 단위 벡터는 기록할 수 있다.

${\displaystyle{\begin{정렬}{\boldsymbol{\hat{\lambda}}}(\lambda ,\varphi)&, =\sec{\varphi}{\frac{\partial \mathbf{r}}{\lambda\partial}};={\frac{\partial \mathbf{r}}{\varphi\partial}}=(-\cos{\lambda}\cd{나는}+(\cos{\lambda})\mathbf{j}\,,\\[8pt]{\boldsymbol{\hat{\varphi}}}(\lambda ,\varphi)& =(-\sin{\lambda})\mathbf.고르\sin {\varphi }}\mathbf {i} +(-\sin {\sina }\cdot \sin {\varphi }}}\mathbf {j} +(\cos {\varphi }}\mathbf {k} \lined}}}}}}}}}}}}}})}$

스칼라 제품을 가지고 있는

${\displaystyle {\boldsymbol {\hat {\lambda }}}\cdot {\boldsymbol {\hat {\varphi }}}={\boldsymbol {\hat {\lambda }}}\cdot \mathbf {r} ={\boldsymbol {\hat {\varphi }}}\cdot \mathbf {r} =0\,.}$

상수 φ에 대한 λ latitude은 위도의 평행선을 추적하고 상수 for에 대한 longitude traces은 경도의 자오선을 추적하며, 함께 구에 접하는 평면을 생성한다.

단위 벡터

${\displaystyle \mathbf{\hats{\hats{\\\barphi )}}}(\chatsymbol {\chota }}+(\cos{\cos{\\cosymbol {\\\bphi }}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}}).$

스칼라 제품은 λ과 φ에 대하여 단위 벡터 φ̂과 일정한 각도 β를 가진다.

${\displaystyle {\hat symbol {\hat {\barphi }}\cdot {\cdmbol {\hats {\varphi }}}=\cos {\cos }\\,}$

록소드롬은 경도의 모든 경맥과 일정한 각도 β를 갖는 구상의 곡선으로 정의되며, 따라서 단위 벡터 β̂에 평행해야 한다. 결과적으로, 록소드롬을 따라 길이 ds가 차등 변위를 생성한다.

${\displaystyle{\begin{정렬}d\mathbf{r}&={\boldsymbol{\hat{\beta}}}\,ds\\[8px]{\frac{\partial \mathbf{r}}{\lambda\partial}}\,d\lambda +{\frac{\partial \mathbf{r}}{\varphi\partial}}\,d\varphi&=((\sin{\beta})\,{\boldsymbol{\hat{\lambda}}}+(\cos{\beta})\,{\boldsymbol{\hat{\varphi}}})ds\\[8px](\cos{\varphi})\,d\la.mbda \,{\boldsymbol{\hat{\lambda}}}+d\varphi \,{\boldsymbol{\hat{\varphi}}}&=(\sin{\beta})\,ds\,{\boldsymbol{\hat{\lambda}}}+(\cos{\beta})\,ds\,{\boldsymbol{\hat{\varphi}}}\\[8px]ds&, ={\frac{\cos{\varphi}}{\sin{\beta}}}\,d\lambda ={\frac{d\varphi}{\cos{\beta}}}\\[8px]{\frac{d\lambda}{d\varphi}}&=\tan{\beta}\cdot \se.c{\varphi}\\[8px]\lambda(\varphi),\,\beta ,\lambda_{0}일 경우 ,\varphi_{0})&,=\tan \beta \cdot{\big(}\operatorname{artanh}(\sin \varphi)-\operatorname{artanh}(\sin \varphi_{0}){\big)}+\lambda _ᆱ\\[8px]\varphi(\lambda),\,\beta ,\lambda_{0}일 경우 ,\varphi_{0})&,=\arcsin{\Big(}\tanh{\big(}(\lambda -\lambda_{0})\cot\beta +\operatorname{artanh}.(\sin)varphi _{0}{\Big )}{\Big )}\end{arged}}}}$

이러한 λ과 φ의 관계와 함께 반지름 벡터는 하나의 변수의 파라메트릭 함수가 되어 구체의 록소드롬을 추적한다.

${\displaystyle \mathbf {r} (\lambda \, \,\beta ,\lambda _{0},\varphi _{0})={\Big (}\cos {\lambda }\cdot \operatorname {sech} \psi {\Big )}\mathbf {i} +{\Big (}\sin {\lambda }\cdot \operatorname {sech} \psi {\Big )}\mathbf {j} +{\Big (}\tanh \psi {\Big )}\mathbf {k} \,,}$

어디에

${\displaystyle \equiv (\data -\basda _{0})\reasonname {artanh}(\sin \varphi _{0}}=\sin \varphi )}$

등위도 입니다.^[5] 지구중심 위도와 등축 위도는 구더만 함수를 통해 서로 연관된다.

${\displaystyle \varphi =\photname {gd}(\properties )\,}$

룸 선에서 지오콘티크리트 위도가 극에 치우치는 경향이 있기 때문에 → → ±//2, sin → → ±1, 등축 위도 아르탄(sin )) → ± ∞, 경도 λ은 폴을 향한 나선형으로 구를 그렇게 빠르게 돌면서 바운드 없이 증가하며, 동시에 유한한 총 호 길이 Δs에 의해 주어진다.

${\displaystyle \Delta s={\big}(\pm \pi /2-\varphi _{0}\cdot \sec \big}})$

메르카토르 투영에 대한 연결

λ 구에 있는 점의 경도가 되게 하고, 그 위도를 φ으로 한다. 그런 다음 메르카토르 투영의 지도 좌표를 다음과 같이 정의하면

${\displaystyle {\partified}x&=\boda -\bodda _{0}\\\y&=\nftname {arth}(\sin \varphi )\\\ended{arged}}}}}$

(이전 절의 표현 사용) 이후, 진정한 북쪽으로부터 일정한 베어링 β를 갖는 록소드롬은 직선이 될 것이다.

${\displaystyle y=mx}$

경사져서

$\displaystyle m=\cHB \cHB \,}$

주어진 두 점 사이의 로크소드롬을 찾는 작업은 메르카토르 지도에서 그래픽으로 수행하거나, 두 개의 미지의 m = cot β와 and에서₀ 두 개의 방정식의 비선형 시스템을 풀어서 수행할 수 있다. 해결책은 무한히 많다; 가장 짧은 것은 실제 경도 차이를 커버하는 것이다. 즉, 여분의 회전도 하지 않고, "잘못된 방향"도 가지 않는다.

록소드롬을 따라 측정한 두 점 Δs 사이의 거리는 단순히 베어링(azimuth)의 2분의 1이 남북 거리를 곱한 절대값이다(거리가 무한대가 되는 위도 원은 제외).

${\displaystyle \Delta s=R\,{\big}(\varphi -\varphi _{0})\cdot \sec \big}}$

여기서 R은 지구 평균 반지름의 하나이다.

적용

항법에서 그것의 용도는 특정 항법 지도의 스타일 또는 투영과 직접 연결된다. 메르카토르 투영 지도에서 루움 선이 직선으로 나타난다.^[1]

이름은 각각 "rumb" 또는 "rumbo"와 같은 각도에서 모든 경맥들을 교차하는 차트의 선인 "rumbo"에서 유래되었다.^[1] 평면에서 이것은 두 점 사이의 최단 거리일 것이다. 낮은 위도의 지구 표면 위 또는 단거리에서 차량, 항공기 또는 선박의 항로를 계획하는 데 사용할 수 있다.^[1] 더 긴 거리 및/또는 더 높은 위도에서 큰 원 경로는 동일한 두 점 사이의 점선보다 상당히 짧다. 그러나 큰 원을 그리며 이동하면서 베어링을 계속 교체해야 하는 불편함이 있어 경우에 따라 룸라인 내비게이션이 매력적이다.^[1]

이 지점은 적도를 따라 경도 90도 이상의 동서 통로로 그려질 수 있으며, 이 경우 원과 덤불선 거리는 10,000km(5,400해리)에서 동일하다. 북위 20도에서 원거리의 최대 원거리는 4,997마일(8,042km)인 반면, 덤불선 거리는 8,166km(5,074마일)로 약 8,166km이다. 1+1/2% 더. 그러나 북위 60도에서는 원형의 거리가 2,485마일(3,999km)인 반면, 러브 선은 4,300km(2,700마일)로 8+1/2%의 차이가 난다. 더 극단적인 경우는 뉴욕시와 홍콩 사이의 항공로인데, 이 노선의 경우, 이 노선은 9,700해리(18,000km)이다. 북극 상공의 거대한 원 경로는 7000해리(1만3000km)로 일반적인 순항속도로 비행시간이 5+1⁄2시간 단축된다.

메르카토르 투영에 있는 일부 오래된 지도는 위도와 경도의 선으로 구성된 그리드를 가지고 있지만 북향, 북향, 북향의 직각, 또는 북향의 어떤 각도에서 직각으로 이루어진 룸바선을 보여주기도 한다. 이것은 직각의 단순한 합리적인 부분이다. 이 굵은 선들은 지도의 특정 지점에서 수렴되도록 그려질 것이다: 모든 방향으로 가는 선들은 이 지점들 각각에서 수렴될 것이다. 나침반 장미를 보라. 그러한 지도는 반드시 메르카토르 투영에 있었을 것이므로 모든 오래된 지도들이 우렁찬 선 표시를 보여줄 수 있는 것은 아닐 것이다.

나침반 장미의 방사선은 럼브라고도 한다. "엉덩이를 타고 통곡"이라는 표현은 16-19세기에 특정한 나침반 제목을 나타내기 위해 사용되었다.^[1]

해양 크로노미터가 발명되기 전 초기 항해자들은 긴 대양 항로에서 우렁우렁한 선 코스를 사용했는데, 그 이유는 태양이나 별을 목격함으로써 배의 위도를 정확하게 설정할 수 있었지만 경도를 정확하게 판단할 수 있는 방법이 없었기 때문이다. 그 배는 목적지의 위도에 도달할 때까지 북이나 남으로 항해할 것이고, 그 후 그 배는 덤불선(실제로도 평행인 것은 덤불선의 특수한 경우)을 따라 동쪽이나 서쪽으로 항해할 것이며, 일정한 위도를 유지하고 육지의 증거가 보일 때까지 항해한 거리에 대한 정기적인 추정치를 기록하게 된다.^[6]

일반화

리만 구에

지구의 표면은 수학적으로 리만 구체, 즉 구를 복잡한 평면에 투영하는 것으로 이해할 수 있다. 이 경우 록소드롬은 뫼비우스 변환의 특정 부류로 이해할 수 있다.

스피로이드

위의 공식은 쉽게 경구까지 확장될 수 있다.^{[7][8][9][10][11]} 우렁텅이 선의 경로는 타원체 등위도를 사용하는 것만으로 찾을 수 있다. 마찬가지로 타원성 자오선 호 길이에 방위각의 2분의 1을 곱하면 거리가 발견된다.

참고 항목

• 대권
• 타원체의 측지학
• 그레이트 타원
• 이소아지무탈
• 룸블라인 네트워크
• 세이퍼트의 나선형
• 작은 원

참조

참고: 이 기사는 1878년판 《유니버셜 정보 백과사전》의 텍스트를 포함하며, 이 책은 공공영역의 저작물이다.

추가 읽기

외부 링크

• MathPages의 상수 제목 및 굵은 선.
• RhumbSolve(1)는 타원형 림프 라인 계산(GeographicLib의 구성 요소)을 위한 유틸리티로, 보충 문서.
• RumbSolve의 온라인 버전.
• 항법 알고리즘 문서: 세일링스.
• 차트 작업 - 항법 알고리즘 차트 작업 무료 소프트웨어: 룸 라인, 그레이트 서클, 복합 항해, 메리디온 부품. 위치 선 파일럿 - 전류 및 해안 고정 장치
• 수학월드 록소드롬.