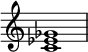감소된 삼합회

Diminished triad
"감소된 화음"은 여기서 방향을 바꾼다. 일곱 번째 화음은 일곱 번째 화음 축소를 참조하십시오.
쇠약해진 삼총사
루트에서 구성 요소 간격
5위 감소.
미성년자 제3의
뿌리를 내리다
튜닝
45:54:64;[1] 54:45=6:5 & 64:45[2]
포르테 번호 / 보완책
3-10 / 9-10

음악 이론에서, 감소된 3중주(일명 마이너 플랫 5중주[citation needed])는 뿌리 위 3분의 2의 마이너로 구성된 3중주곡이다.[3] 그것은 5번째로 낮은 (평활하게) 3중창이다. 코드 기호를 사용할 때는 "dim", "",o "m♭5" 또는 "MI(♭5)"[4] 기호로 표시할 수 있다. 그러나 대부분의 대중음악 화음책에서 기호 "딤"과 ""o는 감소된 7번째 화음(네번째 음의 화음)을 나타내며, 일부 현대 재즈 책과 음악 이론 책에서는 "딤7" 또는 ""o7 기호로 표현된다.

예를 들어, C라고o 쓰여진 C에 구축된 감소된 3중창은 C–E♭–G♭를 투구한다.

{ \override Score.TimeSignature #'stencil = ##f \relative c' { \clef treble \time 4/4 \key c \major <c es ges>1 } }

화음은 정수 표기법 {0, 3, 6}로 나타낼 수 있다.

일반적인 연습 기간 동안 감소된 3중량은 감소된 5중(또는 트리톤) 때문에 불협화음으로 간주된다.

조화함수

{ #(set-global-staff-size 14) \override Score.SpacingSpanner.strict-note-spacing = ##t \set Score.proportionalNotationDuration = #(ly:make-moment 1/2) \new PianoStaff << \new Staff << \relative c'' { \clef treble \key g \major \time 24/16 g16 b d g d b d b g b g d e g c e c g c g e g e c a c fis a fis c fis c a c a fis g b d g d b d b g b g d } >> \new Staff << \relative c' { \clef bass \key g \major \time 24/16 g8.[_\markup { \concat { "I" \hspace #20.5 "IV" \hspace #19.5 "vii" \raise #1 \small "o" \hspace #19.5 "I" } } g,] r g' g[ g,] r g' g[ g,] r g' g[ g,] r g' } >> >> }
J. S. Bach의 Well-Tomety Clavier I, Preference in G장조에서 우세한 화음을 대신하는 감소된 3종 화음.[5]

주요 척도에서는 7번째 척도에서만 삼합회 감소 현상이 발생한다. 예를 들어, C의 키에서, 이것은 B가 줄어든 삼합집이다. (B, D, F). 삼합회는 7척도로 지어지기 때문에 선도음 삼합회라고도 한다. 이 화음은 지배적인 기능을 가지고 있다. 우세한 3중창이나 우세한 7중창과는 달리 5중창의 강한 뿌리운동이 없기 때문에 리드 톤의 3중창은 구조적 화음보다는 연장적 화음으로 기능한다.[6]

반면에, 자연적인 사소한 척도에서, 감소된 삼합체는 두 번째 척도 정도에서 발생하며, C 단조에서, 이것은 D 감소 삼합체 (D, F, A a)이다. 이 3중창은 결과적으로 초토닉 감소 3중창이라고 불린다. 주요 키에서 발견되는 초토닉 3중창처럼, 초토닉 감소 3중창은 지배적인 기능을 가지고 있으며, 거의 항상 지배적인 기능적 화음으로 해결된다.[7]

음악이 마이너 키로 되어 있다면, 줄어든 트라이애드도 7번째 음인 ♯vii에서도o 찾을 수 있다. 오름차순 멜로디 단음계가 6, 7도 상승하기 때문이다. 예를 들어 화음 진행 ♯vi-i가o 일반적이다.

화음의 철자가 베이스와 함께 5번째 감소된 형태를 형성하기 때문에 리드 톤 감소된 삼합창과 초토닉 감소 삼합창은 보통 첫 번째 반전(각각 vii와o6 iio6)에서 발견된다.[6] 이것은 완전히 줄어든 일곱 번째 화음과는 다른데, 이것은 일반적으로 뿌리 위치에서 발생한다.[8] 두 경우 모두 베이스가 위로 풀리고 상반된 동작으로 상부 음성이 아래로 움직인다.[8]

대중음악에서

Walter Everett writes that "In rock and pop music, the diminished triad nearly always appears on the second scale degree, forming a generally maudlin and dejected iio with its members, 2–4–♭6."[9] Songs that feature iio include Santo & Johnny's "Sleep Walk", Jay and the Americans' "Cara Mia", and The Hollies' "The Air That I Breathe".[9] 록 뮤지션의 지식 및 의식적 회피가 암시될 정도로 희귀하지는 않지만, 그 사용의 예로는 오아시스의 "분노 속에서 돌아보지 말라", 데이비드 보위의 "우주 기괴함", 그리고 대릴 홀의 "Everything You Go Away"[10]에 있는 두 가지가 있다.

주요 키의 7번o 키는 덜 흔하지만 여전히 존재한다. I–vio–V7/vi–vi와 같은 진행 과정에서 거의 항상 상대적 소수를 강장시키기 위해 사용된다. 진행의 7-Vo7/v-vi 부분은 상대적 부차에서 i-V-i와o7 유사하다.

튜닝

감소된 트라이어드 튜닝의 비교(센트)

12음 균등 기질에서, 감소된 삼합체는 3과 5사이에 세 개의 반, 3과 3사이에 세 개의 반, 그리고 6개의 반을 가지고 있다.

5 한계만 억양으로 VII(C: B–D–F)의 감소된 화음은 15:8, 9:8, 4:3, II(C: D–F–Aa)의 감소된 화음은 9:8, 4:3 및 8:5(135:160:192)이다. 게오르크 안드레아스 소르지에 따르면, 트럼펫은 C에 대한 오버톤 시리즈에서 삼합집산 E–G–B = = 5:6:7("완벽한 화음")[11]을 주지만, 7은 너무 평평하고 45:54:64가 더 좋다.[1] 헬름홀츠는 음악 이론의 생리학적 기초로서 톤의 감응에 사용된 표기법에서 감소된 3중주를 1- D F로 설명하며, 피타고라스의 3중주(45:54:64)는 "음악 이론의 생리학적 기초로서 톤의 감응에 대하여"에서 사용된 표기법에서 단지 3중주(45:54:64)에 불과하다.[12]

C에서 Perfect(도움말/인포), Preferred(도움말/인포)(5 limit major) 또는 5 limit minor(도움말/인포)를 재생하십시오.

소르지 (완벽한)/
7시 15분 		소르지(선호)/
5학번 소령 		5소조
(D,F,A♭)
고조파
뿌리 E 5 386.31 F♯+ 45 590.22 C♯ 135 92.18
세 번째 G 6 701.96 A+ 54 905.87 E 160 386.31
다섯번째 B7♭ 7 968.83 C 64 1200 G 192 701.96
B에서
뿌리 B 15:8 1088.27 B 15:8 1088.27 B 15:8 1088.27
세 번째 D 9:8 203.91 D 9:8 203.91 D- 10:9 182.40
다섯번째 F7+ 21:16 470.78 F 4:3 498.04 F 4:3 498.04
C에
뿌리 C 1:1 0 C 1:1 0 C 1:1 0
세 번째 E♭ 6:5 315.64 E♭ 6:5 315.64 이- 32:27 294.13
다섯번째 G7♭ 7:5 582.51 G♭- 64:45 609.78 G♭- 64:45 609.78

화음표 감소

화음 뿌리 마이너 세 번째 감소된 5번째
시딤 C E♭ G♭
Cimdim C♯ E G
도딤 D♭ F♭ (E) Adouble flat(G)
딤 D F A♭
도딤 D♯ F♯ A
에짐 E♭ G♭ Bdouble flat (A)
에딤 E G B♭
프딤 F A♭ C♭ (B)
Fimdim F♯ A C
Gimdim G♭ Bdouble flat (A) Ddouble flat(C)
그딤 G B♭ D♭
Gimdim G♯ B D
A♭dim A♭ C♭ (B) Edouble flat(D)
아딤 A C E♭
A♯dim A♯ C♯ E
비딤 B♭ D♭ F♭ (E)
비딤 B D F

참고 항목

참조

  1. ^ a b 셜로, 매튜(2012년). 화합의 이론, 페이지 304. 잊혀진 책들. ISBN978-1-4510-1534-8
  2. ^ 파트치, 해리(1979년). 음악의 창세기, 페이지 68-69. ISBN 978-0-306-80106-8
  3. ^ Benward; Saker (2003). Music: In Theory and Practice, Vol. I (7th ed.). p. 68. ISBN 978-0-07-294262-0.
  4. ^ 벤워드 & 세이커(2003년), 페이지 77.
  5. ^ Jonas, Oswald (1982) [1934]. Das Wesen des musikalischen Kunstwerks: Eine Einführung in Die Lehre Heinrich Schenkers [Introduction to the Theory of Heinrich Schenker]. Translated by Rothgeb, John. p. 25. ISBN 0-582-28227-6.
  6. ^ a b Roig-Francoli 2011, 페이지 248.
  7. ^ Roig-Francoli 2011, 174페이지.
  8. ^ a b Benward; Saker (2009). Music in Theory and Practice: Volume II (8th ed.). p. 76. ISBN 978-0-07-310188-0.
  9. ^ a b Everett, Walter (2009). The Foundations of Rock. p. 195. ISBN 978-0-19-531023-8.
  10. ^ Stephenson, Ken (2002). What to Listen for in Rock: A Stylistic Analysis. p. 85. ISBN 978-0-300-09239-4.
  11. ^ Fétis, François-Joseph; Arlin, Mary I. (1994). Esquisse de l'histoire de l'harmonie. p. 139n9. ISBN 978-0-945193-51-7.
  12. ^ Helmholtz, Hermann (1885). On the Sensations of Tone as a Physiological Basis for the Theory of Music. Longmans, Green. p. 344.

원천