월드 라인

물체의 월드라인(또는 월드라인)은 물체가 4차원 시공간에서 추적하는 경로입니다.그것은 현대 물리학, 특히 이론 물리학에서 중요한 개념이다.

"월드 라인"의 개념은 시간 차원에 의해 "궤도" 또는 "여행"과 같은 개념과 구별되며, 일반적으로 지각적으로 직선 경로가 더 많은 절대 위치를 보여주기 위해 재계산되는 시공간 영역을 포함합니다.tes—특수 상대성 이론 또는 중력 상호작용의 특성을 드러냅니다.

세계선에 대한 생각은 물리학에서 비롯되었고 헤르만 민코프스키에 의해 개척되었다.이 용어는 현재 상대성 이론에서 가장 자주 사용된다.

물리에서의 사용법

물리학에서 물체의 세계선(world line)은 물체의 역사에 대응하는 시공간 사건의 연속이다.월드 라인은 시공간에서 특별한 형태의 곡선입니다.이하에서는, 동등한 정의에 대해 설명합니다.월드 라인은 시공간에서의 시간과 같은 곡선이다.월드 라인의 각 점은 해당 시점의 객체의 시간 및 공간 위치로 레이블을 지정할 수 있는 이벤트입니다.

예를 들어, 우주에서 지구의 궤도는 대략 원, 3차원(닫힌) 곡선이다: 지구는 매년 태양의 상대적인 우주의 같은 지점으로 돌아온다.하지만, 그것은 다른 시간에 그곳에 도착한다.지구의 세계선은 시공간에서 나선형(4차원 공간의 곡선)이며 같은 지점으로 돌아오지 않는다.

시공간은 사건을 식별하는 연속적이고 부드러운 좌표계와 함께 사건의 집합이다.각 사건에는 시간 좌표와 3개의 공간 좌표라는 4개의 숫자로 라벨을 붙일 수 있습니다. 따라서 시공간은 4차원 공간입니다.시공간의 수학 용어는 4차원 다양체이다.이 개념은 고차원 공간에도 적용될 수 있습니다.4차원을 쉽게 시각화하기 위해 종종 2개의 공간 좌표가 생략됩니다.그런 다음 사건은 민코프스키 다이어그램에서 점으로 표현됩니다. 민코프스키 다이어그램은 일반적으로 시간 좌표( $예$ : t $\displaystyle$ t $t$ 가 위쪽으로 표시되고 공간 좌표( $예$ : x $\displaystyle$ x)가 수평으로 $x$ 표시된 평면입니다.F.R.에 의해 표현된 대로.하비

[spacetime]의 곡선 M은 각 점에서 탄젠트가 미래의 타임라이크인 경우 입자의 월드라인이라고 불립니다.arclength 파라미터는 적정시간이라고 불리며 보통 τ으로 표시됩니다.M의 길이는 입자의 적절한 시간이라고 불립니다.월드라인 M이 선분일 경우 입자는 자유낙하 ^[1]^{: 62–63}상태라고 합니다.

월드 라인은 시공간에서 단일 지점의 경로를 추적합니다.월드 시트는 시공간을 이동하는 1차원 선(줄과 같은)에 의해 추적된 유사한 2차원 표면입니다.오픈 스트링(루즈 엔드)의 월드 시트는 스트립이며, 클로즈드 스트링(루프)의 월드 시트는 튜브와 유사합니다.

일단 물체가 단순한 점으로 근사되지 않고 부피가 커지면, 그것은 세계선이 아닌 세계관을 추적한다.

이벤트를 설명하는 도구로서의 월드 라인

입자, 끈, 지느러미에서 파생된 월드 라인, 월드 시트 및 월드 볼륨.

1차원 선 또는 곡선은 하나의 파라미터의 함수로서 좌표로 나타낼 수 있다.파라미터의 각 값은 시공간상의 한 점에 대응하며 파라미터를 변화시키면 선이 트레이스됩니다.따라서 수학적 용어로 곡선은 그리드의 좌표에 설정된 하나의 $\tau$ 에 따라 x a $x^{a}(\tau ),\;a=0,1,2,3$ ( $x^{a}(\tau ),\;a=0,1,2,3$ ) , a $x^{a}(\tau ),\;a=0,1,2,3$ , $x^{a}(\tau ),\;a=0,1,2,3$ , $x^{a}(\tau ),\;a=0,1,2,3$ , $x^{a}(\tau ),\;a=0,1,2,3$ (x $x^{0}$ \ $displaystyle$ x $^$ { $0$ $}$ ) , \ ; a $= 0$ , $1, 2,$ 3 $x^{a}(\tau ),\;a=0,1,2,3$ ( $x^{0}$ 서 x 0 \ $displaystyle$ x^ { $0}$ 은 $x^{0}$ 시간 좌표를 나타냅니다 $\tau$ 의 4 개의 $x^{a}(\tau ),\;a=0,1,2,3$ x a ( $=$ 0 , 1, 2, 3 )에 의해 정의됩니다.4개의 좌표 함수 중 3개가 상수로 설정되어 있는지 여부를 구한다.

때때로 세계선이라는 용어는 시공간에서의 곡선에 대해 느슨하게 사용됩니다.이 용어는 혼동을 일으킵니다.보다 적절하게는, 월드 라인은 입자, 관찰자 또는 작은 물체의 (시간) 이력을 추적하는 시공간에서의 곡선입니다.일반적으로 물체 또는 관찰자의 적절한 시간을 곡선의 파라미터 $\tau$ δ(\ $displaystyle\tau)$ 로 $\tau$ 사용하여 월드라인을 따라갑니다.

시공간 곡선의 간단한 예

세 개의 다른 세계선은 서로 다른 일정한 4개의 속도로 이동하는 것을 나타냅니다. t는 시간과 x 거리입니다.

수평선 세그먼트(항정 좌표 시간에 있는 선)로 구성된 곡선은 시공간에서 막대를 나타낼 수 있으며 적절한 의미에서 월드 라인이 아닐 수 있습니다.매개 변수는 로드 길이를 추적합니다.

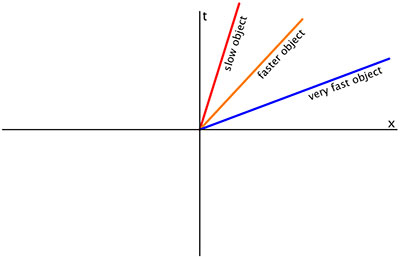
일정한 공간 좌표에서의 선(위에서 채택된 규약의 수직선)은 정지 상태의 입자(또는 정지 상태의 관찰자)를 나타낼 수 있다.기울어진 선은 좌표 속도가 일정한 입자를 나타냅니다(시간 좌표가 증가함에 따라 공간 좌표가 일정하게 변화함).선이 수직에서 기울어질수록 속도가 커집니다.

개별적으로 시작되어 교차하는 두 개의 월드 라인은 충돌 또는 "반대"를 나타냅니다.시공간에서 동일한 사건에서 시작하여 각각 자신의 경로를 따라가는 두 개의 세계선은 한 입자가 다른 두 개의 입자로 붕괴되거나 다른 입자에 의해 한 개의 입자가 방출되는 것을 나타낼 수 있다.

입자와 관찰자의 세계선은 광자의 세계선(빛의 경로)과 상호 연결되어 관찰자에 의해 후속적으로 관찰(또는 다른 입자에 의해 흡수)되는 입자에 의한 광자의 방출을 나타내는 도표를 형성할 수 있다.

월드 라인에 대한 접선 벡터: 4단 속도

월드라인을 정의하는 4개의 $x^{a}(\tau ),\;a=0,1,2,3$ $x^{a}(\tau ),\;a=0,1,2,3$ ( $x^{a}(\tau ),\;a=0,1,2,3$ $x^{a}(\tau ),\;a=0,1,2,3$ $x^{a}(\tau ),\;a=0,1,2,3$ $x^{a}(\tau ),\;a=0,1,2,3$ $x^{a}(\tau ),\;a=0,1,2,3$ , $x^{a}(\tau ),\;a=0,1,2,3$ , 3 $x^{a}(\tau ),\;a=0,1,2,3$ (\ $displaystyle$ x $^{a}$ (\displaystyle x^{ $a},\;a=0,1,2,3)$ 는 $x^{a}(\tau ),\;a=0,1,2,3$ 실수변수 $\tau$ \ $displaystyle \display }$ 의 $\tau$ 실함수이며, 일반 미적분에서는 간단히 구분할 수 있다.메트릭이 존재하지 않는 경우(이 점을 인식하는 것이 중요함) 파라미터 $\tau _{0}$ ${\$ 0의 곡선상의 $포인트$ p $(\displaystyle$ \ $tau _{$ 0 $\tau _{0}$ })와 $p$ 곡선상의 포인트(파라미터 $\tau _{0}+\Delta \tau$ 0 + $\tau _{0}+\Delta \tau$ \ $displaystyle$ \ $tau _0+\Delta \tau$ 의 차이를 알 수 있습니다.한계 $\Delta \tau \to 0$ 0 ${\displaystyle \Delta$ \to 0 $\Delta \tau \to 0$ 에서 이 차이를 $\Delta \tau$ it { $displaystyle \Delta \to$ 0 $\Delta \tau \to 0$ $}$ 으로 $\Delta \tau$ 나눈 값에 의해 p{ $displaystyle$ p $p$ $p$ 에서 월드 라인의 접선 벡터가 정의됩니다. 이 벡터는 p{\ $displaystyle$ p $p$ 지점에서 $p$ 된 4차원 벡터입니다.물체의 M차원 속도(동일하지 않음)를 나타내므로 ${\vec {v}}$ v $→(\$ {v ${\vec {v}}$ 또는 구성 요소:

({displaystyle {vc {v}}=\left(v^{0},v^{1},v^{2},v^{2},v^{right}=\left\frac{0}}{d\frac}}}\;,{\frac}{d}\,{\frac}}},{\frac},{\frac},{frac}}},{frac}}}}},{frac}}}}}},{\frac}}}}}}},{\frac}}}}}}}

여기서 도함수는 p $(\displaystyle$ p $p$ $p$ 에서 구합니다. 즉, $\tau =\tau _{0}$ $=$ $\tau =\tau _{0}$ 0 $(\$ =\ $display_{0$ 에서 구합니다.

점 p를 통과하는 모든 곡선에는 월드 라인뿐만 아니라 탄젠트 벡터가 있습니다.두 벡터의 합은 다시 다른 곡선에 대한 접선 벡터이며 스칼라 곱셈에도 동일하게 유지됩니다.따라서 p 지점의 모든 접선 벡터는 p 지점의 접선 공간이라고 하는 선형 공간에 걸쳐 있습니다.예를 들어, 지구의 (곡선된) 표면과 같은 2차원 공간을 사용할 경우, 특정 지점의 접선 공간은 곡선 공간의 평평한 근사치가 됩니다.

특수 상대성 이론의 세계선

지금까지 사건 사이의 간격을 수량화하는 수단 없이 월드 라인(및 탄젠트 벡터의 개념)을 설명했습니다.기본 수학은 다음과 같습니다.특수상대성이론은 가능한 세계선에 몇 가지 제약을 가한다.특수 상대성 이론에서 시공간의 설명은 관성 좌표계라고 불리는 가속되지 않는(따라서 회전하지 않는) 특수 좌표계로 제한된다.이러한 좌표계에서 빛의 속도는 일정합니다.시공간 구조는 각 사건 쌍에 대한 실수를 제공하는 쌍선형 형태 θ에 의해 결정된다.쌍선형 형태는 때때로 시공간 측정법이라고 불리지만, 수학의 미터법 공간의 측정법과는 달리, 별개의 사건들이 때때로 0의 값을 초래하기 때문에, 쌍선형 형태는 시공간에서의 수학적 측정법이 아니다.

자유롭게 낙하하는 입자/물체의 세계선은 측지학이라고 불립니다.특수 상대성 이론에서 이것들은 민코프스키 공간의 직선이다.

시간 단위는 빛의 속도가 수직(시간) 축과 원뿔을 형성하면서 고정 각도(보통 45도)의 선으로 표현되도록 선택되는 경우가 많다.일반적으로 시공간에서 유용한 곡선은 세 가지 유형으로 나눌 수 있다(다른 유형은 부분적으로 하나, 일부는 다른 유형).

빛의 속도를 가진 빛과 같은 곡선그들은 시공간에서 원뿔을 형성하고, 그것을 두 부분으로 나눕니다.원뿔은 시공간에서 3차원이며, 2차원이 억제된 도면에서는 선으로, 1차원이 억제된 도면에서는 원뿔로 나타납니다.

광원추의 예로서 시공간 한 점에 도달하거나 시공간에서 발생하는 모든 가능한 광선의 3차원 표면이다.여기서, 그것은 하나의 공간적 차원이 억압된 채 묘사된다.

빠르게 가속하는 관찰자(중앙)의 궤적("세계선")을 따라 순간적으로 함께 움직이는 관성 프레임.수직 방향은 시간을 나타내며 수평 방향은 거리를 나타내며, 파선은 관찰자의 시공간입니다.작은 점들은 시공간에서의 특정 사건들이다.관찰자가 가속할 때 순간적으로 함께 움직이는 관성 프레임이 어떻게 변화하는지 주목하십시오.

빛의 속도보다 느린 시간 같은 곡선이러한 곡선은 빛과 같은 곡선으로 정의된 원뿔 안에 있어야 합니다.위의 정의에 따르면 세계선은 시공간에서의 시간적인 곡선입니다.
공간 같은 곡선이 광원추 밖으로 떨어집니다.이러한 곡선은 예를 들어 물리적 물체의 길이를 나타낼 수 있습니다.원통 둘레와 막대 길이는 공간 같은 곡선입니다.

월드 라인상의 특정 이벤트에서 시공간(민코프스키 공간)은 세 부분으로 나뉜다.

주어진 사건의 미래는 미래의 광원뿔 안에 있는 시간과 같은 곡선을 통해 도달할 수 있는 모든 사건에 의해 형성됩니다.
특정 이벤트의 과거는 이벤트에 영향을 줄 수 있는 모든 이벤트(즉, 과거 광원뿔 내의 월드 라인으로 특정 이벤트에 연결할 수 있음)에 의해 형성됩니다.
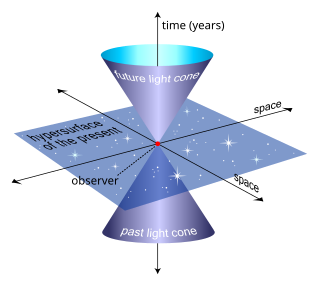
- 주어진 이벤트의 라이트콘은 빛 광선을 통해 이벤트와 연결될 수 있는 모든 이벤트에 의해 형성됩니다.우리가 밤에 하늘을 관찰할 때, 우리는 기본적으로 전체 시공간에서 과거의 광원추만을 보게 된다.
다른 곳은 두 개의 광원뿔 사이의 영역입니다.관찰자의 다른 점에는 액세스할 수 없습니다. 과거의 점만 관찰자에게 신호를 보낼 수 있습니다.일반적인 실험실 경험에서는 일반적인 단위와 측정 방법을 사용하여 현재를 보는 것처럼 보일 수 있지만 사실 빛이 전파되는 데는 항상 지연 시간이 있습니다.예를 들어, 우리는 태양을 "지금 당장"이 아니라 약 8분 전으로 봅니다.갈릴레오/뉴턴 이론의 현재와 달리, 다른 것들은 두껍다; 그것은 3차원 부피가 아니라 4차원 시공간 영역이다.
- "elsewhere"에는 동시 초평면이 포함되며, 이는 주어진 관찰자에 대해 월드 라인에 대해 쌍곡선 직교하는 공간에 의해 정의됩니다.도표상으로는 2면이지만, 알기 쉬운 그림을 만들기 위해서는 1차원을 버려야 했기 때문에, 이것은 정말로 3차원입니다.광원추는 주어진 시공간 이벤트의 모든 관측자에 대해 동일하지만 속도는 다르지만 시공간 이벤트(점)에서 일치하는 다른 관측자는 상대 속도에 의해 결정된 각도로 서로 교차하는 세계선을 가지며, 따라서 동시에 서로 다른 하이퍼플레인을 갖는다.
- 현재란 종종 고려 중인 단일 시공간 사건을 의미합니다.

동시 하이퍼플레인

$w(\tau )\in R^{4}$ $w(\tau )\in R^{4}$ $w(\tau )\in R^{4}$ $w(\tau )\in R^{4}$ $(\$ w $(\displaystyle$ w)\ $in$ R $^{4})$ 에 $w(\tau )\in R^{4}$ 의해 속도 $v={\frac {dw}{d\tau }}$ v $v={\frac {dw}{d\tau }}$ $v={\frac {dw}{d\tau }}$ $v={\frac {dw}{d\tau }}$ d $v={\frac {dw}{d\tau }}$ {\({ $displaystyle$ v $=display$ frac ${d}{d\d}}}})$ 가 $v={\frac {dw}{d\tau }}$ 결정되므로 민코프스키 형태 $,$ $)$ 는 선형 $R^{4}\rightarrow R$ \ $eta(x)$ 를 결정한다 $\eta (v,x)$ . $x\mapsto \eta (v,x).$ } N을 $x\mapsto \eta (v,x).$ 이 선형함수의 늘공간으로 합니다 $.$ 그러면 N은 v에 대한 동시 하이퍼플레인이라고 불립니다.동시성의 상대성은 N이 v에 의존한다는 진술이다. 실제로, N은 θ에 대한 v의 직교 보완체이다.When two world lines u and w are related by ${\frac {du}{d\tau }}={\frac {dw}{d\tau }},$ then they share the same simultaneous hyperplane.이 초평면은 수학적으로 존재하지만 상대성 이론에서의 물리적 관계는 빛에 의한 정보의 움직임을 포함한다.예를 들어, 쿨롱의 법칙에 의해 묘사된 전통적인 정전력은 동시 초평면에서 그려질 수 있지만, 상대론적 전하와 힘의 관계는 지연된 전위를 포함한다.

일반상대성이론의 세계선

일반 상대성 이론에서 세계선을 사용하는 것은 기본적으로 특수 상대성 이론과 동일하지만 시공간이 곡선이 될 수 있다는 차이가 있다.지표는 존재하며 그 역학은 아인슈타인 장 방정식에 의해 결정되며 시공간에서의 질량 에너지 분포에 의존합니다.다시 메트릭은 빛과 같은(늘), 공간적 및 시간적 곡선을 정의합니다.또한, 일반 상대성 이론에서, 세계선은 시공간에서의 시간적인 곡선으로, 시간적인 곡선이 광원추 안에 있습니다.그러나 라이트콘이 시간축에 대해 45도 기울어져 있다고는 할 수 없습니다.그러나 이는 선택된 좌표계의 인공물이며 일반 상대성 이론의 좌표 자유도(차동형 불변성)를 반영한다.어떤 타임라이크 커브라도 그 커브에 대응하는 "시간축"을 가진 콤보 옵서버를 받아들일 수 있으며, 옵서버는 특권이 없기 때문에 우리는 항상 광원자가 시간축에 대해 45도로 기울어져 있는 국소 좌표계를 찾을 수 있다.에딩턴-핀켈슈타인 좌표의 예를 참조하십시오.

자유 낙하하는 입자 또는 물체의 세계선은 측지학이라고 불린다.

양자장 이론의 세계선

현대 입자 물리학의 모든 것이 묘사되는 틀인 양자장 이론은 보통 양자화된 장 이론으로 묘사된다.하지만, 널리 인정받지는 못했지만, 많은 양자장 이론들이 세계선으로 동등하게 묘사될 수 있다는 것은 파인만 이후로^[2] 알려져 왔다.양자장 이론의 세계선 공식화는 게이지^[3]^[4]^[5] 이론의 다양한 계산과 전자기장의 ^[6]^[7]비선형 효과를 설명하는 데 특히 효과적이었다.

문학계의 세계선

1884년 C. H. 힌튼은 에세이 "4차원이란 무엇인가?"를 썼고, 그는 그것을 과학적 로맨스로 출판했다.그는 썼다.

그렇다면 왜 4차원의 존재는 우리 자신이 되어서는 안 되며, 우리의 의식이 갇힌 ^[8]^{: 18–19}3차원의 공간을 통과하는 것을 연속적으로 말하고 있는 것일까.

J.C.는 인간 세계선에 대한 대중적인 묘사를 했다. 상대성 이론의 초기 토론토 대학의 필드.토론토 변호사 Norman Robertson의 설명에 따르면:

필즈가 토요일 저녁 왕립 캐나다 연구소에서 강의를 했던 것을 기억한다.그것은 "수학적 환상"이라고 광고되었고, 그랬다!연습의 내용은 다음과 같다.그는 모든 인간은 자신의 탄생과 함께 긴 필라멘트나 실이 연결된 일종의 영적인 아우라를 가지고 있다고 가정했다. 그것은 그의 일생 동안 그의 뒤를 따라다녔다.그리고 나서 그는 모든 개인이 다른 사람들과의 관계에 관여하게 된 복잡한 얽힘을 묘사하면서, 젊은 시절의 단순한 얽힘을 이후의 삶에서 ^[9]발전하는 복잡한 매듭에 비유했다.

Kurt Bonnegut은 소설 '슬러트하우스-5'에서 스타와 사람의 세계선을 묘사합니다.

"빌리 필그림은 트랄파마도르에서 온 생명체들에게 우주가 밝고 작은 점처럼 보이지 않는다고 말합니다.이 생물들은 각각의 별이 어디에 있었고 어디로 가고 있는지 볼 수 있기 때문에 하늘은 희박하고 빛나는 스파게티로 가득 차 있다.그리고 트랄파마도리안들도 인간을 두 다리 달린 동물로 보지 않는다.빌리 필그림은 "한쪽 끝에는 아기들의 다리가 있고 다른 한쪽 끝에는 노인들의 다리가 있는 훌륭한 젖 짜는 동물"이라고 말합니다.

시간여행을 가능하게 하는 것과 같이 이 개념을 적극적으로 사용하는 거의 모든 공상과학소설은 이 개념을 일차원 타임라인으로 지나치게 단순화시켜 현실의 모델에 맞지 않는 선형 구조에 맞도록 한다.이러한 타임머신은 종종 순간적인 것으로 묘사되며, 콘텐츠는 한 번에 출발하고 다른 곳에 도착하지만 공간의 문자 그대로 동일한 지리적 지점에 있습니다.이것은 종종 기준 프레임의 주석 없이 또는 기준 프레임이 국소적이라는 암묵적인 가정 하에 수행된다. 따라서, 이것은 회전하는 행성이 관성 프레임이 아니기 때문에 정확한 순간이동 또는 타임머신이 같은 장소에 있는 동안 그 내용을 '동결'해야 한다.

작가 Oliver Franklin은 2008년에 World Lines라는 제목의 공상과학 작품을 출판했는데, 이 책에서 그는 평신도를 ^[10]위한 가설에 대한 간략한 설명을 다루었다.

단편소설 Life-Line에서 작가 Robert A. 하인라인은 사람의 ^[11]세계선을 다음과 같이 묘사한다.

그는 기자 중 한 명에게 다가갔다."당신을 예로 든다면요.당신 이름이 로저스 아닌가요?좋아, 로저스 넌 시공간 사건이야 지속시간이 4가지야키는 6피트도 안 되고 너비는 20인치 정도 되고 두께는 10인치 정도 됩니다.시간이 지나면, 여러분 뒤로 더 많은 시공간 사건이 펼쳐지고, 아마도 16세까지 도달합니다. 그 중 시간축과 직각으로 현재만큼 두꺼운 단면을 볼 수 있습니다.저쪽 끝에는 시큼한 우유 냄새가 나는 아기가 턱받이에 아침 식사를 침 흘리고 있다.다른 쪽 끝에는 아마도 1980년대 노인이 누워 있을 것이다.

로저스를 핑크색 긴 벌레라고 부르는 시공간적 사건을 상상해 보세요.그것은 몇 년 동안 계속되며 한쪽은 어머니의 자궁에서, 다른 한쪽은 무덤에서 계속됩니다.."

하인라인의 '메두셀라의 아이들'과 제임스 블리쉬의 '시간의 퀸쿤스' (Beep에서 확장)도 이 용어를 사용한다.

스틴스라는 이름의 시각 소설5pb.에서 제작한 Gate는 세계 라인의 변화를 바탕으로 한 이야기다.스틴게이트는 "사이언스 어드벤처" 시리즈의 한 부분이다.세계선과 디락해와 같은 다른 물리적 개념도 시리즈 내내 사용된다.

닐 스티븐슨의 소설 아나템은 플라토닉 리얼리즘과 유명주의 사이의 철학적인 논쟁의 한가운데에서 저녁을 먹으며 세계선에 대한 긴 토론을 포함한다.

Absolute Choice(절대 선택)는 다양한 월드 라인을 하위 플롯 및 설정 장치로 나타냅니다.

찰스 스트로스가 쓴 '싱글러티 스카이'의 배경과 주요 줄거리 장치는 전략적 기동으로 폐쇄된 시간과 같은 길을 완성하려는 우주 함대이다.

「」를 참조해 주세요.

특정 유형의 월드 라인
- 측지학
- 닫힌 타임라이크기
- 인과 구조, 다양한 유형의 월드 라인을 나타내는 곡선
- 등방성 선
파인만 도표
시간 지리학

레퍼런스

^ Harvey, F. Reese (1990). "Special Relativity" section of chapter "Euclidiean / Lorentzian Vector Spaces". Spinors and Calibrations. Academic Press. pp. 62–67. ISBN 9780080918631.
^ Feynman, Richard P. (1951). "An operator calculus having applications in quantum electrodynamics" (PDF). Physical Review. 84 (1): 108–128. Bibcode:1951PhRv...84..108F. doi:10.1103/PhysRev.84.108.
^ Bern, Zvi; Kosower, David A. (1991). "Efficient calculation of one-loop QCD amplitudes". Physical Review Letters. 66 (13): 1669–1672. Bibcode:1991PhRvL..66.1669B. doi:10.1103/PhysRevLett.66.1669. PMID 10043277.
^ Bern, Zvi; Dixon, Lance; Kosower, David A. (1996). "Progress in one-loop QCD computations" (PDF). Annual Review of Nuclear and Particle Science. 46: 109–148. arXiv:hep-ph/9602280. Bibcode:1996ARNPS..46..109B. doi:10.1146/annurev.nucl.46.1.109.
^ Schubert, Christian (2001). "Perturbative quantum field theory in the string-inspired formalism". Physics Reports. 355 (2–3): 73–234. arXiv:hep-th/0101036. Bibcode:2001PhR...355...73S. doi:10.1016/S0370-1573(01)00013-8. S2CID 118891361.
^ Affleck, Ian K.; Alvarez, Orlando; Manton, Nicholas S. (1982). "Pair production at strong coupling in weak external fields". Nuclear Physics B. 197 (3): 509–519. Bibcode:1982NuPhB.197..509A. doi:10.1016/0550-3213(82)90455-2.
^ Dunne, Gerald V.; Schubert, Christian (2005). "Worldline instantons and pair production in inhomogenous fields" (PDF). Physical Review D. 72 (10): 105004. arXiv:hep-th/0507174. Bibcode:2005PhRvD..72j5004D. doi:10.1103/PhysRevD.72.105004. S2CID 119357180.
^ Hinton, C. H. (1884). "What is the fourth dimension?". Scientific Romances: First Series. S. Sonnenschein. pp. 1–32.
^ Robinson, Gilbert de Beauregard (1979). The Mathematics Department in the University of Toronto, 1827–1978. University of Toronto Press. p. 19. ISBN 0-7727-1600-5.
^ Oliver Franklin (2008). World Lines. Epic Press. ISBN 978-1-906557-00-3.
^ "Technovelgy: Chronovitameter". Retrieved 8 September 2010.

Minkowski, Hermann (1909), "Raum und Zeit" , Physikalische Zeitschrift, 10: 75–88

Wikisource에서의 다양한 영어 번역: 공간과 시간

루드윅 실버슈타인(1914)상대성 이론, 페이지 130, 맥밀런과 컴퍼니.

외부 링크

h2g2에 관한 월드라인 기사.

세계선과 특수상대성이론에 관한 상세한 텍스트

[1] Harvey, F. Reese (1990). "Special Relativity" section of chapter "Euclidiean / Lorentzian Vector Spaces". Spinors and Calibrations. Academic Press. pp. 62–67. ISBN 9780080918631.

[2] Feynman, Richard P. (1951). "An operator calculus having applications in quantum electrodynamics" (PDF). Physical Review. 84 (1): 108–128. Bibcode:1951PhRv...84..108F. doi:10.1103/PhysRev.84.108.

[3] Bern, Zvi; Kosower, David A. (1991). "Efficient calculation of one-loop QCD amplitudes". Physical Review Letters. 66 (13): 1669–1672. Bibcode:1991PhRvL..66.1669B. doi:10.1103/PhysRevLett.66.1669. PMID 10043277.

[4] Bern, Zvi; Dixon, Lance; Kosower, David A. (1996). "Progress in one-loop QCD computations" (PDF). Annual Review of Nuclear and Particle Science. 46: 109–148. arXiv:hep-ph/9602280. Bibcode:1996ARNPS..46..109B. doi:10.1146/annurev.nucl.46.1.109.

[5] Schubert, Christian (2001). "Perturbative quantum field theory in the string-inspired formalism". Physics Reports. 355 (2–3): 73–234. arXiv:hep-th/0101036. Bibcode:2001PhR...355...73S. doi:10.1016/S0370-1573(01)00013-8. S2CID 118891361.

[6] Affleck, Ian K.; Alvarez, Orlando; Manton, Nicholas S. (1982). "Pair production at strong coupling in weak external fields". Nuclear Physics B. 197 (3): 509–519. Bibcode:1982NuPhB.197..509A. doi:10.1016/0550-3213(82)90455-2.

[7] Dunne, Gerald V.; Schubert, Christian (2005). "Worldline instantons and pair production in inhomogenous fields" (PDF). Physical Review D. 72 (10): 105004. arXiv:hep-th/0507174. Bibcode:2005PhRvD..72j5004D. doi:10.1103/PhysRevD.72.105004. S2CID 119357180.

[8] Hinton, C. H. (1884). "What is the fourth dimension?". Scientific Romances: First Series. S. Sonnenschein. pp. 1–32.

[9] Robinson, Gilbert de Beauregard (1979). The Mathematics Department in the University of Toronto, 1827–1978. University of Toronto Press. p. 19. ISBN 0-7727-1600-5.

[Franklin-10] Oliver Franklin (2008). World Lines. Epic Press. ISBN 978-1-906557-00-3.

[11] "Technovelgy: Chronovitameter". Retrieved 8 September 2010.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

Search

월드 라인

네임스페이스

더

목차

물리에서의 사용법